FILOGENETYKA

Bioinformatyka, wyk

Bioinformatyka, wyk

ł

ł

ad 7

ad 7

(2

(2

4

4

.XI.200

.XI.200

8

8

)

)

[e-mail]

[e-mail]

Filogenetyka

Cel

–

rekonstrukcja historii ewolucji wszystkich

organizmów.

Klasyczne podejście:
historia ewolucji jest odtwarzana na podstawie
porównań

cech morfologicznych i fizjologicznych

badanych organizmów.

•

zadaniem

filogenetyki molekularnej

jest

zrekonstruowanie związków filogenetycznych
między badanymi sekwencjami

ƒ

ƒ

sekwencje przodka mutuj

sekwencje przodka mutuj

ą

ą

w sekwencje potomk

w sekwencje potomk

ó

ó

w

w

ƒ

ƒ

podobne gatunki s

podobne gatunki s

ą

ą

genetycznie blisko spokrewnione

genetycznie blisko spokrewnione

•

•

podstawowe za

podstawowe za

ł

ł

o

o

ż

ż

enia w filogenetyce molekularnej:

enia w filogenetyce molekularnej:

•

wyrazem analiz filogenetycznych są

drzewa filogenetyczne

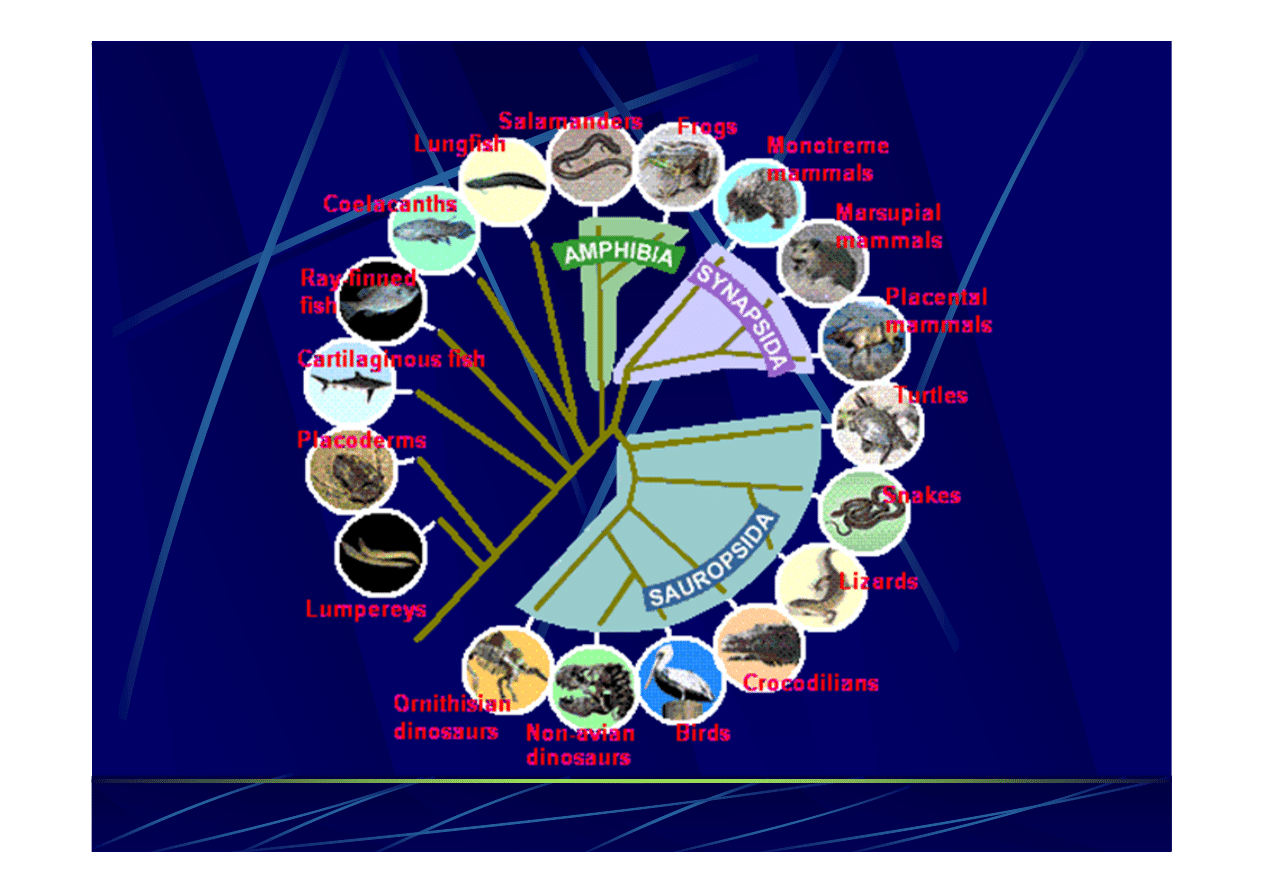
Tree

of

life

(Darwin)

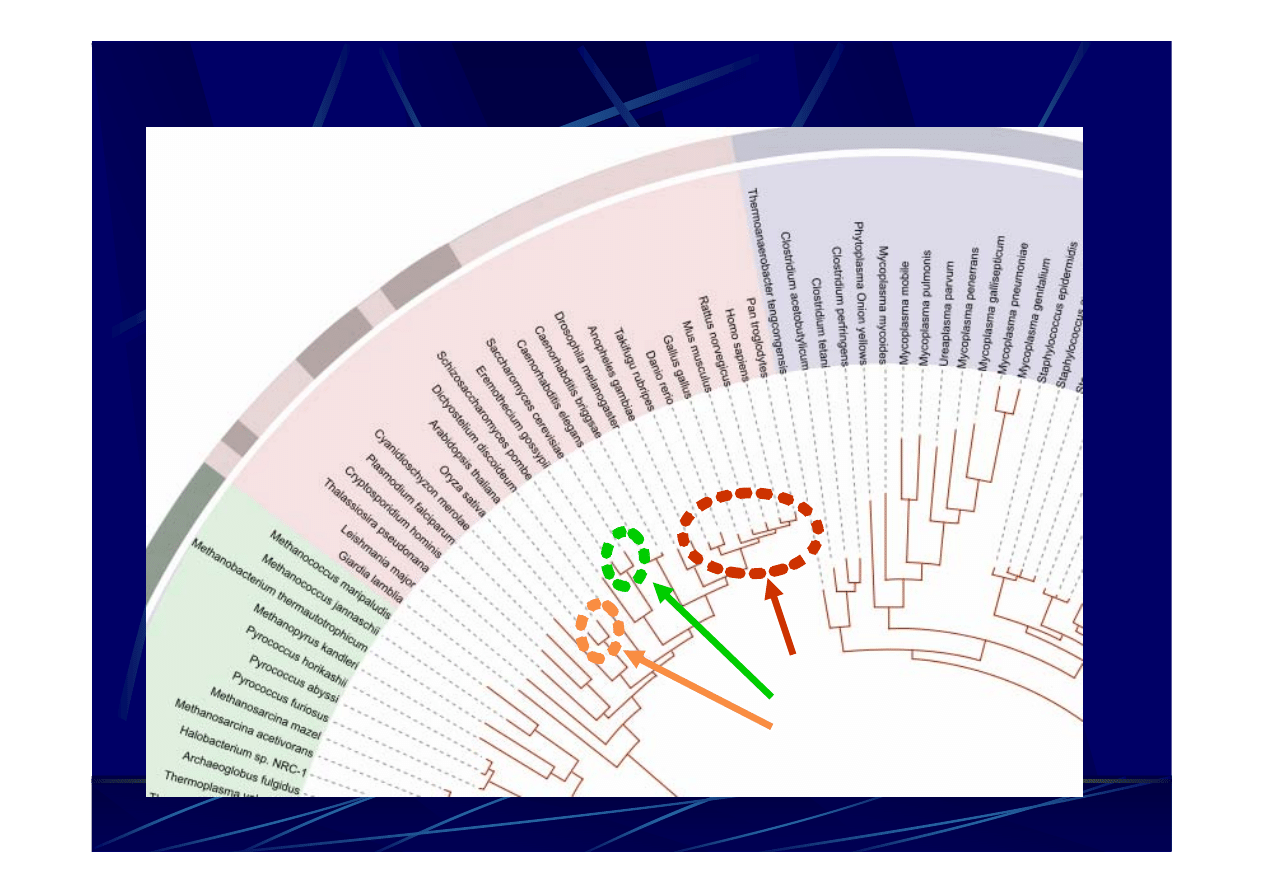
eukarionty

archea

bakterie

Tree

of

life

(dziś)

kręgowce

grzyby

rośliny

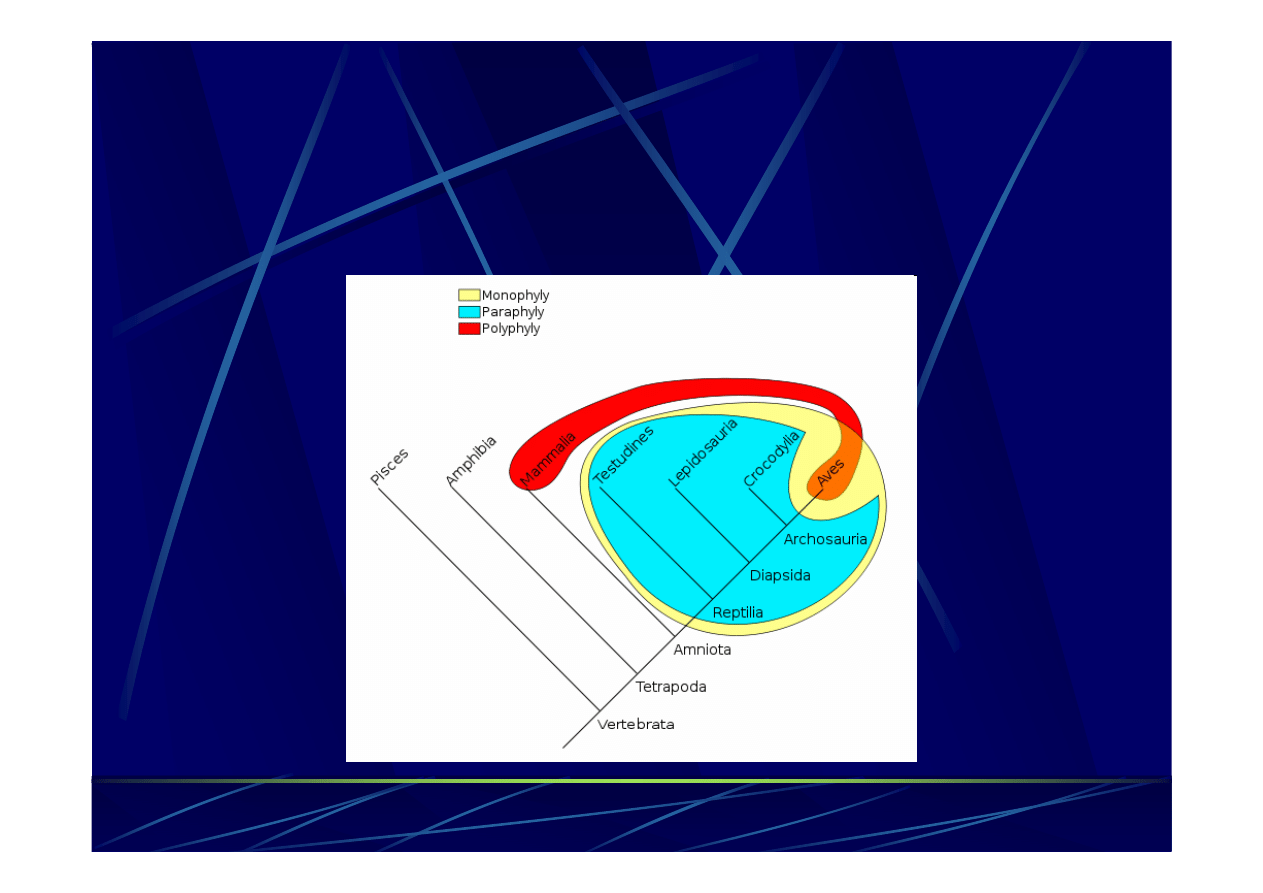
Taksony mono-

i polifiletyczne

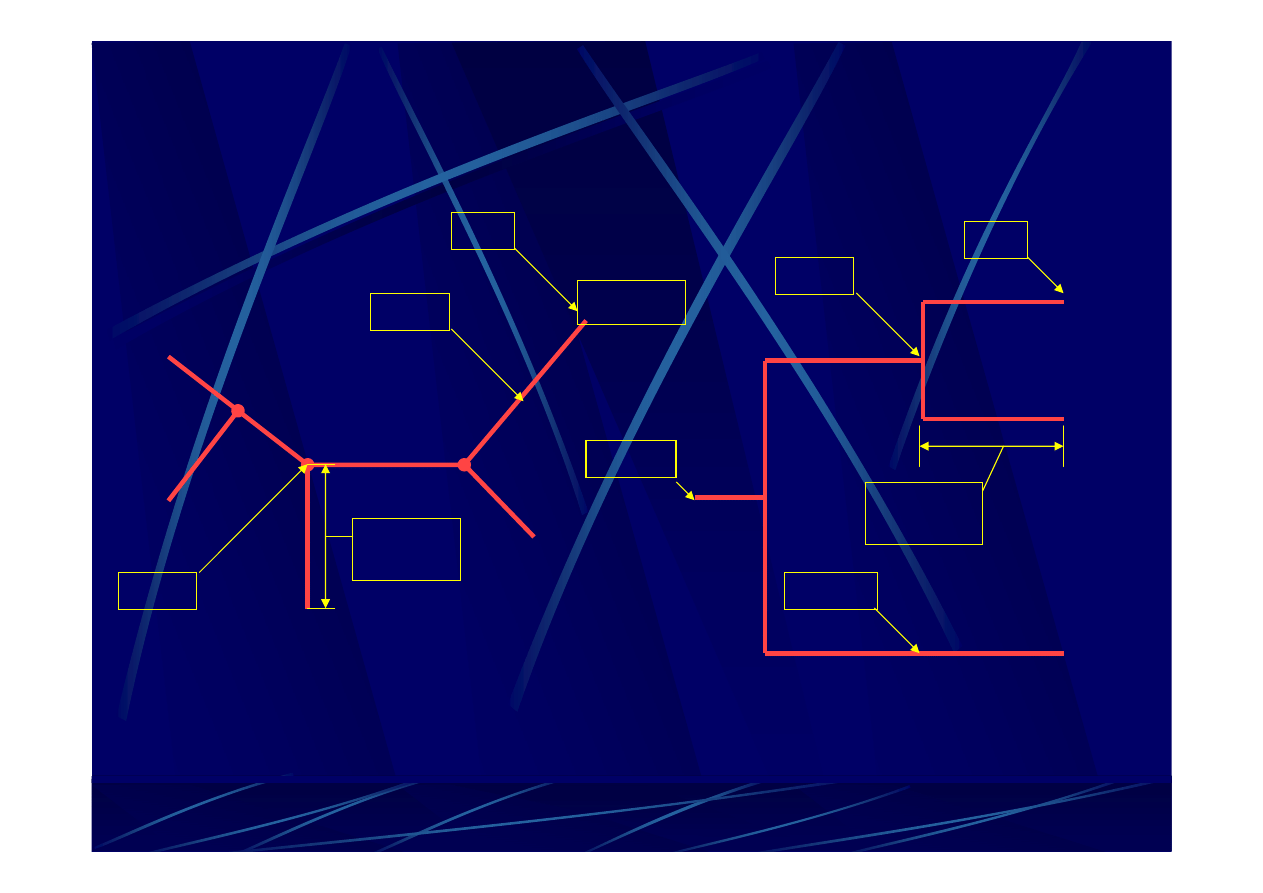
gatunek A

gatunek A

gatunek B

gatunek B

gatunek C

gatunek C

gatunek D

gatunek D

gatunek E

gatunek E

ga

ga

łąź

łąź

w

w

ę

ę

ze

ze

ł

ł

korze

korze

ń

ń

przykładowe

nieukorzenione

drzewo filogenetyczne

przykładowe

ukorzenione

drzewo filogenetyczne

d

d

ł

ł

ugo

ugo

ść

ść

ga

ga

łę

łę

zi

zi

gatunek A

gatunek A

gatunek B

gatunek B

gatunek C

gatunek C

w

w

ę

ę

ze

ze

ł

ł

ga

ga

łąź

łąź

d

d

ł

ł

ugo

ugo

ść

ść

ga

ga

łę

łę

zi

zi

li

li

ść

ść

li

li

ść

ść

Ga

Ga

łąź

łąź

-

-

obrazuje związki ewolucyjne między porównywanymi

jednostkami taksonomicznymi.

D

D

ł

ł

ugo

ugo

ść

ść

ga

ga

łę

łę

zi

zi

-

-

zazwyczaj reprezentuje liczbę

zmian, które się

zdarzyły

w danej linii ewolucyjnej.

Korze

Korze

ń

ń

-

-

wspólny przodek dla wszystkich taksonów.

Li

Li

ść

ść

-

-

reprezentuje aktualnie analizowaną

jednostkę

taksonomiczną.

W

W

ę

ę

ze

ze

ł

ł

-

-

reprezentuje jednostkę

taksonomiczną

(populację, organizm, gen).

Może przedstawiać

współcześnie istniejący takson, jak i jego przodka.

Mechanizmy ewolucji

-

Mutacje w genach.
Mutacje są

rozprzestrzeniane w populacji

poprzez dryf genetyczny

lub/i

selekcję

naturalną

-

Duplikacja i rekombinacja genów.

Etapy analizy filogenetycznej

Dobór i dopasowane sekwencji

Wybór modelu substytucji

Wybór metody oceny odległości ewolucyjnej

Konstrukcja drzewka

Ocena i analiza skonstruowanego drzewka

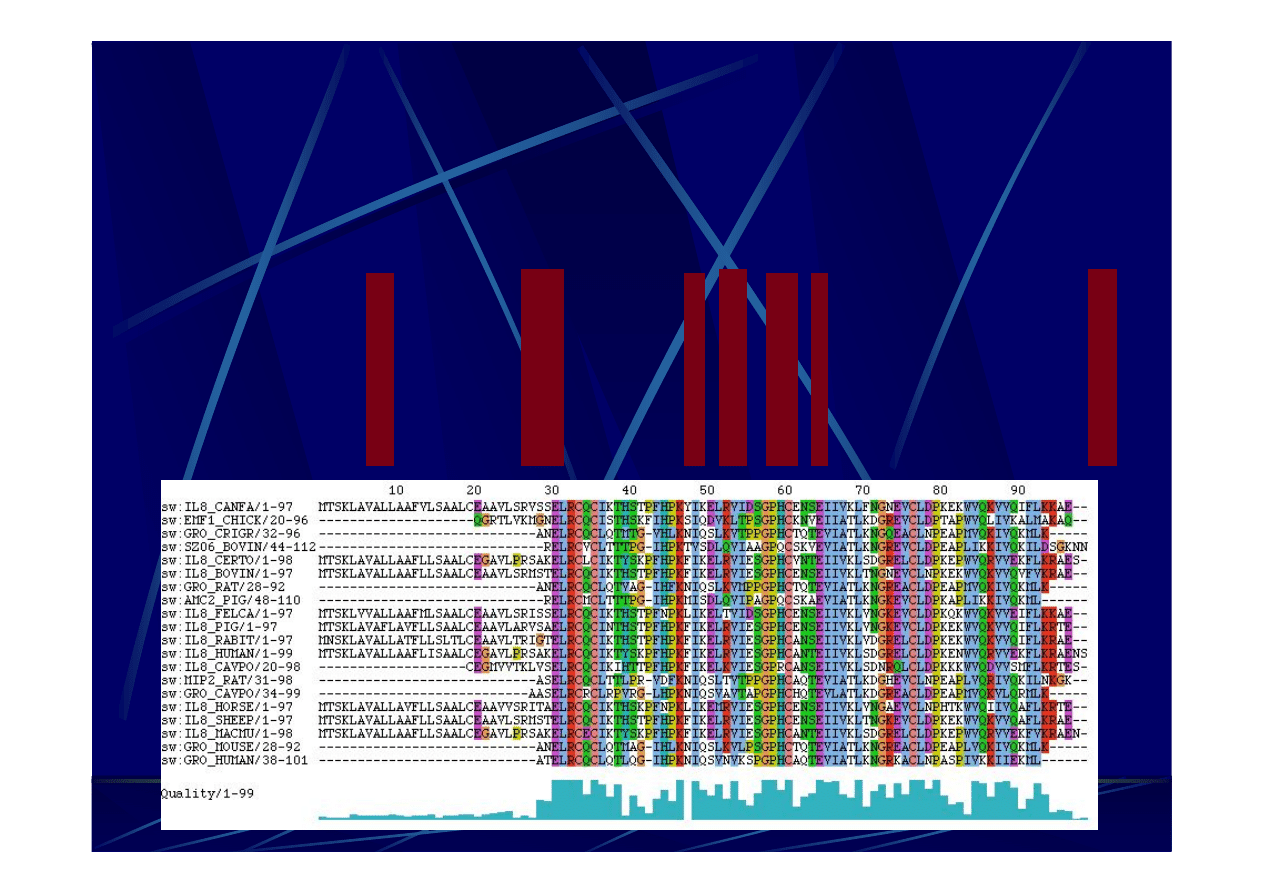
16S

16S

rRNA

rRNA

Dopasowanie wielu sekwencji

Dopasowanie wielu sekwencji

–

–

M

Multiple

sequence alignment (MSA)

E.coli

UCAGAUGU-GAAAUC-CCCGGG=CUCAA=CCUGGG=AACU=GCAUCUGA

Th. thermophilus UCCCAUGU-GAAAGA-CCACGG=CUCAA=CCGUGG=GGGA=GCGUGGGA

B.subtilis

UCUGAUGU-GAAAGC-CCCCGG=CUCAA=CCGGGG=AGGG=UCAUUGGA

Ancyst.nidulans UCUGUUGU-CAAAGC-GUGGGG=CUCAA=CCUCAU=ACAG=GCAAUGGA

Chl.aurantiacus UCGGCGCU-GAAAGC-GCCCCG=CUUAA=CGGGGC=GAGG=CGCGCCGA
match

** *** * ** ** * **

Thermus ruber

UCCGAUGC-UAAAGA-CCGAAG=CUCAA=CUUCGG=GGGU=GCGUUGGA

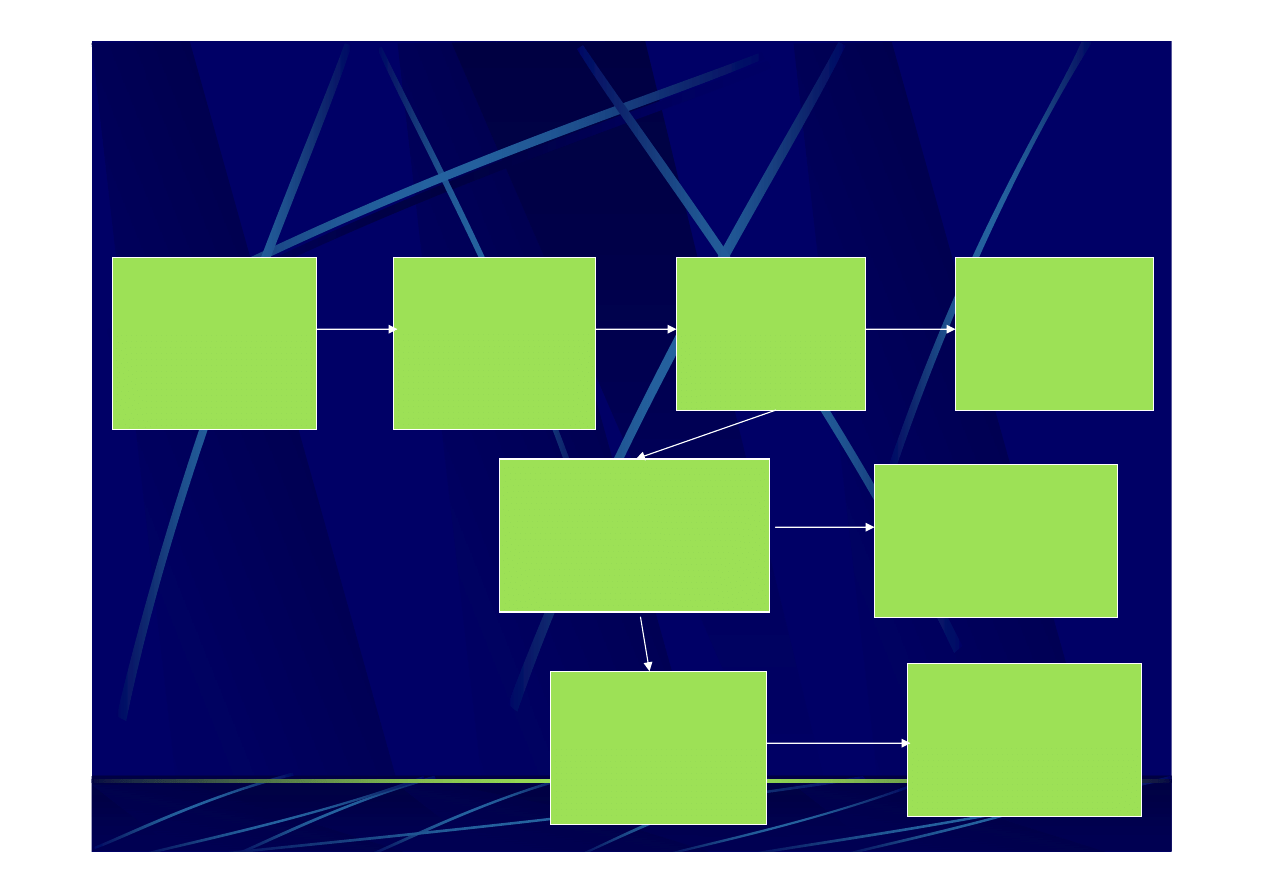
Grupa sekwencji

homologicznych

Dopasowanie

wielu sekwencji

Silne

podobieństwo

sekwencji?

Metoda

maksymalnej

parsymoni

-

MP

Rozpoznawalne

podobieństwo

sekwencji?

Metody oparte

na

odległościach

(dystansowe)

Metoda

maksymalnej

wiarygodności

-ML

Sprawdzanie

poprawności

rekonstrukcji

tak

tak

nie

nie

tak

tak

nie

nie

Metody tworzenia drzewek filogenetycznych

Metoda maksymalnej

Metoda maksymalnej

parsymonii

parsymonii

-

-

MP

MP

Drzewko filogenetyczne skonstruowane

metodą

MP

to takie, które wymaga

najmniejszej liczby zmian aby wyjaśnić

obserwowane różnice w analizowanych

sekwencjach

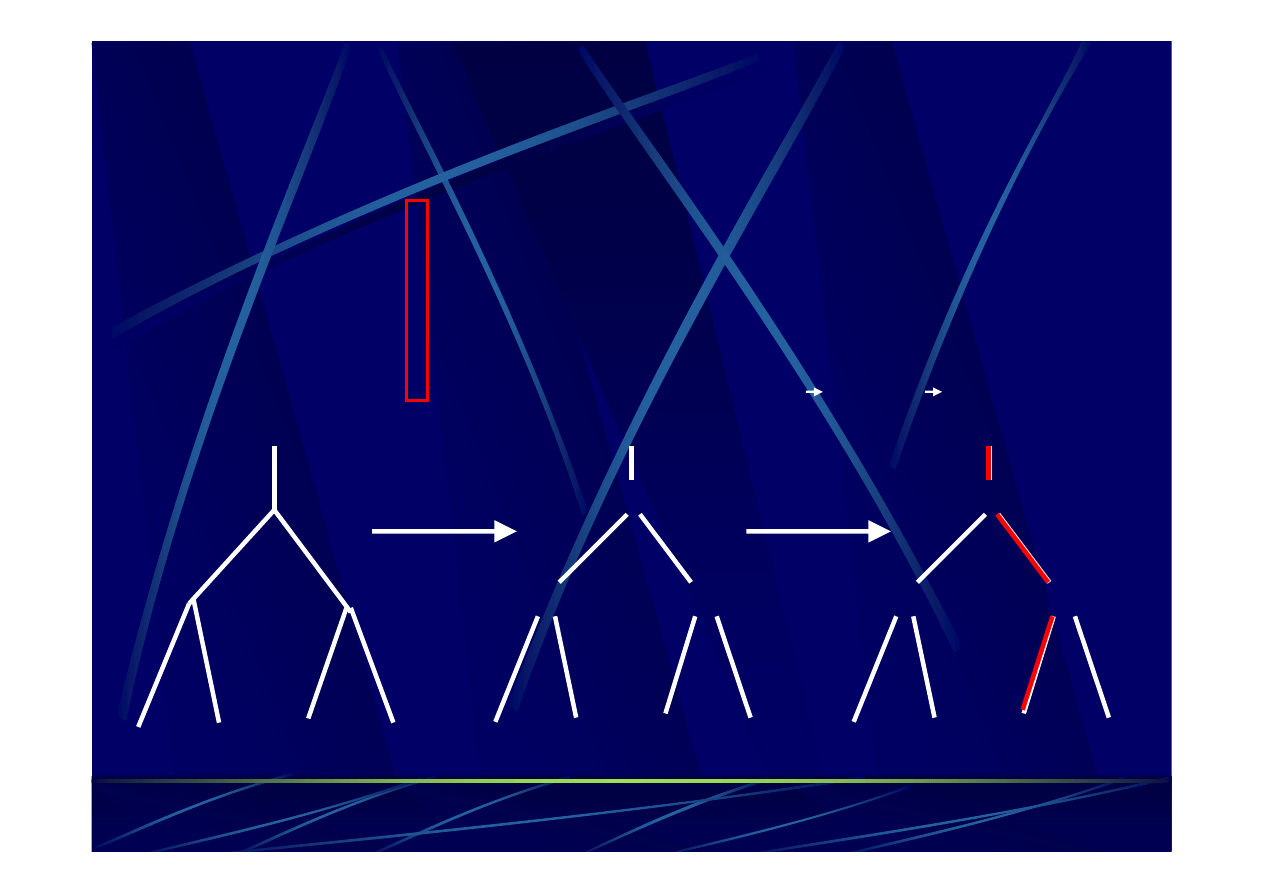
Metoda

Metoda

MP

MP

Seq1

Seq1

A

A

A G A G

A G A G

T

T

G

G

C

C

A

A

Seq2

Seq2

A

A

G C C G

G C C G

T

T

G

G

C

C

G

G

Seq3

Seq3

A

A

G A T A

G A T A

T

T

C

C

C

C

A

A

Seq4

Seq4

A

A

G A G A

G A G A

T

T

C

C

C

C

G

G

1

1

1

1

1

1

2

2

2

2

2

2

3

3

3

3

3

3

4

4

4

4

4

4

Miejsce „informatywne”

dla

sekwencji nukleotydowych to

takie, w którym obserwuje się

przynajmniej dwa różne

nukleotydy i są

one

prezentowane przynajmniej

w dwóch sekwencjach.

1 2

1 2

3 4

3 4

1 3

1 3

2 4

2 4

1 2

1 2

4 3

4 3

Position 2

Position 2

Position 3

Position 3

Position 4

Position 4

Position 5

Position 5

Position 7

Position 7

Position 8

Position 8

Seq1

Seq1

A

A

A G A G

A G A G

T

T

G

G

C

C

A

A

Seq2

Seq2

A

A

G C C G

G C C G

T

T

G

G

C

C

G

G

Seq3

Seq3

A

A

G A T A

G A T A

T

T

C

C

C

C

A

A

Seq4

Seq4

A

A

G A G A

G A G A

T

T

C

C

C

C

G

G

Sum

Sum

11

11

10

10

12

12

Position of

Position of

sequences on the

sequences on the

tree

tree

mutacja

Metoda maksymalnej wiarygodności

–

Maksimum likelihood

(ML)

Drzewko filogenetyczne

skonstruowane metodą

ML

to takie,

które z największym

prawdopodobieńswtem

odtwarza

obserwowane dane

Maximum

likelihood

method

(ML)

1. Wyliczana jest
wiarygodność

(prawdopodobieństwo -

L)

dla każdego
informatywnego

miejsca

2. Następnie sumowane są

wszystkie wartości L dla
każdego możliwego drzewa

3. Porównywane są

ze

sobą

wartości L dla

każdego możliwego drzewa
i wybierane jest to, które
ma najwyższą

wartość

L -

całościowe
czyli
Wybierane jest to drzewo,
które przy danym modelu
najbardziej pasuje do
analizowanych danych

Sekwencja 1: ACGCGTTGGG

Sekwencja 2: ACGCGTTGGG

Sekwencja 3: ACGCAATGAA

Sekwencja 4: AGACAGGGAA

1

2

3

4

T

T

A

G

?

ATGC

?

ATGC

?

ATGC

T

T

A

G

T

G

T

Rekonstrukcja drzewa metod

Rekonstrukcja drzewa metod

ą

ą

ML

ML

Analizujemy kolumnę

Proponujemy układ drzewa

Proponujemy układ nukleotydów

Przydzielenie
nukleotydów

Prawd = P(T) * P(T

G) * P(G

A) = 0.25*10

-6

*10

-6

Likelihood

konkretnej pozycji jest sumą

prawdopodobieństw wszystkich możliwych

rekonstrukcji przodków dla wybranego modelu .

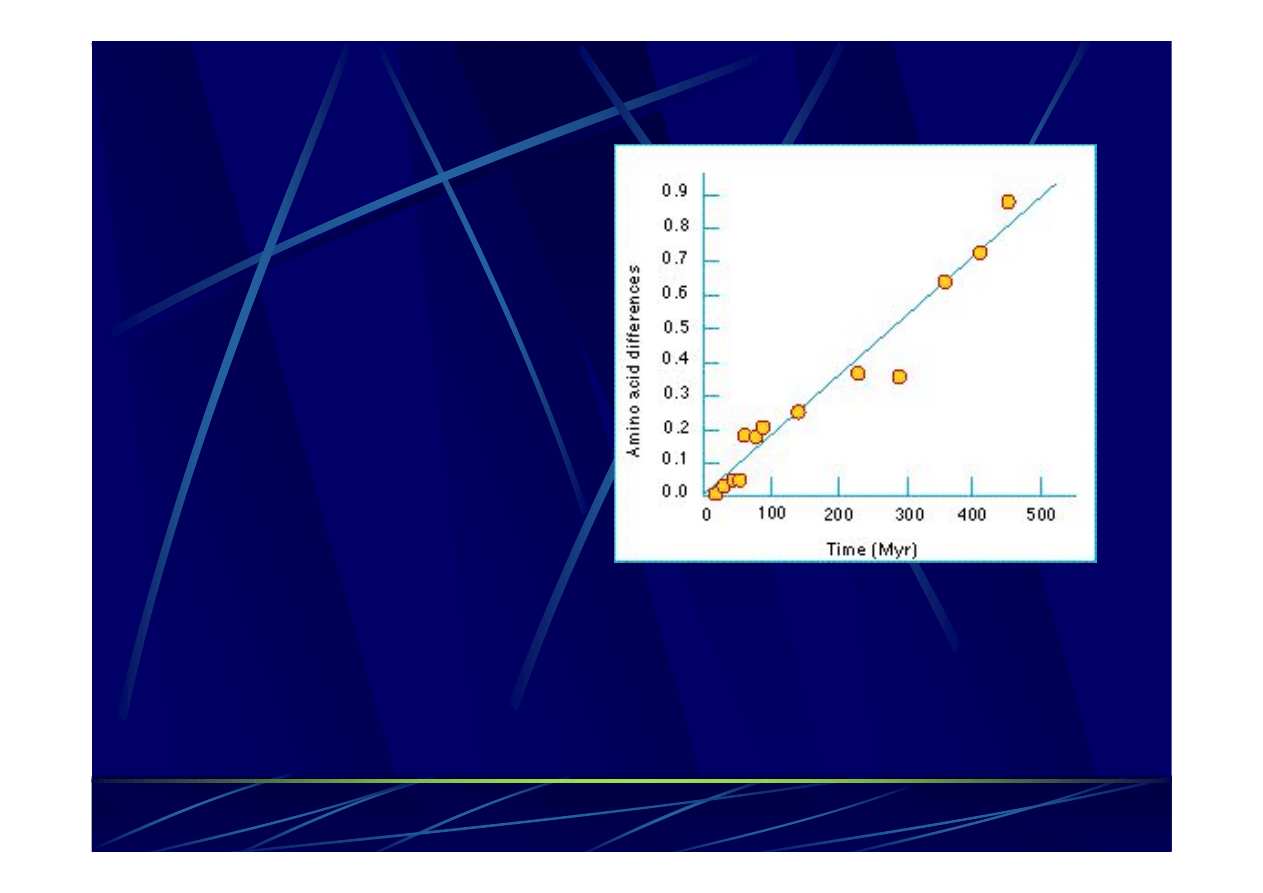
Czyli różnice między sekwencjami dwóch gatunków są

proporcjonalne do czasu jaki upłynął

od momentu gdy oba

gatunki miały wspólnego przodka.

Hipoteza zegara molekularnego (MC)

Hipoteza zegara molekularnego (MC)

Zaproponowana przez
Zuckerkandla

i Paulinga

w

roku 1962.

Opiera się

na założeniu, że

tempo ewolucji (akumulacja
mutacji) sekwencji
nukleotydowej czy
aminokwasowej

jest w

przybliżeniu stałe.

•

•

mo

mo

ż

ż

liwo

liwo

ść

ść

wyst

wyst

ą

ą

pienia wielokrotnych podstawie

pienia wielokrotnych podstawie

ń

ń

•

•

rewersja

rewersja

•

•

rzadko obserwuje si

rzadko obserwuje si

ę

ę

podstawienia mi

podstawienia mi

ę

ę

dzy a

dzy a

minokwasami pe

minokwasami pe

ł

ł

ni

ni

ą

ą

cymi

cymi

wa

wa

ż

ż

ne role w bia

ne role w bia

ł

ł

kach, jak

kach, jak

:

:

cysteina

cysteina

(C)

(C)

czy

czy

tryptofan

tryptofan

(W)

(W)

•

•

cz

cz

ęś

ęś

ciej obserwuje si

ciej obserwuje si

ę

ę

podstawienia mi

podstawienia mi

ę

ę

dzy a

dzy a

minokwasami podobnymi do

minokwasami podobnymi do

siebie, ze wzgl

siebie, ze wzgl

ę

ę

du na swoje w

du na swoje w

ł

ł

a

a

ś

ś

ciwo

ciwo

ś

ś

ci biochemiczne,

ci biochemiczne,

biofizyczne

biofizyczne

np

np

.

.

:

:

ƒ

ƒ

izoleucyna

izoleucyna

(I)

(I)

leucyna

leucyna

(L),

(L),

ƒ

ƒ

valina

valina

(V)

(V)

izoleucyna

izoleucyna

(I),

(I),

ƒ

ƒ

kwas asparaginowy

kwas asparaginowy

(D)

(D)

kwas glutaminowy

kwas glutaminowy

(

(

E),

E),

•

•

rzadko obserwuje si

rzadko obserwuje si

ę

ę

podstawienia mi

podstawienia mi

ę

ę

dzy aminokwasami bardzo

dzy aminokwasami bardzo

r

r

ó

ó

ż

ż

ni

ni

ą

ą

cymi si

cymi si

ę

ę

swoimi w

swoimi w

ł

ł

asno

asno

ś

ś

ciami

ciami

ƒ

ƒ

tryptofan

tryptofan

(W)

(W)

izoleucyna

izoleucyna

(I)

(I)

•

•

niekt

niekt

ó

ó

re aminokwasy, takie jak:

re aminokwasy, takie jak:

asparagina

asparagina

(N)

(N)

, kwas asparaginowy

, kwas asparaginowy

(D)

(D)

,

,

seryna

seryna

(S)

(S)

mutuj

mutuj

ą

ą

cz

cz

ęś

ęś

ciej ni

ciej ni

ż

ż

inne

inne

•

•

cz

cz

ęś

ęś

ciej obserwuje si

ciej obserwuje si

ę

ę

podstawienia typu

podstawienia typu

tranzycji

tranzycji

ni

ni

ż

ż

transwersji

transwersji

•

•

cz

cz

ęś

ęś

ciej obserwuje si

ciej obserwuje si

ę

ę

podstawienia w III pozycjach kodon

podstawienia w III pozycjach kodon

ó

ó

w

w

•

•

tempo mutacji zale

tempo mutacji zale

ż

ż

y od regionu w genomie, genie, rodzaju genu,

y od regionu w genomie, genie, rodzaju genu,

Protein

Rate (mean replacements per site

per 10

9

years)

Fibrinopeptides

8.3

Insulin C

2.4

Ribonuclease

2.1

Haemoglobins

1.0

Cytochrome C

0.3

Histone H4

0.01

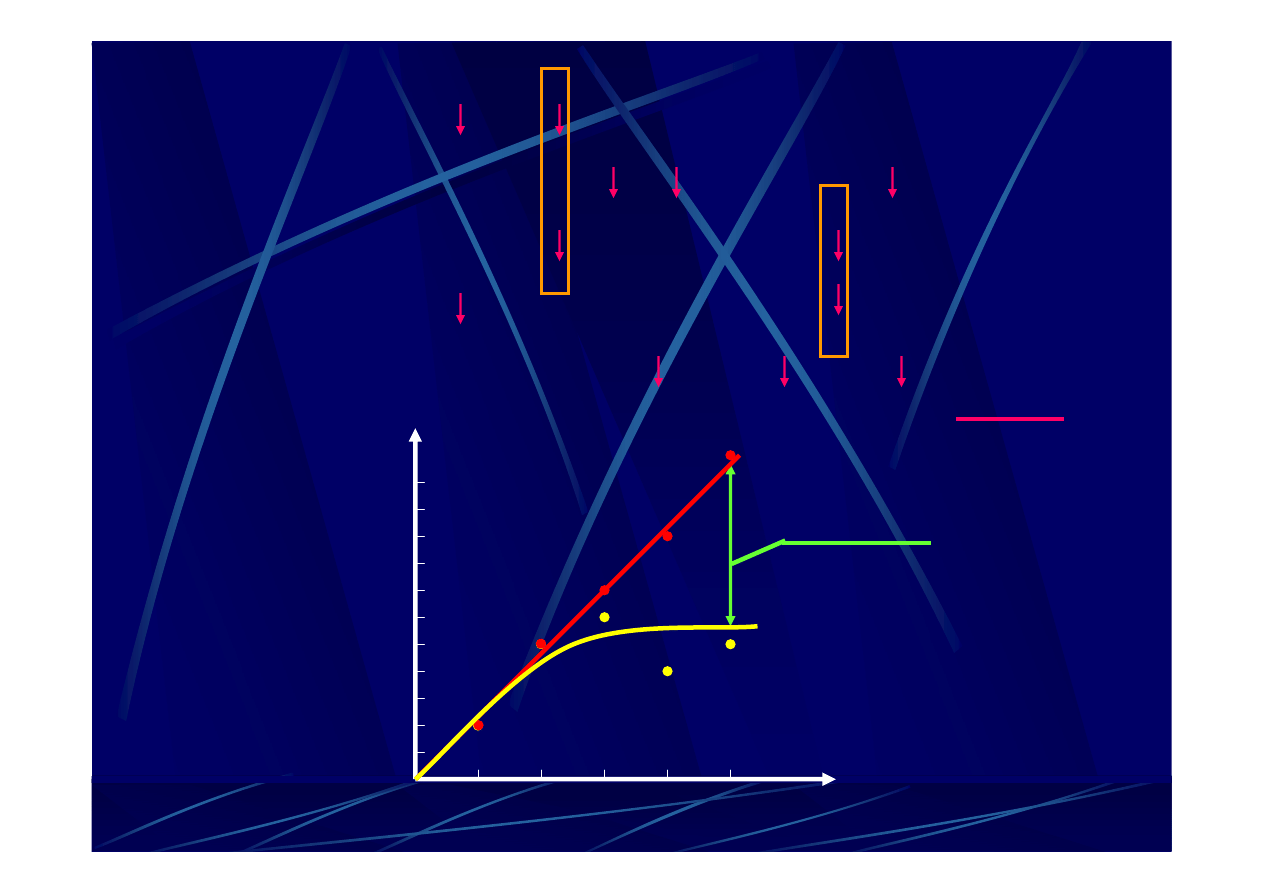
przodek

rzeczywista liczba podstawie

rzeczywista liczba podstawie

ń

ń

zaobserwowana

zaobserwowana

liczba r

liczba r

ó

ó

ż

ż

nic

nic

MELSK

L

TGDPAR

Q

KEL

S

ML

WK

LSKLTGD

R

APFVYRV

L

KRL

MELSK

L

TGDPAR

Q

KEL

S

MLM

K

LSKLTGDPAPF

V

YRV

G

KRL

MELSK

T

TGDPAR

Q

KEL

S

MLM

K

LSKLTGDPAPF

Y

YRV

G

KRL

MELSK

T

TGDPAR

R

KEL

S

MLM

K

LSKLTGDPAPFVYRV

G

KRL

MELSK

T

TGDPAR

R

KELKMLMELSKLTGDPAPFVYRVLKRL

MELSKLTGDPAREKELKMLMELSKLTGDPAPFVYRVLKRL

potomek

3 zmiany

3 zmiany

2 zmiany

2 zmiana

2 zmiany

= 12 zmian

2 zmiany w stosunku do przodka

5 zmian w stosunku do przodka

6 zmian w stosunku do przodka

4 zmian w stosunku do przodka

5 zmian w stosunku do przodka

czas ewolucji

czas ewolucji

r

r

ó

ó

ż

ż

nice mi

nice mi

ę

ę

dz

y sek

w

encjami

dz

y sek

w

encjami

niedoszacowanie

niedoszacowanie

tranzycje

i transwersje

Juckes-Cantor

K80

–

(Kimura)

TN93 –

rozróżnia

tranzycje

i transwersje,

oraz typ tranzycji:

czy

zaszła ona między
purynami czy
pirymidynami

TN93

(Tamura-Nei, 93)

Macierze

Macierze

substutucji

substutucji

nukleotyd

nukleotyd

ó

ó

w

w

Ala Arg Asn Asp Cys Gln Glu Gly His Ile Leu Lys Met Phe Pro Ser Thr Trp Tyr Val

A

R

N

D

C

Q

E

G

H

I

L

K

M

F

P

S

T

W

Y

V

Ala A 9867

2

9

10

3

8

17

21

2

6

4

2

6

2

22

35

32

0

2

18

Arg R

1

9913

1

0

1

10

0

0

10

3

1

19

4

1

4

6

1

8

0

1

Asn N

4

1

9822

36

0

4

6

6

21

3

1

13

0

1

2

20

9

1

4

1

Asp D

6

0

42

9859

0

6

53

6

4

1

0

3

0

0

1

5

3

0

0

1

Cys C

1

1

0

0

9973

0

0

0

1

1

0

0

0

0

1

5

1

0

3

2

Gln Q

3

9

4

5

0

9876

27

1

23

1

3

6

4

0

6

2

2

0

0

1

Glu E

10

0

7

56

0

35

9865

4

2

3

1

4

1

0

3

4

2

0

1

2

Gly G

21

1

12

11

1

3

7

9935

1

0

1

2

1

1

3

21

3

0

0

5

His H

1

8

18

3

1

20

1

0

9912

0

1

1

0

2

3

1

1

1

4

1

Ile I

2

2

3

1

2

1

2

0

0

9872

9

2

12

7

0

1

7

0

1

33

Leu L

3

1

3

0

0

6

1

1

4

22

9947

2

45

13

3

1

3

4

2

15

Lys K

2

37

25

6

0

12

7

2

2

4

1

9926

20

0

3

8

11

0

1

1

Met M

1

1

0

0

0

2

0

0

0

5

8

4

9874

1

0

1

2

0

0

4

Phe F

1

1

1

0

0

0

0

1

2

8

6

0

4

9946

0

2

1

3

28

0

Pro P

13

5

2

1

1

8

3

2

5

1

2

2

1

1

9926

12

4

0

0

2

Ser S

28

11

34

7

11

4

6

16

2

2

1

7

4

3

17

9840

38

5

2

2

Thr T

22

2

13

4

1

3

2

2

1

11

2

8

6

1

5

32

9871

0

2

9

Trp W

0

2

0

0

0

0

0

0

0

0

0

0

0

1

0

1

0

9976

1

0

Tyr T

1

0

3

0

3

0

1

0

4

1

1

0

0

21

0

1

1

2

9945

1

Val V

13

2

1

1

3

2

2

3

3

57

11

1

17

1

3

2

10

0

2

9901

Elementy pomnożone zostały przez 10 000

P

ercent

A

ccepted

M

utation

PAM1 -

M.

M.

Dayhoff

Dayhoff

1978r.

1978r.

element

M

IJ

tej macierzy reprezentuje

prawdopodobieństwo z jakim aminokwas
w kolumnie

j

zostanie podstawiony przez

aminokwas z wiersza

i

w czasie

ewolucyjnym 1 PAM

element diagonalny

M

ii

określa

prawdopodobieństwo, że dany

aminokwas nie ulegnie

substytucji w tym czasie

JEDNOSTKA PAM

JEDNOSTKA PAM

(

(

P

P

ercent

ercent

A

A

ccepted

ccepted

M

M

utation

utation

)

)

–

–

miara odleg

miara odleg

ł

ł

o

o

ś

ś

ci ewolucyjnej mi

ci ewolucyjnej mi

ę

ę

dzy sekwencjami

dzy sekwencjami

.

.

M.

M.

Dayhoff

Dayhoff

i wsp

i wsp

ó

ó

ł

ł

pracownicy

pracownicy

–

–

1978r.

1978r.

1 PAM

1 PAM

–

–

odpowiada takiemu czasowi ewolucyjnemu,

odpowiada takiemu czasowi ewolucyjnemu,

podczas kt

podczas kt

ó

ó

rego, w por

rego, w por

ó

ó

wnywanych sekwencjach,

wnywanych sekwencjach,

zmianie ulegnie 1 aminokwas na 100 (ok. 1

zmianie ulegnie 1 aminokwas na 100 (ok. 1

mln

mln

lat)

lat)

MELSKLT

G

DPAPFVYR

V

LKR ..... SKLT

G

DPAP ..... KVVFRIS

E

SP

M

IFKA

Y

PLDI ..... MELSK

L

TGDPA ... REKEL

K

MLMELSKLTGDPAPFVYRV

L

KRL ..... LDIVLSSLIHER

E

KELKML

MELSKLT

D

DPAPFVYR

Y

LKR ..... SKLT

Q

DPAP ..... KVVFRIS

R

SP

W

IFKA

V

PLDI ..... MELSK

T

TGDPA ... REKEL

D

MLMELSKLTGDPAPFVYRV

F

KRL ..... LDIVLSSLIHER

R

KELKML

1000 aminokwasów

10

zmienionych aminokwasów

Zmianie uległo 10/1000 = 1/100 aminokwasów, czyli 1%

Ewolucyjna macierz PAM

Ewolucyjna macierz PAM

Macierz PAM

Macierz PAM

-

-

Percent

Percent

Accepted

Accepted

Mutations

Mutations

(

(

Dayhoff

Dayhoff

i

i

wsp

wsp

ó

ó

ł

ł

pr

pr

. 1978)

. 1978)

Utworzona przez por

Utworzona przez por

ó

ó

wnanie blisko spokrewnionych sekwencji bia

wnanie blisko spokrewnionych sekwencji bia

ł

ł

ek (ponad

ek (ponad

85% identyczno

85% identyczno

ś

ś

ci) o znanych powi

ci) o znanych powi

ą

ą

zaniach filogenetycznych; naliczenie 1572

zaniach filogenetycznych; naliczenie 1572

zmian zaakceptowanych (przez selekcj

zmian zaakceptowanych (przez selekcj

ę

ę

) w 71 grupach bia

) w 71 grupach bia

ł

ł

ek.

ek.

Uwzgl

Uwzgl

ę

ę

dnia

dnia

mutabilno

mutabilno

ś

ś

ci

ci

poszczeg

poszczeg

ó

ó

lnych aminokwas

lnych aminokwas

ó

ó

w

w

MWT

MWT

V

V

SALV

SALV

G

G

Q

Q

MWT

MWT

A

A

SALV

SALV

G

G

Q

Q

MWT

MWT

V

V

SALV

SALV

L

L

Q

Q

MWT

MWT

V

V

SALV

SALV

G

G

Q

Q

MWT

MWT

A

A

SALV

SALV

G

G

Q

Q

MWT

MWT

V

V

SALV

SALV

L

L

Q

Q

V

V

-

-

>

>

A

A

G

G

-

-

>

>

L

L

Macierz PAM

Macierz PAM

–

–

log

log

odds

odds

je

je

ż

ż

eli

eli

log

log

odds

odds

<

<

0

0

:

:

dana substytucja zachodzi rzadziej ni

dana substytucja zachodzi rzadziej ni

ż

ż

nale

nale

ż

ż

a

a

ł

ł

o si

o si

ę

ę

spodziewa

spodziewa

ć

ć

je

je

ż

ż

eli

eli

log

log

odds

odds

>

>

0

0

:

:

dana substytucja zachodzi cz

dana substytucja zachodzi cz

ęś

ęś

ciej ni

ciej ni

ż

ż

nale

nale

ż

ż

a

a

ł

ł

o si

o si

ę

ę

spodziewa

spodziewa

ć

ć

(

(

np

np

. +1 oznacza,

. +1 oznacza,

ż

ż

e dana substytucja jest obserwowana 10 razy cz

e dana substytucja jest obserwowana 10 razy cz

ęś

ęś

ciej ni

ciej ni

ż

ż

nale

nale

ż

ż

a

a

ł

ł

o si

o si

ę

ę

spodziewa

spodziewa

ć

ć

)

)

je

je

ż

ż

eli

eli

log

log

odds

odds

=

=

0

0

:

:

dana substytucja zachodzi z tak

dana substytucja zachodzi z tak

ą

ą

sam

sam

ą

ą

cz

cz

ę

ę

sto

sto

ś

ś

ci

ci

ą

ą

jak w sekwencji

jak w sekwencji

losowej

losowej

Wyliczenie warto

Wyliczenie warto

ś

ś

ci log

ci log

odds

odds

:

:

P

P

o

o

–

–

obserwowana cz

obserwowana cz

ę

ę

stotliwo

stotliwo

ść

ść

wyst

wyst

ę

ę

powania mutacji

powania mutacji

P

P

e

e

–

–

oczekiwana cz

oczekiwana cz

ę

ę

stotliwo

stotliwo

ść

ść

wyst

wyst

ę

ę

powania mutacji

powania mutacji

(losow

(losow

a

a

)

)

log

log

odds

odds

= log (P

= log (P

o/

o/

P

P

e

e

)

)

A R N D C Q E G H I L K M F P S T W Y V

A R N D C Q E G H I L K M F P S T W Y V

A

A

2

2

R

R

-

-

2 6

2 6

N 0 0 2

N 0 0 2

D 0

D 0

-

-

1 2 4

1 2 4

C

C

-

-

2

2

-

-

4

4

-

-

4

4

-

-

5 12

5 12

Q 0 1 1 2

Q 0 1 1 2

-

-

5 4

5 4

E 0

E 0

-

-

1 1 3

1 1 3

-

-

5 2 4

5 2 4

G 1

G 1

-

-

3 0 1

3 0 1

-

-

3

3

-

-

1 0 5

1 0 5

H

H

-

-

1 2 2 1

1 2 2 1

-

-

3 3 1

3 3 1

-

-

2 6

2 6

I

I

-

-

1

1

-

-

2

2

-

-

2

2

-

-

2

2

-

-

2

2

-

-

2

2

-

-

2

2

-

-

3

3

-

-

2 5

2 5

L

L

-

-

2

2

-

-

3

3

-

-

3

3

-

-

4

4

-

-

6

6

-

-

2

2

-

-

3

3

-

-

4

4

-

-

2 2 6

2 2 6

K

K

-

-

1 3 1 0

1 3 1 0

-

-

5 1 0

5 1 0

-

-

2 0

2 0

-

-

2

2

-

-

3 5

3 5

M

M

-

-

1 0

1 0

-

-

2

2

-

-

3

3

-

-

5

5

-

-

1

1

-

-

2

2

-

-

3

3

-

-

2 2 4 0 6

2 2 4 0 6

F

F

-

-

4

4

-

-

4

4

-

-

4

4

-

-

6

6

-

-

4

4

-

-

5

5

-

-

5

5

-

-

5

5

-

-

2 1 2

2 1 2

-

-

5 0 9

5 0 9

P 1 0

P 1 0

-

-

1

1

-

-

1

1

-

-

3 0

3 0

-

-

1

1

-

-

1 0

1 0

-

-

2

2

-

-

3

3

-

-

1

1

-

-

2

2

-

-

5 6

5 6

S 1 0 1 0 0

S 1 0 1 0 0

-

-

1 0 1

1 0 1

-

-

1

1

-

-

1

1

-

-

3 0

3 0

-

-

2

2

-

-

3 1 2

3 1 2

T 1

T 1

-

-

1 0 0

1 0 0

-

-

2

2

-

-

1 0 0

1 0 0

-

-

1 0

1 0

-

-

2 0

2 0

-

-

1

1

-

-

3 0 1 3

3 0 1 3

W

W

-

-

6 2

6 2

-

-

4

4

-

-

7

7

-

-

8

8

-

-

5

5

-

-

7

7

-

-

7

7

-

-

3

3

-

-

5

5

-

-

2

2

-

-

3

3

-

-

4 0

4 0

-

-

6

6

-

-

2

2

-

-

5 17

5 17

Y

Y

-

-

3

3

-

-

4

4

-

-

2

2

-

-

4 0

4 0

-

-

4

4

-

-

4

4

-

-

5 0

5 0

-

-

1

1

-

-

1

1

-

-

4

4

-

-

2 7

2 7

-

-

5

5

-

-

3

3

-

-

3 0 10

3 0 10

V 0

V 0

-

-

2

2

-

-

2

2

-

-

2

2

-

-

2

2

-

-

2

2

-

-

2

2

-

-

1

1

-

-

2 4 2

2 4 2

-

-

2 2

2 2

-

-

1

1

-

-

1

1

-

-

1 0

1 0

-

-

6

6

-

-

2 4

2 4

Rzadkie aminokwasy maj

Rzadkie aminokwasy maj

ą

ą

du

du

ż

ż

e wagi

e wagi

Pospolite

Pospolite

aminokwasy maj

aminokwasy maj

ą

ą

ma

ma

ł

ł

e wagi

e wagi

A R N D C Q E G H I L K M F P S T W Y V

A R N D C Q E G H I L K M F P S T W Y V

A

A

2

2

R

R

-

-

2 6

2 6

N 0 0 2

N 0 0 2

D 0

D 0

-

-

1 2 4

1 2 4

C

C

-

-

2

2

-

-

4

4

-

-

4

4

-

-

5 12

5 12

Q 0 1 1 2

Q 0 1 1 2

-

-

5 4

5 4

E 0

E 0

-

-

1 1 3

1 1 3

-

-

5 2 4

5 2 4

G 1

G 1

-

-

3 0 1

3 0 1

-

-

3

3

-

-

1 0 5

1 0 5

H

H

-

-

1 2 2 1

1 2 2 1

-

-

3 3 1

3 3 1

-

-

2 6

2 6

I

I

-

-

1

1

-

-

2

2

-

-

2

2

-

-

2

2

-

-

2

2

-

-

2

2

-

-

2

2

-

-

3

3

-

-

2 5

2 5

L

L

-

-

2

2

-

-

3

3

-

-

3

3

-

-

4

4

-

-

6

6

-

-

2

2

-

-

3

3

-

-

4

4

-

-

2 2 6

2 2 6

K

K

-

-

1 3 1 0

1 3 1 0

-

-

5 1 0

5 1 0

-

-

2 0

2 0

-

-

2

2

-

-

3 5

3 5

M

M

-

-

1 0

1 0

-

-

2

2

-

-

3

3

-

-

5

5

-

-

1

1

-

-

2

2

-

-

3

3

-

-

2 2 4 0 6

2 2 4 0 6

F

F

-

-

4

4

-

-

4

4

-

-

4

4

-

-

6

6

-

-

4

4

-

-

5

5

-

-

5

5

-

-

5

5

-

-

2 1 2

2 1 2

-

-

5 0 9

5 0 9

P 1 0

P 1 0

-

-

1

1

-

-

1

1

-

-

3 0

3 0

-

-

1

1

-

-

1 0

1 0

-

-

2

2

-

-

3

3

-

-

1

1

-

-

2

2

-

-

5 6

5 6

S 1 0 1 0 0

S 1 0 1 0 0

-

-

1 0 1

1 0 1

-

-

1

1

-

-

1

1

-

-

3 0

3 0

-

-

2

2

-

-

3 1 2

3 1 2

T 1

T 1

-

-

1 0 0

1 0 0

-

-

2

2

-

-

1 0 0

1 0 0

-

-

1 0

1 0

-

-

2 0

2 0

-

-

1

1

-

-

3 0 1 3

3 0 1 3

W

W

-

-

6 2

6 2

-

-

4

4

-

-

7

7

-

-

8

8

-

-

5

5

-

-

7

7

-

-

7

7

-

-

3

3

-

-

5

5

-

-

2

2

-

-

3

3

-

-

4 0

4 0

-

-

6

6

-

-

2

2

-

-

5 17

5 17

Y

Y

-

-

3

3

-

-

4

4

-

-

2

2

-

-

4 0

4 0

-

-

4

4

-

-

4

4

-

-

5 0

5 0

-

-

1

1

-

-

1

1

-

-

4

4

-

-

2 7

2 7

-

-

5

5

-

-

3

3

-

-

3 0 10

3 0 10

V 0

V 0

-

-

2

2

-

-

2

2

-

-

2

2

-

-

2

2

-

-

2

2

-

-

2

2

-

-

1

1

-

-

2 4 2

2 4 2

-

-

2 2

2 2

-

-

1

1

-

-

1

1

-

-

1 0

1 0

-

-

6

6

-

-

2 4

2 4

Dodatnie warto

Dodatnie warto

ś

ś

ci dla cz

ci dla cz

ę

ę

stszych

stszych

podstawie

podstawie

ń

ń

A R N D C Q E G H I L K M F P S T W Y V

A R N D C Q E G H I L K M F P S T W Y V

A

A

2

2

R

R

-

-

2 6

2 6

N 0 0 2

N 0 0 2

D 0

D 0

-

-

1 2 4

1 2 4

C

C

-

-

2

2

-

-

4

4

-

-

4

4

-

-

5 12

5 12

Q 0 1 1 2

Q 0 1 1 2

-

-

5 4

5 4

E 0

E 0

-

-

1 1 3

1 1 3

-

-

5 2 4

5 2 4

G 1

G 1

-

-

3 0 1

3 0 1

-

-

3

3

-

-

1 0 5

1 0 5

H

H

-

-

1 2 2 1

1 2 2 1

-

-

3 3 1

3 3 1

-

-

2 6

2 6

I

I

-

-

1

1

-

-

2

2

-

-

2

2

-

-

2

2

-

-

2

2

-

-

2

2

-

-

2

2

-

-

3

3

-

-

2 5

2 5

L

L

-

-

2

2

-

-

3

3

-

-

3

3

-

-

4

4

-

-

6

6

-

-

2

2

-

-

3

3

-

-

4

4

-

-

2 2 6

2 2 6

K

K

-

-

1 3 1 0

1 3 1 0

-

-

5 1 0

5 1 0

-

-

2 0

2 0

-

-

2

2

-

-

3 5

3 5

M

M

-

-

1 0

1 0

-

-

2

2

-

-

3

3

-

-

5

5

-

-

1

1

-

-

2

2

-

-

3

3

-

-

2 2 4 0 6

2 2 4 0 6

F

F

-

-

4

4

-

-

4

4

-

-

4

4

-

-

6

6

-

-

4

4

-

-

5

5

-

-

5

5

-

-

5

5

-

-

2 1 2

2 1 2

-

-

5 0 9

5 0 9

P 1 0

P 1 0

-

-

1

1

-

-

1

1

-

-

3 0

3 0

-

-

1

1

-

-

1 0

1 0

-

-

2

2

-

-

3

3

-

-

1

1

-

-

2

2

-

-

5 6

5 6

S 1 0 1 0 0

S 1 0 1 0 0

-

-

1 0 1

1 0 1

-

-

1

1

-

-

1

1

-

-

3 0

3 0

-

-

2

2

-

-

3 1 2

3 1 2

T 1

T 1

-

-

1 0 0

1 0 0

-

-

2

2

-

-

1 0 0

1 0 0

-

-

1 0

1 0

-

-

2 0

2 0

-

-

1

1

-

-

3 0 1 3

3 0 1 3

W

W

-

-

6 2

6 2

-

-

4

4

-

-

7

7

-

-

8

8

-

-

5

5

-

-

7

7

-

-

7

7

-

-

3

3

-

-

5

5

-

-

2

2

-

-

3

3

-

-

4 0

4 0

-

-

6

6

-

-

2

2

-

-

5 17

5 17

Y

Y

-

-

3

3

-

-

4

4

-

-

2

2

-

-

4 0

4 0

-

-

4

4

-

-

4

4

-

-

5 0

5 0

-

-

1

1

-

-

1

1

-

-

4

4

-

-

2 7

2 7

-

-

5

5

-

-

3

3

-

-

3 0 10

3 0 10

V 0

V 0

-

-

2

2

-

-

2

2

-

-

2

2

-

-

2

2

-

-

2

2

-

-

2

2

-

-

1

1

-

-

2 4 2

2 4 2

-

-

2 2

2 2

-

-

1

1

-

-

1

1

-

-

1 0

1 0

-

-

6

6

-

-

2 4

2 4

Ujemne warto

Ujemne warto

ś

ś

ci dla rzadkich

ci dla rzadkich

podstawie

podstawie

ń

ń

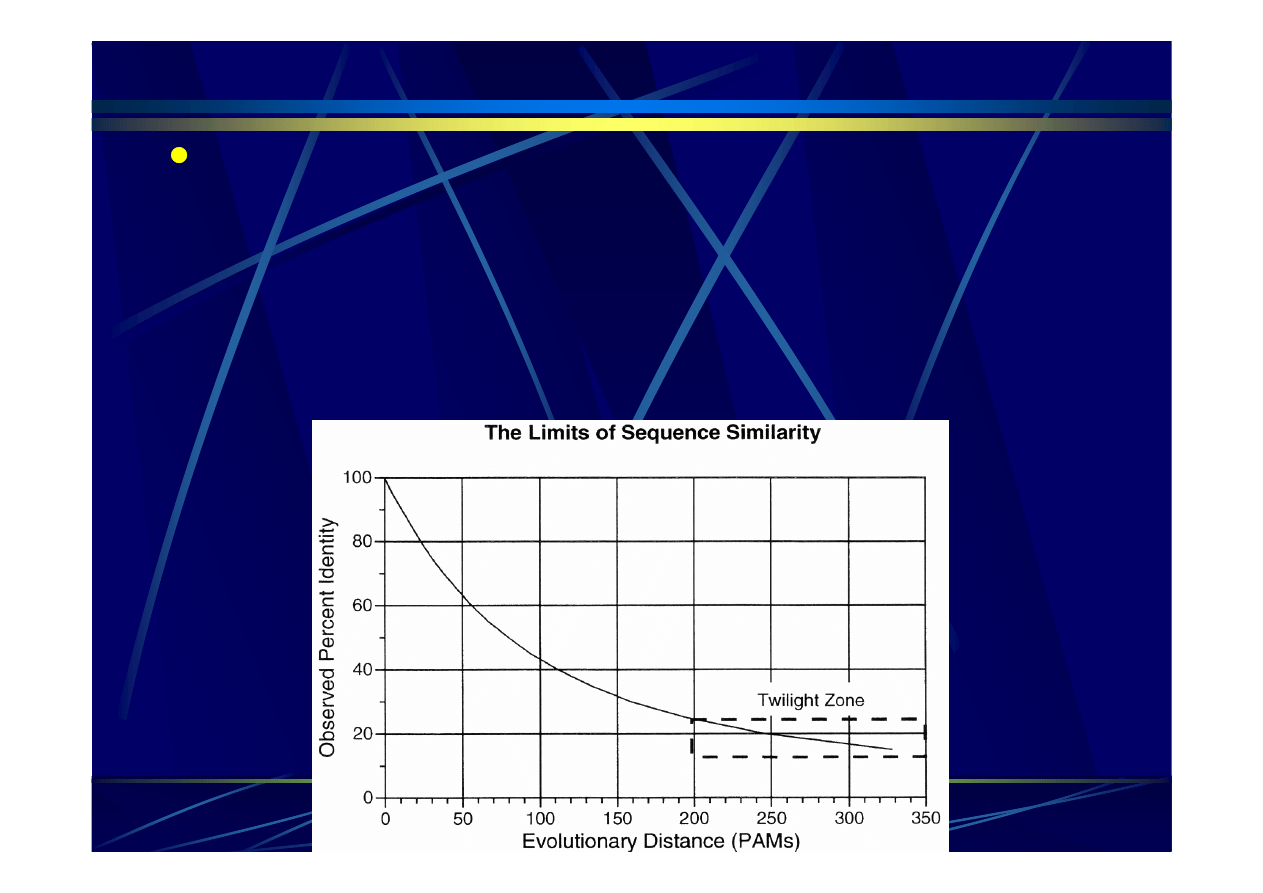
Ewolucyjna macierz PAM

Ewolucyjna macierz PAM

Ekstrapolowanie cz

Ekstrapolowanie cz

ę

ę

sto

sto

ś

ś

ci

ci

podstawie

podstawie

ń

ń

zaobserwowanych na kr

zaobserwowanych na kr

ó

ó

tkich

tkich

dystansach na d

dystansach na d

ł

ł

u

u

ż

ż

sze

sze

dystansy

dystansy

ewolucyjne

ewolucyjne

–

–

mno

mno

ż

ż

enie macierzy przez siebie

enie macierzy przez siebie

–

–

uzyskanie serii tablic PAM:

uzyskanie serii tablic PAM:

PAM1

PAM1

-

-

> PAM60, PAM80, PAM120,

> PAM60, PAM80, PAM120,

PAM250

PAM250

Podobie

Podobie

ń

ń

stwo:

stwo:

99%

99%

60%

60%

50%

50%

40%

40%

20%

20%

Liczba podstawie

Liczba podstawie

ń

ń

na miejsce:

na miejsce:

0.01

0.01

0.6

0.6

0.8

0.8

1.2

1.2

2.5

2.5

Macierz PAM

Macierz PAM

–

–

wady z powodu za

wady z powodu za

ł

ł

o

o

ż

ż

e

e

ń

ń

:

:

Podstawienia

Podstawienia

aminokwas

aminokwas

ó

ó

w zachodz

w zachodz

ą

ą

niezale

niezale

ż

ż

nie od

nie od

siebie. W rzeczywisto

siebie. W rzeczywisto

ś

ś

ci zmiany w r

ci zmiany w r

ó

ó

ż

ż

nych regionach

nych regionach

sekwencji s

sekwencji s

ą

ą

ze sob

ze sob

ą

ą

skorelowane.

skorelowane.

Te same tempo podstawie

Te same tempo podstawie

ń

ń

w r

w r

ó

ó

ż

ż

nych regionach

nych regionach

sekwencji. W rzeczywisto

sekwencji. W rzeczywisto

ś

ś

ci r

ci r

ó

ó

ż

ż

ne regiony wykazuj

ne regiony wykazuj

ą

ą

r

r

ó

ó

ż

ż

ny

ny

stopie

stopie

ń

ń

konserwatywno

konserwatywno

ś

ś

ci i ewoluuj

ci i ewoluuj

ą

ą

z r

z r

ó

ó

ż

ż

n

n

ą

ą

pr

pr

ę

ę

dko

dko

ś

ś

ci

ci

ą

ą

.

.

W r

W r

ó

ó

ż

ż

nych regionach r

nych regionach r

ó

ó

ż

ż

ne

ne

podstawienia

podstawienia

zdarzaj

zdarzaj

ą

ą

si

si

ę

ę

z r

z r

ó

ó

ż

ż

n

n

ą

ą

cz

cz

ę

ę

sto

sto

ś

ś

ci

ci

ą

ą

.

.

Cz

Cz

ę

ę

sto

sto

ść

ść

poszczeg

poszczeg

ó

ó

lnych podstawie

lnych podstawie

ń

ń

nie zmieniaj

nie zmieniaj

ą

ą

si

si

ę

ę

w czasie. W rzeczywisto

w czasie. W rzeczywisto

ś

ś

ci cz

ci cz

ę

ę

sto

sto

ś

ś

ci podstawie

ci podstawie

ń

ń

mog

mog

ą

ą

si

si

ę

ę

zmienia

zmienia

ć

ć

w czasie.

w czasie.

Macierz BLOSUM

Macierz BLOSUM

Macierz BLOSUM

Macierz BLOSUM

–

–

BLOcks

BLOcks

Substitution

Substitution

Matrix

Matrix

(

(

Henikoff

Henikoff

i

i

Henikoff

Henikoff

1992)

1992)

Utworzona przez por

Utworzona przez por

ó

ó

wnanie oko

wnanie oko

ł

ł

o 2000

o 2000

zachowanych

zachowanych

blok

blok

ó

ó

w (region

w (region

ó

ó

w

w

sekwencji) w ponad 500 rodzinach bia

sekwencji) w ponad 500 rodzinach bia

ł

ł

ek o r

ek o r

ó

ó

ż

ż

nej odleg

nej odleg

ł

ł

o

o

ś

ś

ci ewolucyjnej. Bloki s

ci ewolucyjnej. Bloki s

ą

ą

regionami sekwencji odpowiedzialnymi za podobn

regionami sekwencji odpowiedzialnymi za podobn

ą

ą

funkcj

funkcj

ę

ę

biochemiczn

biochemiczn

ą

ą

lub

lub

struktur

struktur

ę

ę

.

.

Macierze dla r

Macierze dla r

ó

ó

ż

ż

nych odleg

nych odleg

ł

ł

o

o

ś

ś

ci ewolucyjnych zosta

ci ewolucyjnych zosta

ł

ł

y wyliczone z por

y wyliczone z por

ó

ó

wnania

wnania

sekwencji odpowiednio odleg

sekwencji odpowiednio odleg

ł

ł

ych:

ych:

BLOSUM30

BLOSUM30

–

–

bloki sekwencji o co najmniej 30% identyczno

bloki sekwencji o co najmniej 30% identyczno

ś

ś

ci reszt aminokwasowych

ci reszt aminokwasowych

BLOSUM62

BLOSUM62

–

–

bloki sekwencji o co najmniej 62% identyczno

bloki sekwencji o co najmniej 62% identyczno

ś

ś

ci reszt aminokwasowych

ci reszt aminokwasowych

BLOSUM80

BLOSUM80

–

–

bloki sekwencji o co najmniej 80% identyczno

bloki sekwencji o co najmniej 80% identyczno

ś

ś

ci reszt aminokwasowych

ci reszt aminokwasowych

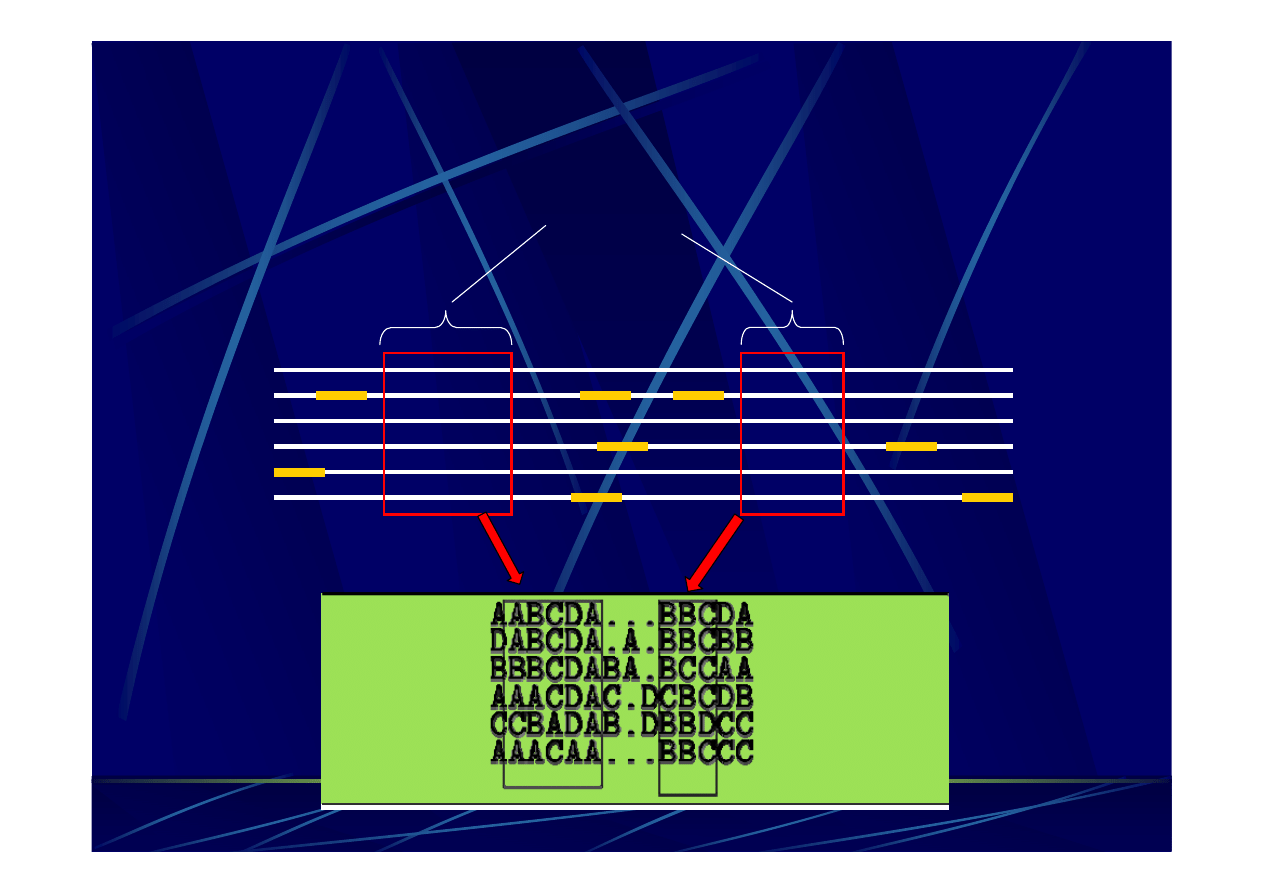
Macierz BLOSUM

Macierz BLOSUM

–

–

BLOcks

BLOcks

Substitution

Substitution

Matrix

Matrix

bloki

bloki

A R N D C Q E G H I L K M F P S T W Y V

A R N D C Q E G H I L K M F P S T W Y V

A 4

A 4

R

R

-

-

1 5

1 5

N

N

-

-

2 0 6

2 0 6

D

D

-

-

2

2

-

-

2 1 6

2 1 6

C 0

C 0

-

-

3

3

-

-

3

3

-

-

3 9

3 9

Q

Q

-

-

1 1 0 0

1 1 0 0

-

-

3 5

3 5

E

E

-

-

1 0 0 2

1 0 0 2

-

-

4 2 5

4 2 5

G 0

G 0

-

-

2 0

2 0

-

-

1

1

-

-

3

3

-

-

2

2

-

-

2 6

2 6

H

H

-

-

2 0 1

2 0 1

-

-

1

1

-

-

3 0 0

3 0 0

-

-

2 8

2 8

I

I

-

-

1

1

-

-

3

3

-

-

3

3

-

-

3

3

-

-

1

1

-

-

3

3

-

-

3

3

-

-

4

4

-

-

3 4

3 4

L

L

-

-

1

1

-

-

2

2

-

-

3

3

-

-

4

4

-

-

1

1

-

-

2

2

-

-

3

3

-

-

4

4

-

-

3 2 4

3 2 4

K

K

-

-

1 2 0

1 2 0

-

-

1

1

-

-

3 1 1

3 1 1

-

-

2

2

-

-

1

1

-

-

3

3

-

-

2 5

2 5

M

M

-

-

1

1

-

-

1

1

-

-

2

2

-

-

3

3

-

-

1 0

1 0

-

-

2

2

-

-

3

3

-

-

2 1 2

2 1 2

-

-

1 5

1 5

F

F

-

-

2

2

-

-

3

3

-

-

3

3

-

-

3

3

-

-

2

2

-

-

3

3

-

-

3

3

-

-

3

3

-

-

1 0 0

1 0 0

-

-

3 0 6

3 0 6

P

P

-

-

1

1

-

-

2

2

-

-

2

2

-

-

1

1

-

-

3

3

-

-

1

1

-

-

1

1

-

-

2

2

-

-

2

2

-

-

3

3

-

-

3

3

-

-

1

1

-

-

2

2

-

-

4 7

4 7

S 1

S 1

-

-

1 1 0

1 1 0

-

-

1 0 0 0

1 0 0 0

-

-

1

1

-

-

2

2

-

-

2 0

2 0

-

-

1

1

-

-

2

2

-

-

1 4

1 4

Macierz BLOSUM62

Macierz BLOSUM62

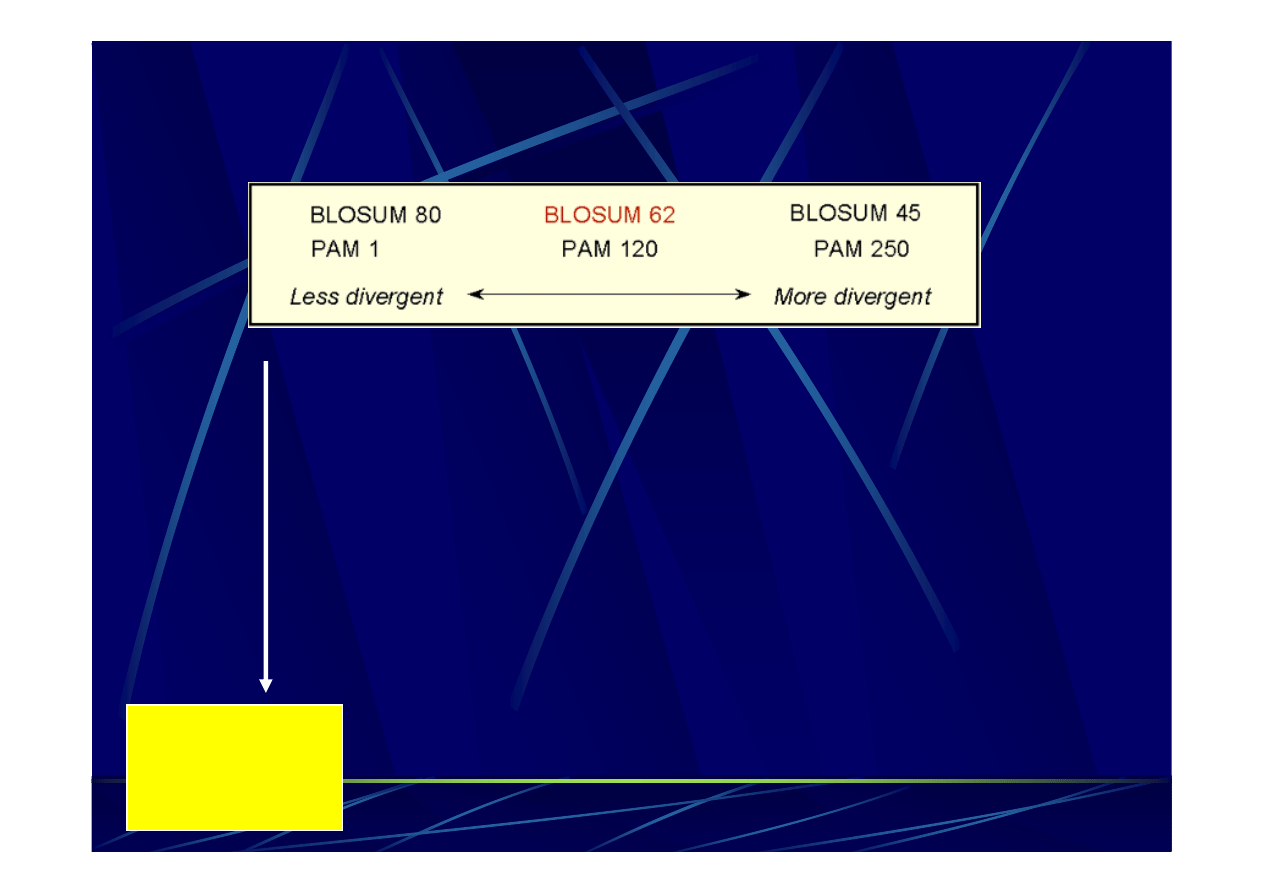
PAM Vs. BLOSUM

PAM100 =~ BLOSUM90

PAM120 =~ BLOSUM80
PAM160 =~ BLOSUM60
PAM200 =~ BLOSUM52
PAM250 =~ BLOSUM45

Bardziej odległe

sekwencje

Inne macierze

Inne macierze

substutucji

substutucji

aminokwasow

aminokwasow

ó

ó

w

w

Oparte na kodzie genetycznym

Oparte na kodzie genetycznym

-

-

zwi

zwi

ą

ą

zane z kodowaniem aminokwas

zane z kodowaniem aminokwas

ó

ó

w przez

w przez

kodony (

kodony (

Fitch

Fitch

1966;

1966;

Benner

Benner

i

i

wsp

wsp

ó

ó

ł

ł

pr

pr

. 1994)

. 1994)

Uwzgl

Uwzgl

ę

ę

dniaj

dniaj

ą

ą

ce w

ce w

ł

ł

a

a

ś

ś

ciwo

ciwo

ś

ś

ci fizyko

ci fizyko

-

-

chemiczne aminokwas

chemiczne aminokwas

ó

ó

w (

w (

Vogt

Vogt

i

i

wsp

wsp

ó

ó

ł

ł

pr

pr

. 1995)

. 1995)

i podobie

i podobie

ń

ń

stwo strukturalne

stwo strukturalne

ł

ł

a

a

ń

ń

cuch

cuch

ó

ó

w bocznych (

w bocznych (

Feng

Feng

i

i

wsp

wsp

ó

ó

ł

ł

pr

pr

. 1985)

. 1985)

Uwzgl

Uwzgl

ę

ę

dniaj

dniaj

ą

ą

ce struktur

ce struktur

ę

ę

trzeciorz

trzeciorz

ę

ę

dow

dow

ą

ą

(

(

Risler

Risler

i

i

wsp

wsp

ó

ó

ł

ł

pr

pr

. 1988; Johnson i

. 1988; Johnson i

Overington

Overington

1993;

1993;

Henikoff

Henikoff

i

i

Henikoff

Henikoff

1993;

1993;

Sander

Sander

i Schneider 1991)

i Schneider 1991)

Macierz

Macierz

dwupeptyd

dwupeptyd

ó

ó

w

w

(

(

Gonnet

Gonnet

i

i

wsp

wsp

ó

ó

ł

ł

pr

pr

. 1994)

. 1994)

-

-

400 x 400, uwzgl

400 x 400, uwzgl

ę

ę

dnia wp

dnia wp

ł

ł

yw

yw

przyleg

przyleg

ł

ł

ych aminokwas

ych aminokwas

ó

ó

w na cz

w na cz

ę

ę

sto

sto

ść

ść

substytucji

substytucji

Macierz PAM z uwzgl

Macierz PAM z uwzgl

ę

ę

dnieniem bia

dnieniem bia

ł

ł

ek transmembranowych (Jones i

ek transmembranowych (Jones i

wsp

wsp

ó

ó

ł

ł

pr

pr

.

.

1994)

1994)

Etapy analizy filogenetycznej

Dobór i dopasowane sekwencji

Wybór modelu substytucji

Wybór metody oceny odległości ewolucyjnej

Konstrukcja drzewka

Ocena i analiza skonstruowanego drzewka

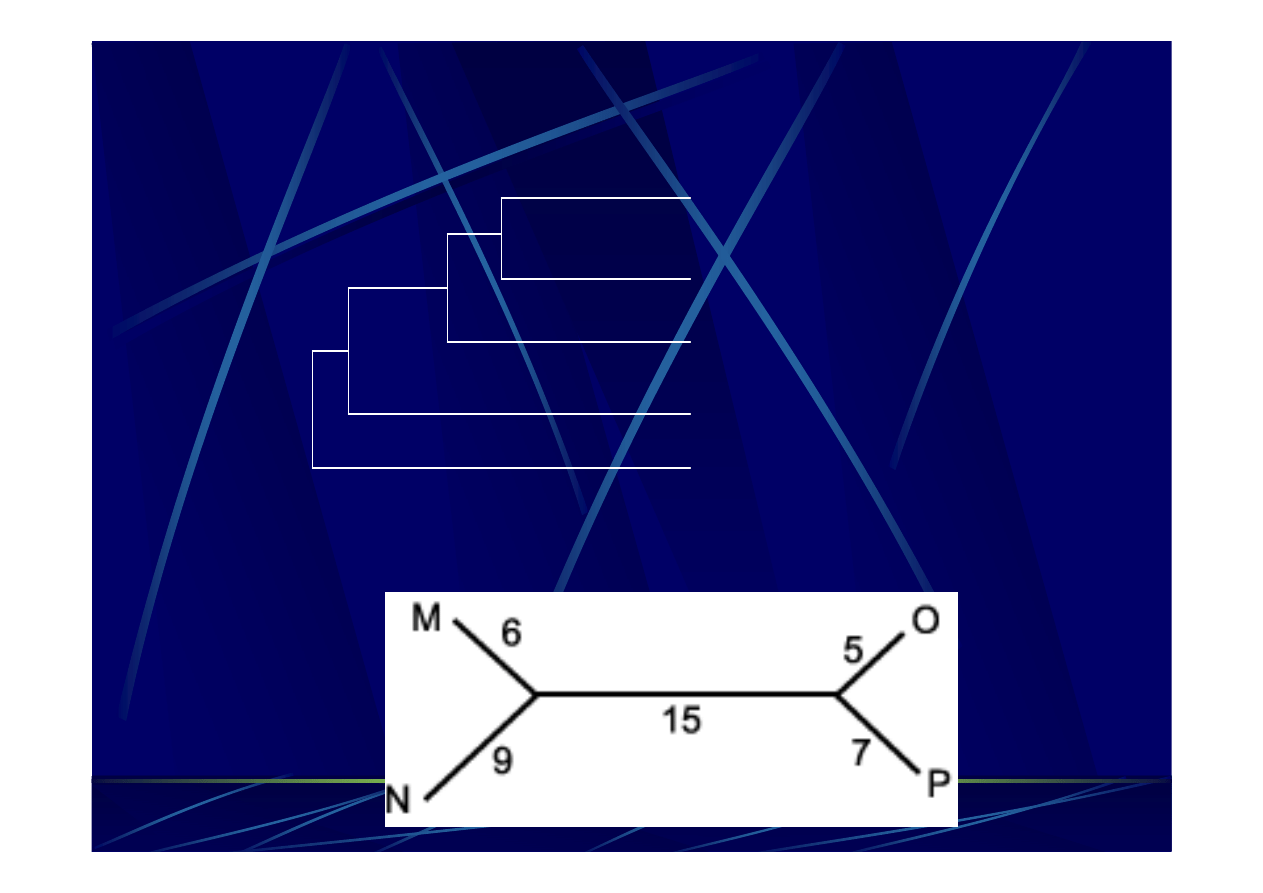
FM

–

Fitch

-

Margoliash

0.047

Human

Chimpanzee

Gorilla

0.056

0.047

Orangutan

0. 094

0.108

Gibbon

UPMGA –

Unweighted

Pair

Group

Method

with

Arithmetic

Mean

A

B

C

D

E

A

B

E

D

C

A

B

NJ -

Neighbour

joining

Ocena poprawności rekonstrukcji
filogenetycznej –

metoda bootstrap

Site

OTU 1

2

3 4 5 6 7 8

9

10

1

2

3

4

A

A

C

C

Site

OTU

1

2

3

4 5 6 7 8 9 10

1

2

3

4

T

C

A

G A T C T A G

T

T

A

G A A C T A G

T

T

C

G A T C G A G

T

T

C

T A A G G A C

C

T

T

T

T

A

T

A

A

A

A

A

G

G

G

C

C

C

C

G

A

A

A

A

T

A

T

A

T

T

T

T

A

A

A

A

oryginalne

dopasowanie

powtórne dopasowanie

1

2

3

4

1

3

2

4

Losujemy nowe kolumny dopasowania (z powtórzeniami!)

Powtarzamy 100 -

1000 i tworzymy drzewko konsensusowe

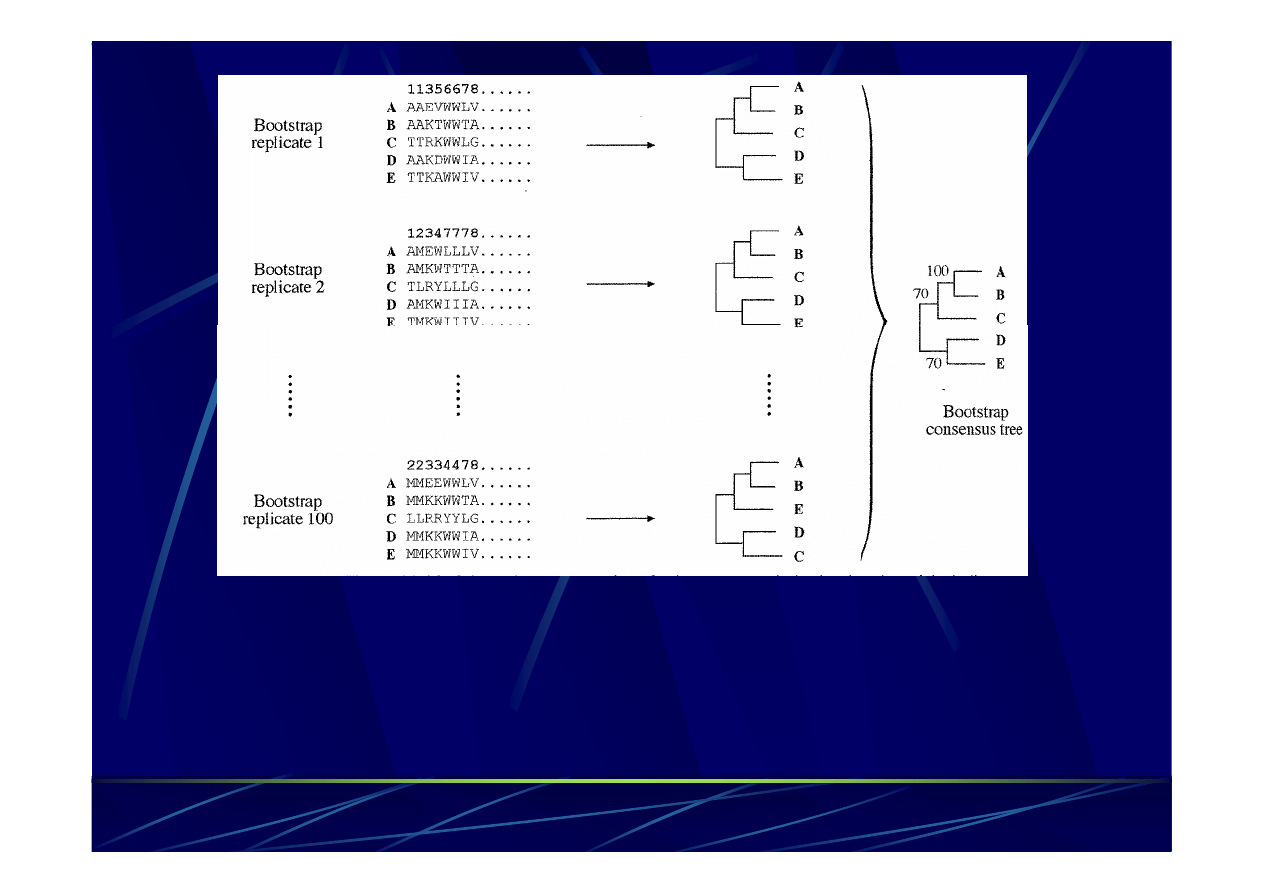
Wartości bootstrap:

> 95% topologia drzewka bardzo prawdopodobna

< 75% nie ma wystarczająco silnych dowodów potwierdzających
taką

topologię

drzewka co wcale nie oznacza, że nie jest ona

prawidłowa!!!