
Bioinformatyka, wykład 6
(18.XI.2008)
krzysztof_pawlowski@sggw.pl
Dopasowanie sekwencji
Dopasowanie sekwencji
–
–
c.d.
c.d.
Sequence
Sequence
alignment
alignment

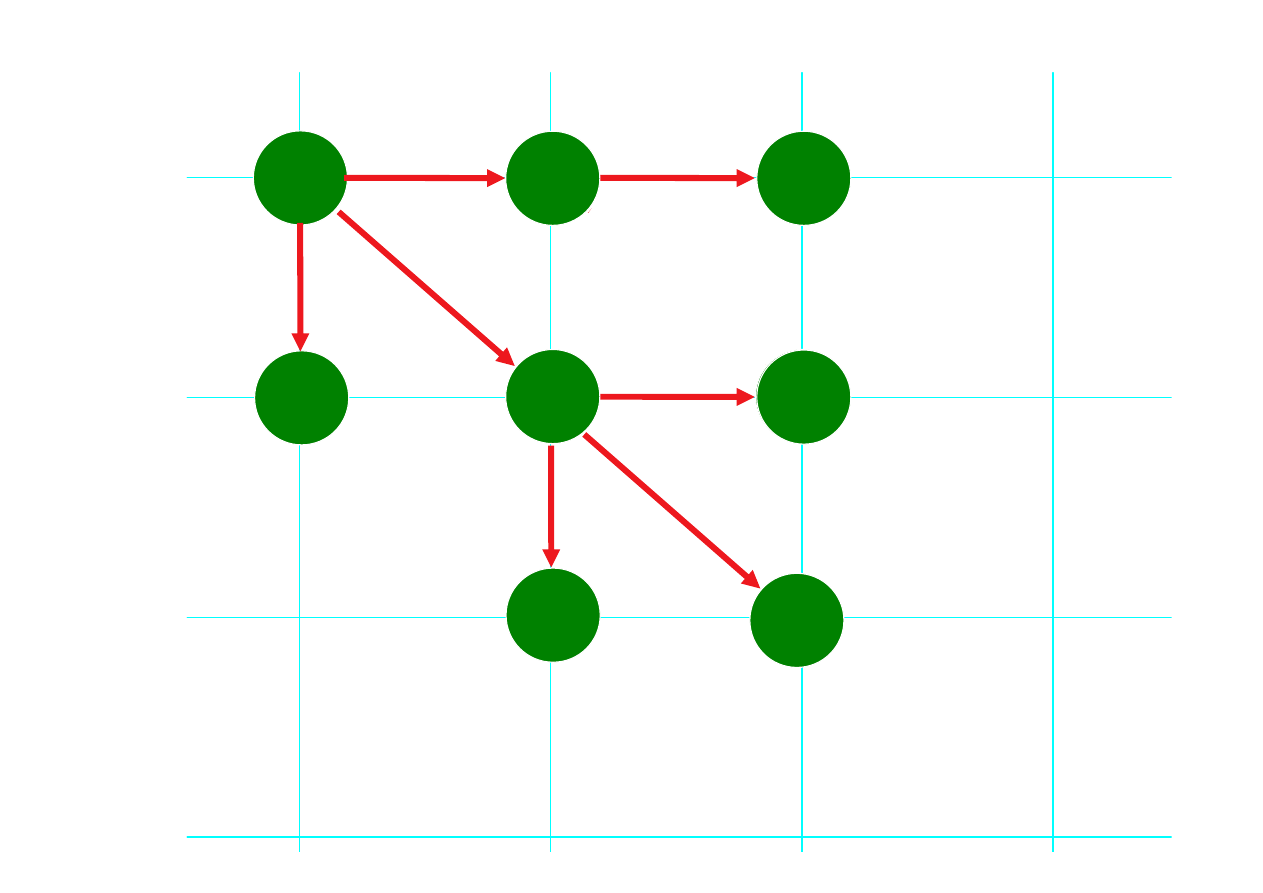
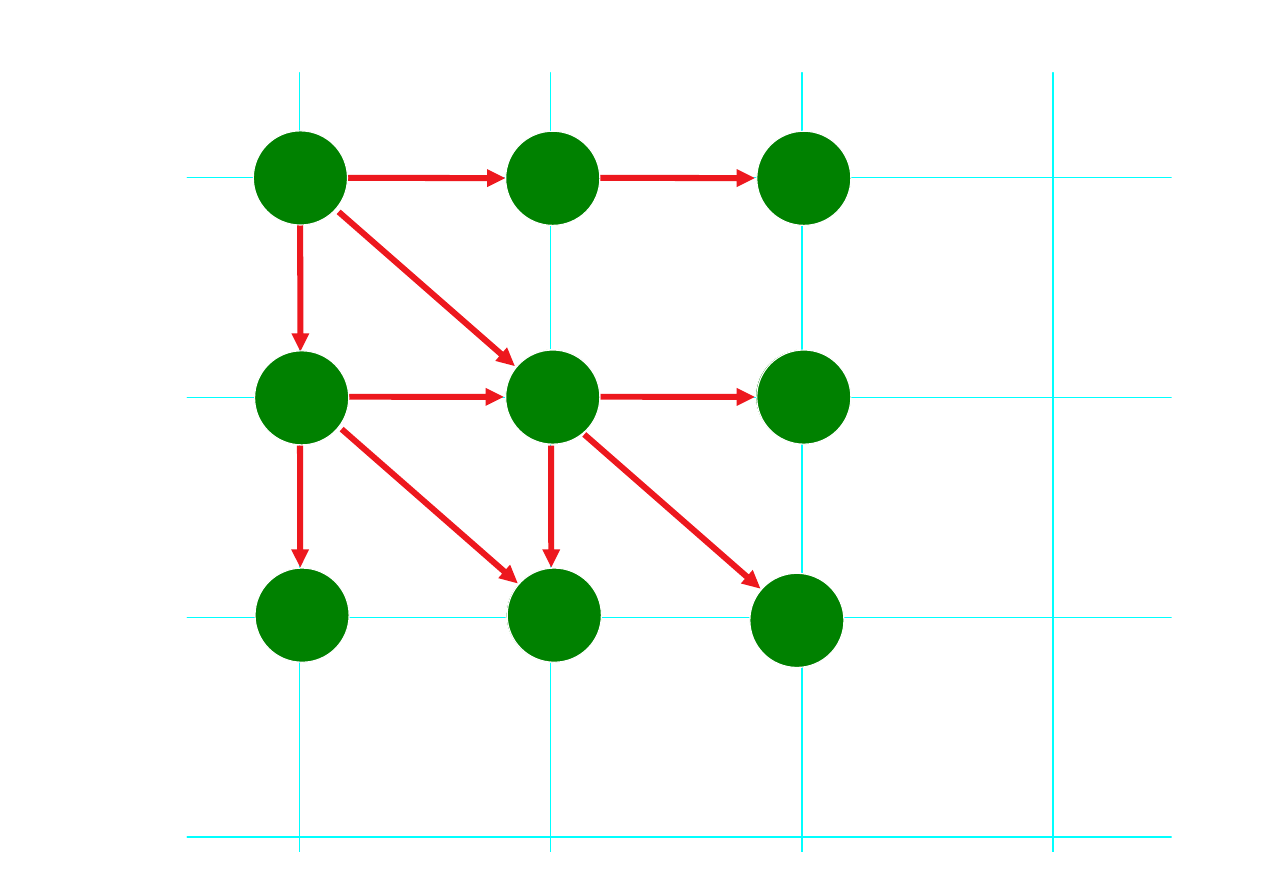
Programowanie dynamiczne
Programowanie dynamiczne
Porównuje każdą
parę
znaków dwóch sekwencji i tworzy dopasowanie
Uwzględnia wszystkie możliwe przyrównania uwzględniając:
dopasowania (matches),
niedopasowania (mismatches),
przerwy (gaps).
Przerwy są
wstawiane, aby uzyskać
wzrost liczby dopasowań
w innych miejscach.
Przyjmuje pewien system punktacji (scoring system)
Rozpatruje wszystkie możliwości
Stara się
uzyskać
maksymalną
liczbę
dopasowań
między identycznymi lub
podobnymi znakami
Znajduje optymalne dopasowanie (może istnieć
więcej niż
jedno
takie dopasowanie)
Czas obliczeń
proporcjonalny do iloczynu długości sekwencji
Programowanie dynamiczne
Programowanie dynamiczne
Przyjęty system punktacji:
dopasowanie (match): +1
niedopasowanie (mismatch): -1
przerwa (gap): -1
AGA--TTGATACCCA
AGACATTAA---CTA
match
mismatch
gap
Programowanie dynamiczne
Programowanie dynamiczne
Programowanie dynamiczne uwzględnia każdą
dodawaną
parę
znaków
i z powrotem przelicza optymalne dopasowanie.
C
A
sekwencja 1:
G A T A C T A
sekwencja 2:
G A T T A C C A
T
|
T
A
T
+
=
Dotychczasowe dopasowanie musi być
optymalne!
A
|
A
G
|
G
T
|
T
A
T
A
|
A
G
|
G
C
A
+1 +1 +1 –1 –1 = +1
G A T - A C
| | | |
G A T T A -
+1 +1 +1 –1 +1 –1 = +2
- - G A T A C
G A T T A - -
–1 –1 –1 –1 –1 –1 –1 = –7
+1 +1 +1 –1 = +2
Już
utworzone dopasowanie, do którego jest dodawana kolejna para znaków,
musi być
optymalne.
- G A T A C
| |
G A T T A -
–1 –1 –1 +1 +1 –1 = –2

Tworzenie macierzy punktacji, w której każda komórka reprezentuje punktację
dla
najlepszego dopasowania kończącego się
w danej pozycji
Programowanie dynamiczne
Programowanie dynamiczne
Cofanie się
w macierzy, aby znaleźć
optymalne dopasowanie
sekwencja 1:
G A T A C T A
sekwencja 2
:
G A T T A C C A
Przyjęty system punktacji:
dopasowanie (match): +1
niedopasowanie (mismatch): -1
przerwa (gap): -1
G A T A C T A
G
A
T
T
A
C
C
A
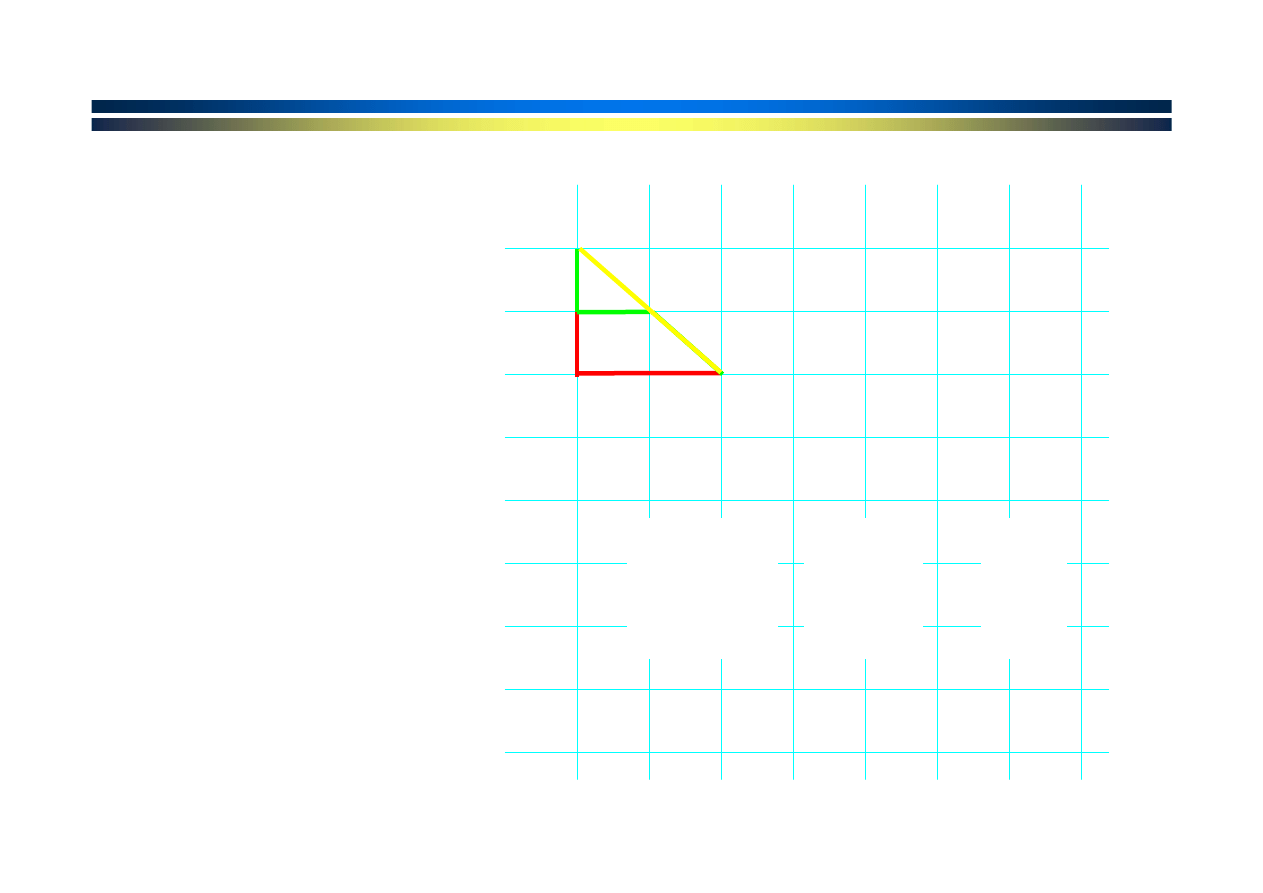
Znaki sekwencji
ułożone wzdłuż
dwu-wymiarowej
siatki
Węzły siatki
znajdują
się
między znakami
Programowanie dynamiczne
Programowanie dynamiczne
–
–
dopasowanie jako
dopasowanie jako
ś
ś
cie
cie
ż
ż
ka w macierzy
ka w macierzy
G A T A C T A
G
A
T
T
A
C
C
A
Celem jest
znalezienie
optymalnej ścieżki
stąd
dotąd
Programowanie dynamiczne
Programowanie dynamiczne
–
–
dopasowanie jako
dopasowanie jako
ś
ś
cie
cie
ż
ż
ka w macierzy
ka w macierzy
G A T A C T A
G
A
T
T
A
C
C
A
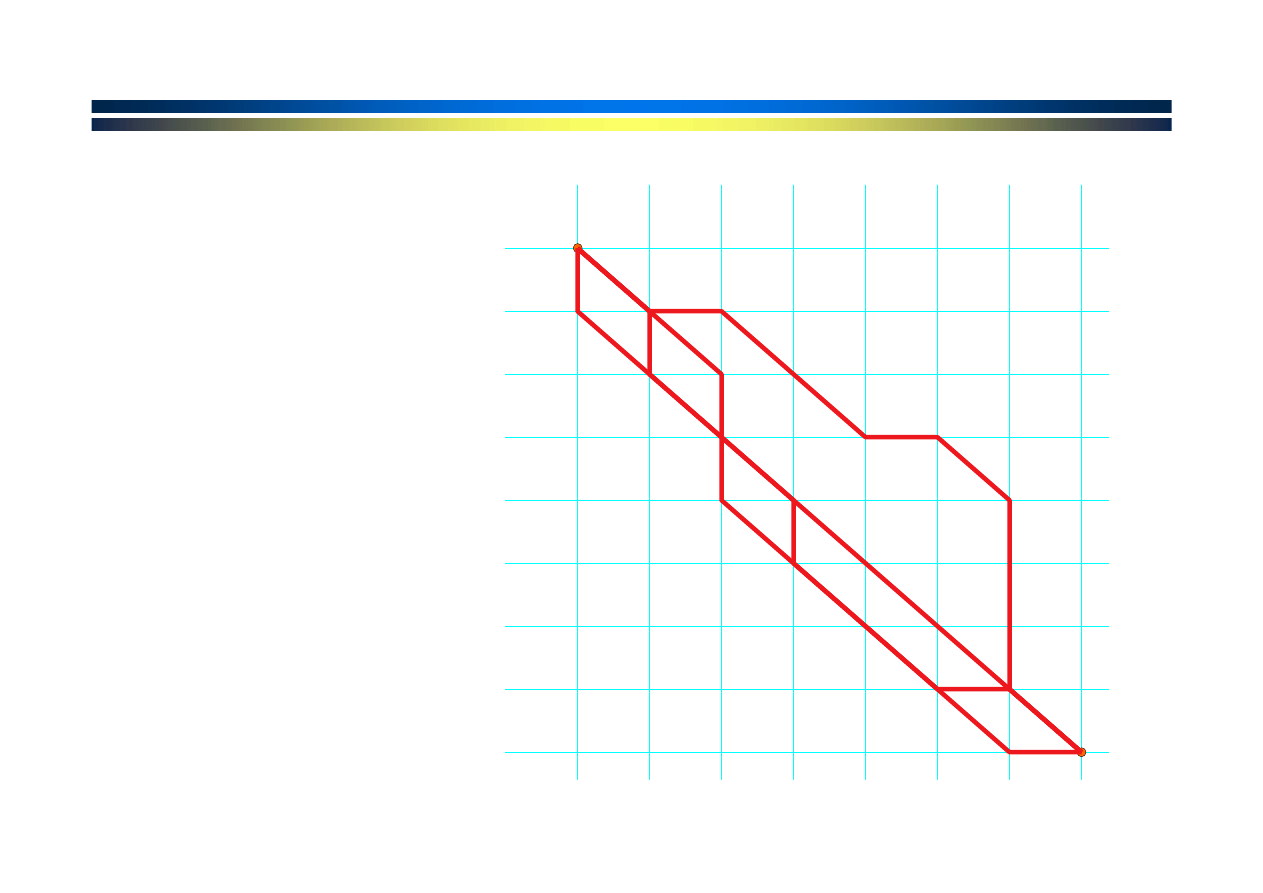
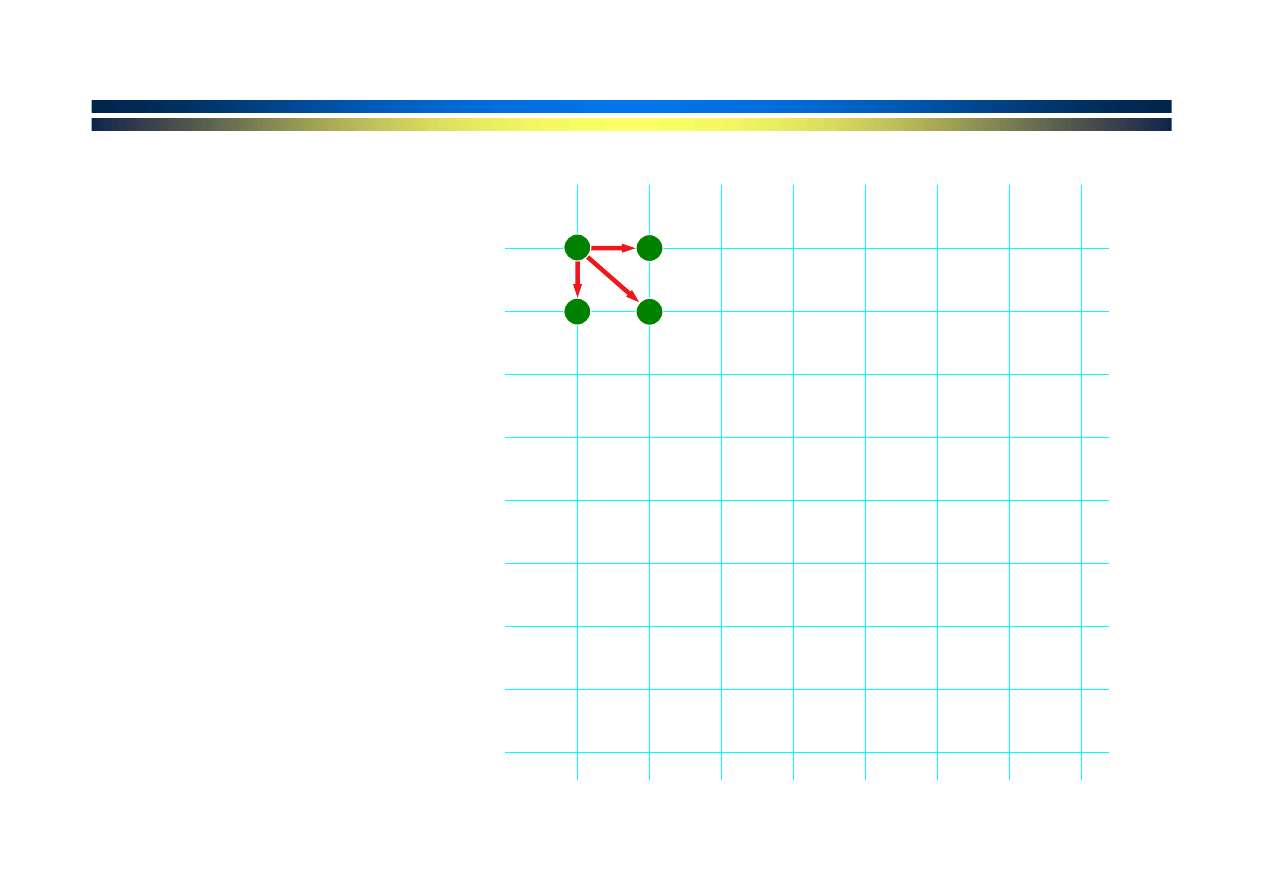
Każda ścieżka
odpowiada
pewnemu
dopasowaniu
Które
dopasowanie
jest optymalne?
Programowanie dynamiczne
Programowanie dynamiczne
–
–
dopasowanie jako
dopasowanie jako
ś
ś
cie
cie
ż
ż
ka w macierzy
ka w macierzy
G A T A C T A
G
A
T
T
A
C
C
A
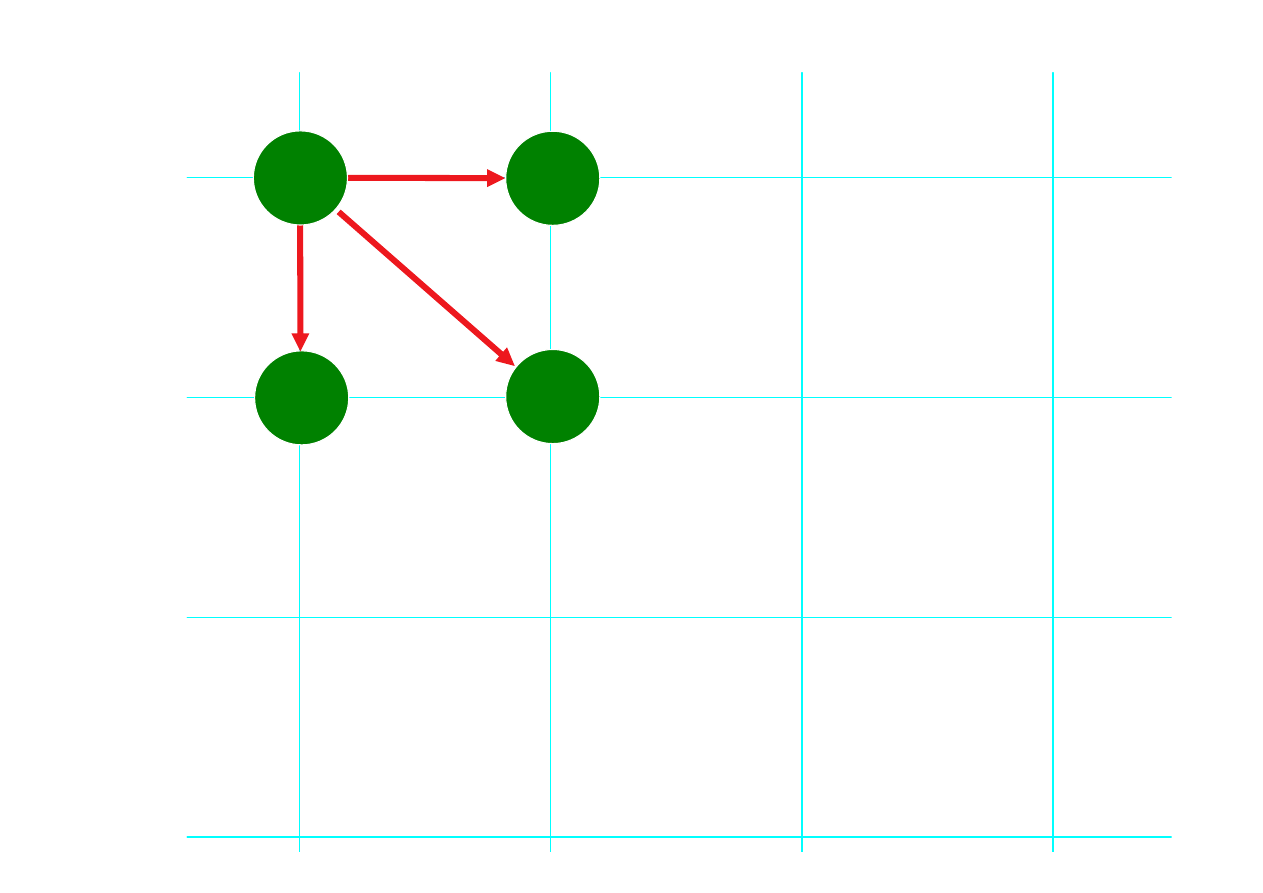
punktacja dla
ścieżki jest sumą
przyrastających
punktacji
krawędzi.
A
porównane z
A
match
= +1
Programowanie dynamiczne
Programowanie dynamiczne
–
–
dopasowanie jako
dopasowanie jako
ś
ś
cie
cie
ż
ż
ka w macierzy
ka w macierzy
G A T A C T A
G
A
T
T
A
C
C
A
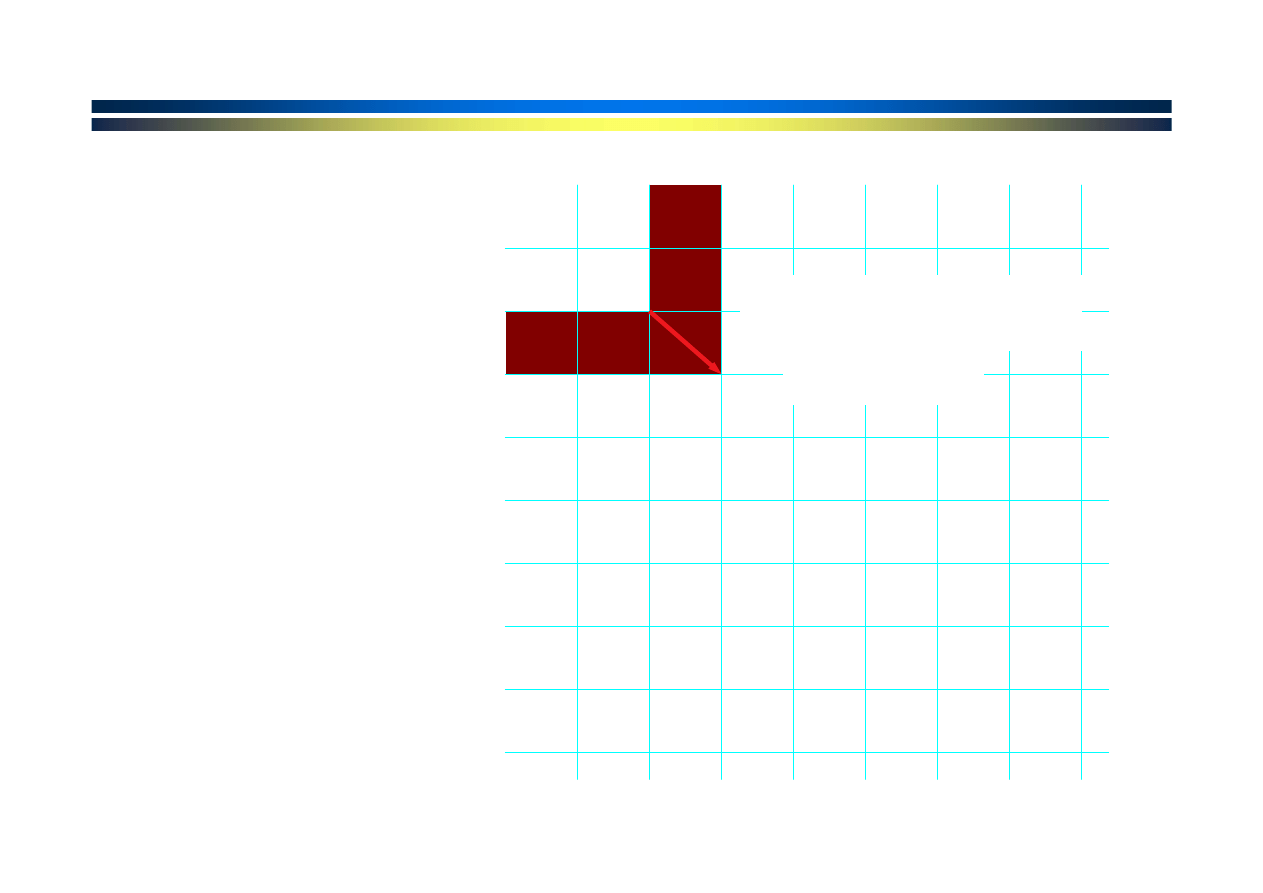
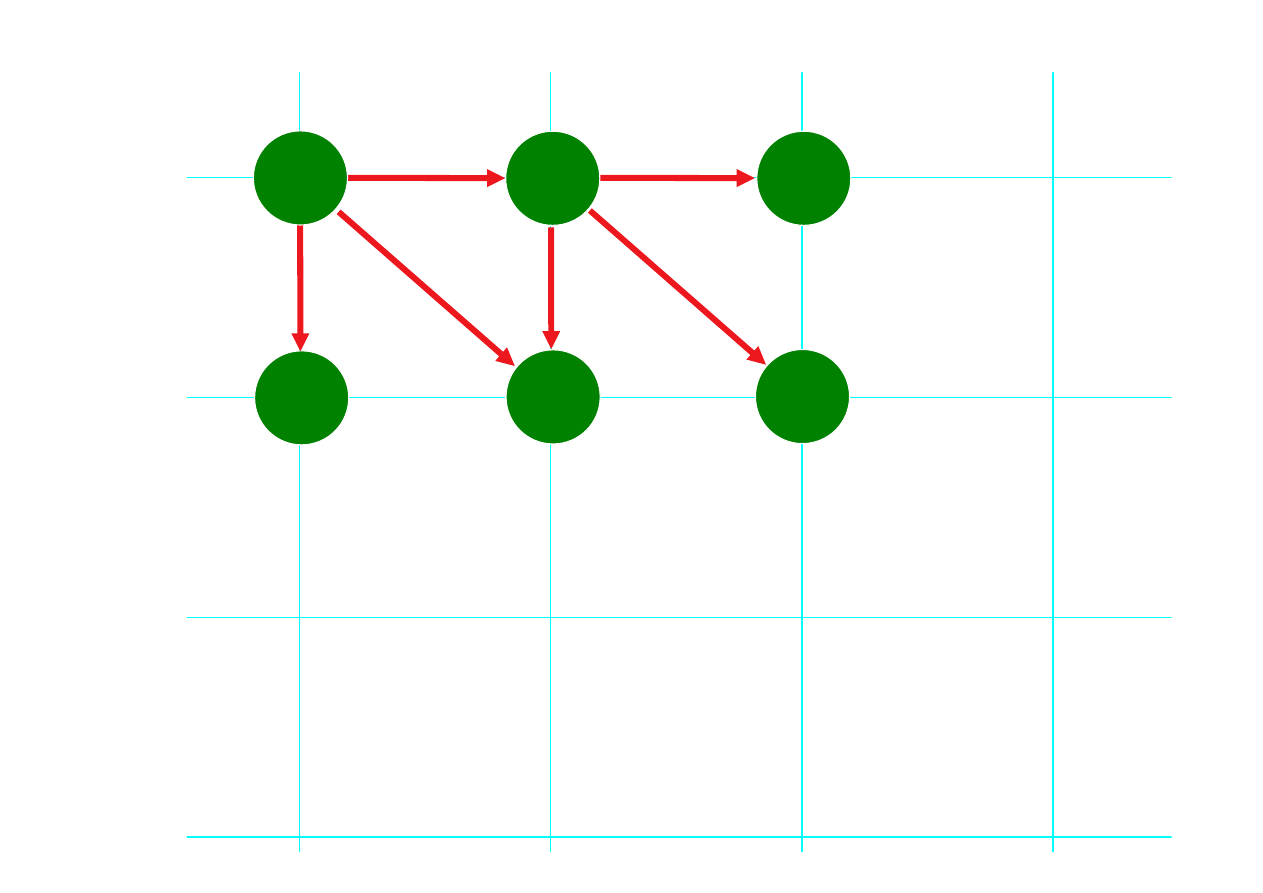
A
porównane z
T
mismatch
= -1
punktacja dla
ścieżki jest sumą
przyrastających
punktacji
krawędzi.
Programowanie dynamiczne
Programowanie dynamiczne
–
–
dopasowanie jako
dopasowanie jako
ś
ś
cie
cie
ż
ż
ka w macierzy
ka w macierzy
G A T A C T A
G
A
T
T
A
C
C
A
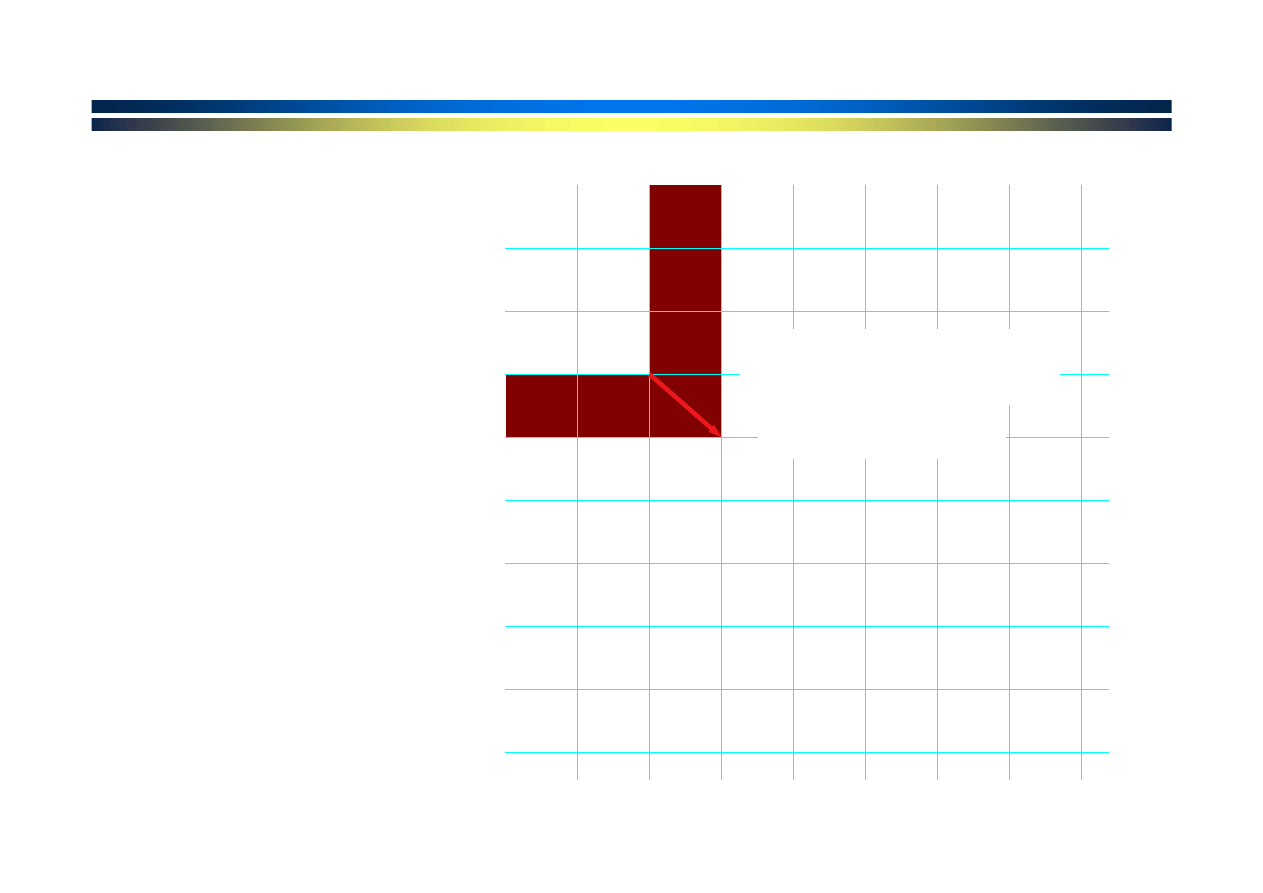
T
porównane z przerwą
gap
= -1
przerwa porównana z
T
punktacja dla
ścieżki jest sumą
przyrastających
punktacji
krawędzi.
Programowanie dynamiczne
Programowanie dynamiczne
–
–
dopasowanie jako
dopasowanie jako
ś
ś
cie
cie
ż
ż
ka w macierzy
ka w macierzy
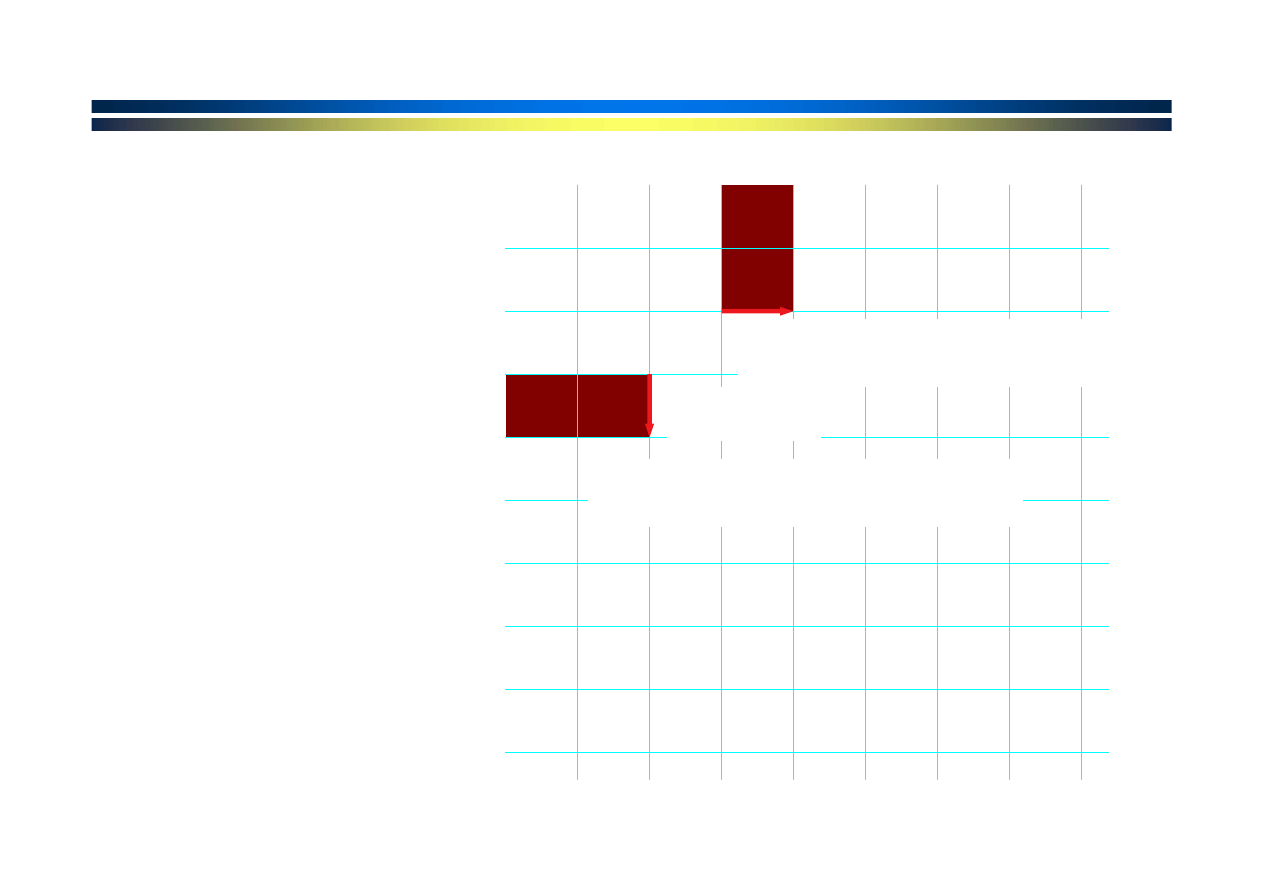
G A T A C T A
G
A
T
T
A
C
C
A
Programowanie dynamiczne
Programowanie dynamiczne
–
–
dopasowanie jako
dopasowanie jako
ś
ś
cie
cie
ż
ż
ka w macierzy
ka w macierzy
Znaczenie punktu w
macierzy:
wszystkie znaki do
tego miejsca są
ze
sobą
porównane,
czego można dokonać
na wiele sposobów
(ścieżek).
Pozycja
“
x
”
oznacza:
przyrównanie
GA
z
GA
x
--GA
GA--
-GA
G-A
GA
GA
G A T A C T A
G
A
T
T
A
C
C
A
Rozszerzanie się
ścieżki i
przyrastanie
punktacji.
0
-1
+1
-1
Programowanie dynamiczne
Programowanie dynamiczne
–
–
dopasowanie jako
dopasowanie jako
ś
ś
cie
cie
ż
ż
ka w macierzy
ka w macierzy
G
G
A
T
A
T
-1
0 -1= -1
-1
0 -1
= -1
+1
0 +
1= +
1
0
G
G
A
T
A
T
-2
-1 -1= -2
-2
-1
-1=
-2
-1
+1
-1
0 -1= -1
0 -1
= -1
0 +
1= +
1
-1 -1
= -2
-2
0
-2
-1
-1=
-2
G
G
A
T
A
T
-2
-1 -1= -2
0
+2
+1 +
1= +
2
+1-1
= 0
0
0
+1 -1= 0
-1
+1
-1
0 -1= -1
0 -1
= -1
0 +
1= +
1
-2
G
G
A
T
A
T
-2
-1 -1= -2
0
+1 -1= 0
-1
+1
0 -1= -1
0 -1
= -1
0 +
1= +
1
0
+2
+1 +
1= +
2
+1-1
= 0
0
-2
-1 -1= 0
-1
-2
-1 -
1= -2
-1-1
= -2
-2
G A T A C T A
G
A
T
T
A
C
C
A
Rozszerzanie się
ścieżki i
przyrastanie
punktacji.
0
-1
+1
-1
Programowanie dynamiczne
Programowanie dynamiczne
–
–
dopasowanie jako
dopasowanie jako
ś
ś
cie
cie
ż
ż
ka w macierzy
ka w macierzy
G A T A C T A
G
A
T
T
A
C
C
A
0
+1
-1
-2
-2
-1
Wybierana jest
najlepsza ścieżka
prowadząca do
każdego punktu
na siatce.
Rozszerzanie się
ścieżki i
przyrastanie
punktacji.
Programowanie dynamiczne
Programowanie dynamiczne
–
–
dopasowanie jako
dopasowanie jako
ś
ś
cie
cie
ż
ż
ka w macierzy
ka w macierzy
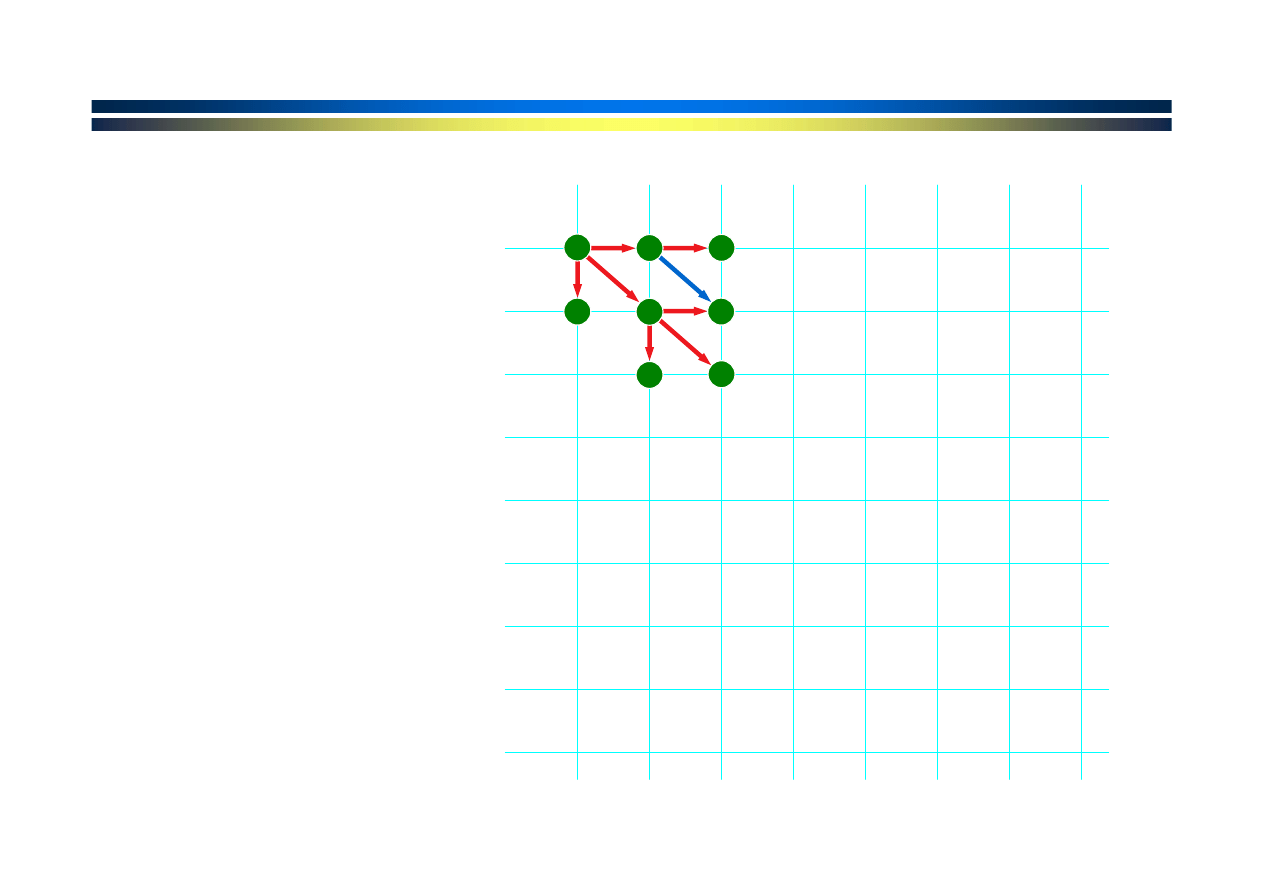
G A T A C T A
G
A
T
T
A
C
C
A
0
-1
-2
0
+2
+1
-1
-2
0
Wybierana jest
najlepsza ścieżka
prowadząca do
każdego punktu
na siatce.
Rozszerzanie się
ścieżki i
przyrastanie
punktacji.
Programowanie dynamiczne
Programowanie dynamiczne
–
–
dopasowanie jako
dopasowanie jako
ś
ś
cie
cie
ż
ż
ka w macierzy
ka w macierzy
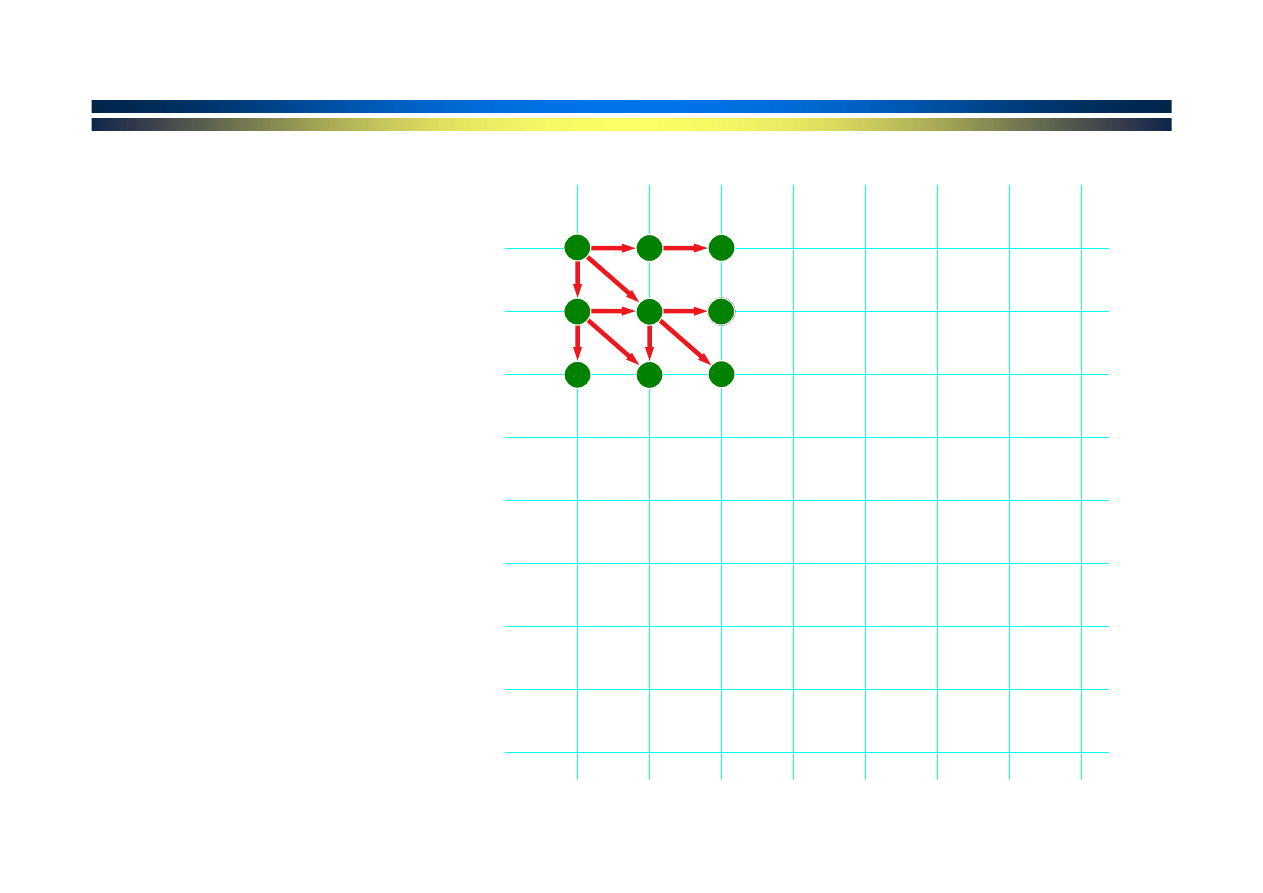
G A T A C T A
G
A
T
T
A
C
C
A
0
-2
0
+2
+1
-1
-2
0
-2
-1
Wybierana jest
najlepsza ścieżka
prowadząca do
każdego punktu
na siatce.
Rozszerzanie się
ścieżki i
przyrastanie
punktacji.
Programowanie dynamiczne
Programowanie dynamiczne
–
–
dopasowanie jako
dopasowanie jako
ś
ś
cie
cie
ż
ż
ka w macierzy
ka w macierzy
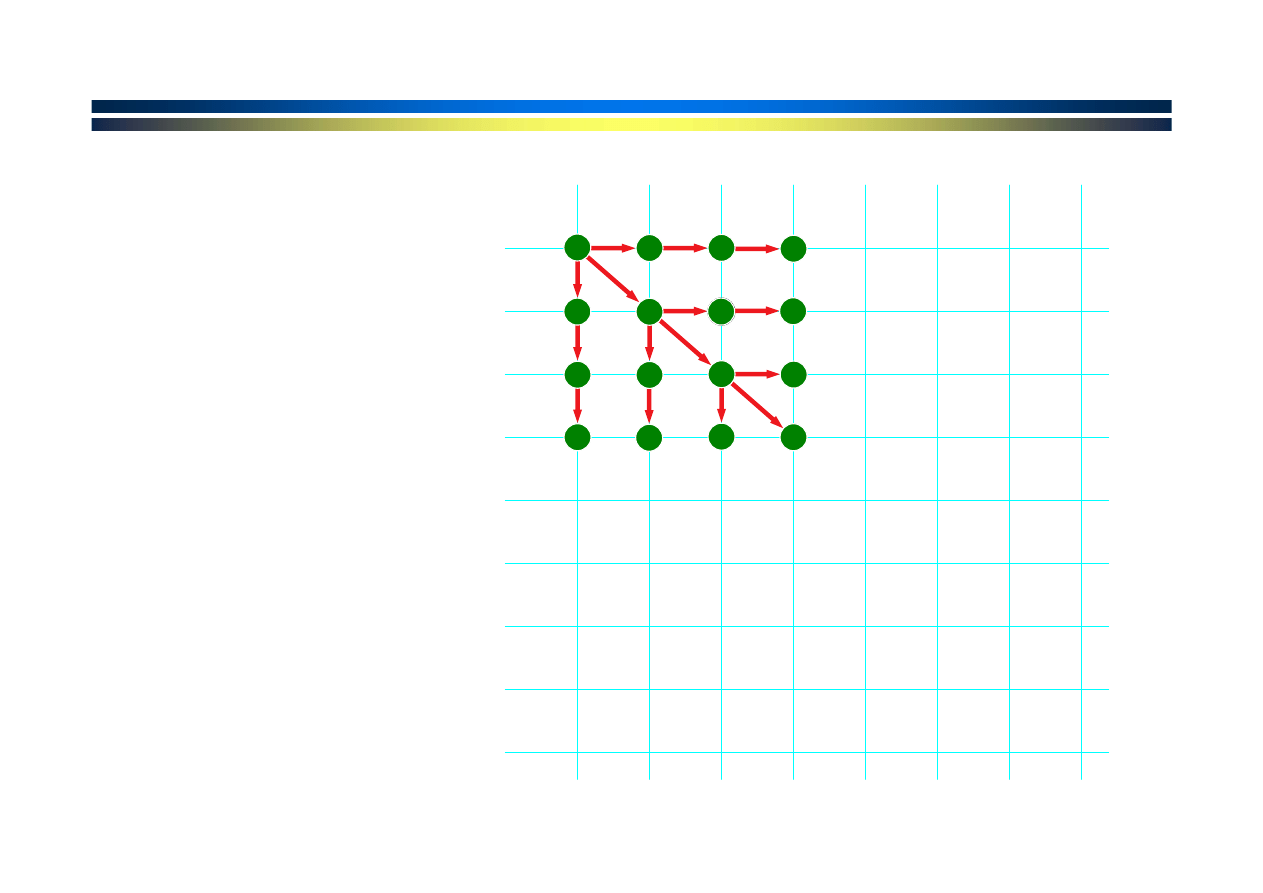
G A T A C T A
G
A
T
T
A
C
C
A
0
+1
-1
-2
-1
-3
-2
-3
-2
+3
-1
-1
0
0
+1
+1
+2
Wybierana jest
najlepsza ścieżka
prowadząca do
każdego punktu
na siatce.
Rozszerzanie się
ścieżki i
przyrastanie
punktacji.
Programowanie dynamiczne
Programowanie dynamiczne
–
–
dopasowanie jako
dopasowanie jako
ś
ś
cie
cie
ż
ż
ka w macierzy
ka w macierzy
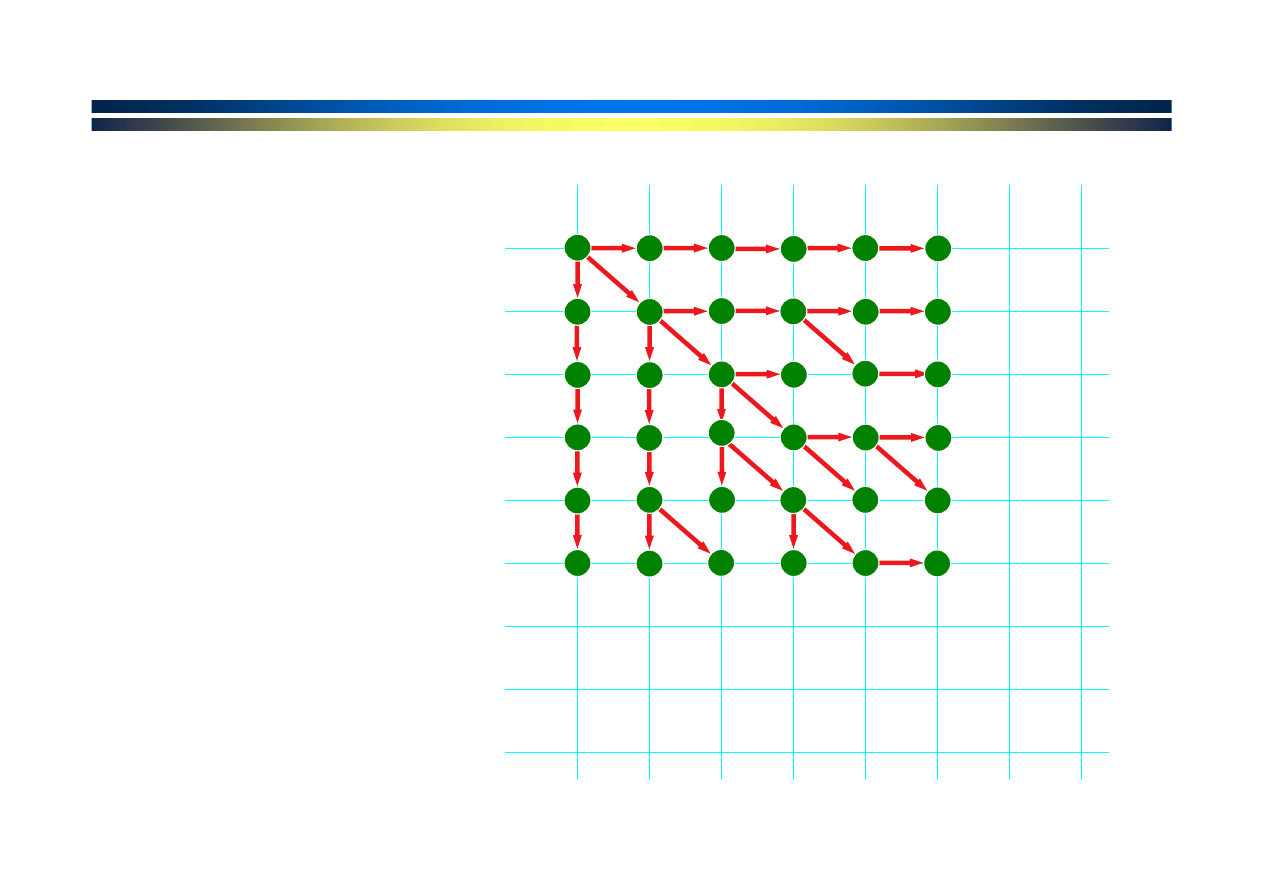
G A T A C T A
G
A
T
T
A
C
C
A
0
+1
-1
-1
-2
-2
0
0
+1
+2
-5
-4
-5
-4
-3
-3
-1
-3
-2
-1
0
+1
+2
0
+1
-1
+2
-3
-1
-2
+1
+3
+2
+1
+2
+3
Wybierana jest
najlepsza ścieżka
prowadząca do
każdego punktu
na siatce.
Rozszerzanie się
ścieżki i
przyrastanie
punktacji.
Programowanie dynamiczne
Programowanie dynamiczne
–
–
dopasowanie jako
dopasowanie jako
ś
ś
cie
cie
ż
ż
ka w macierzy
ka w macierzy
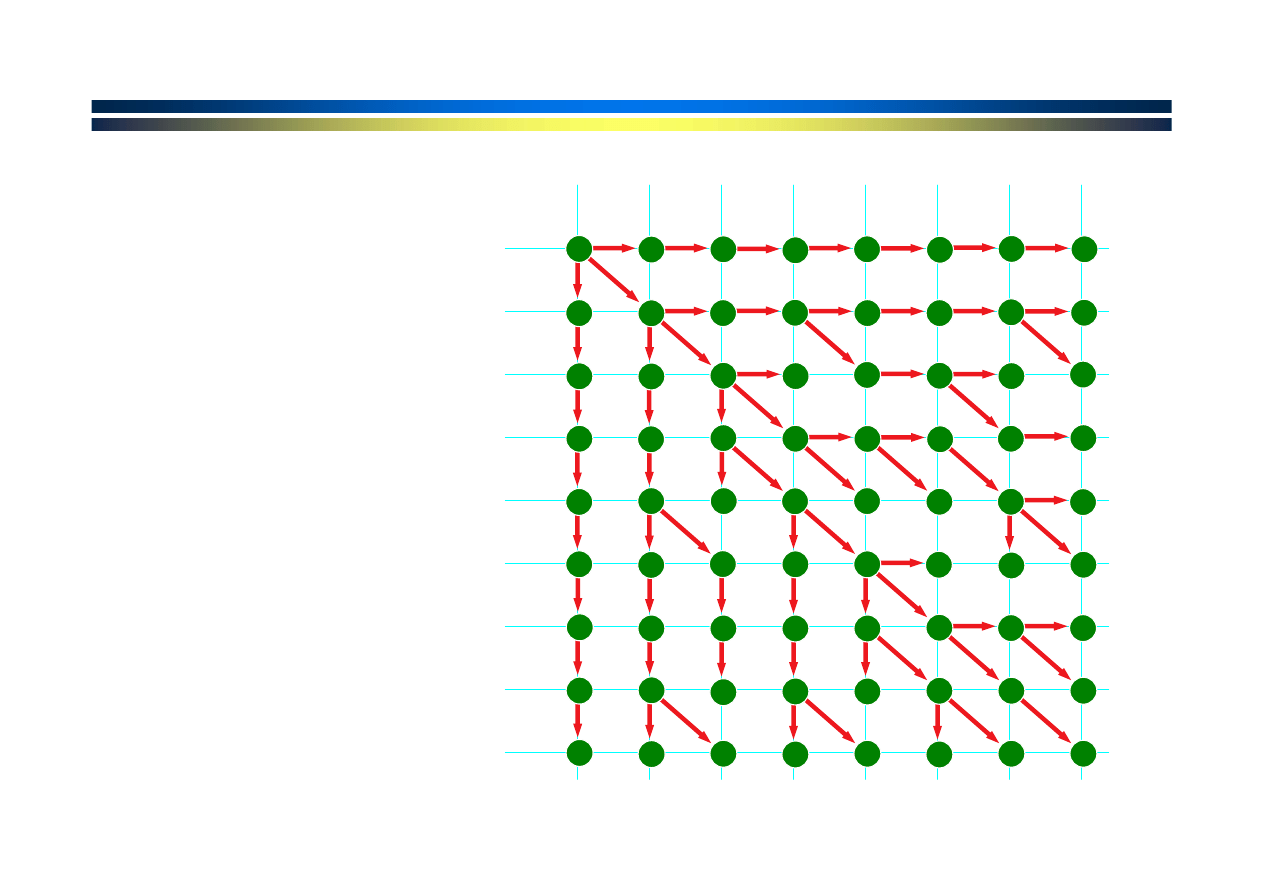
G
G A T A C T A
A
T
T
A
C
C
A
0
+1
-1
-1
-2
-2
0
0
+1
+2
-4
-4
-3
-3
-1
-2
0
+2
0
+1
-1
+2
-2
+2
+1
+2
+3
-8
-7
-6
-5
-7
-6
-5
-5
-3
-2
-3
-4
-1
-1
0
+1
+1
+1
+3
+2
-4
-6
-3
-2
-3
-1
-4
-5
+1
+3
+1
0
+2
+4
+4
+3
+2
+2
+3
-2
0
-1
+2
+2
+3
Wybierana jest
najlepsza ścieżka
prowadząca do
każdego punktu
na siatce.
Rozszerzanie się
ścieżki i
przyrastanie
punktacji.
Programowanie dynamiczne
Programowanie dynamiczne
–
–
dopasowanie jako
dopasowanie jako
ś
ś
cie
cie
ż
ż
ka w macierzy
ka w macierzy
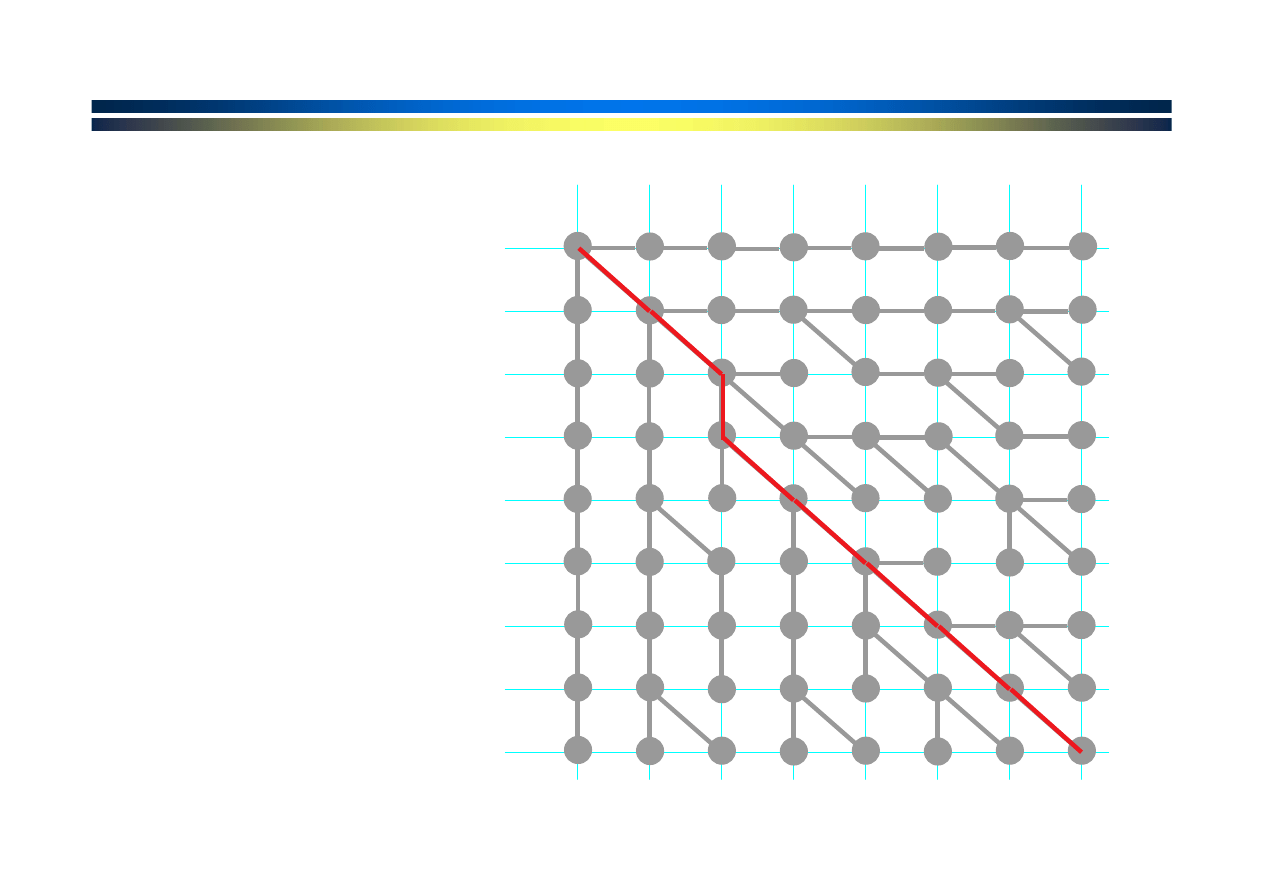
G A T A C T A
G
A
T
T
A
C
C
A
Cofanie się
do
tyłu i wybór
optymalnej
ścieżki i
dopasowania.
0
+1
-1
-1
-2
-2
0
0
+1
+2
-4
-4
-3
-3
-1
-2
0
+2
0
+1
-1
+2
-2
+2
+1
+2
+3
-8
-7
-6
-5
-7
-6
-5
-5
-3
-2
-3
-4
-1
-1
0
+1
+1
+1
+3
+2
-4
-6
-3
-2
-3
-1
-4
-5
+1
+3
+1
0
+2
+4
+4
+3
+2
+2
+3
-2
0
-1
+2
+2
+3
Programowanie dynamiczne
Programowanie dynamiczne
–
–
dopasowanie jako
dopasowanie jako
ś
ś
cie
cie
ż
ż
ka w macierzy
ka w macierzy
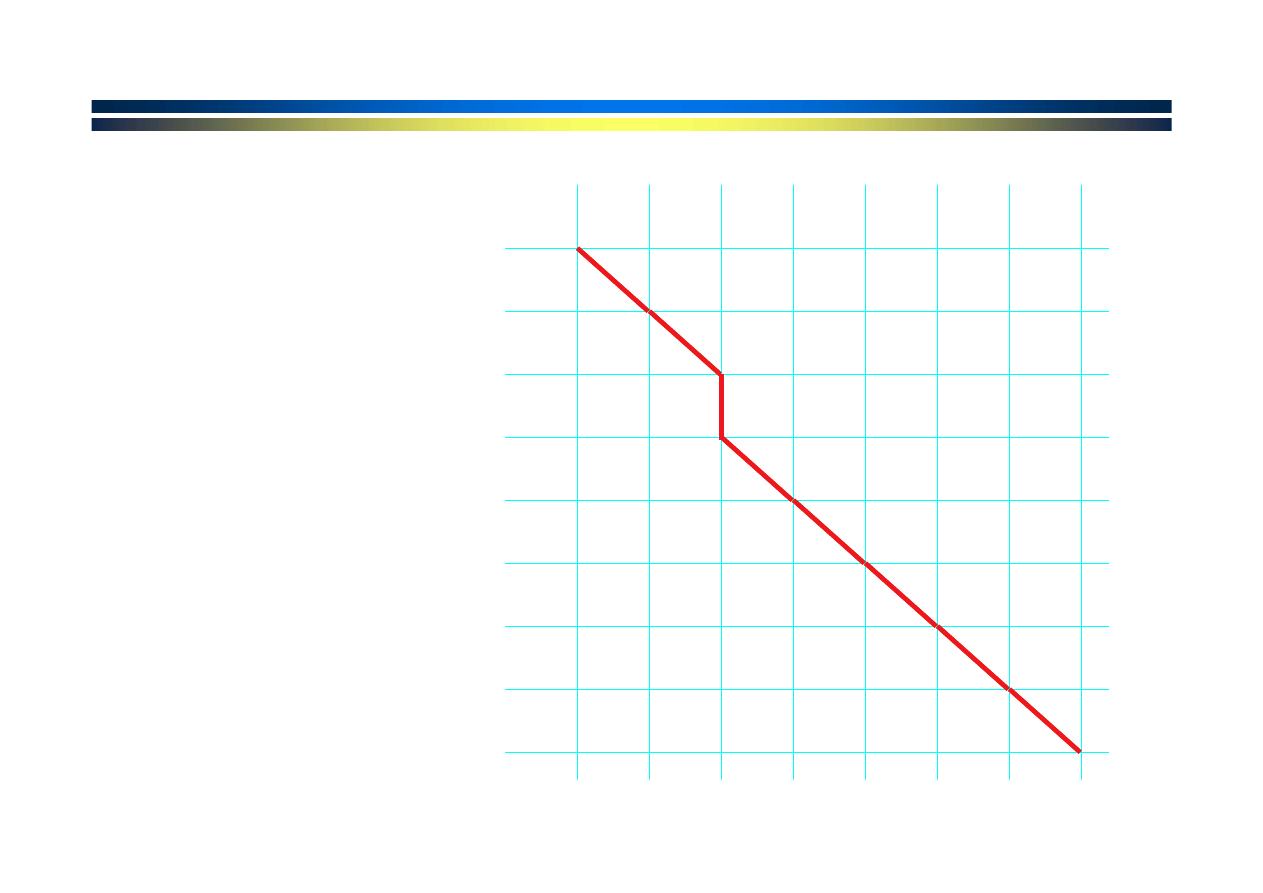
G A T A C T A
G
A
T
T
A
C
C
A
Uzyskane
dopasowanie
A
A
-
T
T
T
A
A
C
C
T
C
A
A
G
G
Programowanie dynamiczne
Programowanie dynamiczne
–
–
dopasowanie jako
dopasowanie jako
ś
ś
cie
cie
ż
ż
ka w macierzy
ka w macierzy

Optimalne
dopasowanie
globalne
Optymal ne
dopasowanie
lolalne
dopasowanie globalne i lokalne
dopasowanie globalne i lokalne
dopasowanie globalne
(Needleman & Wunsch, 1970)
–
przyrównuje sekwencje na
całej długości; wykorzystuje tak dużo znaków, jak to jest tylko możliwe.
dopasowanie lokalne
(
Smith & Waterman
, 1981)
–
przyrównuje fragmenty sekwencji,
które wykazują
największe podobieństwo; poszukuje najlepiej pasujących regionów;
znajduje regiony konserwowane. Gdy obliczana wartość
punktacji w macierzy jest
mniejsza od zera, to wartość
ta jest ustawiana na zero, a dopasowanie ulega
zakończeniu do tego miejsca i rozpoczynany jest nowe` dopasowanie od nowego
miejsca
LGPSSKQTGKGS-SRIWDN
| | ||| | |
LN-ITKSAGKGAIMRLGDA
-------TGKG--------
|||
-------AGKG--------
sekwencje o podobnej
długości, blisko
spokrewnione
sekwencje o różnych
długościach, posiadające
regiony
i domeny zachowane,
podobne tylko
w niektórych obszarach

System punktacji
System punktacji
Zaawansowany system punktacji (nadawanie różnych wag dla
niedopasowań
i przerw w zależnosci
od ich długości):
Macierze podstawień
aminokwasów (PAM, BLOSUM)
Macierze podstawień
nukleotydów
System punktacji dla przerw: gap penalties, affine gap penalty
Prosty system punktacji:
match
: +1
+1
mismatch
: -1
0
gap
: -1
-1

Typowe systemy punktacji
Typowe systemy punktacji
z
sekwencje DNA
–
Match = +1
–
Mismatch = -3
–
Gap penalty = -5
–
Gap extension penalty = -2
z
sekwencje białkowe
–
Macierz Blossum62
–
Gap open penalty = -11
–
Gap extension = -1

Istotno
Istotno
ść
ść
dopasowania
dopasowania
Czy punktacja dopasowanie jest znacząco większa od punktacji
oczekiwanej dla dopasowania losowych sekwencji o tej samej
długości i składzie?
3 > Z
–
brak homologii
3 < Z < 6
–
istnieje homologia
Z > 6
–
silna homologia
Tworzenie metodą
Monte Carlo
losowych(-ej) sekwencji (o tej samej
długości i składzie co rzeczywiste).
Przyrównanie losowych(-ej) sekwencji (powtórzenie 100-1000 razy) przy
tych samych parametrach.
Określenie rozkładu punktacji, średniej i odchylenie standardowego (SD).
Wyliczenie Z-score: Z = (score
obs
–
score
ran
)/SD
ran
Rozkład „score-ów”
nie jest normalny i dlatego nie można przekształcić
Z-score
na prawdopodobieństwo.
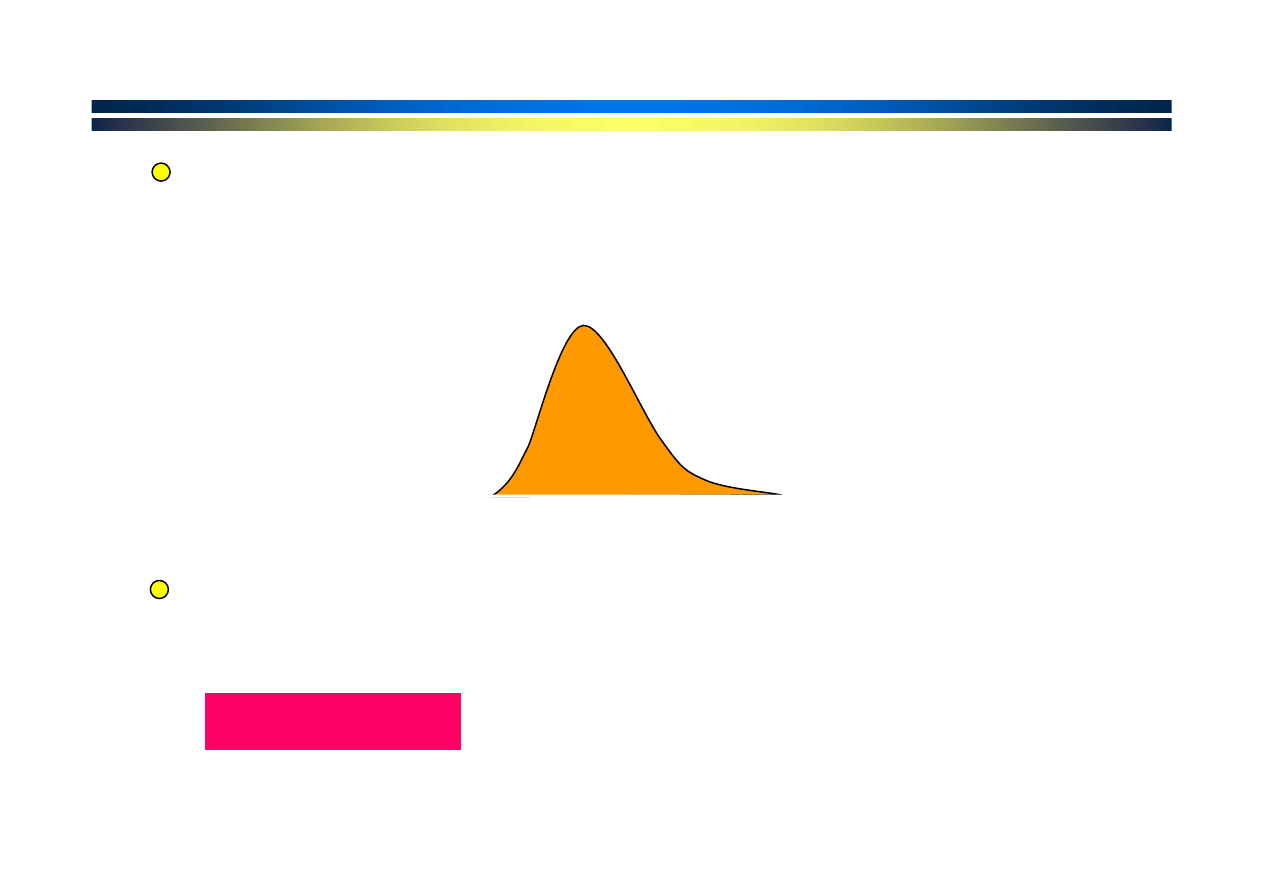
Istotno
Istotno
ść
ść
dopasowania
dopasowania
Wykres zależności logarytmu ułamka dopasowań
z punktacją
S równą
lub większą
od wartości punktacji S’
Określenie E-value –
Oczekiwana liczba przypadkowych dopasowań
z punktacją
większą
niż
obserwowana
Dla dopasowań
lokalnych rozkład maksymalnych „scorów”
dopasowania
dla sekwencji losowych przyjmuje rozkład wartości ekstremalnych
(extreme
values
distribution)(Karlin
i Altschul
1990).
S’
Log
p(S>=S’)
S
e
Kmn
E
λ
−
⋅
=
Oczekiwana (wg rozkładu prawdopodobieństwa)
liczba dopasowań
z punktacją
równą
przynajmniej S
'
2
S
mn
E
−
=
2
ln
ln
'
K
S
S
−
=
λ
!
a
E
e
a
E
−
Bit score-
znormalizowana punktacja uwzględniająca
warunki jego naliczania i przyjęte systemy punktacji
(parametry lambda i K)
Prawdopodobieństwo
znalezienia dokładnie a
dopasowań
o punktacji >= S:
Prawdopodobieństwo
znalezienia przynajmniej 1
dopasowania o punktacji >=S
E
e
p
−
−
= 1
Jeżeli spodziewamy się
znaleźć
przynajmniej 3
dopasowania o punktacji >= S, to
prawdopodobieństwo tego że znajdziemy co
najmniej jedno wynosi 0,95. Programy z grupy
BLAST posługują
się
wartością
E zamiast
bezpośrednim prawdopodobieństwem ze względu
na łatwiejsze rozróżnienie

dopasowanie wielu sekwencji (MSA)
dopasowanie wielu sekwencji (MSA)
przyrównanie (porównanie) wielu (co najmniej trzech) sekwencji
HBB_HUMAN --------VHLTPEEKSAVTALWGKVN--VDEVGGEALGRLLVVYPWTQRFFESFGDLST
HBB_HORSE --------VQLSGEEKAAVLALWDKVN--EEEVGGEALGRLLVVYPWTQRFFDSFGDLSN
HBA_HUMAN ---------VLSPADKTNVKAAWGKVGAHAGEYGAEALERMFLSFPTTKTYFPHF-DLS-
HBA_HORSE ---------VLSAADKTNVKAAWSKVGGHAGEYGAEALERMFLGFPTTKTYFPHF-DLS-
GLB5_PETMA PIVDTGSVAPLSAAEKTKIRSAWAPVYSTYETSGVDILVKFFTSTPAAQEFFPKFKGLTT
MYG_PHYCA ---------VLSEGEWQLVLHVWAKVEADVAGHGQDILIRLFKSHPETLEKFDRFKHLKT
LGB2_LUPLU --------GALTESQAALVKSSWEEFNANIPKHTHRFFILVLEIAPAAKDLFSFLKGTSE
*: : : * . : .: * :
* : .
HBB_HUMAN PDAVMGNPKVKAHGKKVLGAFSDGLAHLDN-----LKGTFATLSELHCDKLHVDPENFRL
HBB_HORSE PGAVMGNPKVKAHGKKVLHSFGEGVHHLDN-----LKGTFAALSELHCDKLHVDPENFRL
HBA_HUMAN ----HGSAQVKGHGKKVADALTNAVAHVDD-----MPNALSALSDLHAHKLRVDPVNFKL
HBA_HORSE ----HGSAQVKAHGKKVGDALTLAVGHLDD-----LPGALSNLSDLHAHKLRVDPVNFKL
GLB5_PETMA ADQLKKSADVRWHAERIINAVNDAVASMDDT--EKMSMKLRDLSGKHAKSFQVDPQYFKV
MYG_PHYCA EAEMKASEDLKKHGVTVLTALGAILKKKGH-----HEAELKPLAQSHATKHKIPIKYLEF
LGB2_LUPLU VP--QNNPELQAHAGKVFKLVYEAAIQLQVTGVVVTDATLKNLGSVHVSKG-VADAHFPV
. .:: *. : . : *. * . : : .
HBB_HUMAN LGNVLVCVLAHHFGKEFTPPVQAAYQKVVAGVANALAHKYH------
HBB_HORSE LGNVLVVVLARHFGKDFTPELQASYQKVVAGVANALAHKYH------
HBA_HUMAN LSHCLLVTLAAHLPAEFTPAVHASLDKFLASVSTVLTSKYR------
HBA_HORSE LSHCLLSTLAVHLPNDFTPAVHASLDKFLSSVSTVLTSKYR------
GLB5_PETMA LAAVIADTVAAG---------DAGFEKLMSMICILLRSAY-------
MYG_PHYCA ISEAIIHVLHSRHPGDFGADAQGAMNKALELFRKDIAAKYKELGYQG
LGB2_LUPLU VKEAILKTIKEVVGAKWSEELNSAWTIAYDELAIVIKKEMNDAA---
: : .: ... . :

Dopasowania wielu sekwencji
Dopasowania wielu sekwencji
-
-
zastosowanie
zastosowanie
Określanie powiązań
filogenetycznych między sekwencjami
Poszukiwanie odległych homologów
Poszukiwanie wspólnych, konserwowanych wzorów, motywów
i domen w sekwencjach, odpowiedzialnych za odpowiednie
funkcje biochemiczne lub strukturę
przestrzenną.
Grupowanie białek w rodziny o wspólnej funkcji biochemicznej
lub historii ewolucyjnej. Identyfikowanie członków rodzin białek.
Identyfikowanie zachodzących fragmentów sekwencji powstałych
w wyniku losowego sekwencjonowania genomów i ułatwienie ich
składania w jedną
całą
sekwencję.
Najbardziej wiarygodny dla sekwencji o podobnej długości
i posiadających zachowanie regiony.

Dopasowania wielu sekwencji a analizy filogenetyczne
Dopasowania wielu sekwencji a analizy filogenetyczne
sekw1
N
F
L
AWSQ
G
A
sekw2
N
F
I
AWSQ
G
A
sekw3
N
F
I
AWTQ
-
A
sekw4
N
-
I
AWSQ
G
A
N
-
I
AWSQ
G
A
N
F
L
AWSQ
G
A
N
F
I
AWSQ
G
A
N
F
I
AWTQ
-
A
+
F
I
->
L
-
G

Dopasowania wielu sekwencji
Dopasowania wielu sekwencji
-
-
metody
metody
Programowanie dynamiczne (PD) -
zbyt skomplikowane dla wielu
sekwencji; stosowany dla niewielu krótkich sekwencji
program MSA
(dopasowanie globalne)
Progresywne dopasowanie globalne (hierarchiczne)
programy: CLUSTALW, CLUSTALX
Metody iteracyjne
programy: MultAlin, PRRP, DIALIGN,
SAGA (algorytm genetyczny)
Metody aproksymacyjne:
Dopasowanie wielu sekwencji i PD
Dopasowanie wielu sekwencji i PD
-
-
z
z
ł
ł
o
o
ż
ż
ono
ono
ść
ść
problemu
problemu
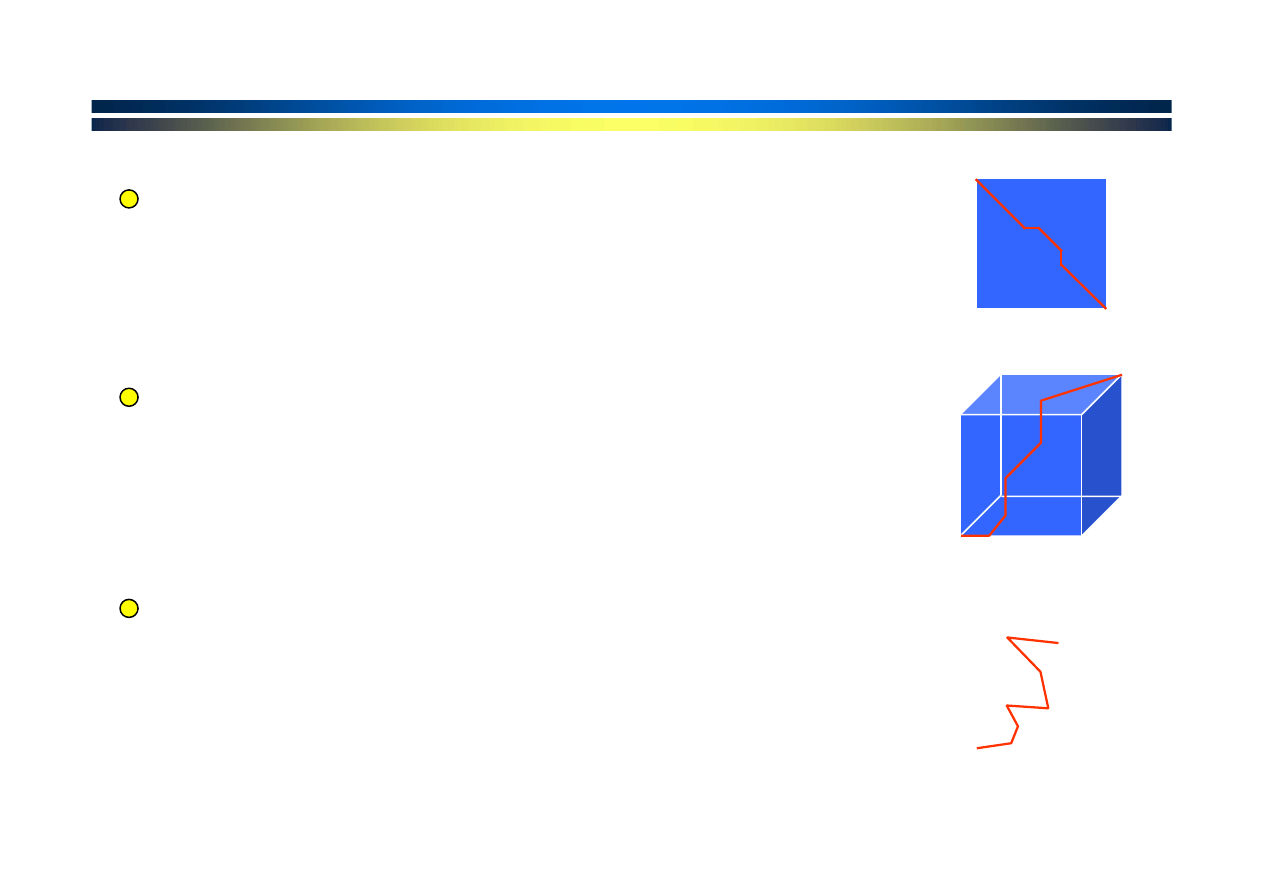
Optymalne dopasowanie dwóch sekwencji przy pomocy
programowania dynamicznego -
macierz punktacji
w kwadracie, wymagany czas: L
2
; L -
długość
sekwencji
Optymalne dopasowanie trzech sekwencji przy pomocy
programowania dynamicznego -
macierz punktacji w
sześcianie; wymagany czas: L
3
Optymalne dopasowanie N sekwencji przy pomocy
programowania dynamicznego -
macierz punktacji w N
wymiarach: wymagany czas: L
N
- rośnie wykładniczo ze
wzrostem liczby sekwencji (N)
Dopasowanie wielu sekwencji
Dopasowanie wielu sekwencji
-
-
trzy sekwencje
trzy sekwencje
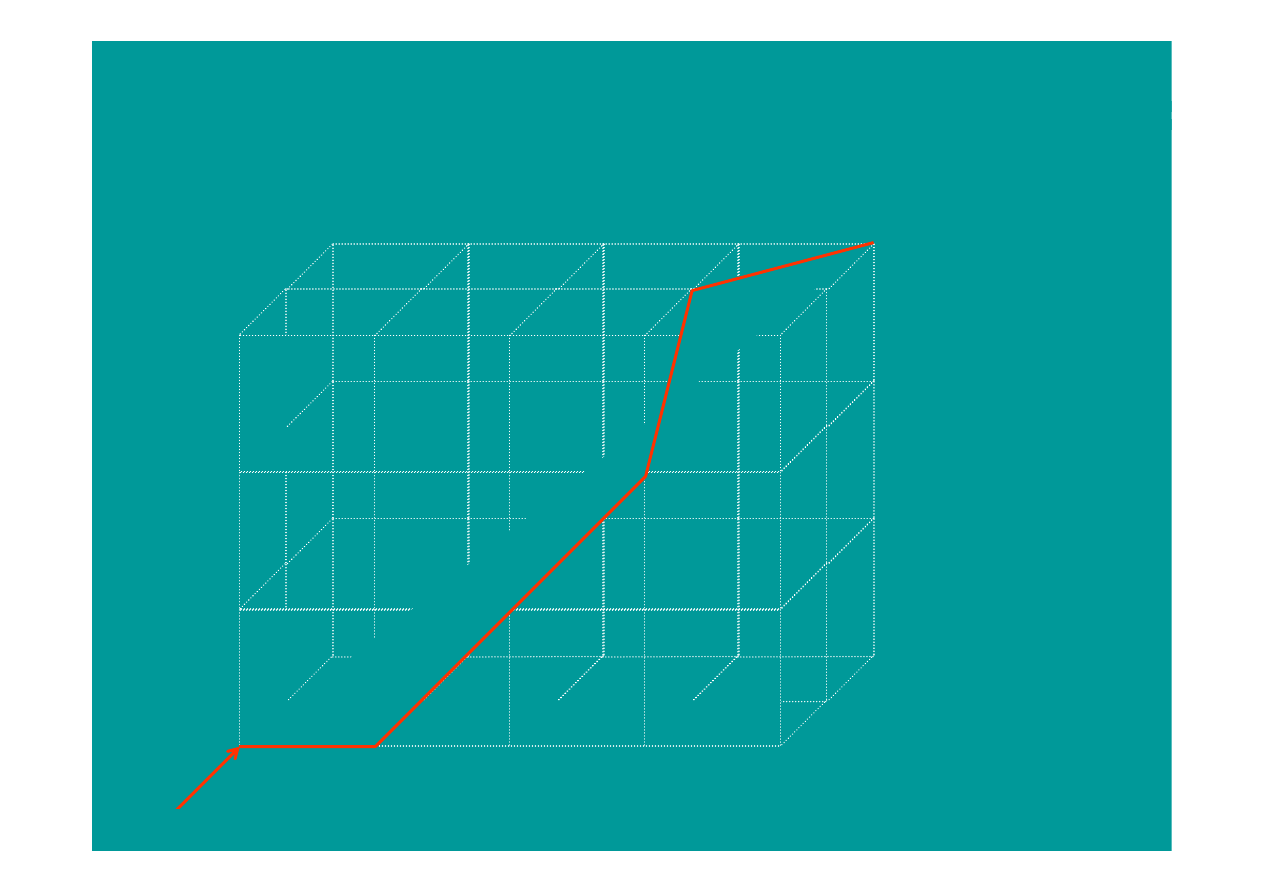
V
S
N
S
S
N
A
A
S
V S N - S
- S N A
- - - A S
start
Szukanie optymalnego dopasowania w objętości sześcianu.
Dopasowanie wielu sekwencji i PD
Dopasowanie wielu sekwencji i PD
–
–
program MSA
program MSA
Liczenie w objętości (w przestrzeni N-wymiarowej) punktacji dla
wielokrotnego dopasowania.
Optymalne dopasowanie to takie, który posiada najlepszy SP score.
Punktacja dla wielokrotnego dopasowania jest sumą
punktacji
uzyskanych dla porównania wszystkich par sekwencji w wielokrotnym
alignment-cie
(miara SP –
sum of
pairs).

Progresywne
Progresywne
dopasowanie
dopasowanie
globalne
globalne
-
-
program CLUSTALW
program CLUSTALW
>HBB_HUMAN
VHLTPEEKSAVTALWGKVNVDEVGGEALGRLLVVYPWTQRFFESFGDLSTPDAVMGNPKVKAHGKKVLGAFSDGLAHLDNLKGTFA
TLSELHCDKLHVDPENFRLLGNVLVCVLAHHFGKEFTPPVQAAYQKVVAGVANALAHKYH*
>HBB_HORSE
VQLSGEEKAAVLALWDKVNEEEVGGEALGRLLVVYPWTQRFFDSFGDLSNPGAVMGNPKVKAHGKKVLHSFGEGVHHLDNLKGTFA
ALSELHCDKLHVDPENFRLLGNVLVVVLARHFGKDFTPELQASYQKVVAGVANALAHKYH*
>HBA_HUMAN
VLSPADKTNVKAAWGKVGAHAGEYGAEALERMFLSFPTTKTYFPHFDLSHGSAQVKGHGKKVADALTNAVAHVDDMPNALSALSDL
HAHKLRVDPVNFKLLSHCLLVTLAAHLPAEFTPAVHASLDKFLASVSTVLTSKYR*
>HBA_HORSE
VLSAADKTNVKAAWSKVGGHAGEYGAEALERMFLGFPTTKTYFPHFDLSHGSAQVKAHGKKVGDALTLAVGHLDDLPGALSNLSDL
HAHKLRVDPVNFKLLSHCLLSTLAVHLPNDFTPAVHASLDKFLSSVSTVLTSKYR*
>MYG_PHYCA
VLSEGEWQLVLHVWAKVEADVAGHGQDILIRLFKSHPETLEKFDRFKHLKTEAEMKASEDLKKHGVTVLTALGAILKKKGHHEAEL
KPLAQSHATKHKIPIKYLEFISEAIIHVLHSRHPGDFGADAQGAMNKALELFRKDIAAKYKELGYQG*
>GLB5_PETMA
PIVDTGSVAPLSAAEKTKIRSAWAPVYSTYETSGVDILVKFFTSTPAAQEFFPKFKGLTTADQLKKSADVRWHAERIINAVNDAVA
SMDDTEKMSMKLRDLSGKHAKSFQVDPQYFKVLAAVIADTVAAGDAGFEKLMSMICILLRSAY*
>LGB2_LUPLU
GALTESQAALVKSSWEEFNANIPKHTHRFFILVLEIAPAAKDLFSFLKGTSEVPQNNPELQAHAGKVFKLVYEAAIQLQVTGVVVT
DATLKNLGSVHVSKGVADAHFPVVKEAILKTIKEVVGAKWSEELNSAWTIAYDELAIVIKKEMNDAA*
Sekwencje globin

•
Porównujemy zestaw 7 sekwencji :HAHU, HBHU,HAHO, HBHO, MYWHP,
PILHB i LGHB
•
Dopasowujemy osobno każdą
możliwą
parę
sekwencji i obliczamy
według pewnego algorytmu wzajemne podobieństwo sekwencji w
obrębie każdej z 21 par
•
Wynik przedstawiamy w macierzy podobieństw
DOPASOWANIA WIELOKROTNE
DOPASOWANIA WIELOKROTNE
(MULTIALIGNMENT)
(MULTIALIGNMENT)
Metoda hierarchiczna
Metoda hierarchiczna
HAHU
HBHU
HAHO
HBHO
MYWHP
PILHB
HBHU
21.1
HAHO
32.9
19.7
HBHO
20.7
39.0
20.4
MYWHP
11.0
9.8
10.3
9.7
PILHB
9.3
8.6
9.6
8.4
7.0
LGHB
7.1
7.3
7.5
7.4
7.3
4.3

Tworzenie drzewa przewodniego
Tworzenie drzewa przewodniego
LGHB
LGHB
PILHB
PILHB
MYWHB
MYWHB
HAHU
HAHU
HAHO
HAHO
HBHU
HBHO
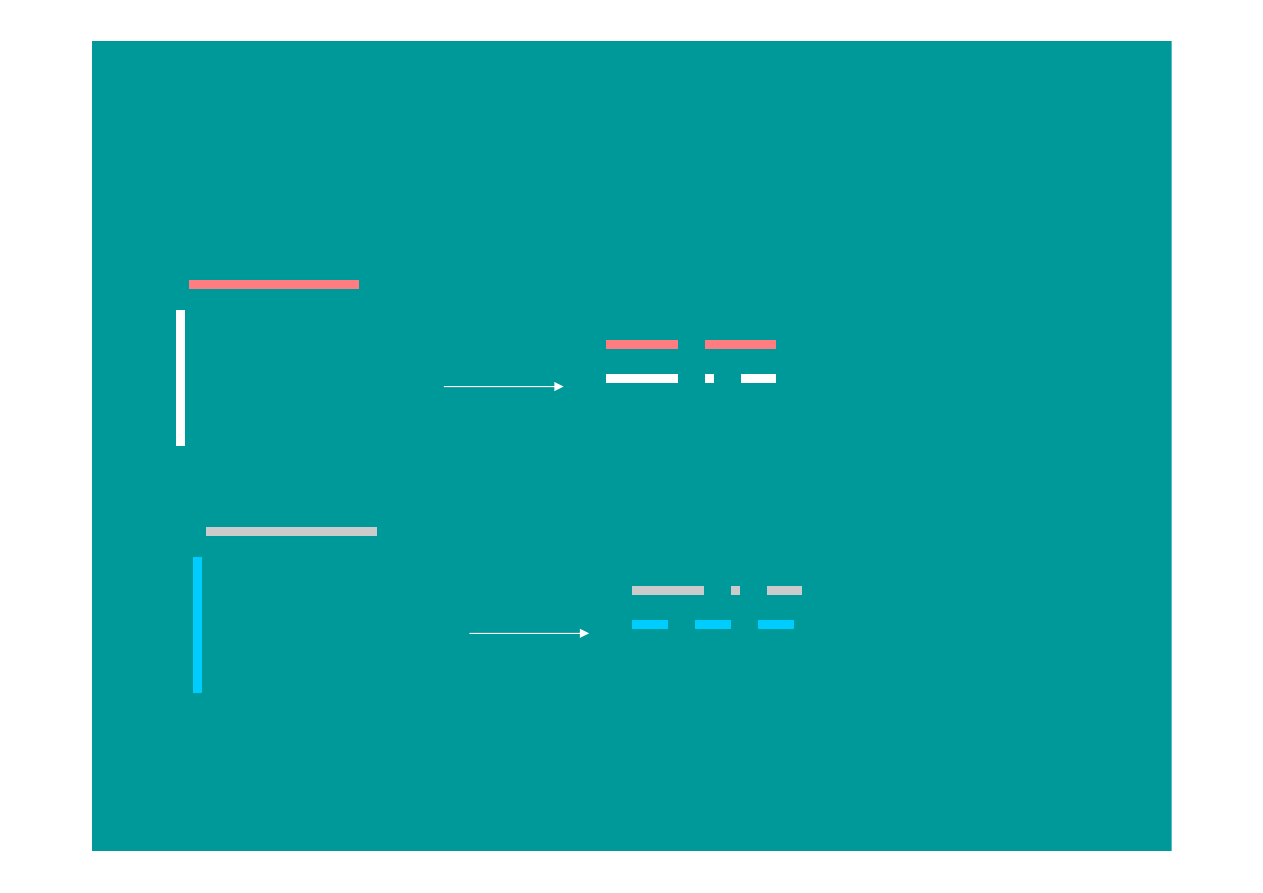
Stopniowe zestawianie sekwencji
Stopniowe zestawianie sekwencji
dopasowanych
dopasowanych
HBHO
HBHU
Programowanie
dynamiczne
dopasowanie
HBHO
HBHU
HAHU
HAHO
Programowanie
dynamiczne
dopasowanie
HAHU
HAHO
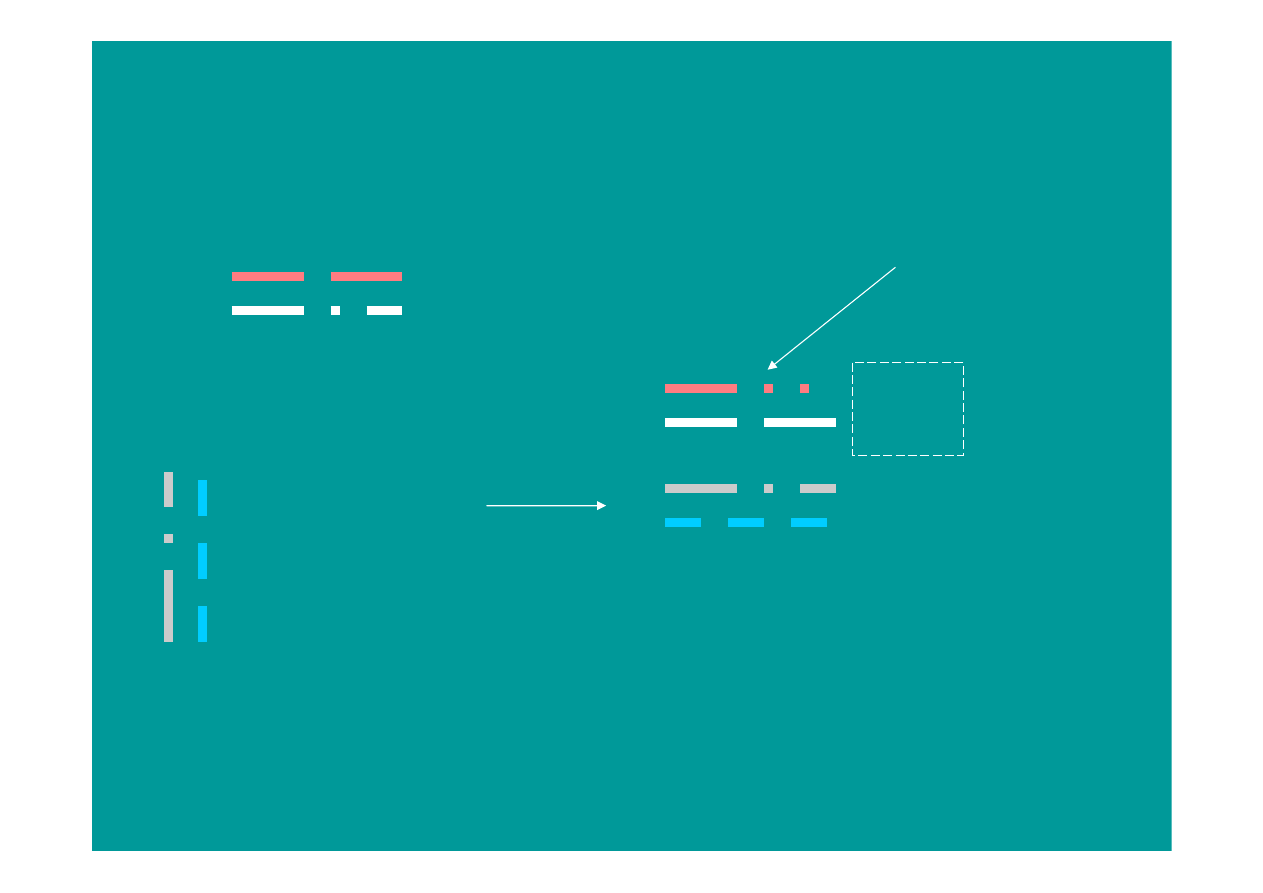
HBHO
HBHU
HAHU
HAHO
Programowanie
dynamiczne
HBHO
HBHU
HAHU
HAHO
Nowa
przerwa
dopasowanie czterech sekwencji
-
Dodawanie kolejnych sekwencji, coraz
bardziej odległych według drzewa
przewodniego

Sekwencyjne przyrównywanie sekwencji, ze względu na podobieństwo opisane na
drzewie: przyrównanie najpierw sekwencji najbardziej podobnych, a następnie
dołączanie do już
utworzonego dopasowania pozostałych najbardziej podobnych
sekwencji wg przewodniego drzewa filogenetycznego. Sekwencje po dopasowaniu są
traktowane jako całość.
HBB_HUMAN VHLTPEEKSAVTALWGKVNVDEVGGEALGRLLVVYPWTQRFFESFGDLSTPDAVMGNPKVKAHGKKVLGAFSDGLAHLDNLK
HBB_HORSE VQLSGEEKAAVLALWDKVNEEEVGGEALGRLLVVYPWTQRFFDSFGDLSNPGAVMGNPKVKAHGKKVLHSFGEGVHHLDNLK
HBB_HUMAN GTFATLSELHCDKLHVDPENFRLLGNVLVCVLAHHFGKEFTPPVQAAYQKVVAGVANALAHKYH
HBB_HORSE GTFAALSELHCDKLHVDPENFRLLGNVLVVVLARHFGKDFTPELQASYQKVVAGVANALAHKYH
HBA_HUMAN VLSPADKTNVKAAWGKVGAHAGEYGAEALERMFLSFPTTKTYFPHFDLSHGSAQVKGHGKKVADALTNAVAHVDDMPNALSA
HBA_HORSE VLSAADKTNVKAAWSKVGGHAGEYGAEALERMFLGFPTTKTYFPHFDLSHGSAQVKAHGKKVGDALTLAVGHLDDLPGALSN
HBA_HUMAN LSDLHAHKLRVDPVNFKLLSHCLLVTLAAHLPAEFTPAVHASLDKFLASVSTVLTSKYR
HBA_HORSE LSDLHAHKLRVDPVNFKLLSHCLLSTLAVHLPNDFTPAVHASLDKFLSSVSTVLTSKYR
+
HBB_HUMAN VHLTPEEKSAVTALWGKVN--VDEVGGEALGRLLVVYPWTQRFFESFGDLSTPDAVMGNPKVKAHGKKVLGAFSDGLAHLDNLK
HBB_HORSE VQLSGEEKAAVLALWDKVN--EEEVGGEALGRLLVVYPWTQRFFDSFGDLSNPGAVMGNPKVKAHGKKVLHSFGEGVHHLDNLK
HBA_HUMAN -VLSPADKTNVKAAWGKVGAHAGEYGAEALERMFLSFPTTKTYFPHF-DLS-----HGSAQVKGHGKKVADALTNAVAHVDDMP
HBA_HORSE -VLSAADKTNVKAAWSKVGGHAGEYGAEALERMFLGFPTTKTYFPHF-DLS-----HGSAQVKAHGKKVGDALTLAVGHLDDLP
HBB_HUMAN GTFATLSELHCDKLHVDPENFRLLGNVLVCVLAHHFGKEFTPPVQAAYQKVVAGVANALAHKYH
HBB_HORSE GTFAALSELHCDKLHVDPENFRLLGNVLVVVLARHFGKDFTPELQASYQKVVAGVANALAHKYH
HBA_HUMAN NALSALSDLHAHKLRVDPVNFKLLSHCLLVTLAAHLPAEFTPAVHASLDKFLASVSTVLTSKYR
HBA_HORSE GALSNLSDLHAHKLRVDPVNFKLLSHCLLSTLAVHLPNDFTPAVHASLDKFLSSVSTVLTSKYR

HBB_HUMAN --------VHLTPEEKSAVTALWGKVN--VDEVGGEALGRLLVVYPWTQRFFESFGDLSTPDAVMGNPKVKAHGKKVLGAFSD
HBB_HORSE --------VQLSGEEKAAVLALWDKVN--EEEVGGEALGRLLVVYPWTQRFFDSFGDLSNPGAVMGNPKVKAHGKKVLHSFGE
HBA_HUMAN ---------VLSPADKTNVKAAWGKVGAHAGEYGAEALERMFLSFPTTKTYFPHF-DLS-----HGSAQVKGHGKKVADALTN
HBA_HORSE ---------VLSAADKTNVKAAWSKVGGHAGEYGAEALERMFLGFPTTKTYFPHF-DLS-----HGSAQVKAHGKKVGDALTL
GLB5_PETMA PIVDTGSVAPLSAAEKTKIRSAWAPVYSTYETSGVDILVKFFTSTPAAQEFFPKFKGLTTADQLKKSADVRWHAERIINAVND
HBB_HUMAN GLAHLDN---LKGTFATLSELHCDKLHVDPENFRLLGNVLVCVLAHHFGKEFTPPVQAAYQKVVAGVANALAHKYH
HBB_HORSE GVHHLDN---LKGTFAALSELHCDKLHVDPENFRLLGNVLVVVLARHFGKDFTPELQASYQKVVAGVANALAHKYH
HBA_HUMAN AVAHVDD---MPNALSALSDLHAHKLRVDPVNFKLLSHCLLVTLAAHLPAEFTPAVHASLDKFLASVSTVLTSKYR
HBA_HORSE AVGHLDD---LPGALSNLSDLHAHKLRVDPVNFKLLSHCLLSTLAVHLPNDFTPAVHASLDKFLSSVSTVLTSKYR
GLB5_PETMA AVASMDDTEKMSMKLRDLSGKHAKSFQVDPQYFKVLAAVIADTVAAG---------DAGFEKLMSMICILLRSAY-
HBB_HUMAN VHLTPEEKSAVTALWGKVN--VDEVGGEALGRLLVVYPWTQRFFESFGDLSTPDAVMGNPKVKAHGKKVLGAFSDGLAHLDNLK
HBB_HORSE VQLSGEEKAAVLALWDKVN--EEEVGGEALGRLLVVYPWTQRFFDSFGDLSNPGAVMGNPKVKAHGKKVLHSFGEGVHHLDNLK
HBA_HUMAN -VLSPADKTNVKAAWGKVGAHAGEYGAEALERMFLSFPTTKTYFPHF-DLS-----HGSAQVKGHGKKVADALTNAVAHVDDMP
HBA_HORSE -VLSAADKTNVKAAWSKVGGHAGEYGAEALERMFLGFPTTKTYFPHF-DLS-----HGSAQVKAHGKKVGDALTLAVGHLDDLP
HBB_HUMAN GTFATLSELHCDKLHVDPENFRLLGNVLVCVLAHHFGKEFTPPVQAAYQKVVAGVANALAHKYH
HBB_HORSE GTFAALSELHCDKLHVDPENFRLLGNVLVVVLARHFGKDFTPELQASYQKVVAGVANALAHKYH
HBA_HUMAN NALSALSDLHAHKLRVDPVNFKLLSHCLLVTLAAHLPAEFTPAVHASLDKFLASVSTVLTSKYR
HBA_HORSE GALSNLSDLHAHKLRVDPVNFKLLSHCLLSTLAVHLPNDFTPAVHASLDKFLSSVSTVLTSKYR
GLB5_PETMA PIVDTGSVAPLSAAEKTKIRSAWAPVYSTYETSGVDILVKFFTSTPAAQEFFPKFKGLTTADQLKKSADVRWHAERIINAVND
GLB5_PETMA AVASMDDTEKMSMKLRDLSGKHAKSFQVDPQYFKVLAAVIADTVAAGDAGFEKLMSMICILLRSAY
+

Progresywne
Progresywne
dopasowanie
dopasowanie
globalne
globalne
-
-
program CLUSTALW
program CLUSTALW
HBB_HUMAN --------VH
L
TPEEKSAVTAL
W
GKVN--VDEVGGEALGRLLVVY
P
WTQRF
F
ESFGDLST
HBB_HORSE --------VQ
L
SGEEKAAVLAL
W
DKVN--EEEVGGEALGRLLVVY
P
WTQRF
F
DSFGDLSN
HBA_HUMAN ---------V
L
SPADKTNVKAA
W
GKVGAHAGEYGAEALERMFLSF
P
TTKTY
F
PHF-DLS-
HBA_HORSE ---------V
L
SAADKTNVKAA
W
SKVGGHAGEYGAEALERMFLGF
P
TTKTY
F
PHF-DLS-
GLB5_PETMA PIVDTGSVAP
L
SAAEKTKIRSA
W
APVYSTYETSGVDILVKFFTST
P
AAQEF
F
PKFKGLTT
MYG_PHYCA ---------V
L
SEGEWQLVLHV
W
AKVEADVAGHGQDILIRLFKSH
P
ETLEK
F
DRFKHLKT
LGB2_LUPLU --------GA
L
TESQAALVKSS
W
EEFNANIPKHTHRFFILVLEIA
P
AAKDL
F
SFLKGTSE
*
: : :
*
. : .:
*
:
*
: .
HBB_HUMAN PDAVMGNPKVKA
H
GKKVLGAFSDGLAHLDN-----LKGTFAT
L
SEL
H
CDKLHVDPENFRL
HBB_HORSE PGAVMGNPKVKA
H
GKKVLHSFGEGVHHLDN-----LKGTFAA
L
SEL
H
CDKLHVDPENFRL
HBA_HUMAN ----HGSAQVKG
H
GKKVADALTNAVAHVDD-----MPNALSA
L
SDL
H
AHKLRVDPVNFKL
HBA_HORSE ----HGSAQVKA
H
GKKVGDALTLAVGHLDD-----LPGALSN
L
SDL
H
AHKLRVDPVNFKL
GLB5_PETMA ADQLKKSADVRW
H
AERIINAVNDAVASMDDT--EKMSMKLRD
L
SGK
H
AKSFQVDPQYFKV
MYG_PHYCA EAEMKASEDLKK
H
GVTVLTALGAILKKKGH-----HEAELKP
L
AQS
H
ATKHKIPIKYLEF
LGB2_LUPLU VP--QNNPELQA
H
AGKVFKLVYEAAIQLQVTGVVVTDATLKN
L
GSV
H
VSKG-VADAHFPV
. .::
*
. : . :
*
.
*
. : : .
HBB_HUMAN LGNVLVCVLAHHFGKEFTPPVQAAYQKVVAGVANALAHKYH------
HBB_HORSE LGNVLVVVLARHFGKDFTPELQASYQKVVAGVANALAHKYH------
HBA_HUMAN LSHCLLVTLAAHLPAEFTPAVHASLDKFLASVSTVLTSKYR------
HBA_HORSE LSHCLLSTLAVHLPNDFTPAVHASLDKFLSSVSTVLTSKYR------
GLB5_PETMA LAAVIADTVAAG---------DAGFEKLMSMICILLRSAY-------
MYG_PHYCA ISEAIIHVLHSRHPGDFGADAQGAMNKALELFRKDIAAKYKELGYQG
LGB2_LUPLU VKEAILKTIKEVVGAKWSEELNSAWTIAYDELAIVIKKEMNDAA---
: : .: ... . :
α-helisa

Metody
Metody
iteracyjne
iteracyjne
Problemy dopasowania progresywnego: dalsze przyrównania zależą
od
początkowej pary sekwencji (szczególnie jeśli są
to sekwencje odległe); błędy
powstałe przy pierwszym przyrównaniu będą
powielane dalej.
Metody iteracyjne -
wielokrotnie przeprowadzają
dopasowania podgrup
sekwencji, a następnie wykonują
przyrównanie tych podgrup w dopasowanie
globalne wszystkich sekwencji. Podgrupy są
wybierane ze względu na ułożenie
na drzewie filogenetycznym lub losowo.

FASTA
FASTA
-
-
algorytm
algorytm
Tworzenie listy słów znaków o zadanej długości (k-tup dla DNA: 4-6; dla białek:
1, 2) i określenie ich położenia w sekwencjach.
MRSCNSCMI
MR
1
RS
2
SC
3, 6
CN
4
NS
5
CM
7
MI
8
MIRSCNCN
MI
1
IR
2
RS
3
SC
4
CN
5, 7
NC
6
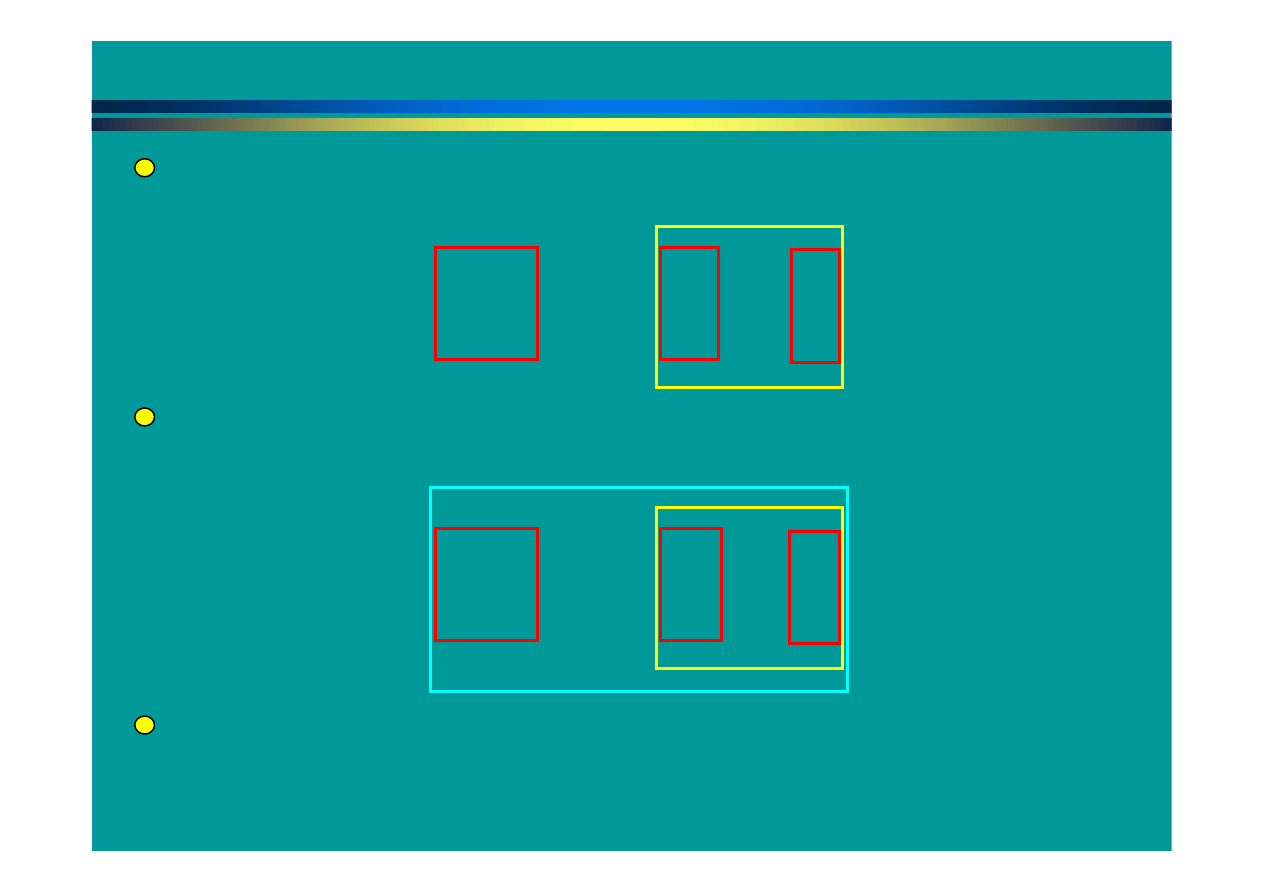
Liczenie różnicy położenia dla odpowiednich słów. Słowa, które wykazują
tą
samą
różnicę
w położeniu i znajdują
się
w fazie są
regionem, gdzie sekwencje
pasują
do siebie.
MRSCNSCG
RS
2
SC
3, 6
CN
4
MI
8
IRSCNCN
RS
3
SC
4
CN
5, 7
MI
1
-
=
RS
-1
SC
-1, 2
CN
-1, -3
MI
7
FASTA
FASTA
-
-
algorytm
algorytm
Łączenie znalezionych par słów w regiony początkowe bez przerw znajdujące
się
w pewnej odległości od siebie.
-MRSCNSCMIGWQIAAWYA
MIRSCNCNA--WQAGSWYLA
Łączenie regionów początkowych w większe regiony najlepiej pasujące
(o największej punktacji) i mogące uwzględniać
przerwy.
-MRSCNSCMIGWQIAAWYA
MIRSCNCNA--WQAGSWYLA
Przeprowadzenie optymalnego lokalnego dopasowania w oparciu o algorytm
Smith-Watermana dla wybranych regionów, a następnie pomiędzy całą
sekwencją
wysłaną
i znalezioną
w bazie o najlepszej punktacji. Określenie
istotności statystycznej dopasowań
(E-value).

BLAST
BLAST
-
-
algorytm
algorytm
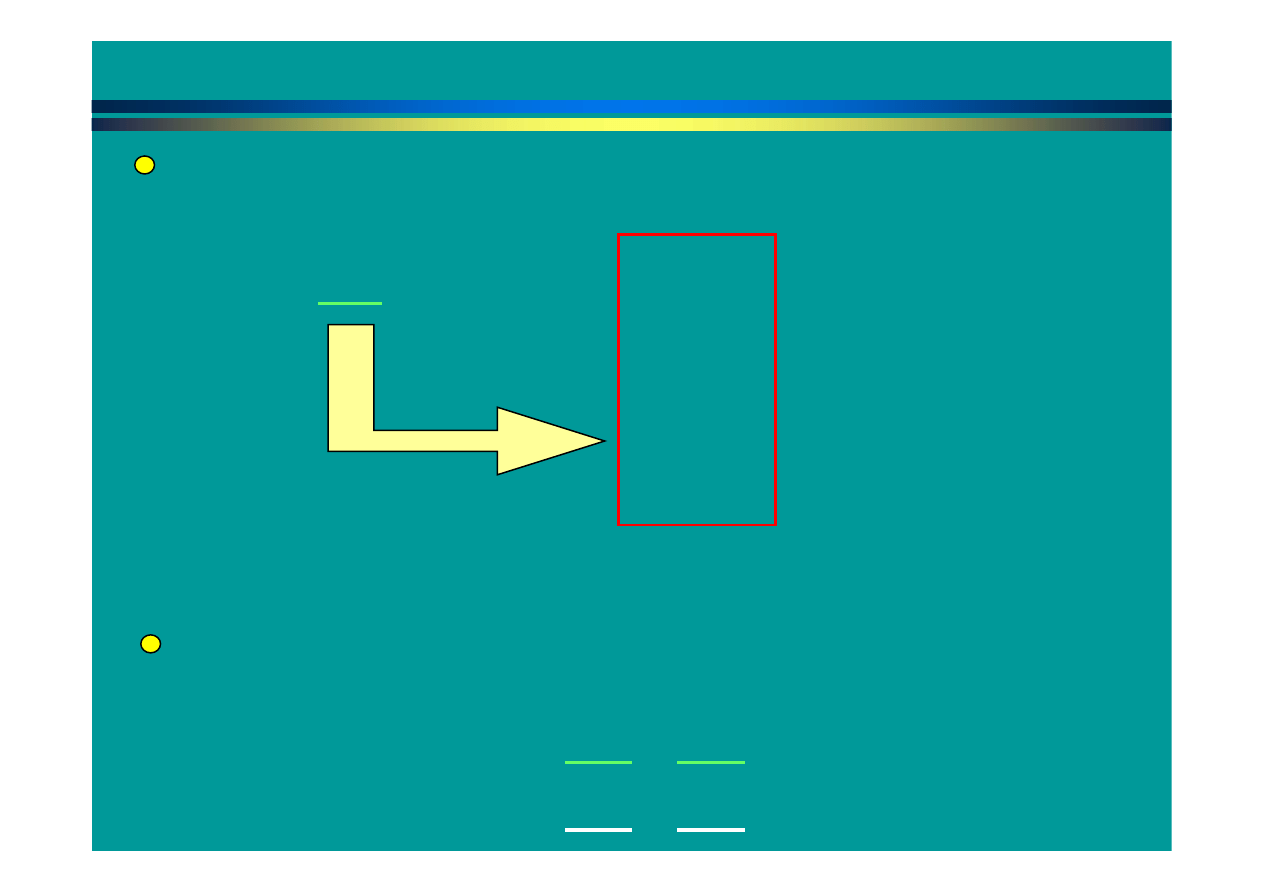
Tworzenie listy słów znaków o zadanej długości (k-tup dla DNA: 11, 3 w
przypadku tłumaczenia; dla białek: 2, 3) i określenie sąsiadujących
(podobnych) słów –
neighorhood words
(dla sekwencji aminokwasowych).
MLIPQGDELVISWA
MLI
LIP
IPQ
PQG
QGD
GDE
DEL
ELV
LVI
VIS
ISW
SWA
PEG,PRG,PSG,PQA,PAA,LQW,...
GDA,GDF,ASE,QDE,IDL,ADE...
BLAST
BLAST
-
-
algorytm
algorytm
MLIPQGDELVISWA
PQG 18
PEG 15
PRG 14
PKG 14
PNG 13
PDG 13
PHG 13
PMG 13
PSG 13
PQA 12
PQN 12
...
Zidentyfikowanie w obrębie sąsiadujących (podobnych) słów tylko takich (~50),
które najmniej różnią
się
od wzorca wg macierzy BLOSUM62
(>T –
punktacja progowa, score
threshold).
T>13
Poszukiwanie wybranych słów w sekwencjach w bazie danych i ich
przyrównywanie (dopasowywanie). Dla sekwencji DNA szukane są
identyczne
słowa.
GQTERFCVLMLIPQGDELVISWANASSCS
NQWGYASCAALLPRGDFLVLGWIGHAALI
BLAST
BLAST
-
-
algorytm
algorytm
Rozszerzanie dopasowania w regionie, w którym zostały znalezione
przynajmniej dwa słowa, aż
do regionów o niskiej punktacji. Określenie
regionów HSP (high-scoring
segment pair).
GQTERFCVLMLIPQGDELVISWANASSCS
NQWGYASCAALLPRGDFLVLGWIGHAALI
HSP
Przeprowadzenie optymalnego lokalnego dopasowania w oparciu o algorytm
Smith-Watermana uwzględniającego wszystkie znalezione regiony HSP.
Określenie istotności statystycznej dopasowań
(E-value).

Filtrowanie region
Filtrowanie region
ó
ó
w o s
w o s
ł
ł
abej z
abej z
ł
ł
o
o
ż
ż
ono
ono
ś
ś
ci
ci
Maskowanie (nieuwzględnianie w porównaniach sekwencji) regionów
o niskiej złożoności składu, niskiej entropii -
LCR (low-complexity
regions):
powtórzenia nukleotydów lub aminokwasów
ciągi tych samych, dwóch lub jednego znaku
Regiony te mogą
dawać
wysokie wartości punktacji dla sekwencji
w rzeczywistości niehomologicznych
-
wyniki fałszywe pozytywne
Programy do poszukiwania i maskowania tych regionów:
PRSS (w pakiecie FASTA)
SEG (wykorzystywany przez BLASTP)
PSEG
NSEG
DUST (wykorzystywany przez BLASTN)
XNU
RepeatMasker
Filtrowanie tych regionów jest opcją
domyślną
w programie BLAST.
X -
dla aminokwasów, N -
dla nukleotydów
Ponad połowa sekwencji białkowych w bazach posiada przynajmniej jeden LCR
>gi|730028|sp|P40692|MLH1_HUMAN DNA mismatch repair protein Mlh1 1)
Length = 756
Score = 233 bits (593), Expect = 8e-62
Identities = 117/131 (89%), Positives = 117/131 (89%)
Query: 1 IETVYAAYLPKNTHPFLYLSLEISPQNVDVNVHPTKHEVHFLHEESILERVQQHIESKLL 60
IETVYAAYLPKNTHPFLYLSLEISPQNVDVNVHPTKHEVHFLHEESILERVQQHIESKLL
Sbjct: 276 IETVYAAYLPKNTHPFLYLSLEISPQNVDVNVHPTKHEVHFLHEESILERVQQHIESKLL 335
Query: 61 GSNSSRMYFTQTLLPGLAGPSGEMVKXXXXXXXXXXXXXXDKVYAHQMVRTDSREQKLDA 120
GSNSSRMYFTQTLLPGLAGPSGEMVK DKVYAHQMVRTDSREQKLDA
Sbjct: 336 GSNSSRMYFTQTLLPGLAGPSGEMVKSTTSLTSSSTSGSSDKVYAHQMVRTDSREQKLDA 395
Query: 121 FLQPLSKPLSS 131
FLQPLSKPLSS
Sbjct: 396 FLQPLSKPLSS 406
Filtrowanie region
Filtrowanie region
ó
ó
w o s
w o s
ł
ł
abej z
abej z
ł
ł
o
o
ż
ż
ono
ono
ś
ś
ci
ci
LCR (low-complexity
regions
Por
Por
ó
ó
wnanie program
wnanie program
ó
ó
w FASTA i BLAST
w FASTA i BLAST
BLAST
FASTA
może podawać
więcej niż
jeden
region o wysokiej punktacji
podaje tylko jedno najlepsze
dopasowanie
lepszy dla sekwencji białek niż
DNA
lepszy dla sekwencji DNA niż
białek
szybszy niż
FASTA
wolniejszy niż
BLAST
mniej czuły niż
FASTA przy użyciu
domyślnych ustawień
bardziej czuły niż
BLAST
daje gorsze rozróżnienie między
prawdziwymi i fałszywymi homologami
daje lepsze rozróżnienie między
prawdziwymi i fałszywymi homologami
Document Outline
- Dopasowanie sekwencji – c.d. Sequence alignment
- Slide Number 2
- Slide Number 3
- Slide Number 4
- Slide Number 5
- Slide Number 6
- Slide Number 7
- Slide Number 8
- Slide Number 9
- Slide Number 10
- Slide Number 11
- Slide Number 12
- Slide Number 13
- Slide Number 14
- Slide Number 15
- Slide Number 16
- Slide Number 17
- Slide Number 18
- Slide Number 19
- Slide Number 20
- Slide Number 21
- Slide Number 22
- Slide Number 23
- Slide Number 24
- Slide Number 25
- Slide Number 26
- Slide Number 27
- Slide Number 28
- Slide Number 30
- Slide Number 31
- Slide Number 32
- Slide Number 33
- Slide Number 34
- Slide Number 35
- Slide Number 36
- Slide Number 37
- Slide Number 38
- Slide Number 39
- Slide Number 40
- Slide Number 41
- DOPASOWANIA WIELOKROTNE (MULTIALIGNMENT) Metoda hierarchiczna
- Tworzenie drzewa przewodniego
- Stopniowe zestawianie sekwencji dopasowanych
- Slide Number 45
- Slide Number 46
- Slide Number 47
- Slide Number 48
- Slide Number 49
- Slide Number 50
- Slide Number 51
- Slide Number 52
- Slide Number 53
- Slide Number 54
- Slide Number 55
- Slide Number 56
- Slide Number 57
Wyszukiwarka
Podobne podstrony:
bioinformatyka w13 2008 9 web
bioinformatyka w2 2008 web
bioinformatyka w9 2008 web
bioinformatyka w11 2008 web
bioinformatyka w4 2008 web
bioinformatyka w10 2008 web
bioinformatyka w12 2008 9 web
bioinformatyka w3 2008 web
bioinformatyka w7 2008 web
bioinformatyka w1 2008 web
bioinformatyka w8 2008 web
bioinformatyka w5 2008 web
bioinformatyka w13 2008 9 web
bioinformatyka w2 2008 web
bioinformatyka w9 2008 web
więcej podobnych podstron