Podstawy Metrologii i Technik Eksperymentu
Laboratorium
SPRAWDZANIE I WZORCOWANIE
APARATURY POMIAROWEJ
Instrukcja do ćwiczenia nr 4
Zakład Miernictwa i Ochrony Atmosfery
Wrocław, listopad 2010 r.
2
Podstawy Metrologii i Technik Eksperymentu Ćwiczenie laboratoryjne nr 4
SPRAWDZANIE I WZORCOWANIE APARATURY POMIAROWEJ
1.C
EL ĆWICZENIA
Celem
ćwiczenia jest:
-sprawdzenie mie
rnika do pomiaru napięć termoelektrycznych
-sprawdzenie i wyznaczenie poprawek mierników do pomiarów temperatur dla
termoelementu typu K
-sprawdzenie i wyznaczenie poprawek termometrów oporowych Pt100 klasy 2.
2. W
STĘP [1]
Jednym z kryterium podziałów przyrządów do pomiaru temperatury związane jest z rodzajem
wielkości fizycznej w nich wykorzystywanych. Wyróżnia się przyrządy nieelektryczne, w
których sygnał temperatury zamieniany jest na wielkość nieelektryczną, oraz przyrządy
elektryczne
, w których sygnał od temperatury zamieniany jest na jedną z wielkości
elektrycznych. Przykłady termometrów nieelektrycznych to: termometry cieczowe,
bimetalowe czy manometryczne. Do drugiej grupy
należą: kwarcowe, termometry
rezystancyjne (oporowe), termoelektryczne. Dw
a ostatnie stosowanie są najczęściej w
energetyce np. do bilansowych pomiarów maszyn i
urządzeń energetycznych (np. kotły,
turbiny, młyny).
2.1 TERMOMETRY TERMOELEKTRYCZNE; ZASADA
DZIAŁANIA [1,2]
Termoelem
enty tworzą dwa różne materiały: metale czyste, stopy metali, lub niemetale
połączone na jednym końcu. W termoelementach sygnał od temperatury zamieniany zostaje
na napięcie.
Zasada działania opiera się na dwóch zjawiskach:
- zjawisku Peltiera: wyst
ępowania siły (napięcia) termoelektrycznego w punkcie połączenia
dwóch metali
- zjawiska Thomsona:
występowania siły termoelektrycznej na długości poszczególnych
przewodów obwodu zamkniętego.
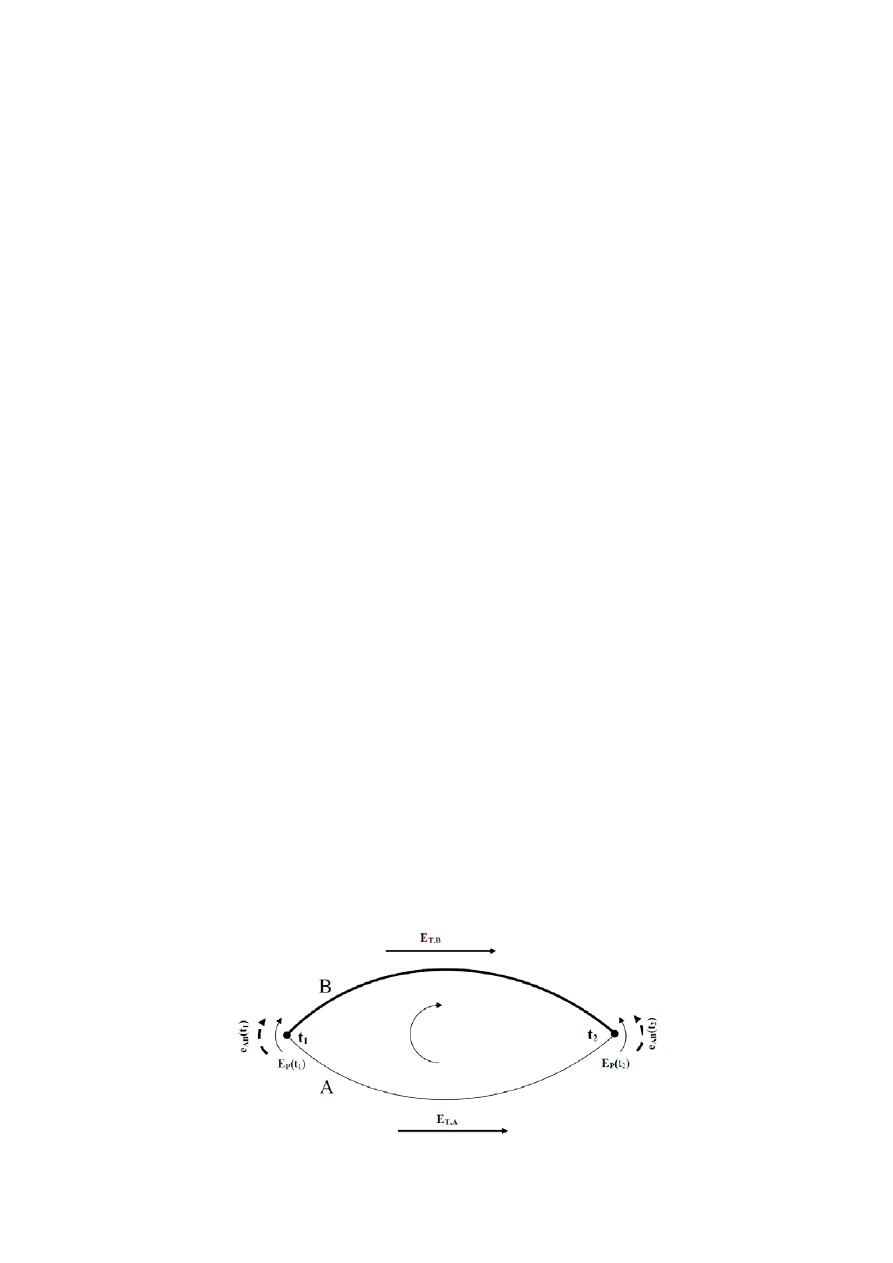
Ilustruje to rysunek 1. W wyniku
połączenia dwóch metali znajdujących się w różnych
temperaturach t
1
i t
2
występują cztery siły termoelektryczne:
E
P
(t
1
)-
siła termoelektryczna Peltiera w spoinie 1
E
P
(t
2
)-
siła termoelektryczna Peltiera w spoinie 2
E
T,A
(t
1
)-
siła termoelektryczna Thomsona w przewodzie A
E
T, B
(t
1
)-
siła termoelektryczna Thomsona w przewodzie B [1].
Rys.
1. Zamknięty obwód termoelektryczny [1]
3
Przyjmując kierunek sumowania sił termoelektrycznych zgodnie z ruchem wskazówek zegara
wypadkową siłe termoelektryczną w obwodzie można zapisać w postaci:
E = E
P
(t
1
) + E
T,B
− E
P
(t
2
) − E
T,A
= �E
P
(t
1
) + E
T,B
� − �E
P
(t
2
) + E
T,A
�
(1)
e
AB
(t
1
) e
AB
(t
2
)
Wobec trudności w zidentyfikowaniu wartości poszczególnych sił termoelektrycznych,
umownie przyjmuje się, że siły te umiejscowione są w spoinach obwodu i oznacza się je
przez: e
AB
(t
1
) oraz e
AB
(t
2
) (linia kreskowana na rysunku 1) [1]
Wypadkowa siła termoelektryczna wyraża się wtedy równaniem:
E
AB
(t
1
, t
2
) = e
AB
(t
1
) − e
AB
(t
2
) = f
1
(t
1
, t
2
)
(2)
Wypadkowa siła termoelektryczna w obwodzie zależy jedynie od obu metali A i B od
temperatur t
1
i t
2
–
jest zatem funkcją dwóch zmiennych. Ponieważ trudno jest operować
funkcją dwóch zmiennych temperaturę t
2
przyjmuje się stałą, tzn. t
2
= t
0
. Spoina ta nazywa się
spoiną odniesienia, zaś spoina o temperaturze t
1
- jest
spoiną mierniczą. Równanie można
zatem napisać:
E
AB
(t
1
, t
2
) = E
AB
(t
1
, t
0
) = e
AB
(t
1
) − e
AB
(t
0
) = f
1
(t
1
)
(3)
W celu wyznaczenia temperatury
należy w obwód z rysunku 1 włączyć miliwoltomierz i
zmierzyć napięcie, które jest proporcjonalne do siły termoelektrycznej. Włączenie
miliwoltomierza równoznaczne jest z wprowadzeniem do tego obwodu trzeciego metalu, z
którego wykonane s
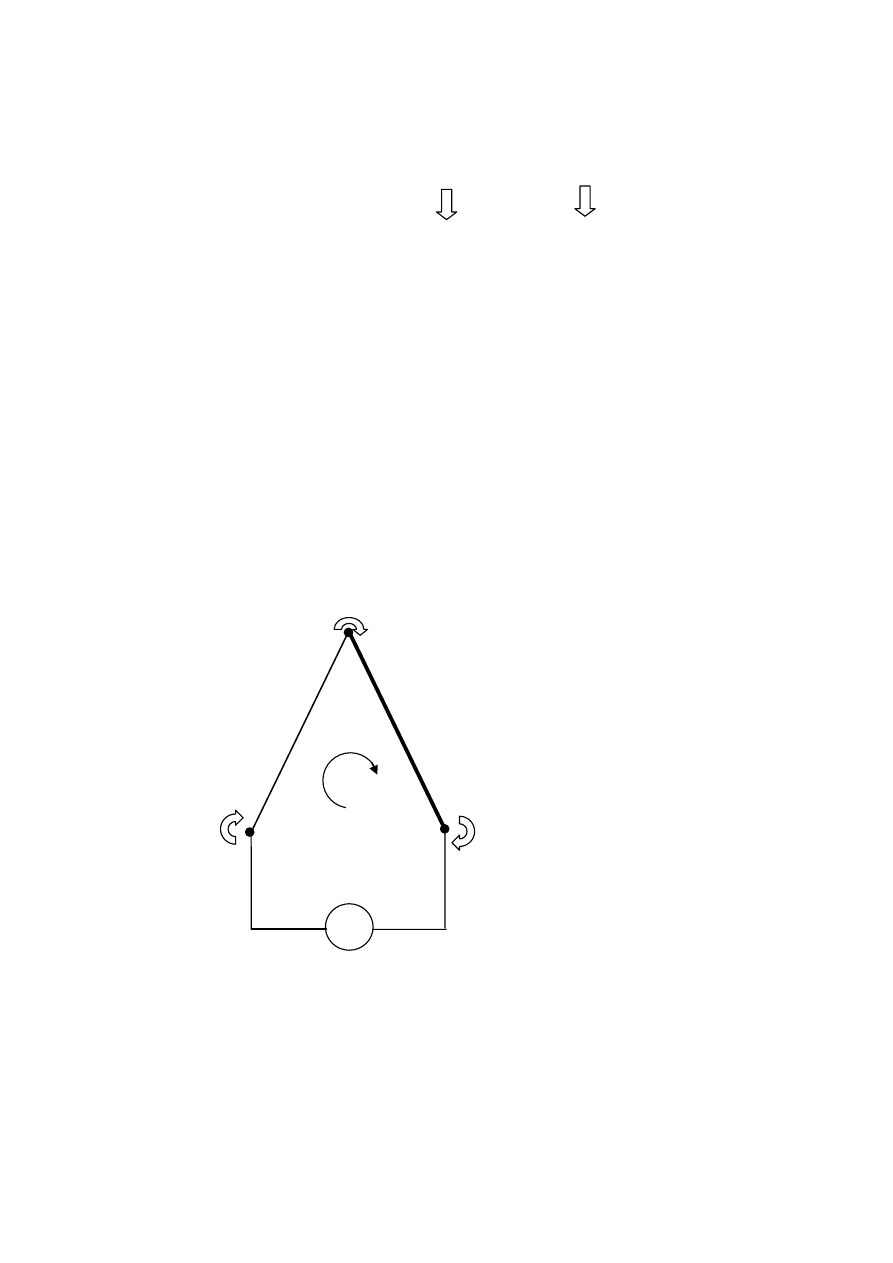
ą przewody miernika. Przedstawia to rysunek 2.
Rys.2.
Trzeci metal w obwodzie termoelektrycznym rozciętym w spoinie [1]
Wypadkowa siła termoelektryczna wynosi:
E = e
AB
(t
1
) + e
BC
(t
2
) + e
CB
(t
2
)
(4)
A
B
C
C
U
t
1
t
2
t
2
e
AB
(t
1
)
e
BC
(t
2
)
e
CB
(t
2
)
4
Dla t
1
= t
2
otrzymamy:
e
AB
(t
2
) + e
BC
(t
2
) + e
CB
(t
2
) = 0
(5)
Stąd:
e
BC
(t
2
) + e
CB
(t
2
) = −e
AB
(t
2
)
(6)
i dalej, wstawiając tą zależność do równania otrzymamy:
E = e
AB
(t
1
)−e
AB
(t
2
)
(7)
Zależność ta umożliwia sformułowanie prawa trzeciego metalu:
Wprowadzenie do obwodu metali A i B trzeciego metalu nie wpływa na wartość wypadkowej
siły termoelektrycznej pod warunkiem, że oba końce przewodu wykonanego z metalu C
znajdują się w tej samej temperaturze [1].
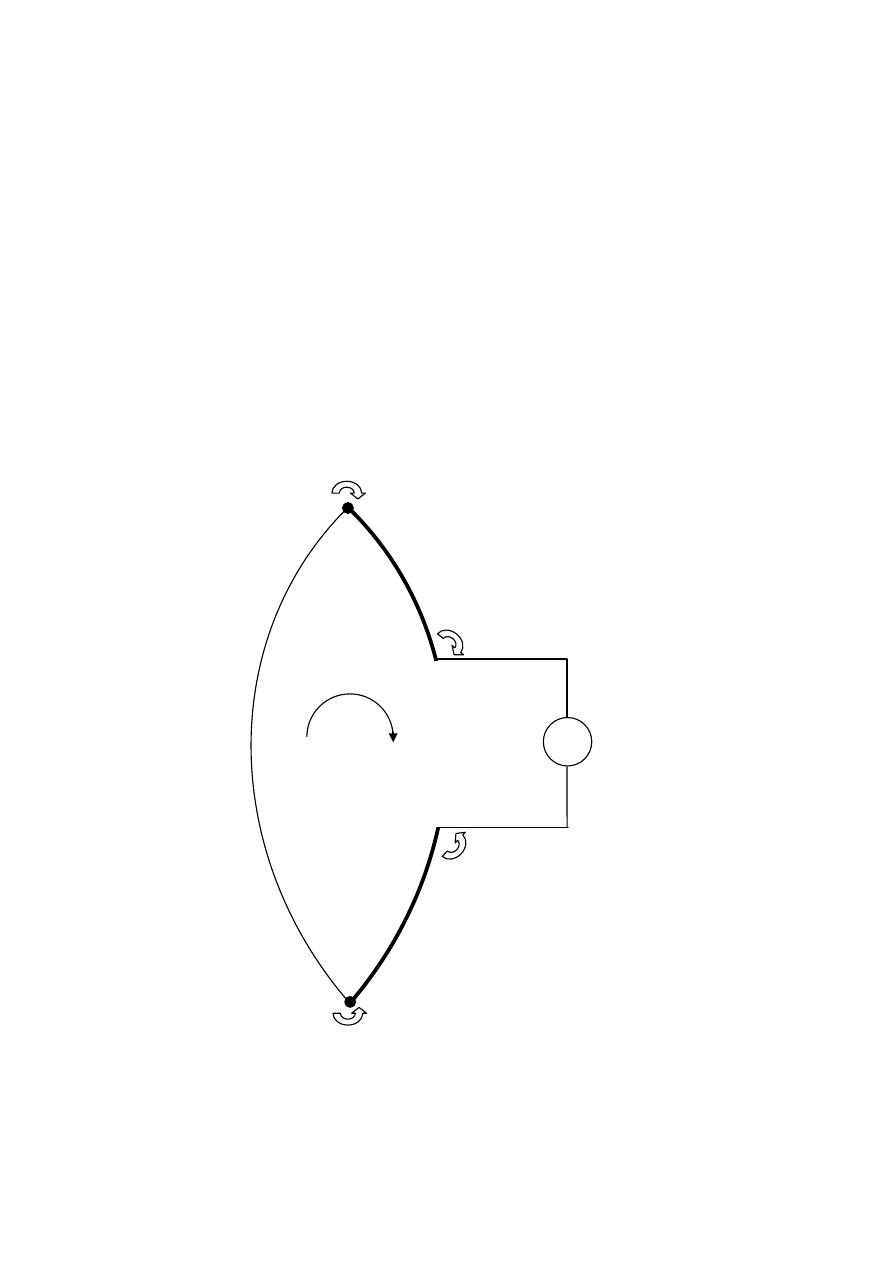
Miejsce
włączenia trzeciego metalu jest dowolne. Ilustruje to rysunek 3.
Rys.3.
Trzeci metal w obwodzie termoelektrycznym rozcięty w dowolnym napięciu [1]
t
1
t
0
t
2
t
2
A
B
B
U
e
AB
(t
1
)
C
C
e
BC
(t
2
)
e
BC
(t
2
)
e
AB
(t
0
)
5
Siła termoelektryczna wynosi:
E = e
AB
(t
1
) + e
BC
(t
2
) − e
BC
(t
2
) − e
AB
(t
0
)
(8)
Stąd:
E = e
AB
(t
1
) − e
AB
(t
0
).
(9)
Charakterystyk
ę termoelementu przedstawia zależność napięcia termoelektrycznego w
funkcji temperatury przy stałej temperaturze spoiny odniesienia t
0
–
najczęściej jest to
temperatura równa t
0
=0.
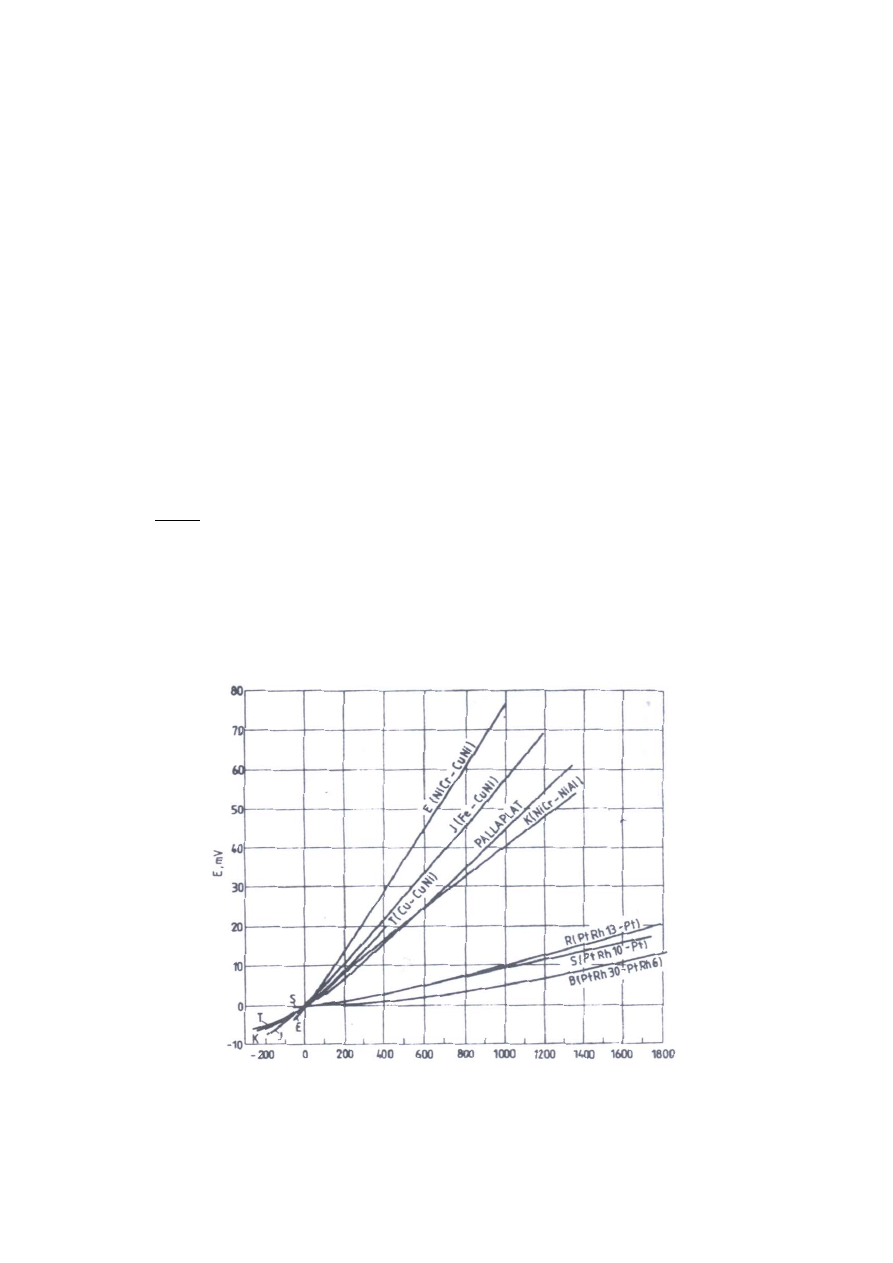
Przykładowe charakterystyki termoelementów przedstawia
rysunek 4. [1]
Pomiaru
temperatury wykonuje się bardzo często metodą wychyłową, wg rysunku 2.
Zakładając, że opór wewnętrzny miliwoltomierza wynosi R
W
, a opory wszystkich przewodów
R
P
, zgodnie z prawem Ohma otrzymamy:
E − IR
p
= U
(10)
U = IR
w
(11)
I
dalej po przekształceniach:
U = E
R
w
R
w
+R
p
(12)
Ponieważ opór wewnętrzny miernika R
w
>> R
p
to
można przyjąć, że U=E. Znając wartość U
z charakterystyki termoelementu można odczytać wartość temperatury t
1
oczywiście dla danej
temperatury t
0
.
Jeżeli temperatura t
0
zmieni się to popełniamy błąd systematyczny, dla t
01
> t
0
mierzona temperatura
będzie mniejsza od t
1
, a jeżeli t
01
< t
0
to mierzona temperatura
będzie
większa od t
1
.
Rys.4
. Przykładowe charakterystyki termoelementów [1]
6
Do
najczęściej stosowanych w pomiarach termoelementów o znormalizowanych
charakterystykach wg PN-
EN60584 należą:
• termoelement typu K nikiel-chrom/nikiel- aluminium (NiCr-NiAl)- do temperatury 1200 °C
•
termoelement typu J żelazo/miedź-nikiel (Fe- CuNi) do temperatury 750 °C
•
termoelement typu T miedź/miedź- nikiel ( Cu-CuNi) do temperatury 500°C
Każdy z termoelementów o grubości przewodu od 0,25 mm do 3 mm może zostać wykonany
w 2 lub 3 klasach
dokładności Tabela 1 przedstawia klasy dokładności dla wyżej
wymienionych termoelementów
wraz z błędami granicznymi wskazań. [2]
Tabela 1
Klasy dokładności dla termoelementów [2]
typ K
Klasa 1
Klasa2
Klasa3
-40… +1000°C ± 0,004 t lub ±1,5°C
-40… +1200°C ± 0,0075 t lub ±2,5°C
-200…+40°C ± 0,015 t lub ±2,5°C
typ J
Klasa 1
Klasa2
-40… +750°C ± 0,004 t lub ±1,5°C
-40… +750°C ± 0,0075 t lub ±2,5°C
typ T
Klasa 1
Klasa2
Klasa3
-0… +350°C ± 0,004 t lub ±0,5°C
-40… +350°C ± 0,0075 t lub ±1,0°C
-200…+40°C ± 0,015 t lub ±1,0°C
Dla przykładu termoelement typ K klasy 2 pokazuje temperaturę 200 °C przy temperaturze
spoiny odniesienia 0°C. Jako b
łąd graniczny ( tolerancja) przyjmujemy większą z wartości
0,0075·200°C = 1,5 °C i
±2,5 °C. Oznacza to że wartość prawdziwa temperatury znajduje
się w przedziale <197,5°C – 202,5°C>. [2]
2.2. TERMOMETRY REZYSTANCYJNE METALOWE [2]
Zasada działania tych termometrów polega na wzroście rezystancji metali wraz ze wzrostem
temperatury.
Ze względu na wymaganie łatwej odtwarzalności metali na termometry
rezystancyjne stosuje się wyłącznie czyste metale – najczęściej platyna [1]. Charakterystykę
termometru oporowego platynowego
można przedstawić w postaci dwóch równań:
w zakresie -200
°
C…0
°
C
R(t) = R
0
(1 + At + Bt
2
+ C[t − 100
°
C]t
3
)
(13)
w zakresie 0
°
C…850
°
C
R(t) = R
0
(1 + At + Bt
2
)
(14)
gdzie:
R
o
– rezystancja w temperaturze 0
°
C
A= 3,90802·10
-3
·
°
C
-1
B = -5,775·10
-7
·
°
C
-2
C = -4,2735·10
-12
·
°
C
-4
Innym parametrem charakterystycznym dla termometrów rezystancyjnych jest cieplny
współczynnik zmian rezystancji α podawany najczęściej w zakresie 0
°
C do 100
°
C, w postaci
równania:
α =
1
R
0
R
100
−R
0
100
, 1/°C
(15)
Termometrem rezystancyjnym, czysto wykorzystywanym w pomiarach temperatur jest
termometr Pt100 , o rezystancji 100Ω w 0
°
C i 138
Ω w 100
°
C
oraz
współczynniku
α równym
α =3,925 10
-3
°
C
-1
( co oznacza ok. 40% wzrost oporu na 100
°
C).
W pomiarach stosowane są
również termometry oporowe Pt500 i Pt 1000.
7
W
ielkością charakterystyczną dla termometrów rezystancyjnych jest również ich czułość.
Można ją określić jako zmianę oporu przypadającą na 1
°
C. Dla termometrów Pt 100 wynosi
ona
ok. 0,4 Ω/
°
C, dla termometrów Pt 5
00 ok. 2Ω/
°
C, a termometrów Pt1000 ok.
4Ω/
°
C.
Wynika z tego, że termometry Pt 500 i Pt1000 mogą mierzyć temperaturę z większą
dokładnością niż Pt100.
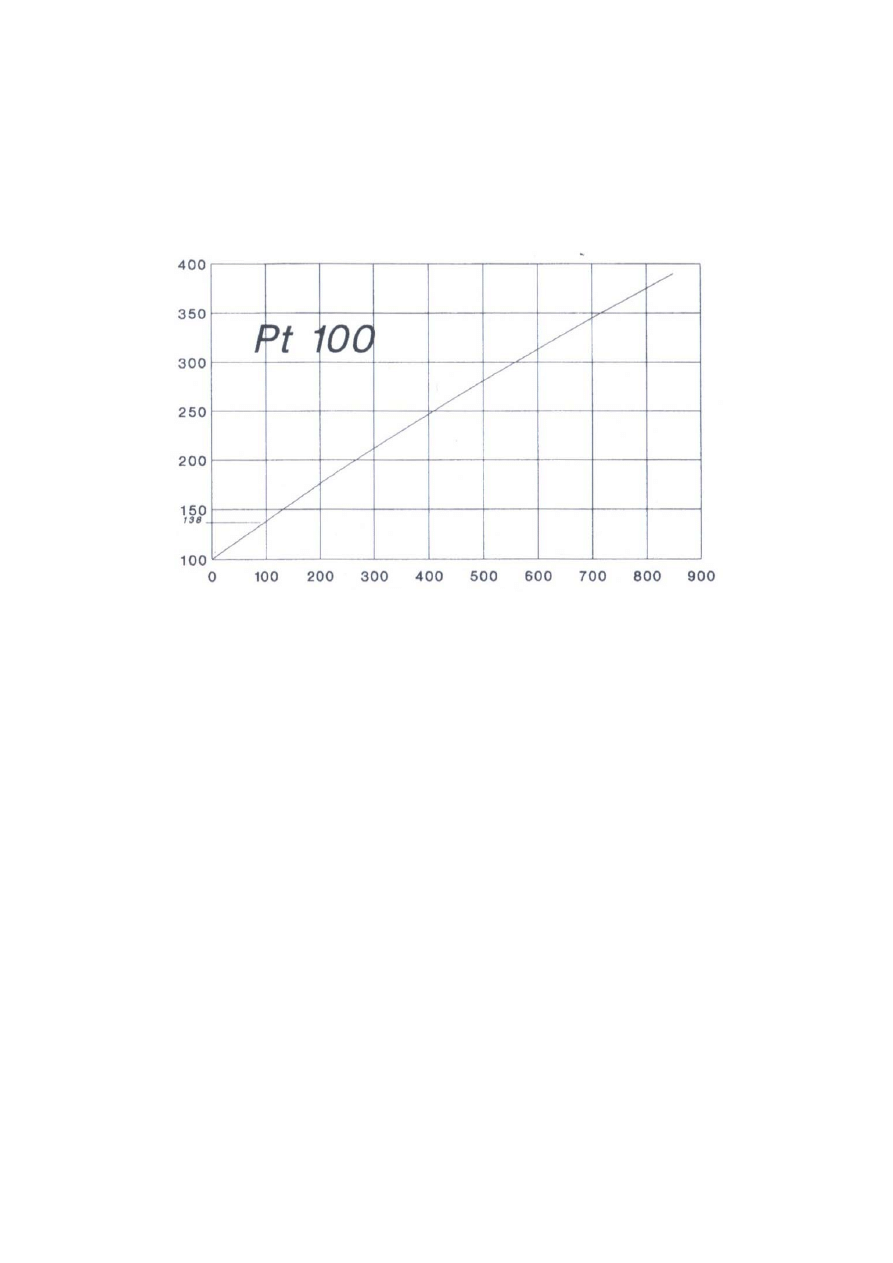
Charakterystykę termometru rezystancyjnego Pt100 przedstawia rysunek 5. [2]
Rys.5. Charakterystyka termometru rezystancyjnego Pt100 [2]
Oprócz termometrów platynowych do pomiaró
w wykorzystuje się: termometry niklowe
Ni100 i miedziane Cu100.
Zastępują one w niższych temperaturach platynę.
Termometry rezystancyjne wykonuje się w dwóch klasach dokładności A i B. Dla
termometrów platynowych
błędy graniczne (tolerancje) wynoszą:
Klasa A -
Δt
g
= ±(0,15 +0,002·t)
(16)
Klasa B -
Δt
g
= ±(0,30 +0,005·t), t w
°
C
(17)
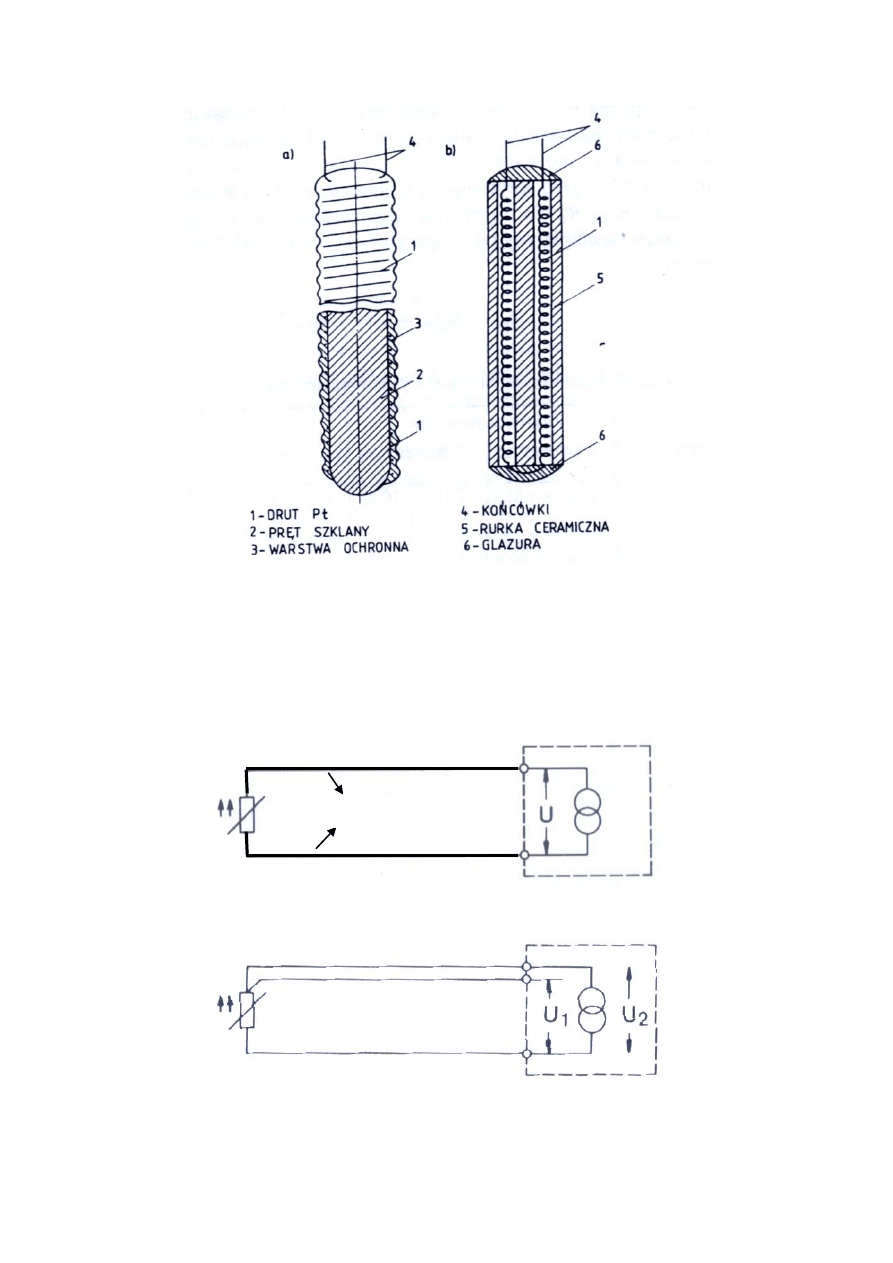
Najbardziej rozpowszechnioną formą platynowych rezystorów termometrycznych są
rezystory pałeczkowe przedstawione na rysunku 6. Uzwojenie rezystancyjne jest nawiniete
na pręcie lub rurce ze szkła lub kwarcu – rysunek 6a lub uzwojenie rezystancyjne w formie
spirali umieszczone w otworkach poosiowych rurki ceramicznej – rysunek 6b.
temperatura/
°
C
o
pór
/Ω
8
Rys.6. Rezystory pałeczkowe [1]
Układy pomiarowe przedstawione są na rysunkach:7 – układ z linią dwuprzewodową i 8-
układ z linia trójprzewodową. Zaletą tego drugiego układu jest to, że zmiana oporu linii
łączących rezystor z miernikiem nie wpływa na wartość mierzonej temperatury. W
pierwszym przypadku dla linii dwuprzewodowej , dla przewodów miedzianych o przekroju
0,5mm
2
, oporności właściwej ρ= 0,0175Ωmm
2
/m i długości przewodów l= 100 m popełnia
się błąd pomiaru temperatury termometrem Pt100 wynoszący ok. 18,5
°
C [2].
Rys.7.
Układ z linią dwuprzewodową [2]
Rys.8.
Układ z linią trójprzewodową [2]
t
przewody połączeniowe
t
9
Temperaturę mierzoną wyznacza się z prawa Ohma: U= I·R. Przy stałej wartości prądy I
płynącego w tym układzie pomiarowym napięcie U~R a tym samym jest funkcja temperatury
mierzonej t. Prąd pomiarowy I płynący przez rezystor powoduje jego nagrzewanie, co przy
przekroczeniu dopuszczalnych
wartości może powodować błąd pomiaru. Przyjmuje się że
wartość tego prądu nie powinna przekraczać wartości 5-10 mA, zależy ona od powierzchni
oddawania ciepła przez rezystor, rodzaju osłony i ośrodka w którym znajduje się rezystor.[2]
3.
WZORCOWANIE I SPRAWDZANIE PRZYRZĄDÓW POMIAROWYCH [3]
Według [3] wzorcowanie (kalibracja) to zbiór operacji ustalających w określonych warunkach
relację między wartościami wielkości mierzonej wskazanymi przez przyrząd pomiarowy lub
układ pomiarowy albo wartościami reprezentowanymi przez wzorzec miary lub przez
materiał odniesienia a odpowiednimi wartościami wielkości realizowanymi przez wzorce
„jednostki miary” .
Zgodnie z t
ą definicją wynik wzorcowania pozwala na przypisanie wskazaniom
odpowiednich
wartości wielkości mierzonej lub na wyznaczenie poprawek do wskazań [3].
Błąd systematyczny wskazania wyraża równanie [3]:
∆
s
W = W
� − N
(18)
w którym:
W
� - wartość średnia z nieskończonej liczby wyników wskazań przyrządu uzyskanych przy
pomiarach wzorca
N –
wartość odtwarzana przez wzorzec
W
g definicji poprawka to błąd systematyczny ze znakiem przeciwnym, zatem wyraża ją
równanie:
P
w
= -
∆
s
W = N − W
�
(19)
Z równania tego można jedynie oszacować poprawkę, ponieważ seria pomiarów jest zawsze
skończona. Równanie na poprawkę można zapisać zatem w postaci:
P
w
=
N − W
� ± U(P
w
)
(20)
Równanie to można rozszerzyć poprzez uwzględnienie w nim poprawki na rozdzielczość
przyrządu P
rw
oraz poprawki P
wo
– na
rozbieżność między charakterystykami przyrządu i
wzorca w zakresie warunków odniesienia i zapisać w postaci: [3]
P
w
=
(N − W
� + P
rw
+
P
wo
) ± U(P
w
)
(21)
Wzór na złożoną niepewność standardową dany jest równaniem:
u(P
w
) = �u
2
(N) + u
2
(W
� ) + u
2
(P
rw
) + u
2
(P
wo
)
(22)
Poszczególne składowe niepewności oblicza się w następując sposób:
u(N) –
na podstawie świadectwa wzorcowania wzorca
u(
W
� ) – metodą statystyczną wg równania:
u(W
� ) = �
∑(W
i
−W
���)
2
n(n−1)
(23)
n- liczba pomiarów w wybranym punkcie zakresu.
Wzorcowanie wymaga wyznaczenia poprawek wskazań P
w
w wybranych punktach zakresu
pomiarowego, a liczba pomiarów n w danym punkcie wskazania musu być odpowiednio
duża to przyjmuje się, że rozrzut wskazań w całym zakresie pomiarowym jest podobny i dużą
10
serię pomiarów n
d
wykonuje się w jednym wybranym punkcie. Może być to na przykład
podprz
edział w którym błędy wskazań są największe [3]. Wtedy niepewność wskazania u(W
� )
liczy się z równania:
u(W
� ) =
�
∑�Wi−W
�����2
(nd−1)
√n
=
�
∑(W
i
−W
���)
2
n(n
d
−1)
(24)
gdzie n –
ilość pomiarów w wybranym punkcie zakresu pomiarowego.
u(
𝑃
𝑟𝑤
) - oblicza się zakładając, że rozdzielczość przyrządu d ma rozkład prostokątny i
wyznacza z równania:
u(P
rw
) =
d
√12
(25)
Poprawkę tą uwzględnia się wtedy gdy obliczona niepewność wskazania u(W
� ) będzie
mniejsza od niepewności tej poprawki liczonej z równania(25).
u(
P
wo
)- jeżeli poprawką tą jest poprawka temperaturowa(P
ws
= Wαδt); W- wskazanie
przyrządu, α - uśredniony współczynnik rozszerzalności cieplnej, δt - różnica temperatur
przyrządu i mierzonego elementu)
to niepewność jej można ja wyznaczyć z następującego równania: [3]
u(P
ws
) = Wαu(δt)
(26)
Sprawdzanie narzędzia pomiarowego to czynności stwierdzające zgodność narzędzia
pomiarowego z wymaganiami przepisów legalizacyjnych, zaleceniami norm lub warunkami
technicznymi [3].
Sprawdza się czy błędy wskazań przyrządu pomiarowego nie przekraczają błędów
granicznych ±Δ
g
.
Błędy wskazań przyrządu należy wyznaczyć w kilku wybranych punktach
zakresu np.: w okolicy początku, połowie i przy końcu zakresu [3]. Pojedyncze wskazania w
wybranych punktach nie powinny być obarczone błędami większymi niż bledy
graniczne, a niepewność wyznaczenia błędów powinna być co najmniej 3 razy mniejsza
od błędu granicznego [3].
Błąd wskazania E
w
liczy się z równania [3]:
E
w
= W − N
(27)
gdzie:
W-
pojedyncze wskazanie przyrządu
N-
wartość odtwarzana przez wzorzec
Po
uwzględnieniu rozdzielczości δ
rw
i warunków środowiskowych δ
rw
równanie to przybiera
postać [3]:
E
w
= W − N + δ
rw
+ δ
wo
.
(28)
Równanie na niepewność standardową złożoną wskazania wyznacza się z równania:
u(E
w
) = �u
2
(W) + u
2
(N) + u
2
(δ
rw
) + u
2
(δ
wo
)
(29)
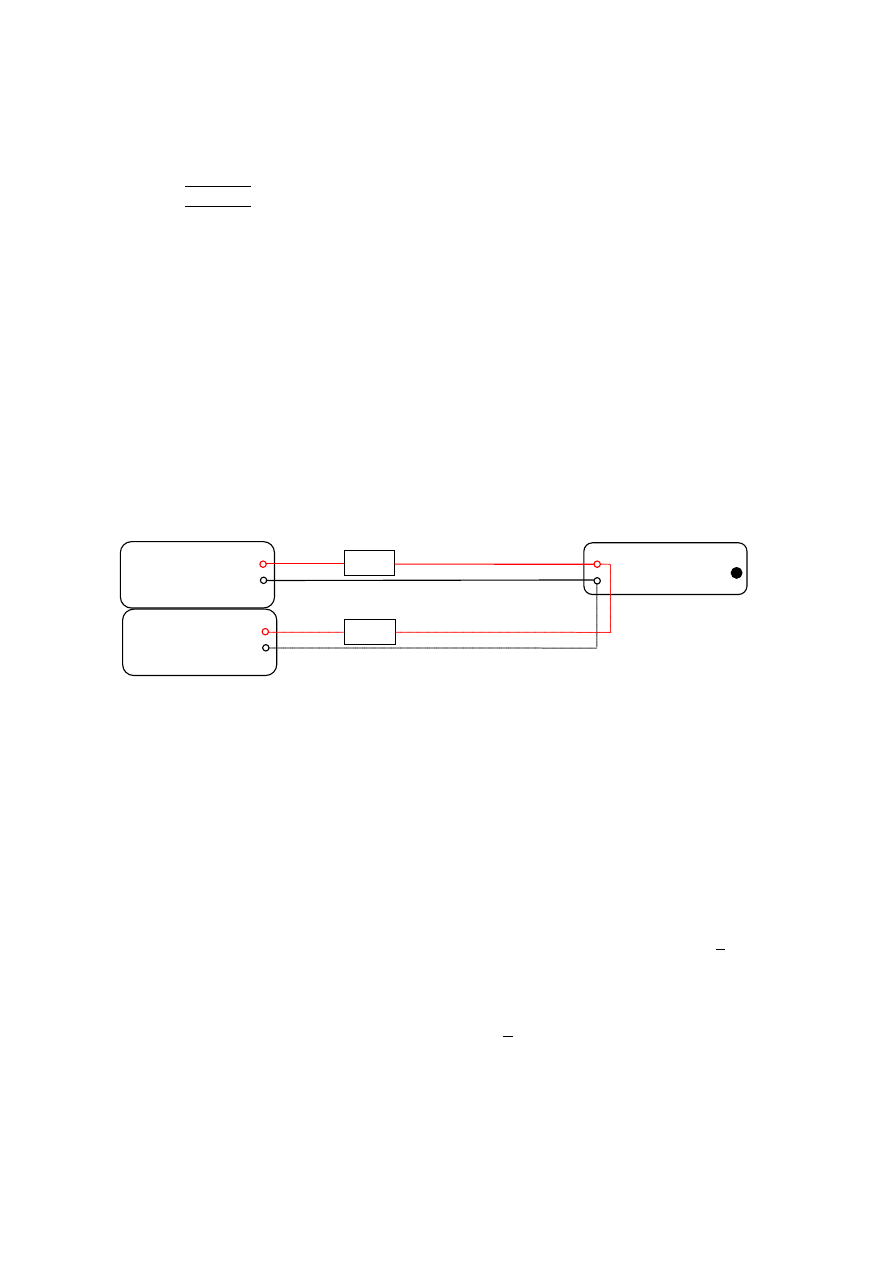
11
Składowe niepewności wyznacza się analogicznie jak w przypadku wzorcowania i są one
opisane równaniami od 22 do 26
. Niepewność wskazania u(W) wyznacza się jak dla
pojedynczego pomiaru wg równania:
u(W
� ) = �
∑(W
i
−W
���)
2
(n−1)
(30)
W którym n
≥ 10 [3].
Podsumowując: celem wzorcowania jest przede wszystkim przyporządkowanie
wskazaniom
przyrządu poprawek lub błędów , które będą wykorzystywane podczas
jego eksploatacji. Końcowym efektem wzorcowania może być krzywa kalibracji [3].
Sprawdzanie natomiast ma na celu ustalenie za pomocą pomiarów, czy błędy wskazań
przyrządu nie przekraczają dopuszczalnych wartości granicznych. [3].
4.
SPOSÓB REALIZACJI ĆWICZENIA
4.1
SPRAWDZENIE MIERNIKÓW DO POMIARU TEMPERATURY Z
TERMOELEMENTU TYPU K ORAZ WYZNACZENIE POPRAWEK I KRZYWEJ
KALIBRACJI
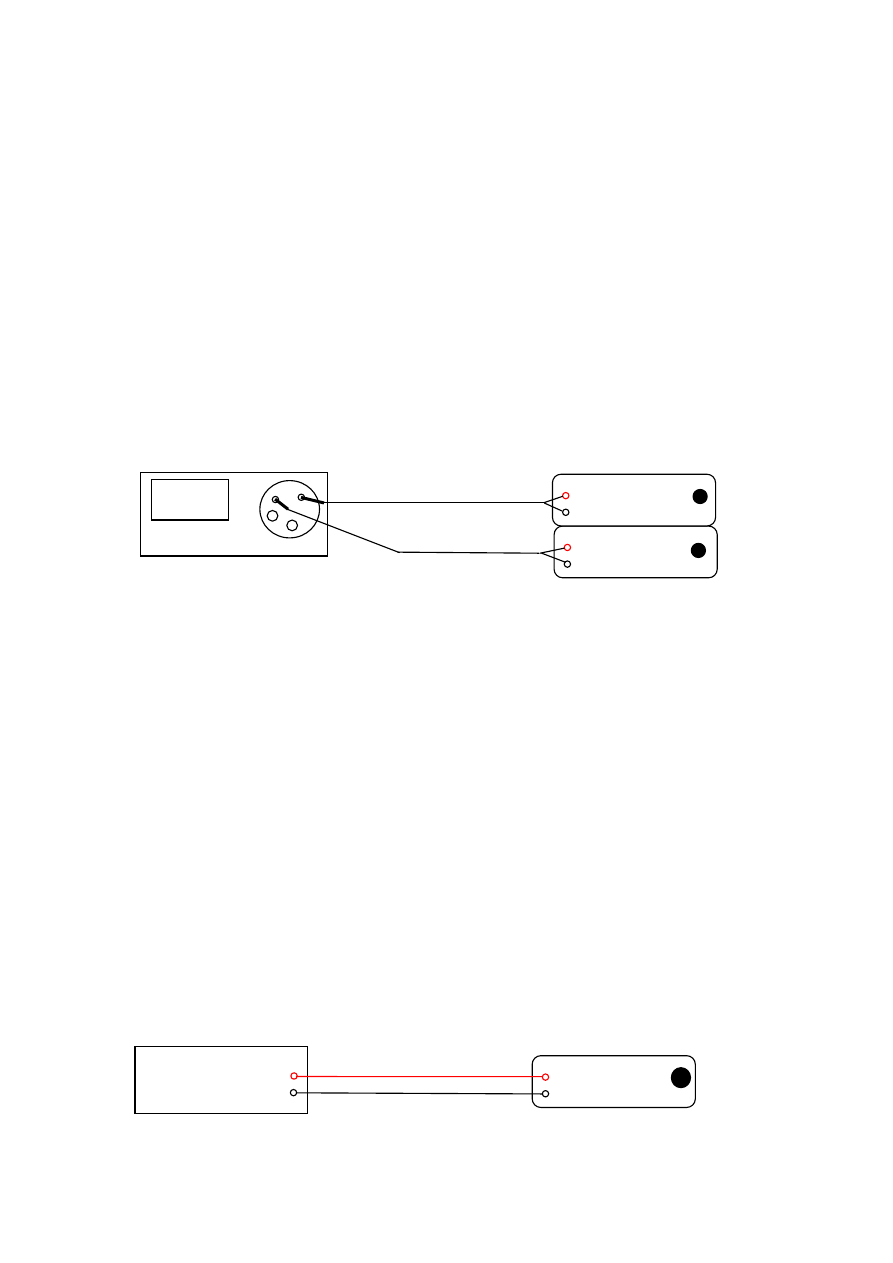
Schemat stanowiska :
Sprawdzenie miernika nr 2 odbywa się dla trzech temperatur: 200
°
C, 400
°
C i 600
°
C w
następujący sposób:
•
wcisnąć w kalibratorze przycisk K oznaczający typ termoelementu oraz przycisk cal.
•
podłączyć do układu opór linii 10Ω
•
pokrętłem nastawić temperaturę np. 200
°
C
•
odczytać 10 krotnie temperaturę na mierniku
•
obliczyć błąd wskazania E
w
wg równania (28) oraz (29)
•
obliczyć niepewność błędu u(E
w
) wg równania błędu, przyjmując:
j
eżeli nie ma rozrzutu wyników to u(W) = 0
δ
rw
= 0, a u(
δ
rw
) liczyć z równania (25) przyjmując, że rozdzielczość temperatury
wynosi d= 20
°
C.
u(N) -
przyjąć z danych technicznych kalibratora: błąd graniczny
Δ
g
= ±0,1%
wartości wskazanej ±1
°
C; niepe
wność u(N) liczyć z równania u(N) = Δ
g
/
√3.
o
dczytać temperaturę otoczenia t
o
.
Miernik wzorcowany był przy temperaturze
t
ow
=20
°
C-
jeżeli temperatura t
o
jest mniejsza od t
ow
to
𝛿
𝑤𝑜
= t
ow
- t
o
w przeciwnym
razie
δ
wo
= t
o
- t
ow
. Błąd graniczny temperatury otoczenia przyjąć Δ
g
= ±1
°
C, a
niepew
ność liczyć z równania: u(δ
wo
) = Δ
g
/
√3
obliczyć niepewność rozszerzoną na poziomie ufności α=0,95 (współczynnik
rozszerzenia k=2); Niepewność rozszerzona U= k·u.
s
prawdzić czy E
w
±U(E
w
) <= Δ
gm
; bład graniczny miernika Δ
gm
= ± klasa·zakres/100
Miernik 1:
Zakres 20-1200
°
C
Klasa 1,5
R
L
=10Ω
Miernik 2:
Zakres 20-1200
°
C
Klasa 1,5
R
L
=10Ω
Kalibrator napięć
termoelektrycznych C402
12
4.2. WYZNACZENIE POPRAWEK DLA MIERNIKA NR 1
Poprawki należy wyznaczyć dla temperatur: 100
°
C, 200
°
C, 300
°
C, 400
°
C….1000
°
C, w
następujący sposób:
•
wcisnąć w kalibratorze przycisk K oznaczający typ termoelementu oraz przycisk cal.
•
podłączyć do układu opór linii 10Ω
•
nastawić na kalibratorze t
k
= 100
°
C i odczytać temperaturę na mierniku t
m
Błąd systematyczny wynosi ∆
s
t = t
m
− t
k
, a poprawka P
t
= -
∆
s
t
•
procedurę powtórzyć dla następnych temperatur od 200
°
C do 1000
°
C z krokiem co 100
°
C
i dla
każdej z nich wyznaczyć poprawkę
•
sporządzić wykres zależności poprawki od temperatury na kalibratorze tzn. P
t
= f(t
k
)
• spo
rządzić krzywą kalibracji miernika – zależność temperatury na kalibratorze
(rzeczywistej)
t
k
od temperatury wskazywanej przez miernik t
m
i podać równanie
analityczne tej krzywej przyjmując np., że jest ona linią prostą.
4.3. WYZNACZENIE POPRAWEK DLA CZUJNIKA Pt 100
Schemat stanowiska:
Poprawki
wyznaczyć dla temperatur ustawianych w piecyku: 50
°
C, 100
°
C, 150
°
C, 200
°
C,
250
°
C, 300
°
C i 350
°
C w następujący sposób:
-
ustawić w piecyku temperaturę 50
°
C
i poczekać aż nastawiona temperatura ustali się
-
włączyć w kalibratorach przycisk Pt>200
-
podłączyć oba termometry Pt 100 wejść kalibratora o rezystancji linii 0Ω ( zaciski HI,
LO)
-
odczytać temperaturę w piecyku t
p
,
temperaturę t
1
pokazywaną przez Pt
1
100 , oraz
temperaturę t
2
pokazywaną przez Pt
2
100
-
obliczyć różnicę Δt
p
= t
1
- t
p
i sprawdzić, czy różnica ta jest mniejsza od błędu granicznego
wynikającego z klasy termometru platynowego Pt
1
100 –
błąd graniczny dla termometru
platynowego wykonanego w klasie 2 wyraża się równaniem (17)
-
dla nastawionej e temperatury w piecyku obliczyć błąd systematyczny Δ
t2
=t
2
- t
1
, a
następnie poprawkę P
t2
= -
Δ
t2
-
procedurę powtórzyć dla wszystkich temperatur wymienionych na początku tzn.: 100
°
C….350
°
C.
-
sporządzić wykres zależności P t
2
= f(t
1
)
4.4. SPRAWDZENIE
MIERNIKA DO POMIARU NAPIĘCIA
TERMOELEKTRYCZNEGO (MULTIMETRU)
Schemat stanowiska:
100
°
C
Kalibrator
termo rezystancji C403
Kalibrator
termo rezystancji C403
Pt
1
100,
t
1
Pt
2
100,
t
2
Piecyk Fluke
Klibrator
termorezystancji C403
Multimetr
TH1942
Kalibrator napięć i
prądów stałych C401
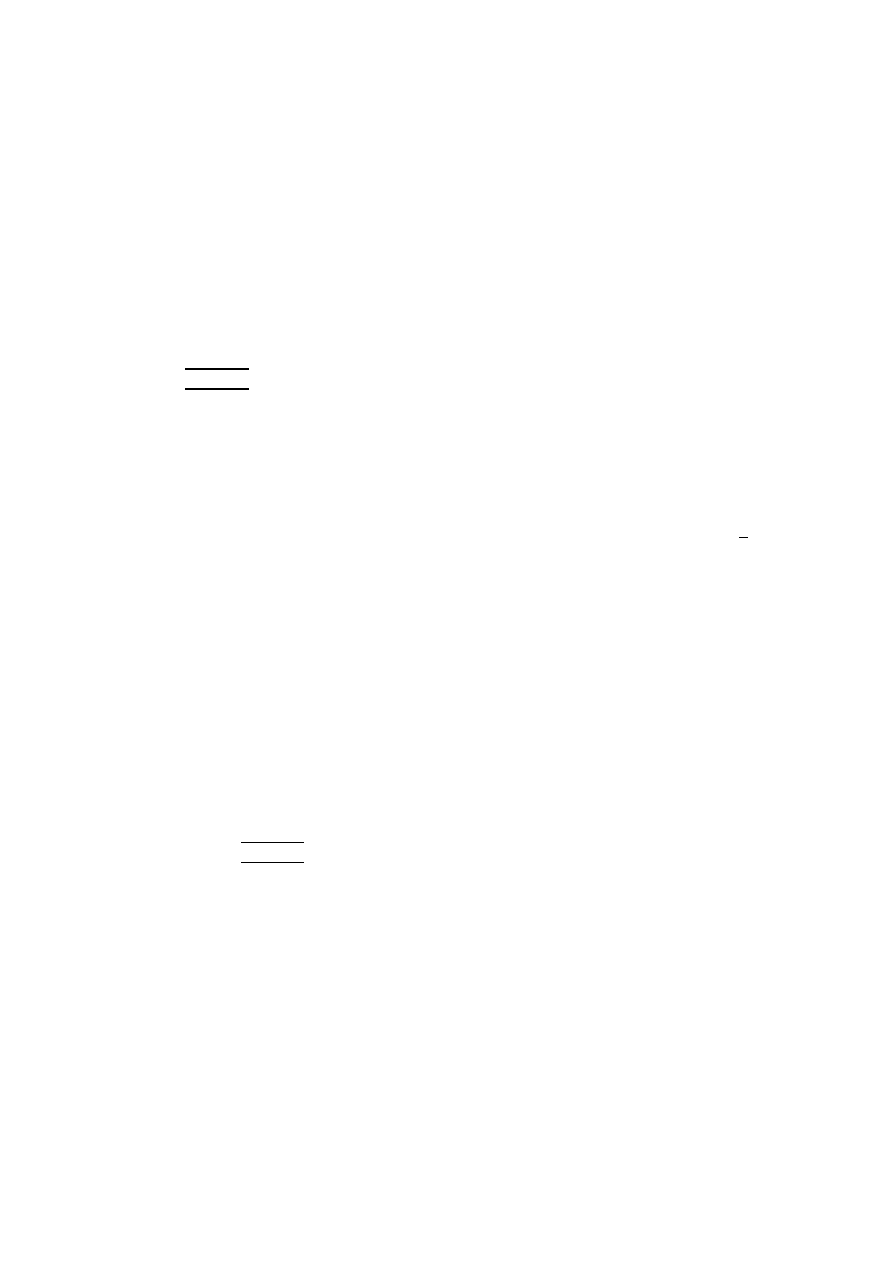
13
Sprawdzenie wykonać tylko w jednym punkcie pomiarowym zgodnie z następującą
procedurą:
•
włączyć kalibrator- przycisk Power
•
wcisnąć przycisk kalibracji cal i przycisk mV
•
włączyć multimetr
•
nastawić pokrętłem kalibratora np. wartość napięcia U= 20mV i odczekać chwilę aż
napięcie na kalibratorze ustabilizuje się
•
dla tej wartości napięcia odczytać 10 razy wartość napięcia pokazywaną przez
multimetr u
1
, u
2
, …, u
10
O
bliczyć niepewność błędu u(E
w
) wg równania
błędu, przyjmując:
u(W
� ) = �
∑(w
i
−W
���)
2
n(n−1)
w
i
=u
i
,
w� = U�
przyjąć δ
rw
= 0, a u(
δ
rw
) liczyć z równania (25) przyjmując, że rozdzielczość
temperatury wynosi d= 0,01
mV.
u(N) -
przyjąć z danych technicznych kalibratora : błąd graniczny Δ
g
= ±0,1%
wartości nastawionej + 6cyfr ; 6 cyfr oznacza:6*wartość napięcia odpowiadająca
ostatniej cyfrze maksymalnego wskazania
Wmax - dla zakresu
napięć do 100mV
maksymalne wskazanie to 99,99 ostatnia cyfra to 0,01
więc błąd graniczny Δ
g
/mV=
±0,1% wartości nastawionej + 6·0,01; u(N) liczy się z równania u(n) = Δ
g
/
√3.
przyjąć δ
wo
= 0 oraz u(δ
wo
) = 0
p
oliczyć wartość błędu wskazania E
w
z równania (28)
, niepewność u(E
w
) z równania
(29)
oraz niepewność rozszerzoną na poziomie ufności α=0,95 (współczynnik
rozszerzenia k=2); Niepewność rozszerzona U= k·u.
Sprawdzić czy E
w
±U(E
w
) <= Δ
gm
;
błąd graniczny multimetru Δ
gm
= ±0,02%
wartości wskazanej +0,016%zakresu ( dla zakresu z= 500 mV)
Sprawdzić następnie czy błąd pojedynczego wskazania wartości napięcia na
multimetrze zawiera się w przedziale ± Δ
gm
, wg procedury:
•
Wybrać największe wskazanie z 10 odczytanych wartości napięcia na
multimetrze U
MAX
•
obliczyć błąd pomiaru E
w
= U
MAX
– U
•
policzyć odchylenie standardowe pojedynczego pomiaru wg równania
𝑢(𝑊) = �
∑(𝑤
𝑖
−𝑊
� )
2
(𝑛−1)
, gzie n= 10
•
sprawdzić czy u(W) jest większe od błędu rozdzielczości liczonego z równania ,
gdzie d= 0,01 mV: jeżeli tak to przyjąć, że δ
rw
= 0 i u(
δ
rw
) = 0
•
u(N) liczyć tak jak w poprzednim przykładzie
•
przyjąć δ
wo
= 0 oraz u(δ
wo
) = 0
Policzyć wartość błędu wskazania E
w
z równania,
niepewność u(E
w
) oraz
niepewność rozszerzoną na poziomie ufności α=0,95 ( współczynnik rozszerzenia
k=2); Niepewność rozszerzona U(E
w
)= k·u(E
w
).
Sprawdzić czy E
w
±U(E
w
) <= Δ
gm
;
błąd graniczny multimetru Δ
gm
= ±0,02%
wartości wskazanej +0,016%zakresu ( dla zakresu z= 500 mV)
14
5. PYTANIA KONTROLNE
1. Za
sada działania termoelementów
2.
Zasada działania termometrów oporowych
3.
Wymienić przykładowe termoelementy i termometry oporowe
4.
Co to jest wzorcowanie przyrządów
5.
Co to jest sprawdzanie przyrządów
6. Równanie na
błąd wskazania, z wyjaśnieniem wielkości wchodzących w jego skład.
7. Co to jest
błąd symetryczny i poprawka
6. LITERATURA
1. L. Michalski, K. Eckersdorf, J. Kucharski:
Termometria. Przyrządy i metody, Politechnika
Łódzka, Łódź 1998
2. M. Nau: Elektrische Temperaturmessung, JUMO GmbH ECO.KG, Fulda, Fulda
November 2004
3. J. Arendarski:
Niepewność pomiarów, Oficyna wydawnicza Politechnika Warszawskiej,
Warszawa 2006
Data wykonania instrukcji:
19.10.2010