12.

Stochastyczne podejście do stopy procentowej.

( Zmienność stopy procentowej)

12.1 Wprowadzenie

Poprzednie rozdziały w tej książce prezentowały teorię stopy procentowej, w dużej

mierze na podłożu deterministycznym. Rozdział 12 wprowadza czytelnika w stochastyczne

(przypadkowe) podejście do stopy procentowej.

W rzeczywistości, pojawiły się dwie dziedziny w poprzednich rozdziałach, w których

wyraźnie przedstawione zostały prawdopodobieństwa. Pierwszą dziedziną było rozważenie

domniemanych prawdopodobieństw w Sekcji 9.8, drugą zaś była hipoteza odnosząca się do

wycofania ze świadectwa ilustracji depozytowej w Sekcji 11.9. Wzór (11.17) na pochodną

trwania został również oznaczony rozbieżnym zapisem dla łatwości prezentacji. Ostatecznie,

pojawiło się domniemane rozpoznanie ryzyka oraz niepewność w tychże dziedzinach, jako

praktyki obligacji płatnych na żądanie oraz rat stawek kredytów hipotecznych. Jednak,

wcześniejsze podejście przedstawione w książce było w dużej mierze deterministyczne.

W rozdziale 12 najpierw rozważymy stopę procentową jako przypadkową zmienną.

Następnie, uwzględnimy zasadnicze przedstawienie kilku modeli wraz ze stochastycznym

podłożem, co ma ważne zastosowanie w praktyce. Na koniec, zbadamy obszernie używanego

podejścia scenariusza testowania jako środka dotyczącego przyszłej niepewności.

Zakładamy, iż czytelnik posiada podstawową wiedzę w statystykach matematycznych.

Poziom statystyk użytych w tym rozdziale nie jest zaawansowany. Czytelnicy, którzy

chcieliby odświeżyć wiedzę dotyczącą rezultatów statystyk, użytych w tym rozdziale, niech

odniosą się do Załącznika D.

12.2

Niezależna Stopa Oprocentowania

Rozważmy teraz stopę oprocentowania jako przypadkową zmienną. W Sekcji 12.2 i

12.3 rozważymy przypadek w którym stopa procentowa w jednym okresie jest

niezależna od stóp oprocentowania w innym okresie. Zaczynając od Sekcji 12.4

usuniemy niezależna hipotezę i zbadamy niektóre modele, w których kolejne stopy

procentowe korelują pod pewnymi względami.

Wstępna ilustracja

Na początku pokażemy, iż przewidywane skumulowane i obecne wartości nie są

jednakowe w stosunku do skumulowanych i obecnych wartości w oczekiwanej stopie

procentowej. W celu zaprezentowania tej możliwości, rozważmy inwestycję jednostki

na 10 lat w stosunku do stałej efektywnej stopy procentowej, która jest nieznana ale

równa prawdopodobieństwu bycia 7%, 8% lub 9%.

Niech

będzie oznaczało efektywną stopę procentową. Z podstawowych statystyk

oczekiwana stopa procentowa jest obliczana w ten sposób:

Przewidywana skumulowana wartość jest obliczana:

Jednakże, skumulowana wartość przewidywanej stopy procentowej obliczana jest:

Dlatego też, na tej ilustracji, przewidywana skumulowana wartość nie jest równa

skumulowanej wartości przewidywanej stopy procentowej. Stopa procentowa j, która

przedstawiłaby przewidywaną skumulowaną wartość może być uwarunkowana poprzez:

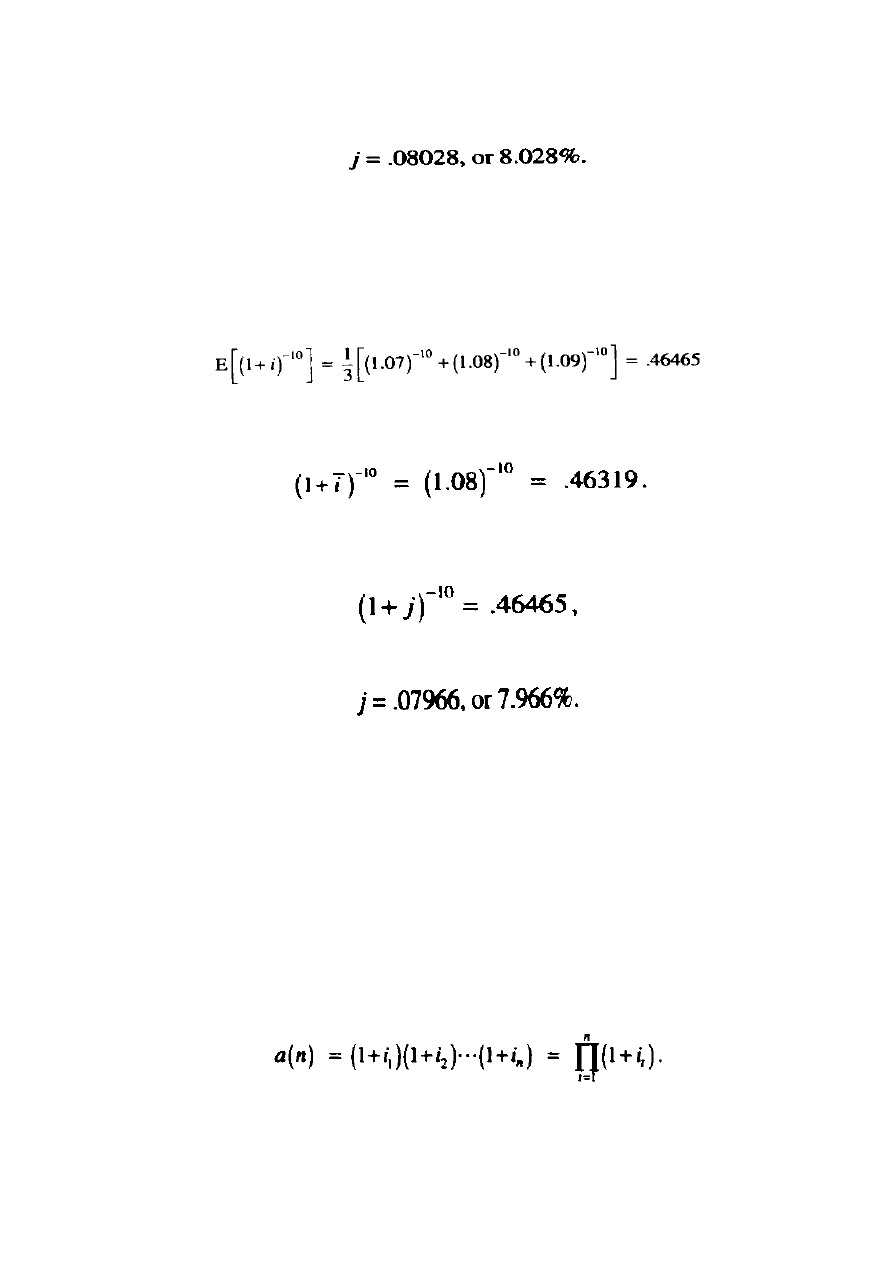
Co może być rozwiązane poprzez:

Podobny rezultat może również występować dla obecnych wartości. Zakładając, iż

chcemy zainwestować dziś określoną kwotę, dotyczącą jednej jednostki, na dziesięć lat, na

warunkach opisanych powyżej, dotyczącej nieznanej stałej stopy procentowej.

Przewidywana obecna stopa procentowa obliczana jest:

Podczas gdy obecna wartość przewidywanej stopy procentowej obliczana jest:

Stopa procentowa j , która przedstawiałaby przewidywaną obecną wartość może być

uwarunkowana poprzez:

Co może być rozwiązane poprzez:

Skumulowane wartości

Na powyższych ilustracjach założyliśmy, iż niepewna stopa procentowa była stała od

dziesięciu lat. Obecnie rozważamy sytuację, w której stopa procentowa może być różna w

różnych okresach, według niektórych prawdopodobieństw, które nie zmieniają się z czasem.

Przyjmiemy zapisy użyte w Rozdziale 1 i pozwolimy aby stopa procentowa podczas

okresu rth, i.e. od czasu t – l do t, była oznaczona poprzez i, dla t+1,2,……,n. Skumulowana

wartość inwestycji l na koniec okresu n jest obliczana poprzez wzór (1.40) ze zmianą w

zapisie

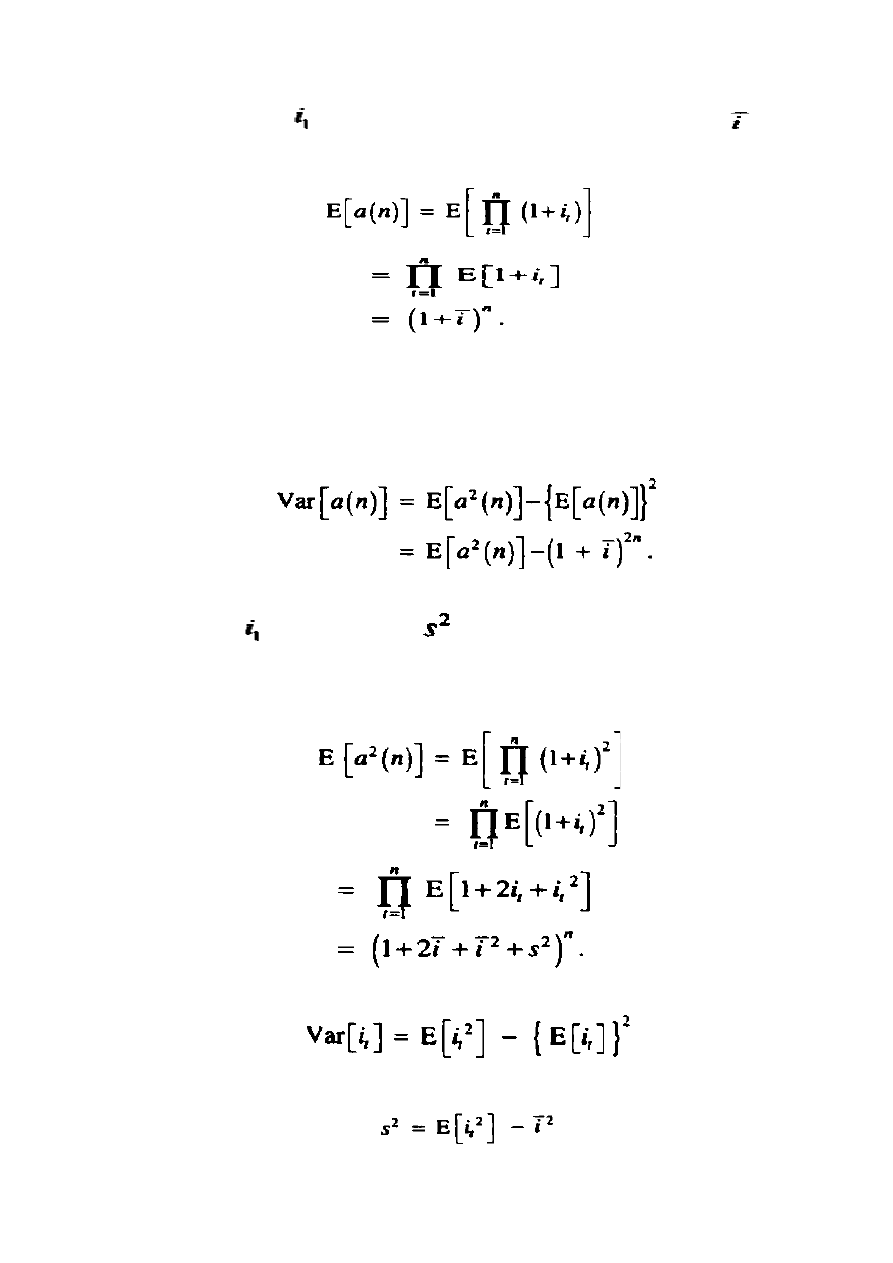
A teraz załóżmy, iż

są niezależnie i identycznie rozprowadzane ze środkiem

.

Ś

rodek skumulowanej wartości obliczany jest:

Zauważ, iż w tym przypadku przewidywana skumulowana wartość nie jest równa

skumulowanej wartości przewidywanej stopy procentowej.

Następnie rozważymy wariancję skumulowanej wartości, która jest:

Załóżmy, iż

mają stałą wariancję

. Następnie będziemy mogli obliczyć drugi

moment źródła a(n).(moment pochodzenia)

Ten wynik oparty jest na fakcie, iż dla każdej wartości t

Lub

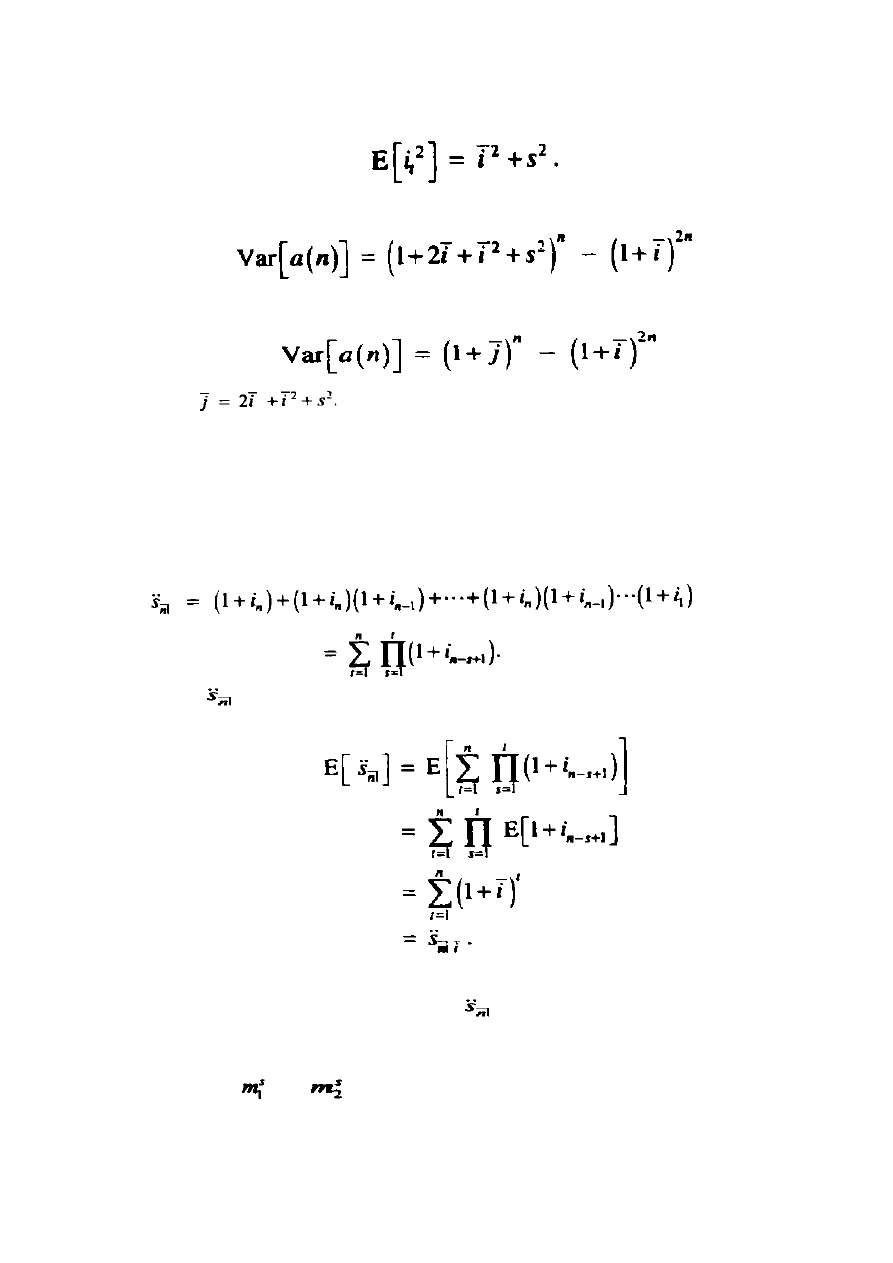
Co daje

Dlatego też, różnica skumulowanej wartości obliczana jest:

Co może być zapisane jako:

Gdzie

Teraz poszerzymy powyższą analizę, dotyczącą pojedynczej płatności do poziomu

rocznej raty. Rozważmy okres – n jako obowiązek spłaty rocznej raty. Podążając poglądem

opracowanym w Sekcji 3.8 dla metody stopy, skumulowana wartość roczna raty to:

Ś

rednia

może być uzyskana poprzez wzór:

Następnie postaramy się znaleźć wariancję

. Różnica serii tych form jest złożona i

przedstawiona jest w Załączniku 12 na końcu rozdziału.

Zdefiniujmy

oraz

jako pierwszy i drugi moment l+i, pod kątem źródła,

odpowiednio:

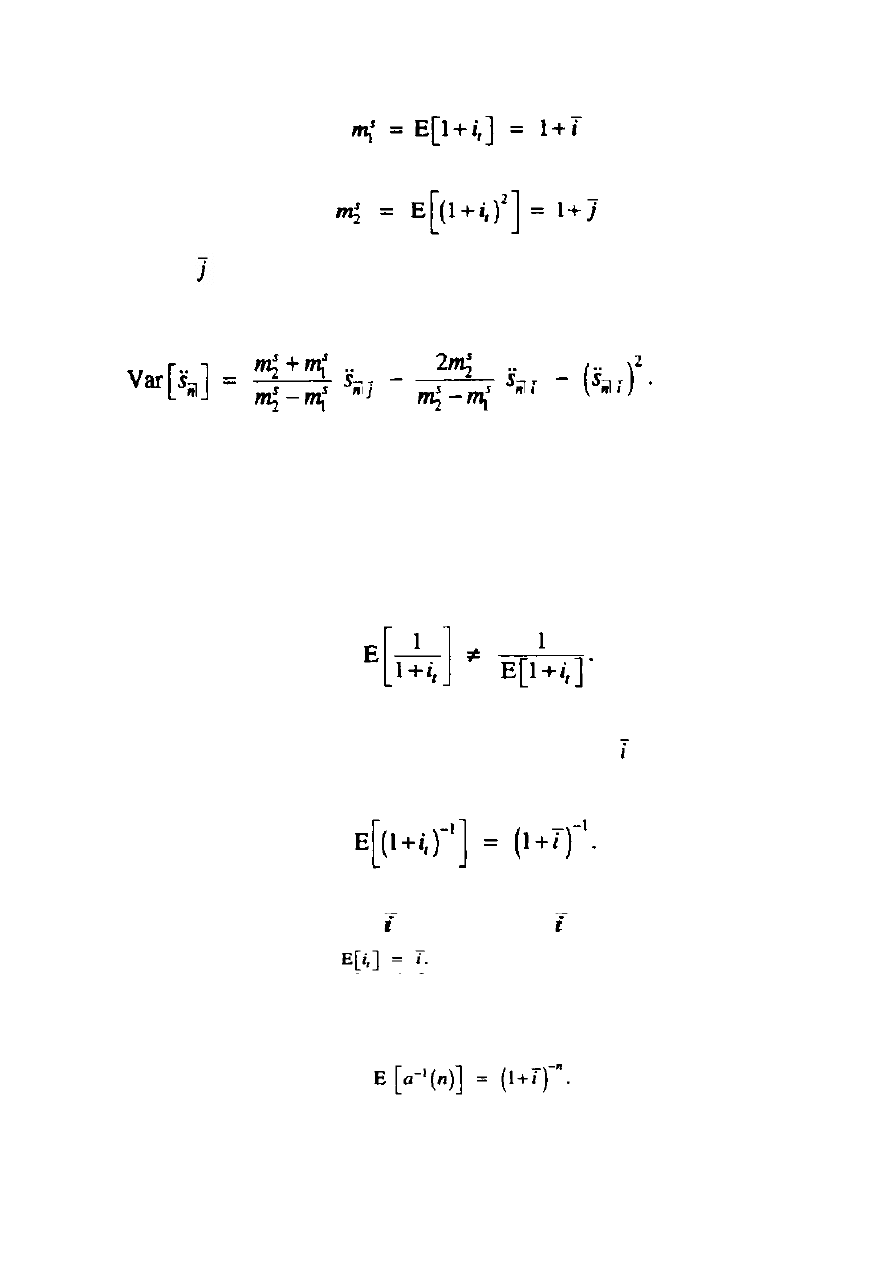
Oraz:

Gdzie

jest określone we wzorze (12.4b). Następnie stosując rezultaty z Załącznika

12, otrzymujemy:

Obecne wartości

Podobne rezultaty do tych powyżej dla skumulowanych wartości mogą być także

opracowane dla obecnych wartości. Jednakże, musimy być ostrożni przy wyborze stopy

procentowej, Ogólnie rzecz biorąc, otrzymujemy:

Dlatego też, prezentując obecne wartości musimy zdefiniować

jako:

Musimy zaznaczyć, iż wartość różni się od wartości , użytej powyżej dla

skumulowanych wartości gdzie

Nasz pierwszy wynik to rozwinięcie wzoru dla średniej obecnej wartości, pojedynczej

płatności, analogicznie do wzoru (12.1), otrzymamy:

Uzyskany wzór (12.9) jest podobny do wzoru (12.1) i pozostaje ćwiczeniem.

Dla wariancji obecnej wartości otrzymujemy:

Gdzie:

Niestety, bez wiedzy rozprowadzenia

, nie będziemy w stanie dowiedzieć się w jaki

sposób opracować

. Pogląd przedstawiony powyżej, w celu znalezienia drugiego momentu

dla skumulowanych wartości, nie będzie miał zastosowania dla obecnych wartości. Wzór

(12.10) wymaga obliczenia drugiego momentu opartego na konkretnej gęstości

prawdopodobieństwa.

Tymczasem, powróćmy do obecnej wartości okresu – n , bezpośredniej rocznej raty z

Sekcji 3.8

Ś

rednia

jest oczekiwanym wynikiem:

Uzyskany wzór (12.11) jest podobny do wzoru (12.5) i pozostaje ćwiczeniem.

W końcu rozważmy wariancję

. Zdefiniujmy

oraz

jako pierwszy i

drugi moment

pod względem źródła pochodzenia:

Powtórnie otrzymując wyniki z Załącznika 12, otrzymujemy:

Wynik numerycznych rozwiązań

Zatem, jeśli znamy pierwszy i drugi moment

oraz

, możemy znaleźć

ś

rednią i różnicę skumulowanej wartości lub obecnej wartości, zarówno pojedynczej płatności

jak i poziomu raty rocznej. Możemy przyjąć prawdopodobieństwo ścisłości funkcji dla

.

Niestety, powyższe wzory nie dają wyniku dla gęstości prawdopodobieństwa, nawet jeśli

ś

rednia i różnica są nam znane.

Standardowym rozwiązaniem dla tej sytuacji w praktyce, jest użycie symulacji.

Procedurę przedstawiamy poniżej:

1.

Założyć prawdopodobieństwo ścisłości funkcji dla

i jej parametrów

2.

Przygotować przypadkową serię liczb oraz przeprowadzić tak dużo prób jak tylko jest

to możliwe. Jeśli próby m będą zamierzone, wtedy przypadkowe liczby mn będą

niezbędne.

3.

Używając standardowych technik symulacji, używać tylko przypadkowych liczb, w

celu obliczenia mnogości m dla wartości

4.

Dla każdej mnogości m

, obliczyć wymaganą funkcję finansową, np.

, lub inne funkcje.

5.

Wyniki m mogą być użyte w celu rozwinięcia przybliżonej prawdopodobności

ś

cisłości funkcji, dla tej właśnie funkcji finansowej. Oszacowane prawdopodobności

dla możliwych wyników mogą być obliczone z wyników m.

Nie będziemy omawiać bliżej techniki symulacji ponieważ zakładamy, iż czytelnik jest

zaznajomiony w tym temacie. Czytelnicy, którzy nie są zaznajomieni z tą techniką

proszeni są o odniesienie się bezpośrednio do całej książki.

Przykład 12.1 Załóżmy, że i jest obowiązującą stopą procentową, oddzieloną przedziałem

czasowym

dla t = 1,2 i 3. Dla skumulowanej wartości inwestycji 1 w

przeciągu ostatnich 3 lat, znajdź:

(1)

Ś

rednią

(2)

Odchylenie standardowe

1.

Dla jednolitego podziału otrzymujemy:

Bezpośrednie zastosowanie wzoru (12.1) daje nam:

2.

Dla jednolitego podziału otrzymujemy:

Bezpośrednie zastosowanie wzoru (12.4a) daje nam:

Dlatego też, odchylenie standardowe to

. Ta odpowiedź wydaje się

racjonalna w stosunku do związku z maksymalnym zakresem możliwych wyników, tzn.:

do

Przykład 12.2. Przeróbmy Przykład 12.2 dla skumulowanej wartości inwestycji 1, na

początku każdego roku w przeciągu trzech lat.

1.

Bezpośrednie zastosowanie wzoru (12.5) daje:

2.

Stosując wzory (12.6) oraz (12.7) otrzymujemy:

i

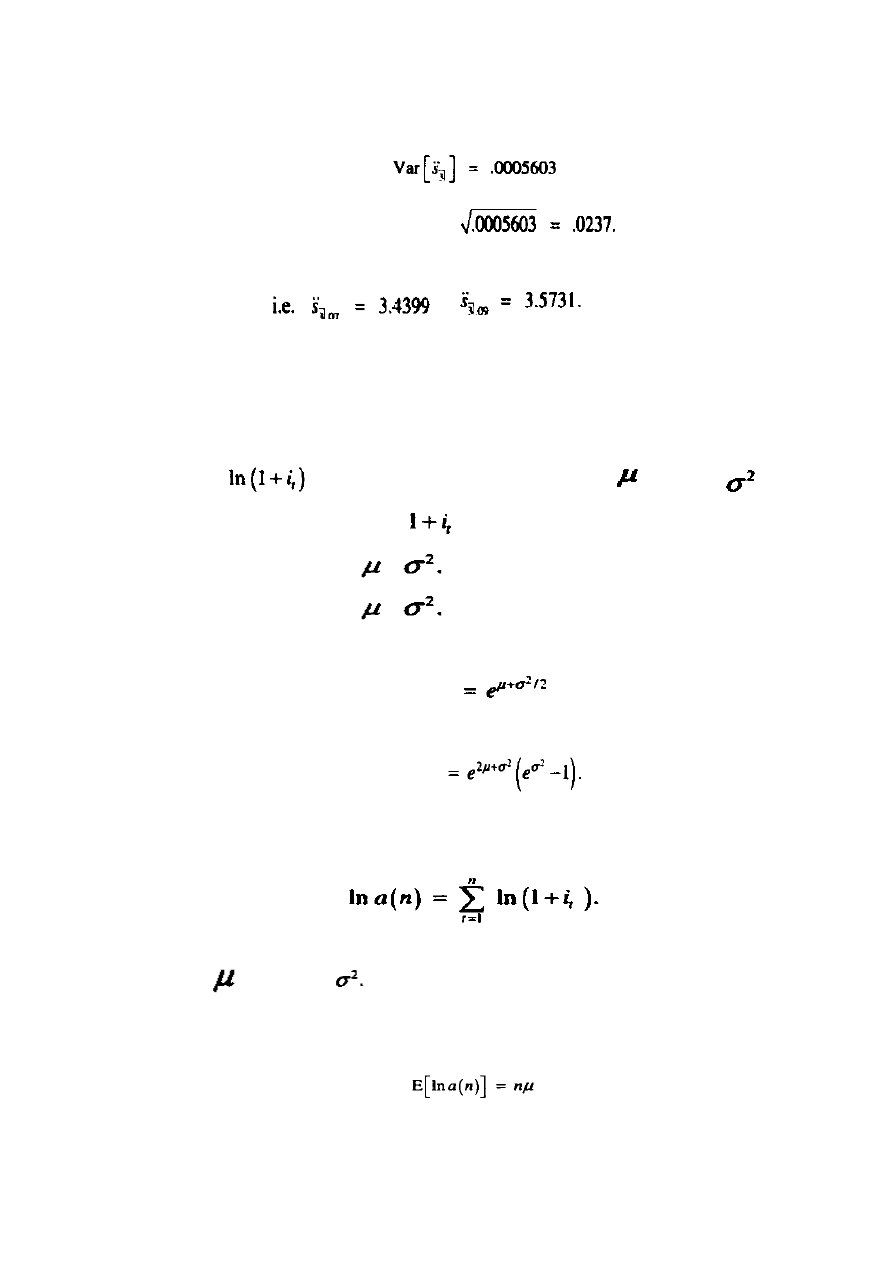
Stosując wzór (12.8) otrzymujemy:

Tak, że standardowe odchylenie wynosi

. Ten wynik wydaje

być się racjonalnym w stosunku do związku z maksymalnym zakresem możliwych

wyników, tzn.:

do

12.3 Model Logarytmicznie - Normalny

Występuje jeden ważny przypadek modelu ukazanego w Sekcji 12.2 dla

którego przydatny wynik może być uzyskany analitycznie. Załóżmy, iż przypadkowa

zmienna

poprzedza zwykłe rozdzielenie ze średnią

i wariancją

.

Następnie przypadkowa zmienna

poprzedza logarytmicznie-normalne

rozdzielenie z parametrami

i

Średnia i różnica logarytmicznie-normalnego

rozdzielenia z parametrami

i

dają:

Ś

rednia

I

Wariancja

Zaczynając od wzoru (1.40), jak w Sekcji 12.2, otrzymujemy:

Prawa strona równania jest sumą n – niezależnych przypadkowych zmiennych ze

ś

rednią

i wariancją

Ponieważ średnie i wariancje są zależne od siebie, kiedy występuje niezależne

rozdzielenie, otrzymujemy:

I

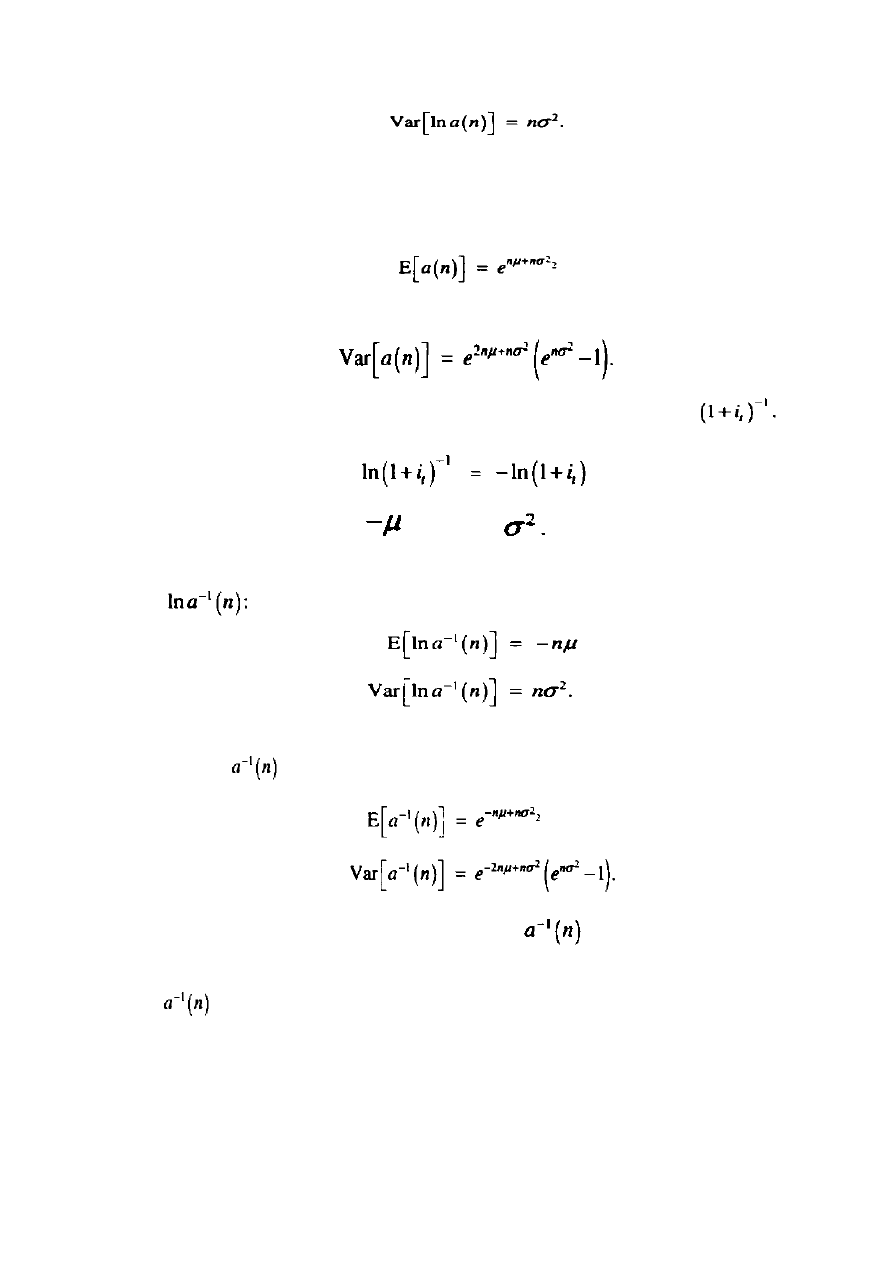
Bezpośrednio a(n) idzie w parze z logarytmicznie-normalnym rozdzieleniem, którego

ś

rednie i wariancje są od siebie zależne, w takim przypadku otrzymujemy:

I

Omówmy obecne wartości dla których musimy zanalizować rozdzielenie

:

co rozłożone jest na średnią

i wariancję

Dlatego też, otrzymujemy następujące rozszerzone wzory (12.18) oraz (12.19) dla

W podobnym przypadku, otrzymujemy także rozszerzone wzory (12.20) oraz (12.1)

tylko dla

:

Powyższe wariancje wzorów dla a(n) oraz

, tzn. wzory (12.21) oraz

(12.25) są skomplikowane i trudne do opracowania. W praktyce, logarytmy a(n) oraz

są zwykle stosowane, co pozwala nam zastosować normalne rozdzielenie i

pracować z o wiele prostszymi wzorami (12.19) oraz (12.23), w momencie gdy

potrzebujemy różnic.

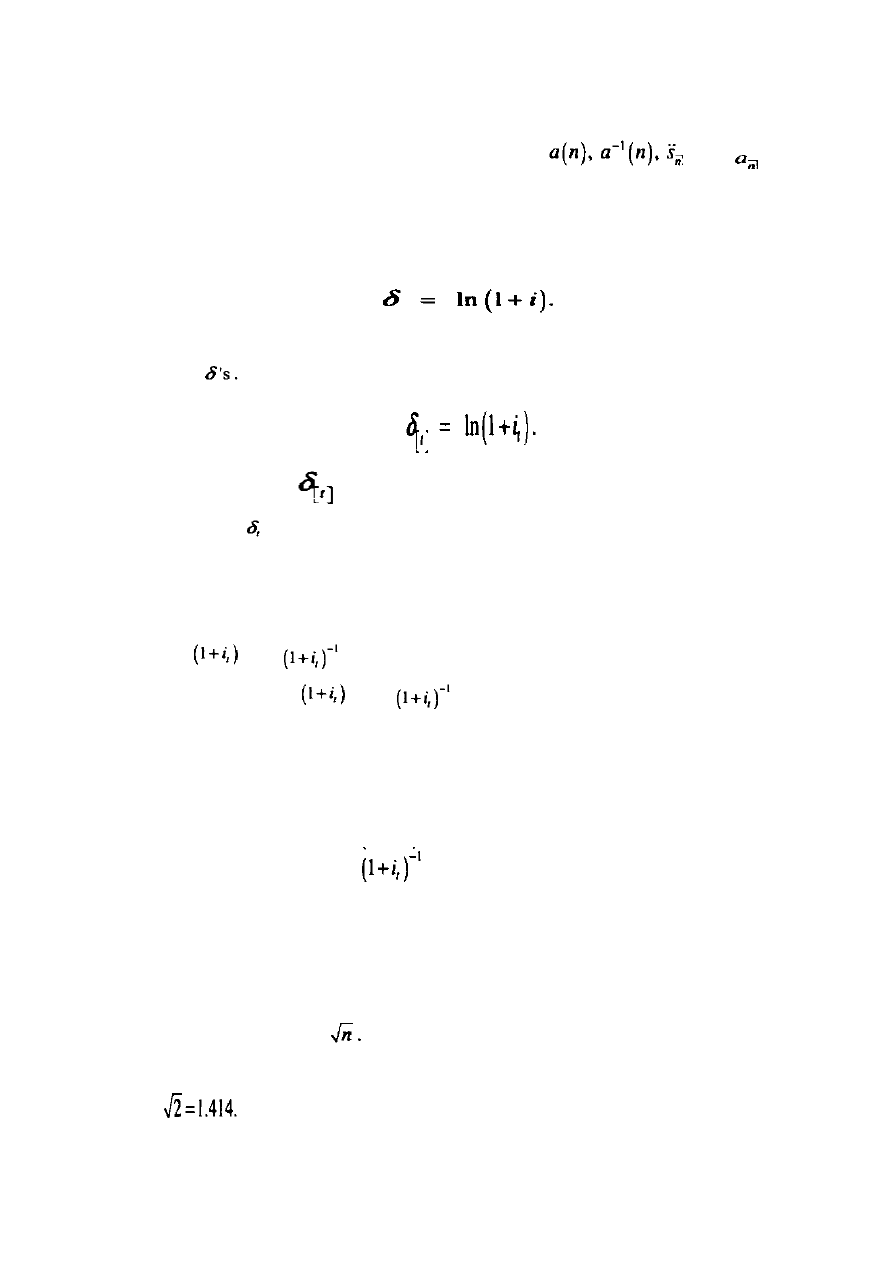
Wraz z powyższymi wzorami, jesteśmy w stanie znaleźć momenty i oszacować

prawdopodobne zestawienia, o możliwych wynikach

oraz

bez odnoszenia się do symulacji.

Przypomnijmy wzór (1.33) dla natężenia stopy procentowej:

Zatem, widzimy, iż wzór po prawej stronie (12.17) może być zinterpretowany jako

suma

Tak jak w Sekcji 1.10 definiujemy:

Nawias odróżnia

, które jest poziomem odpowiedniego natężenia do przedziału

t – 1 do t, z , które jest odpowiednim natężeniem tylko dla chwilowego momentu t.

To wydaje się być racjonalne w niektórych przypadkach aby przypuszczać, że

wahania w natężeniu stopy procentowej wiążą się ze zwykłą dystrybucją. Kiedy ta

hipoteza potwierdza się, wtedy połączone nagromadzenie oraz pominięte czynniki ,

tzn:

oraz

, będą szły wraz z logarytmicznie-normalnym rozkładem.

Nawet jeśli

oraz

nie idą w parze z logarytmicznie-normalnym

rozkładem, jest wciąż możliwe aby użyć logarytmów przy zastosowaniu normalnego

rozkładu, w celu poszerzenia n. Jest to zastosowaniem Centralnego Twierdzenia

Limitu w statystykach. To twierdzenie udowadnia zastosowanie wzorów: (12.18) i

(12.19) oraz wzorów (12.22) i (12.23) jako dopuszczalnych przybliżeń dla poszerzenia

n, niezależnie jak l + i oraz

są rozdzielone. Centralne Twierdzenie Limitu

może być wtedy użyte jako prawdopodobne przewidywania oraz aby rozwinąć pewne

już przedziały dla różnych wyników. Będzie to przedstawione w Przykładzie 12.4.

Jednym z końcowych spostrzeżeń jest zauważenie średnich i wariancji dla

normalnego rozkładu proporcjonalnie do n. Jednakże, odchylenie standardowe

proporcjonalne jest do

Na przykład, w analizie ln a(n), jeśli podwoimy n,

podwoi się średnia. Jednak, odchylenie standardowe tylko podwyższy czynnik

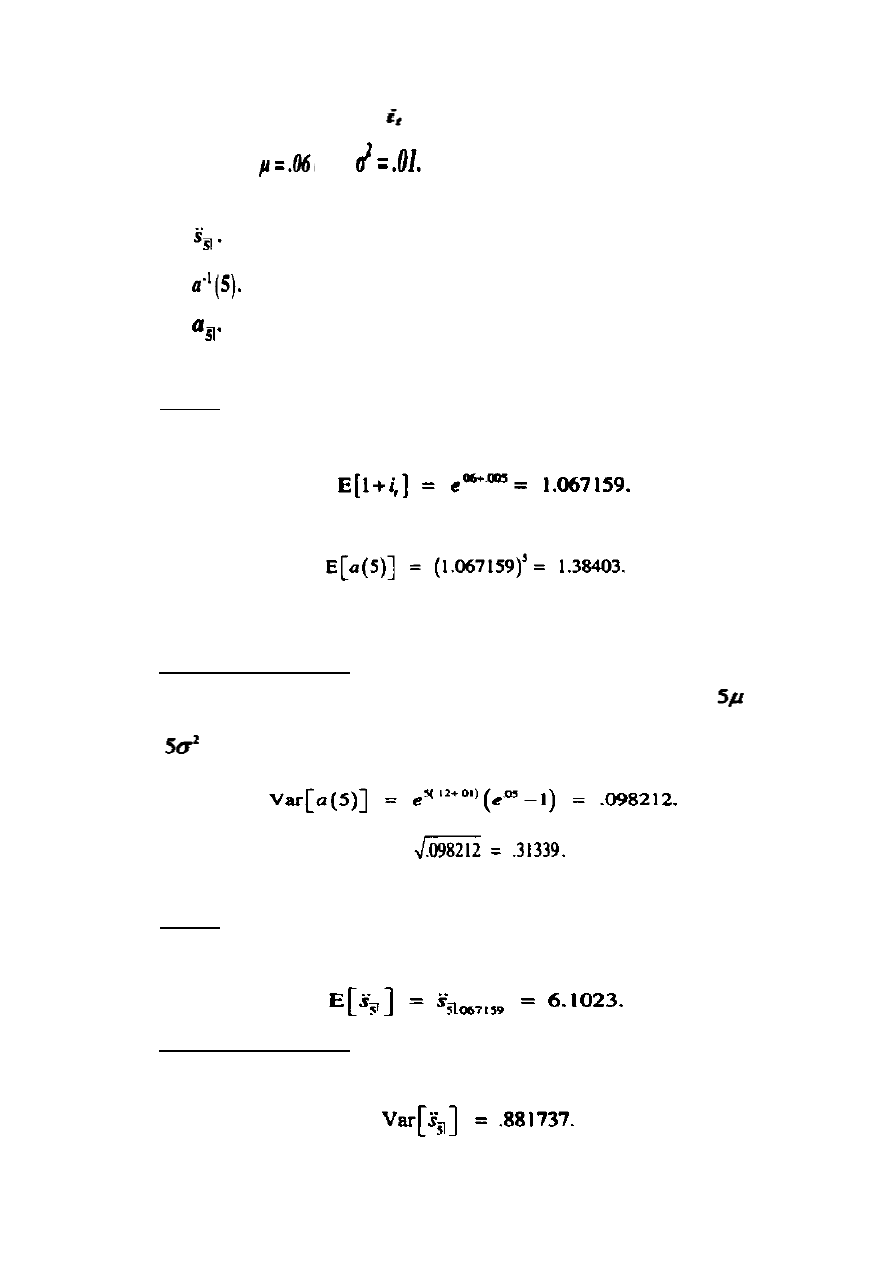
Przykład 12.3 Załóżmy, iż 1 +

idzie w parze z logarytmicznie – normalnym

rozkładem z

oraz

. Znajdź średnią i odchylenie standardowe dla:

(1)

a(5).

(2)

(3)

(4)

1.

Średnia

Ze wzoru (12.15) otrzymujemy:

Stosując wzór (12.1) otrzymujemy średnią:

Wynik może być także uzyskany poprzez bezpośrednie zastosowanie wzoru (12.20)

Odchylenie standardowe

W tym przypadku a(5) ma logarytmicznie-normalny rozkład z parametrami

oraz

, tak więc ze wzoru otrzymujemy:

Zatem, odchylenie standardowe to

. Ćwiczeniem będzie tutaj

potwierdzenie tej odpowiedzi poprzez alternatywne podejście do wzoru (12.4a).

2.

Średnia

Ze wzoru (12.8) otrzymujemy:

Odchylenie standardowe

Ze wzoru (12.8) otrzymujemy:

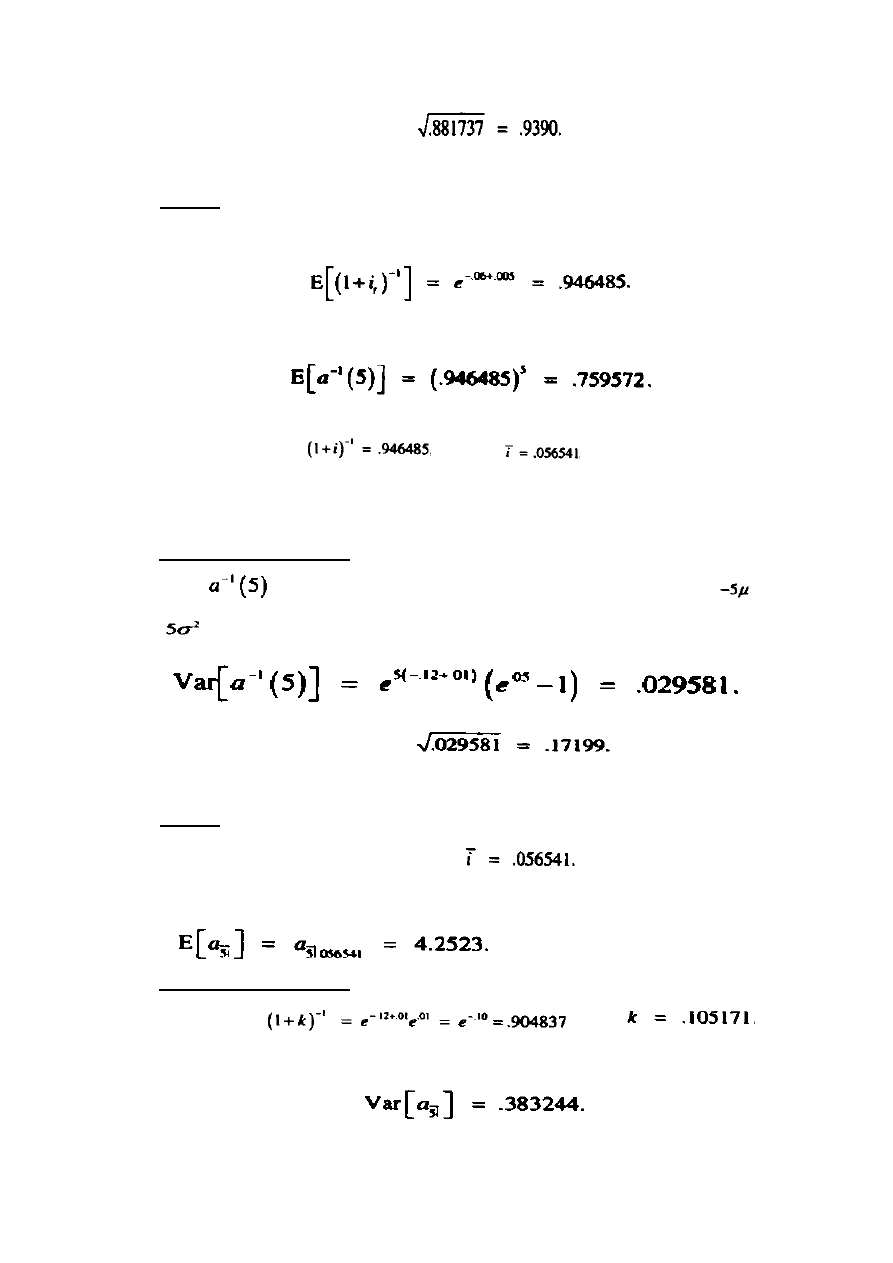
Zatem, odchylenie standardowe to

3.

Średnia

Ze wzoru (12.15) otrzymujemy:

Stosując wzór (12.9) otrzymujemy:

Ten wynik może być także uzyskany poprzez bezpośrednie zastosowanie wzoru

(12.24). Zauważ, iż

, tak więc

, co różni się w częściach 1 i

2 powyżej.

Odchylenie standardowe

Teraz

posiada logarytmiczno-normalną dystrybucję z parametrami

oraz

, tak więc ze wzoru (12.25) otrzymujemy:

Zatem, odchylenie standardowe to

4.

Średnia

W części 3 powyżej dowiadujemy się, że

. Zatem ze wzoru (12.11)

otrzymujemy:

Odchylenie standardowe

Otrzymaliśmy

, gdzie

Stosując wzór (12.14) otrzymujemy:

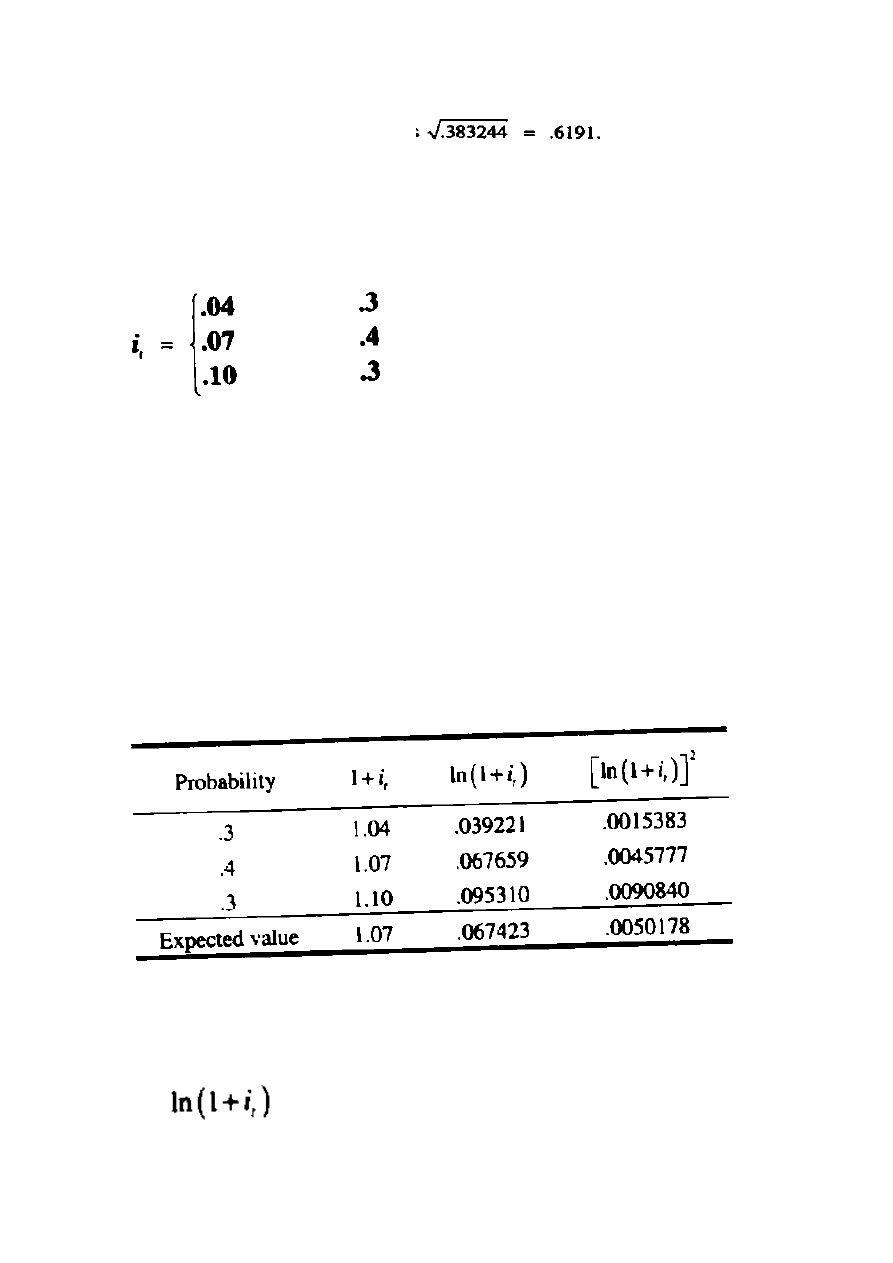
Zatem, odchylenie standardowe to

Przykład 12.4 35- latek odziedziczył $100,000 i chciałby zainwestować wszystko w

emeryturę w wieku 65 lat. Fundusz inwestycyjny zarobi na tym 4%, 7% lub 10% o

następujących prawdopodobieństwach:

Zwrot w każdym roku będzie zależał od zwrotów w latach poprzednich. Zastosuj Centralne

Twierdzenie Limitu w celu określenia sumy, jaką inwestor zgromadzi w wieku 65 lat z 95%

prawdopodobieństwem.

Tabela 12.1 zawiera kalkulacje potrzebne do sprawdzenia wymaganych wzorów w tej sekcji.

Pamiętaj, że po użyciu logarytmów będziemy zajmować się wartościami, które są normalnie

rozprowadzane.

Tabela 12.1 Kalkulacje dla Przykładu 12.4

Probability – Prawdopodobieństwo

Expected value – oczekiwana wartość

Ś

rednia

to

Wariancja

to

Otrzymujemy n= 30. Wzór (12.18) daje nam:

A wzór (12.19) daje nam:

Wartość, która może być osiągnięta występuje w pozostałych 5%. W standardowej

normalnej rozkładzie otrzymujemy:

Niech A będzie skumulowaną wartością na jednego zainwestowanego dolara i w ten sposób

otrzymamy:

Rozwiązując to równanie otrzymujemy:

Lub

Na każdego jednego zainwestowanego dolara. Zatem, odpowiedź to:

Co może być skumulowane z 95% prawdopodobieństwem w wieku 65 lat.

Jest to pouczające aby porównać tą odpowiedź ze środkiem skumulowanej wartości co daje

nam:

12.4 Czasowe modele szeregowe

W Sekcji 12.2 i 12.3 założyliśmy, iż stopy procentowe

, w każdym kolejnym

okresie są niezależne. W Sekcjach 12.4 i 12.6 rozważamy modele w których to założenie nie

sprawdza się.

Zależne stopy maja zdecydowanie intuicyjne odwołanie. Na przykład, jeśli stopa

procentowa w jednym okresie jest znacznie wyższa niż długoterminowa przeciętna stopa,

wtedy uzasadnione jest założenie, iż następująca stopa w danym okresie będzie

najprawdopodobniej wyższa niż przeciętna. To samo założenie wydaje się być uzasadnione

dla stóp niższych od przeciętnych.

Innymi słowy, historyczne doświadczenia sugerują, że bardziej prawdopodobne dla

stóp jest aby zostały wyższe lub niższe dla kilku kolejnych okresów niż dla stóp wyższych

przypadkowych lub niższych przeciętnych. To wydaje się bardziej wiarygodne, gdy

rozważamy fakt, iż poziom stóp jest związany z warunkami ekonomicznymi oraz z polityką

rządową.

Jest wiele różnych modeli, które mogą być utworzone w celu rozważenia zależności.

Niektóre z nich są poniżej możliwości tej książki. Jednakże, będziemy omawiać niektóre z

prostszych przypadków, zaczynając od szeregu czasowego analizowanych statystyk.

Kilka rodzajów modeli czasowych szeregowych zostało tutaj rozbudowanych. Główne

modele to średnia krocząca(MA), auotregresywne modele(AR) lub pomieszanie tych dwóch.

Ukażemy tylko autoregresywne modele w tej sekcji ponieważ są łatwiejsze do zastosowania.

Jednakże, czytelnicy którzy mają podstawy w czasowych modelach szeregowych powinni

rozważyć zastosowanie średniej ruchomej.

Jako przykład tego prostego założenia, rozważmy jednolity rozkład, która miał

zastosowanie w przykładach 12.1 oraz 12.12. Załóżmy, iż jednolity rozkład zastosowany jest

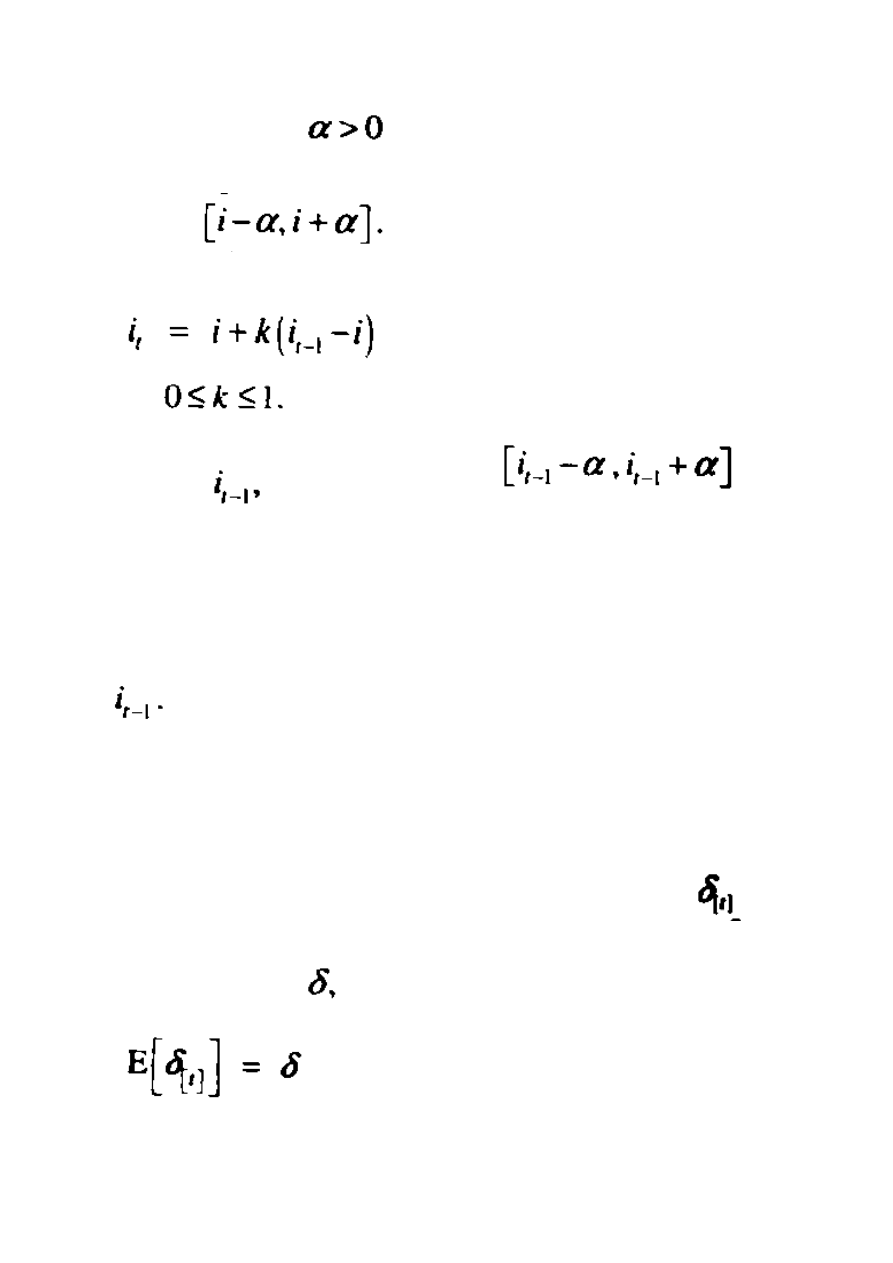
w przedziale większym niż

po stronie średniej stopy procentowej. Zatem, jeśli

długoterminowa przeciętna stopa to i, otrzymujemy więc jednolity rozkład zgodnie z

przedziałem

Teraz załóżmy, iż kolejne stopy procentowe mogą być połączone poprzez wzór:

Gdzie

. Ta zależność pokazuje, iż jednolita dystrybucja ma zastosowanie

centralnie w

, to jest zgodnie z przedziałem

dla

każdej kolejnej wartości t – 1.

Stała k jest względna do ciężaru otrzymanego w długoterminowej przeciętnej stopie

procentowej i poprzedniego okresu stopy. Jeśli k=0, wtedy otrzymujemy niezależność i

stosujemy wynik z Sekcji 12.2. Jeśli k=1, wtedy otrzymujemy całkowitą wagę w stosunku do

poprzedniego okresu stopy. Tymczasowa wartość k daje nam częściowy ciężar dla i oraz dla

. W rzeczywistości wykonujemy liniową interpolację pomiędzy dwoma z nich.

Ta prosta ilustracja dotyczy zastosowania autoregresywnego procesu pojedynczej

kolejności AR(1). Taki proces powoduje, iż stopa procentowa w jednym okresie jest wyższa

niż w poprzednim.

Kolejne wyniki zostały uzyskane poprzez zastosowanie logarytmicznie – normalnego

rozkładu w sposób zależny. Zostanie to zrealizowane poprzez specyfikacje formy

jako

określonego wzoru (12.26). Zakładamy, iż długoterminowa przeciętna siła stopy procentowej

otrzymywana jest poprzez

to jest :

Dla t = 1,2,3…..

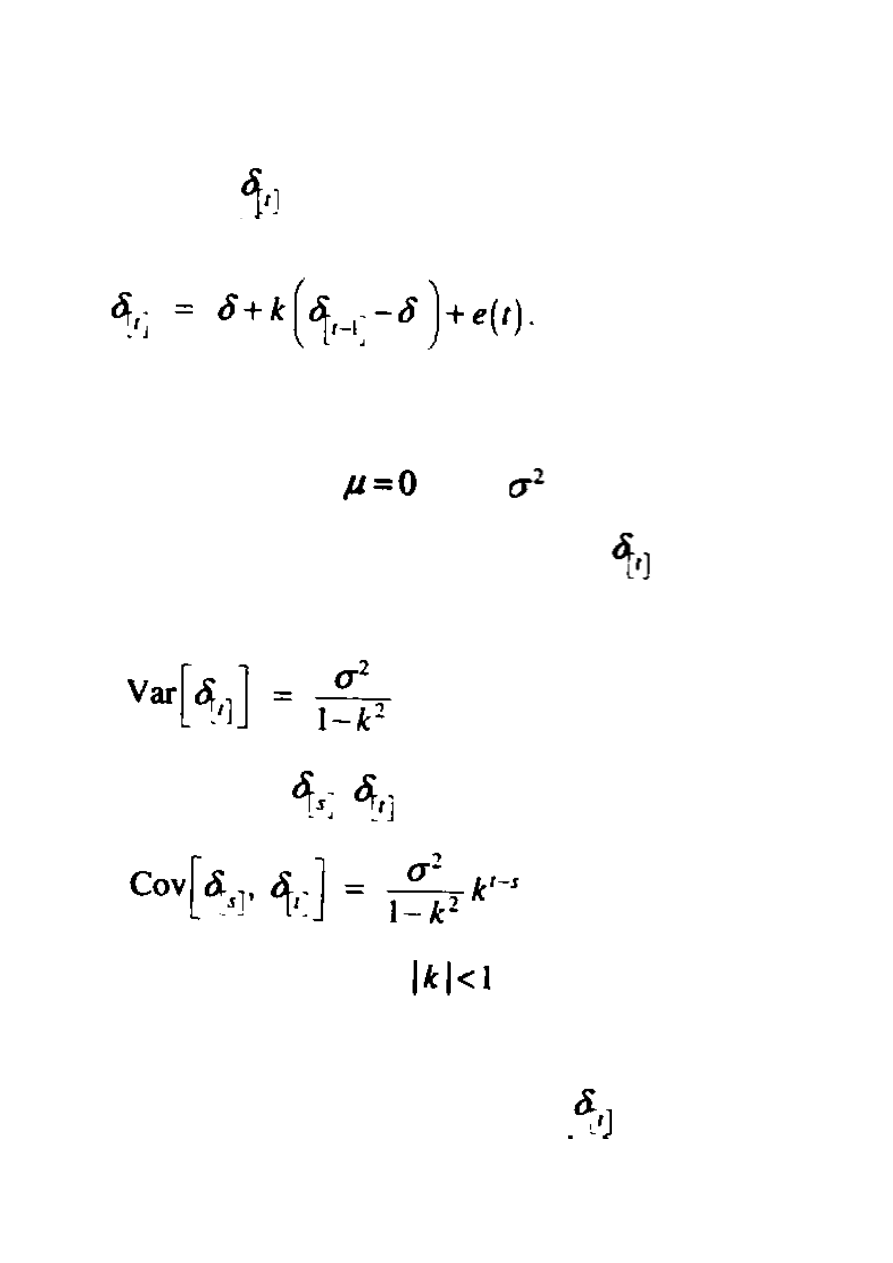
Teraz zastosujmy proces AR(1) i rozwińmy go szerzej niż przedstawiliśmy go powyżej. Ten

proces zakłada, iż

jest oparty na długoterminowej przeciętnej sile okresu

poprzedniego. Zatem, ma ono następująca formę:

Widać tutaj ewidentne podobieństwo do wzoru (12.27). Wyrażenie e(t) jest mylnym pojęciem

i zakłada, iż e(t) jest dla t = 1,2,3…. są niezależne i identycznie rozpowszechnione według

rozkładu normalnego ze średnią

i wariancją

.

Potwierdzamy te rezultaty beż żadnych dowodów. Wariancja

przedstawiona

jest jako:

A kowariancja pomiędzy

a

ukazana jest jako:

Dla t>s. Powyższe wzory wymagają aby

. Zauważ, iż k = 0, mamy więc

niezależność i wyniki, zastosowane w Sekcji 12.2.

Bardziej rozwinięta czasowo szeregowa procedura znajduje się w autoregresywnym

procesie podwójnej kolejności – AR(2). Ten proces zakłada, iż

oparte jest na

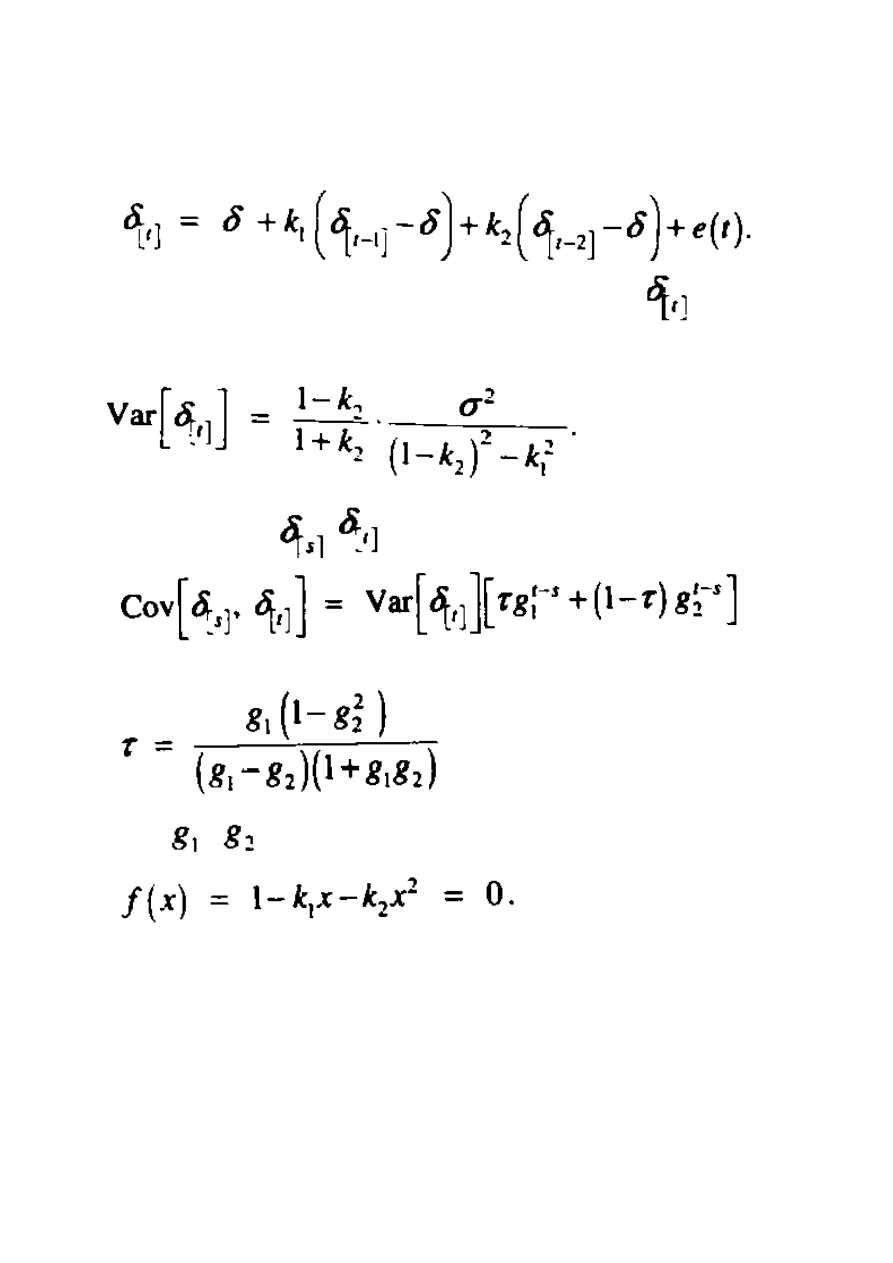
długoterminowej przeciętnej sile i siłach z poprzednich okresów. Zatem, uzyskujemy

następującą formę:

Błędne pojęcie e(t) jest określone tak samo jak w procesie AR(1). Różnica

ukazana jest

następująco:

Kowariancja pomiędzy

a

przedstawiona jest jako:

Dla t>s, gdzie

I gdzie

i

są odwzajemnione jako główne źródło charakterystycznego równania

Jest możliwe, iż powyższe równanie posiada nierzeczywiste źródło. Wyżej wymienione

wzory wymagają trzech warunków:

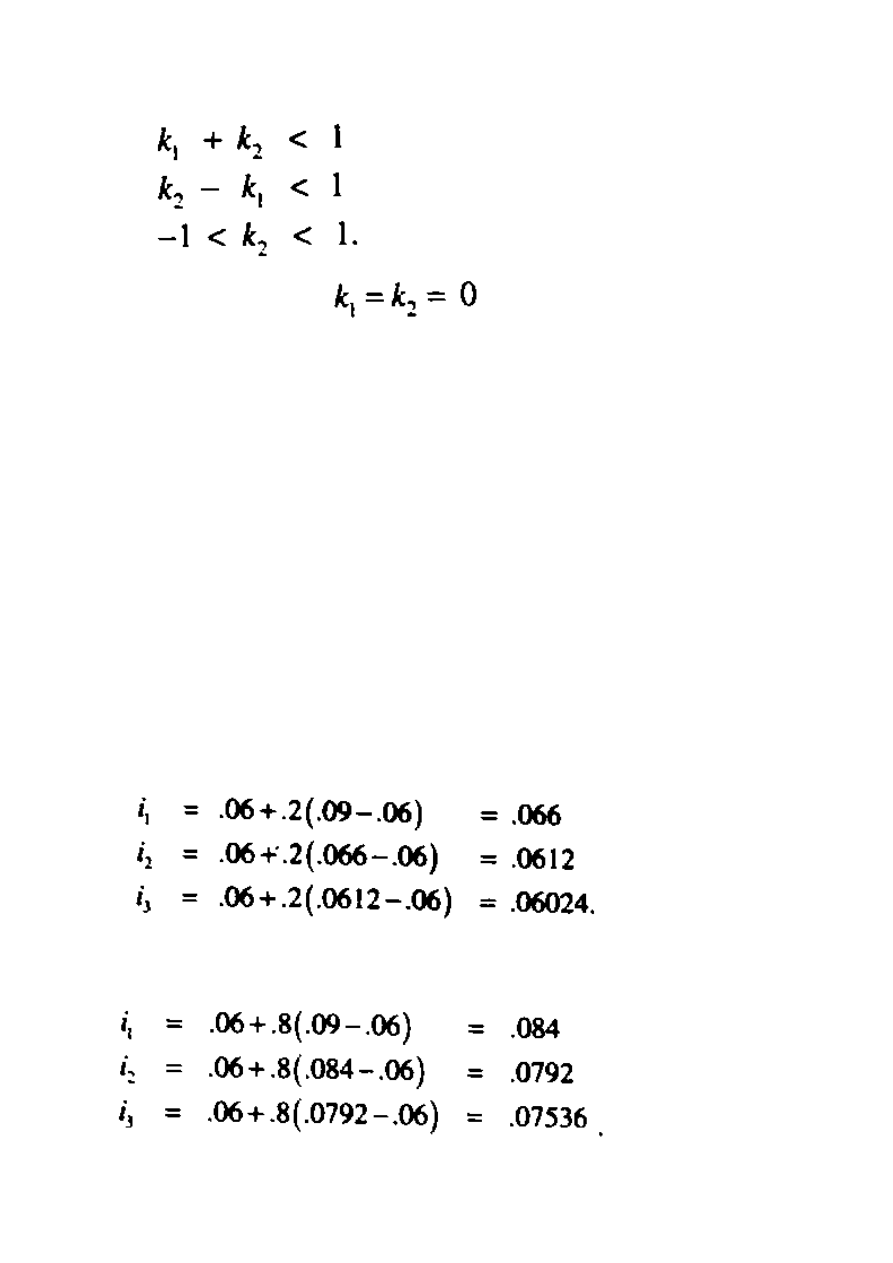
Ponownie zauważmy, że jeśli

, mamy wtedy niezależność i wyniki

zastosowane w Sekcji 12.2.

Powyższe zastosowanie procesów AR(1) oraz AR(2) jest w rzeczywistości

analityczne. Jednakże, kolejnym podejściem, które może być zastosowane jest symulacja.

Inne modele stosujące zależność, mogą być również użyte oraz realizowane wraz z

symulacją. Ważne jest, iż żaden model nie może być stosowany z empirycznymi danymi,

przed użyciem, w celu sprawdzenia jak radzi sobie model z aktualnymi wynikami.

Przykład 12.5 Załóżmy, iż długoterminowa obowiązująca stopa procentowa w

określonej sytuacji wynosi 6% a w poprzednim roku 9%. Porównaj zależność przedstawioną

we wzorze (12.27) w okresie 3 lat, zakładając, iż stopa w każdym roku jest dokładnie równa

stopie opartej na długoterminowej przeciętnej stopie i stopie z poprzedniego roku.

(1)

Jeśli k = .2.

(2)

Jeśli k = .8.

1.

Załóżmy, że:

Regresja wartości do średniej stopy 6% jest natychmiastowa.

2.

Załóżmy, że:

W tym przypadku regresja w stosunku do średniej jest znacznie wolniejsza.

Celem tego przykładu jest zilustrowanie domniemanej zależności przedstawionej przez różne

wartości k. Oczywiście w praktyce aktualna roczna stopa procentowa jest bardziej

prawdopodobna niż oszacowana stopa oparta na długoterminowej przeciętnej stopie i stopy z

poprzedniego roku, tak że powyższa równa zależność będzie znacznie podwyższona.

Jednakże, efekt wyboru k, będzie wyraźny w pojęciach wielkości regresji w stosunku do

długoterminowej przeciętnej stopy procentowej jak na powyższej ilustracji.

Przykład 12.6 Wiemy, iż

idzie w parze z procesem AR(1) ze średnią = .09,

różnicą = .003, oraz kowariancją pomiędzy sąsiadującymi wartościami = .002. Oszacowana

wartość

wynosi .075. Znajdź aktualną wartość

.

Podzieliliśmy wzór (12.31) wzorem (12.30) aby uzyskać:

Oznaczmy aktualne wartości poprzez

oraz oczekiwane wartości poprzez

. Ze

wzoru (12.29) otrzymujemy:

Co daje nam:

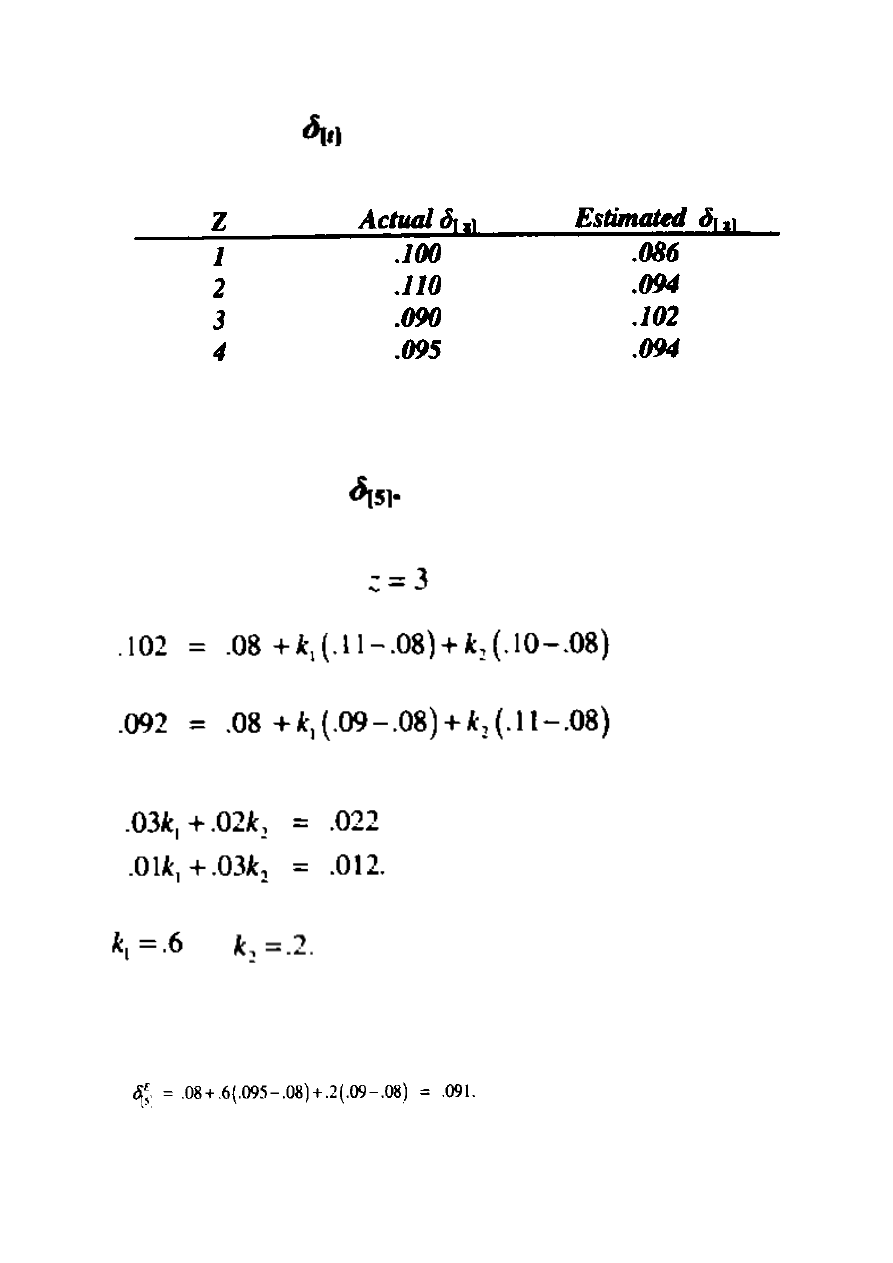
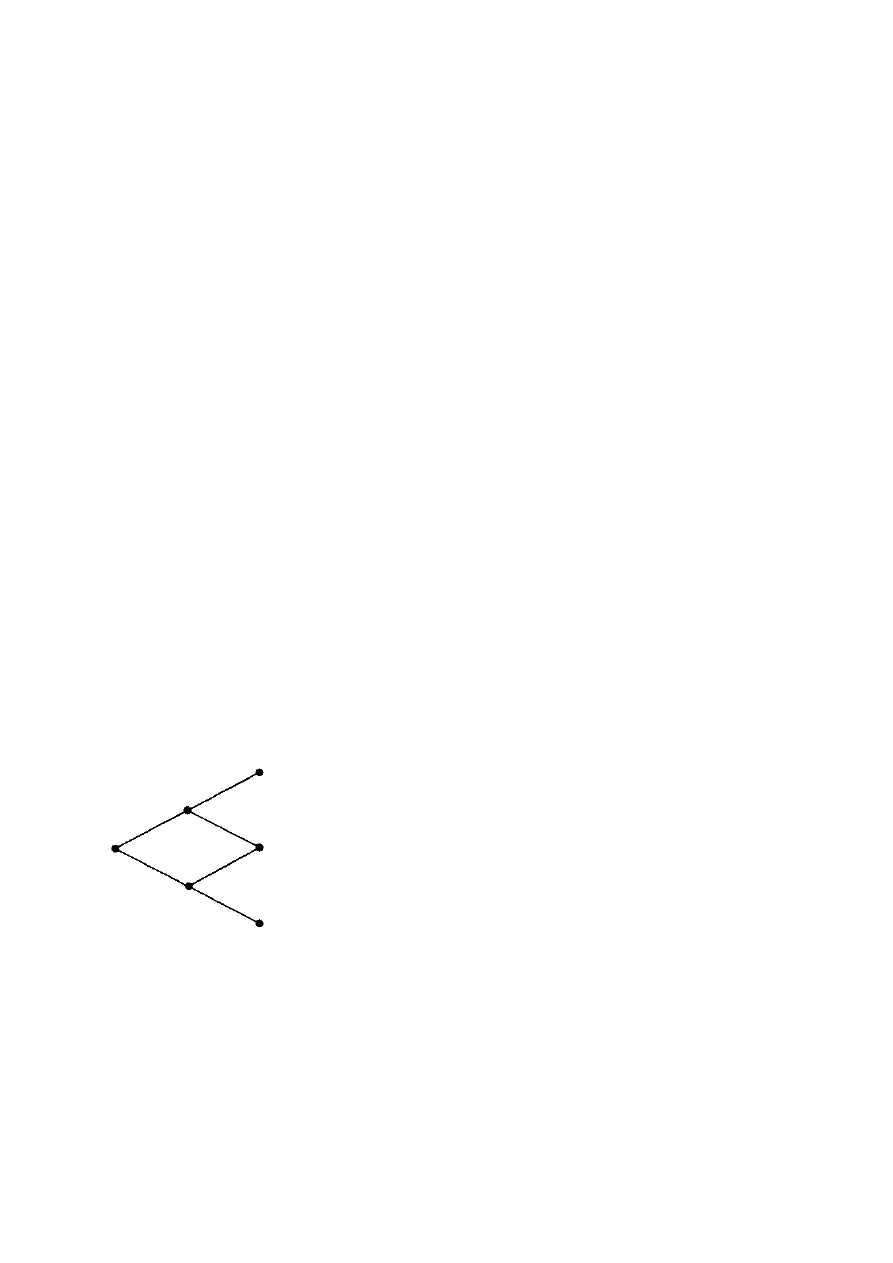
Przykład 12.7 Wiemy, że

idzie w parze z procesem AR(2) ze średnią równą .08.

Następujące wartości przedstawione są poprzez tabelę

Actual – Aktualnie

Estimated – Oczekiwane

Znajdź oczekiwaną wartość dla

Jeśli zastosujemy wzór (12.32) dla

oraz 4, otrzymamy:

W skróconym zapisie otrzymujemy:

Są to dwa równania z dwoma niewiadomymi, które mogą być rozwiązane stosując

oraz

. Zauważ, iż wartości k spełniają trzy wymagane warunki.

Zatem, otrzymujemy:

12.5 Drzewo Dwumianowe

Kolejnym zależnym modelem stopy procentowej jest model dwumianu. Ten model

tworzy szereg przyszłych ścieżek stopy procentowej, dotyczących ciągu ruchów górnych i

dolnych w stopie procentowej. Przedstawiona graficznie prezentacja zwana jest zwykle

dwumianem kratowym lub drzewem dwumianu.

Model dwumianu rozpoczyna się obecną stopą procentową, co pozostaje poziomem

ponad niektóre określone okresy a następnie porusza się zarówno w górę jak i w dół z

ustanowionym prawdopodobieństwem. Nie może pozostawać to poziomem, zatem, nazwa

„dwumian” dotyczy faktu, iż są dwie możliwości wyniku, gdzie prawdopodobieństwo

sumuje się.

Proces powtarza się w kolejnych okresach w przyszłości. Ilość okresów jest wyższa w

stosunku do modelu opartego na określonym zastosowanemu. Każdy kolejny okres jest

równy pod względem długości a prawdopodobieństwa ruchów górnych i dolnych pozostają

niezmienione w każdym okresie.

Metoda dwumianu jest przykładem błądzenia losowego, terminu uzyskanego w

zastosowanych statystykach. Początkowa wartość dla każdego okresu jest końcowym

punktem poprzedniego okresu. Również i wynik w każdym okresie jest niezależny od

okresów poprzednich.

Drzewo dwumianu ilustruje graficznie różnicę.

Zamknięte drzewo

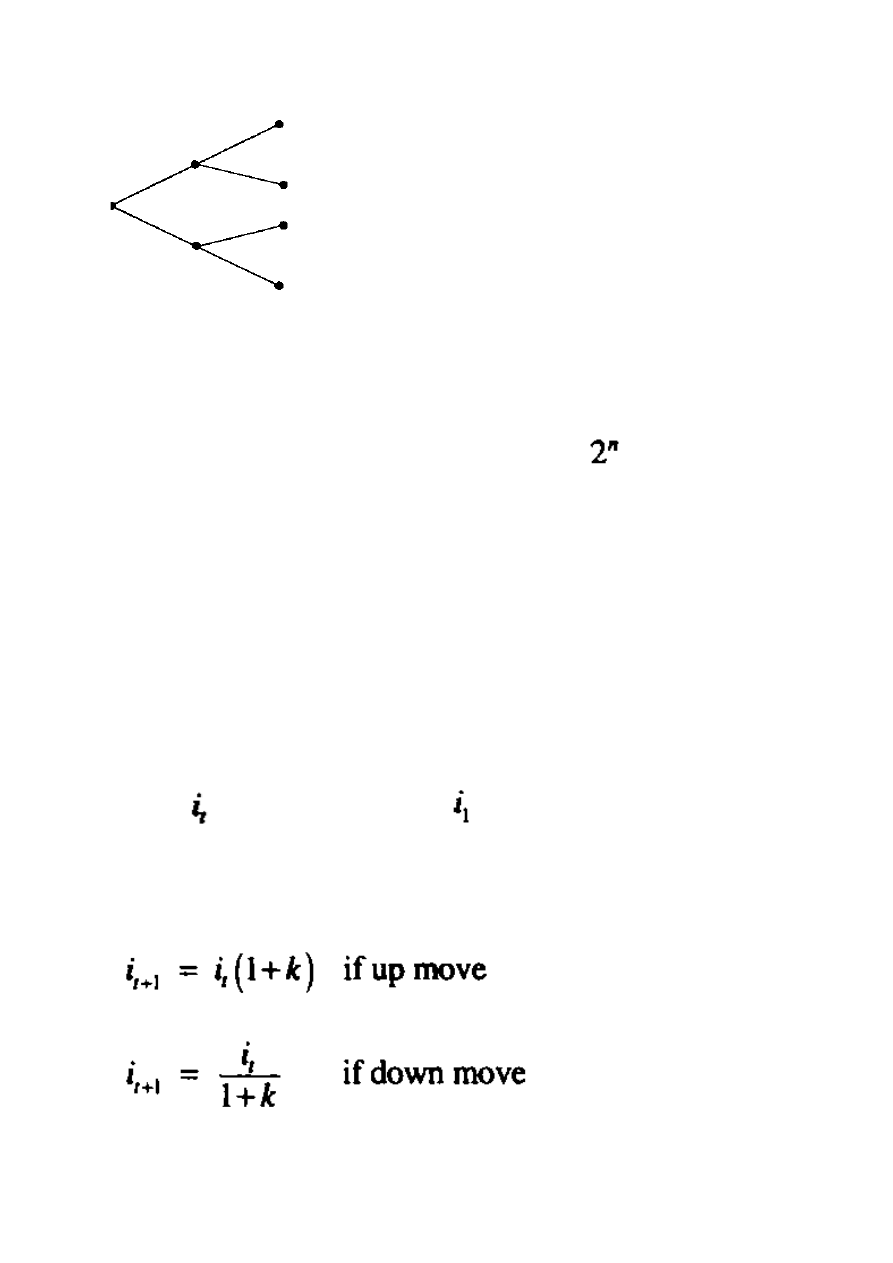
Otwarte drzewo

Po okresach n, zamknięte drzewo będzie miało n + 1 zamknięte punkty a otwarte

drzewo bez żadnych podwojeń, będzie posiadało końcowe punkty

. Otwarte drzewa są

bardziej złożone niż zamknięte.

Zamknięte drzewo nazywane jest dwumianem dodatkowym jeśli górne i dolne ruchy

mają taką samą wartość. Na przykład, jeśli każdy ruch stopy procentowej jest mniej więcej

1%-towy, model nazywany wtedy jest „dodatkowym”.

Zamknięte drzewo nazywane jest wielokrotnym modelem dwumianu jeśli każdy górny

i dolny ruch jest stale wielokrotny do poprzedniej stopy procentowej. Model ten posiada

wyraźną zaletę – stopy procentowe nigdy nie będą negatywne tak jak przy modelu

dodatkowym.

Tak jak w poprzednich rozdziałach, określamy stopę procentową dla okresu czasu t –

1 do t jako

. Zatem, drzewo zaczyna się od

, stopą procentową dla pierwszego okresu,

a następnie odgałęzia się od niego.

Często stosowany wielokrotny model przedstawiony jest jako:

If up move – jeśli jest to ruch górny

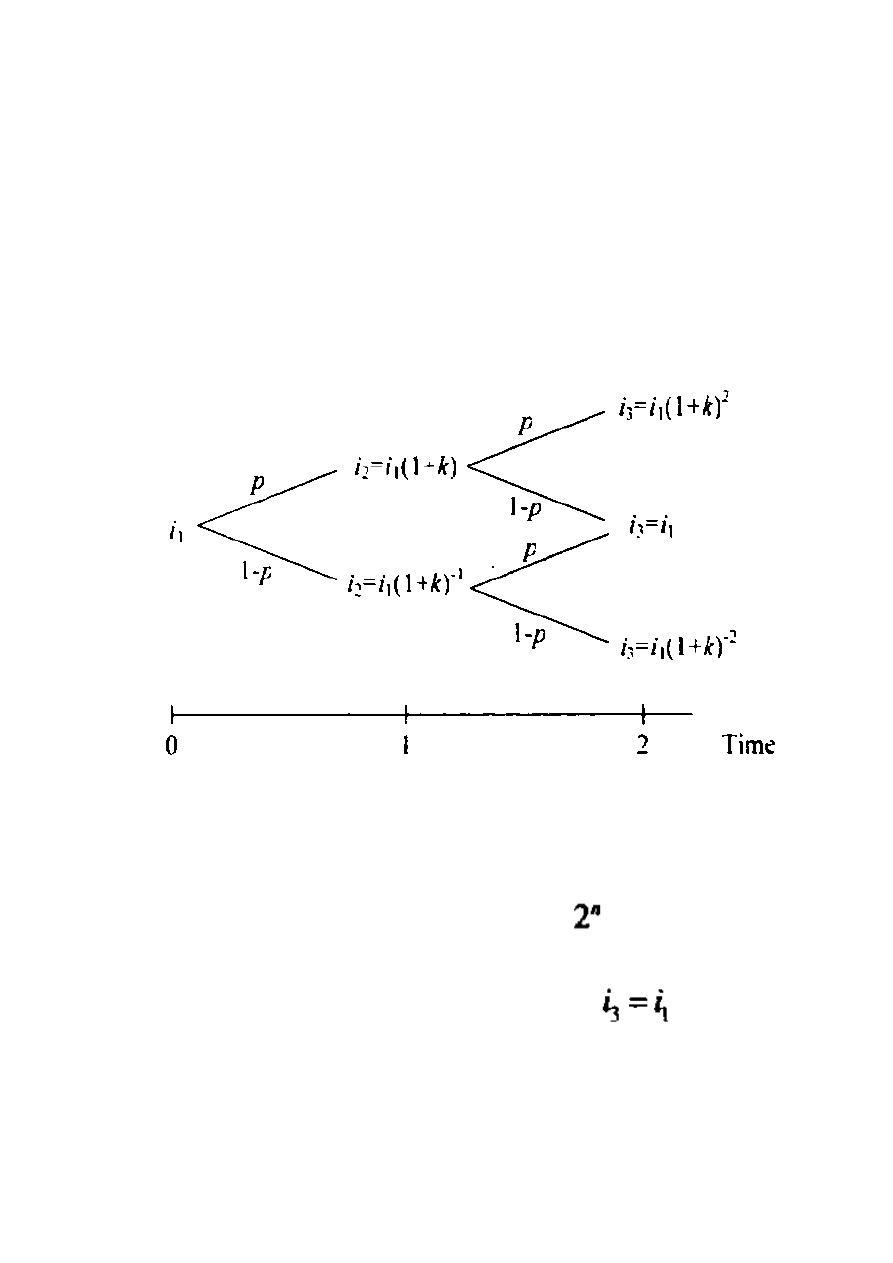
If down move – jeśli jest to ruch dolny

Parametr k jest często określany jako parametr lotności w tym rodzaju modelu wielokrotnego.

Określmy prawdopodobieństwo ruchu górnego i dolnego. Prawdopodobieństwo ruchu

dolnego będzie wynosiło 1 – p. Rysunek 12.2 przedstawia ogólne dwuokresowe drzewo

wielomianu wielokrotnego opartego na powyższym zapisie.

Rysunek 12.2 Dwuokresowe drzewo wielomianu

Następnie rozważmy ilość źródeł stopy procentowej w stosunku do drzewa. Jeśli

byłyby n okresy w tym modelu, wtedy pojawi się maksymalnie

takie źródła.

Niektóre źródła mogą lub nie mogą być podwojone co zależy od określonego

zastosowania. Na przykład, na Rysunku 12.2 środkowa wartość dla

oparta jest na

jednym górnym i jednym dolnym ruchu w takiej samej kolejności. Jednak, dwa źródła nie są

równoważne jeśli chodzi o obliczenie obecnych wartości od ponad dwóch lat. Oba źródła

stosują stopę procentową

w pierwszym roku ale mają różną

w kolejnym roku.

Chociaż pokazaliśmy jak budować drzewo stopy procentowej, jest jeszcze coś o czym

warto wspomnieć. Typowym powodem budowy takiego drzewa na pierwszym miejscu jest

kalkulacja finansowej wartości dla wszystkich źródeł, które mogą być obliczone

Jednym z najpowszechniejszych zastosowań drzewa stopy procentowej jest ocena

obligacji. Przedstawimy ilustracyjnie niektóre obligacje kalkulacyjne w Przykładach 12.9 oraz

12.10.

Technika oceny jest procesem rekursywnym, które zaczyna się po prawej stronie

końca drzewa i powraca do początku lewej strony. Załóżmy więc obligacje kuponu, gdzie

okres opłacenia kuponu zachodzi w tym samym czasie co okres drzewa.

Niech V będzie wartością obligacji, to jest obecną wartością przyszłego przepływu

gotówki, na początku okresu. Następnie, określmy obecne wartości na koniec okresu:

- gotówka przepływa w ruchu górnym

- gotówka przepływa w ruchu dolnym

- wartość w ruchu górnym

- wartość w ruchu dolnym

Zauważ różnicę pomiędzy przepływami gotówki występującymi na koniec okresu,

oznaczonym poprzez R, oraz obecną wartość przyszłego przepływu gotówki występującą

później, oznaczonym poprzez V.

Wzór rekursywny otrzymujemy poprzez:

Gdzie

jest stopą procentową dla określonego okresu w kwestii ukazanej na drzewie.

Czytelnik może być ciekawy wyboru długości okresów. We wzorze (12.38)

wybieramy okres drzewa tak aby współistniał z częstotliwością kuponu obligacji dla

ułatwienia. To daje nam typowy wynik w półrocznej częstotliwości dla obligacji, ale także

typową miesięczną częstotliwość dla kredytu hipotecznego.

Praktyczne zastosowania są opracowane na komputerze a także krótszy okres może

być wybrany aby uniknąć przepływu gotówki w środku okresu. Wzór (12.38) wciąż działa,

jeśli nie ma przepływu gotówki poprzez ustanowienie, iż

. W

rzeczywistości, stosowanie drzew z wieloma gałęziami i krótszymi okresami według

ustalonego terminu przedziału dla całej kalkulacji, może poprawić ścisłość wyników w wielu

zastosowaniach.

Jest także możliwe pod pewnymi warunkami aby skrócić okres do zera i stworzyć

model prawdopodobieństwa. Nie będziemy próbować rozwinąć tego modelu w tej sekcji.

Jednakże, zauważmy ze Sekcja 12.6 będzie prezentowała niektóre stochastyczne modele

prawdopodobieństwa stopy procentowej.

Przykład 12.8 Drzewo dwumianu z roczną obowiązującą stopą procentową jest

zbudowane wg wartości 3 letniego zerowego kuponu obligacji i wynosi 1000$ do zapłaty.

Początkowa stopa procentowa w drzewie to 10%. Model wielokrotności z

prawdopodobieństwem p = 5 i parametrem przesunięcia k = .2 będzie tutaj zastosowany.

(1)

Przelicz wartość tej obligacji z drzewa

(2)

Przelicz wartość tej obligacji używając 10%-towego wskaźnika poziomu

dochodowości..

1.

Wraz z zerowym kuponie obligacyjnym nie mamy przepływu gotówki w stosunku do

czasu t = 3. Drzewo ma 3 okresy i jest to ukazane na Rysunku 12.3

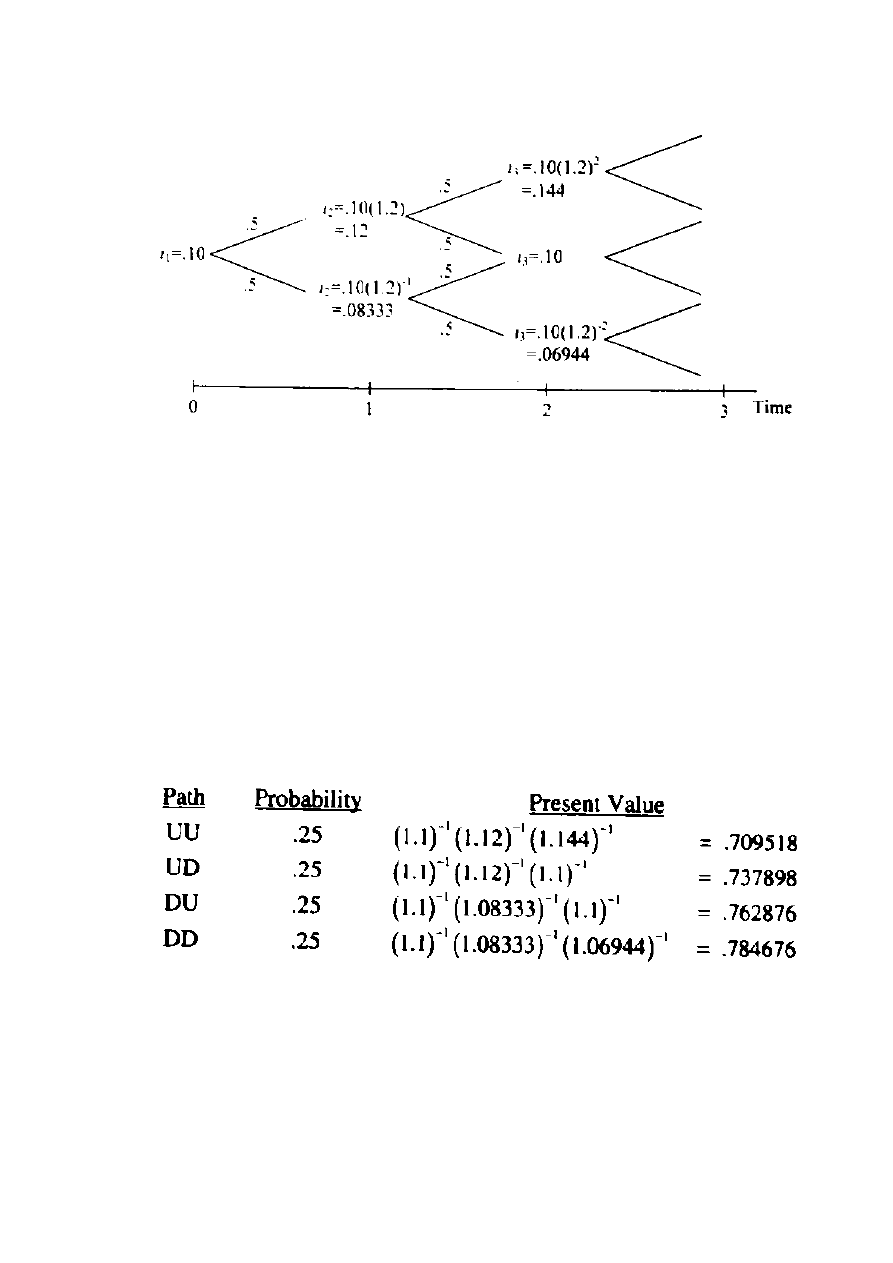
Rysunek 12.3 Drzewo wielomianu dla Przykładu 12.5

Zauważmy, iż gałęzie pomiędzy czasami t = 2 oraz t = 3 nie będą stosowane dla

jakichkolwiek kalkulacji w tym przykładzie. Wszystkie stopy procentowe, które zostaną

użyte są już znane w czasie t = 2. ( to jest: początek 3 roku).

Ponieważ nie ma przepływu gotówki do czasu t = 3, możemy przyspieszyć proces opisany

w tej sekcji. Bardziej niż używając wzoru (12.38), możemy pominąć wartość do zapłaty

$1000 na okres 3 lat w prawidłowych stopach procentowych z drzewa. Wartości

wymagane przy kalkulacji są określone poniżej:

Path – ścieżka

Probablility – prawdopodobieństwo

Present value – obecna wartość

Wartość 3-letniego zerowego kuponu obligacyjnego jest przeciętna w stosunku do

różnych ścieżek stopy procentowej, to jest:

2.

Wartość tej obligacji, użytej jako stały dochód 10% stopy jest równa:

Zauważmy, iż wartość jest większa niż wartość uzyskana w części 1 pomimo całkowitej

symetrii stóp procentowych w części 1 przy początkowej wartości

Intuicyjnie ma to sens. Część 1 ma ważną stopę procentową, podczas gdy część 2 już jej

nie posiada. Większa stopa procentowa prowadzi do wyższego dochodu stóp a zatem i

niższych cen. Jest to prawdą nawet dla zerowego kuponu obligacyjnego.

Przykład 12.9 Chciałbyś zainwestować $1000 na jeden rok, gdzie norma wartości

obligacji wynosiłaby 7.6% wraz z półrocznymi kuponami. Obecna dochodowa stopa

procentowa wynosi 8% zamiennie co pół roku. Drzewo dwumianu z półrocznymi

okresami zostanie tu zastosowane. Model wielokrotności gdzie p = .4 oraz przesunięcie

parametru k = .2 jest wybrany. Przekalkuluj wartość tej obligacji, używając drzewa

wielomianu.

Początkowa stopa procentowa jest obecną półroczną stopą dochodu równą .08/2 = 4.

Drzewo dwumianu jest przedstawione na Rysunku 12.4

Time (half years) – czas (pół roku)

Rys. 12.4 Drzewo dwumianowe dla Przykładu 12.6

Podobnie jak w Przykładzie 12.8, wartości

nie musza być obliczane, ponieważ

nie będą używane do żadnych kalkulacji. Wszystkie stopy procentowe, które będą użyte

są już znane, jako czas zakładamy t = 1 (to jest: początek okresu 2).

Ponieważ jest to obligacja kuponu, musimy zastosować wzór (12.38) , cofając się do

drzewa. Czas oznaczamy t = 2 we wszystkich przypadkach, otrzymujemy więc:

(wartość płatności + kupon)

Oraz

V = O ( wiązanie zostało spłacone)

Stosując wzór (12.38) jako czas t = 1 na górnej gałęzi, otrzymujemy:

Stosując wzór (12.38) gdzie t = 1 na dolnej gałęzi, otrzymujemy:

W końcu, stosując wzór (12.38) gdzie czas t = o, otrzymujemy:

Przykład 12.10 Opracujmy po raz kolejny Przykład 12.9, jeśli jest to obligacja płatna na

żą

danie na każdej akcji o wartości nominalnej.

Obligacja nie pojawi się od razu o czasie t = 0 ponieważ jej wartość $997.02 jest

mniejsza niż jej wartość nominalna $1000. Także nie pojawi się w czasie t = 1 jeśli stopy

procentowe wzrosną, ponieważ ich wartość na tym etapie będzie równa $990.46.

Jednakże, obligacja pojawi się w czasie t = 1, jeśli stopy procentowe obniżą się,

ponieważ wartość na tym etapie będzie wynosiła $1004.25. Zatem, musimy ponownie

obliczyć wartość w czasie t = 0 zastępując $1004.52 i wywołując wartość $1000. To daje

wartości w czsie t = 0

Zatem, wartość obligacji płatnej na żądanie jest mniejsza niż wartość innej niepłatnej

na żądanie obligacji. Obligacje płatne na żądanie wiążą się z większą niepewnością, cena

takiej obligacji powinna być niższa aby rekompensować ilość kupców dla większej

niepewności.

W rzeczywistości, w praktycznym zastosowaniu jednym z podstawowych użyć

drzewa dwumianowego jest wycena papierów wartościowych i innych finansowych

zagadnień w procentowych przepływach gotówki. Obligacje płatne na żądanie są bardzo

ważnym przykładem takiej gwarancji.

12.6

Stochastyczne Modele Prawdopodobieństwa

Końcowa kategoria zależności stopy procentowej to model stochastyczny

prawdopodobieństwa. To w rzeczywistości jest rodzina modeli, zbudowana w podobny

sposób ale z innymi właściwościami i charakterystyką. Omówimy cztery takie modele

we wzrastającej kolejności złożoności i zaawansowania.

Teoria poniższych modeli stochastycznych prawdopodobieństwa, jest stosunkowo

zaawansowana. Wymaga ona zastosowania stochastycznych rachunków oraz

rozwiązania różniczkowych równań.

Nie będziemy próbować rozwinąć wszystkich poniższych teorii w tej prostej książce.

Zatem, zaprezentujemy materiał logicznie i użyjemy nieciągłych przybliżeń w różnych

zastosowaniach modeli.

Ponieważ modele są prawdopodobieństwem w naturze, jest oczywiste użycie siły

stopy procentowej

omówionej w Rozdziale 1. Oczywiście, różna siła odsetek

zawsze może być przekształcona w równoważność stopy procentowej nad przedziałem

czasowym, jeśli to konieczne. Dlatego też, te modele stosują początkową wartość,

, i tworzą następnie wartości

z tych modeli. Wszystkie modele przedstawione

w Sekcji 12.6 sa oparte na procesie Weinera. Jeżeli zmienna

następuje po Procesie

Weinera, wtedy zmiany zachodzące w

w niewielkich odstępach czasowych, będą

niezależne i będą podążać według normalnego rozkładu. Następnie zastosujemy prawo

własności, tak, że średnia normalnego rozkładu jest proporcjonalna do czasu t, a

odchylenie standardowe jest proporcjonalne do

.

Niech y będzie wartością standardowego zwykłego rozkładu, to jest: z

i

Kolejno utworzy się następująca relacja w stosunku do krótkiego okresu

czasu:

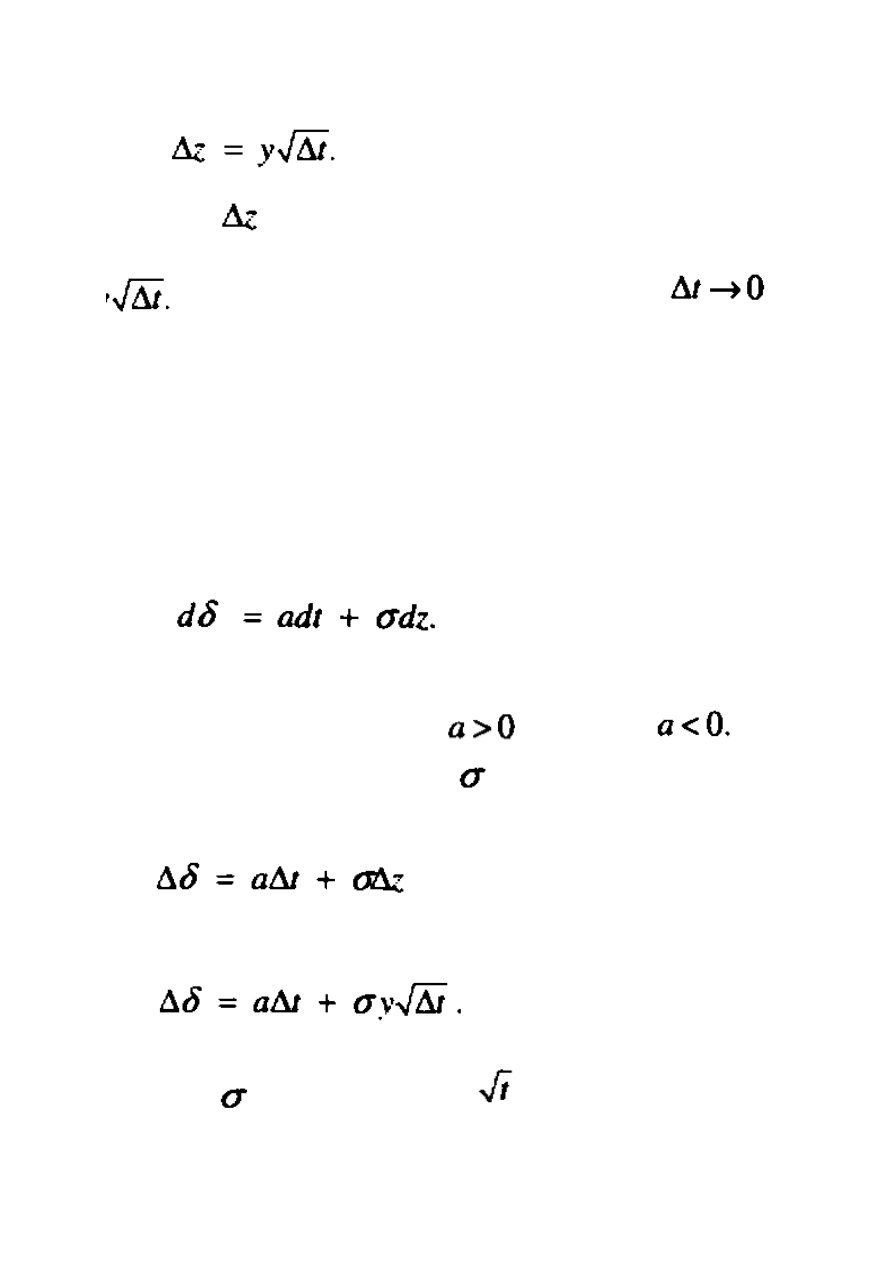
W ten sposób

jest normalnie rozłożone ze średnią 0 i odchyleniem standardwoym

W końcu, uzyskujemy model ciągły poprzez określenie limitu jako

i

oznaczenia wyniku poprzez różniczkę dz

Błądzenie losowe ( Ruchy Browna)

Najprostszym stochastycznym modelem prawdopodobieństwa jest błądzenie losowe,

które często nazywane jest Ruchami Browna. Jest to bardzo dobrze znany model w

stosowanych statystykach z wieloma rodzajami zastosowań. Czytelnik zauważy, iż

prezentujemy odrębną wersje błądzenia losowego. W Sekcji 12.5.

Błądzenie losowe opisane jest jako:

Parametr a zwykle zwany jest parametr dryft, ponieważ powoduje błądzenie losowe w

stosunku do przesunięcia wolnego w górę jeśli

lub w dół jeśli

.

Standardowe odchylenie w tym procesie, to jest

, często zwane jest parametrem lotności.

Odrębnym przybliżeniem dla tego modelu jest:

Który staje się następującym wzorem zastępczym (12.39)

Zauważ, iż parametr dryft a, jest proporcjonalny do t, podczas gdy standardowe

odchylenie

procesu jest proporcjonalne do

.

Innymi słowy, w porównaniu do okresów t, średnia tego procesu to:

A wariancja to:

Następujące obserwacje dotyczące tego modelu są ważne, ponieważ:

1.

Zastosowanie parametru dryft a, w stosunku do długich przedziałów

czasowych jest wątpliwy, ponieważ jego rezultatem będzie nieokreślony

długotrwały wzrost lub spadek

. Jednakże, jego zastosowanie może być

odpowiednie dla krótszych przedziałów, zależnie od sytuacji. Zauważmy

również, iż dryft może być całkowicie wyeliminowany poprzez regulację a =

0.

2.

Wynik tego modelu może okazać się negatywnymi wartościami dla

, co

jest wyraźnie nieuzasadnione.

3.

Lotność jest taka sama bez względu czy

jest większe czy mniejsze. Wiele

modeli mogłoby być wygodniejszych jeśli chodzi o lotność, zależną od

wielkości

,podanego w punkcie czasu.

4.

Wartości

nie posiadają średniej zwrotu warunkowego. Innymi słowy, nie

ukazują tendencji stopniowego ruchu w kierunku długoterminowego

wskaźnika w stosunku do czasu. Zatem, jeśli długoterminowa przeciętna

wynosi 5% a obecna

= 10%, jest prawdopodobne, iż następny ruch

będzie wyższy od aktualnego, ponieważ będzie wolniejszy.

Rendleman – Bartter Model

Rendleman – Bartter Model może być opisany jako geometryczne błądzenie losowe.

Model określony jest następująco:

Główną koncepcją jest utworzenie dwóch parametrów

oraz

proporcjonalnych do

obecnej wagi

Odrębne przybliżenie dla tego modelu to:

Lub

Obserwacja 1 powyżej jest również zastosowaniem tego modelu. Jednakże, ten model nie

posiada słabych punktów, które opisane są w obserwacjach 2 i 3, będących podstawowymi

motywacjami dla ich rozwoju. Chociaż słaby punkt jest wciąż obecny w obserwacji 4.

Na dodatek, ten model ma kolejny słaby punkt. Ponieważ lotność jest proporcjonalna

do wielkości

określonego punktu w czasie, wzrostowe ruchy zastosowane są w wysokiej

wartości

, co może spowodować, iż wartości

mogą osiągnąć nierealistyczne wysokie

poziomy.

Vasicek Model

Naszym trzecim modelem jest Model Vasicek. Podstawowym celem tego modelu jest

ukazanie średniej zwrotu warunkowego. Model ten jest przedstawiony w następujący sposób:

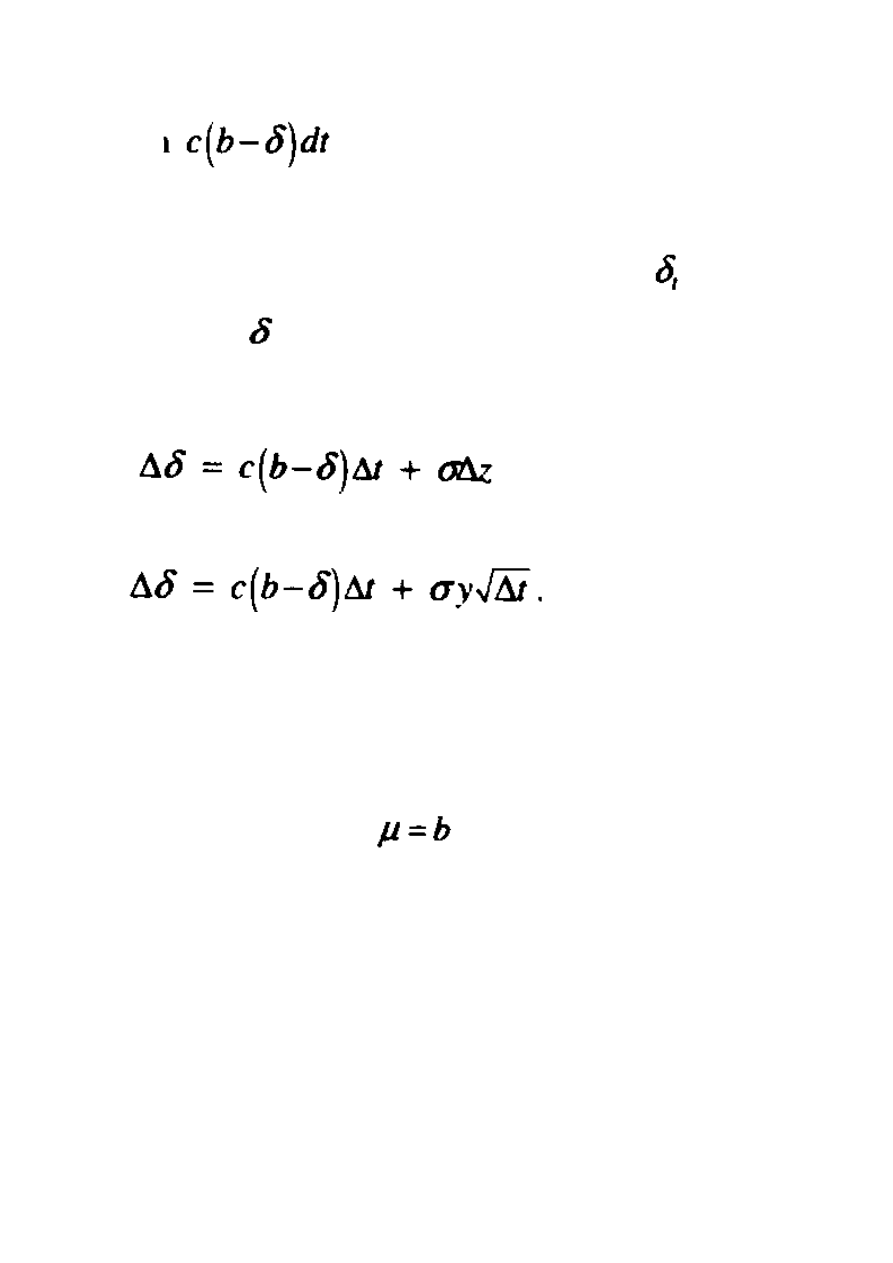
Termin

dotyczy średniej zwrotu warunkowego. Parametr b jest

długoterminową siłą odsetek w stosunku do tego co prezentuje model. Parametr c mierzy

wskaźnik zwrotu warunkowego w stosunku do średniej. Na przykład, jeśli c = .2, wtedy

przeciętnie model zamykać będzie się w 20% odstępie pomiędzy obecnym

a

długoterminowym

w każdym okresie.

Odrębne przybliżenie dla tego modelu to:

Lub

Wyżej wymieniony słaby punkt w obserwacji 4 jasno jest rozwiązany przez ten model,

który przedłuża podstawową motywację tego modelu na pierwszym miejscu. Również

możliwy słaby punkt w obserwacji 1 nie jest obecny. Jednakże, słaby punkt w

obserwacjach 2 i 3 jest jak najbardziej obecny.

Jest to również ważne aby zauważyć dwa szczególne skrajne przypadki modelu

Vasick. Jeśli c = 0, model staje się błądzeniem losowym bez dryftu. Jeśli zaś c = 1, model

staje się normalnym rozkładem z

. Sedno sprawy leży w tym, iż możemy

uogólnić Model Vasick jako mieszankę normalnego rozkładu oraz Ruchu Browna.

Model Cox-Ingersoll-Ross

Nasz czwarty i ostatni stochastyczny model prawdopodobieństwa to Model Cox-

Ingersoll-Ross. Jest najbardziej zaawansowanym z tych czterech modeli i próbuje

wyeliminować wszystkie słabe punkty, opisane powyżej dla trzech powyższych modeli.

Dzieje się to poprzez modyfikacje Modelu Vasick w celu lotności parametru

proporcjonalnego do

Model ten opisany jest w następujący sposób:

Odrębne przybliżenie dla tego modelu to:

Lub

Z powodu swoich interesujących właściwości, Model Cox-Ingersoll_Ross, stał się dość

powszechnie używany w stopach procentowych, w celu wykorzystania stochastycznego

modelu prawdopodobieństwa.

Praktyczne rozważania:

Zamykamy tą sekcję poprzez wykaz czterech praktycznych rozważań, przydatnych w

zastosowaniu tych modeli.

1.

Odrębne wersje tych modeli wymagają ostrożnego zdefiniowania t, oraz tego

jak często chcemy obliczyć nową siłę odsetek. Na przykład, możemy chcieć

określić t = 1 jako okres jednego roku, ale i poprawić ścisłość modelu poprzez

częstsze zmiany w sile odsetek. Zatem, na przykład, jeśli ustalimy, iż

, utworzymy kwartalne wartości

lub jeśli ustalimy, iż

, utworzymy wartości miesięczne.

2.

Modele te wymagają oszacowania lotności parametrów

i możliwie

innych parametrów a, b i/lub c. Te parametry muszą być spójne z tym jak

określimy pojedynczy okres, to jest: t = 1, jak powyżej.

3.

Modele analogiczne są często realizowane poprzez użycie symulacji.

Głównym założeniem jest utworzenie przypadkowych liczb, które

zastosowanie odnajdą w utworzeniu wartości y ze standardowego normalnego

rozkładu, to jest: z

i

Zatem, jeśli chcielibyśmy utworzyć

wartość

używając miesięcznych wartości z przeciągu roku,

potrzebujemy 12 imitowanych standardowych zwykłych zmiennych y.

4.

W użyciu modeli analogicznych, końcowa wartość jednego okresu staje się

początkową wartością następnego okresu. Zatem, modele są stosowane

rekursywnie z okresu na okres.

Przykład 12.11 Obecna siła odsetek wynosi .07. Oszacuj siłę odsetek z jednego roku na

przyszły, to jest: w czasie t = 1. Użyj błądzenia losowego (Ruch Browna) z kwartalnym

dopasowaniem, to jest:

. Lotność parametru

oraz

parametr dryft a = -.004. Następne cztery standardowe zwykłe zmienne były utworzone

używając symulacji +2, -.5, +1, 0.

Cztery standardowe normalne zmienne mogą być rozumiane jako ilość standardowych

odchyleń ponad lub poniżej średniej wynoszącej 0. Były one wybrane dowolnie aby

przedstawić wyraźniej działanie modelu. Przeciętnie te cztery określone wartości są w pewien

sposób większe niż średnia.

Interpretacja parametru dryft polega na tym, iż zredukujemy siłę odsetek poprzez

.004 lub .4% na rok pod wpływem neutralnych warunków. Wyjaśnienie parametru lotności

jest takie, iż standardowe odchylenie siły odsetek w ciągu jednego roku wynosi .01 lub 1%, w

stosunku do obecnej siły odsetek, która wynosi 7%.

Teraz zastosujmy wzór (12.41b) rekursywnie cztery razy:

Z początkową wartością

. To daje nam następujące wyniki:

Zatem odpowiedź to .0785 lub 7.85%.

Wynik parametr dryft a = -.004, to ruch dolny w kierunku siły odsetek ze stopą

procentową -.001 na kwartał. Jednakże, ten wynik to więcej niż potrącenie przez pozytywne

powyższe wartości y ponad średnią. Cała tendencja w czwartym kwartale jest przypisana

dryftu. Jeśli parametr dryft będzie wynosił zero, wtedy siła odsetek pozostanie niezmienna w

ciągu tego kwartału.

Przykład 12.12 Opracuj ponownie Przykład 12.11 używając Modelu Rendeiman-

Bartter.

Zastosujmy wzór (12.45b) rekursywnie 4 razy. W celu osiągnięcia wyników

porównywalnych do Przykładu 12.11, pomnóżmy parametry a oraz

przez 1/.07 aby

zneutralizować wynik poprzez umieszczenie

we wzorze

Otrzymujemy:

Co daje wynik:

Zatem, odpowiedź to .0783, lub 7.83%.

Wynik użycia geometrycznej wersji Ruchu Browna jest nie do końca oczywistym w

ciągu tak krótkiego okresu ze stosunkowo małymi zmianami w sile odsetek. Rezultat stałby

się bardziej oczywisty jeśli poziom odsetek wzrósłby lub spadł drastycznie.

Przykład 12.13 Opracuj ponownie Przykład 12.11 używając Modelu Vasicek z

parametrami b - .05 oraz c = .20.

Wytłumaczenie parametru b = .05 jest takie, iż długoterminowa siła odsetek jest to 2%

poniżej obecnego poziomu. Wytłumaczenie dla parametru c = .20 jest takie, iż wskaźnik

zwrotu warunkowego do średniej to 20% na rok. Zastosujemy wzór (12.47b) rekursywnie

cztery razy:

Otrzymujemy więc:

Zatem, odpowiedź to .0774 lub 7.74%

Wyniki w tym przykładzie są zbliżone do wyników z Przykładu 12.11. Ten wynik jest

przypisany faktowi, iż zwrot warunkowy do średniej jest przybliżony .2 (.05-.07) = -.004 na

rok, i jest taki sam jak parametr dryft a, z Przykładu 12.11

Przykład 12.14 Opracuj ponownie Przykład 12.13 używając Modelu Cox-Ingersoll-

Ross.

Zastosujemy wzór (12.49b) rekursywnie cztery razy. W celu uzyskania wyników

porównywalnych do Przykładu 12.13 pomnożymy parametr

przez

. Aby

zneutralizować wynik poprzez umieszczenie

we wzorze.

Otrzymujemy więc:

Co daje wynik:

Zatem odpowiedź to .0774 lub 7.74%.

Według tych warunków w ciągu krótkiego okresu czasu Model Cox-Ingersoll_Ross

daje prawie identyczne wyniki jak Model Vasicek. Większe różnice powstałyby wraz z

większymi tendencjami poziomu odsetek górnych lub dolnych w ciągu dłuższych okresów

czasu.

12.7

Test Scenariusza

W praktycznym zastosowaniu dla wielu sytuacji w Rozdziałach 11 i 12 podejście

zwane testem scenariusza, stało się bardzo popularne. Ta technika, jest w istocie

rodzajem zaawansowanej symulacji, która wymaga obszernych zdolności

komputerowych do jej zrealizowania, ponieważ ilość obliczeń jest bardzo wysoka. W

tym podejściu, każdy „scenariusz” odnosi się do innego rodzaju stopy procentowej.

Na przykład, rozważmy analizę dopasowania wkładów i zobowiązań wobec instytucji

finansowych. Ważne jest aby oszacować przyszłe przepływy gotówki z wkładów i

przyszłe wypływy gotówki z zobowiązań.

Te napływy i wypływy gotówkowe mogą wiązać się z naturalną niepewnością

jeśli chodzi o ilość, prawdopodobieństwo spłaty oraz synchronizację. Ważne jest też,

aby rozpoznać w budowie scenariusza, iż te przepływy gotówki mogą być także

uzależnione od rodzajów stopy procentowej . Na przykład, jeżeli chodzi o wkład,

wspomniany już wcześniej, napływy gotówki wzrastają wraz z obligacjami oraz z

przedpłatą hipoteki co uzależnione jest od poziomu stóp procentowych.

Poziom nadwyżek, co może być pozytywne lub negatywne, jest obliczany na koniec

okresu projektu dla każdego scenariusza. Te wyniki powodują symptom zakresu możliwych

rezultatów. Także inne statystyczne pomiary mogą być obliczane w miejscach wyników, na

przykład średnia i standardowe odchylenie.

Wiele decyzji musi być podjętych w zastosowaniu testu scenariusza. Jedna z nich to

ilość używanych scenariuszy, to jest ilość różnych dróg stopy procentowej, które musza być

rozwiązane. Zwiększając ilość dróg prawdopodobnie zapewnia się lepszy obraz możliwych

wyników rozkładów. Jednakże, „prawo malejących zysków” w pewnym stopniu zajmuje tu

miejsce. Nie jest prawdą, iż podwajając stos komputerowych wydruków wytwarzamy więcej

cennych informacji. Także, czas i rozważania wydatkowe są bardzo ważne. Zatem, znaczenie

nauki zależy od wysiłku, który w nią włożymy. W końcowej analizie, ilość stosowanych

scenariuszy nie jest jednoznaczna.

Kolejną decyzją jest częstotliwość zmian w stopach procentowych używanych w teście

scenariusza, to jest miesięcznie, kwartalnie, rocznie, itd. Ponownie jest to wymiana pomiędzy

wzrostem poziomu zaawansowania a wzrostem złożoności, czasu oraz kosztu analizy. Tu

również decyzja jest niejednoznaczna i oparta na wielu takich samych rozważaniach jak przy

określaniu ilości stosowanych scenariuszy.

Ważnym przemyśleniem jest rozwinięcie ścieżek stopy procentowej dla różnych

scenariuszy krzywej dochodowości. W rzeczywistości, w wielu przypadkach testu

scenariusza, krzywa j dochodowości jest zaplanowana. Doświadczenie pokazuje, że ogólne

krótkoterminowe stopy procentowe są niestałe niż długoterminowe stopy procentowe. Zatem,

różnice przyszłych zachowań krzywej dochodowości powinny być nieodłączną częścią testu

scenariusza. Innymi słowy, analityk nie powinien ignorować krzywej dochodowości i tym

samym bezwarunkowo przypuszczać, że jej kształt jest taki sam w każdym scenariuszu.

Podobny temat to przypuszczenie wystąpienia wskaźników reinwestycji. To

przypuszczenie jest ważne, jeśli analiza dotyczy szczegółowego okresu czasu. Może to

wiązać się z przypuszczeniami na temat przyszłych zachowań, jak i wyłącznie z finansowymi

przypuszczeniami.

Kolejnym ważnym rozważaniem w tworzeniu scenariuszów jest możliwość wolnego od

ryzyka arbitrażu w jednej lub w większej ilości ścieżek stopy procentowej. Wraz z istnieniem

możliwości wolnego od ryzyka arbitrażu w podanej ścieżce stopy procentowej lub

umiejscowienia ścieżek podczas planowania całej krzywej dochodowości, wzrasta zapytanie

o wewnętrzną zwięzłość dotyczącą scenariusza lub scenariuszy. Istnieją techniki dla

wyeliminowania wolnego od ryzyka arbitrażu, lecz te techniki są poniżej poziomu tej książki.

Istnieją ogólne metody występujące w określaniu ścieżek stopy procentowej w teście

scenariusza. Pierwszą jest metoda teraźniejsza. Pod wpływem tej metody analityk

bezpośrednio określa wszystkie stopy procentowe w różnych ścieżkach. Ta metoda oferuje

maximum elastyczności dla analityka w kwestii wyboru scenariusza. Jest to również

wyszczególnione poprzez głównych ustawodawców instytucji finansowych.

Typowe testowane scenariusze zawierają mieszankę optymistycznych wartości

ś

rodkowych oraz pesymistycznych scenariuszy z przynajmniej jednym „najgorszym

przypadkiem”. Stopa procentowa zawiera zarówno wyższą jak i niższą lotność. Ścieżki

odzwierciedlają główną długotrwałą koniunkturę wzrostową lub obniżoną w ciągu okresu

czasu. Ścieżki ukazują również główny zastój gospodarczy lub hiperinflację, wykorzystywane

podczas rozważania nad „najgorszym przypadkiem” scenariusza.

Jednakże, przy tworzeniu wyników opartych na scenariuszach, ważne jest dla analityka

aby przydzielić prawdopodobieństwa do różnych scenariuszy. Jednym z powszechnym

błędów jest założenie, iż wszystkie scenariusze są równie prawdopodobne. Jednym razem

prawdopodobieństwa są przydzielone do różnych scenariuszy a kolejnym razem statystyczne

pomiary takie jak średnia i standardowe odchylenie mogą być obliczane poprzez wszystkie

scenariusze.

Chociaż oferując dużą elastyczność analitykowi, obecna metoda ma ważne słabe

punkty. Jednym z nich jest to, iż metoda jest nieodłącznie dowolna ponieważ ścieżki stopy

procentowej są oparte na subiektywnym postanowieniu analityka lub ścieżek opisanych przez

ustawodawców. Kolejnym słabym punktem , jest to, iż metoda może być całkiem

czasochłonna, ponieważ ważne jest aby określić różne stopy procentowe wymagane dla

różnych scenariuszy. Kolejne dwie metody nie wymagają subiektywnych postanowień

analityka i określają ścieżki stopy procentowej w bardziej systematyczny i skuteczny sposób.

Drugim typem metody jest metoda prawdopodobieństwa. Jedną z powszechnych metod

prawdopodobieństwa jest użycie techniki drzewa dwumianu. Powinno być zauważone, iż

występuje dokładna odwrotność pomiędzy cenami obligacji a stopą procentową. Zatem,

zakładając, iż ceny obligacji poruszają się dzięki błądzeniu losowemu, to jest to

równoznaczne do założenia, iż stopy procentowe poruszają się dzięki błądzeniu losowemu.

Pod wpływem tej metody, prawdopodobieństwo ruchu wzrostowego w stopie procentowej

danego okresu wynosi p, podczas gdy prawdopodobieństwo obniżonego ruchu wynosi 1 – p.

Jeśli p = ½, wtedy wskaźniki podwyższą się lub obniżą przypadkowo w stosunku do ich

obecnego poziomu, zakładając, iż czynniki wzrostu i obniżenia są odwzajemnione. Jeśli p

, wtedy nastąpi długotrwała koniunktura wzrostowa w przeciągu czasu, podczas

gdy przeciwna okaże się prawdziwa w momencie kiedy

Lotność wyników

jest hamowana poprzez wielkość możliwych wzrostowych i obniżonych ruchów.

Trzecim rodzajem tej metody jest metoda stochastyczna. Prawdopodobnie

najpowszechniejsza stosowana metoda stochastyczna polega na założeniu, iż kolejne wartości

następują po logarytmicznie normalnym rozkładzie. Jedną z zalet stochastycznej

metody jest zdolność do łatwości rozliczenia lotności stopy procentowej. Może być również

ukazane to, że powszechne założenia są całkowicie stosowane co powoduje, iż ta metoda staje

się skrajnym przypadkiem metody drzewa dwumianu w momencie kiedy drzewa podziału

zmniejszają się do zera. Jednym z problemów metody prawdopodobieństwa jak i

stochastycznej jest taki, iż stopy procentowe mogą pojawiać się w niektórych ścieżkach po

ilości okresów czasowych, co wydaje się nieracjonalnie wysokie lub niskie. Jednym z

rozwiązań jest zmniejszenie założonych lotności w ruchu stóp procentowych. Kolejnym

rozwiązaniem jest zastosowanie granic na wysokość lub niskość wskaźników. Jednakże,

ż

adna z tych metod, które są w stanie rozwiązać problem, nie jest idealna.

Analiza czasowa jest użyteczna w połączeniu z tworzeniem scenariuszy. To zmusza

analityka do rozważań na temat przeszłych danych w budowie scenariuszy. Jednakże, ważne

jest aby zapamiętać, iż „przyszłość nie kopiuje przeszłości”. Zatem, niektóre scenariusze

mogą dotyczyć warunków, które nie występowały wcześniej.

W końcu, ważne jest także to aby nie ignorować znaczenia przejściowych wyników,

poprzez zbytnie koncentrowanie się na rezultatach na koniec okresu planowania. Na przykład,

dla określonego scenariusza, jeśli ukażemy pozytywny rezultat na koniec okresu planowania,

ale w negatywnym świetle w połowie okresu, możemy nie uzyskać korzystnego scenariusza.

W skrócie, bliższa analiza tego określonego scenariusza jest niezbędna.

Powyższe rozważania są krótkim streszczeniem na temat dyskusji testu scenariusza.

Ciężko jest być tutaj bardzo dokładnym w dyskusji o tej technice ponieważ jest tak wiele

różnych możliwości przeprowadzenia testu scenariusza, które są prowadzone przez

analityków ( a nawet więcej!). Niemniej jednak, ta sekcja powinna być użyteczna w

zapewnieniu czytelnikowi ogólnej aprecjacji różnych stosowanych metod i dotyczących ich

rozważań.

Przykład 12.15 Zainwestowano $1000 na pięć lat w nieznana siłę odsetek, które

zmieniają się co roku. Założone jest, iż siła odsetek wiąże się z AR(1) procesem gdzie

, Pięć przypadkowych utworzonych liczb, które tworzą

następujące wartości ze standardowej zwykłej dystrybucji:

. Siła odsetek w ciągu roku zakończona jest

na .10. Znajdź skumulowaną wartość inwestycji na koniec pięciu lat dla tej ścieżki stopy

procentowej.

Pięć kolejnych wartości

zostało utworzonych we wzorze (12.29):

Zatem, skumulowana wartość na koniec pięciu lat dla tej ścieżki stopy procentowej

będzie wynosiła:

Dla najbliższej wartości dolara.

W tymże rodzaju problemu, duża ilość ścieżek stopy procentowej będzie utworzona w

ten sposób. Statystyczne pomiary, takie jak średnia i standardowe odchylenie, mogą być

obliczane dla rozkładów skumulowanych wartości, które utworzone zostały poprzez

symulację.

Przykład 12.16 Firma ubezpieczająca wydaje roczny zabezpieczony kontrakt

inwestycyjny (GIC), który udziela rocznych kredytów ze wskaźnikiem odsetek równym 8.5%.

Firma decyduje się zainwestować wyniki ze sprzedaży GIC w trzymiesięczne papiery

wartościowe na początku każdego kwartału. Stopa procentowa zarobiona przez pierwszy

kwartał wynosi 8.4% wymiennie co kwartał. Zakładamy, iż przyszłe stopy procentowe

poruszają się według błądzenia losowego, gdzie prawdopodobieństwo ruchu wzrostu w stopie

procentowej wynosi .4 a ilość ruchów wzrostu i obniżeń w każdym kwartale wynosi .5% oraz

.4% odpowiednio wymiennie co kwartał. Znajdź prawdopodobieństwo tego, iż firma straci

pieniądze w GIC.

Drzewo dwumianu w tym przypadku, jest drzewem otwartym, co jest przedstawione na

Ilustracji 12.1 a nie typowym drzewem zamkniętym. Zatem, są

ścieżki stopy

procentowej.

Będziemy pracować nad kwartalnymi stopami procentowymi. Stopą procentową dla

pierwszego kwartału jest .021. Ilość każdego ruchu wzrostu w stopie procentowej wynosi

.00125, podczas gdy ilość obniżonego ruchu wynosi .001.

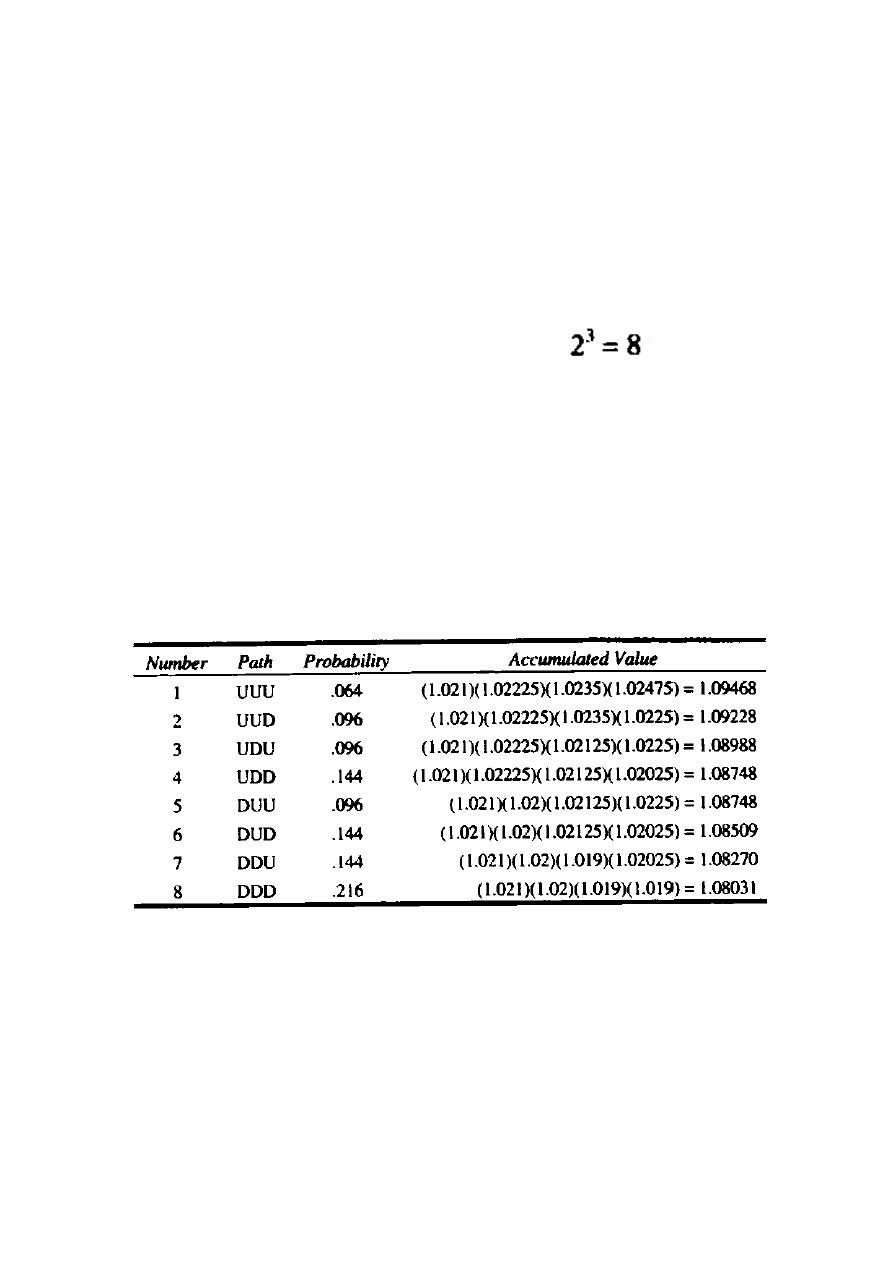
Wyniki dla ośmiu ścieżek stóp procentowych są podsumowane w Tabeli 12.2.

Tabela 12.2 Podsumowanie Ścieżek Stopy Procentowej dla przykładu 12.16

Number – ilość

Path – ścieżka

Probability – prawdopodobieństwo

Accumulated value – skumulowana wartość

Pod wpływem GIC, firma musi zapłacić 1.085 na koniec roku na każdego

zainwestowanego dolara. Firma straci pieniądze dla ścieżek 7 oraz 8 w Tabeli 12.2. Zatem,

prawdopodobieństwo straty wynosi .144 + .216 = .36.

12.8

Modele bardziej zaawansowane

Ten rozdział jest niewątpliwie złożony oraz wymagający dla wielu czytelników.

Pomimo tego, jest on podstawowym wprowadzeniem do stochastycznych modeli stopy

procentowej. Celem tej końcowej sekcji jest zapewnienie krótkiego nietechnicznego

opisu czterech pozostałych zaawansowanych modeli w wszechstronnym zastosowaniu,

co przekracza możliwości tej książki.

1.

Pierwszym z nich jest rozwinięcie wielookresowe modeli wolnych od

arbitrażu, dotyczących krzywej dochodowości. Wymóg dla tego modelu

został opisany w Sekcji 12.7.

2.

Modele Vasicek oraz Cox-Ingersoll-Ross dotyczą zwrotu warunkowego w

stosunku do długoterminowej siły odsetek jako ich podstawowej cechy.

Bardziej złożony model w tej ogólnej kategorii to model powracającej

podwójnej średniej, w którym długoterminowa siła odsetek powraca nawet

na poziomie dłuższym terminowo. Chociaż brzmi to zupełnie zbędnie i

skomplikowanie na początku, ten model udowodnił możliwość utworzenia

bardziej realistycznych scenariuszy odsetek dla testu scenariusza.

3.

Model Black-Derman-Toy jest bardziej złożonym modelem połączonym z

krzywą dochodowości w drzewo dwumianu. Jest także tak zaprojektowany

aby dopasować się do aktualnych światowych danych poprzez proces

zwany wzorcowaniem. Ten model udowadnia, iż świetnie modeluje lotność

krzywej dochodowości z czasem.

4.

W końcu, otrzymujemy różne typy modeli liniowo-zamiennych. Te modele

zamieniają się przypadkowo pomiędzy dwoma lub więcej rozkładami.

Udowadniają skuteczność w pewnych typach zastosowań, w szczególności

w zwrotach kapitału własnego.

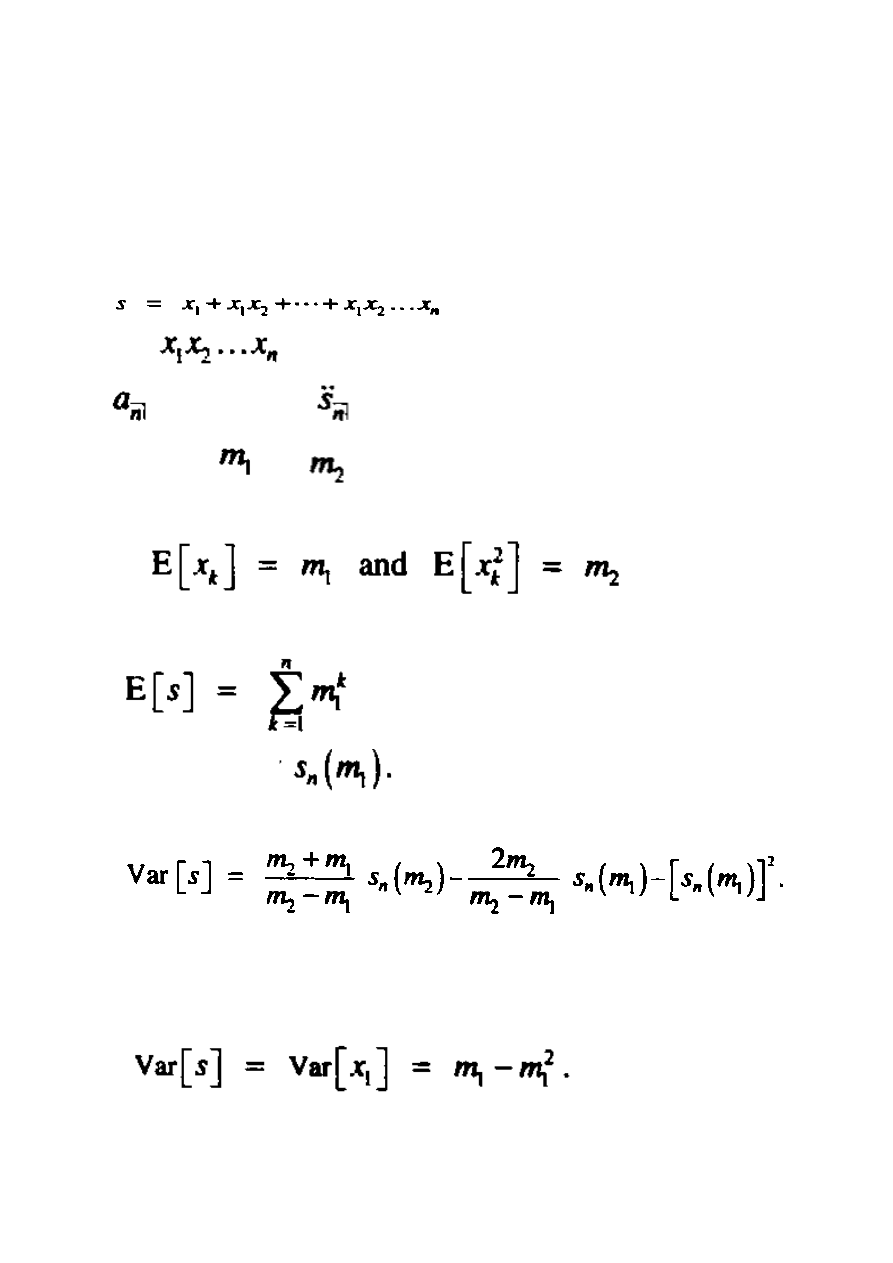
ZAŁĄCZNIK 12

Źródło wariancji opłaty rocznej

Zamierzymy znaleźć wariancję sum

Gdzie

są niezależne i identycznie rozproszone zmienne. Wzór (3.23) dla

oraz wzór (3.25) dla

mają tą samą formę.

Niech

oraz

będą pierwszym i drugim momentem początkowym, to

jest:

Dla k = 1, 2, ……, n. Z niezależności otrzymujemy:

Co oznaczymy poprzez

Wzór, który chcemy udowodnić to:

Dowód osiągnęliśmy poprzez indukcję matematyczną.

Niech n = 1. Wiemy, iż:

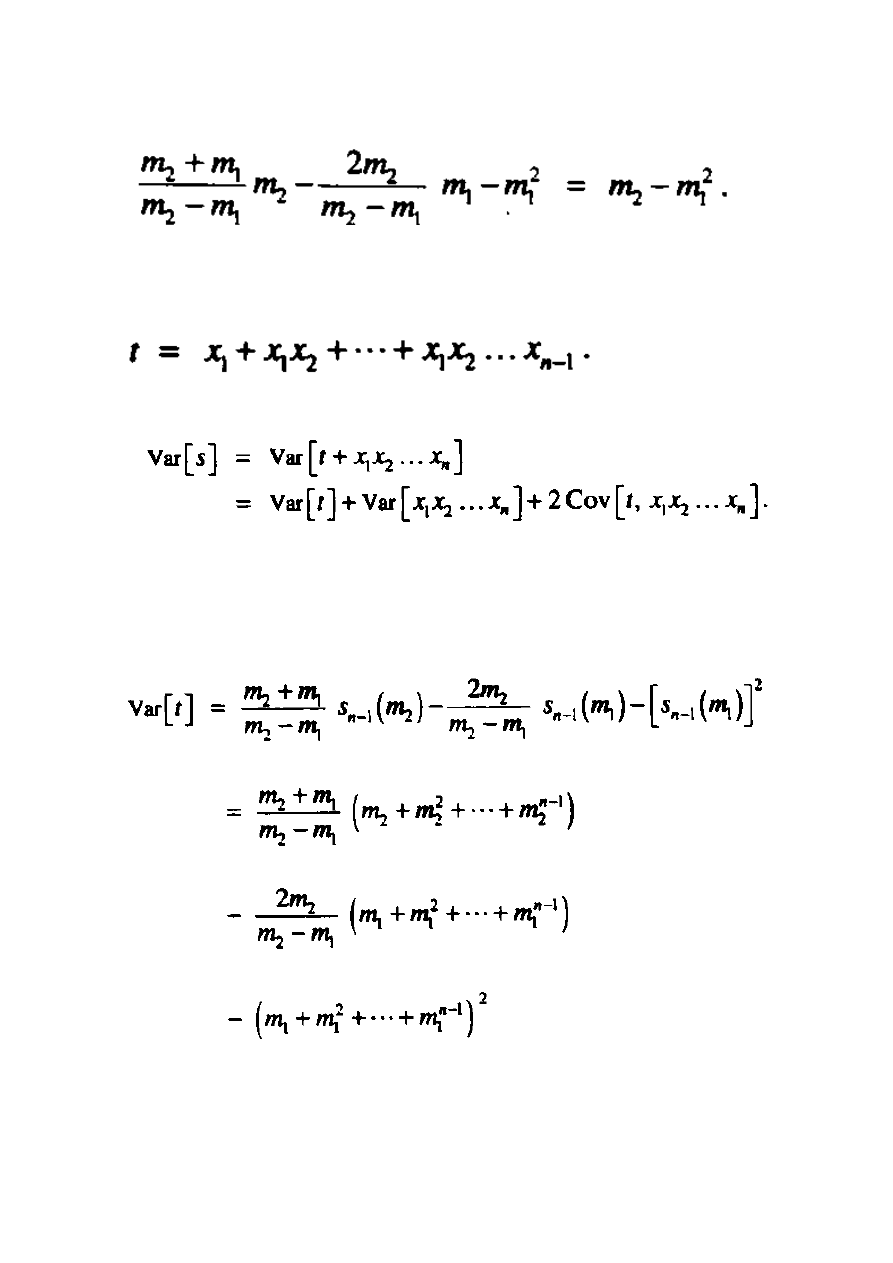
Prawa strona wzoru udowadnia, iż:

Zatem, wzór uzyskujemy dla n = 1.

Teraz załóżmy, iż wzór dotyczy n – 1. Definiując:

Otrzymujemy:

Musimy oszacować te trzy terminy.

Z wywołanego założenia mamy:

Z niezależności otrzymujemy:

Dla kowariancji otrzymujemy:

Musimy pokazać, iż suma tych trzech pojęć potwierdza nam hipotezę. Czytelnik powinien

sprawdzić czy (A) + (D) + (F) daje pierwsze pojęcie we wzorze; (B) + (G) daje drugie

pojęcie; a (C) + (E) + (H) daje trzecie pojęcie.

Zatem, dowód indukcji matematycznej został ukończony.

ĆWICZENIA

12.2 Niezależne stopy procentowe

1. Uzyskaj wzór (12.9)

2. Uzyskaj wzór (12.11)

3. Sumę 1000$ zainwestowano na trzy lata. Obowiązująca stopa procentowa wynosi 8% przez

pierwszy rok. Obowiązująca stopa procentowa w drugim roku jest prawdopodobnie 1%,

wyższa lub niższa niż w pierwszym roku. Podobnie, obowiązująca stopa procentowa w

trzecim roku jest prawdopodobnie 1% wyższa lub niższa niż stopa w drugim roku.

a. Znajdź średnią stopy procentowej w okresie trzech lat

b. Znajdź odchylenie standardowe stopy procentowej w okresie trzech lat

c. Znajdź jak najwięcej możliwych akumulacji na końcu trzech lat

d. Znajdź jak najmniej możliwych akumulacji na końcu trzech lat

e. Znajdź akumulację na końcu trzech lat w średniej stopy procentowej

f. Znajdź średnią wartości akumulacji na końcu trzech lat

g. Znajdź odchylenie standardowe akumulacji na końcu trzech lat

4. Załóżmy, iż

jest obowiązująca stopą procentową przedstawioną w Przykładzie 12.1, to

jest: jednolicie w przedziale [.07,.09] dla t = 1, 2, 3.

a. Znajdź

tak aby

b. Znajdź średnią obecnej wartości 1, zapłaconej na końcu trzech lat.

c. Znajdź

tak aby

.

d. Znajdź odchylenie standardowe obecnej wartości w (b).

5. Opracuj ponownie Ćwiczenie 4(b) oraz (d) dla obecnej wartości płatności 1, dokonanej na

końcu każdego roku w przeciągu trzech lat.

6. Załóżmy, iż

jest nominalną stopą procentową, następującą po rozkładzie

normalnym z

i

dla

a. Znajdź średnią i odchylenie standardowe skumulowanej wartości 100, na końcu

dwóch lat.

b. Opracuj ponownie (a) dla skumulowanej wartości płatności 100, zrealizowanej na

początku każdej połowy roku w przeciągu dwóch lat.

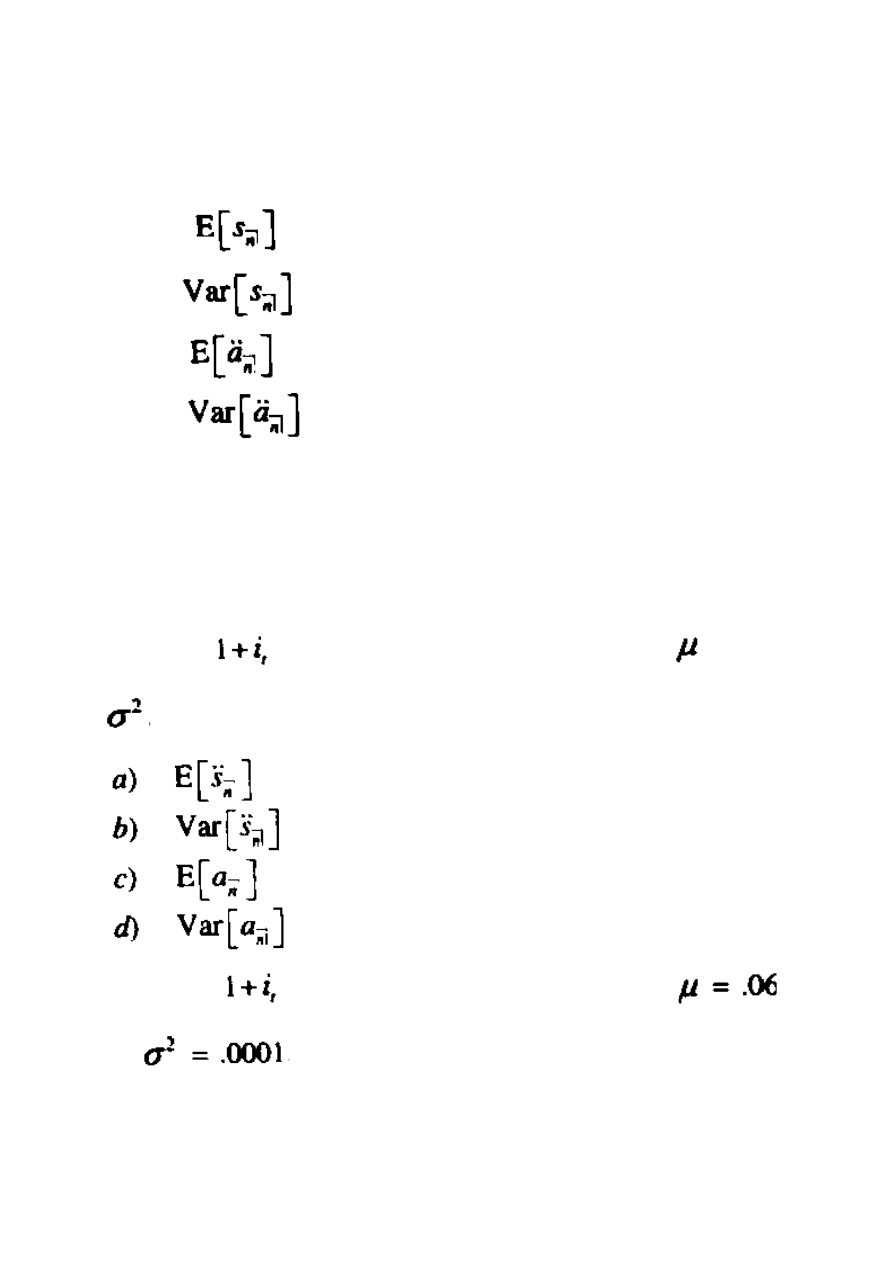
7. Rozwiń wzory dla:

a.

, oparte na wzorze (12.5).

b.

, oparte na wzorze (12.8)

c.

, oparte na wzorze (12.11).

d.

, oparte na wzorze (12.14).

12.3

Model logarytmicznie-normalny

8. W Przykładzie 12.3(1), dla odchylenia standardowego, potwierdź, iż odpowiedź może być

uzyskana poprzez naprzemianległe podejście do zastosowania wzoru (12.4a).

9. Załóżmy, iż

następuje po rozkładzie logarytmicznie-normalnym z

oraz

Znajdź wzory dla:

10. Załóżmy, iż

następuje po rozkładzie logarytmicznie-normalnym z

oraz

. Znajdź średnią i odchylenie standardowe dla:

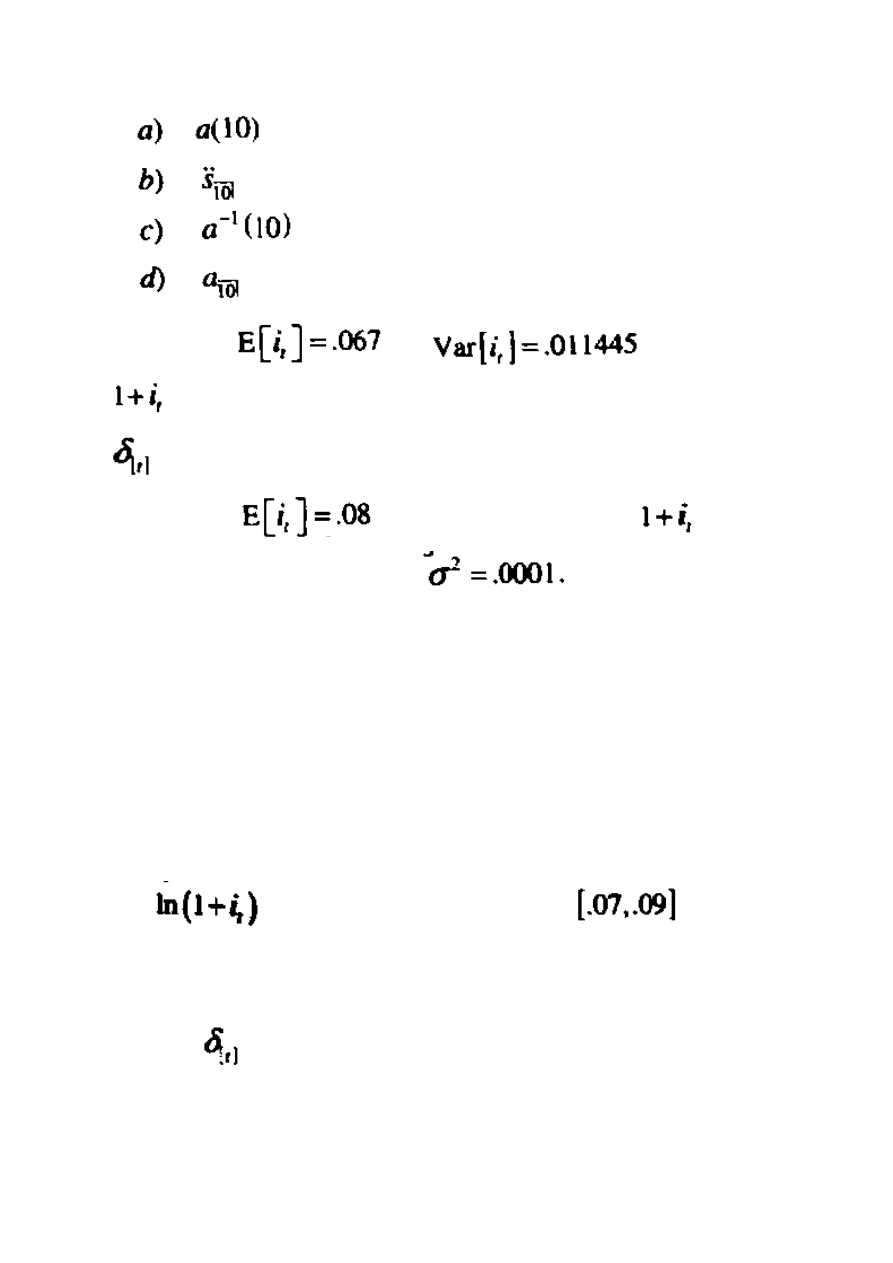
11. Załóżmy, że

oraz

, Załóżmy także, że

następuje po rozkładzie logarytmicznie-normalnym. Znajdź średnią i różnicę

.

12. Załóżmy, iż

dla t = 1, 2, 3. Załóżmy także, iż

następuje

po rozkładzie logarytmicznie-normalnym z

Znajdź dwuczłonowy 95%-

towy przedział prawdopodobieństwa dla skumulowanej wartości inwestycji 1 na końcu trzech

lat.

13. Używając tych samych danych jak w ćwiczeniu 12, znajdź średnią oraz wariancję

skumulowanej wartości inwestycji 1, zrealizowanej na końcu każdego roku w przeciągu

trzech lat.

14. 35-latek zainwestował pewną kwotę aby tym razem uzyskać emeryturę z funduszu,

przynajmniej 100.000 $ w wieku 65 lat. Zwrot w każdym roku jest niezależny od wyników

rocznych. Użyj Twierdzenia Centralnego Limitu aby określić ilość pieniędzy jaką 35-latek

potrzebuje teraz do zainwestowania, aby uzyskać 95% prawdopodobieństwo w momencie

kiedy

jest rozproszone jednolicie w przedziale

.

12.4

Modele szeregu czasowego

15. Oszacuj

dla t = 6, 7, 8 przy wartościach podanych w Przykładzie 12.6, stosując

przyszłe rzeczywiste wartości adekwatne do szacowanych wartości.

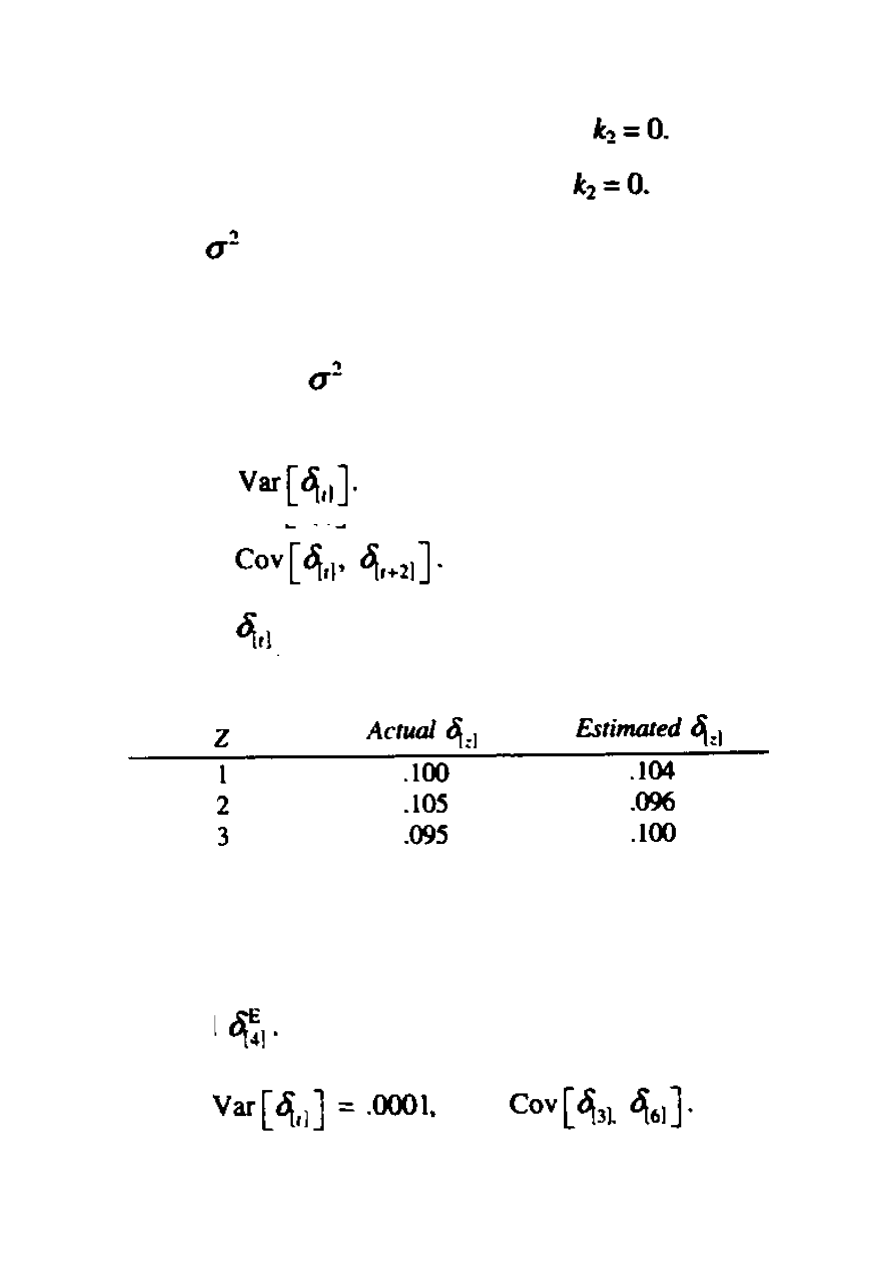
16. a. Pokaż, iż wzór (12.33) upraszcza się do wzoru (12.30) jeżeli

b. Pokaż, iż wzór (12.34) upraszcza się do wzoru (12.31) jeżeli

.

17. Oszacuj

dla procesu AR(2) w Przykładzie 12.7 opartym na danych dla Z = 1, 2, 3,

4, zakładając, iż błędy są rozłożone normalnie ze średnia = 0 i zakładając, iż zbiorowa

wariancja równa jest próbce wariancji.

18. Zakładając, iż wartość

dla procesu AR(2) w Przykładzie 12.7 jest rzeczywiście

równy .0002.

a. Znajdź

b. Znajdź

19. Wiadomo, iż

jest rozłożone normalnie i następuje po procesie AR(1). Następujące

wartości są podane poniżej:

Actual – rzeczywiste

Estimated – szacowane

a.

Znajdź

b.

Jeżeli

, znajdź

.

20. Fundusz inwestycyjny zarobił 6% podczas zeszłego roku. Dla każdego z następnych

dwóch lat dochód z funduszu inwestycyjnego

jest prawdopodobny:

a.

Pokaż, iż

b.

Pokaż, iż

12.5

Drzewa dwumianu

21. Opracuj ponownie Przykład 12.8 (1) stosując wzór (12.38)

22. Model dwumianu z roczną stopą procentową, utworzony jest w stosunku do wartości

trzyletniej obligacji kuponowej, przypadającej do zapłaty 1000$. Początkowa stopa

procentowa w drzewie wynosi 10%. Każda stopa procentowa porusza się wzrostowo z 1% i

prawdopodobieństwem p = 5 lub obniża się poprzez 1% z prawdopodobieństwem 1 – p = .5.

a. Oblicz wartość obligacji z drzewa.

b. Oblicz odchylenie standardowe obecnej wartości tej obligacji z drzewa.

c. Porównaj wartość obligacji z drzewa oraz wartość, używającą średniej stopy

procentowej.

23. Jednoroczna obligacja 9%-towa z półrocznymi kuponami warta jest 1000$. Zastosujemy

tu drzewo dwumianu z półrocznymi okresami. Obecny wskaźnik dochodu wynosi 9%

wymiennie co pół roku. Każda nominalna stopa procentowa wzrasta poprzez 1% z

prawdopodobieństwem p = .3 lub obniża się poprzez 1% z prawdopodobieństwem 1 – p = .7.

a. Przelicz wartość tej obligacji z drzewa.

b. Przelicz poziom prawdopodobnego wskaźnika zwrotu.

24. Opracuj ponownie ćwiczenie 23(a) jeżeli obligacja jest płatna na żądanie na każdym

terminie płatności dywidendy na przyszłe akcje o wartościach nominalnym.

25. Opracuj ponownie Przykład 12.9 jeżeli obecny wskaźnik dochodu wynosi 8% wymiennie

co kwartał. Zastosuj drzewo dwumianu z przedziałami kwartalnymi.

26. Pomnożony model dwumianu z prawdopodobieństwem p = .4 i parametrem lotności k =

.2 jest tutaj wykorzystany. Początkowa stopa procentowa w drzewie wynosi 10%.

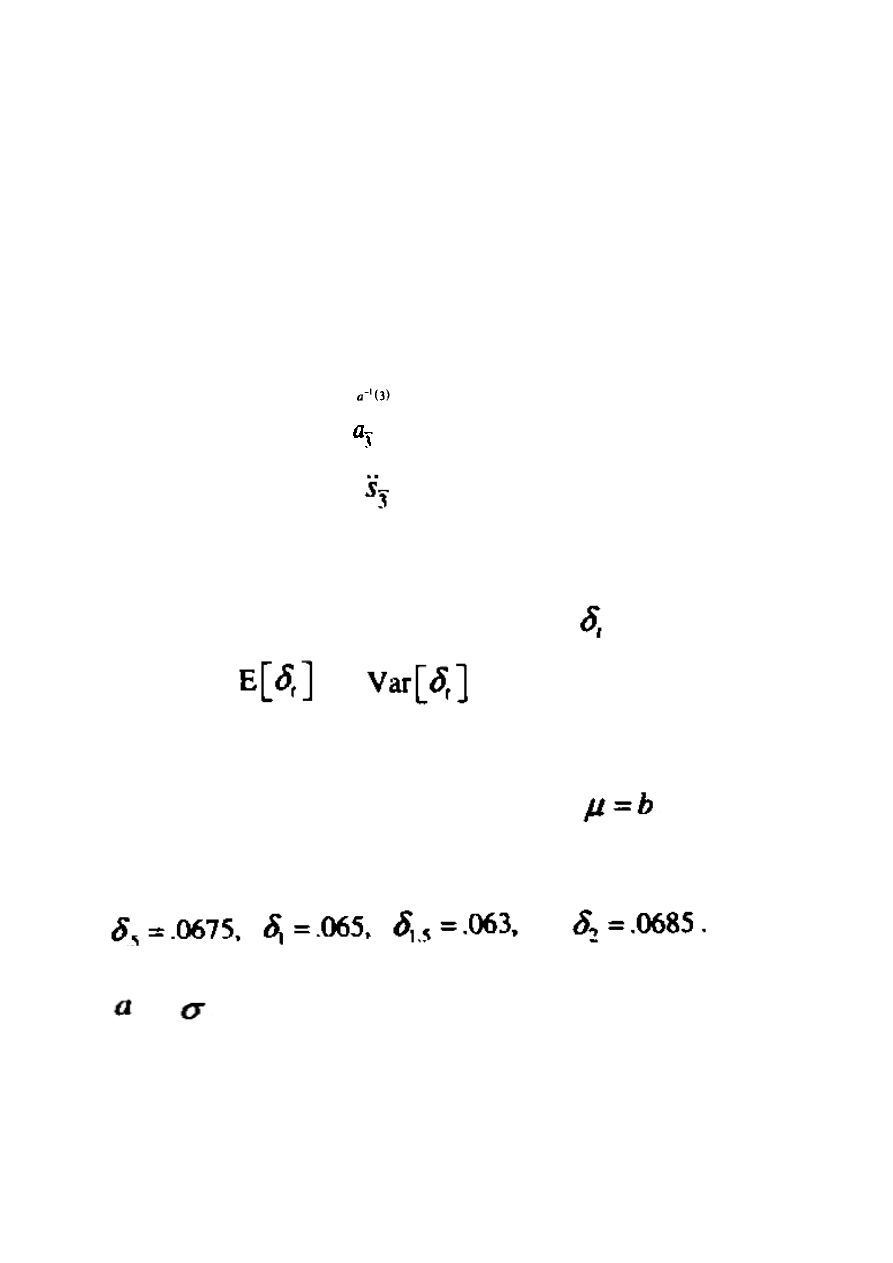
a. Znajdź średnią wartości a(3)

b. Znajdź średnią wartości

c. Znajdź średnią wartości

d. Znajdź średnią wartości

12.6

Modele stochastyczne prawdopodobieństwa

27. Wzory (12.42) oraz (12.43) dają średnią i wariancję procesu

, zgodnie z błądzeniem

losowym. Znajdź

oraz

, zgodnie z trzema modelami.

28. Dla Modelu Vasicek określonego przez wzór (12.46):

a. Pokaż, że kiedy c = 0, model staje się błądzeniem losowym bez dryftu.

b. Pokaż, że kiedy c = 1, model staje się rozkładem normalnym z

.

29. Obecna siła stopy procentowej wynosi .06. Zgodnie z błądzeniem losowym z

dopasowaniem półrocznym, oszacowane siły odsetek wynoszą:

oraz

. Znajdź

oszacowane siły odsetek używając Modelu Rendelman-Bartter z takimi samymi parametrami

oraz

.

30. Norma wartości obligacji w jednym roku wynosi 1000$, i posiada 7.8% półrocznych

kuponów. Obecna siła odsetek wynosi .08. Użyj błądzenia losowego z półrocznymi korektami

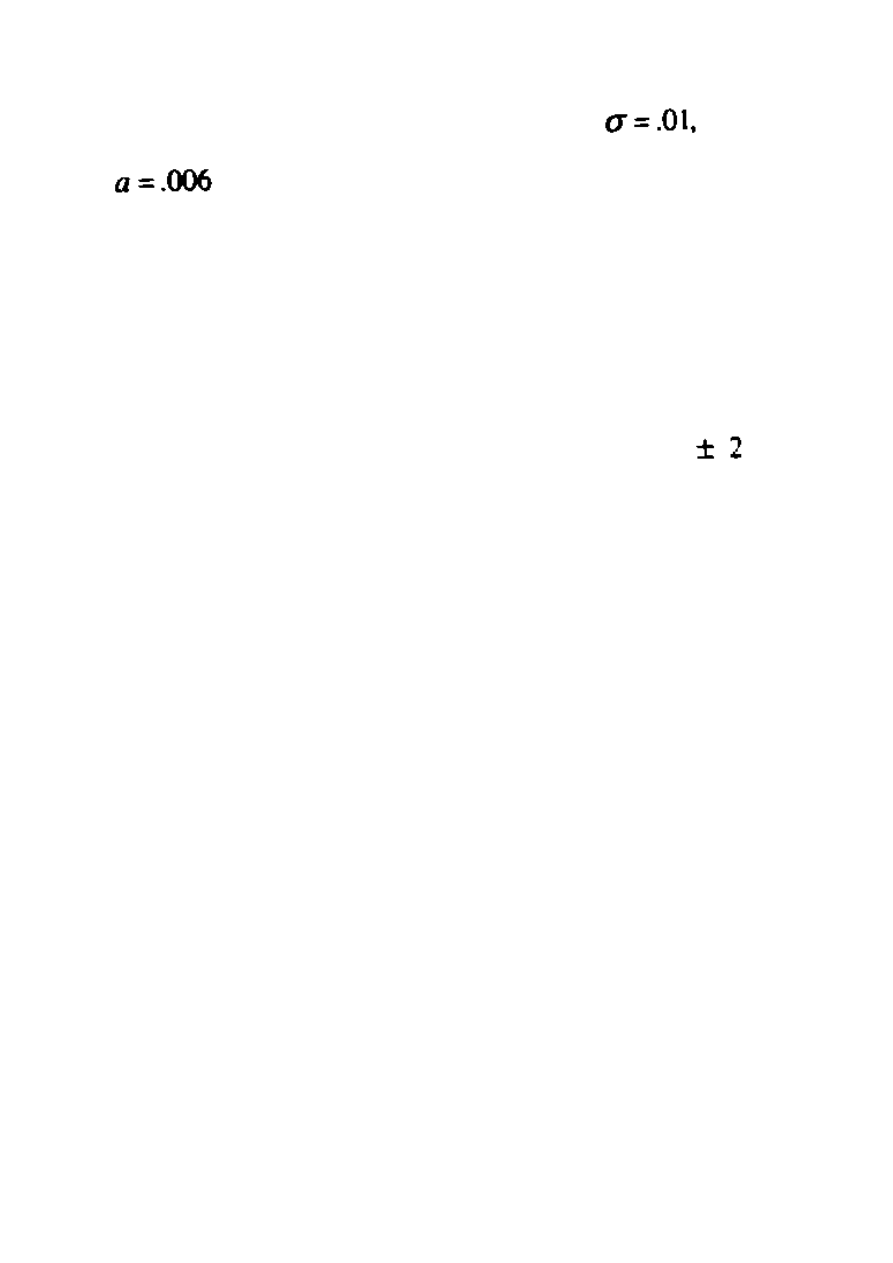
aby oszacować siłę odsetek na przyszłość. Parametr lotności wynosi

oraz

.

a. Znajdź wartość obligacji

b. Znajdź poziom krzywej dochodowości

c. Znajdź wartość obligacji, jeśli standardowa normalna zmienna wynosi .5, używając

symulacji

31. Odrzuć cztery standardowe normalne zmienne utworzone przy użyciu symulacji w

Przykładach 12.11-12.14. Opracuj ponownie te cztery przykłady aby znaleźć jak największą i

jak najmniejszą możliwą siłę stopy procentowej w jednym roku w stosunku do przyszłości.

Załóżmy, iż wskaźnik standardowych normalnych zmiennych wynosi 4., to jest:

standardowych odchyleń.

12.7

Test scenariusza

32. Załóżmy, iż obowiązująca stopa procentowa w ciągu roku zakończona jest na 8%. Ścieżki

stopy procentowej będą utworzone w ciągu najbliższych 10 lat zgodnie z drzewem

dwumianu. Załóżmy, iż obowiązujący wskaźnik zarówno wzrośnie jak i zmaleje o 10% w

byłym poziomie każdego roku i że ruch w każdym kierunku jest równie prawdopodobny.

a.

Znajdź jak najwięcej możliwych obowiązujących wskaźników po 10 latach

b.

Znajdź jak najmniej możliwych obowiązujących wskaźników po 10 latach.

c.

Znajdź obowiązujący wskaźnik po 10 latach, jeśli jest 5 wzrostów i 5 obniżeń.

d.

Wytłumacz dlaczego odpowiedzi z punktu c, nie wynoszą 8%.

e.

Znajdź prawdopodobieństwo wyniku w punkcie c.

f.

Wiemy, iż wynik w nadwyżce 15% jest nierealny. Znajdź prawdopodobieństwo, iż

wskaźnik jest ograniczony w 15% na koniec 10 lat.

33. Krótkoterminowe stopy procentowe są bardziej zmienne niż długoterminowe stopy

procentowe. W celu przyjrzeniu się temu zjawisku, został tu zastosowany projekt techniczny,

dla którego kolejne miejsce wskaźników w ścieżce stopy procentowej jest utworzone przez

wzór:

Gdzie

jest odchyleniem standardowym miejsca wskaźnika .Z - jest wartością z

rozkładu normalnego standardowego a k jest stałą. Odchylenie standardowe

jest

większe dla krótkoterminowych wskaźników niż dla długoterminowych. Załóżmy, iż obecny

jednoroczny wskaźnik miejsca wynosi 7% z odchyleniem standardowym .1, podczas gdy

obecny pięcioletni wskaźnik miejsca wynosi 8% z odchyleniem standardowym .05.

Wskaźniki są zaplanowane na ponad pięć następnych lat dla obu ich miejsc. Pięć

przypadkowych liczb jest utworzonych z normalnego standardowego rozkładu: +1.65, -.26,

+.73, +1.17, +.98. Te wartości są używane w celu zaplanowania ścieżki stopy procentowej dla

obu miejsc wskaźników. Stała k jest równa 1. Znajdź dwa miejsca wskaźników na końcu

pięciu lat i pokaż, iż krzywa dochodowości staje się odwrócona