1

Podstawy Konstrukcji Maszyn

Wykład 4

Połączenia śrubowe część 2

Dr inż. Jacek Czarnigowski

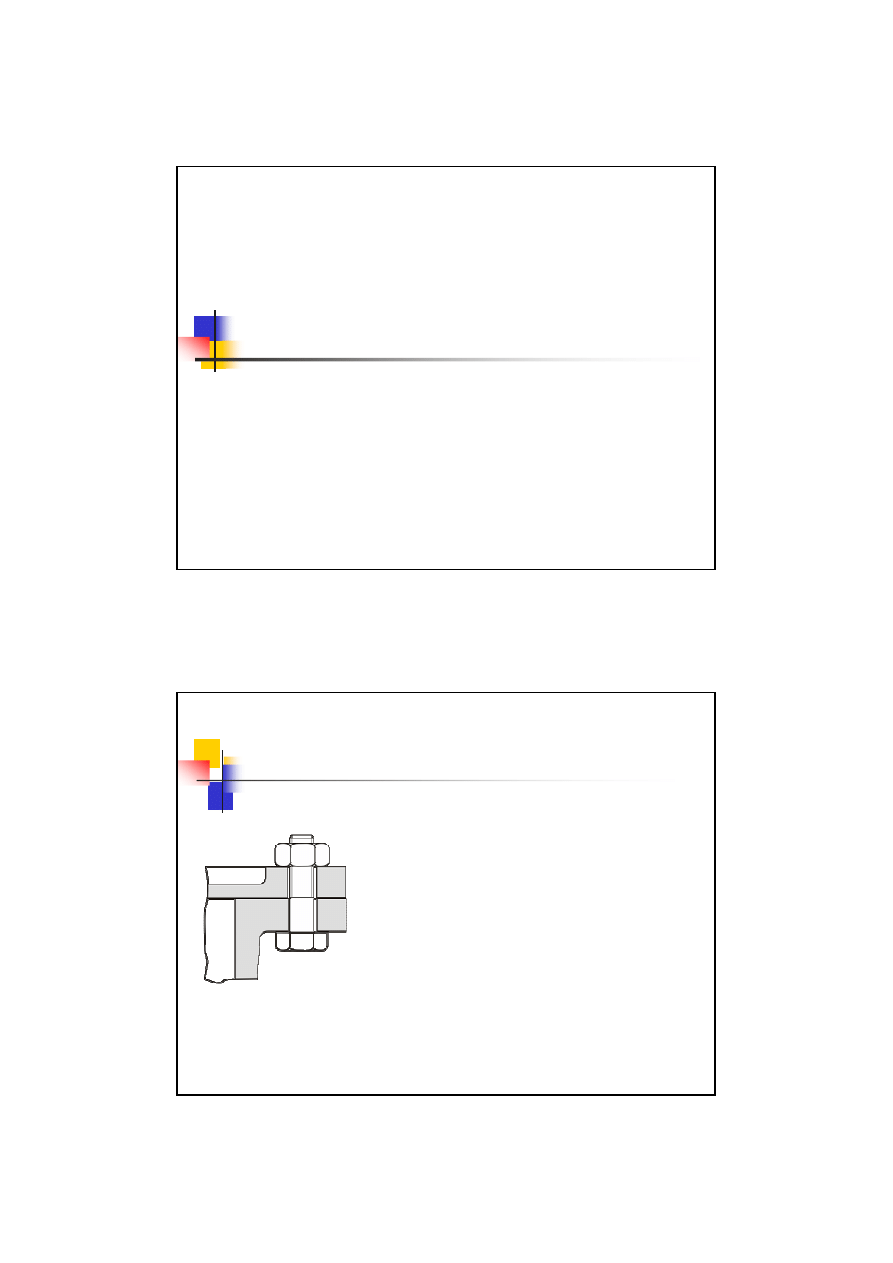
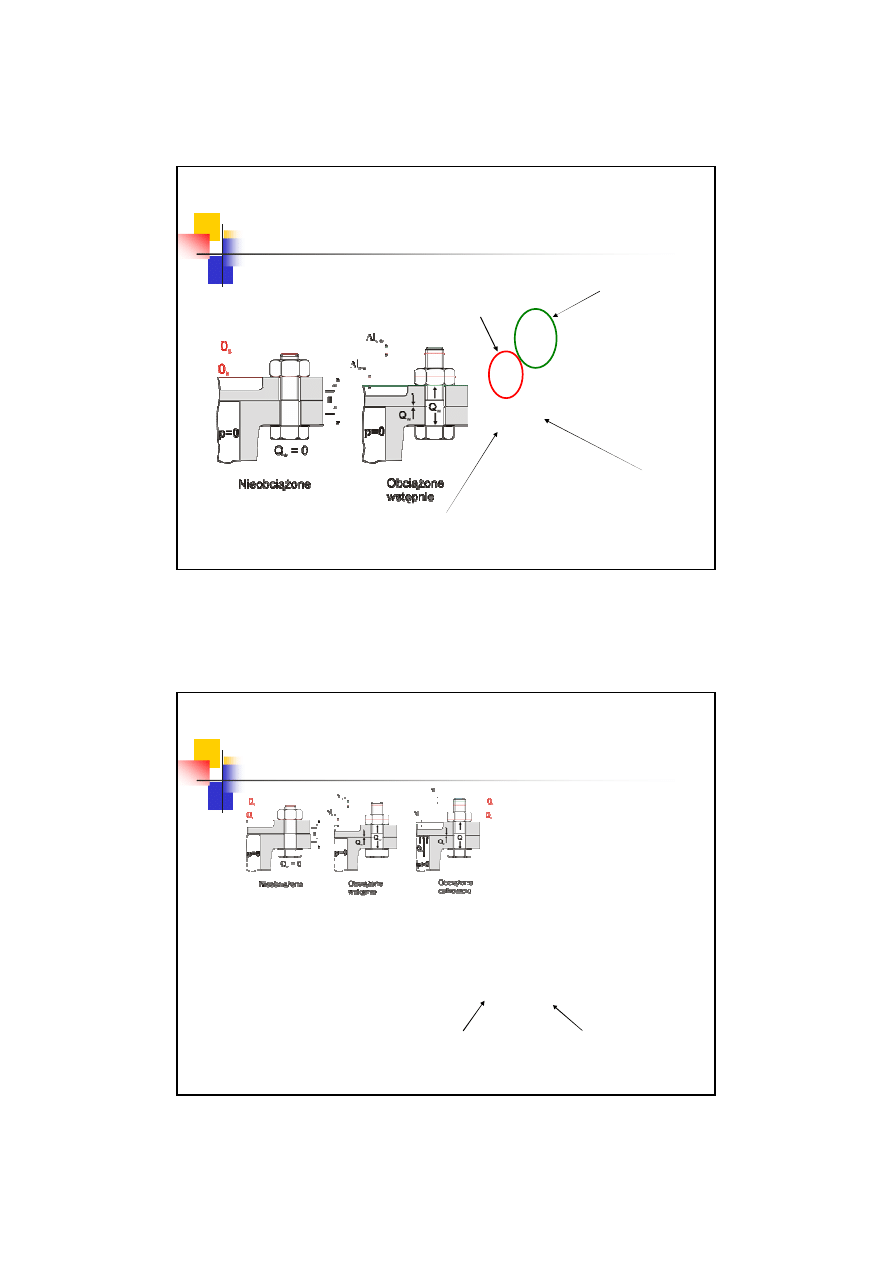
3 przypadek obciążenia śrub

Złącze samohamowne

najpierw napięte

siłą napięcia wstępnego

Q

w

poprzez

skręcenie śruby

momentem

M

c

Przykłady:
- śruby pokryw zbiorników ciśnienia,
- szpilki głowic silnika,
- śruby kołnierzy przewodów rurowych

A

następnie obciążone

siłą roboczą

osiową

Q

p

rozciągającą śrubę.

Zacisk wstępny musi być na tyle duży
aby po obciążeniu śruby

siłą roboczą

osiową

Q

p

nie nastąpił luz między

łączonymi elementami (pozostał

zacisk

resztkowy

Q

z

.

2

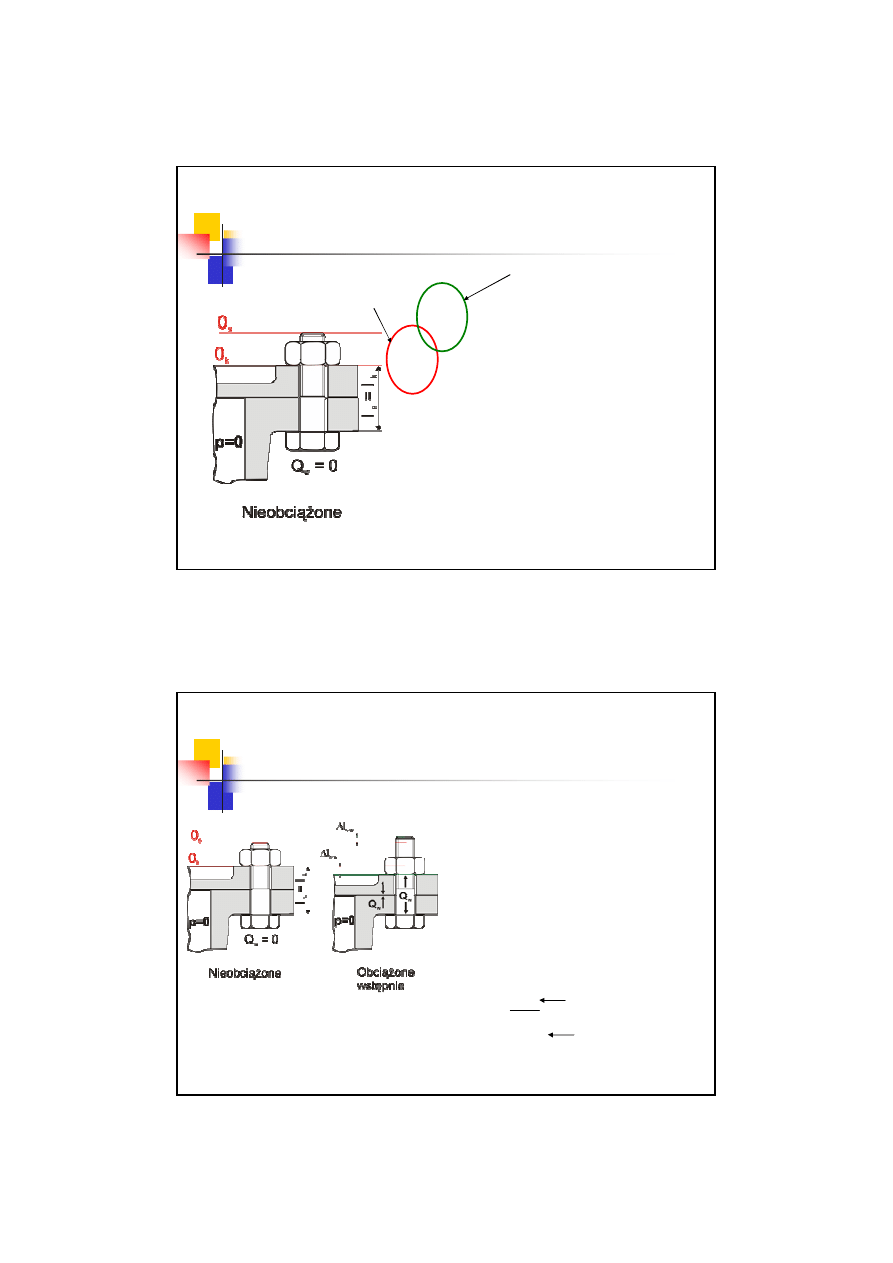
3 przypadek obciążenia śrub

Siła napięcia
wstępnego

Q

w

Ściśnięcie kołnierza

Rozciągnięcie śruby

3 przypadek obciążenia śrub

Odkształcenia występują w

zakresie odkształceń

sprężystych

l

l

⋅

=

∆

δ

Prawo Hooka

E

r

σ

δ

=

Wydłużenie jednostkowe

Naprężenia

rozciągające

Moduł

sprężystości –

Moduł Younga

3

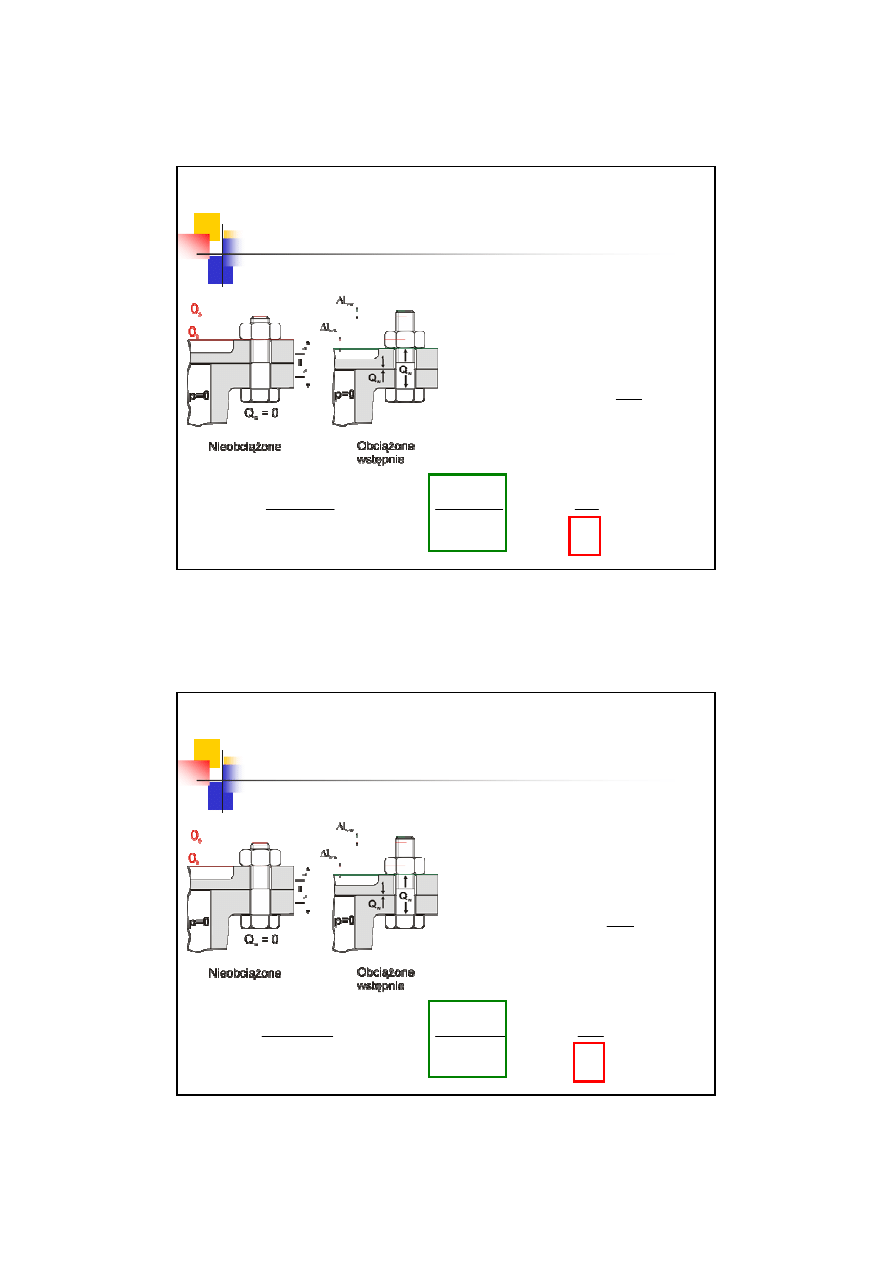
3 przypadek obciążenia śrub

Zatem przy obciążeniu

wstępnym siłą

Q

w

s

s

r

s

s

w

s

l

E

l

l

⋅

=

⋅

=

∆

−

σ

δ

Odkształcenie śruby:

s

w

s

s

s

w

s

s

s

w

w

s

c

Q

E

F

l

Q

l

E

F

Q

l

1

⋅

=

⋅

⋅

=

⋅

⋅

=

∆

−

Podatność śruby

Sztywność

śruby

3 przypadek obciążenia śrub

Zatem przy obciążeniu

wstępnym siłą

Q

w

k

k

r

k

k

w

k

l

E

l

l

⋅

=

⋅

=

∆

−

σ

δ

Odkształcenie kołnierza:

k

w

k

k

k

w

k

k

k

w

w

k

c

Q

E

F

l

Q

l

E

F

Q

l

1

⋅

=

⋅

⋅

=

⋅

⋅

=

∆

−

Podatność kołnierza

Sztywność

kołnierza

4

3 przypadek obciążenia śrub

Sztywność





















=

⋅

=

⋅

=

m

N

m

m

N

m

l

E

F

c

2

2

∆

l

Q

α

c

l

Q

tg

=

∆

=

α

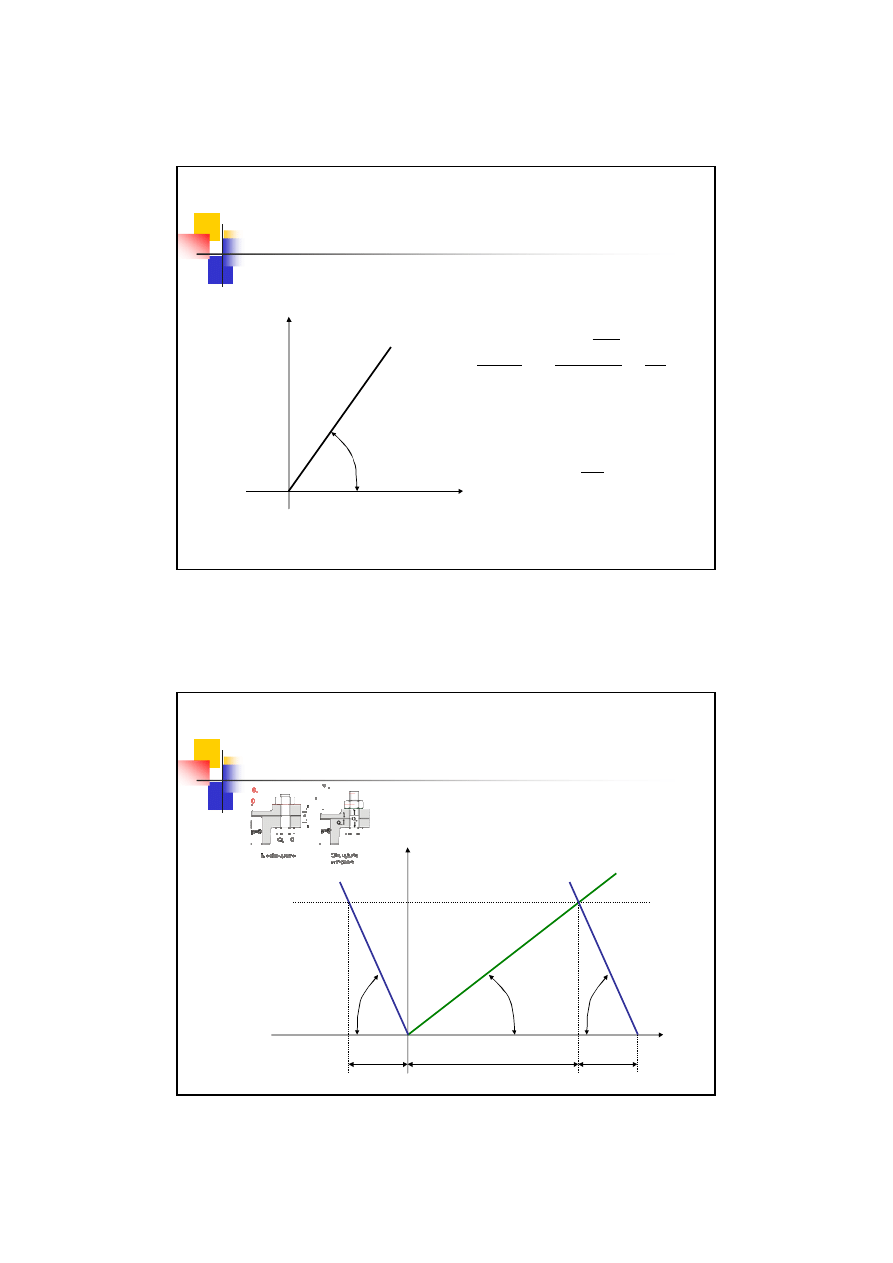
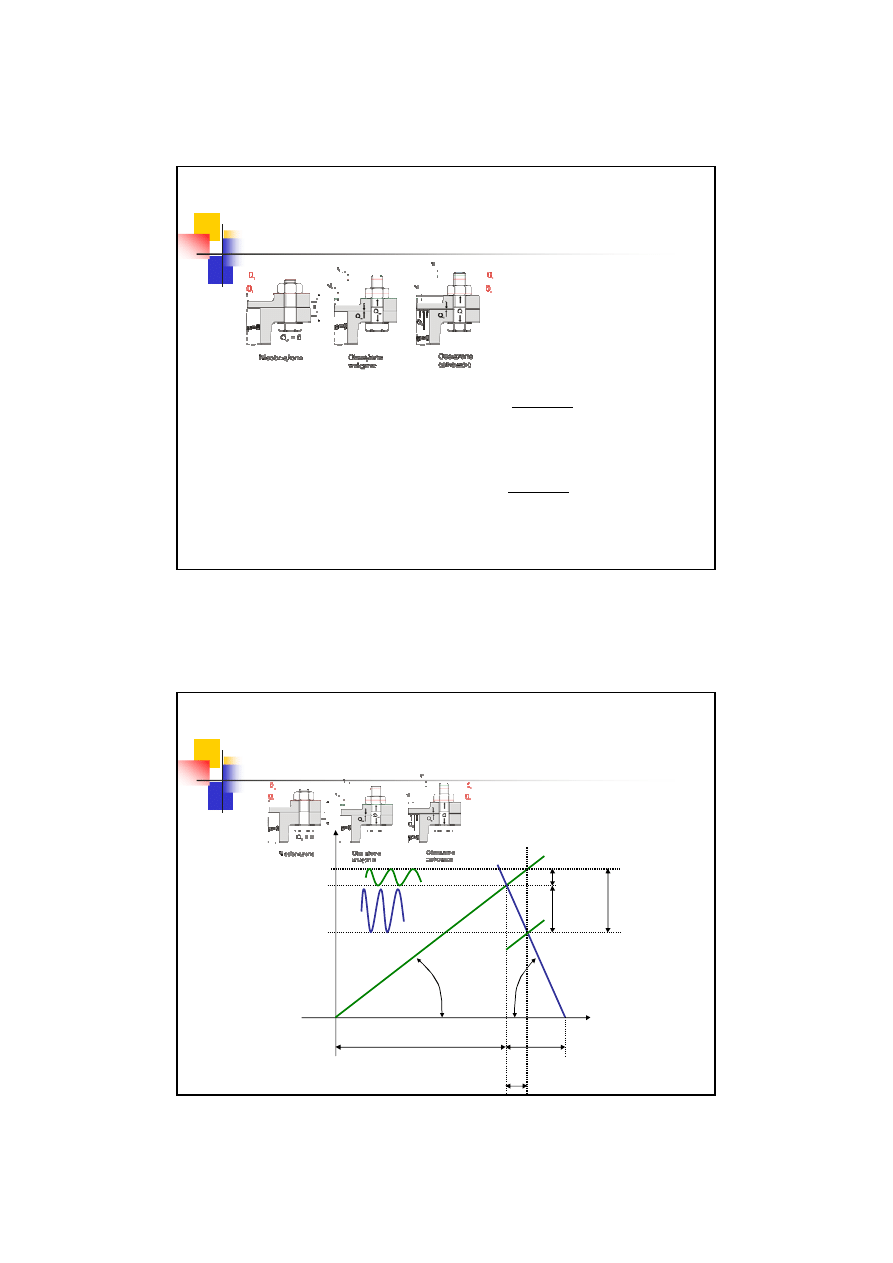
3 przypadek obciążenia śrub

Wykres obciążeń i odkształceń

∆

l

Q

Śruba

Kołnierz

α

s

c

tg

=

α

β

k

c

tg

=

β

Q

w

∆

l

s-w

∆

l

k-w

β

∆

l

k-w

5

3 przypadek obciążenia śrub

Siła robocza

Q

p

Zmniejszenie

ściśnięcia

kołnierza

Dodatkowe

rozciągnięcie

śruby

Zacisk
resztkowy

Q

z

3 przypadek obciążenia śrub

Siła robocza

Q

p

(

)

k

s

p

p

c

c

l

Q

+

⋅

∆

=

k
p

s

p

k

p

s

p

p

Q

Q

c

l

c

l

Q

+

=

⋅

∆

+

⋅

∆

=

Dodatkowe

obciążenie

śruby

Odciążenie

kołnierza

6

3 przypadek obciążenia śrub

Siła robocza

Q

p

k

s

s

p

s
p

c

c

c

Q

Q

+

=

Dodatkowe obciążenie śruby

Odciążenie kołnierza

k

s

k

p

k
p

c

c

c

Q

Q

+

=

3 przypadek obciążenia śrub

Wykres obciążeń i

odkształceń

∆

l

Q

Śruba

Kołnierz

α

Q

w

∆

l

s-w

∆

l

p

β

∆

l

k-w

Q

p

k

Q

p

s

Q

p

Zacisk resztkowy

Q

z

Obciążenie całkowite

Q

max

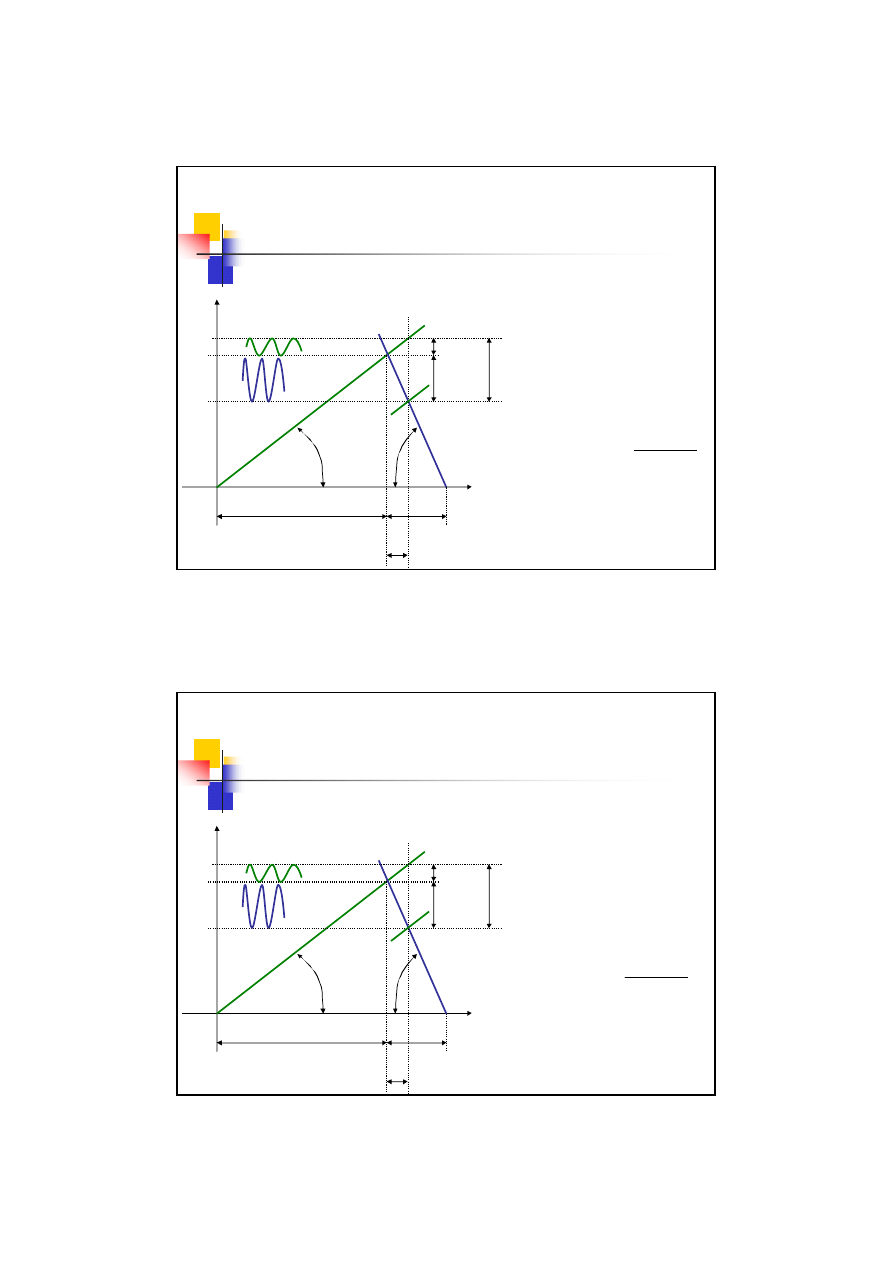
7

3 przypadek obciążenia śrub

Wykres obciążeń i

odkształceń

∆

l

Q

Śruba

Kołnierz

α

Q

w

∆

l

s-w

∆

l

p

β

∆

l

k-w

Q

p

k

Q

p

s

Q

p

Obciążenie całkowite

Q

max

s

p

w

Q

Q

Q

+

=

max

k

s

s

p

w

c

c

c

Q

Q

Q

+

+

=

max

3 przypadek obciążenia śrub

Wykres obciążeń i

odkształceń

∆

l

Q

Śruba

Kołnierz

α

Q

w

∆

l

s-w

∆

l

p

β

∆

l

k-w

Q

p

k

Q

p

s

Q

p

Zacisk resztkowy

Q

z

k
p

w

z

Q

Q

Q

−

=

k

s

k

p

w

z

c

c

c

Q

Q

Q

+

−

=

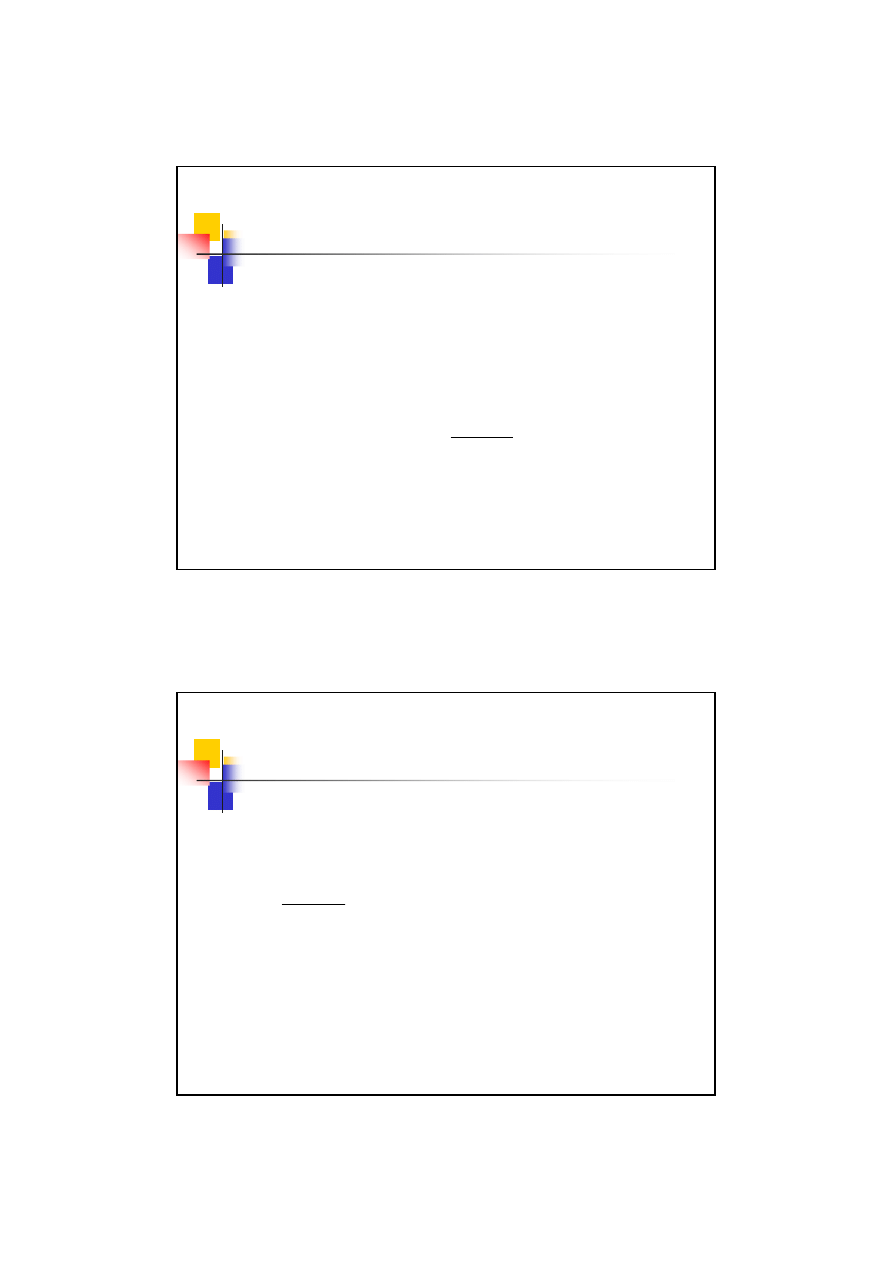
8

3 przypadek obciążenia śrub

Zacisk resztkowy

Q

z

k

s

k

p

w

c

c

c

Q

Q

+

>

Aby na powierzchniach łączonych nie wystąpił luz to

zacisk resztkowy powinien być większy od 0

3 przypadek obciążenia śrub

Zacisk resztkowy

Q

z

Siła zacisku resztkowego nie powinna być zbyt mała i wynosić:

Gdy wymagana jest szczelność:

n

F

p

Q

u

u

z

⋅

=

p

u

- ciśnienie uszczelnienia

F

u

- pole powierzchni uszczelnienia

n – liczba śrub w złączu

Np. dla silników spalinowych:

p

u

= 1,5 – 2

p

max

Gdy nie wymagana jest szczelność:

p

z

Q

Q

⋅

÷

=

6

,

0

2

,

0

9

3 przypadek obciążenia śrub

Wpływ sztywności śruby

∆

l

Q

Śruba

Kołnierz

Q

w

∆

l

s-w

∆

l

p

β

∆

l

k-w

Q

p

Q

z

Q

max

Q

w

= const

Q

p

= const

c

k

= const

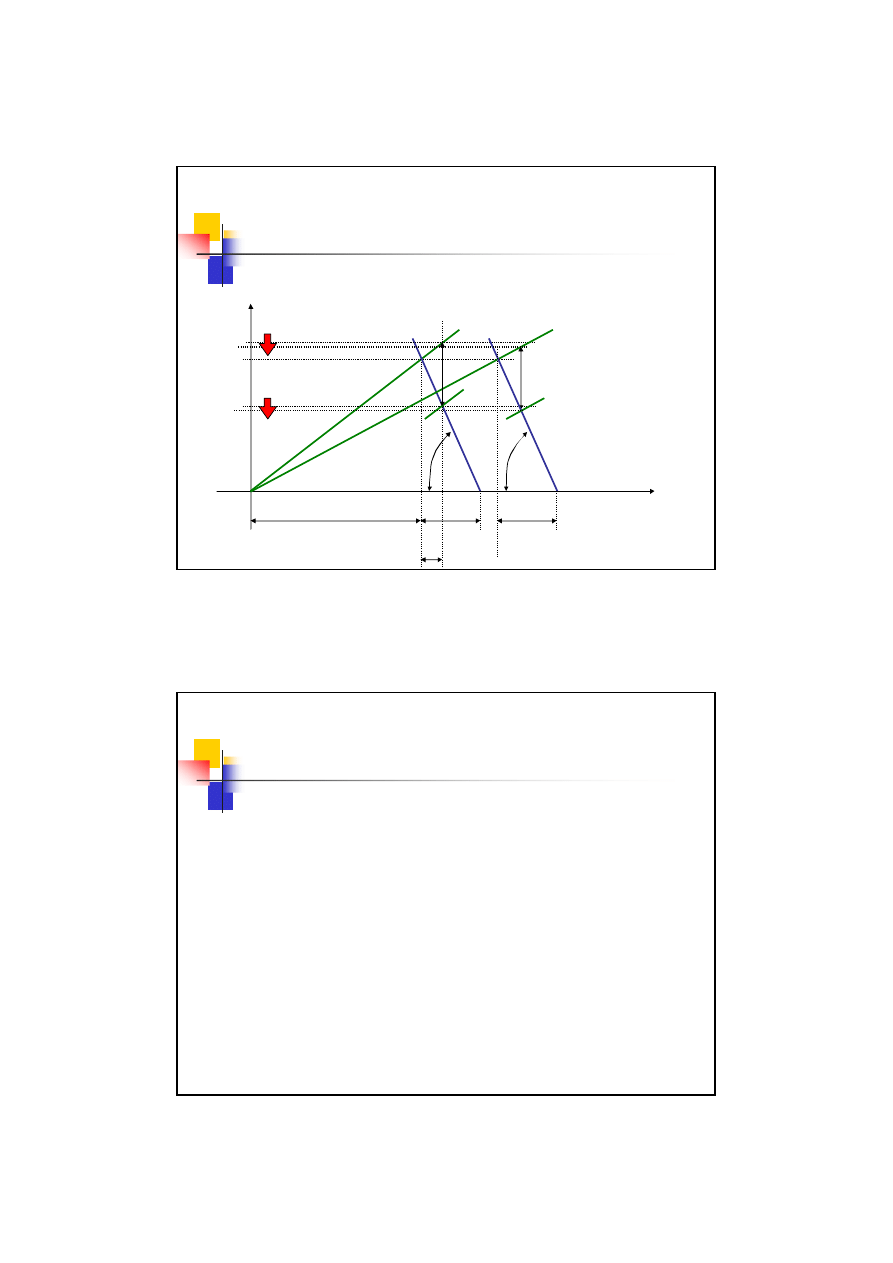
Spadek

sztywności

śruby

β

∆

l

k-w

Q

p

3 przypadek obciążenia śrub

Wpływ sztywności śruby

Spadek sztywności śruby

Zalety:

Spadek obciążenia całkowitego (maksymalnego) w śrubie

Spadek zakresu zmienności obciążenia w śrubie

Spadek naprężeń średnich w kołnierzu

Wady:

Spadek zacisku resztkowego

10

3 przypadek obciążenia śrub

Wpływ sztywności kołnierza

∆

l

Q

Śruba

Kołnierz

Q

w

∆

l

s-w

∆

l

p

∆

l

k-w

Q

p

Q

z

Q

max

Q

w

= const

Q

p

= const

c

s

= const

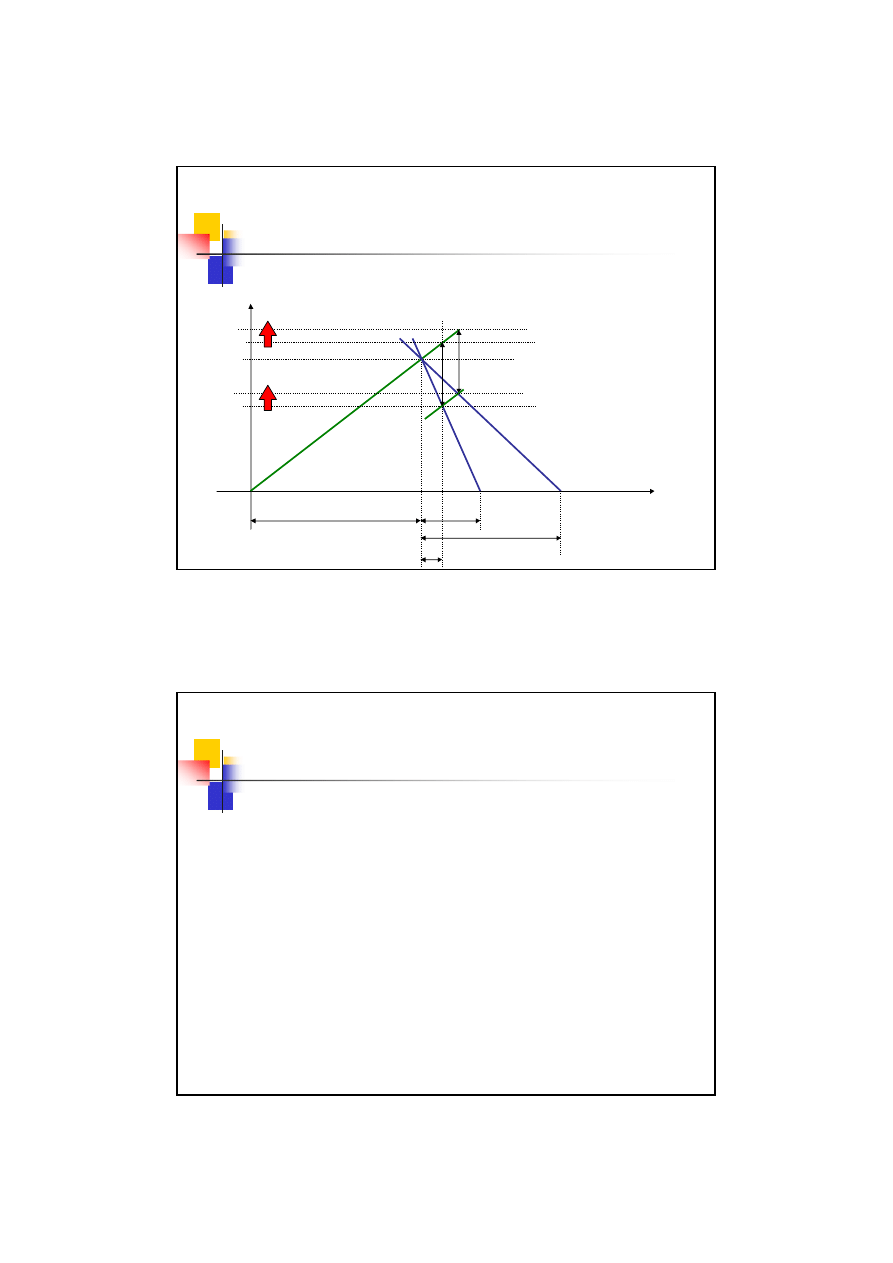
Spadek

sztywności

kołnierza

∆

l

k-w

Q

p

3 przypadek obciążenia śrub

Wpływ sztywności kołnierza

Spadek sztywności kołnierza

Zalety:

Wzrost obciążenia całkowitego (maksymalnego) w śrubie

Wzrost zakresu zmienności obciążenia w śrubie

Wzrost naprężeń średnich w kołnierzu

Wady:

Wzrost zacisku resztkowego

11

3 przypadek obciążenia śrub

Wpływ sztywności śruby i kołnierza

Wniosek

Idealne rozwiązanie to:

Podatna śruba i sztywny kołnierz

3 przypadek obciążenia śrub

Określenie sztywności śruby

Śruba o stałej średnicy

s

s

s

l

E

d

c

⋅

⋅

⋅

=

4

2

π

Śruba o zmiennej geometrii

∑

=

⋅

=

n

i

i

i

s

s

F

l

E

c

1

1

1

12

3 przypadek obciążenia śrub

Określenie sztywności kołnierza

Metoda dokładna – oparta na badaniach doświadczalnych

rzeczywistego elementu

Metoda uproszczona – oparta na „stożkach wpływu”

3 przypadek obciążenia śrub

Określenie sztywności kołnierza

Metoda uproszczona – oparta na „stożkach wpływu”

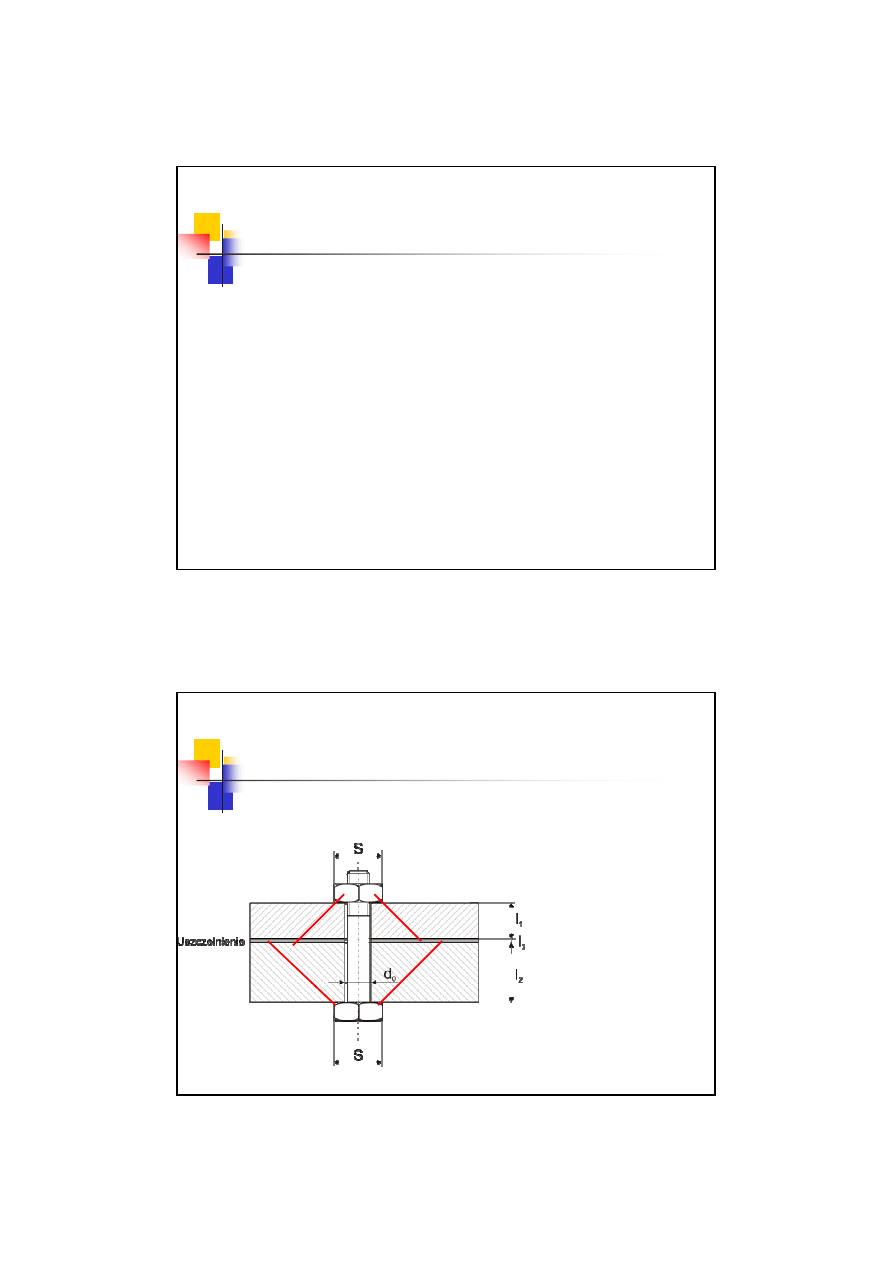
Zakłada się, że

ściskany jest ścięty

stożek o średnicy

mniejszej podstawy

równej wymiarowi

pod klucz

S i

tworzącej pod kątem

45

o

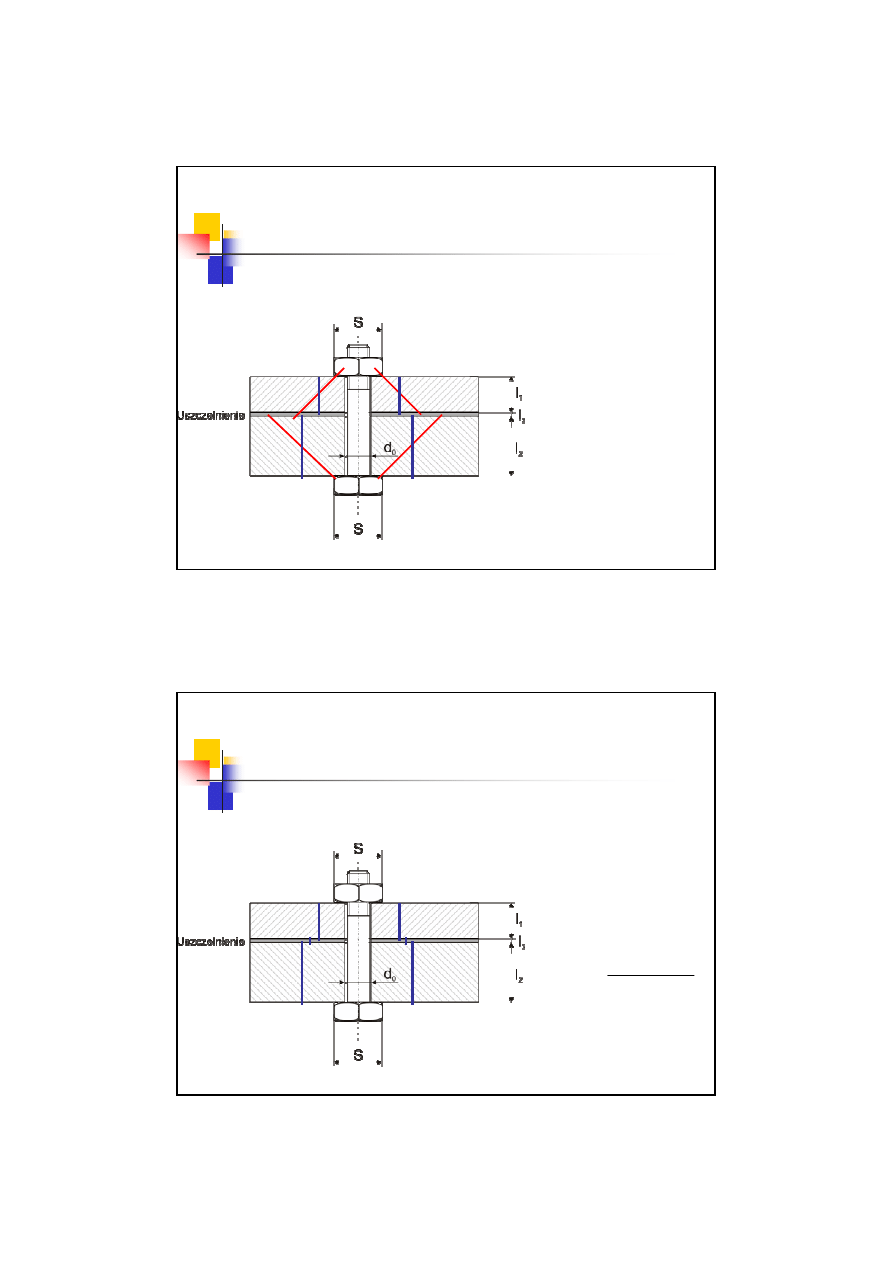
13

3 przypadek obciążenia śrub

Określenie sztywności kołnierza

Metoda uproszczona – oparta na „stożkach wpływu”

Stożki te

zastępowane są

walcami zastępczymi

o średnicy:

D

z

= S+l

D

z1

= S+l

1

D

z2

= S+l

2

3 przypadek obciążenia śrub

Określenie sztywności kołnierza

Metoda uproszczona – oparta na „stożkach wpływu”

Dla uszczelki

przyjmuję się

średnicę pośrednią:

2

2

1

3

z

z

z

D

D

D

+

=

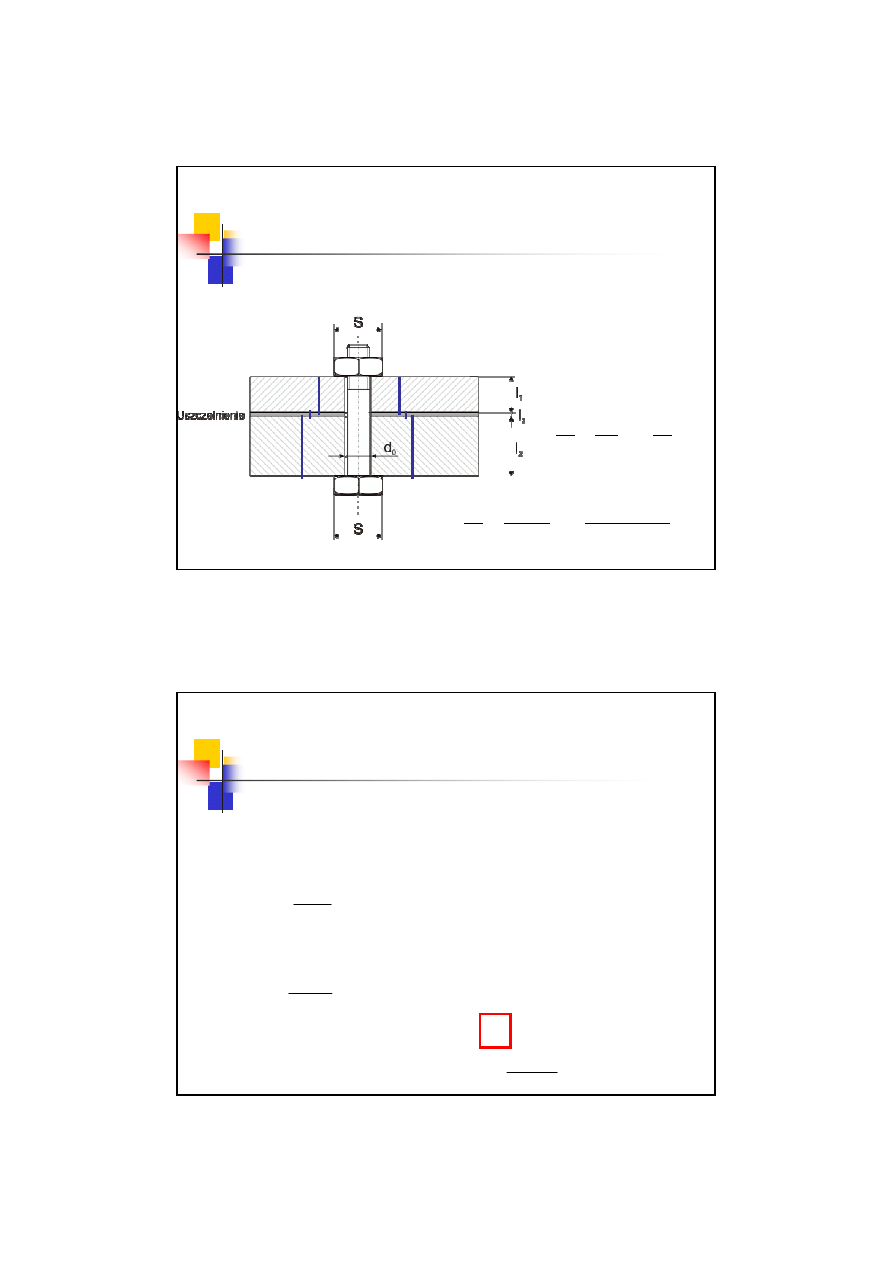
14

3 przypadek obciążenia śrub

Określenie sztywności kołnierza

Metoda uproszczona – oparta na „stożkach wpływu”

Dla tak określonych

walców zastępczych

oblicza się sztywność

jako:

∑

=

⋅

=

n

i

i

i

k

k

F

l

E

c

1

1

1

(

)

∑

=

−

⋅

⋅

=

3

1

2

2

4

1

i

o

zi

i

k

k

d

D

l

E

c

π

3 przypadek obciążenia śrub

Obliczenia wytrzymałościowe

Śruba

Rozciąganie:

min

max

F

Q

r

=

σ

Najmniejsze pole przekroju śruby

Skręcanie:

min

o

c

s

W

M

=

τ

Dla najmniejszego

pole przekroju śruby

Moment całkowity wywołany zaciskiem wstępnym

(

)

[

]

'

5

,

0

ρ

γ

µ

+

⋅

+

⋅

⋅

⋅

=

+

=

tg

d

d

Q

M

M

M

M

s

p

w

c

s

t

c

2

o

p

d

S

d

+

=

15

3 przypadek obciążenia śrub

Obliczenia wytrzymałościowe

Śruba

Naprężenia zastępcze:

r

s

r

z

k

w

⋅

<

⋅

+

=

2

2

3

τ

σ

σ

Zmienność obciążenia:

Tylko rozciąganie – cykl jednostronny siła zmienia się

od

Q

w

do

Q

max

3 przypadek obciążenia śrub

Obliczenia wytrzymałościowe

Kołnierz

Najsłabszym elementem jest uszczelka:

dop

u

w

p

F

Q

p

≤

=

Zmienność obciążenia:

Ściskanie cykl jednostronny siła zmienia się

od

Q

w

do

Q

z

16

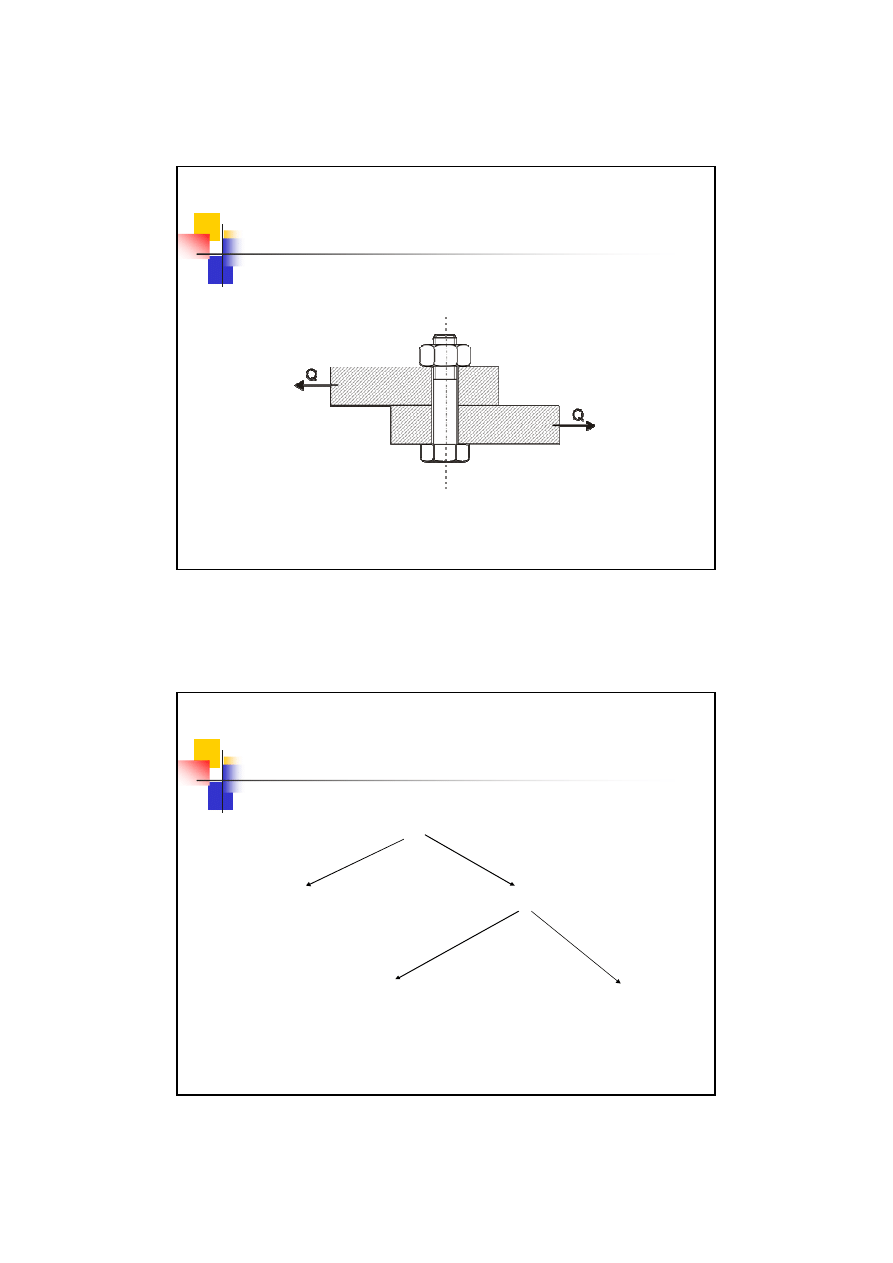
4 przypadek obciążenia śrub

Złącze śrubowe obciążone

siłą prostopadłą

do osi

Przykłady:
- połączenie blach,
- połączenia kołnierzy sprzęgieł,
- …

4 przypadek obciążenia śrub

Sposoby przenoszenia obciążenia:

Śruby ciasnopasowane

Śruby luźnopasowane

Pracujące na zginanie

Obciążenie przenoszone

tarciem

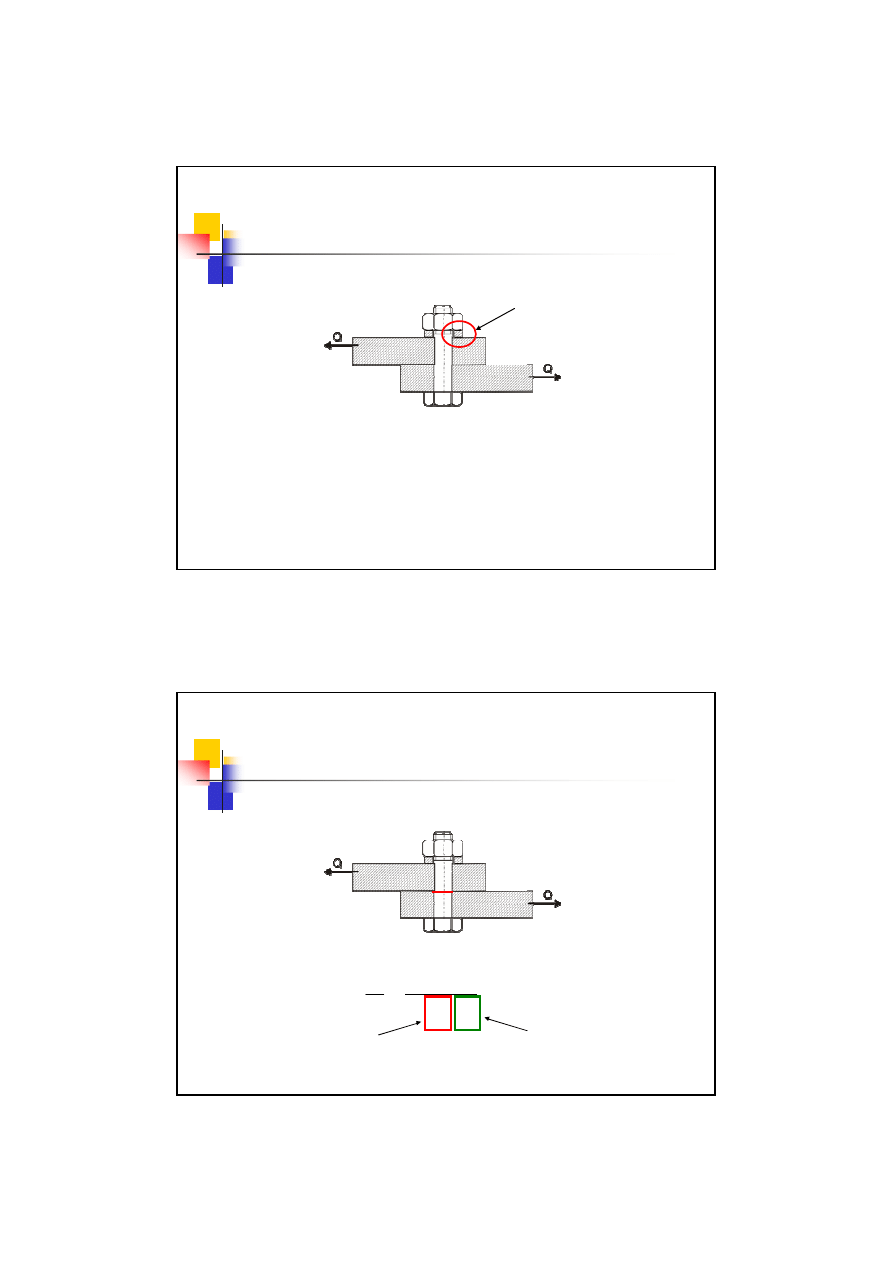
17

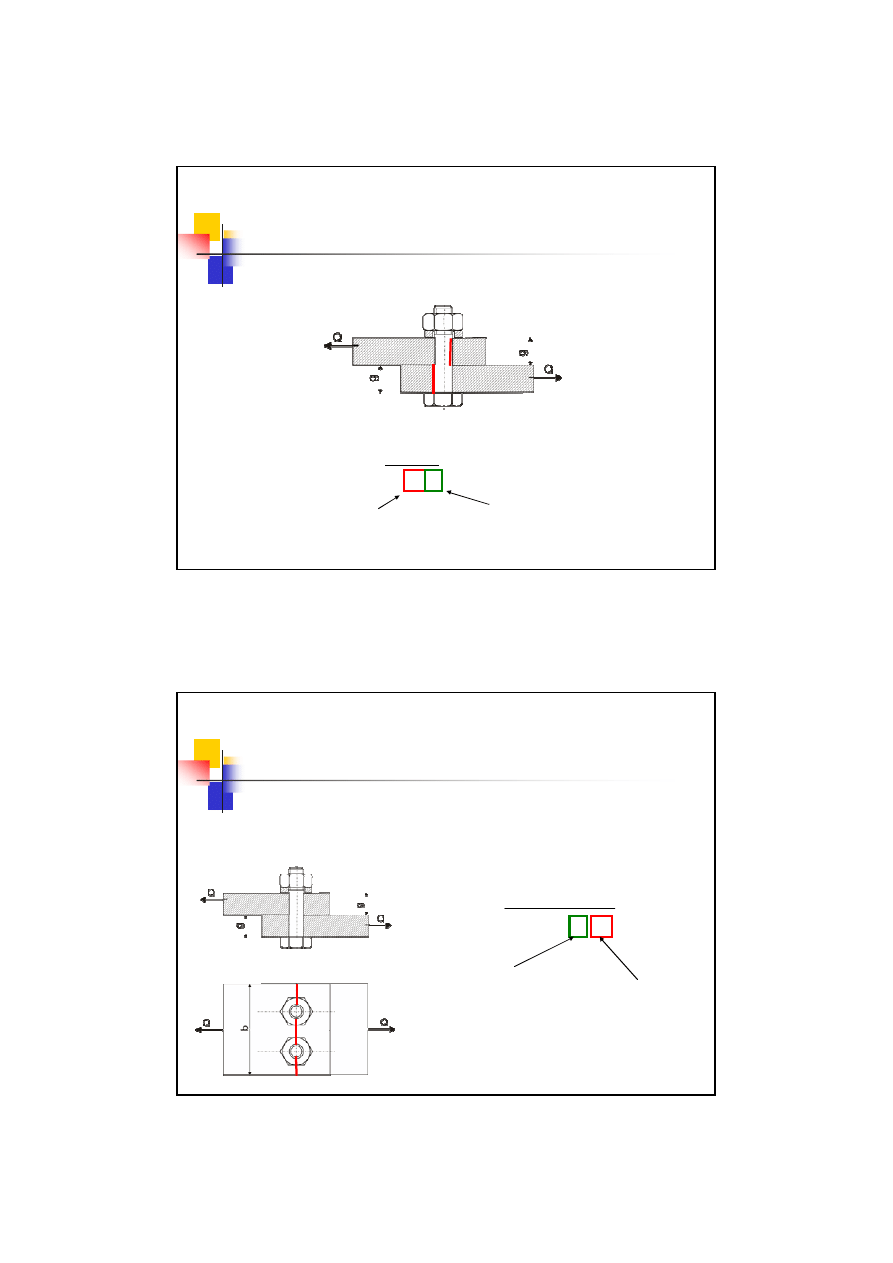
4 przypadek obciążenia śrub
– śruby ciasnopasowane

Śruba jest spasowana w otworach łączonych elementów.

Pracuje w tym przypadku

część niegwintowana

.

Niezbędna jest

podkładka

dystansowa

Śruba pracuje jak

kołek

. Gwint jest tylko elementem

zabezpieczającym

przed rozłączeniem

4 przypadek obciążenia śrub
– śruby ciasnopasowane

Obliczenia wytrzymałościowe

1. Warunek na ścinanie:

t

t

k

m

d

Q

F

Q

≤

⋅

⋅

⋅

=

=

2

4

π

τ

Średnica nominalna gwintu =

średnicy trzpienia

nienagwintowanego

Liczba powierzchni czynnych

18

4 przypadek obciążenia śrub
– śruby ciasnopasowane

Obliczenia wytrzymałościowe

2. Warunek na nacisków:

dop

p

n

d

g

Q

p

≤

⋅

⋅

=

Średnica nominalna gwintu =

średnicy trzpienia

nienagwintowanego

Liczba śrub

4 przypadek obciążenia śrub
– śruby ciasnopasowane

Obliczenia wytrzymałościowe

3. Warunek wytrzymałości płaskowników na rozciąganie:

(

)

r

r

k

d

n

b

g

Q

≤

⋅

−

⋅

=

σ

Średnica nominalna

gwintu = średnicy

trzpienia

nienagwintowanego

Liczba śrub w linii

19

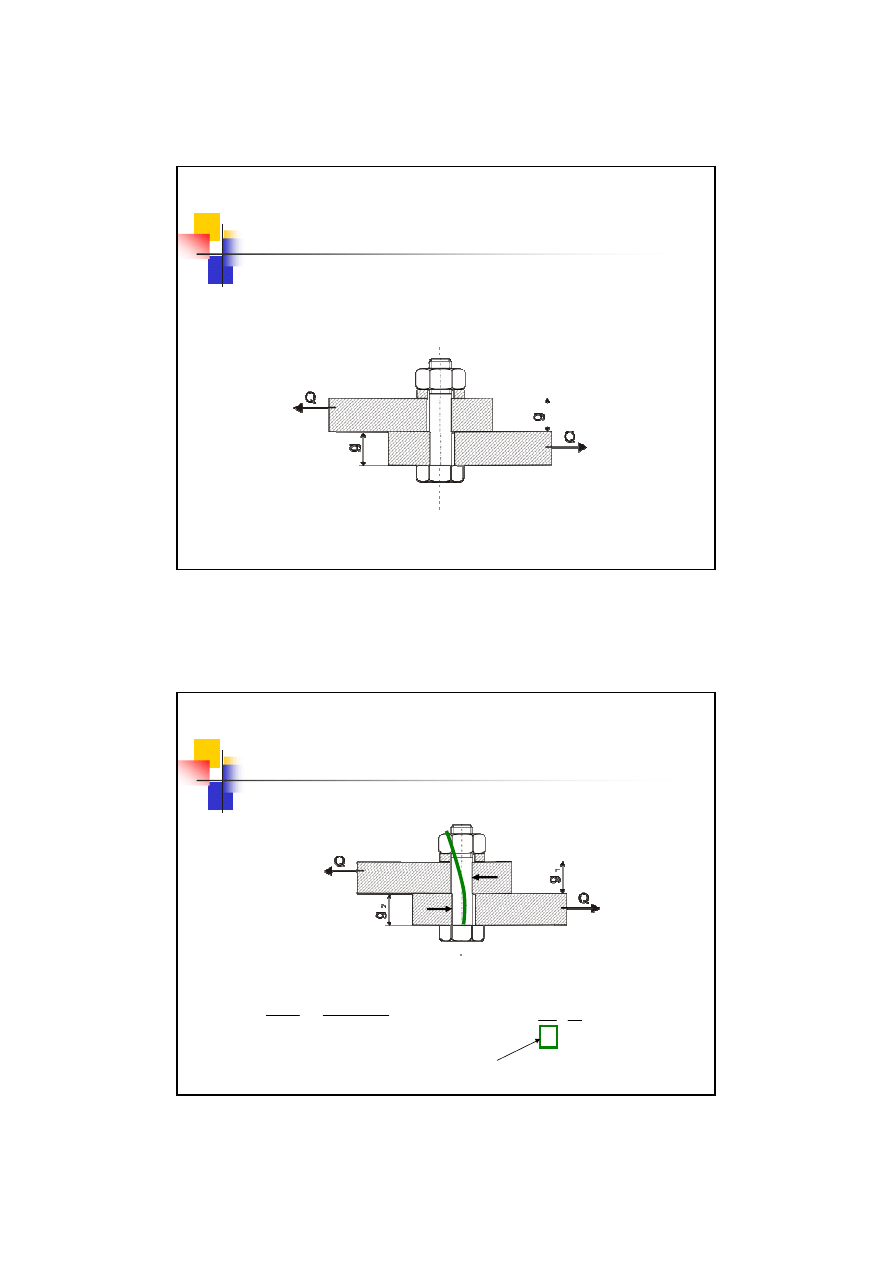
4 przypadek obciążenia śrub
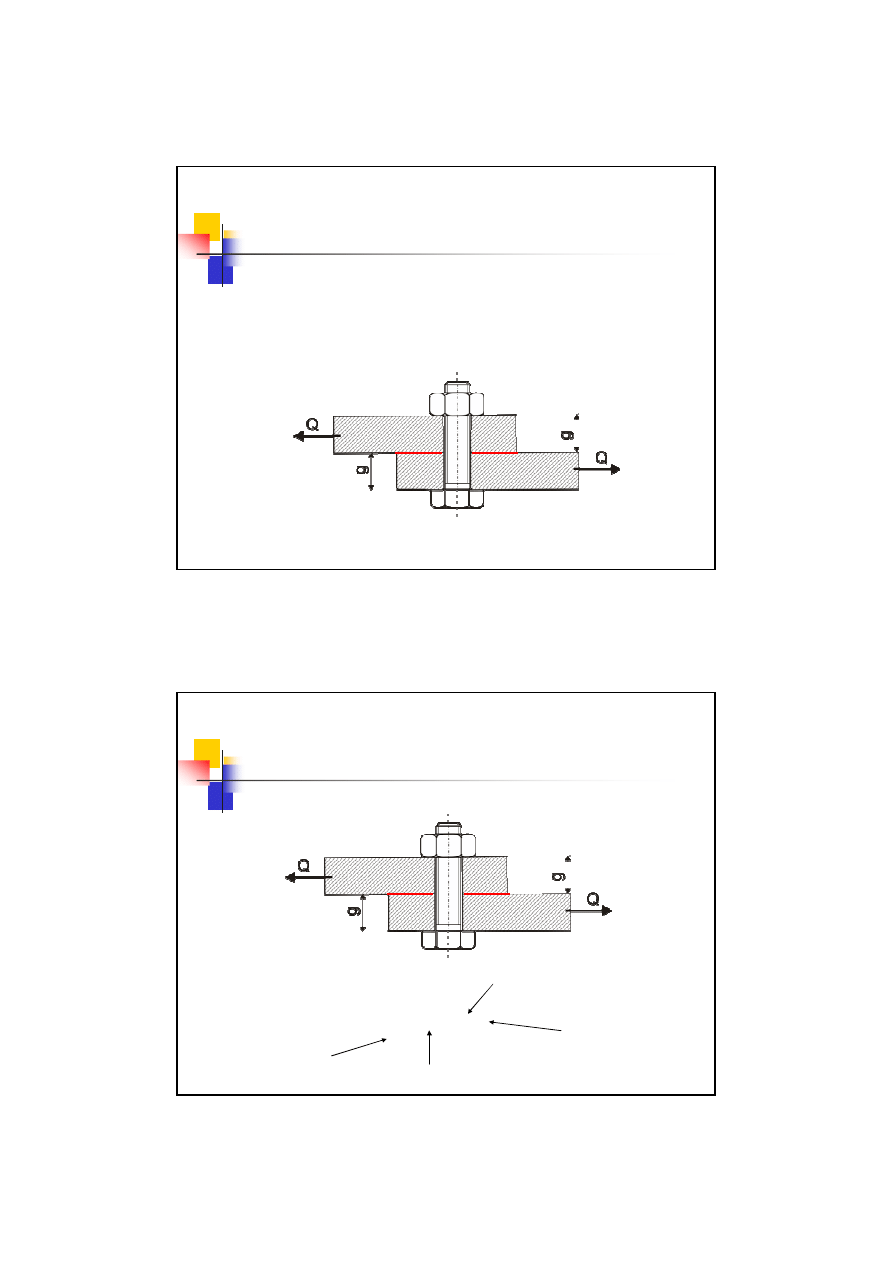
– śruby luźnopasowane zginane

Śruba jest luźno osadzona w otworach łączonych elementów.

Pracuje w tym przypadku

część niegwintowana

.

Śruba pracuje jak

luźny kołek

. Gwint jest tylko elementem

zabezpieczającym

przed rozłączeniem

4 przypadek obciążenia śrub
– śruby luźnopasowane zginane

Obliczenia wytrzymałościowe

1. Warunek na zginanie

g

g

x

g

g

k

d

M

W

M

≤

⋅

⋅

=

=

3

32

π

σ

(

)

2

1

2

1

g

g

n

Q

M

g

+

⋅

=

Liczba śrub

20

4 przypadek obciążenia śrub
– śruby luźnopasowane zginane

Obliczenia wytrzymałościowe

1. Warunek na zginanie

g

g

x

g

g

k

d

M

W

M

≤

⋅

⋅

=

=

3

32

π

σ













+

⋅

=

2

1

4

1

2

1

g

g

n

Q

M

g

Liczba śrub

4 przypadek obciążenia śrub
– śruby luźnopasowane zginane

Obliczenia wytrzymałościowe

2. Warunek na nacisków:

dop

p

n

d

g

Q

p

≤

⋅

⋅

=

Średnica nominalna gwintu =

średnicy trzpienia

nienagwintowanego

Liczba śrub

21

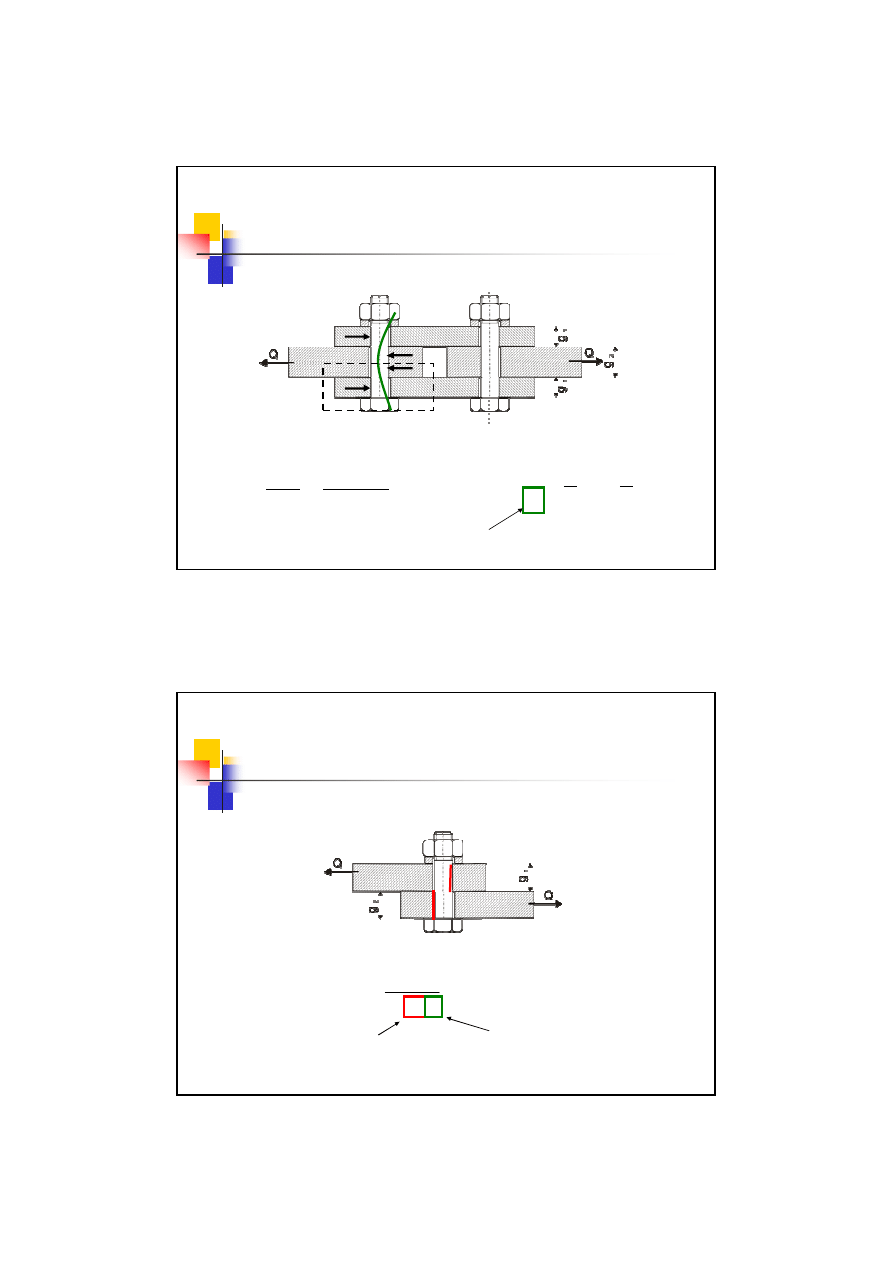
4 przypadek obciążenia śrub
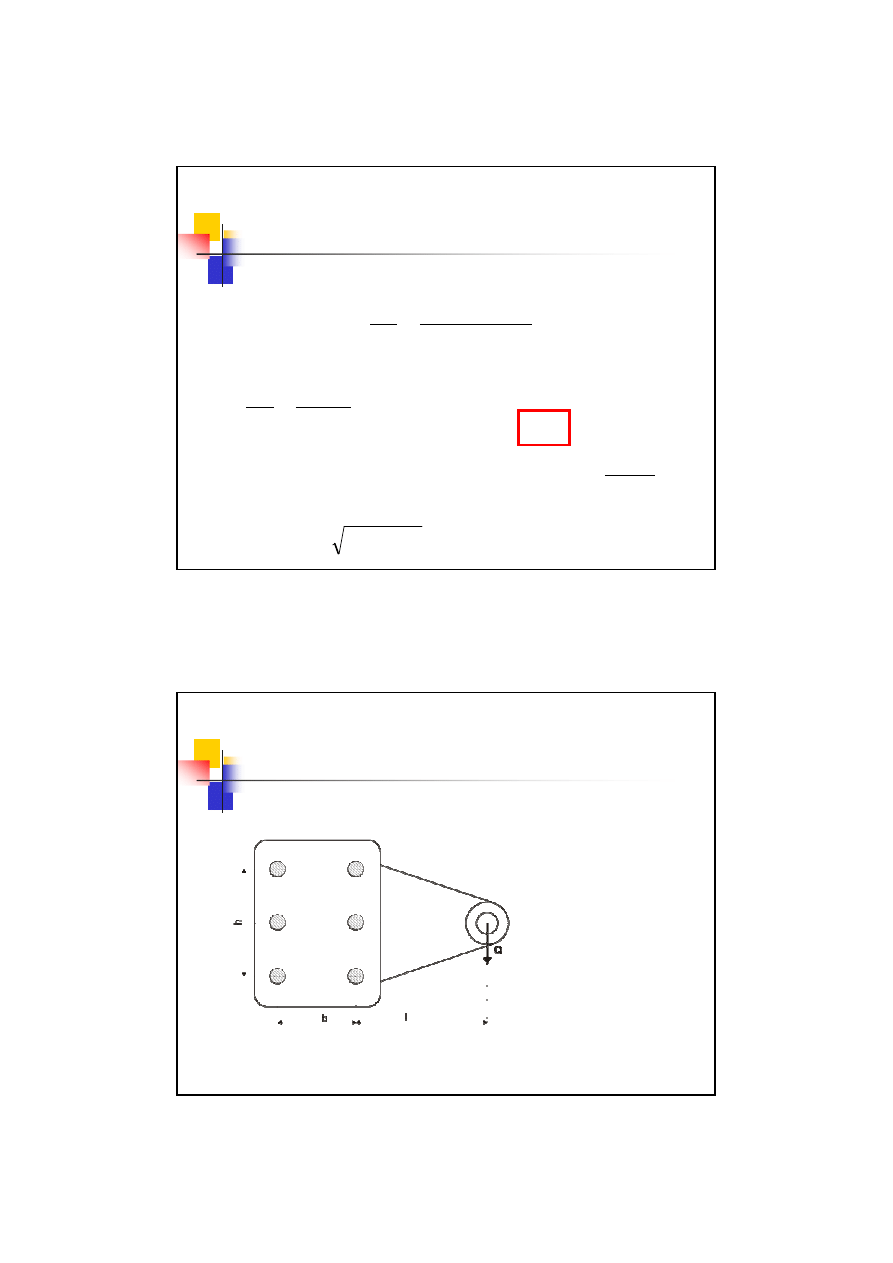
– śruby luźnopasowane tarciowe

Obciążenie przenoszone jest poprzez

tarcie

między łączonymi

elementami. Tarcie to uzyskiwane jest poprzez

nacisk

wywołany

napięciem

śrub.

4 przypadek obciążenia śrub
– śruby luźnopasowane tarciowe

Obliczenia wytrzymałościowe

Założenie:

T>Q

i

n

Q

T

w

⋅

⋅

⋅

=

µ

Metoda uproszczona:

Współczynnik tarcia

Liczba śrub

Siła zacisku wstępnego (jak w

obliczeniach 3 przypadku śrub)

Liczba powierzchni

ciernych

22

4 przypadek obciążenia śrub
– śruby luźnopasowane tarciowe

Obliczenia wytrzymałościowe

Rozciąganie:

i

n

d

Q

F

Q

w

r

⋅

⋅

⋅

⋅

⋅

=

=

µ

π

σ

2

3

4

Skręcanie:

3

3

16

d

M

W

M

c

o

c

s

⋅

⋅

=

=

π

τ

Moment całkowity wywołany zaciskiem wstępnym

(

)

[

]

'

5

,

0

ρ

γ

µ

+

⋅

+

⋅

⋅

⋅

=

+

=

tg

d

d

Q

M

M

M

M

s

p

w

c

s

t

c

2

o

p

d

S

d

+

=

Tarcie między nakrętką a

elementem dociskanym

Naprężenia zastępcze:

r

s

r

z

k

w

⋅

<

⋅

+

=

2

2

3

τ

σ

σ

4 przypadek obciążenia śrub
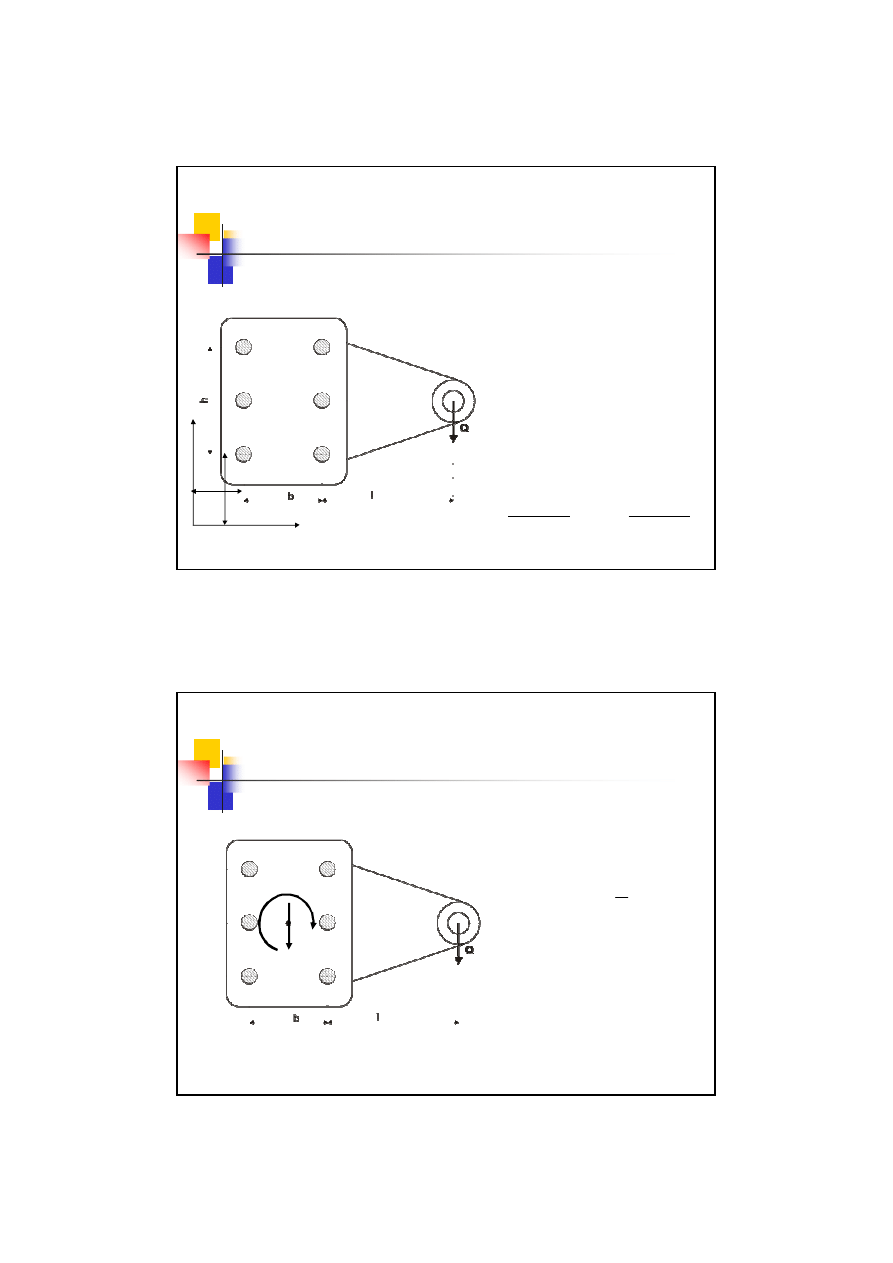
– połączenia grupowe skręcane

Połączenie traktowane jest jak jeden

przekrój (redukuje się na niego

obciążenia zewnętrzne)

23

4 przypadek obciążenia śrub
– połączenia grupowe skręcane

Pierwszym krokiem jest zatem

określenie położenia

środka ciężkości

tego przekroju

1. Wprowadzamy układ

współrzędnych

x

y

2. Obliczenie położenia

środka ciężkości

F

i

x

i

y

i

∑

∑

⋅

=

i

i

i

o

F

x

F

x

∑

∑

⋅

=

i

i

i

o

F

y

F

y

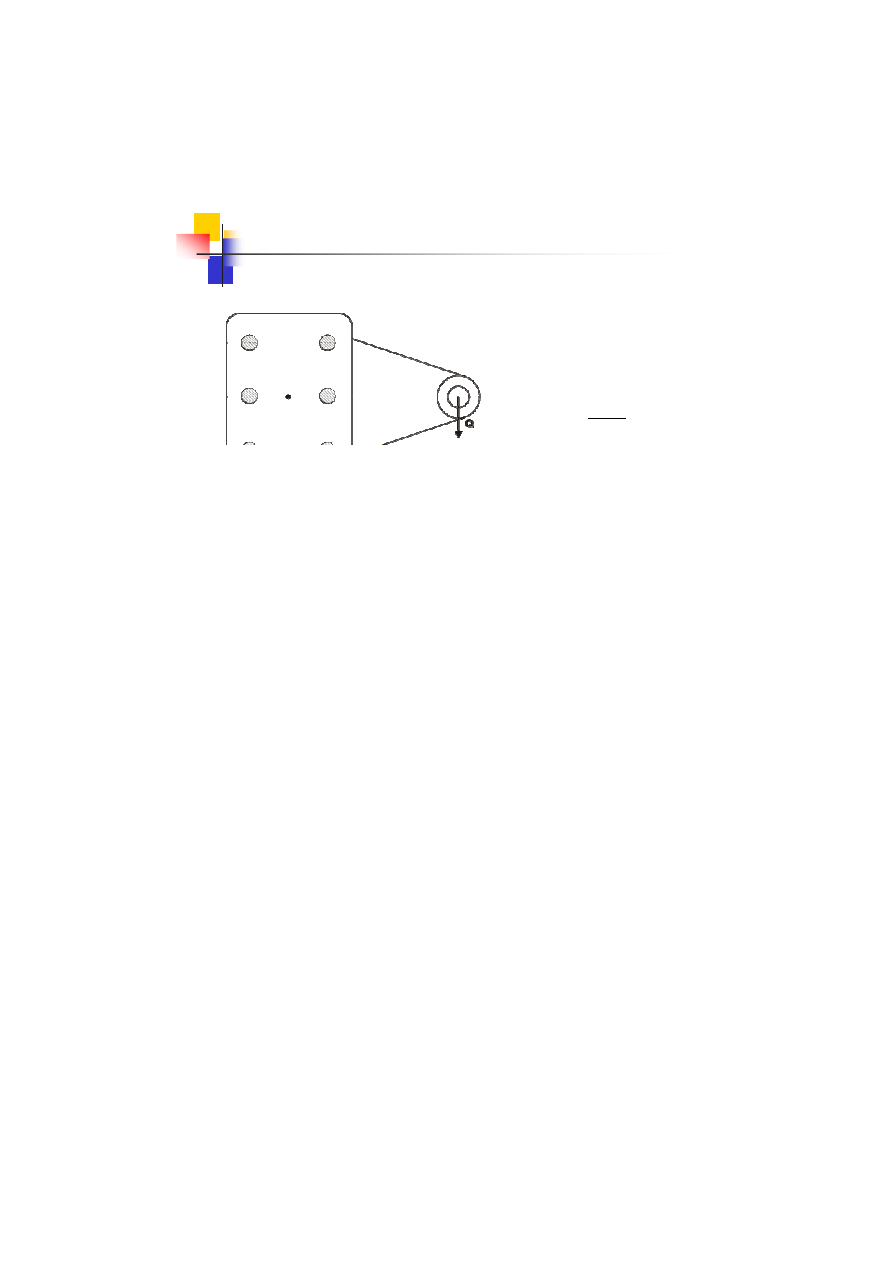
4 przypadek obciążenia śrub
– połączenia grupowe skręcane

Następnie przenosimy obciążenie na

środek ciężkości:













+

⋅

=

2

b

l

Q

M

s

Q

M

s

24

4 przypadek obciążenia śrub
– połączenia grupowe skręcane

Rozdzielamy obciążenie proporcjonalnie

na każdą ze śrub oddzielnie, zastępując

obciążenia zredukowane odpowiednimi

siłami działającymi na śruby

∑

⋅

=

i

i

Qi

F

F

Q

P

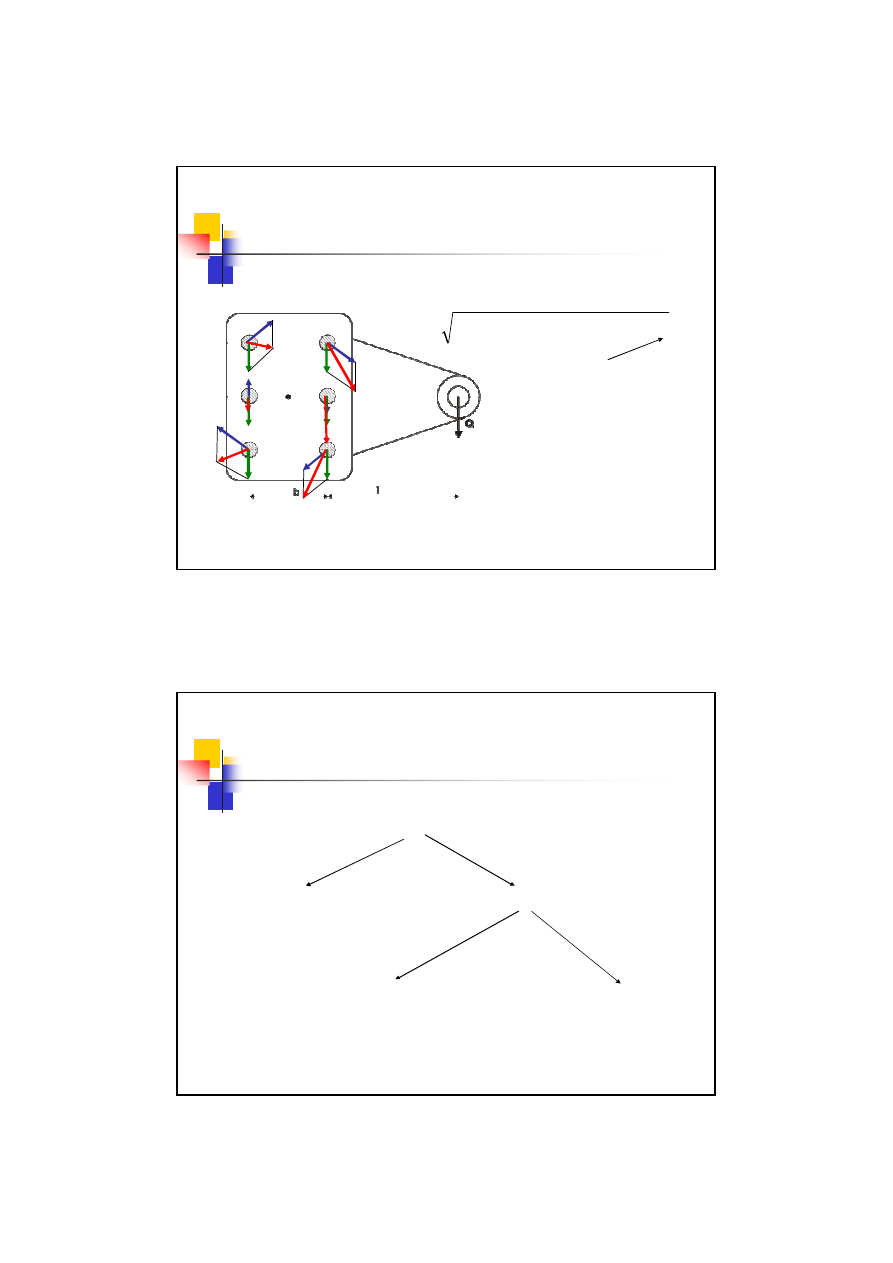
25

4 przypadek obciążenia śrub
– połączenia grupowe skręcane

α

cos

2

2

2

⋅

⋅

⋅

+

+

=

Mi

Qi

Mi

Qi

i

P

P

P

P

P

Wyznaczenie obciążeń wypadkowych dla poszczególnych śrub

P

M1

P

M2

P

M4

P

M6

P

M5

P

M3

P

Q1

P

Q2

P

Q4

P

Q6

P

Q5

P

Q3

P

1

P

2

P

4

P

3

P

5

P

6

Kąt zawarty między siłami

Do dalszych obliczeń

bierze się

największą

z sił

wypadkowych

4 przypadek obciążenia śrub
– połączenia grupowe skręcane

Sposoby przenoszenia obciążenia:

Śruby ciasnopasowane

Śruby luźnopasowane

Pracujące na zginanie

Obciążenie przenoszone

tarciem

Obliczenia warunków na:
- Ścinanie
- Naciski powierzchniowe

Obliczenia warunków na:
- Zginanie
- Naciski powierzchniowe

Obliczenia warunków na:
- Rozciąganie
- Skręcanie

26

4 przypadek obciążenia śrub
– połączenia grupowe skręcane

Obciążenie przenoszone tarciem

Przeniesienie obciążenia przy obciążeniu tylko momentem skręcającym

obliczenia opierają się założeniu równego rozkładu nacisków na całej

powierzchni styku.

Przyjmuje się, że:

M

t

> M

s

Zwykle:

M

t

=(1,2 – 1,4) M

s

Są dużo trudniejsze, ze względów określenia

wymaganej siły zacisku wstępnego elementów

4 przypadek obciążenia śrub
– połączenia grupowe skręcane

Obliczenie momentu tarcia

M

s

dF

τ

∫

⋅

⋅

=

F

t

dF

r

M

τ

r

p

⋅

=

µ

τ

∫

∫

⋅

⋅

⋅

=

⋅

⋅

⋅

=

F

F

t

dF

r

p

dF

r

p

M

µ

µ

o

t

S

p

M

⋅

⋅

=

µ

Biegunowy moment statyczny powierzchni

względem środka ciężkości

27

4 przypadek obciążenia śrub
– połączenia grupowe skręcane

Wymagany nacisk

M

s

dF

τ

o

t

S

M

p

⋅

=

µ

r

F

n

Q

p

w

⋅

=

Uzyskiwany nacisk

n

S

F

M

Q

o

t

w

⋅

⋅

⋅

=

µ

Stąd:

Liczba śrub

Dalsze obliczenia tak jak poprzednio

Wytrzymałość połączenia
gwintowego

Określana jest jako obciążenie jakie może

przenieść zestaw

Śruba-Nakrętka

(

)

dop

p

n

D

d

Q

p

≤

⋅

−

⋅

=

2

1

2

4

π

Obliczenia opierają się na obliczeniu

nacisku

na zwoje gwintu

Liczba zwojów połączenia

D

1

–

śr

e

d

n

ic

a

w

e

w

n

ę

tr

zn

a

n

a

kr

ę

tk

i (

śr

e

d

n

ic

a

o

tw

o

ru

)

d

–

śr

e

d

n

ic

a

z

e

w

n

ę

tr

zn

a

śr

u

b

y

(

w

y

m

ia

r

n

o

m

in

a

ln

y

)

28

Wytrzymałość połączenia
gwintowego

Najczęściej obliczenia wytrzymałości prowadzą do

obliczenia wysokości nakrętki (ilości zwojów gwintu)

(

)

dop

p

D

d

Q

n

⋅

−

⋅

⋅

≥

2

1

2

4

π

Nacisk dopuszczalny na zwoje gwintu

5

,

1

+

=

n

n

rz

Zwoje uszkodzone na wejściu i wyjściu

z

P

n

H

rz

⋅

=

Stąd wysokość nakrętni:

Skok gwintu

Krotność gwintu

Wytrzymałość połączenia
gwintowego

Warunki dodatkowe:

(

)

s

d

H

⋅

÷

=

2

2

,

1

tzw. „warunek dobrego prowadzenia”

d

H

⋅

=

8

,

0

Gwinty złączne (nakrętki znormalizowane)