L

ABORATORIUM FIZYCZNE

Instytut Fizyki Politechniki Krakowskiej

ĆWICZENIE

29

Wyznaczanie szybkości dźwięku w powietrzu

Ćwiczenie 29

2

Oprócz fal mechanicznych, którymi
są fale dźwiękowe, czy fale na po-
wierzchni wody, w przyrodzie wystę-
pują jeszcze fale elektromagnetyczne
i fale materii. Falami elektromagne-
tycznymi są np. fale radiowe i świa-
tło, a rozchodzą się w postaci zabu-
rzenia pola elektromagnetycznego. Z
cząstkami o mikroskopijnych rozmia-
rach, takimi jak elektron lub proton,
związane są fale materii, które wyko-
rzystuje się w mikroskopie elektro-
nowym.

ĆWICZENIE

29

Wyznaczanie szybkości dźwięku w powietrzu

Barbara Oleś

1.

Wprowadzenie

W ćwiczeniu wyznaczymy długość fali dźwiękowej wzbudzonej w słupie powietrza, a

następnie obliczymy szybkość rozchodzenia się w nim dźwięku. Otrzymane wyniki posłużą
do odpowiedzi na pytanie, jak właściwości powietrza (temperatura, wilgotność) wpływają
na szybkość rozchodzenia się w nim dźwięku.

1.1

Fale mechaniczne

Jeżeli w ośrodku materialnym pewien element ośrodka zaczyna drgać wokół położenia równo-

wagi, a dzięki sprężystym właściwościom tego ośrodka jego ruch jest przekazywany sąsiednim ele-
mentom, to w ośrodku rozchodzi się zaburzenie w postaci fali.

Fala mechaniczna

to zaburzenie lub zespół zaburzeń rozchodzących się w ośrodku sprężystym,

które mogą mieć postać impulsu lub drgań.

Fale mechaniczne przenoszą energię, ale nie jest to związane z transportem masy, bowiem czą-

steczki ośrodka nie przesuwają się wraz z rozchodzącą się falą.

Fale dźwiękowe zaliczamy do

podłużnych fal

mechanicznych, ponieważ materialne cząsteczki

ośrodka, którym może być ciało stałe, ciecz lub gaz, drgają wzdłuż kierunku propagacji fali (rys. 1).
Jeśli ruch cząstek odbywa się prostopadle do kierunku rozchodzenia się fali, mówimy o

fali poprzecz-

nej

. Jej przykładem jest zaburzenie rozchodzące się w linie, której jeden koniec poruszany jest w górę

i w dół, jak to przedstawiono na rys. 1.

Do opisu fal potrzebna jest matematyczna funkcja opisująca jej kształt. Jeśli fala rozchodzi się

wzdłuż osi , to dla określonego punktu ośrodka (zadana wartość

) funkcja ta, zwana

funkcją falo-

Fala poprzeczna

Fala podłużna

kierunek propagacji fali

→

kierunek propagacji fali

→

Rys. 1. Fale: podłużna (górny rysunek) i poprzeczna (dolny
rysunek). Na górnym rysunku ruch ręki powoduje ściska-
nie i rozciąganie zwojów, odkształcenie zwojów jest rów-
noległe do kierunku rozchodzenia się fali.
(http://spot.pcc.edu/~aodman/physics%20122/light-
electro-pictures/longitudal%20compresion%20waves.jpg)

Wyznaczanie szybkości dźwięku w powietrzu

3

wą

, opisze jego wychylenia w czasie, np. drgania ustalonego elementu sznura zaznaczone strzałką na

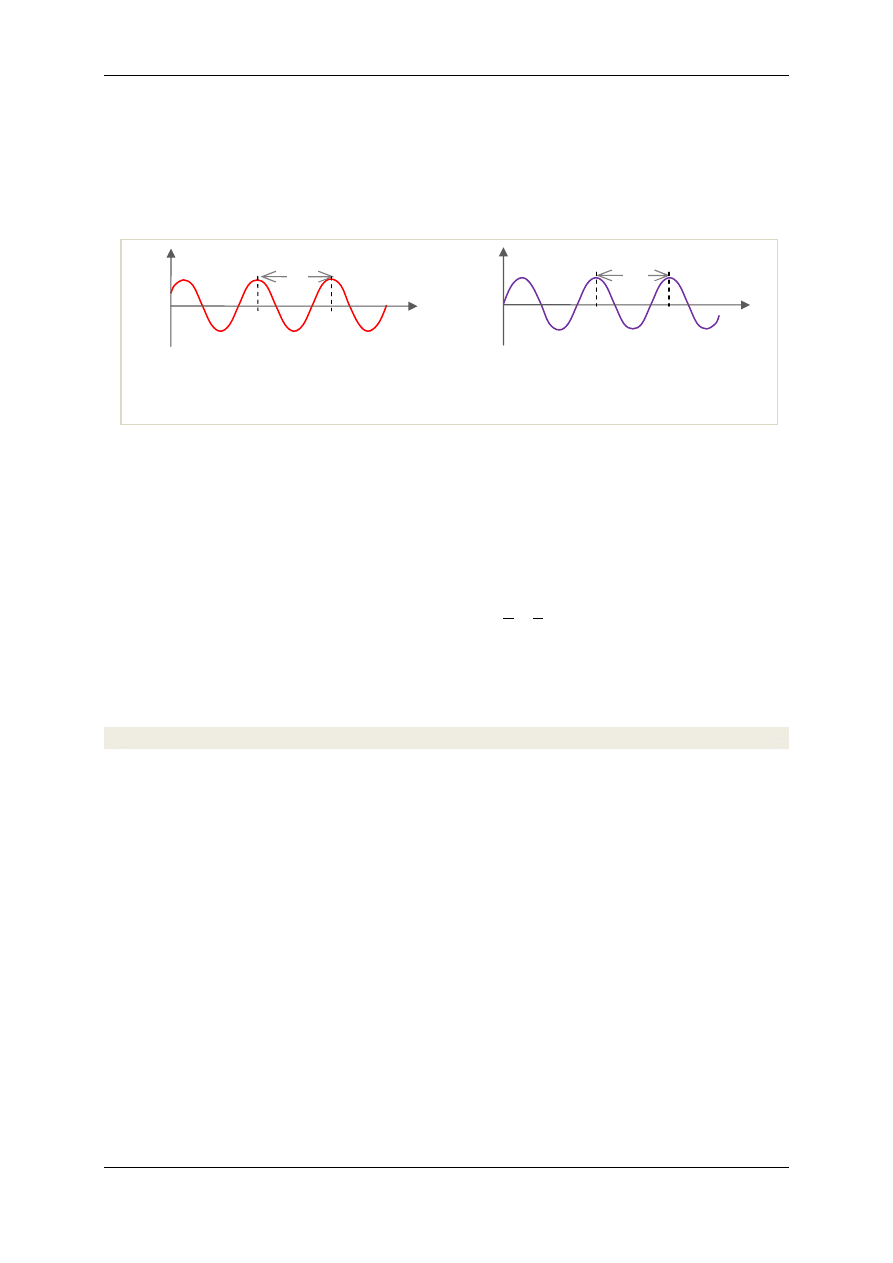
rys. 1. W szczególnym przypadku, gdy każdy element ośrodka drga ruchem harmonicznym prostym,
tj. opisanym funkcją

ψ

( ) =

(2

π

+

ϕ

), gdzie – amplituda drgań, = 1/ – częstotliwość,

– okres,

ϕ

– faza początkowa (patrz rys. 2a), to mamy do czynienia z

falą harmoniczną

. Z kolei

ustalając czas t dostaniemy informację o wychyleniach cząstek ośrodka wzdłuż osi jak na rys. 2b.

Zauważmy, że przedstawiona na nim fala harmoniczna ma kształt sinusoidalny i cechuje ją okreso-
wość przestrzenna. Odległość, między dwoma najbliższymi punktami przestrzeni, w których fazy
funkcji

ψ

w danej chwili t są identyczne, nazywamy

długością fali

λ

. Jeśli prędkość rozchodzenia się

fali wynosi , to zachodzi:

λ

= , gdzie jest okresem, czasem, w którym fala przebiega odległość

równą

λ

.

Dla fali harmonicznej funkcja falowa

ψ

może być zapisana w postaci:

( , ) = sin 2

∓ +

, (1.1)

gdzie znak „–” odnosi się do fali rozchodzącej się w prawo, a „+” w lewo,

jest amplitudą fali,

ϕ

–

fazą początkową. Wzór (1.1) przyjmie zwartą postać, jeśli wprowadzimy nowe wielkości,

liczbę falo-

wą

= 2

π

/

λ

oraz

częstość kołową

ω

= 2

π

/ = 2

π

f:

( , ) = sin(! − + ), (1.2)

1.2

Superpozycja fal

Fale mogą przebiegać w ośrodku niezależnie od siebie, co oznacza, że w danej chwili czasu prze-

mieszczenie dowolnej cząstki jest sumą przemieszczeń wywołanych przez każdą z fal.

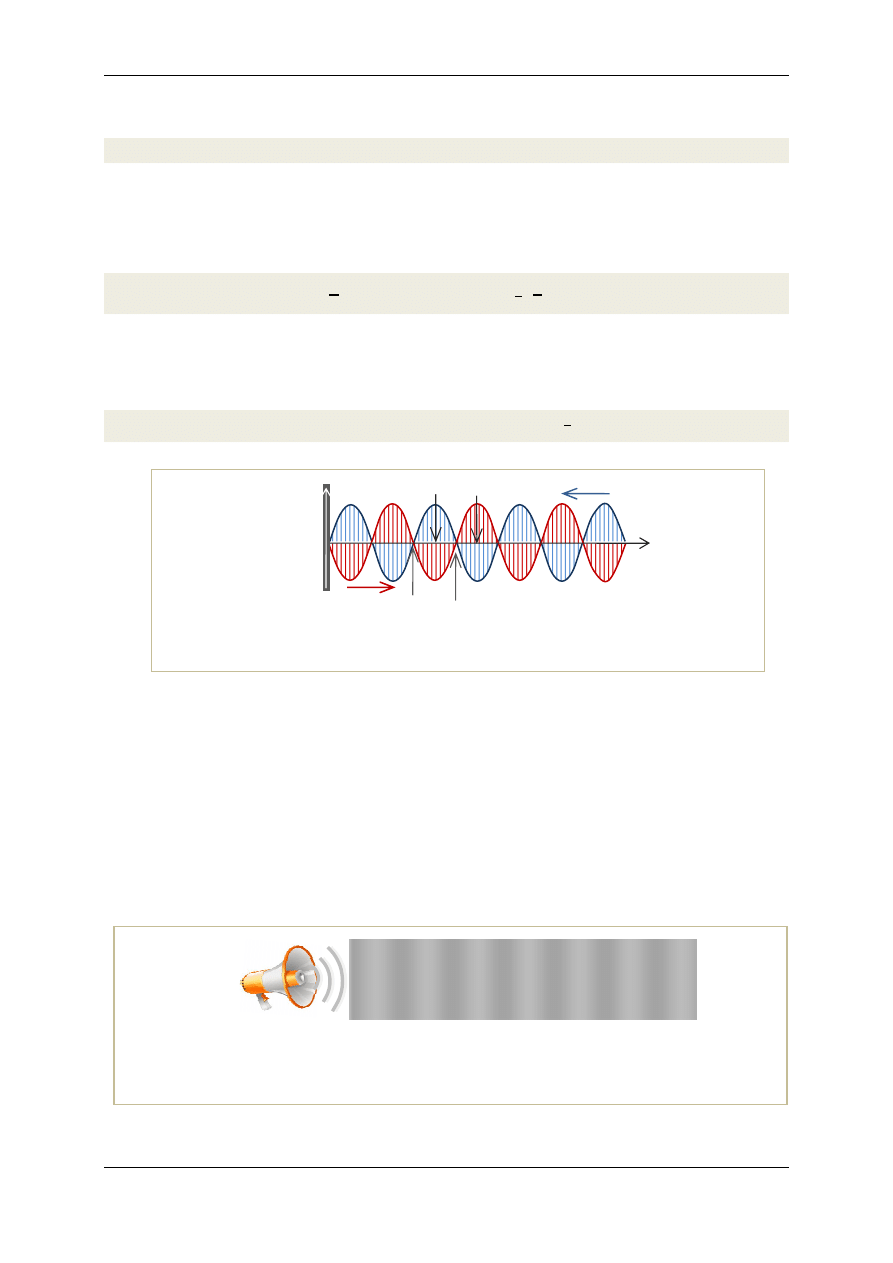
Rozważmy przypadek nakładania się dwóch fal o jednakowych amplitudach, rozchodzących się w

przeciwnych kierunkach. Z sytuacją taką mamy do czynienia przy odbijaniu się fal na przeszkodach
(rys. 3). W wyniku superpozycji fali padającej na przeszkodę z falą odbitą dostajemy

falę stojącą

. W

przypadku padania na ośrodek gęstszy następuje skok fazy

ϕ

fali odbitej o

π

(odpowiadający połowie

okresu). Natomiast przy odbiciu od ośrodka o mniejszej gęstości faza

ϕ

nie ulega zmianie.

Napiszmy równania obu fal, podającej i odbitej, rozchodzących się wzdłuż osi w przeciwnych

kierunkach (dla uproszczenia przyjmujemy fazę początkową fali padającej równą zeru):

#

( , ) = sin(! + )

$

( , ) = sin(! − + ).

Fala wypadkowa jest superpozycją obu tych fal i korzystając ze związku trygonometrycznego

sin(% ± ') = sin % cos ' ± cos % sin '

Rys.2 a. Zależność wychylenia elementu oś-
rodka w ustalonym położeniu od czasu ,
gdy w ośrodku rozchodzi się fala harmoniczna

Rys.2 b. Wychylenia elementów ośrodka w
ustalonym czasie t, gdy w ośrodku rozchodzi
się fala harmoniczna

x

A

−

−

A

−

λ

t

A

−

−

A

−

Ćwiczenie 29

4

oraz z tego, że

sin(% + ) = − sin %, dostajemy

równanie fali stojącej

:

*+,

( , ) =

#

( , ) +

$

( , ) = 2 sin( ) cos(! ). (3)

Ze wzoru (3) wynika, że każda cząstka drga prostym ruchem harmonicznym danym wyrażeniem

cos(! ) i częstość drgań jest taka sama dla wszystkich cząstek. Wyrażenie |2 sin( )| odgrywa tu
rolę, zależnej od położenia i charakterystycznej dla fali stojącej, amplitudy drgań. W punktach zwa-
nych

strzałkami

i spełniających warunek:

= (2 + 1) 2 , czyli dla = 4 +

#

$

5 2 , gdzie = 0,1,2,…. (4)

drgania osiągają maksymalną amplitudę

2 .

Natomiast w punktach zwanych

węzłami

drgania nie występują. Ich współrzędne dane są wzo-

rem:

=

, czyli dla =

;
$

, gdzie = 0,1,2, …. (5)

1.3

Szybkość fali akustycznej

Fale rozchodzące się w powietrzu, które docierając do naszego ucha wywołują wrażenie dźwięku

mają częstotliwość f z przedziału od 16 do 20 000 Hz. Prędkość propagacji fali zależy od mechanicz-
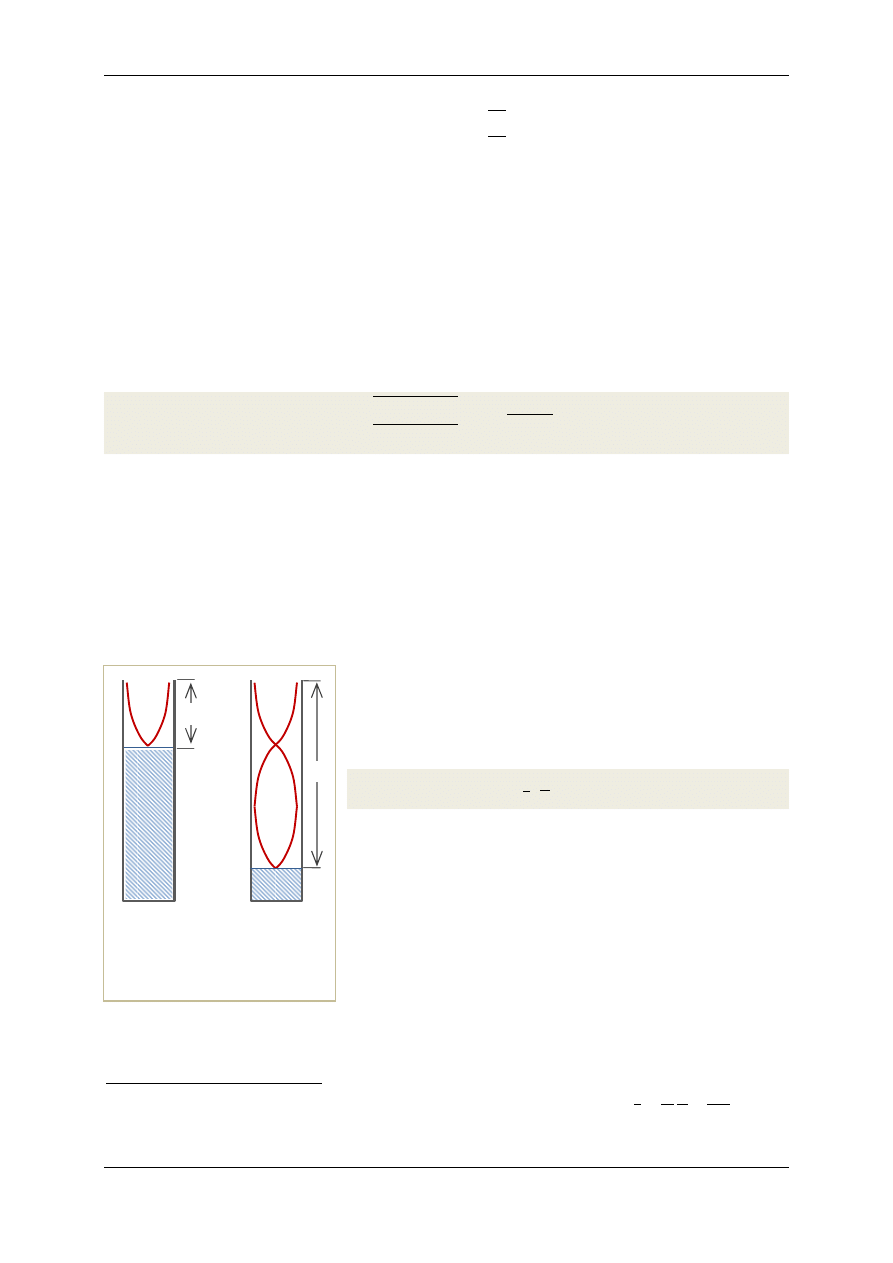
nych właściwości ośrodka. Rozchodząca się w gazie fala dźwiękowa jest falą podłużną, polegającą na
przemieszczaniu się jego zagęszczeń i rozrzedzeń (rys. 4). Ze względu na dużą szybkość rozchodzenia
się fali możemy przyjąć, że mamy do czynienia z procesami adiabatycznymi, a wówczas otrzymujemy
wzór na jej szybkość w postaci:

Rys.3. Fala padająca (niebieski linia) i odbita od ośrodka gęstszego (czerwona linia) nakładają
się na siebie dając falę stojącą, której charakterystycznymi elementami są strzałki i węzły

ψ

( , )

Strzałki

Węzły

Rys.4. Fala dźwiękowa rozchodząca się w powietrzu (mechaniczna fala podłużna) polega na rozcho-
dzeniu się zagęszczeń i rozrzedzeń powietrza, czyli obszarów o podwyższonym i obniżonym ciśnieniu.
Molekuły gazu wykonują ruchy w kierunku równoległym do kierunku rozchodzenia się fali.

Wyznaczanie szybkości dźwięku w powietrzu

5

= =

>?

@ , (6)

gdzie

κ

= B

,

/B

C

jest to stosunek ciepła właściwego przy stałym ciśnieniu do ciepła właściwego przy

stałej objętości,

? – ciśnienie, @ – gęstość gazu

.

Szybkość dźwięku w powietrzu zależy od jego temperatury i wilgotności. Uwzględniając, że

zależność gęstości gazu od temperatury dana jest wyrażeniem

1

:

@( ) = @

D

(1 + % )

⁄

,

gdzie

@

0

jest gęstością w t = 0°C,

α

= 1/273,15°C

–1

współczynnikiem rozszerzalności objętościowej

gazu, t temperaturą w skali Celsjusza, otrzymujemy wzór na szybkość fali dźwiękowej w powietrzu:

= =

>?

D

(1 + % )

@

D

=

D

√1 + % , (7)

gdzie v

0

to szybkość rozchodzenia się dźwięku w powietrzu w temperaturze 0°C, bez względu na jego

ciśnienie. W suchym powietrzu v

0

= 331,4 m/s. Jeśli zmienia się zawartość pary wodnej w powietrzu,

to zmienia się jego gęstość – wilgotne powietrze ma mniejszą gęstość niż suche. Ze wzorów 6 i 7
widzimy, że będzie to miało wpływ na na szybkość rozchodzenia się fali; im większa wilgotność, tym
większa szybkość.

2.

Metoda pomiaru

Akustyczne fale stojące można wzbudzić w słupach powie-

trza. Jeśli jeden koniec rury jest zamknięty, to fale wzbudzane u
wylotu rury rozchodzą się w powietrzu i odbijają na jej końcu.
Fala stojąca powstaje w wyniku superpozycji fal padających i
odbitych. Jeśli długość półotwartej rury spełnia warunek:

= 4 +

#

$

5 2 , gdzie = 0,1,2,…. (8)

to na zamkniętym końcu rury powstaje węzeł, a na końcu otwar-
tym strzałka fali stojącej (rys.5). Amplituda drgań u wylotu rury
osiąga maksymalną wartość i jednocześnie obserwuje się silne
wzmocnienie dźwięku.

Pomiar długości słupa powietrza, w którym powstaje fala

stojąca, jeśli znamy częstotliwość źródła wymuszającego drga-
nia, pozwala wyznaczyć ze wzoru (8) długość fali

λ

oraz prędkość

dźwięku

=

λ

.

Na rysunku 5 mamy przedstawione dwa przypadki. W pierwszym przypadku w słupie powietrza o

wysokości

I

#

powstaje ćwiartka długości fali

λ

/4 (rys.5a). Natomiast w drugim wysokość słupa powie-

1

Dla gazu w temperaturze (w skali Kelwina), objętości

J i pod ciśnieniem ? mamy:

,
K

=

,C

L

M

M

N

=

,

N

C

N

L

(1 + % )

gdzie

?

D

,

J

D

to odpowiednio ciśnienie i objętość w 0°C (czyli w T

0

= 273,15 K), m – masa gazu, t – temperatura

w °C,

α

= 1/273,15°C

–1

.

I

#

I

$

(a)

(b)

Rys.5. Fale stojące wzbudzone w
słupie powietrza w rurze jedno-
stronnie otwartej

Ćwiczenie 29

6

trza

I

$

jest większa o połówkę długości fali i mieszczą się w nim trzy ćwiartki długości fali

3

λ

/4

(rys.5a).

3.

Wykonanie ćwiczenia

3.1

Opis aparatury

Zdjęcie aparatury przedstawia rys.6. Piono-

wa rura szklana (a), wypełniona częściowo wo-
dą, połączona jest plastikową rurką ze zbiorni-
kiem wody (b). Zbiornik można podnosić lub
opuszczać za pomocą śruby, co prowadzi do
zmiany poziomu wody w rurze, a tym samym
wysokości słupa powietrza ponad wodą. Wyso-
kość słupa powietrza w rurze odczytujemy na
skali milimetrowej. Nad rurą umocowany jest
głośnik (c) podłączony do generatora drgań (d).
U wylotu rury zamocowany jest mikrofon podłą-
czony do oscyloskopu (e), na którym można
obserwować sygnał z mikrofonu.

3.2

Przebieg pomiarów

1.

Podnieś zbiornik z wodą (b) do najwyższego położenia.

2.

Włącz generator sygnału (d) i ustal częstotliwość drgań membrany głośnika f pomiędzy 450–
500 Hz. Należy odczekać ok. 15 min, aby częstotliwość ustabilizowała się. Uwaga: obserwuj
częstotliwość sygnału i zanotuj górną

O

oraz dolną

P

granicę przedziału jej zmian. W razie du-

żych zmian dokonaj korekty częstotliwości.

3.

Sprawdź, czy przewód prowadzący do mikrofonu podłączony jest do zacisków bateryjki (f).

4.

Włącz oscyloskop (e) i obserwuj sygnał z mikrofonu. Przy odpowiednio dobranym zakresie i
włączonej podstawie czasu powinien mieć kształt sinusoidalny.

5.

Powoli opuszczając zbiornik z wodą, obniżaj poziom wody w rurze. Kiedy zbliżysz się do poło-
żenia pierwszej strzałki, zmianie wysokości słupa powietrza będzie towarzyszyć wzrost ampli-
tudy sygnału na oscyloskopie oraz wyraźne wzmocnienie dźwięku. Odczytaj na skali położe-
nie

I

1

poziomu wody dla maksymalnej wartości amplitudy (rys.5a) i zanotuj w tabeli 1. Od-

powiada ono pozycji pierwszej strzałki, kiedy częstotliwość drgań membrany mikrofonu jest
równa częstotliwości powstającej w powietrzu fali stojącej.

6.

Każdy wynik pomiaru od razu wpisuj do tabeli danych 1, której wzór podany jest na końcu
niniejszego paragrafu.

Pomiar

I

1

nie daje nam dokładnie

λ

/4, ponieważ nie uwzględnia powietrza drgającego nad otworem

rury. Dlatego musimy wyznaczyć pozycję drugiej strzałki, wówczas różnica

I

2

–

I

1

=

λ

/2.

Rys.6. Wygląd aparatury służącej do wy-
znaczania szybkości dźwięku w powietrzu

f

a

b

c

d

e

Wyznaczanie szybkości dźwięku w powietrzu

7

7.

Obniżaj dalej poziom wody, aby zaobserwować i odczytać położenie następnej strzałki,

I

2

(rys. 5b).

Wyniki pomiarów

I

1

oraz

I

2

cechuje spory rozrzut wartości, spowodowany trudnością dokładnego

ustalenia położenia, w którym amplituda jest maksymalna (dźwięk najgłośniejszy), jak również precy-
zyjnego odczytanie poziomu wody, z powodu wklęsłego menisku wody w rurce. Zatem należy wyko-
nać po dziesięć pomiarów

I

1

oraz

I

2

.

8.

Powróć do położenia pierwszej strzałki i powtórz pomiary

I

1

dziesięć razy, na przemian obni-

żając i podnosząc poziom wody. Analogicznie zmierz położenie

I

2

.

9.

Odczytaj temperaturę powietrza t w sali laboratoryjnej oraz jego wilgotność.

10.

Odczytaj najmniejszą działkę skali termometru (możesz ją przyjąć za szerokość przedziału
granicznego 2

∆ , jeśli odległości miedzy kreskami skali pozwalają wyznaczyć temperaturę z

dokładnością do ½ działki).

Oszacuj przedział graniczny 2

∆I. Uwaga: z powodu występowania menisku wody nie można

przyjąć, że jest on równy działce skali milimetrowej.

11.

Pomiary można powtórzyć dla innych częstotliwości .

Tabela 1. Ćwiczenie 29. Dane pomiarowe

Wysokość słupa

powietrza

I

#

Wysokość słupa

powietrza

I

$

Częstotliwość

L.p.

[cm]

L.p.

[cm]

Górna granica

O

[Hz]

1.

1.

2.

2.

Dolna granica

P

[Hz]

3.

3.

4.

4.

Temperatura [

o

C]

5.

5.

6.

6.

Przedział graniczny

2∆ [℃]

7.

7.

8.

8.

9.

9.

Przedział graniczny

2∆I [cm]

10.

10.

4.

Obliczenia

1.

Oblicz średnie wartości wysokości słupów powietrza

I̅

#

oraz

I̅

$

.

2.

Oblicz zmierzoną pośrednio długość fali dźwiękowej w powietrzu

λ

= 2(

I

̅

2

− I

̅

1

)

.

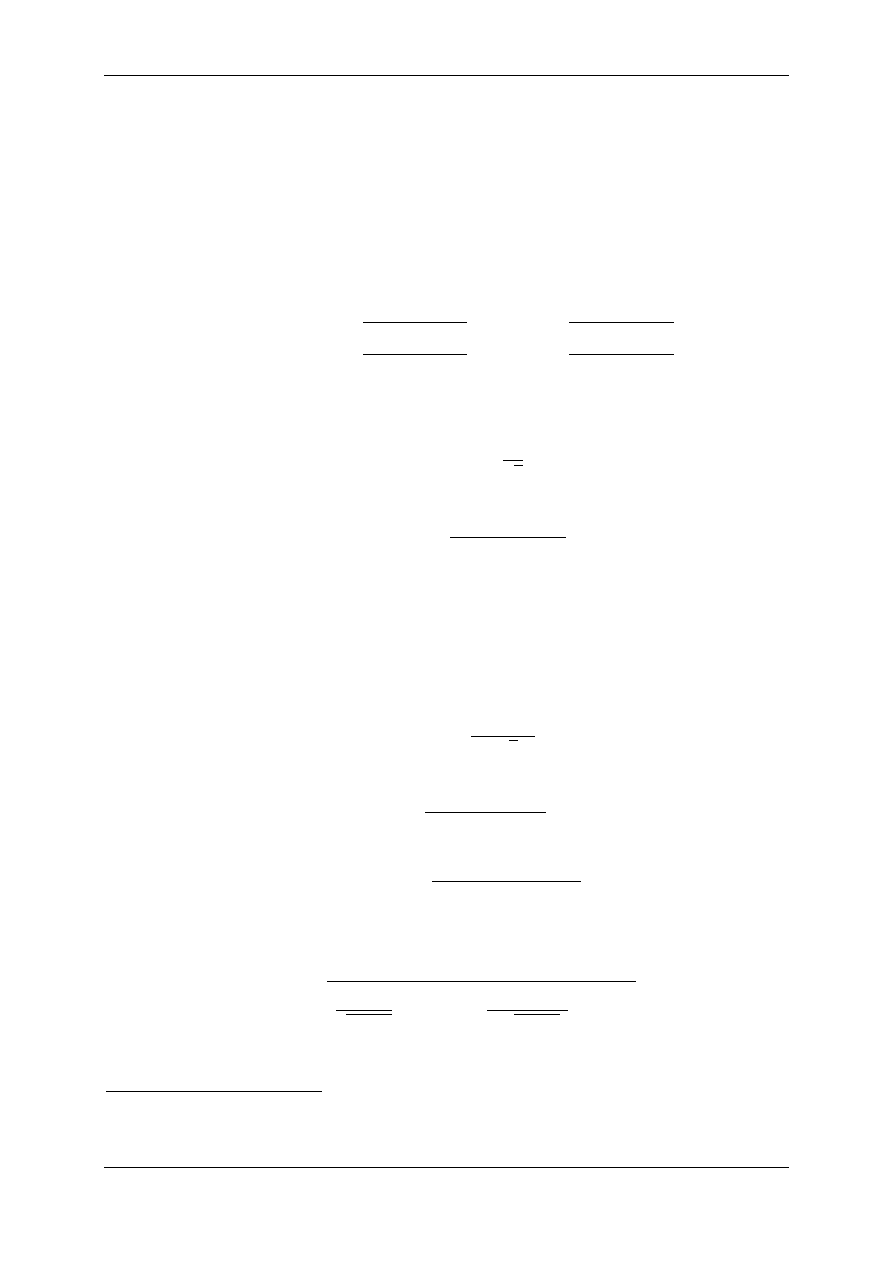
Ćwiczenie 29

8

3.

Oblicz częstotliwość drgań membrany

2

= (

O

+

P

)/2.

4.

Oblicz szybkość dźwięku w powietrzu w warunkach laboratoryjnych

=

λ

.

5.

Ze wzoru (7) oblicz szybkość dźwięku w suchym powietrzu

D

w temperaturze 0°C.

6.

Oszacuj metodą A niepewności pomiaru wysokości słupów powietrza

T

U

(I

#

) i T

U

(I

$

). W tym

celu oblicz odchylenia standardowe średnich arytmetycznych

T

U

(I

#

) = =

∑ WI

#X

− I̅

#

Y

$

Z

X[#

( − 1) , T

U

(I

$

) = =

∑ WI

$X

− I̅

$

Y

$

Z

X[#

( − 1) ,

7.

Oszacuj metodą B niepewność pomiaru wysokości

I, T

\

(I).

T

\

(I) =

∆I

√6

.

8.

Oblicz standardową niepewność złożoną pomiaru wysokości

I

#

słupa powietrza

T

]

(I

#

) = ^T

U

(I

#

)

$

+ T

\

(I)

$

.

i analogicznie oblicz niepewność złożoną

T

]

(I

$

).

9.

Oszacuj niepewność pomiaru temperatury metodą B,

T

\

( ).

10.

Oszacuj metodą B niepewność pomiaru częstotliwości. Ponieważ przyjęliśmy, że rozkład
prawdopodobieństwa na przedziale granicznym

(

O

−

P

) jest prostokątny, niepewność

standardowa wyraża się wzorem

T

\

( ) =

(

O

−

P

)

2√3

.

11.

Oblicz złożoną niepewność standardową długości fali

T

]

(

λ

) = 2^T

]

(I

#

)

$

+ T

]

(I

$

)

$

.

12.

Oblicz złożoną niepewność standardową szybkości dźwięku w powietrzu

T

]

( ) = ^

$

T

]

( )

$

+

$

T

\

( )

$

.

13.

Oblicz złożoną niepewność standardową szybkości dźwięku w suchym powietrzu

D

w tem-

peraturze 0°C

T

]

(

D

) = =

1

√1 + %

$

T

]

( )

$

+ _

%

2W√1 + % Y

`

$

T

]

( )

$

,

a następnie niepewność względną

T

a,]

(

D

).

2

P

rzyjmujemy dla tego pomiaru rozkład prostokątny. Gęstość prawdopodobieństwa wystąpienia dowolnej

wartości częstotliwości mieszczącej się w tym przedziale jest stała. Estymatą częstotliwości , będzie punkt
środkowy przedziału granicznego

= (

O

+

P

)/2.

Wyznaczanie szybkości dźwięku w powietrzu

9

14.

Oblicz niepewność rozszerzoną

b(

D

) pomiaru szybkości dźwięku w suchym powietrzu

D

(w

0°C).

15.

Podaj poprawnie zapisane wyniki pomiarów (łącznie z niepewnościami) i wpisz je do Tabeli 2.

5.

Dyskusja wyników

1.

Porównaj obliczoną szybkość dźwięku w warunkach laboratoryjnych z wartościami z Tabeli
3. Oceń zgodność obu wartości.

2.

Porównaj otrzymaną wartość szybkości dźwięku w suchym powietrzu

D

(w 0°C) z wartością

tabelaryczną. Oceń zgodność obu wartości. Czy wartość tabelaryczna mieści się w wyznaczo-
nym przedziale wyznaczonym

̅

D

± b(

D

), jaki otrzymaliśmy? Jeśli wartość tabelaryczna nie

mieści się w nim, to spróbuj znaleźć błędy, które do tego doprowadziły.

3.

Przyjrzyj się swoim wynikom pomiarów (możesz również skorzystać z wyników innych zespo-
łów) i zastanów się, w jaki sposób wilgotność i temperatura powietrza wpływają na wartość
szybkości dźwięku

i czy potwierdza się zależność teoretyczna.

6.

Uzupełnienia

6.1

Tabele

Tabela 3. Prędkość rozchodzenia się dźwięku w powietrzu wyrażona w m/s

Wilgotność

względna w %

Szybkość

dźwięku w

18℃

Szybkość

dźwięku w

20℃

Szybkość

dźwięku w

22℃

Szybkość

dźwięku w

24℃

0

342.197

343.371

344.540

345.705

30

342.52

343.74

344.96

346.18

40

342.63

343.87

345.10

346.34

50

342.74

343.99

345.24

346.50

60

342.85

344.12

345.38

346.66

70

342.96

344.24

345.53

346.82

80

343.07

344.37

345.67

346.98

90

343.18

344.49

345.81

347.14

100

343.29

344.62

345.95

347.31

Tabela 2. Wyniki obliczeń

λ

, T

]

(

λ

)

[m]

, T

]

( )

[m/s]

± b( )

[m/s]

D

, T

]

(

D

)

[m/s]

D

± b(

D

)

[m/s]

Wartość teore-

tyczna

D

[m/s]

Ćwiczenie 29

10

6.2

Dlaczego wilgotne powietrze jest lżejsze?

Prawo Avogadra mówi, że takie same objętości gazów przy jednakowym ciśnieniu i temperaturze

zawierają taką samą liczbę cząsteczek. Powietrze składa się z cząsteczek azotu N

2

(masa cząsteczkowa

28) i cząsteczek tlenu O

2

(masa cząsteczkowa 32)). Cząsteczka wody, która składa się z atomu tlenu o

masie atomowej 16 i 2 atomów wodoru o masie atomowej 1. Zatem ma masę cząsteczkową równą
18. Dodanie pary wodnej do danej objętości powietrza powoduje zastąpienie cięższych cząsteczek
azotu lub tlenu lżejszymi wody, bo ilość wszystkich cząsteczek w tej objętości musi pozostać stała. W
konsekwencji gęstość wilgotnego powietrza zmniejsza się.

7.

Literatura

1.

Praca pod red. B.Oleś i M. Duraj: Ćwiczenia laboratoryjne z fizyki, cz.I. wyd.4, Wydawnictwo
PK, Kraków 2008.

2.

T.Dryński: Ćwiczenia laboratoryjne z fizyki. PWN, Warszawa 1967.

3.

D.Halliday, R.Resnick, J.Walker: Podstawy fizyki, cz.2. PWN, Warszawa 2008.