Opracowanie do kolowium

Przetwarzania Sygnałów

Część I

Sploty itp

MC_OMEN

1. Sygnał dwuharmoniczny x(t) jest próbkowany z zadaną częstotliwością

próbkowania:
a) ( ) ( ( ) ) ( )

b) ( ) ( ( ) ) ( )

c) ( ) . ( )

/ ( )

System dyskretny nie ma filtru antyaliasingowego, a filtr odbiorczy jest idealny.
Znajdź takie częstotliwości f ( jest ich nieskończenie wiele, podaj wzór), dla których
sygnał wyjściowy jest sygnałem jednoharmonicznym. Dla najmniejszej ze
znalezionych częstotliwości spełniającej warunek narysuj widmo sygnału
wejściowego, widmo sygnału spróbkowanego, widmo sygnału wyjściowego.
Wyznacz sygnał wyjściowy ( ). W przypadku c znajdź dodatkowo takie pary
( ), dla których sygnał wyjściowy równa się zeru.

Rozwiązanie:

Sygnał jedno harmoniczny – taki który ma jedną składową, tzn jego częstotliwości
siępokrywają i można go zapisać jako pojedynczy.

Równanie :

Gdzie:

Wtedy dostajemy równanie gdzie korzystając z okresowości funkcji kosinusoidalnej
otrzymamy na wyjściu

a) ( ) ( ( ) ) ( )

( ) ( ( ) ) ( ( ) )

Sygnał po spróbkowaniu:

, - ( )

( (

) ) ( (

) )

( (

) ) ( (

) )

( (

) ) ( (

) ) ( (

) )

Sygnał po rekonstrukcji:

( ) , -

( ( ) )

b) ( ) ( ( ) ) ( )

( ) ( ( ) ) ( ( ) )

Sygnał po spróbkowaniu:

, - ( )

( (

) ) ( (

) ) ( (

) ) ( (

) )

Sygnał po rekonstrukcji:

( ) , -

( ( ) ) ( ( ) )

c) Nie chce mi się tego rozkladac na fouriera = /

2. Są dane sygnały , - i , -:

a) * , -+ { ̂ } * , -+ * ̂ +
b) * , -+ { ̂ } * , -+ * ̂ +

Oblicz i wykreśl splot liniowy

, - , - , - i kołowy

, - , - , -.

Oblicz i wykreśl widma

(

) ( )

, -( ). Pokaż, że te widma są

następującymi iloczynami

(

) (

) (

)

, - , - , -. Pokaż, że

uzupełniając sygnały zerami ( jaka jest minimalna liczba tych zer?) otrzymamy wynik
splotu kołowego taki sam jak splotu liniowego.

a) * , -+ { ̂ } * , -+ * ̂ +

Zapis w postaci DTFT i DFT
DFT:

, - , - , - , - , -

, - , - , -

DTFT:

(

)

(

)

Korzystamy z własności że splot z delta diraca to po prostu przeniesienie o N
miejsc.

, - , - , -

, - ( , - , - , - , -)( , - , -)

, - , - , - , - , - , -
, - , - , - , - , - , -
, - , - , - , -
, - , - , - , - , - , -
, - , -
, - , - , - , - , - , -

* , -+ * ̂ +

DTFT po prostu przemnażamy:

(

) (

) (

) (

)(

)

(

)

Sploty każdy sobie sam umie policzyć
Jeżeli sygnał , - ma M próbek, a sygnał , - ma N próbek, to aby otrzymać
równy sobie splot liniowy i kołowy to oba sygnały powinno się uzupełnić zerami
do liczby próbek

3. Zadanie na kształt 2, nie robie.
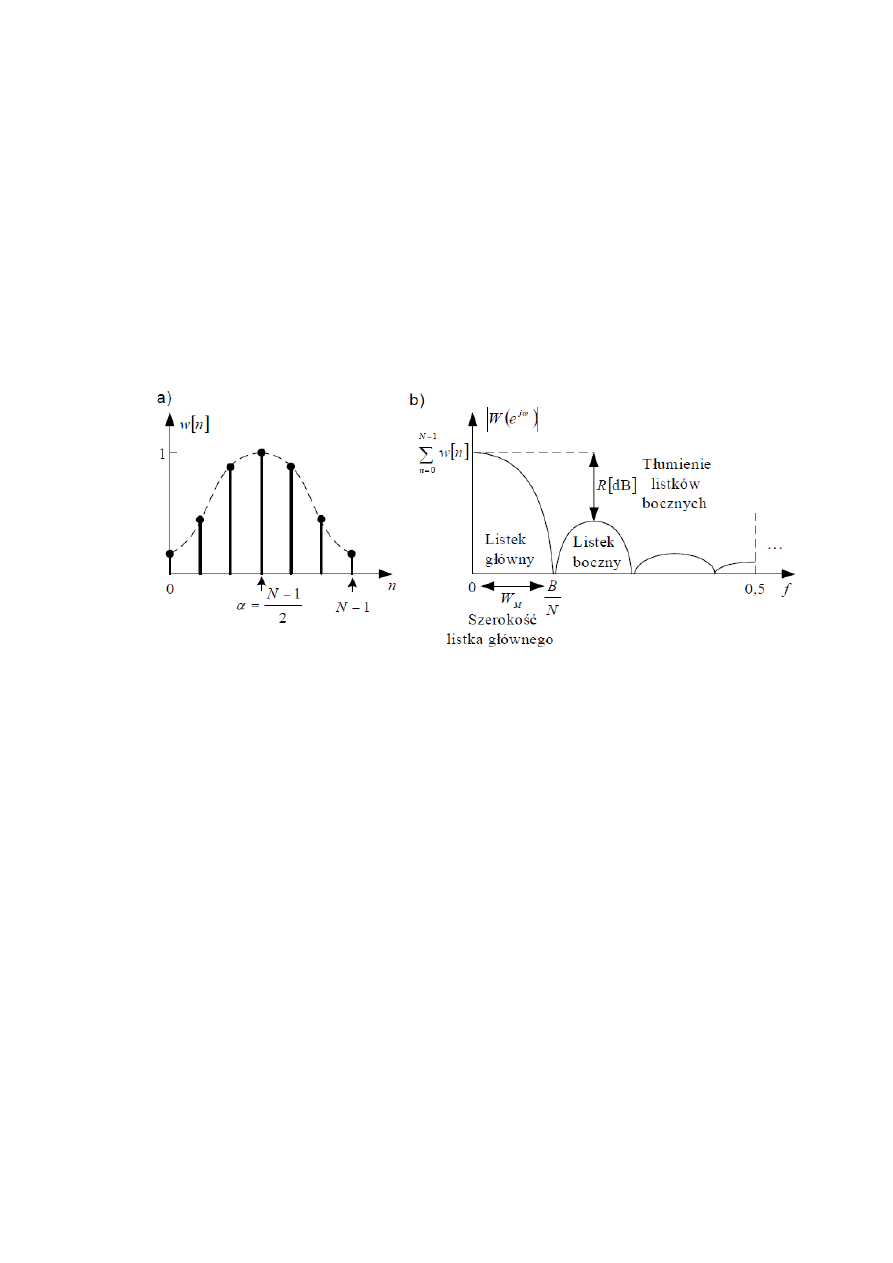
4. Narysuj okno:

A propo okien:

Rozdzielczość częstotliwościowa jest parametrem mówiącym o zdolności rozróżnienia
składowych sumy dwóch sinusoid o jednakowych amplitudach różniących się niewiele
częstotliwościami. Zazwyczaj jest to

O rozdzielczości amplitury decyduje głównie tłumienie listków bocznych R.

Czyli :

, -

a) Prostokątne o N=7

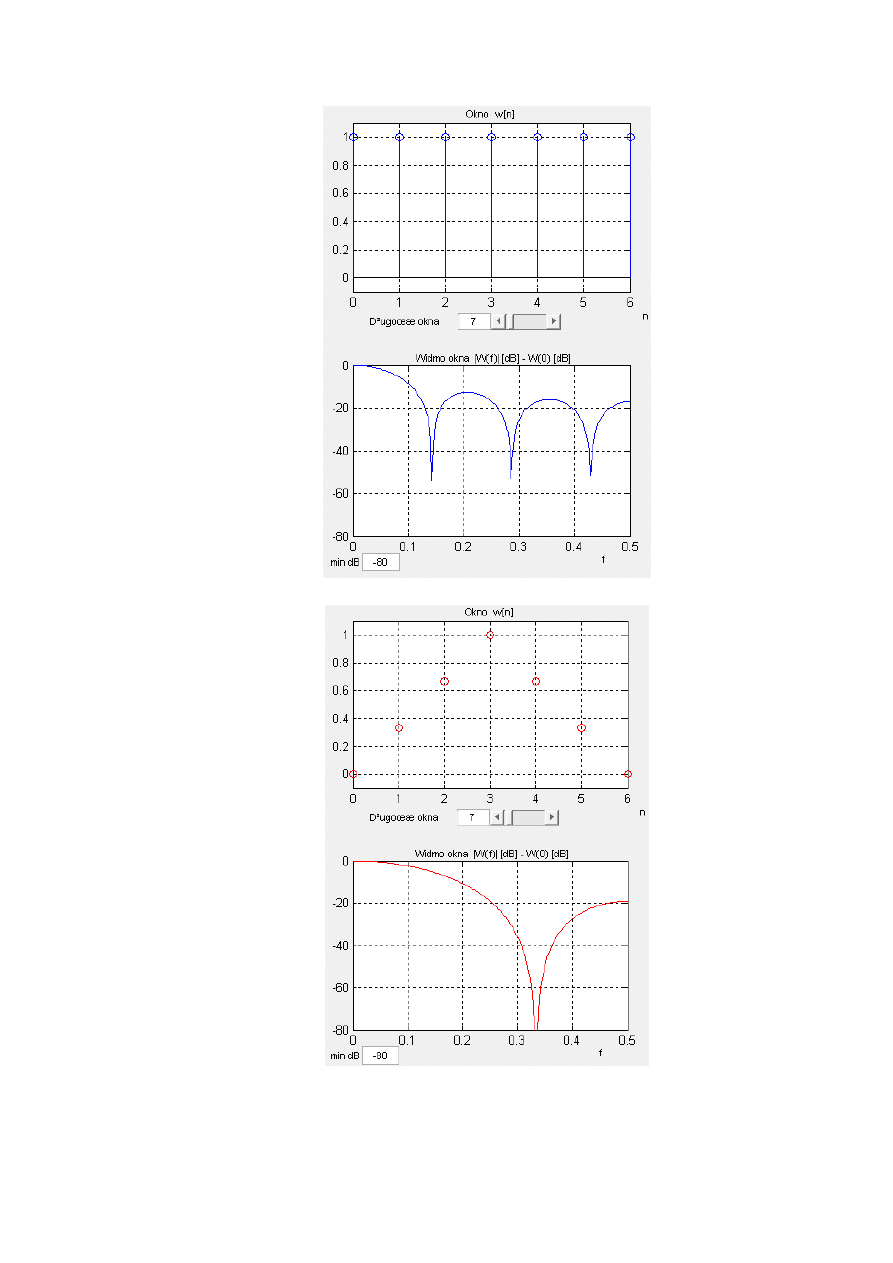
b) Trójkątne o N=7

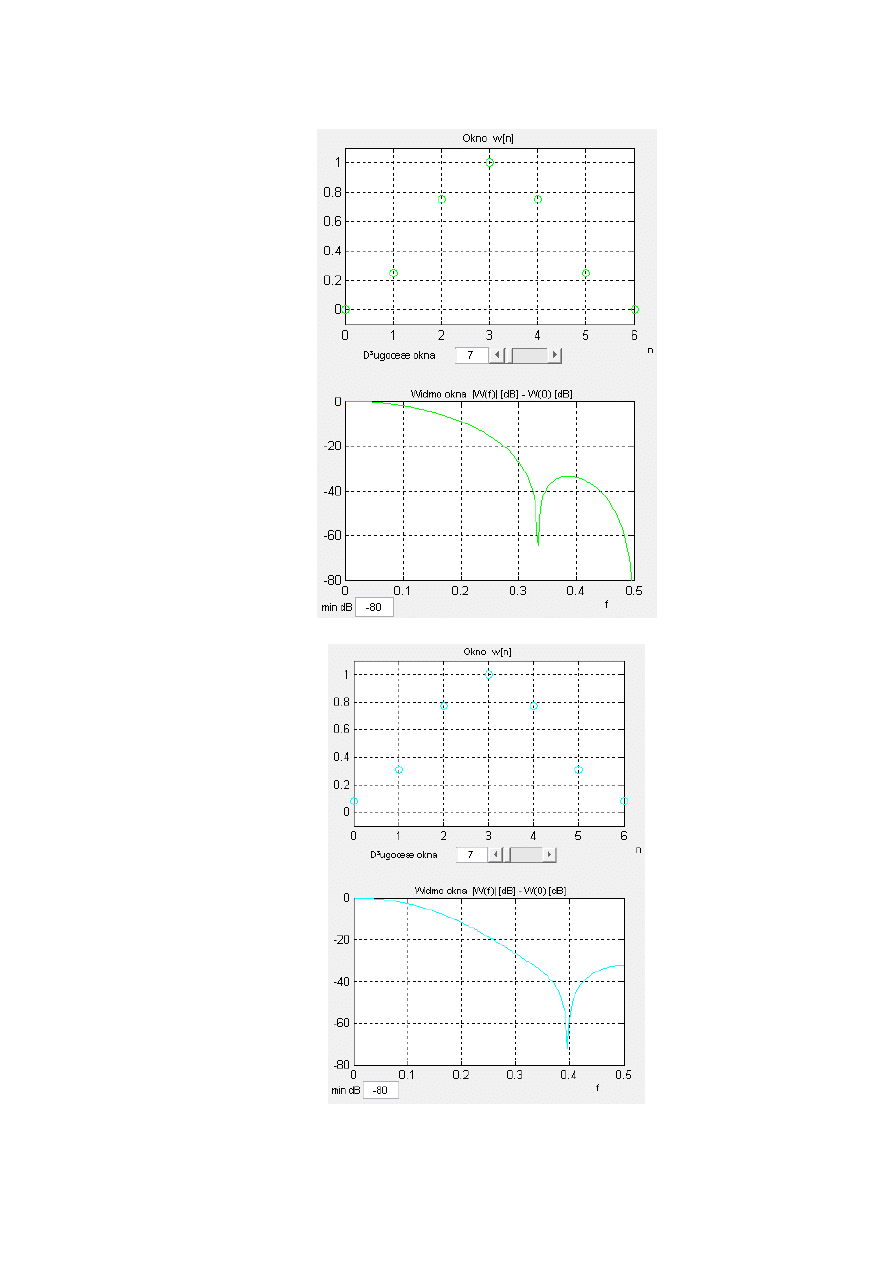
c) Von Hanna o N=7

d) Hamminga o N=7

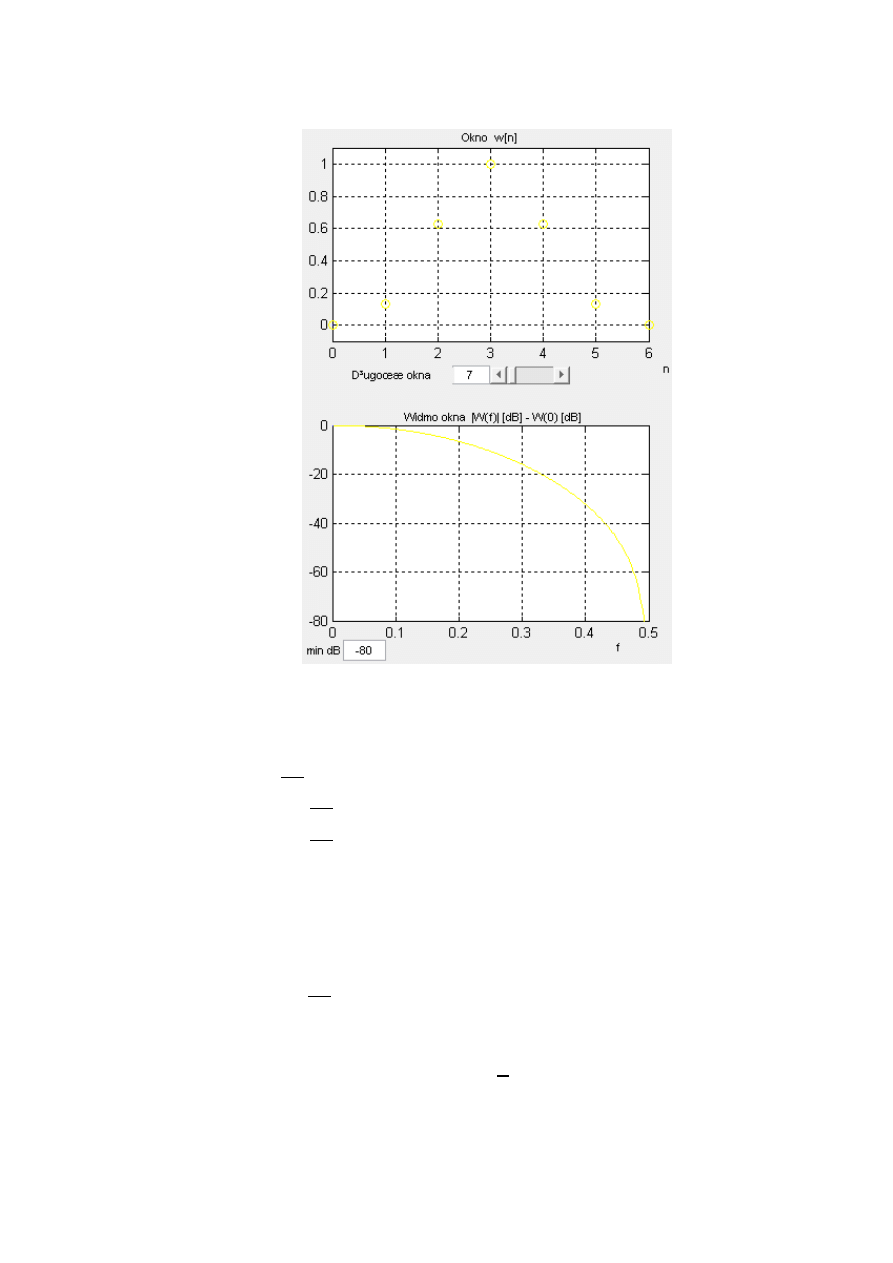
e) Blackmana o N=7

5. Naszkicuj spektrogram sygnału świergotowego ( ) (

) o czasie

trwania od zera do

próbkowanego z częstotliwością

przy następujących

wartościach paramtetrów:
a)

b)

c)

Sygnał świergotowy z liniowo zmieniającą się częstotliwością jest następującą
funkcja: ( ) (

). Wykres tej funkcji jest kosinusoida o stałej

amplitudzie, ale kosinusoida coraz „gęstszą” na osi czasu, w miarę jak w funkcji
czasu rośnie liniowo częstotliwość chwilowa ( )

.

a)

Narastanie sygnału na spektrogramie określamy jako funkcję liniową opisana
wzorem: ( )

Jednakże przy częstotliwości Nquista (

) sygnał „załamuje się” i

symetrycznie leci do

tak jak szedłby liniowo dalej, z tymże jest załamany

( )

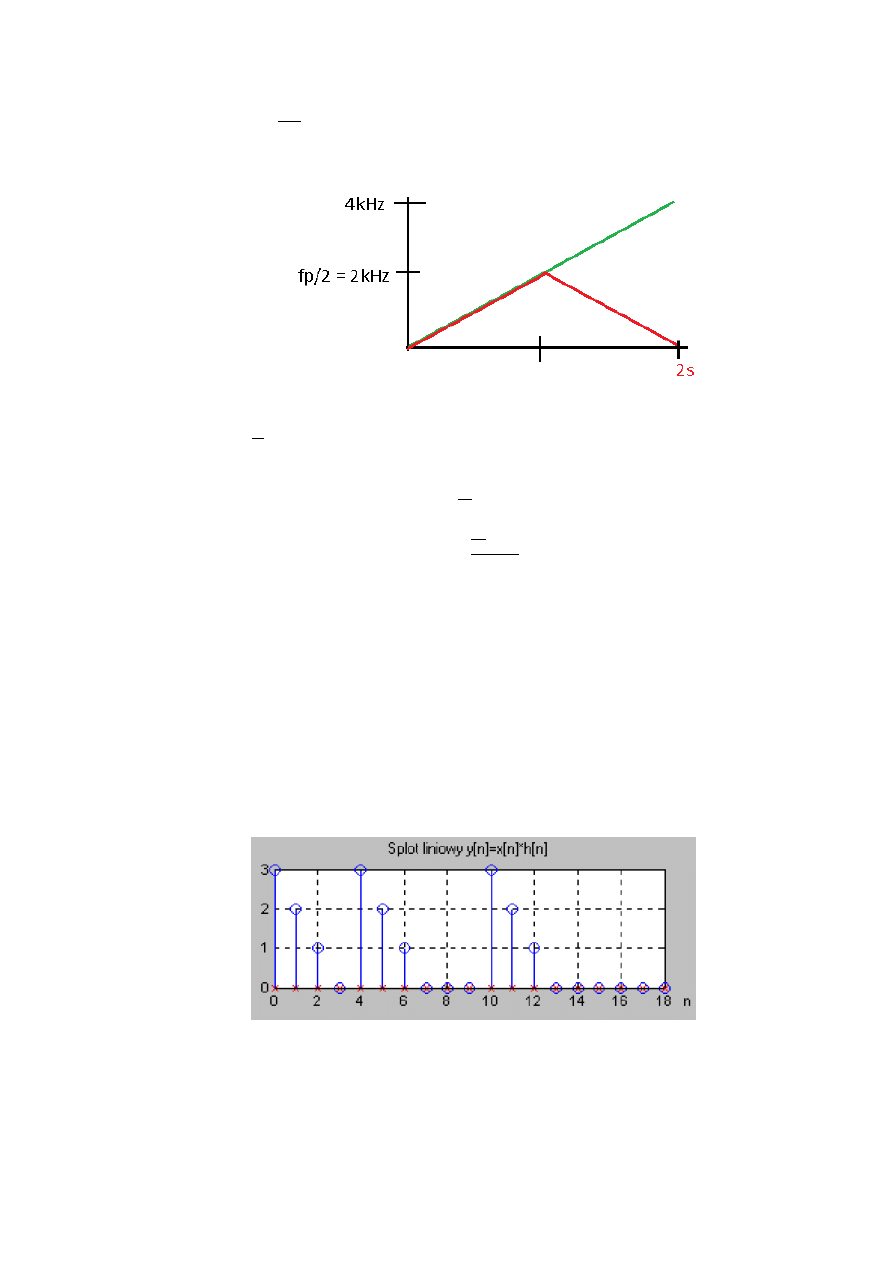
, a czas zmienia się od 0 do 2s, czyli częstotliwość zmienia się od

0 do

Czyli szukamy czasu dla którego liniowo narastająca częstotliwość osiągnie

( )

Obliczenia analogicznie dla b) i c)

6. Co jest wynikiem splotu krótkiego sygnału z ciągiem rzadkich delt?

Jeżeli krótki sygnał , - jest splatany z rzadkim ciągiem delt Kroneckera , -
(rzadkim tzn. odstępy między deltami Kroneckera są większe niż czas trwania
krótkiego sygnału x[n]), to wynikiem splotu jest powtarzający się w chwilach
występowania delt Kroneckera sygnał , -. Na rysunku jest wynik splotu krótkiego
sygnału * , -+ * ̂,2,1,0,…} z rzadkim ciągiem delt Kroneckera , - , -
, - , -. Wynikiem jest sygnał , - powtarzający się począwszy od
pozycji . Gdyby sygnał , - splatać z okresowym ciągiem delt Kroneckera
o okresie równym czasowi trwania sygnały , -, to otrzymalibyśmy sygnał
okresowy, w którym jeden okres równa się sygnałowi , -.

7. Na przykładzie splotu liniowego dwóch impulsów prostokątnych określ czasy

trwania stanów przejściowych i stanu ustalonego splotu
Posplocimy dwa sygnały:

* , -+ { ̂ }

* , -+ { ̂ }

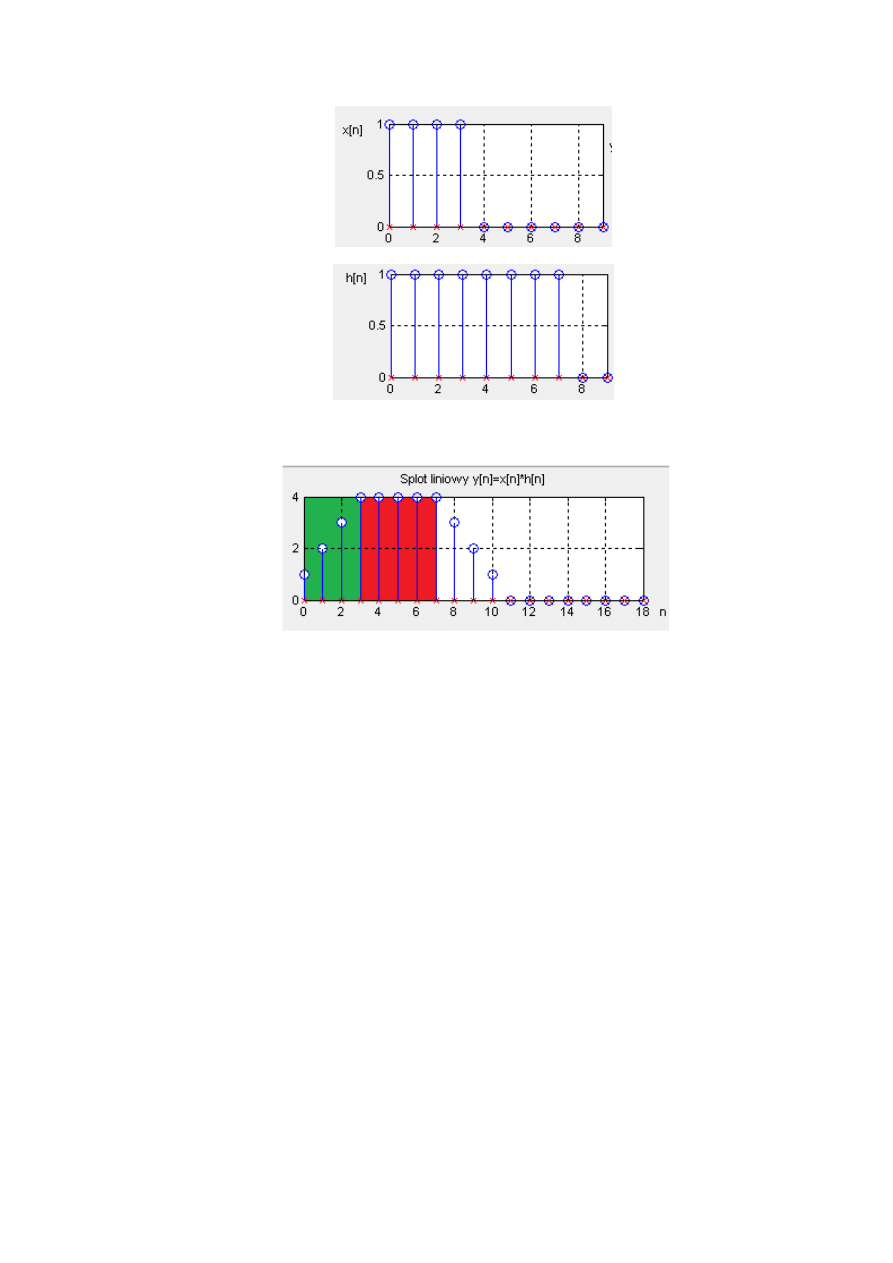
Wynik splotu:

W wyniku splotu zaznaczone zostało na zielono – stan przejściowy, na czerwono stan
ustalony

Długość w taktach stanu ustalonego obliczamy ze wzoru:

Długość stanu przejściowego określamy w taktach jako taktowa długość krótszego
sygnału czyli:

8. Porównaj wynik splotu liniowego i kołowego dwóch identycznych impulsów

prostokątnych. Jaki musi być minimalny zeropadding, aby wynik splotu kołowego
był identyczny ze splotem liniowym.
Jeżeli sygnał , - ma M próbek, a sygnał , - ma N próbek, to aby otrzymać równy
sobie splot liniowy i kołowy to oba sygnały powinno się uzupełnić zerami do liczby
próbek

Załóżmy 2 sygnały:

, - , -

, - , -

Sploty tych sygnałów:

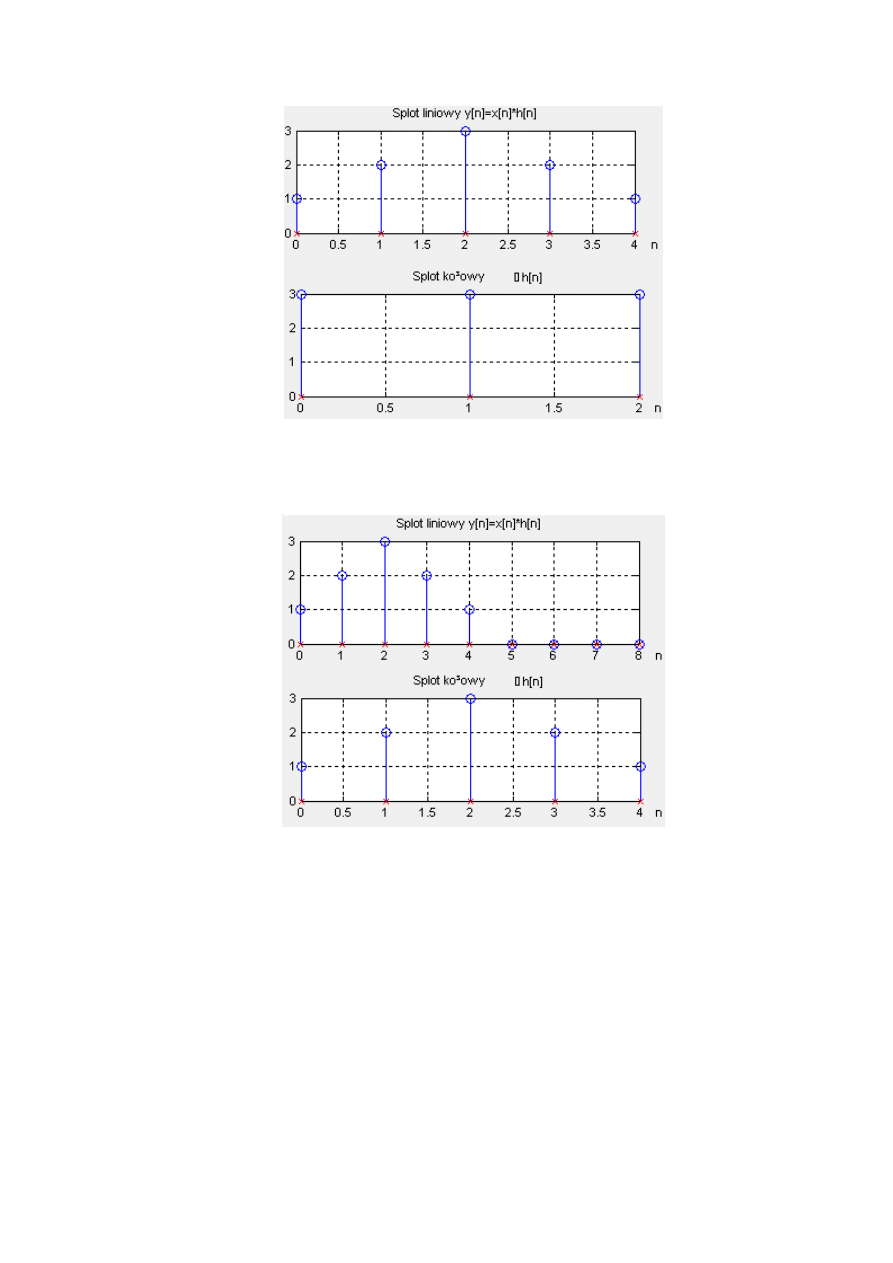
Teraz teoretycznie powinno się rozszerzyć sygnały zerami do 5 miejsca, czyli o 2
zera:

, - , -

, - , -

9. Co jest wynikiem splotu dwóch impulsów prostokątnych? Naszkicuj obwiednie

przebiegów czasowych możliwych wyników. Określ długość i maksymalną wartość
spotu dla dowolnych impulsów prostokątnych. Od jakich parametrów impulsów
zależż te wartości?

Długość splotu liniowego :

Długość splotu kołowego:

( )

Maksymalna wartość splotu zdeterminowana jest długościami obu sygnałów oraz ich
wartościami, jak wiemy splot polega na przemnażaniu przez siebie wartości, czyli
gdy mamy sygnały :

, - , -
, - , -

To przykładowo liczba a będzie przemnażana M krotnie przez liczbę b.
Tak więc jest to funkcja

( )

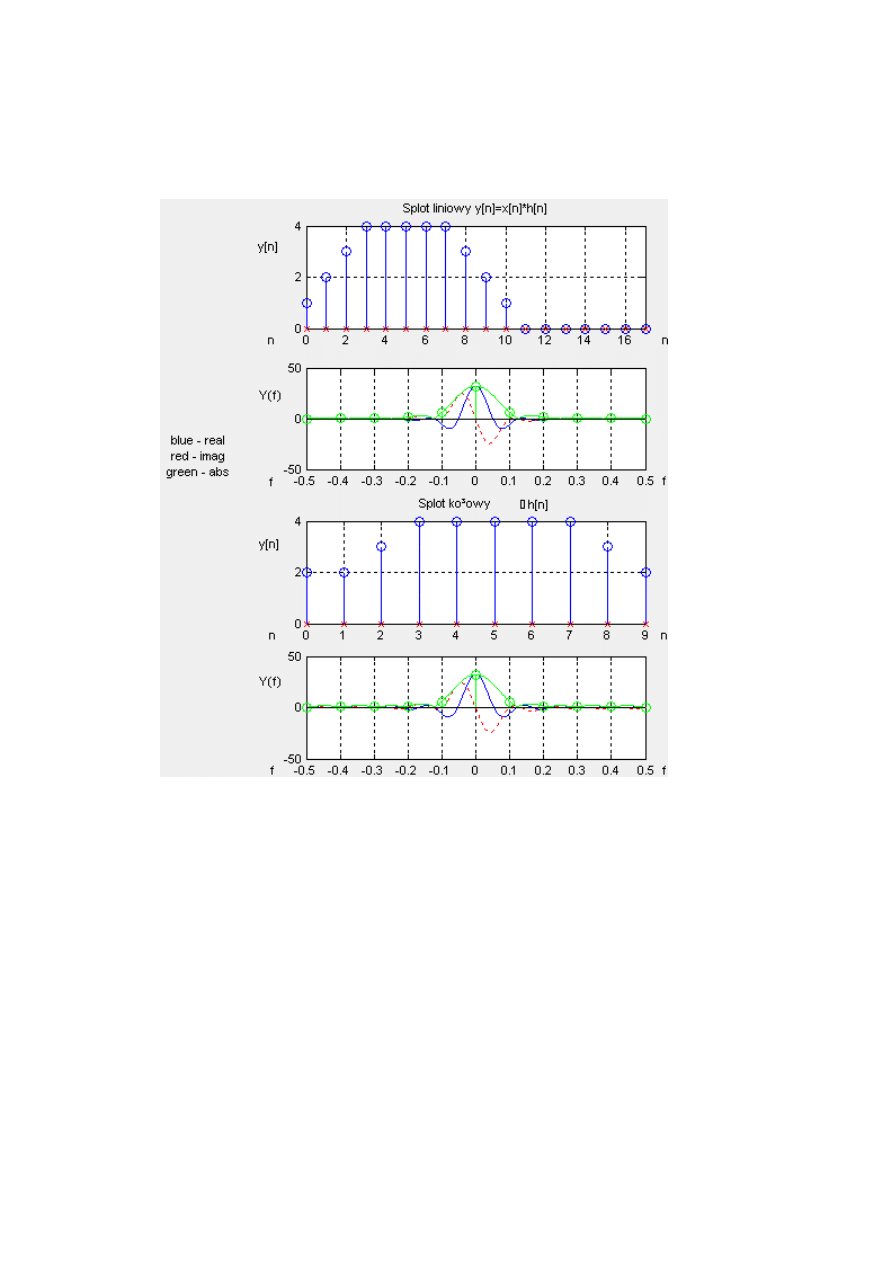
Sygnały opisane są w zadaniu 7. Splotowe obwiednie czasowe (kolejność, lin, koł):