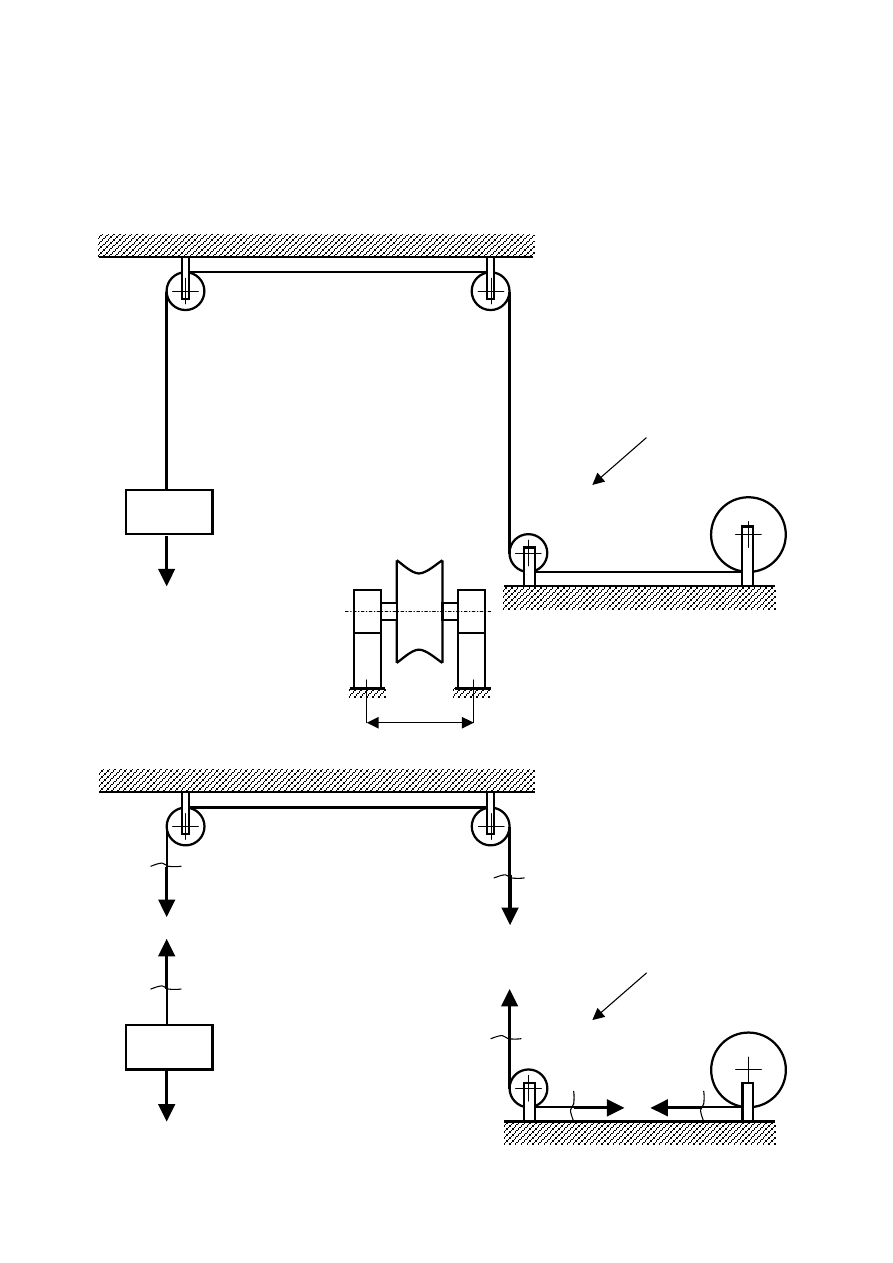
Przykład 1
Obliczyć obciążenie łożysk oraz narysować wykres momentu gnącego osi wskazanej rolki
urządzenia wyciągowego.
Przyjąć następujące dane:
- masa elementu podnoszonego m=500kg
- rozstaw
łożysk L=0,2m
F
m
F
S
S
Przedmiot
zainteresowania
F
F
F
S
m
F
L
Przedmiot
zainteresowania
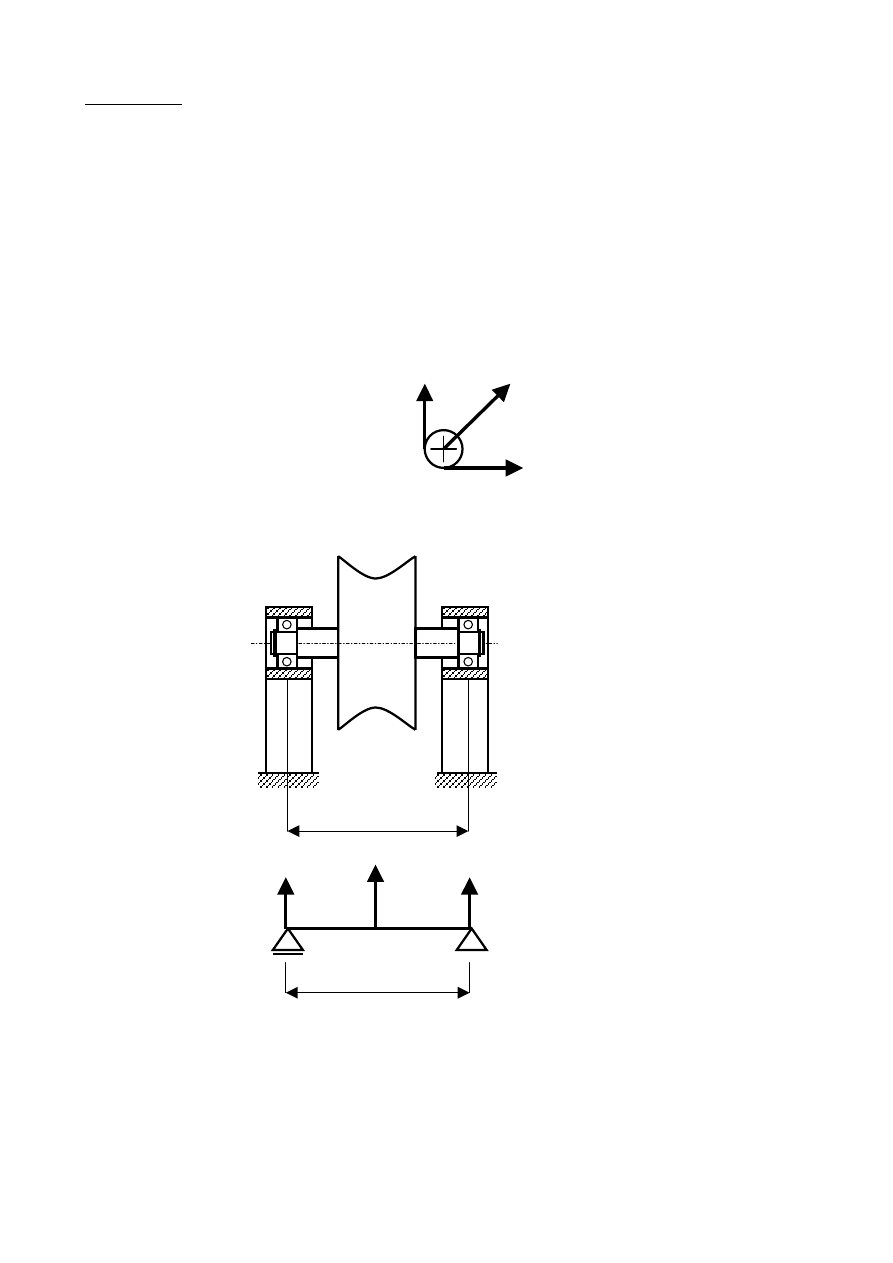
Przypadek 1
1. Obliczenie siły F
F = m*g
F = 500kg * 9,81 m/s
2
= 4905 N
≈ 4,9 kN
2. Siła w linie S
S = F
S = 4,9 kN
3. Obciążenie rolki
Siła wypadkowa P działająca na rolkę
P =
√2 * S
P = 6930 N
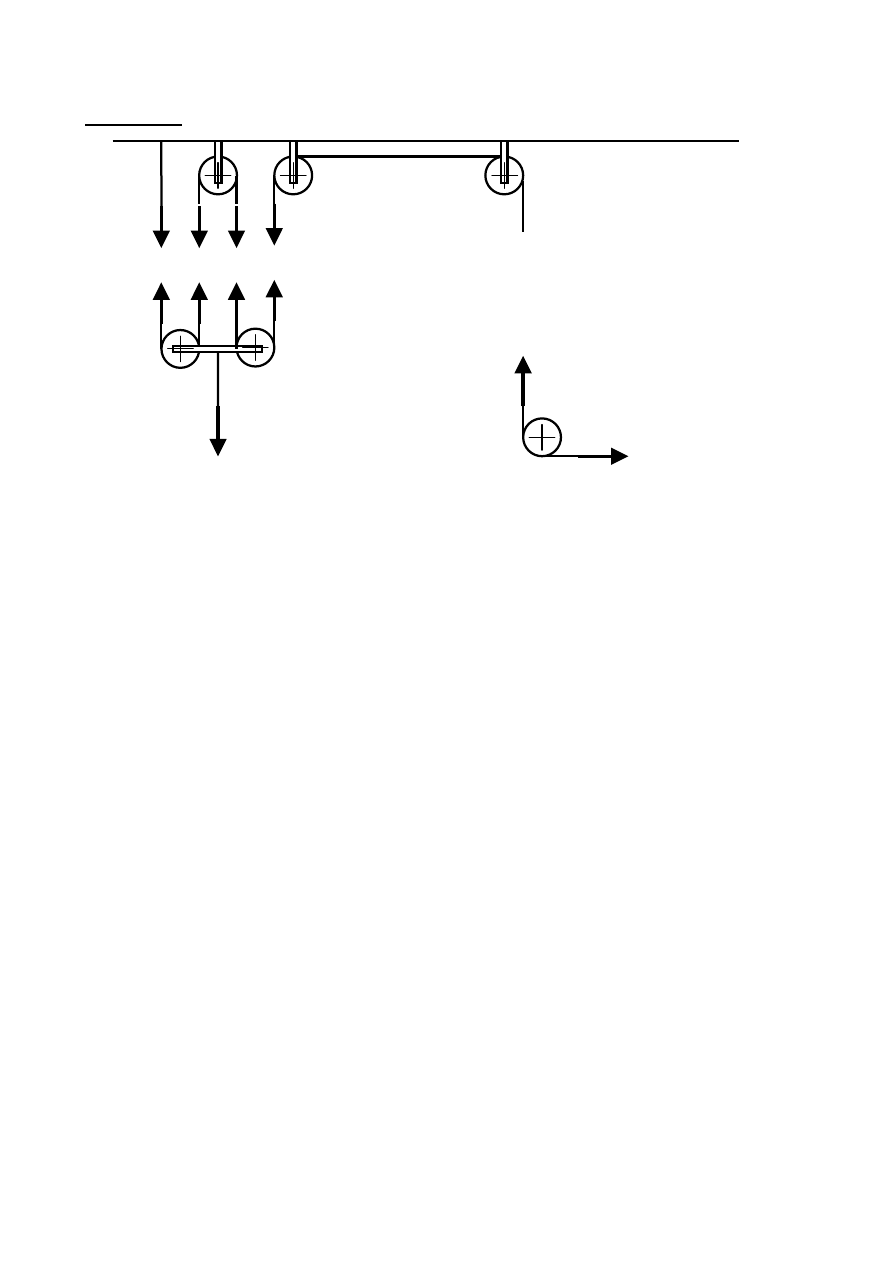
4. Model fenomenologiczny rolki
5. Obliczenie reakcji (obciążenie łożysk)
R
A
= R
B
= P/2 = 3465 N
S
S
P
P
R
A
R
B
L
L
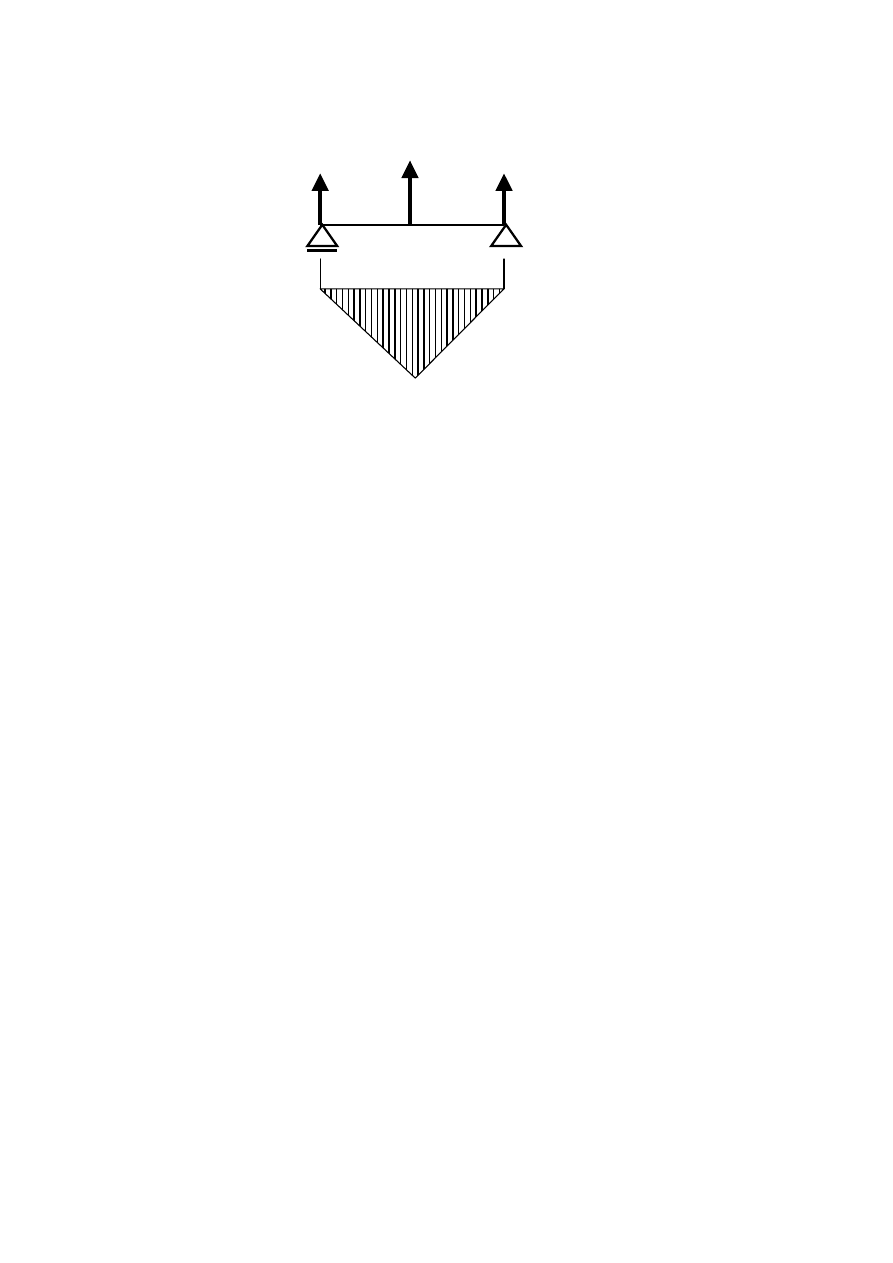
6. Moment gnący
Mg
max
= R
A
*L/2 = 346,5 Nm
P
R
A
R
B
Mg
max
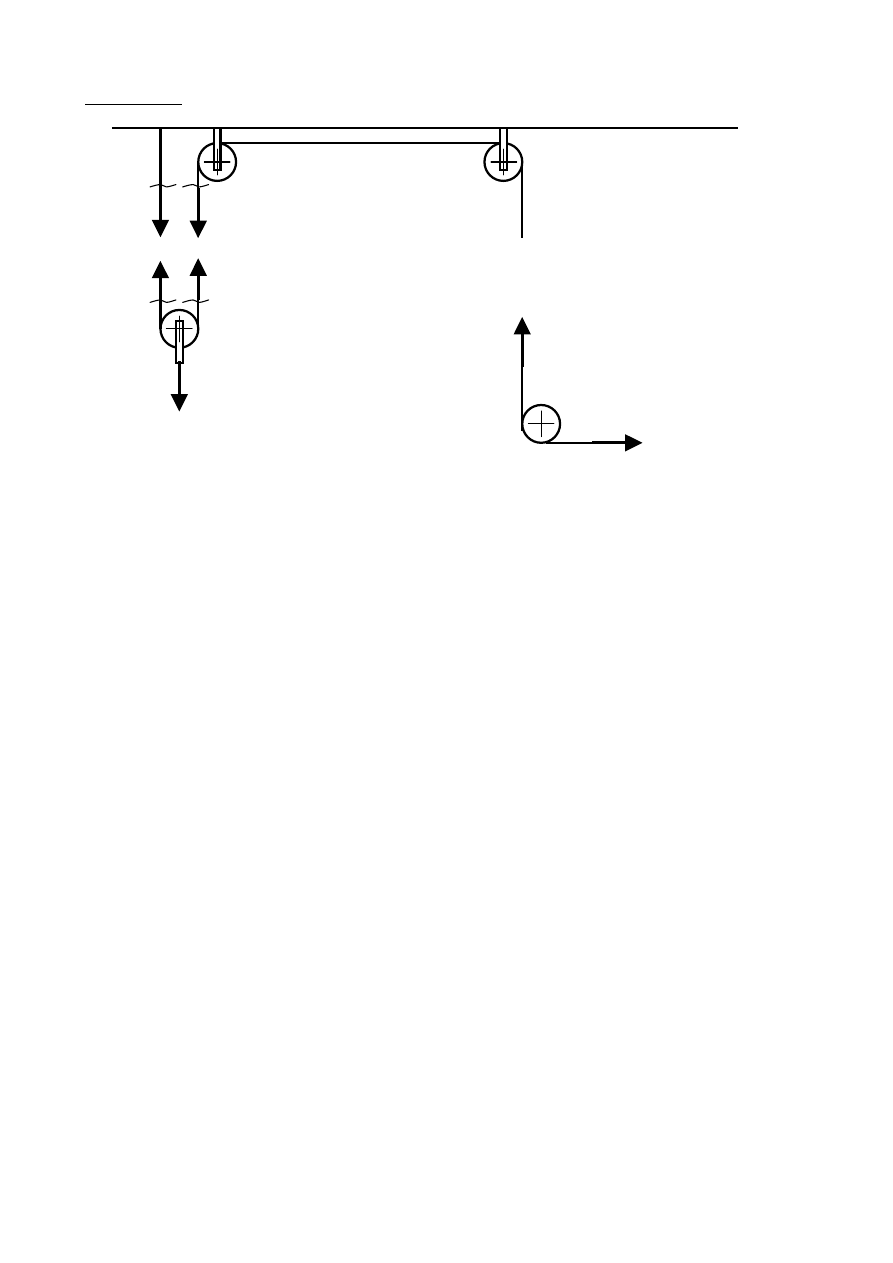
Przypadek 2
1. Obliczenie siły F
F
≈ 4,9 kN
2. Siła w linie S
S = F/2
S = 2450 N
3. Obciążenie rolki
P =3465 N
4. Model bez zmian
5. Obliczenie reakcji (obciążenie łożysk)
R
A
= R
B
= P/2 = 1732 N
6. Moment gnący
Mg
max
= 173 Nm
S
S
F/2
F/2
F
F/2
F/2
Przypadek 3
1. Obliczenie siły F
F
≈ 4,9 kN
2. Siła w linie S
S = F/4
S = 1225 N
3. Obciążenie rolki
P =1732 N
4. Model bez zmian
5. Obliczenie reakcji (obciążenie łożysk)
R
A
= R
B
= P/2 = 866 N
6. Moment gnący
Mg
max
= 86,6 Nm
F
S
S
F/4 F/4 F/4
F/4
F/4 F/4 F/4
F/4
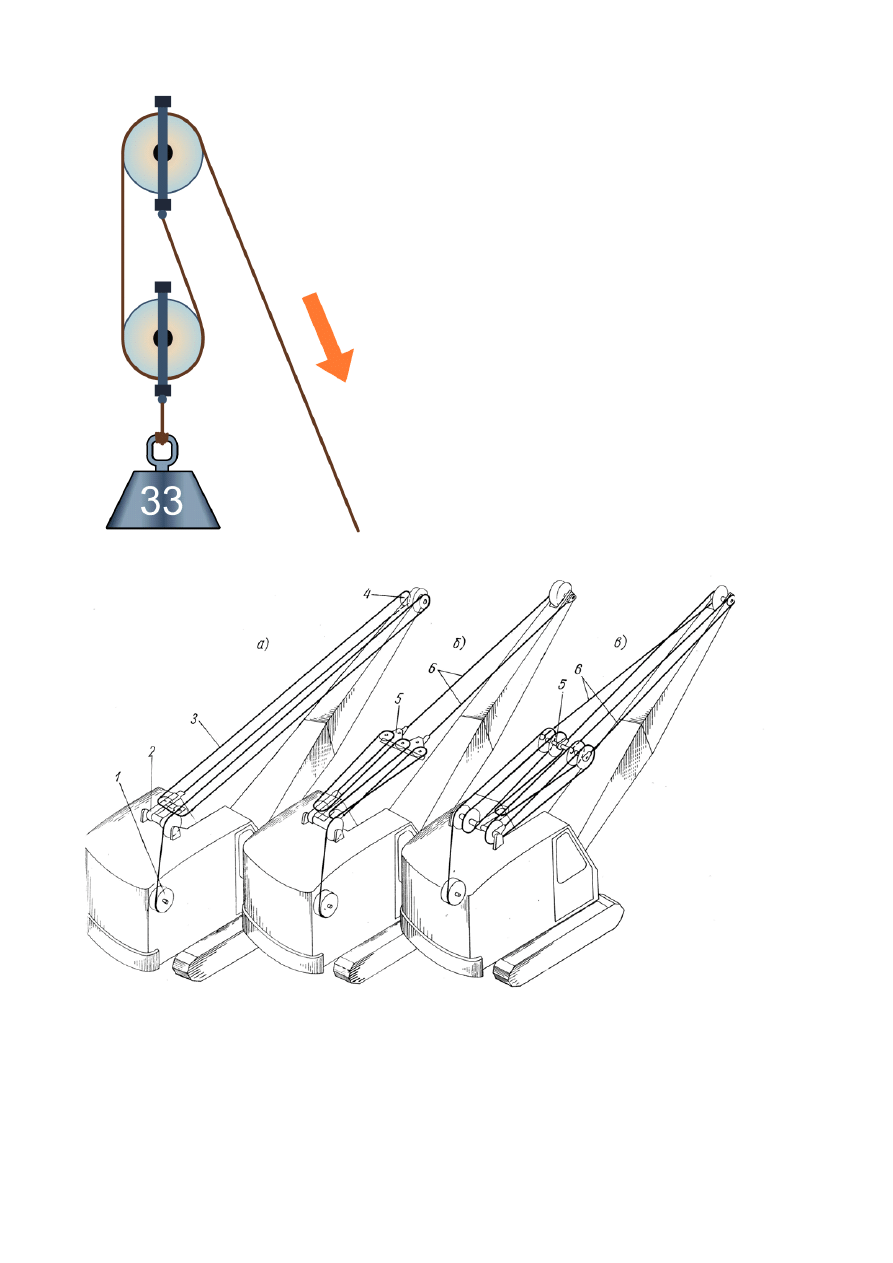
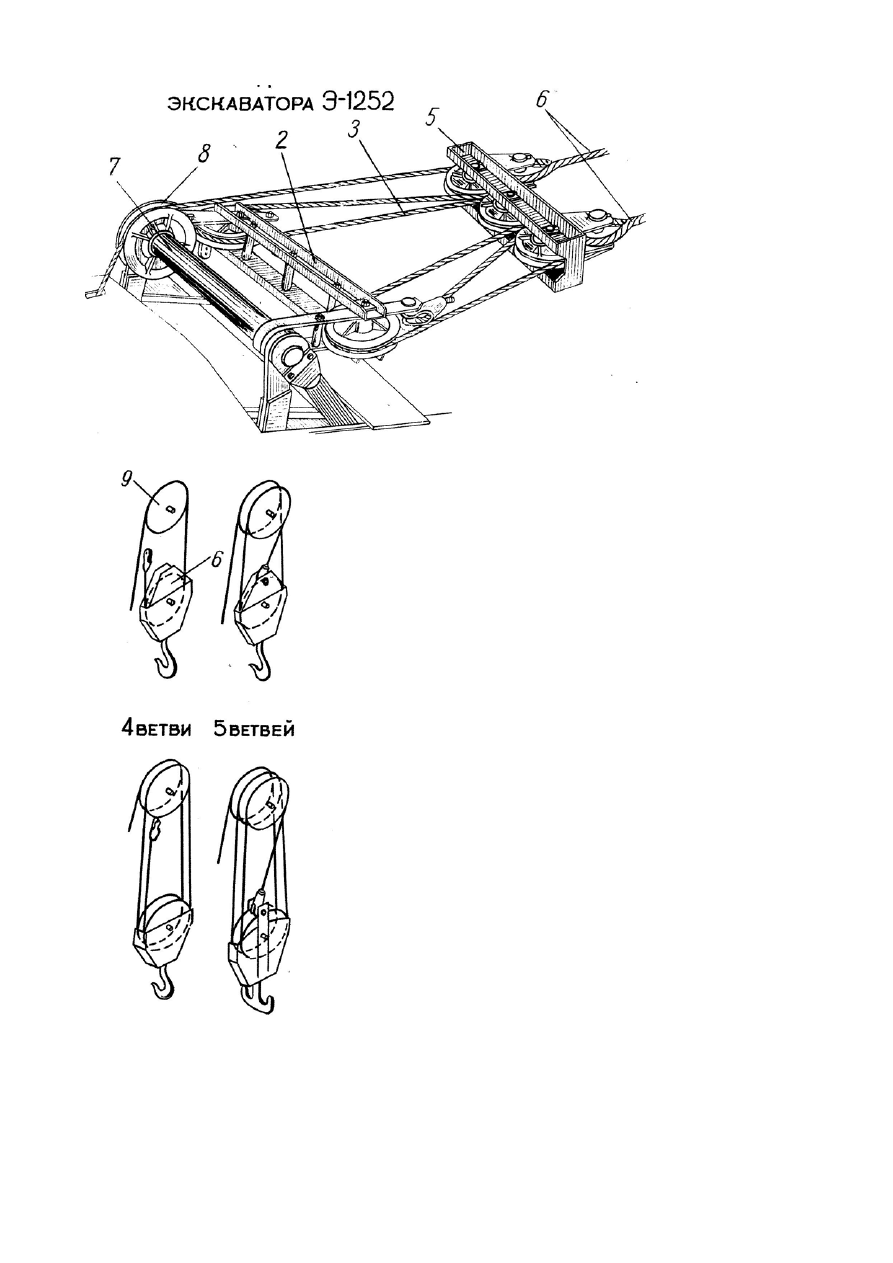
Przykład 2
Na rysunku poniżej przedstawiono postać wysięgnika promieniowego, obrotowego, zamocowanego
do słupa wykonanego z dwuteownika. Obrót wysięgnika realizowany jest w łożyskach tocznych,
zamocowanych w specjalnych oprawach. Górna część wysięgnika została ułożyskowana za pomocą
łożyska kulkowego zwykłego, dolna cześć jest umocowana w łożysku kulkowym skośnym.
Największa masa jaka może być podnoszona przez wysięgnik wynosi m.
Zadanie.
Wyznaczyć reakcje w podporach łożyskowych oraz siły wewnętrzne we wszystkich prętach.
Podnoszona masa wynosi m = 450 kg.
Dane dodatkowe:
V = 2500
[mm]
H = 2000
[mm]
h1 = 300
[mm]
h2 = 1400
[mm]
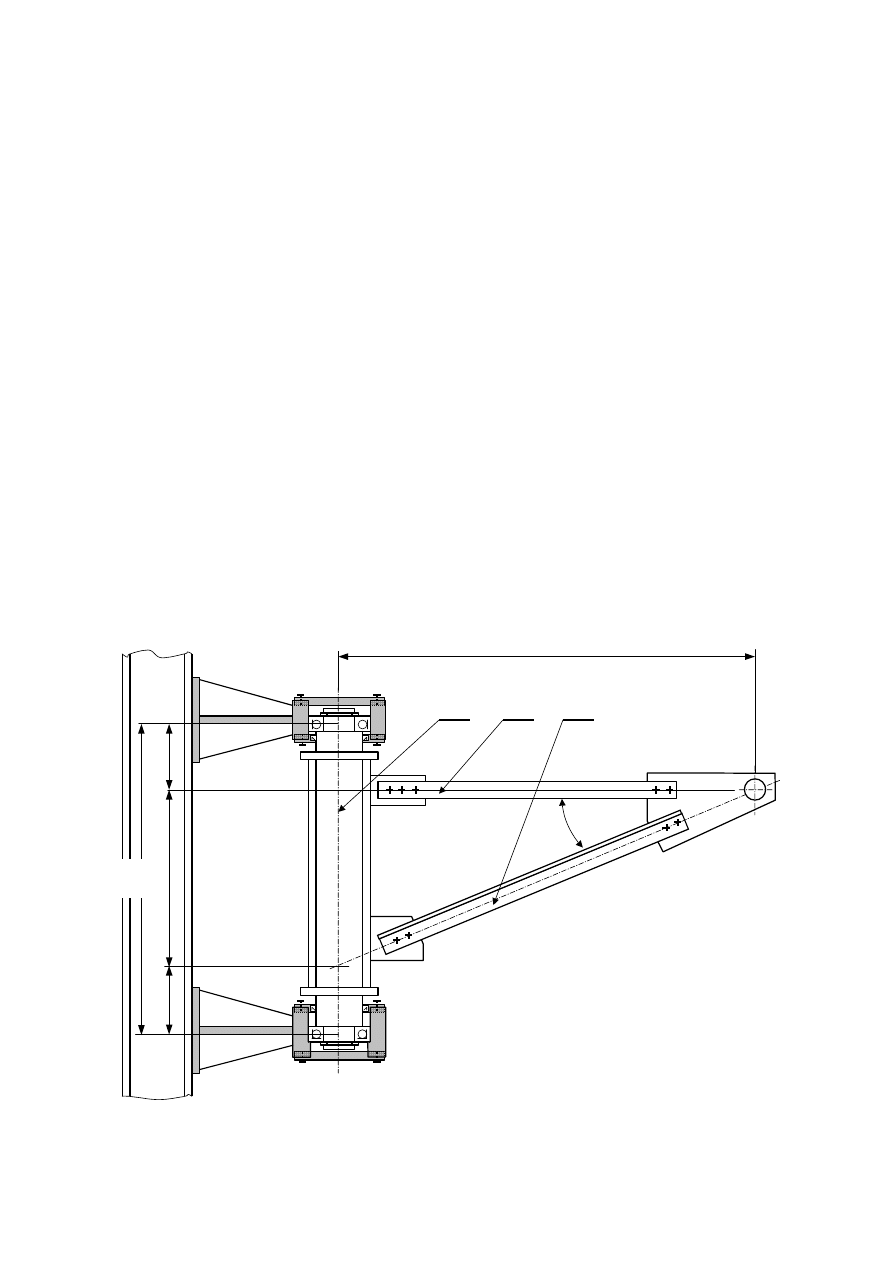
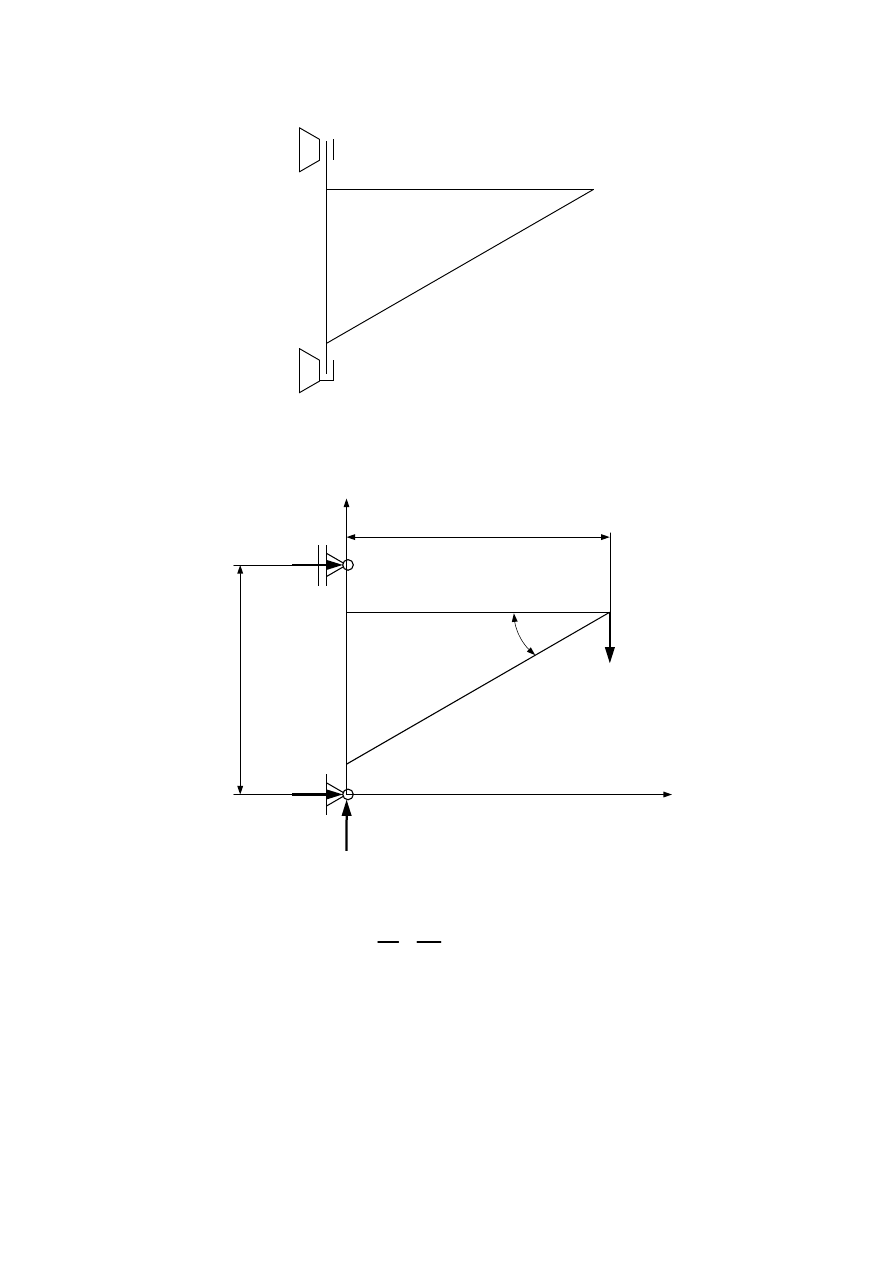
Rysunek wysięgnika.
Konieczne jest naszkicowanie wysięgnika, ze szczególnym uwzględnieniem ułożyskowania i
sposobu połączenia poszczególnych prętów. Pręty wykonane są z następujących elementów:
1 - dwuteownik
2 - dwa
płaskowniki
3 - dwa
kątowniki
1
2
3
α
H
h2
h1
h1
V
W pierwszym kroku zamieniamy elementy wysięgnika na elementy znane z wytrzymałości
materiałów, w tym przypadku na pręty. Należy zwrócić uwagę studentom na podpory łożyskowe
górną – przesuwną i dolną – stałą.
Patrz rysunek poniżej. Na tym rysunku pokazano, że na dolnej podporze opiera się cały wysięgnik.
W kolejnym kroku zamieniamy podpory na oznaczenia znane studentom z mechaniki i
wytrzymałości materiałów. Dorysowujemy obciążenie wysięgnika siłą F oraz reakcje w podporach.
F
R
Ax
R
Bx
R
By
V
H
x
y
α
0
Wyznaczenie kąta
α
:
]
[
25
,
29
56
,
0
56
,
0
5
,
2
4
,
1
2
°
=
=
=
=
=
arctg
V
h
tg
α
α
Wyznaczenie obciążenia:
Obciążenie w układzie pochodzi od podnoszonej masy i wynosi:
]
[
5
,
4414
81
,
9
450
N
F
g
m
F
=
⋅
=
⋅
=
(1)
Wyznaczenie reakcji w podporach:
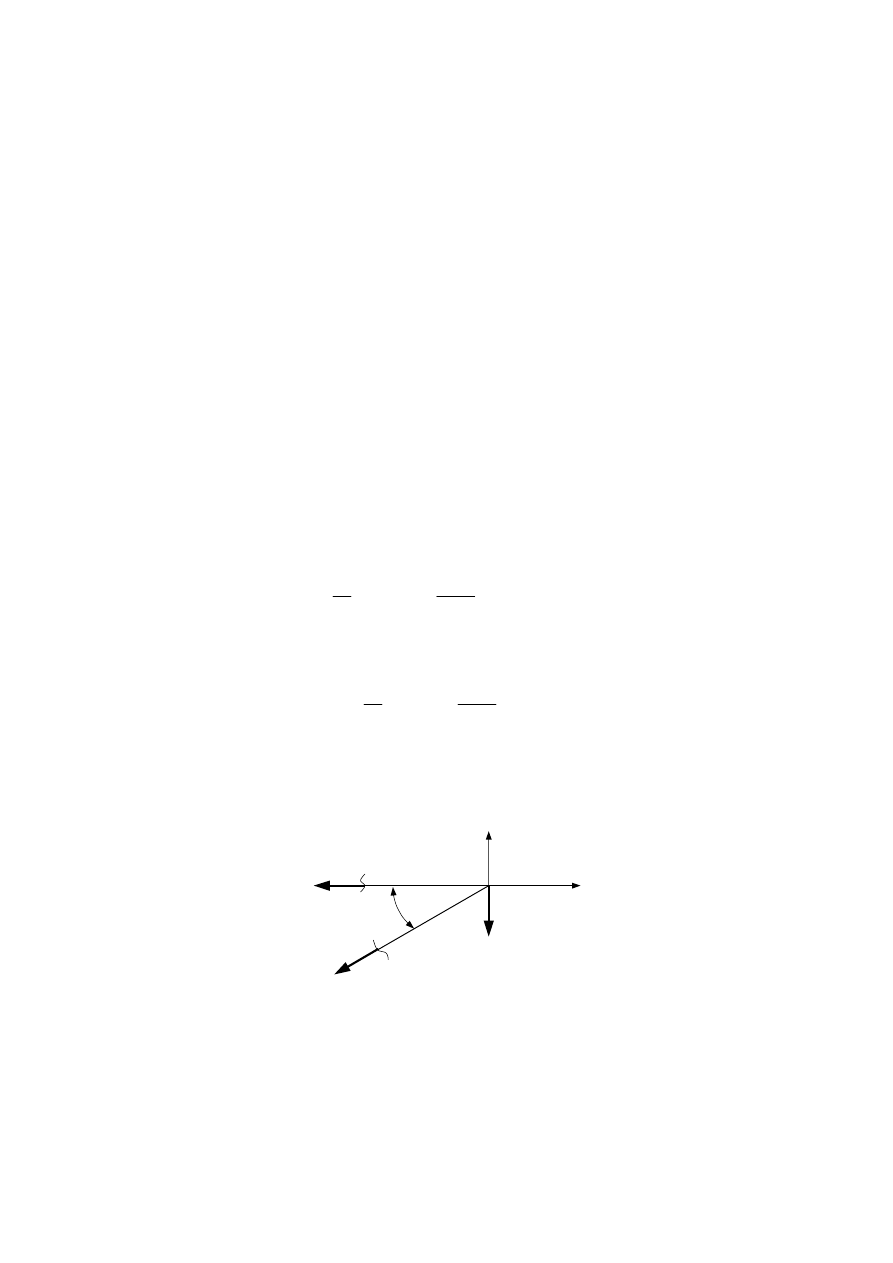
Suma rzutów wszystkich sił na oś x:
0
0
=
+
=
∑
Bx
Ax
ix
R
R
F
(2)
Suma rzutów wszystkich sił na oś y:
0
0
=
+
−
=
∑
By
iy
R
F
F
(3)
Suma momentów wszystkich sił względem punktu 0 (początku układu współrzędnych):
0
0
=
⋅
+
⋅
=
∑
H
R
V
F
M
Ax
io
(4)
z (3) mamy
]
[
5
,
4414
N
F
R
By
=
=
(5)
z (4) mamy
]
[
13
,
5518
2000
2500
5
,
4414
N
H
V
F
R
Ax
−
=
⋅
−
=
⋅
−
=
(6)
z (2) mamy
]
[
13
,
5518
2000
2500
5
,
4414
N
H
V
F
R
R
Ax
Bx
=
⋅
=
⋅
=
−
=
(7)
Wyznaczenie naprężeń i sił wewnętrznych w prętach:
Rozpatrujemy fragment układu w węźle zamocowania obciążenia – siły F. Myślowo rozcinamy
pręty 2 i 3 i zaznaczamy siły wewnętrzne (odpowiednio S
2
i S
3
).
F
S
2
S
3
α
x
y
Wyznaczamy wartości sił wewnętrznych:
0
cos
0
3
2
=
⋅
−
−
=
∑
α
S
S
F
ix
(8)
0
sin
0
3
=
⋅
−
−
=
∑
α
S
F
F
iy
(9)
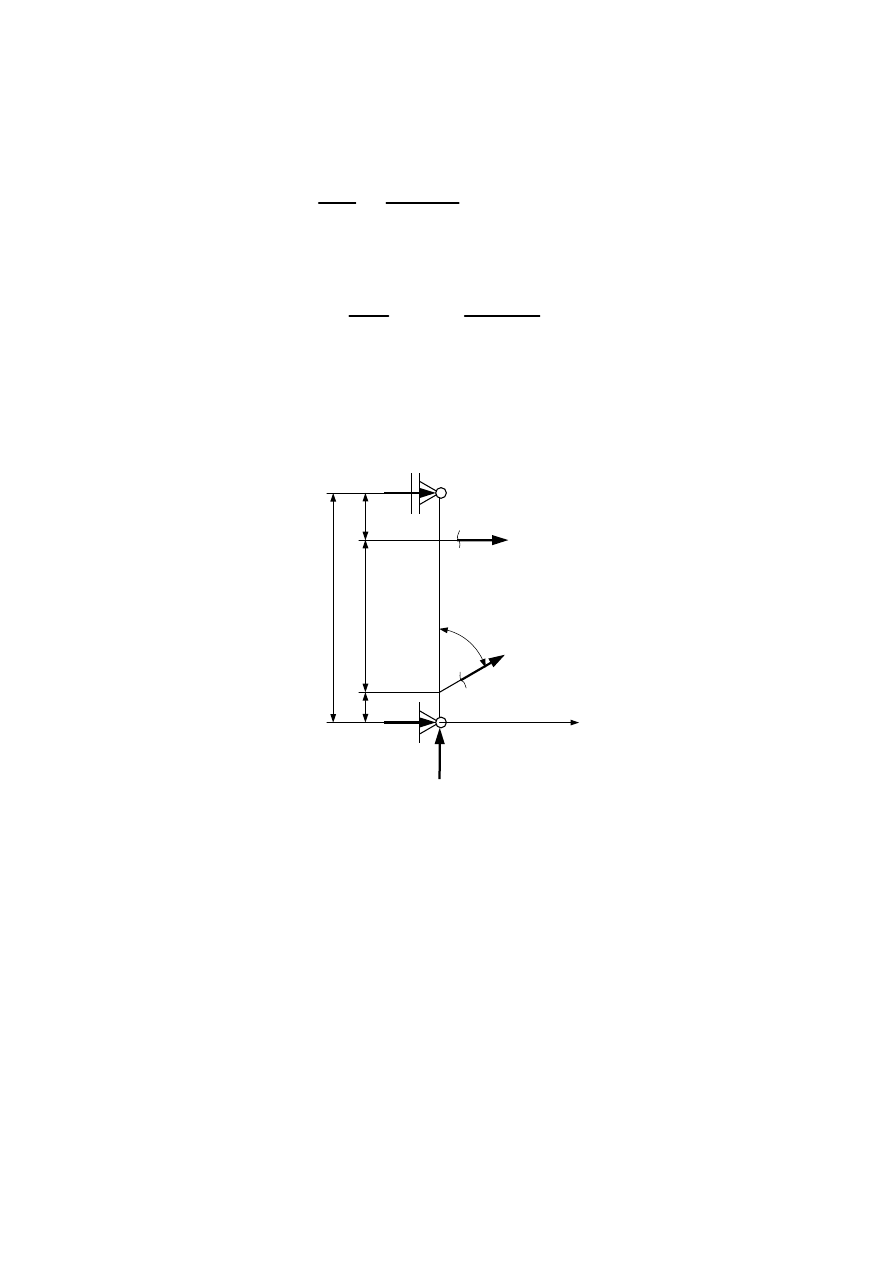
Z (9):
]
[
61
,
9034
25
,
29
sin
5
,
4414
sin
0
3
N
F
S
F
iy
−
=
°
−
=
−
=
=
∑
α
(10)
Z (8):
]
[
66
,
7882
25
,
29
sin
25
,
29
cos
5
,
4414
sin
cos
cos
3
2
N
F
S
S
=
°
°
⋅
=
⋅
=
⋅
−
=
α
α
α
(11)
Z uzyskanych wyników wynika, że pręt 2 będzie rozciągany (dodatnia wartość siły S
2
), zaś pręt 3
będzie ściskany (ujemna wartość siły S
3
).
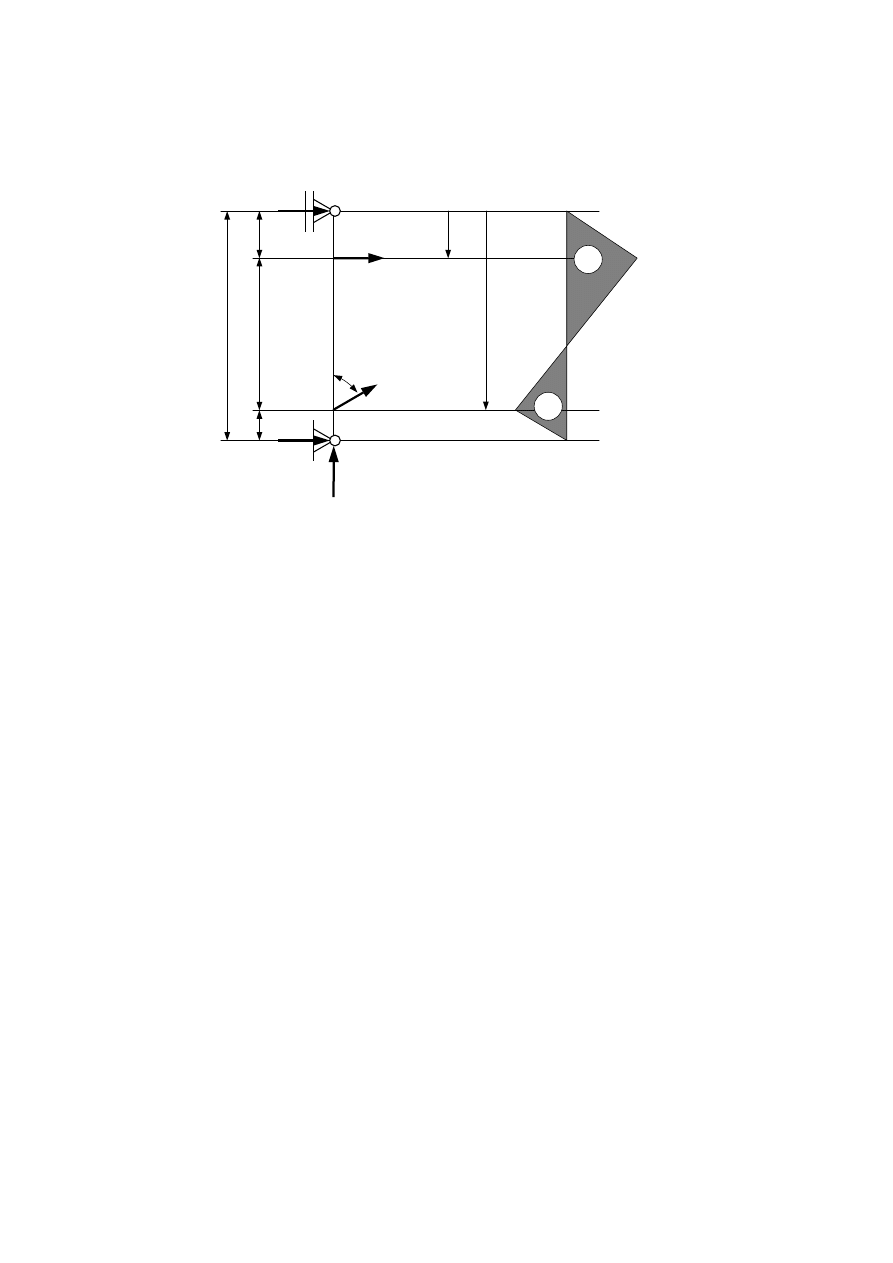
Rozpatrzmy pręt 1. W tym celu należy wydzielić podukład pręta 1.
R
Ax
R
Bx
R
By
H
x
90 −
α
0
S
2
S
3
h
1
h
2
h
1
Element 1 jest belką podpartą w podporach A i B. Obciążenie pochodzące od siły F przenoszone
jest na belkę 1 poprzez pręty 2 i 3. Możemy więc rozpatrywać powyższy układ jako belkę
obciążoną siłami S
2
i S
3
. Reakcje zostały wyznaczone wcześniej. Pozostało przygotowanie
wykresów momentu gnącego. Wartości sił S
2
i S
3
zostały wyznaczone za pomocą wzorów (9) i (10)
i wynoszą:
]
[
61
,
9034
]
[
66
,
7882
3
2
N
S
N
S
−
=
=
(12)
]
[
5
,
4414
]
[
13
,
5518
]
[
13
,
5518
N
R
N
R
N
R
By
Bx
Ax
=
=
−
=
(13)
Wyznaczenie momentów gnących:
(
)
(
)
]
[
90
,
1654
3
,
0
7
,
1
66
,
7882
7
,
1
13
,
5518
1
]
[
44
,
1655
3
,
0
13
,
5518
2
2
2
2
1
1
Nm
h
x
S
x
R
M
Nm
x
R
M
Ax
g
Ax
g
=
−
⋅
+
⋅
−
=
−
⋅
+
⋅
=
−
=
⋅
−
=
⋅
=
(13)
R
Ax
R
Bx
R
By
H
90 −
α
S
2
S
3
h
1
h
2
h
1
M
g1
x
1
x
2
-
+
M
g2