Prawo Hardy’ego - Weinberga

dr in

ż

. Dariusz Kaczmarczyk

Prawo Hardy’ego - Weinberga

Godfrey Harold Hardy (matematyk, Anglia)

Wilhelm Weinberg (fizjolog , Niemcy)

Obydwaj panowie pracuj

ą

c niezale

ż

nie od siebie

sformułowali w roku 1908 tez

ę

głosz

ą

ca

ż

e:

aa

Aa

AA

2pq

H

q

2

p

2

f

a

= q

f

A

= p

Godfrey Harold Hardy

Wilhelm Weinberg

Je

ż

eli w danym locus genowym wyst

ę

puj

ą

dwa allele

(A i a) i je

ż

eli frekwencj

ę

wyst

ę

powania allelu

dominuj

ą

cego (A) oznaczymy jako p, a recesywnego

(a) jako q, to cz

ę

sto

ść

wyst

ę

powania

poszczególnych genotypów w populacji b

ę

dzie

nast

ę

puj

ą

ca:

Zale

ż

no

ść

ta nazywana jest Prawem Hardy’ego - Weinberga

p

2

+2pq+q

2

gdzie:

p- frekwencja cz

ęś

ciej wyst

ę

puj

ą

cego allelu

q- frekwencja rzadziej wyst

ę

puj

ą

cego allelu

Model Hardy’ego-Weinberga

Zało

ż

enia modelu Hardy’ego-Weinberga:

1. liczebno

ść

populacji jest wielka i stała w kolejnych pokoleniach,

2. kojarzenie osobników jest losowe,
3. organizmy s

ą

diploidalne,

4. pokolenia nie zaz

ę

biaj

ą

si

ę

,

5. rozród odbywa si

ę

drog

ą

płciow

ą

,

6. wpływ mutacji i selekcji jest niewielki i mo

ż

na go zaniedba

ć

.

Przebadano populacj

ę

pewnego gatunku

motyla i wykryto ze składa si

ę

ona z

osobników o nast

ę

puj

ą

cych fenotypach i

genotypach

BB - 226 osobników
Bb - 43 osobniki
bb - 1 osobnik
N – 270 osobników

BB

Bb

Bb

bb

N

N

N

p

Bb

BB

2

)

*

2

(

+

=

N

N

N

q

Bb

bb

2

)

*

2

(

+

=

08

,

0

270

*

2

43

)

1

*

2

(

92

,

0

270

*

2

43

)

226

*

2

(

≈

+

=

≈

+

=

q

p

Obliczanie frekwencji alleli

gdzie:
B – p
b - q
p+p=1
N

BB

– liczba osobników

o genotypie BB
N

Bb

– liczba osobników

o genotypie BB
N

bb

– liczba osobników

o genotypie BB

cz

ę

sto

ść

allelu a

c

z

ę

s

to

ś

ć

g

e

n

o

ty

p

u

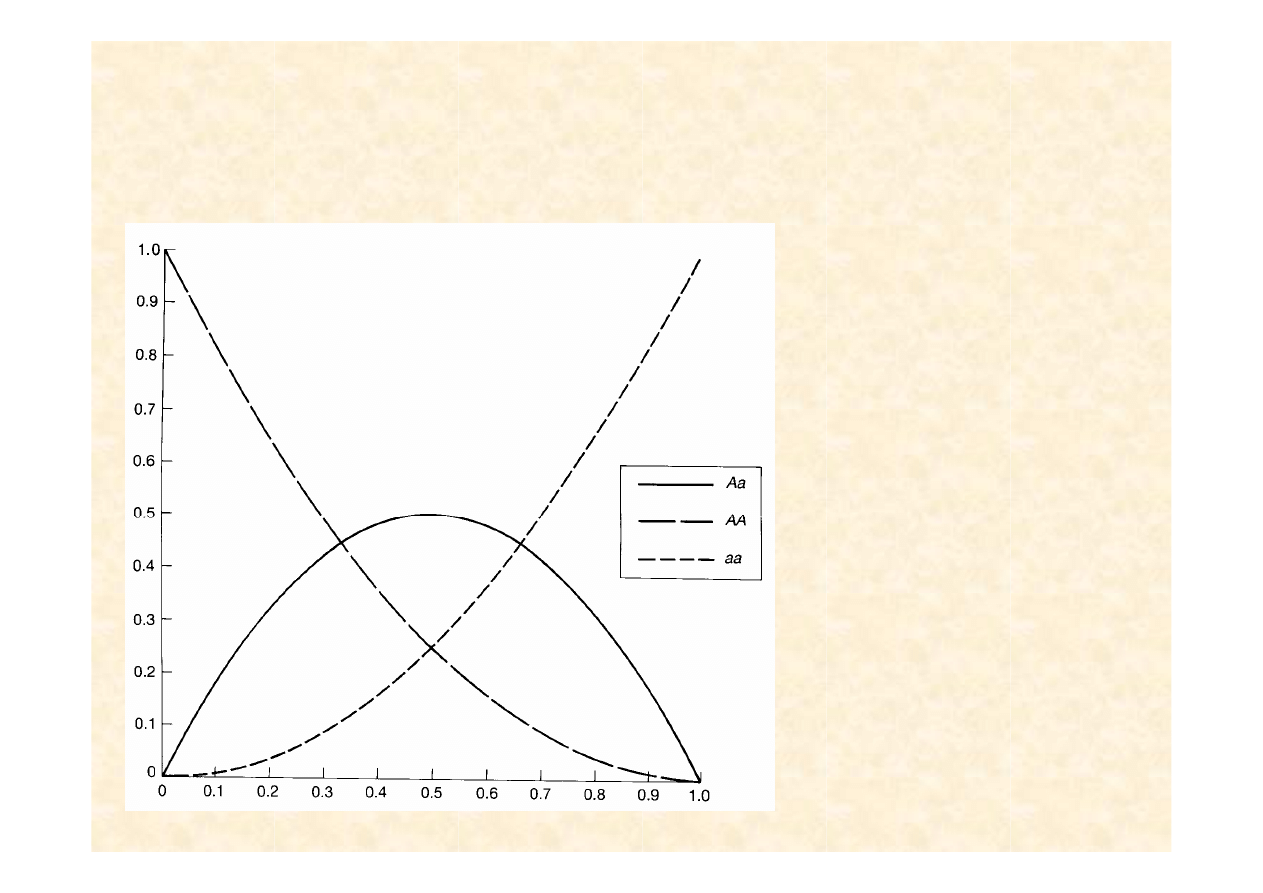
Frekwencja genotypów wynikaj

ą

ca z prawa Hardy’ego i Weinberga

Wnioski:

Gdy allel rzadki, prawie

wyłącznie związany jest w

heterozygotach (które

zazwyczaj nie różnią się

fenotypowo od homozygot

dominujących)

Eliminacja rzadkich alleli

recesywnych jest nieskuteczna

Plan Hitlera eliminacji chorób

genetycznych (zazwyczaj

warunkowanych przez

recesywne układy

homozygotyczne) był zatem nie

tylko zbrodniczy lecz i

nonsensowny

Nawet po eliminacji homozygot

recesywne allele są

dziedziczone za pośrednictwem

układów heterozygotycznych;

nie oddawajmy więc władzy

szaleńcom

Dlaczego tak trudno jest zmieni

ć

frekwencj

ę

alleli

recesywnych, gdy prowadzimy selekcj

ę

na podstawie cech

fenotypowych i nie mo

ż

emy odró

ż

ni

ć

homozygot

dominuj

ą

cych od heterozygot?

)

(

1

0

0

Nq

q

q

n

+

=

Do szacowania skuteczno

ś

ci prób zmiany frekwencji allelu recesywnego na drodze

selekcji stosuje si

ę

nast

ę

puj

ą

cy wzór:

Ocena skuteczno

ś

ci prób wyeliminowania allelu recesywnego ze stada

gdzie:
q

0

- pocz

ą

tkowa frekwencja allelu recesywnego

q

n

– docelowa frekwencja recesywnego allelu po n

pokoleniach
N – liczba pokole

ń

Warto

ść

N informuje nas o liczbie pokole

ń

potrzebnych do osi

ą

gni

ę

cia zamierzonego celu

hodowlanego obliczamy korzystaj

ą

c ze wzoru:

n

n

f

q

f

q

=

=

0

0

0

1

1

q

q

N

n

−

=

gdzie:
f

0

– pocz

ą

tkowa frekwencja osobników b

ę

d

ą

cych

homozygotamu recesywnymi
f

n

– docelowa frekwencja osobników b

ę

d

ą

cych

homozygotamu recesywnymi

Warto

ś

ci q

0

i q

n

obliczamy korzystaj

ą

c ze wzoru:

W stadzie suma kanałowego jest 9% ryb albinotycznych, hodowca chce zredukowa

ć

liczb

ę

albinosów do 0,01% stada, czyli uzyska

ć

stado w którym odsetek sumików

normalnie ubarwionych wynosi 99,99%. Przez ile pokole

ń

suma kanałowego (N)

b

ę

dzie musiał prowadzi

ć

selekcj

ę

aby osi

ą

gn

ąć

zamierzony cel? Ile lat mu to zajmie

wiedz

ą

c ze sum kanałowy dojrzewa płciowo w wieku dwóch lat?

Ocena skuteczno

ś

ci prób eliminacji allelu recesywnego ze stada - Zadanie przykładowe

W pierwszej kolejno

ś

ci obliczamy warto

ś

ci q

0

i q

n

a nast

ę

pnie uzyskane warto

ś

ci

podstawiamy do wzoru na N

01

,

0

0001

,

0

3

,

0

09

,

0

0

0

0

=

=

=

=

=

=

n

n

n

q

f

q

q

f

q

97

67

,

96

3

,

0

1

01

,

0

1

1

1

0

≈

=

−

=

−

=

N

N

q

q

N

n

Odpowied

ź

– hodowca b

ę

dzie musiał prowadzi

ć

selekcj

ę

przez 97 pokole

ń

suma

kanałowego, czyli 194 lata!

Testowanie czy populacja pozostaje w równowadze H-W

Je

ś

li analizujemy populacj

ę

w której mo

ż

emy obliczy

ć

liczb

ę

osobników o

poszczególnych genotypach to jeste

ś

my w stanie okre

ś

li

ć

czy

pozostaje ona w równowadze H-W

(szczegółowy opis ka

ż

dego etapu oblicze

ń

znajduje si

ę

w przewodniku do

ć

wicze

ń

)

Testowanie czy populacja pozostaje w równowadze H-W-

metodyka rozwi

ą

zania zada

ń

1. Obliczenie liczby osobników o ka

ż

dym z analizowanych

genotypów a nast

ę

pnie obliczenie zaobserwowanej frekwencji

genotypów.

2. Okre

ś

lenie frekwencji alleli, wykorzystuj

ą

c zaobserwowane

frekwencje genotypów.

3. Kalkulacja oczekiwanej frekwencji genotypów .
Warno

ś

ci frekwencji alleli nale

ż

y podstawi

ć

do równania H-W a

nast

ę

pnie pomno

ż

y

ć

przez liczebno

ść

stada/populacji,

4. Oznaczenie warto

ść

x

2

wstawiaj

ą

c do wzoru obserwowane i

oczekiwane ilo

ś

ci osobników o danym genotypie. Obliczenia te

prowadzi si

ę

dla jednego stopnia swobody (2 allele).

Obliczanie obserwowanej frekwencji genotypów i frekwencji alleli

Analizuj

ą

c zmienno

ść

genetyczn

ą

w locus koduj

ą

cym białko hemoglobiny

stwierdzono nast

ę

puj

ą

c

ą

liczb

ę

osobników o poszczególnych

genotypach:

AA - 46/100 = 0,46

Aa – 50/100 = 0,50

aa – 4/100 = 0,04

p = 0,71

q=0,29

Frekwencja alleli

Obserwowana frekwencja
genotypów

Obserwowana liczba
genotypów

genotyp

q = 0,29

p = 0,71

0,04

0,50

0,46

4

50

46

aa

Aa

AA

Genotypy

8

42

50

Oczekiwane liczebno

ś

ci genotypów

q

2

2pq

p

2

Frekwencje genotypów zgodne z
prawem H-W

BB

Bb

bb

p = 0,71

q = 0,29

Frekwencja alleli

8

100

*

29

,

0

42

100

*

29

,

0

*

71

,

0

*

2

50

100

*

71

,

0

1

29

,

0

29

,

0

*

71

,

0

*

2

71

,

0

1

2

2

2

2

2

2

2

≈

=

≈

=

≈

=

=

+

+

=

+

+

bb

Bb

BB

F

F

F

q

pq

p

Oczekiwana frekwencja genotypów jest ilorazem frekwencji genotypów
wynikaj

ą

cej z równania HW i liczebno

ś

ci populacji

Obliczanie oczekiwanej frekwencji genotypów

Warto

ść x

2

:

(Obs - Exp)

2

χ

2

=

Σ -------------------

Exp

Interpretacja:

Je

żeli uzyskana wartość testu x

2

( przy stopniu swobody 1), jest wi

ększa od

tabelarycznej. Hipotez

ę, że populacja pozostaje w równowadze H-W należy

odrzuci

ć.

Testowanie istotno

ś

ci odst

ę

pstw od równowagi H-W

H

o

Populacja jest w w stanie równowagi HW

H

1

populacja nie jest w stanie równowagi HW

gdzie:
Obs – obserwowana frekwencja genotypów
Exp – oczekiwana frekwencja genotypów

Zadanie przykładowe

W składzie tarłowym składaj

ą

cym si

ę

z 100 ryb stwierdzono:

50 ryb o normalnym ubarwieniu (genotyp AA)

40 ryb o ubarwieniu palomino (genotyp Aa)

10 ryb

ż

ółtych (genotyp aa)

Obliczono

ż

e w tym stadzie zgodnie z równowag

ą

H-W frekwencja

poszczególnych genotypów powinna wynosi

ć

Genotyp

n osobników

AA

49

Aa

42

aa

9

Oblicz istotno

ść

odst

ę

pstw od równowagi H-W

Testowanie istotno

ś

ci odst

ę

pstw od równowagi H-W

Obliczanie warto

ś

ci statystyki x

2

Testowanie istotno

ś

ci odst

ę

pstw od równowagi H-W

22

,

0

9

)

9

10

(

42

)

42

40

(

49

)

49

50

(

)

(

2

2

2

2

2

2

2

=

−

+

−

+

−

=

−

=

∑

χ

χ

χ

Exp

Exp

Obs

Obliczanie liczby stopni swobody

Dysponujemy trzema klasami danych (frekwencje trzech genotypów), oraz jednym

badanym parametrem zatem:

Liczba stopni swobody = 3 – 1 - 1 = 1

Liczba stopni swobody jest równa liczbie klas danych pomniejszonych o liczb

ę

badanych parametrów i pomniejszon

ą

o jedno

ść

Warto

ść

krytyczna statystyki x2 odczytanej z tabel dla jednego stopnia swobody i

prawdopodobie

ń

stwie 0,05 = 3,84

Wniosek:

Nie ma podstaw do odrzucenia hipotezy

ż

e ta populacja jest w stanie równowagi H-W