dysleksja

MFA-R1A1P-062

EGZAMIN MATURALNY

Z FIZYKI I ASTRONOMII

Arkusz II

POZIOM ROZSZERZONY

Czas pracy 120 minut

Instrukcja dla zdającego
1. Sprawdź, czy arkusz egzaminacyjny zawiera 11 stron (zadania

22 –26). Ewentualny brak zgłoś przewodniczącemu zespołu
nadzorującego egzamin.

2. Rozwiązania i odpowiedzi zapisz w miejscu na to

przeznaczonym przy każdym zadaniu.

3. W rozwiązaniach zadań rachunkowych przedstaw tok

rozumowania prowadzący do ostatecznego wyniku oraz
pamiętaj o jednostkach.

4. Pisz czytelnie. Używaj długopisu/pióra tylko z czarnym

tuszem/atramentem.

5. Nie używaj korektora, a błędne zapisy wyraźnie przekreśl.
6. Pamiętaj, że zapisy w brudnopisie nie podlegają ocenie.
7. Podczas egzaminu możesz korzystać z karty wybranych

wzorów i stałych fizycznych, linijki oraz kalkulatora.

8. Wypełnij tę część karty odpowiedzi, którą koduje zdający.

Nie wpisuj żadnych znaków w części przeznaczonej
dla egzaminatora.

9. Na karcie odpowiedzi wpisz swoją datę urodzenia i PESEL.

Zamaluj

pola odpowiadające cyfrom numeru PESEL.

Błędne zaznaczenie otocz kółkiem

i zaznacz właściwe.

Życzymy powodzenia!

ARKUSZ II

MAJ

ROK 2006

Za rozwiązanie

wszystkich zadań

można otrzymać

łącznie

50 punktów

Wypełnia zdający przed

rozpoczęciem pracy

PESEL ZDAJĄCEGO

KOD

ZDAJĄCEGO

Miejsce

na naklejkę

z kodem szkoły

2

Egzamin maturalny z fizyki i astronomii

Arkusz

II

Zadanie 22. Wahadło balistyczne (10 pkt)

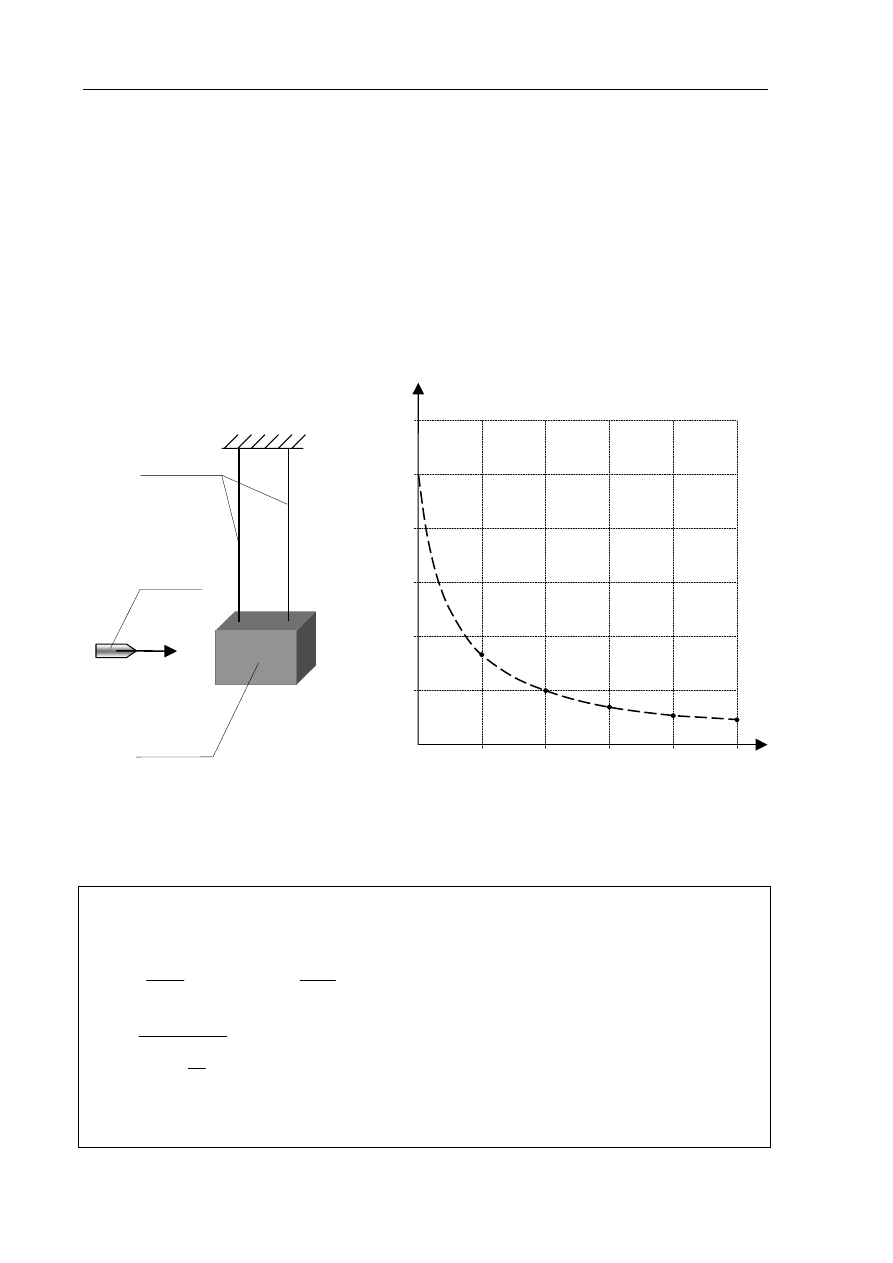
Na rysunku poniżej przedstawiono schematycznie urządzenie do pomiaru wartości prędkości
pocisków wystrzeliwanych z broni palnej. Podstawowym elementem takiego urządzenia jest
tzw. wahadło balistyczne będące (w dużym uproszczeniu) zawieszonym na linkach klockiem,
w którym grzęzną wystrzeliwane pociski. Po trafieniu pociskiem wahadło wychyla się
z położenia równowagi i możliwy jest pomiar jego energii kinetycznej.
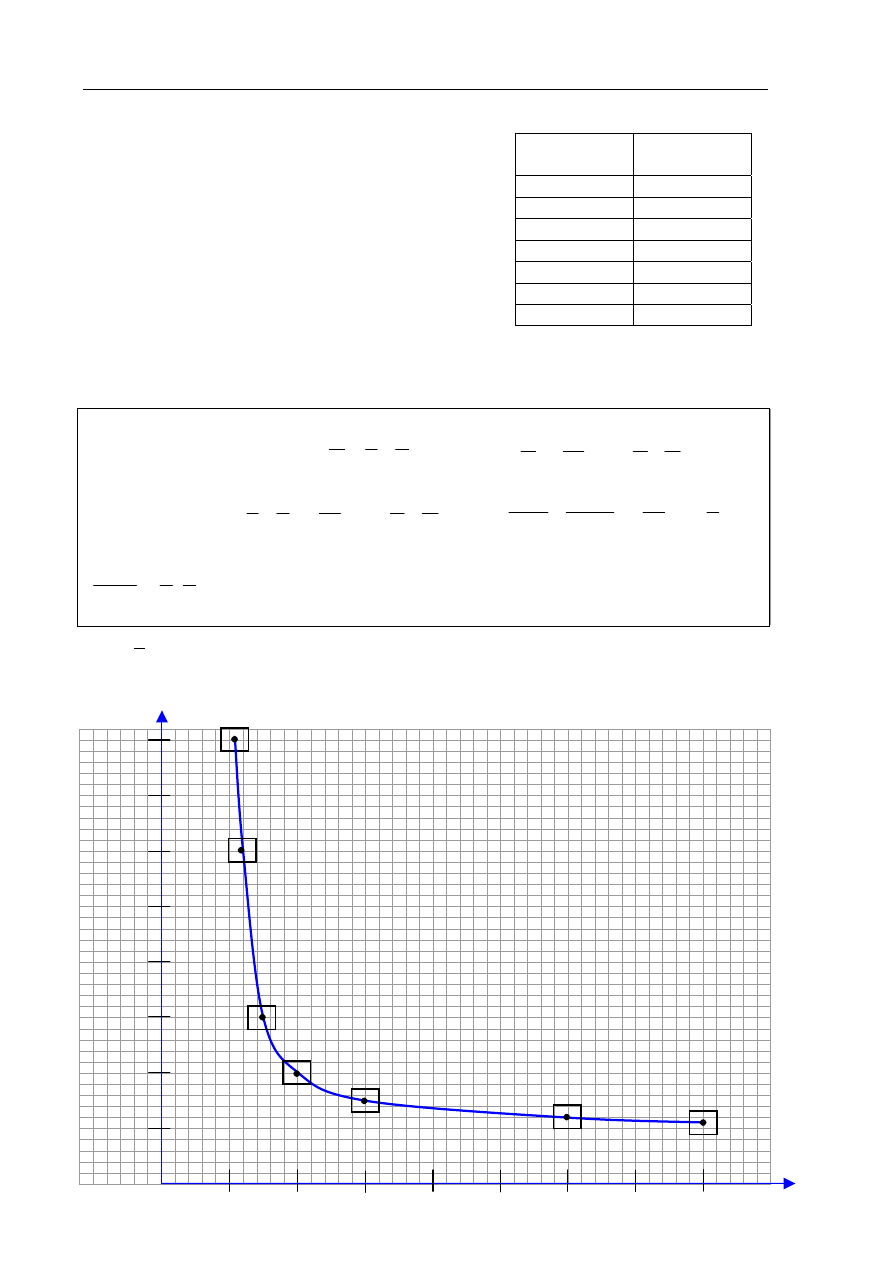
Punkty na wykresie przedstawiają zależność energii kinetycznej klocka wahadła
z pociskiem (który w nim ugrzązł) tuż po uderzeniu pocisku, od masy klocka. Pomiary
wykonano dla 5 klocków o różnych masach (linia przerywana przedstawia zależność
teoretyczną). Wartość prędkości pocisku, tuż przed trafieniem w klocek wahadła, za każdym
razem wynosiła 500 m/s, a odległość od środka masy klocka wahadła do punktu zawieszenia
wynosiła 1 m. W obliczeniach pomiń masę linek mocujących klocek wahadła.

22.1 (3 pkt)

Wykaż, analizując wykres, że masa pocisku jest równa 0,008 kg.

linki

wahadło

pocisk

v

G

200

800

400

600

1000

1200

10

0 2 4 6 8

0

masa wahadła wyrażona jako wielokrotność

masy pocisku

energia kinetyczna wahad

ła z pociskiem

E, J

Analizując wykres można zauważyć, że dla masy klocka równej

0

, energia

kinetyczna wahadła z pociskiem jest równa

1000 J

.

kg

m

s

m

J

m

E

m

m

E

k

k

008

,

0

500

1000

2

2

2

2

2

2

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

=

=

⇒

=

v

v

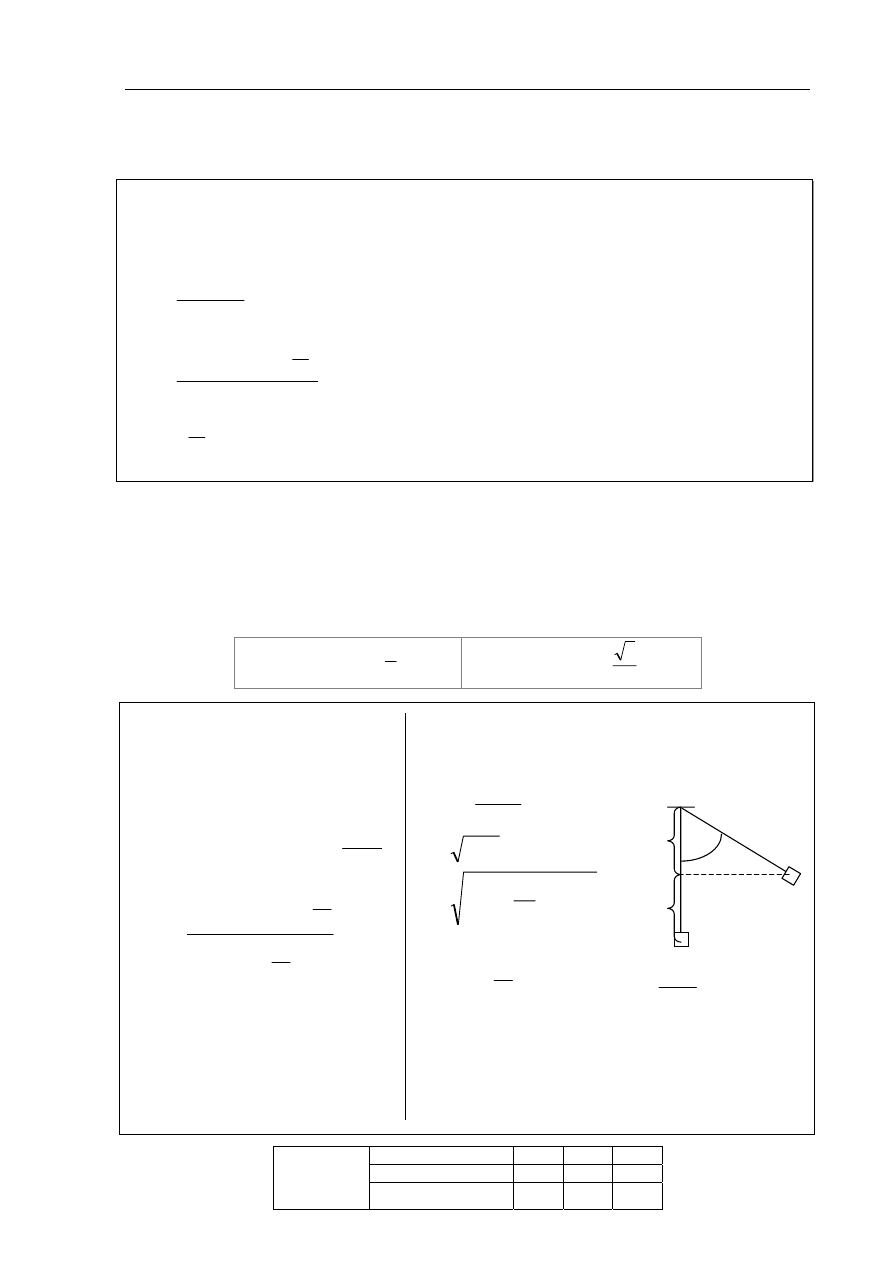
Egzamin maturalny z fizyki i astronomii

3

Arkusz

II

22.2 (3 pkt)

Oblicz wartość prędkości klocka z pociskiem bezpośrednio po zderzeniu w sytuacji, gdy masa
klocka była 499 razy większa od masy pocisku.

22.3 (4 pkt)

Oblicz, jaka powinna być masa klocka wahadła, aby po wychyleniu z położenia równowagi
wahadła o 60

o

, zwolnieniu go, a następnie trafieniu pociskiem w chwili przechodzenia

wahadła przez położenie równowagi, wahadło zatrzymało się w miejscu. Do obliczeń
przyjmij, że masa pocisku wynosi 0,008 kg. W obliczeniach możesz skorzystać z podanych
poniżej wartości funkcji trygonometrycznych.

sin 30

° = cos 60° =

2

1

= 0,50 sin 60° = cos 30° =

2

3

≈ 0,87

Nr zadania

22.1

22.2

22.3

Maks. liczba pkt

3

3

4

Wypełnia

egzaminator!

Uzyskana liczba pkt

Korzystając z zasady
zachowania pędu można zapisać

(

)

(

)

s

m

kg

s

m

kg

m

m

m

m

m

m

k

k

p

k

p

p

k

k

p

k

p

p

1

008

,

0

1

499

500

008

,

0

=

⋅

+

⋅

=

+

=

+

=

v

v

v

v

v

v

Aby wahadło zatrzymało się
w miejscu wartości pędów
pocisku i klocka muszą być
równe.

k

p

p

k

k

k

p

p

m

m

m

m

v

v

v

v

=

⇒

=

kg

m

s

m

s

m

kg

m

k

k

27

,

1

16

,

3

500

008

,

0

≈

⋅

=

gdzie:

v

p

–

wartość prędkości pocisku,

v

k

– wartość prędkości klocka,

m

p

– masa pocisku,

m

k

– masa klocka.

Korzystając z zasady zachowania energii

2

2

k

v

m

mgh

=

, zatem

gh

k

2

=

v

m

s

m

k

5

,

0

10

2

2

⋅

⋅

=

v

s

m

k

16

,

3

≈

v

l-h

h

60˚

m

h

m

h

l

h

l

h

l

5

,

0

)

5

,

0

1

(

1

)

60

cos

1

(

60

cos

=

−

=

°

−

=

°

=

−

4

Egzamin maturalny z fizyki i astronomii

Arkusz

II

Zadanie 23. Ogrzewacz wody (10 pkt)

Turystyczny ogrzewacz wody zasilany jest z akumulatora samochodowego. Element grzejny
wykonano na bocznej powierzchni szklanego naczynia mającego kształt walca. Element
grzejny tworzy kilka zwojów przewodzącego materiału w postaci paska o szerokości 4 mm
i grubości 0,1 mm. Całkowita długość elementu grzejnego wynosi 0,628 m. Opór elektryczny
elementu grzejnego jest równy 0,60 Ω. Siła elektromotoryczna akumulatora wynosi 12,6 V,
a jego opór wewnętrzny jest równy 0,03 Ω.

23.1 (3 pkt)

Oblicz moc elementu grzejnego wykorzystywanego w ogrzewaczu w sytuacji opisanej
w treści zadania.

23.2 (2 pkt)

Wykaż, że opór właściwy elementu grzejnego ma wartość około 3,8·10

-7

Ω·m.

UI

P

=

, oraz

IR

U

=

, zatem

R

I

P

2

=

w

z

R

R

I

+

=

ε

Ω

⋅

=

6

,

0

)

20

(

2

A

P

Ω

+

Ω

=

03

,

0

6

,

0

6

,

12 V

I

W

P 240

=

A

I 20

=

S

l

R

ρ

=

, gdzie

b

a

S

⋅

=

a = 4 mm

,

b = 0,1 mm

.

m

m

m

m

l

b

a

R

l

S

R

⋅

Ω

⋅

=

⋅

⋅

Ω

=

=

=

−7

10

82

,

3

628

,

0

0001

,

0

004

,

0

6

,

0

ρ

ρ

ρ

ρ

Egzamin maturalny z fizyki i astronomii

5

Arkusz

II

23.3 (3 pkt)

Oszacuj, ile razy wydłuży się czas potrzebny do zagotowania wody, jeżeli napięcie na
zaciskach elementu grzejnego zmaleje o 20%. Załóż, że opór elektryczny elementu grzejnego
jest stały, a straty ciepła w obu sytuacjach są pomijalne.

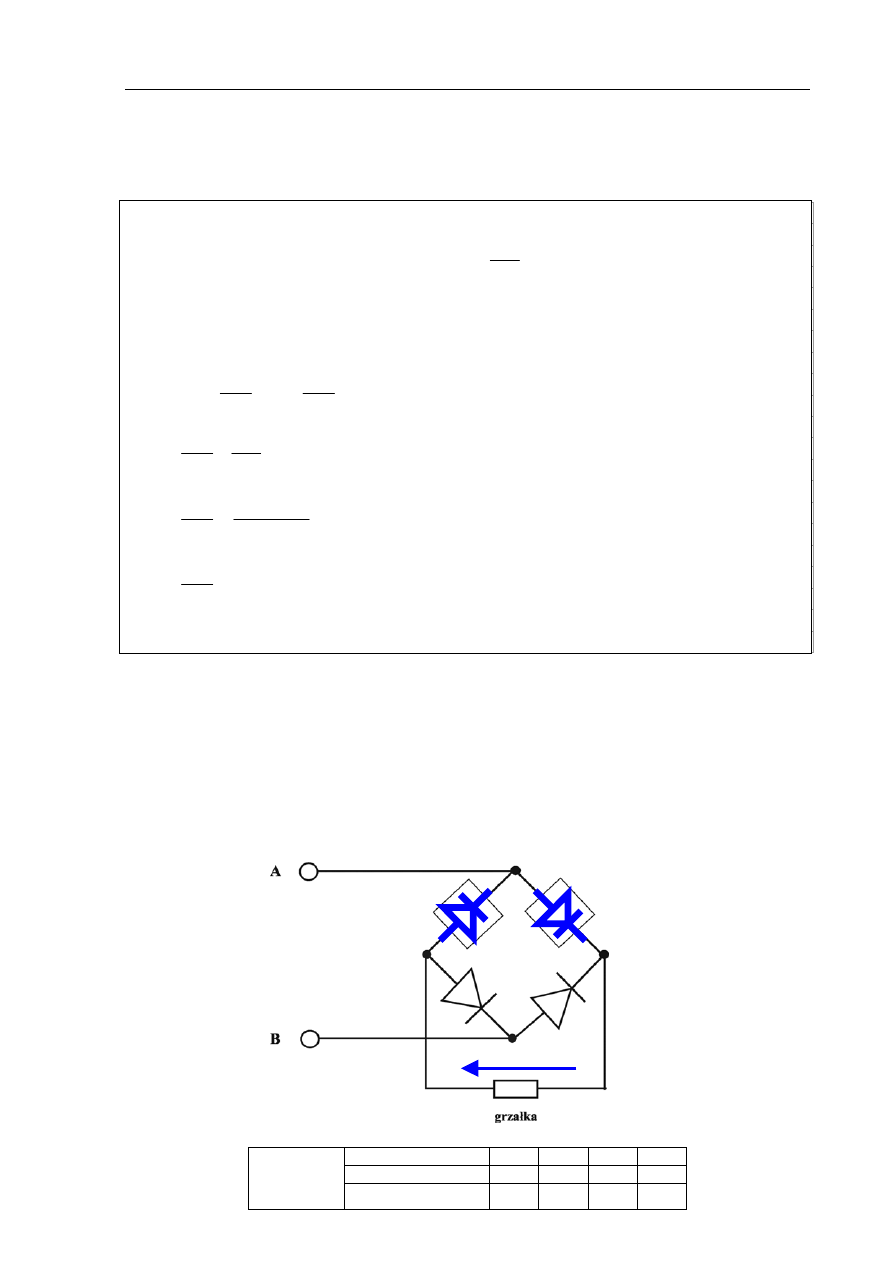
23.4 (2 pkt)

Ogrzewacz może być zasilany ze źródła prądu przemiennego poprzez układ prostowniczy.
Do zacisków A i B układu doprowadzono z transformatora napięcie przemienne. Narysuj na
schemacie, w miejscach zaznaczonych prostokątami, brakujące elementy półprzewodnikowe
tak, aby przez grzałkę płynął prąd wyprostowany dwupołówkowo*). Oznacz na schemacie za
pomocą strzałki kierunek przepływu prądu przez grzałkę.

*) wyprostowany dwupołówkowo – prąd płynie przez grzałkę w obu półokresach

Nr

zadania

23.1 23.2 23.3 23.4

Maks. liczba pkt

3

2

3

2

Wypełnia

egzaminator!

Uzyskana liczba pkt

t

UI

W

Δ

=

i

IR

U

=

, zatem

t

R

U

W

Δ

=

2

Wykonana praca jest w obu wypadkach taka sama, zatem

2

2

2

1

2

1

t

R

U

t

R

U

W

Δ

=

Δ

=

, skąd

(

)

56

,

1

8

,

0

1

2

2

1

2

1

1

2

2

2

2

1

1

2

≈

Δ

Δ

=

Δ

Δ

=

Δ

Δ

t

t

U

U

t

t

U

U

t

t

I

, ponieważ

1

2

8

,

0 U

U

=

6

Egzamin maturalny z fizyki i astronomii

Arkusz

II

Zadanie 24. Soczewka (10 pkt)

W pracowni szkolnej za pomocą cienkiej szklanej
soczewki dwuwypukłej o jednakowych promieniach
krzywizny, zamontowanej na ławie optycznej,
uzyskiwano obrazy świecącego przedmiotu. Tabela
zawiera wyniki pomiarów odległości od soczewki
przedmiotu x i ekranu y, na którym uzyskiwano ostre
obrazy przedmiotu. Bezwzględne współczynniki
załamania powietrza oraz szkła wynoszą odpowiednio
1 i 1,5.

24.1 (3 pkt)

Oblicz promień krzywizny soczewki wiedząc, że jeśli przedmiot był w odległości 0,3 m od
soczewki to obraz rzeczywisty powstał w odległości 0,15 m od soczewki.

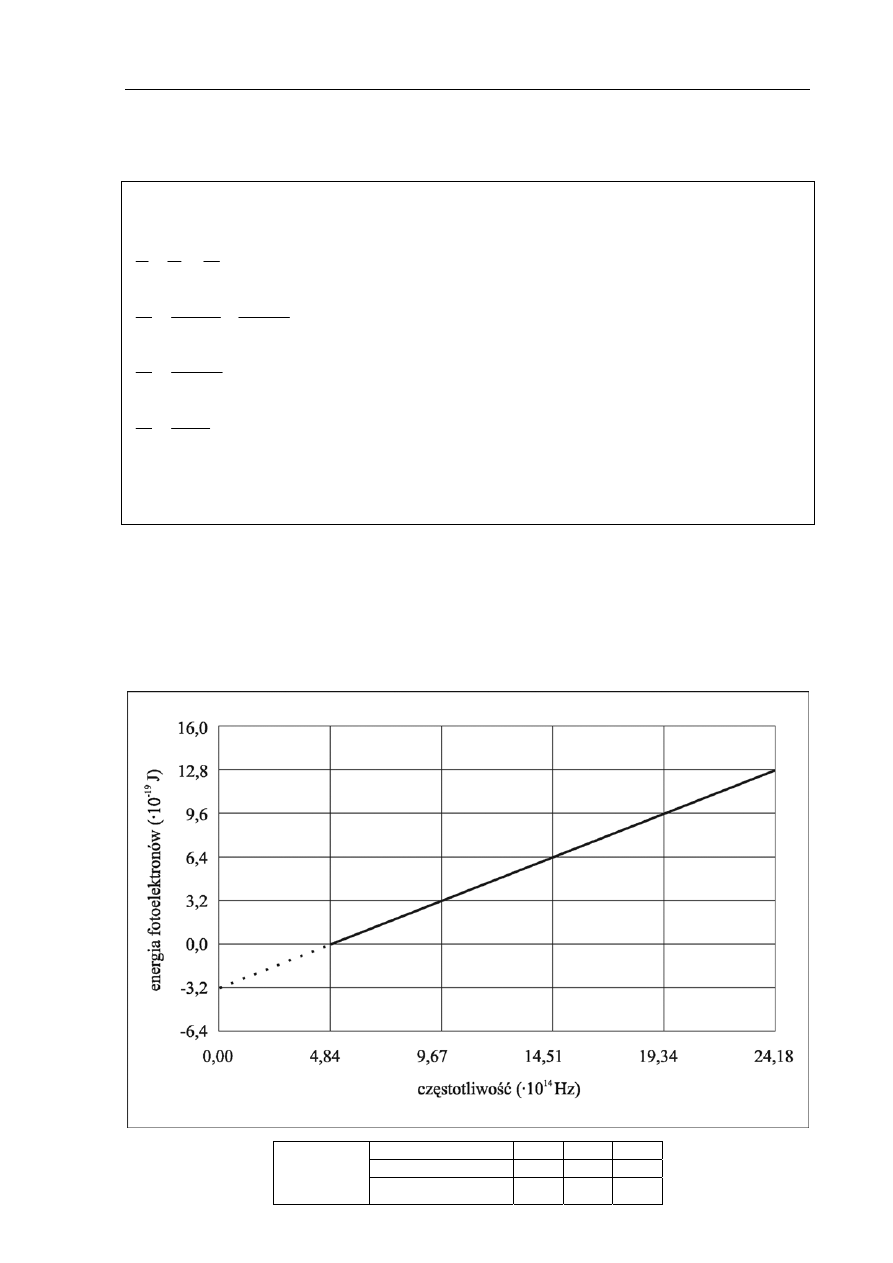
24.2 (4 pkt)

Naszkicuj wykres zależności y(x). Zaznacz niepewności pomiarowe. Wykorzystaj dane
zawarte w tabeli.

x

(m)

∆x

= ± 0,02 m

y

(m)

∆y

= ± 0,02 m

0,11 0,80
0,12 0,60
0,15 0,30
0,20 0,20
0,30 0,15
0,60 0,12
0,80 0,11

Korzystając z zależności

y

1

x

1

f

1

+

=

,

oraz

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

⋅

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

−

=

2

1

p

s

r

1

r

1

1

n

n

f

1

,

można

zapisać

=

+

y

1

x

1

⇒

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

⋅

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

−

2

1

1

1

1

r

r

n

n

p

s

r

m

m

2

1

1

5

,

1

15

,

0

1

3

,

0

1

⋅

⎟

⎠

⎞

⎜

⎝

⎛

−

=

+

m

r

r

m

1

,

0

2

2

1

3

,

0

3

=

⇒

⋅

=

0,6

0,7

0,8

0,2

0,1

0,8

0,7

0,6

0,5

0,4

0,3

0,2

0,1

0,3

0,4

0,5

y, m

x, m

0, 0

Egzamin maturalny z fizyki i astronomii

7

Arkusz

II

24.3 (3 pkt)

Gdy wartość x rośnie, y dąży do pewnej wartości, która jest wielkością charakterystyczną dla
soczewki. Podaj nazwę tej wielkości fizycznej oraz oblicz jej wartość.

Zadanie 25. Fotoefekt (10 pkt)

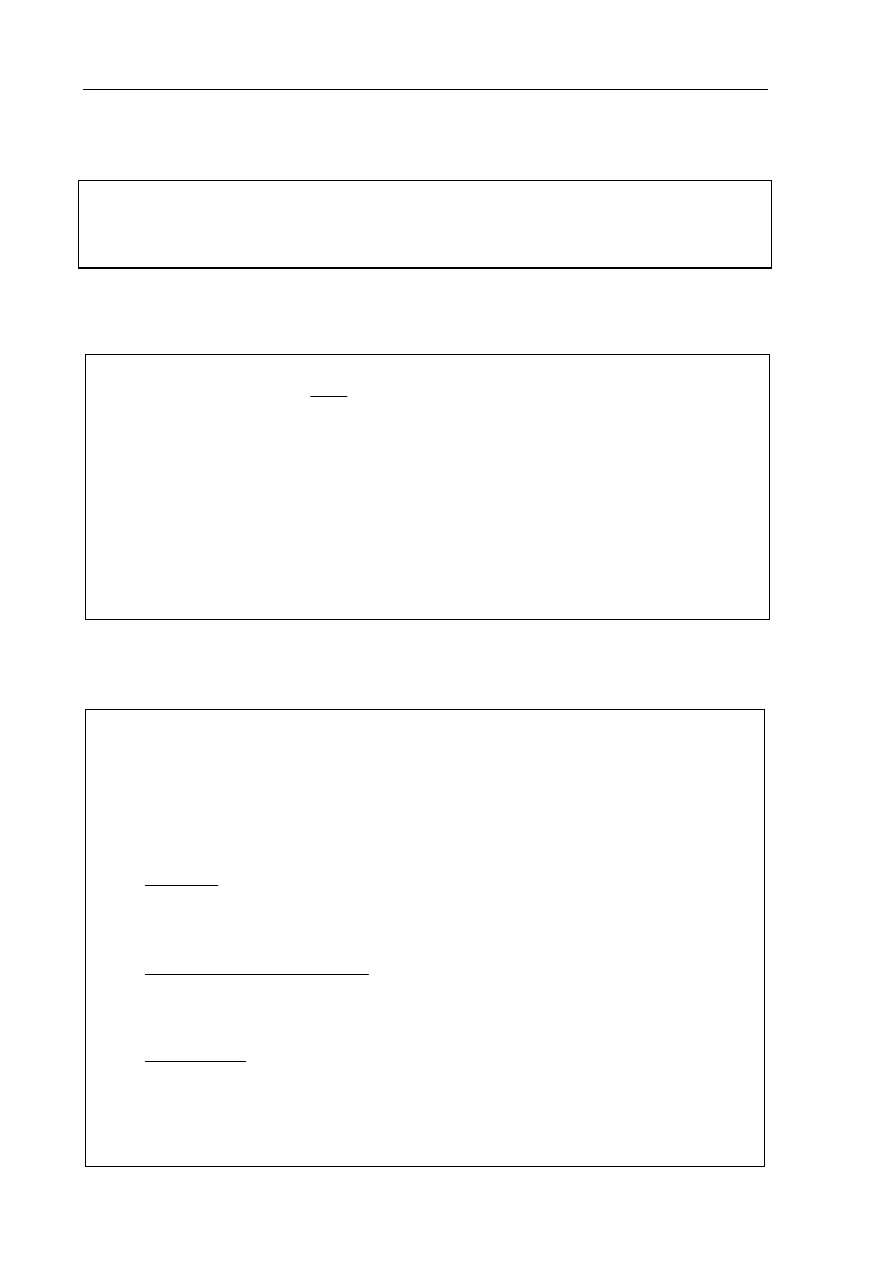
W pracowni fizycznej wykonano doświadczenie mające na celu badanie zjawiska
fotoelektrycznego i doświadczalne wyznaczenie wartości stałej Plancka. W oparciu o wyniki
pomiarów sporządzono poniższy wykres. Przedstawiono na nim zależność maksymalnej
energii kinetycznej uwalnianych elektronów od częstotliwości światła padającego na
fotokomórkę.

Nr zadania

24.1

24.2

24.3

Maks. liczba pkt

3

4

3

Wypełnia

egzaminator!

Uzyskana liczba pkt

Gdy x rośnie y dąży do wartości, która jest ogniskową soczewki.

f

1

y

1

x

1

=

+

m

f

m

f

m

f

m

m

f

1

,

0

1

,

0

1

1

30

,

0

3

1

30

,

0

1

15

,

0

1

1

=

=

=

+

=

8

Egzamin maturalny z fizyki i astronomii

Arkusz

II

25.1 (1 pkt)

Odczytaj z wykresu i zapisz wartość częstotliwości granicznej promieniowania dla tej
fotokatody.

25.2 (2 pkt)

Oblicz, korzystając z wykresu, pracę wyjścia elektronów z fotokatody. Wynik podaj
w elektronowoltach.

25.3 (3 pkt)

Oblicz doświadczalną wartość stałej Plancka, wykorzystując tylko dane odczytane z wykresu
oraz zależność

k

E

W

h

+

=

⋅

ν

.

Wartość częstotliwości granicznej promieniowania jest równa

4,84·10

14

Hz

.

max

2

2 ⎟

⎟

⎠

⎞

⎜⎜

⎝

⎛

+

=

⋅

v

m

W

h

ν

Dla energii kinetycznej fotoelektronów równej

0,

ν

⋅

= h

W

,

zatem

odczytując

z

wykresu

wartość

ν = 4,84·10

14

Hz,

otrzymamy

eV

W

J

W

Hz

s

J

W

2

10

21

,

3

10

84

,

4

10

63

,

6

19

14

34

≈

⋅

=

⋅

⋅

⋅

⋅

=

−

−

Po odjęciu stronami układu równań

⎩

⎨

⎧

+

=

+

=

2

2

1

1

k

k

E

W

h

E

W

h

ν

ν

,

otrzymamy

(

)

s

J

h

Hz

J

h

Hz

Hz

J

J

h

E

E

h

E

E

h

k

k

k

k

⋅

⋅

≈

⋅

⋅

=

⋅

−

⋅

⋅

−

⋅

=

−

−

=

−

=

−

−

−

−

−

34

14

19

14

14

19

19

2

1

2

1

2

1

2

1

10

62

,

6

10

67

,

9

10

4

,

6

10

67

,

9

10

34

,

19

10

2

,

3

10

6

,

9

ν

ν

ν

ν

Egzamin maturalny z fizyki i astronomii

9

Arkusz

II

25.4 (4 pkt)

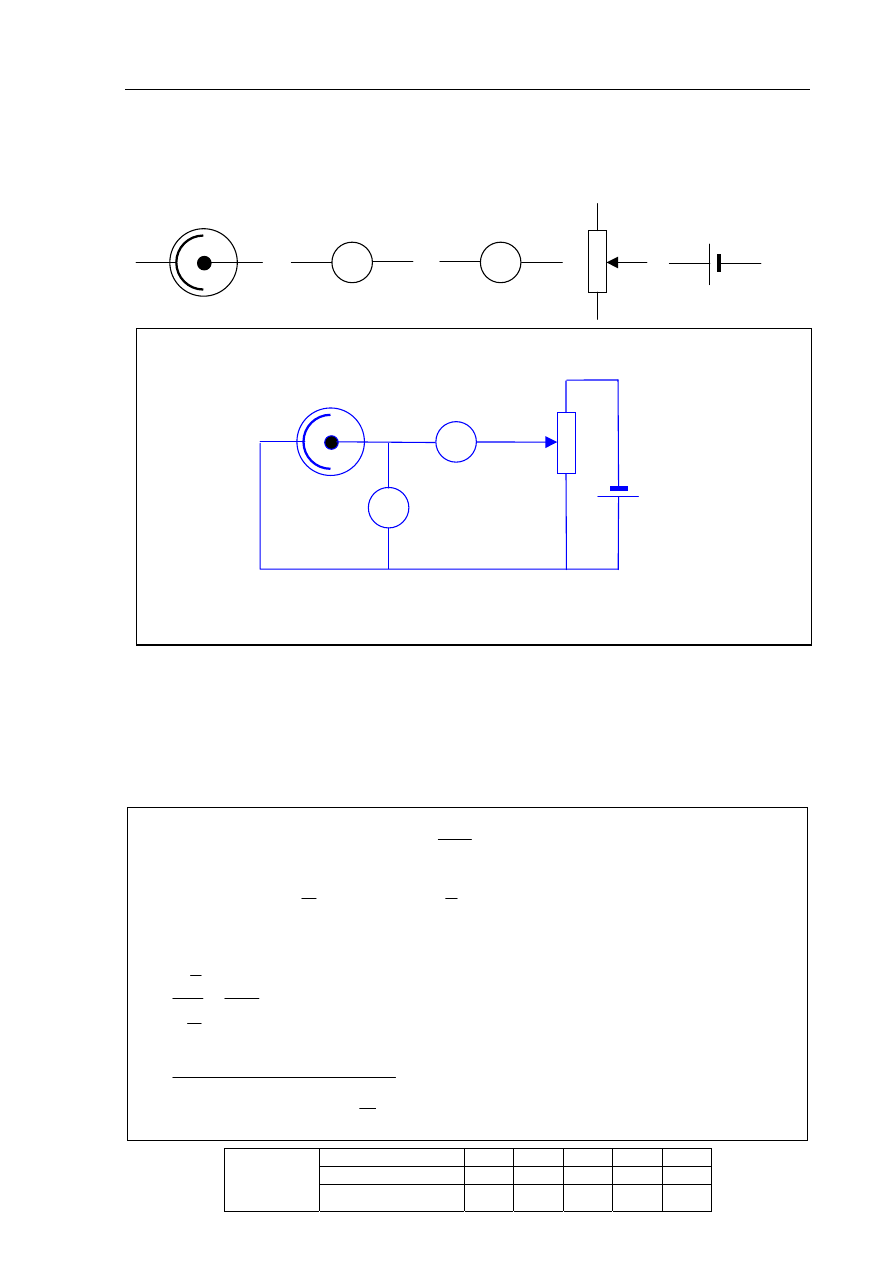
Narysuj schemat układu elektrycznego pozwalającego wyznaczyć doświadczalnie wartość
napięcia hamowania fotoelektronów. Masz do dyspozycji elementy przedstawione poniżej
oraz przewody połączeniowe.

Zadanie 26. Laser (10 pkt)

Laser o mocy 0,1 W emituje w próżni monochromatyczną wiązkę światła o długości fali
633 nm i kołowym przekroju.

26.1 (5 pkt)

Oszacuj liczbę fotonów zawartych w elemencie wiązki światła o długości jednego metra.

Nr

zadania

25.1 25.2 25.3 25.4 26.1

Maks. liczba pkt

1

2

3

4

5

Wypełnia

egzaminator!

Uzyskana liczba pkt

V

μA

+

–

R

A

K

V

μA

+

–

R

A

K

f

nE

W

=

i

t

P

W

Δ

=

,

stąd

f

E

t

P

n

Δ

=

.

Ponieważ

λ

c

h

E

f

=

,

oraz

c

s

t

=

Δ

,

zatem

9

2

8

34

9

2

10

06

,

1

10

3

10

63

,

6

10

633

1

1

,

0

⋅

≈

⎟

⎠

⎞

⎜

⎝

⎛ ⋅

⋅

⋅

⋅

⋅

⋅

⋅

=

=

=

−

−

s

m

s

J

m

m

W

n

hc

Ps

c

h

c

s

P

n

λ

λ

gdzie: s – długość wiązki

światła

c – prędkość

światła

10

Egzamin maturalny z fizyki i astronomii

Arkusz

II

26.2 (3 pkt)

Oblicz wartość siły, jaką wywierałaby ta wiązka światła laserowego padająca w próżni
prostopadle na wypolerowaną metalową płytkę. Do obliczeń przyjmij, że w ciągu jednej
sekundy na powierzchnię płytki pada 10

17

fotonów. Załóż, że płytka odbija w całości padające

na nią promieniowanie.

26.3 (2 pkt)

Oblicz najwyższy rząd widma, jaki można zaobserwować po skierowaniu tej wiązki
prostopadle na siatkę dyfrakcyjną posiadającą 400 rys/mm.

Nr zadania

26.2

26.3

Maks. liczba pkt

3

2

Wypełnia

egzaminator!

Uzyskana liczba pkt

t

a

Δ

Δ

= v

i

m

F

a

=

, zatem

t

p

t

m

F

Δ

Δ

=

Δ

Δ

=

v

.

Ponieważ

f

np

p 2

=

Δ

, gdzie

n

– liczba fotonów, a

p

f

– wartość

pędu

fotonu

λ

h

p

f

=

,

zatem

t

nh

F

Δ

=

λ

2

s

m

s

J

F

1

10

633

10

63

,

6

10

2

9

34

17

⋅

⋅

⋅

⋅

⋅

⋅

=

−

−

N

F

10

10

2

−

⋅

≈

α

λ

sin

d

n

=

Najwyższy rząd widma uzyskamy dla kąta

°

→ 90

α

, czyli

1

sin

→

α

.

d

n

=

λ

λ

d

n

=

95

,

3

10

633

10

400

1

9

3

≈

⋅

⋅

=

−

−

n

m

m

n

Najwyższy rząd widma jaki można zaobserwować w opisanej sytuacji jest
równy 3.

Egzamin maturalny z fizyki i astronomii

11

Arkusz

II

BRUDNOPIS