Politechnika Wrocławska

Wrocław, 06.06.2013r.

Wydział Budownictwa Lądowego i Wodnego

Budownictwo Ogólne

Projekt

Wykonał:

Przemysław Różycki

Nr indeksu: 186216

Projekt Budownictwo Ogólne II

2

Wydział Budownictwa Wodnego i Lądowego

Dane wyjściowe:

Dane do projektowania:

Konstrukcja dachu:

jętkowa

Maksymalny rozstaw krokwi:

1,0 m

Nachylenie połaci dachowej:

Pokrycie dachu:

dachówka ceramiczna zakładkowa o

szerokości pokrycia (rozstawie łat) 0,35 m

Izolacja:

folia paraizolacyjna, wełna mineralna

Lokalizacja budynku:

Głogów

Obciążenie śniegiem (tablica NB.1):

strefa 1

Obciążenie wiatrem I strefa (tablica NB.1):

strefa 1

Więźba będzie wykonana z drewna sosnowego klasy wytrzymałości C22. W tabeli
przedstawiono najważniejsze właściwości tej klasy drewna.

Tabela 1.1 Właściwości charakterystyczne drewna sosnowego klasy C22 wg [8], tab.1

Właściwości wytrzymałościowe [N/mm

2

=MPa]

zginanie

22

rozciąganie wzdłuż włókien

13

rozciąganie w poprzek włókien

0,5

ściskanie wzdłuż włókien

20

ściskanie w poprzek włókien

2,4

ścinanie

2,4

Właściwości sprężyste [ kN/mm

2

]

średni moduł sprężystości wzdłuż włókien

10

5% kwanty modułu sprężystości wzdłuż
włókien

6,7

średni moduł sprężystości w poprzek
włókien

0,33

średni moduł odkształcenia postaciowego

0,63

Gęstość [ kg/m

3

]

gęstość charakterystyczna

340

średnia gęstość

410

Projekt Budownictwo Ogólne II

3

Wydział Budownictwa Wodnego i Lądowego

Obciążenie zmienne -śnieg

Obciążenie zmienne wywołane opadami śniegu wyznaczono w oparciu o PN-EN 1991-1-3 .
Głogów należy do 1 strefy obciążenia śniegiem gruntu (rys. NB. 1). Dla powyższego terenu,
według tablicy NB.1, wartość charakterystyczna obciążenia śniegiem gruntu wynosi:

s

k

=0,7 kN/m

2

o

Wartość charakterystyczna obciążenia śniegiem

Wartość charakterystyczną obciążenia śniegiem dachu wyznaczono ze wzoru 5.1,

gdzie:

-współczynnik kształtu dachu

- współczynnik ekspozycji

– współczynnik termiczny

- wartość charakterystyczna obciążenia śniegiem gruntu

Współczynnik ekspozycji

Przyjęto, iż obliczenia dotyczą terenu normalnego, gdzie nie występuje znaczne przenoszenie
śniegu przez wiatr, co wg tablicy 5.1odpowiada współczynnikowi ekspozycji C

e

=1,0.

Współczynnik termiczny

Dach nie ma podwyższonego współczynnika przenikania ciepła, dlatego współczynnik
termiczny C

t

=1,0.

Współczynnik kształtu dachu

Wyznaczenie współczynnika kształtu dachu przeprowadzono dla dachu dwupołaciowego w
oparciu o rysunek 5.3 oraz tablicę 5.2 normy [12].

Przypadki obciążenia śniegiem:

a) obciążenie równomiernie rozłożone

Wartość charakterystyczna obciążenia śniegiem dachu :

=0,4

Wartość obliczeniowa obciążenia śniegiem dachu :

Projekt Budownictwo Ogólne II

4

Wydział Budownictwa Wodnego i Lądowego

=0,28

b) Obciążenie nierównomiernie rozłożone

Wartość charakterystyczna obciążenia śniegiem dachu

:

=0,4

=0,5

0,4

Wartość obliczeniowa obciążenia śniegiem dachu :

=0,28

=0,5

0,28

Obciążenia zmienne -oddziaływanie wiatru

Obciążenie zmienne wywołane oddziaływaniem wiatru wyznaczono w oparciu o PN-EN 1991-
1-4. Miejsce lokalizacji budynku należy do 1 strefy obciążenia wiatrem (rys. NB. 1). Założono
wysokość bezwzględną projektowanego obiektu jako średnią wysokość bezwzględną Głogowa,
czyli 86 m n.p.m. Dla powyższego terenu określono wg tab. NB. 1

podstawowa wartość bazowej prędkości wiatru:

wartość bazowa ciśnienia prędkości wiatru:

Na podstawie tablicy 4.1określono kategorię terenu, na którym będzie wzniesiona budowla.
Jest to teren kategorii III. Tereny regularnie pokryte roślinnością lub budynkami albo o
pojedynczych przeszkodach, oddalonych od siebie najwyżej na odległość równą ich 20
wysokościom (takie jak wsie, tereny podmiejskie, stałe lasy).

Ciśnienie sumaryczne działające na dach jest różnicą algebraiczną ciśnień po dwóch stronach
przegrody. Dlatego należy wyznaczyć ciśnienie działające na stronę wewnętrzną konstrukcji, a
następnie odjąć je od ciśnienia po stronie zewnętrznej(wg pkt.5.2, ).

o

ciśnienie wiatru działające na powierzchnie zewnętrzne

Na podstawie [12] wartość obciążenia charakterystycznego wiatrem powierzchni zewnętrznych
konstrukcji wyznaczono ze wzoru 5.1[12]:

pe

e

p

e

c

z

q

w





)

(

gdzie

-wartość szczytowa ciśnienia prędkości

-współczynnik ciśnienia zewnętrznego

Projekt Budownictwo Ogólne II

5

Wydział Budownictwa Wodnego i Lądowego

-wysokość odniesienia dla ciśnienia zewnętrznego wg rozdziału 7

o

ciśnienie wiatru działające na powierzchnie wewnętrzne

Na podstawie] wartość obciążenia charakterystycznego wiatrem powierzchni wewnętrznych
konstrukcji wyznaczono ze wzoru:

pi

i

p

i

c

z

q

w





)

(

gdzie

-wartość szczytowa ciśnienia prędkości

-współczynnik ciśnienia wewnętrznego

-wysokość odniesienia dla ciśnienie wewnętrznego wg rozdziału 7

Wartości charakterystyczne obciążenia wiatrem dachu oraz współczynniki ciśnienia należy
wyznaczyć dla dwóch kierunków wiatru wg pkt. 7.2.5.

a) kierunek wiatru Θ=0°

1234

0

8050

Wiatr

Rys.3.1 wymiary budynku dla Θ=0°

Wymiary budynku:
b=12340mm d=8050mm h=7,475m

b) kierunek wiatru Θ=90°

Projekt Budownictwo Ogólne II

6

Wydział Budownictwa Wodnego i Lądowego

12340

8050

Wiatr

Rys.3.2 wymiary budynku dla Θ=90°

Wymiary budynku:
b=12340mm d=8050mm h=7,475m

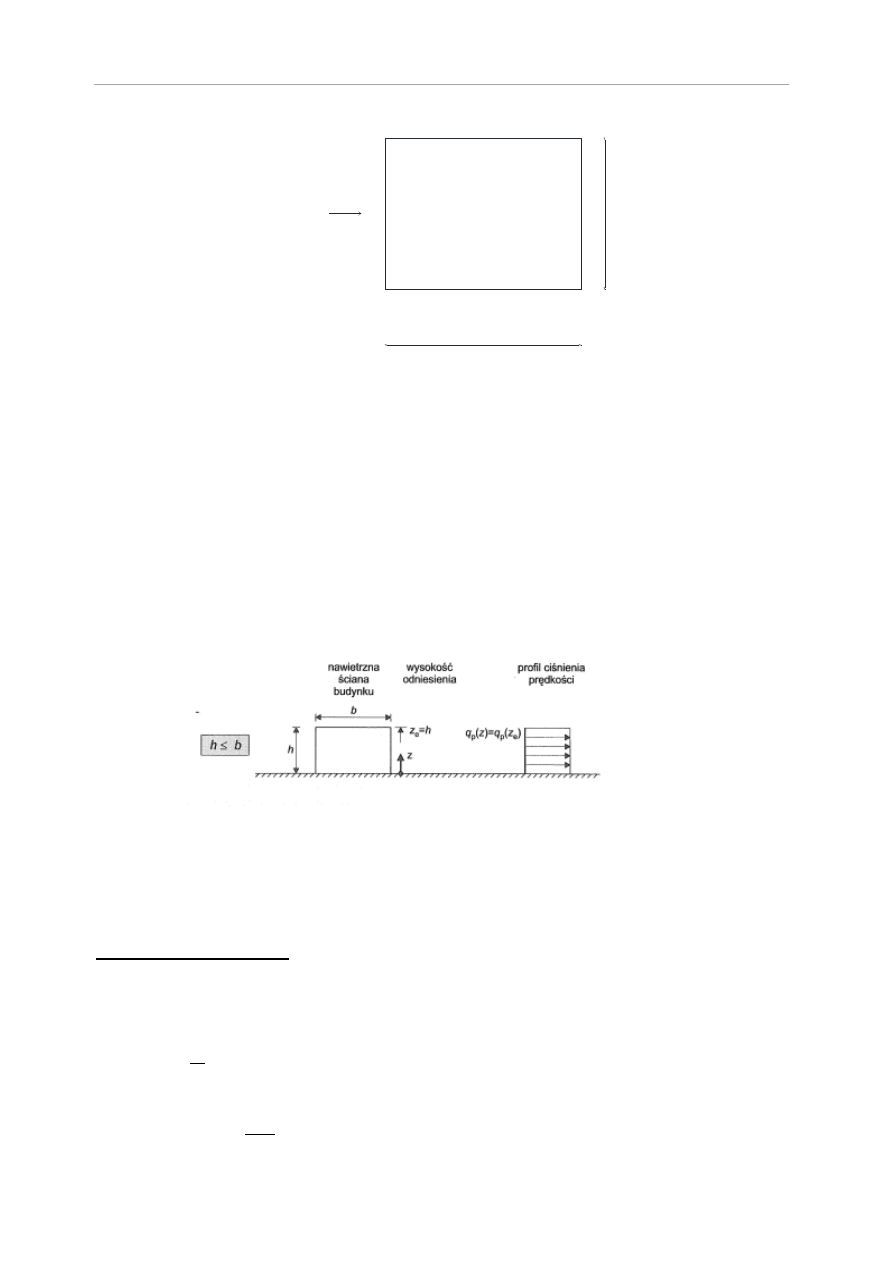
Określenie wysokości odniesienia przeprowadzono zgodnie z rozdziałem siódmym [12].

Rys.3.3 Wysokości odniesienia, z

e

, zależne od h i b oraz odpowiadające im rozkłady ciśnienia

prędkości

Dla obu sytuacji h<b, więc zgodnie z rysunkiem 3.3:

, z

e

=h=7,475m

Współczynnik ekspozycji

Na podstawie tablicy NB.3 dla terenu kategorii III odczytano wzór na obliczenie
współczynnika ekspozycji:

gdzie: z –wysokość odniesienia dla budynku wg rozdziału 7

=1,762

Projekt Budownictwo Ogólne II

7

Wydział Budownictwa Wodnego i Lądowego

Wartość szczytowa ciśnienia prędkości

Wartość szczytową ciśnienia prędkości określono wg wzoru 4.8

gdzie:

=

=0,3 kN/m

2

(wg NB.1, [12])

=1,762

Tak jak wspomniano wcześniej rozpatrujemy dwie sytuacje obliczeniowe.
Podział dachu na pola obliczeniowe przeprowadzono wg rys. 7.8

1) kierunek wiatru Θ=0°

e=min{b;2h}=min{12,34; 14,95}=12,34m
e/10=12,34/10=1,23m, e/4=12,34/4=3,09m

12340

8050

Wiatr

H

G

F

F

J

I

Rys. 3.4 Sytuacja obliczeniowa 1, Θ=0°

Wartości współczynników ciśnienia zewnętrznego dla kąta nachylenia połaci

wyznaczono wg tablicy 7.4a, i przedstawiono w tabeli 3.1.

Projekt Budownictwo Ogólne II

8

Wydział Budownictwa Wodnego i Lądowego

Tab.3.1 Wartości współczynników ciśnienia zewnętrznego dla dachu dwuspadowego o kącie

nachylenia połaci

Według Uwagi 1, tab.7.4a, należy rozważyć cztery przypadki, w których najmniejsze lub
największe wartości w polach F, G, H są w kombinacji z najmniejszymi lub największymi
wartościami w polach I, J. Zestawienie poszczególnych przypadków zamieszczono w tabeli.

Tab.3.2 Zestawienie przypadków współczynników c

pe,10

dla

Θ=0°

wartość

pole dla kierunku wiatru Θ=0°

przypadki

c

pe,10

F

G

H

I

J

0,0

0,0

0,0

-0,2

-0,3

0,0

0,0

0,0

0,0

0,0

0,7

0,7

0,6

-0,2

-0,3

0,7

0,7

0,6

0,0

0,0

Po podstawieniu do wzoru (5.4) współczynników ciśnienia zewnętrznego z powyższej tabeli
otrzymano następujące wartości ciśnienia zewnętrznego:

Tab.3.3 Zestawienie wartości ciśnienia wiatru działającego na powierzchnie zewnętrzne dla

Θ=0°

wartość

pole dla

kierunku wiatru Θ=0°

w

e

F

G

H

I

J

0,0

0,0

0,0

-0,106

-0,159

0,0

0,0

0,0

0,0

0,0

0,371

0,371

0,318

-0,106

-0,159

0,371

0,371

0,318

0,0

0,0

Współczynniki ciśnienia wewnętrznego c

pi

przyjęto zgodnie z Uwagą 2 do punktu 7.2.9 [12]

jako jedną z dwóch wartości:

0,2 lub

-0,3

Wartości ciśnienia wiatru działającą na powierzchnie wewnętrzne wyznaczono ze wzoru (4.5) i
przedstawiono w tabeli.

Tab.3.4 Zestawienie wartości ciśnienia wiatru działającego na powierzchnie wewnętrzne

wartość

c

pi

=0,2

c

pi

=-0,3

w

i

0,106

-0,159

wartość

pole dla kierunku wiatru Θ=0°

c

pe,10

F

G

H

I

J

0,0

0,0

0,0

-0,2

-0,3

+0,7

+0,7

+0,6

+0,0

+0,0

Projekt Budownictwo Ogólne II

9

Wydział Budownictwa Wodnego i Lądowego

Wartości sumarycznego ciśnienia działającego na konstrukcje otrzymano jako różnicę ciśnienia
zewnętrznego i wewnętrznego wg pkt.5.2, [12]. Przedstawia je tabela 5.7.

Tab.3.5 Wartości ciśnienia sumarycznego działającego na dach dla

Θ=0°

wartość

pole dla kierunku wiatru Θ=0°

wartości charakterystyczne

w

net

(c

pi

=0,2)

F

G

H

I

J

-0,106

-0,106

-0,106

-0,212

-0,265

-0,106

-0,106

-0,106

-0,106

-0,106

0,265

0,265

0,212

-0,212

-0,265

0,265

0,265

0,212

-0,106

-0,106

w

net

(c

pi

=-0,3)

0,159

0,159

0,159

0,053

0,0

0,159

0,159

0,159

0,159

0,159

0,530

0,530

0,477

0,053

0,0

0,530

0,530

0,477

0,159

0,159

wartości obliczeniowe

w

net

(c

pi

=0,2)

F

G

H

I

J

-0,159

-0,159

-0,159

-0,318

-0,398

-0,159

-0,159

-0,159

-0,159

-0,159

0,398

0,398

0,318

-0,318

-0,398

0,398

0,398

0,318

-0,159

-0,159

w

net

(c

pi

=-0,3)

0,239

0,239

0,239

0,08

0,0

0,239

0,239

0,239

0,239

0,239

0,795

0,795

0,716

0,08

0,0

0,795

0,795

0,716

0,239

0,239

2) kierunek wiatru Θ=90°

e=min{b;2h}=min{8,05; 14,95}=8,05m
e/10=8,05m /10=0,81m, e/4=8,05m /4=2,01m, e/2=8,05m /2=4,03m

12340

8050

Wiatr

I

I

H

H

F

G

G

F

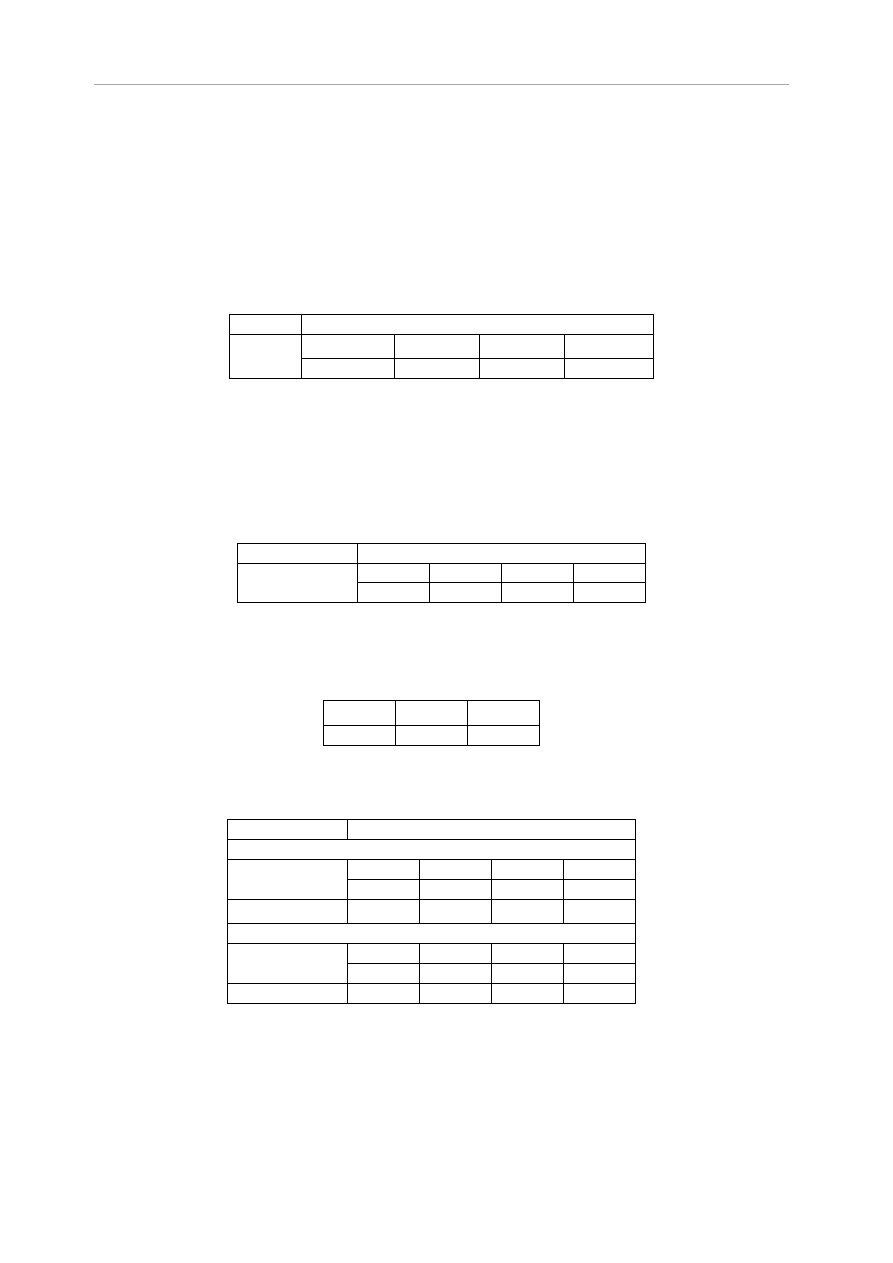
Projekt Budownictwo Ogólne II

10

Wydział Budownictwa Wodnego i Lądowego

Rys.3.5Sytuacja obliczeniowa 2, Θ=90°

Współczynniki ciśnienia zewnętrznego dla kierunku wiatru Θ=90° są podane w tablicy 7.4b,
[12]. Dla kąta nachylenia połaci

Tab.3.6 Wartości współczynników ciśnienia zewnętrznego dla dachu dwuspadowego o kącie

nachylenia połaci

,

Θ=90°

Tab.3.7 Zestawienie wartości ciśnienia wiatru działającego na powierzchnie zewnętrzne dla

Θ=90°

Współczynniki ciśnienia wewnętrznego wynoszą:

0,2 lub

-0,3

wartość

c

pi

=0,2

c

pi

=-0,3

w

i

0,106

-0,159

Tab.3.8 Wartości ciśnienia sumarycznego działającego na dach dla

Θ=90°

wartość

pole dla kierunku wiatru Θ=90°

wartości charakterystyczne

w

net

(c

pi

=0,2)

F

G

H

I

-0,689

-0,848

-0,583

-0,371

w

net

(c

pi

=-0,3)

-0,424

-0,583

-0,318

-0,106

wartości obliczeniowe

w

d

(c

pi

=0,2)

F

G

H

I

-1,034

-1,272

-0,875

-0,557

w

d

(c

pi

=-0,3)

-0,636

-0,875

-0,477

-0,159

obciążenie użytkowe

wartość

pole dla kierunku wiatru Θ=90°

c

pe,10

F

G

H

I

-1,1

-1,4

-0,9

-0,5

wartość

pole dla kierunku wiatru Θ=90°

w

e

F

G

H

I

-0,583

-0,742

-0,477

-0,265

Projekt Budownictwo Ogólne II

11

Wydział Budownictwa Wodnego i Lądowego

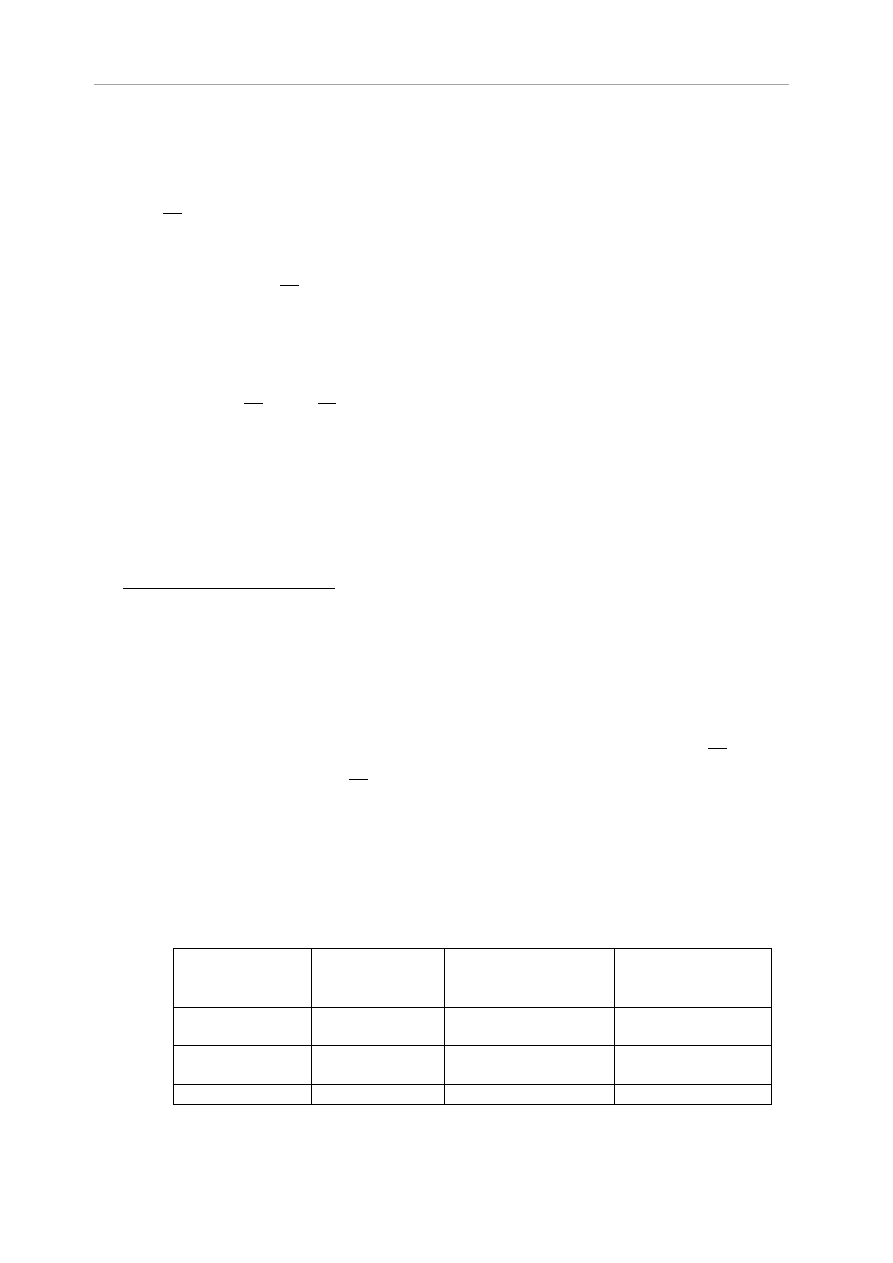
Projektowany dach będzie dostępny wyłącznie dla napraw i zwykłego utrzymania, dlatego wg
tab.6.9, [10] należy do kategorii H pod względem obciążonej powierzchni. Zalecane obciążenie
użytkowe dla tej kategorii jest podane w tablicy 6.10, [10] i wynosi:

0,4

,

Wartość obliczeniowa tego obciążenia wynosi:

=0,4

1,5=0,6

,

=1

1,5=1,5 kN

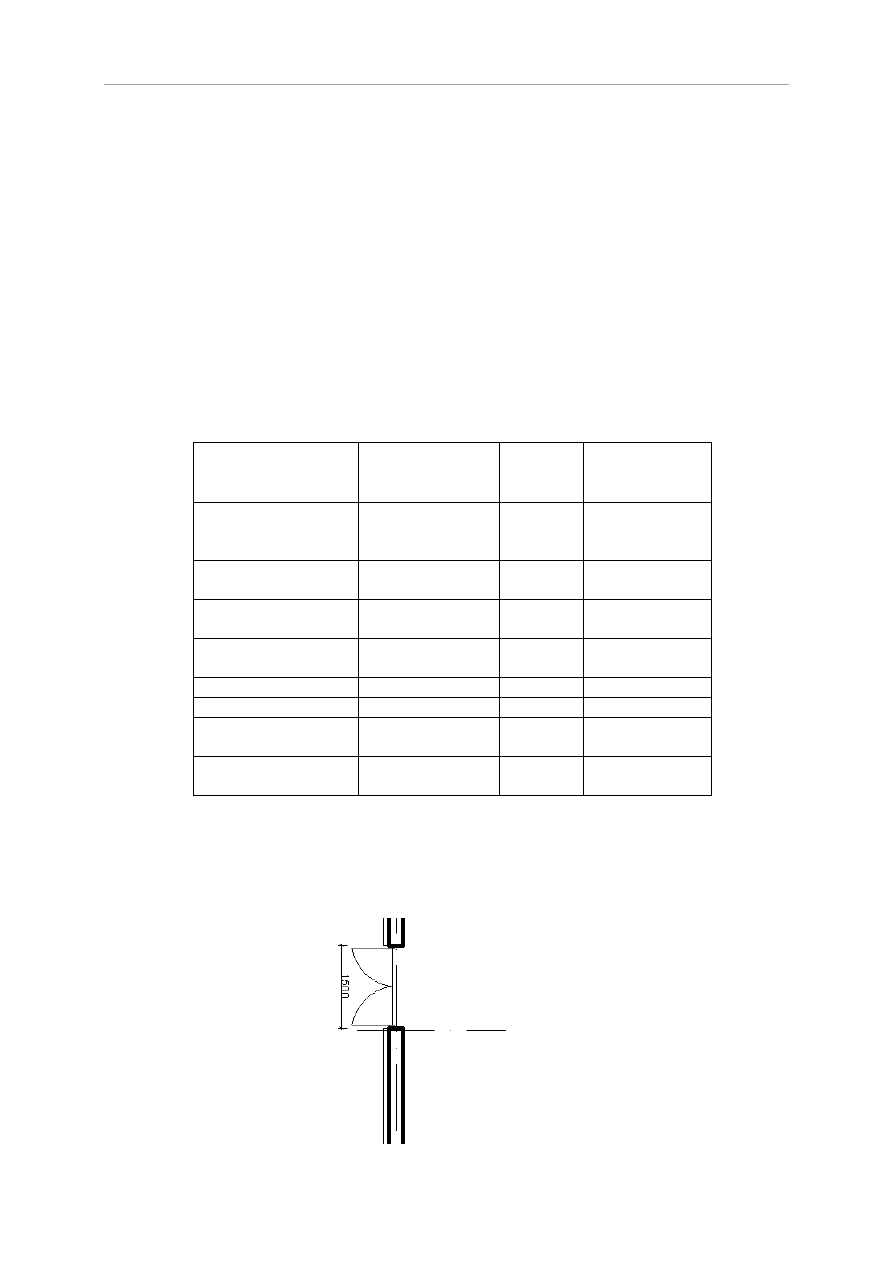
Obliczenie łaty

Przyjęto do projektowania łaty z drewna sosnowego 45x50 mm o polu przekroju poprzecznego
A=0,00225m

2

. Łata będzie wykonana z drewna klasy C22. Jego średnia gęstość wg tablicy 1,

[8] wynosi

.

Przyjęto długość przęseł równą maksymalnemu rozstawowi krokwi

.

Rozstaw łat wynosi 0,35m.

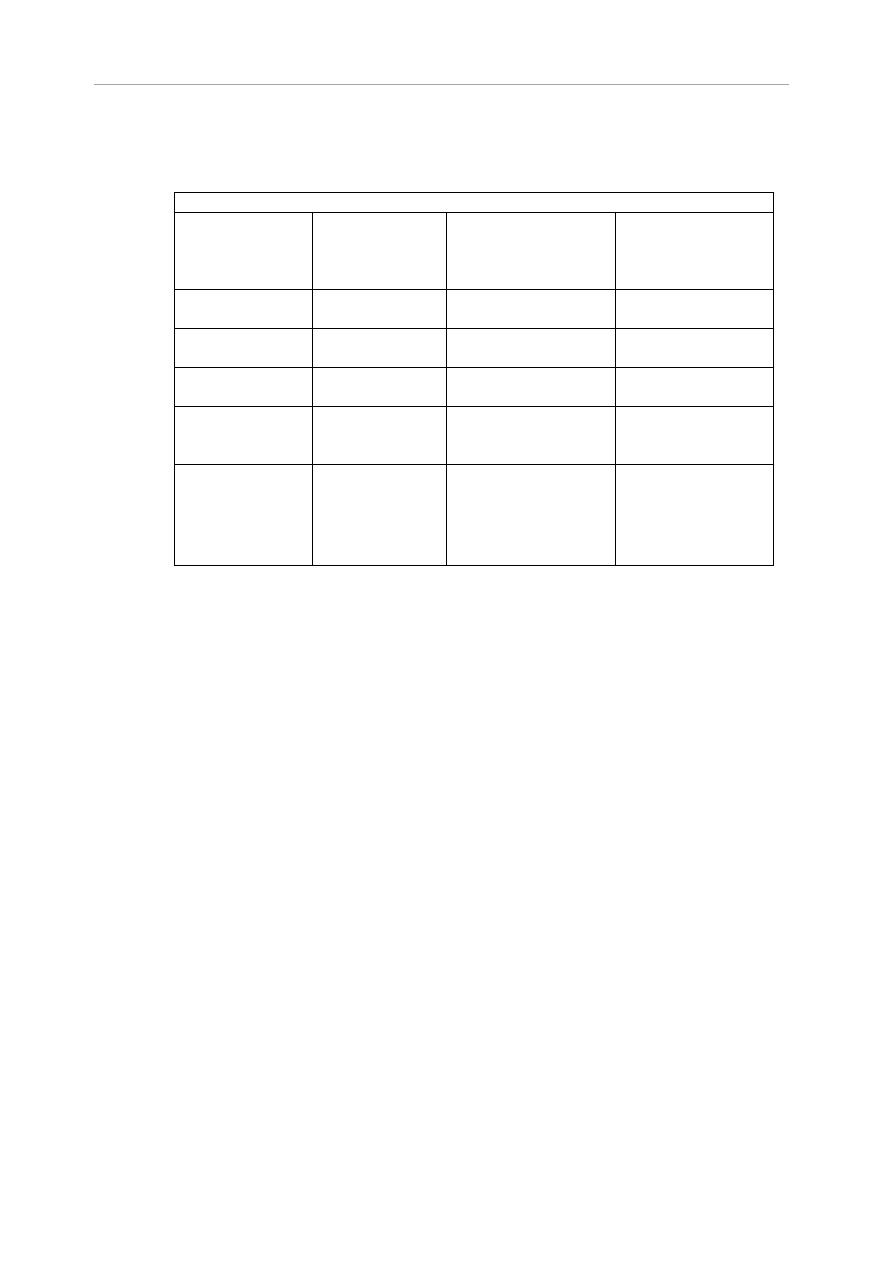
Zestawienie obciążeń

Łatę obliczono przy uwzględnieniu obciążenia prostopadłego i równoległego.

Składowe obciążeń wynoszą:

Według punktu 3.3.1, [10] w obliczeniach konstrukcji z powierzchniami, które są poddane
różnym kategoriom obciążenia, należy uwzględnić najbardziej niekorzystny przypadek. Punkt
3.3.2, [10] podaje, że nie należy obciążeń użytkowych od śniegu i wiatru działających na
dachach uwzględniać jako obciążeń przyłożonych równocześnie. Zgodnie z punktem 6.3.4.2,
[10] należy przeprowadzać oddzielne sprawdzanie dachów przy założeniu oddzielnie
działającego obciążenia użytkowego skupionego oraz równomiernie rozłożonego.
Dlatego do obliczeń przyjęto obciążenie charakterystyczne od śniegu

obciążenie od wiatru

.

Łatę obliczono przy uwzględnieniu dwóch wariantów obciążenia: wariant I- obciążenie od
ciężaru własnego, pokrycia, wiatru oraz siły skupionej, wariant II-obciążenie od ciężaru
własnego, pokrycia, śniegu oraz obciążenia użytkowego równomiernie rozłożonego.

Tab.6.1 Zestawienie obciążeń stałych g

obciążenie

wartość

charakterystyczna

współczynnik

obciążenia

wartość obliczeniowa

[kN/m]

γf

[kN/m]

ciężar własny łaty

0,00225*4,1

0,009

1,35

0,012

ciężar pokrycia

0,037*12*0,35

0,155

1,35

0,210

RAZEM

0,165

0,220

Projekt Budownictwo Ogólne II

12

Wydział Budownictwa Wodnego i Lądowego

Tab.6.2 Zestawienie obciążeń na łatę

ZESTAWIENIE OBCIĄZEŃ NA ŁATĘ

obciążenie

wartość

charakterystyczna

współczynnik

obciążenia

wartość obliczeniowa

[kN/m]

γ

f

[kN/m]

g-

ciężar własny i

pokrycia

0,165

1,35

0,222

S-

śnieg

0,35*0,28

0,098

1,50

0,147

q- wiatr

0,35*0,53

0,186

1,50

0,278

Q-

obciążenie

użytkowe skupione

[kN]

1,000

1,50

1,500

q-

obciążenie

użytkowe

równomiernie

rozłożone

0,4*0,35

0,140

1,50

0,210

W wariancie I obciążeniem zmiennym dominującym jest obciążenie użytkowe siłą skupioną,
więc dla obciążenia wiatrem należy zastosować współczynnik wartości kombinacyjnej
obciążeń

=0,6 (wg tab.A1.1, [9]).

W wariancie II obciążeniem zmiennym dominującym jest obciążenie śniegiem, dlatego dla
obciążenia użytkowego zastosowano współczynnik wartości kombinacyjnej obciążeń

=0,0

(wg tab. A1.1, [9]).

Zestawienie obciążeń na łatę po zastosowaniu współczynników wartości kombinacyjnej
obciążeń wraz z ich rozkładem na składowe prostopadłe i równoległe przedstawia tabela 4.13

- obciążenia stałe: G┴ = G · cos , G║ = G · sin

- obciążenie śniegiem: s┴ = s · cos 2 , s║ = s · sin · cos

- obciążenie wiatrem: w┴ = w = w, w║ = 0

- obciążanie użytkowe: Q┴ = Q · cos , Q║ = Q · sin

Projekt Budownictwo Ogólne II

13

Wydział Budownictwa Wodnego i Lądowego

, sin

Tab.6.3 Zestawienie obciążeń na łatę po zastosowaniu współczynników jednoczesności
obciążeń

obciążenie

wartość

charakteryst

yczna

współczynni

k obciążenia

wartość

obliczeniow

a

wartości składowe

prostopadłe obciążenia

wartości składowe równoległe

obciążenia

[kN/m]

γ

f

[kN/m]

charakterystycz

na [kN/m]

obliczenio
wa [kN/m]

charakterysty

czna [kN/m]

obliczeniowa

[kN/m]

g-

ciężar

własny i

pokrycia

0,165

1,35

0,222

0,126

0,170

0,106

0,143

S-

śnieg

0,35*0,28

0,098

1,50

0,147

0,069

0,104

0,069

0,104

q- wiatr

0,53*0,35*0,6

0,111

1,50

0,167

0,111

0,167

0,000

0,000

Q-

obciążenie

użytkowe

skupione [kN]

1,000

1,50

1,500

0,707

1,061

0,707

1,061

q-

obciążenie

użytkowe

równomiernie

rozłożone

0,4*0,35*0

0,000

1,50

0,000

0,000

0,000

0,000

0,000

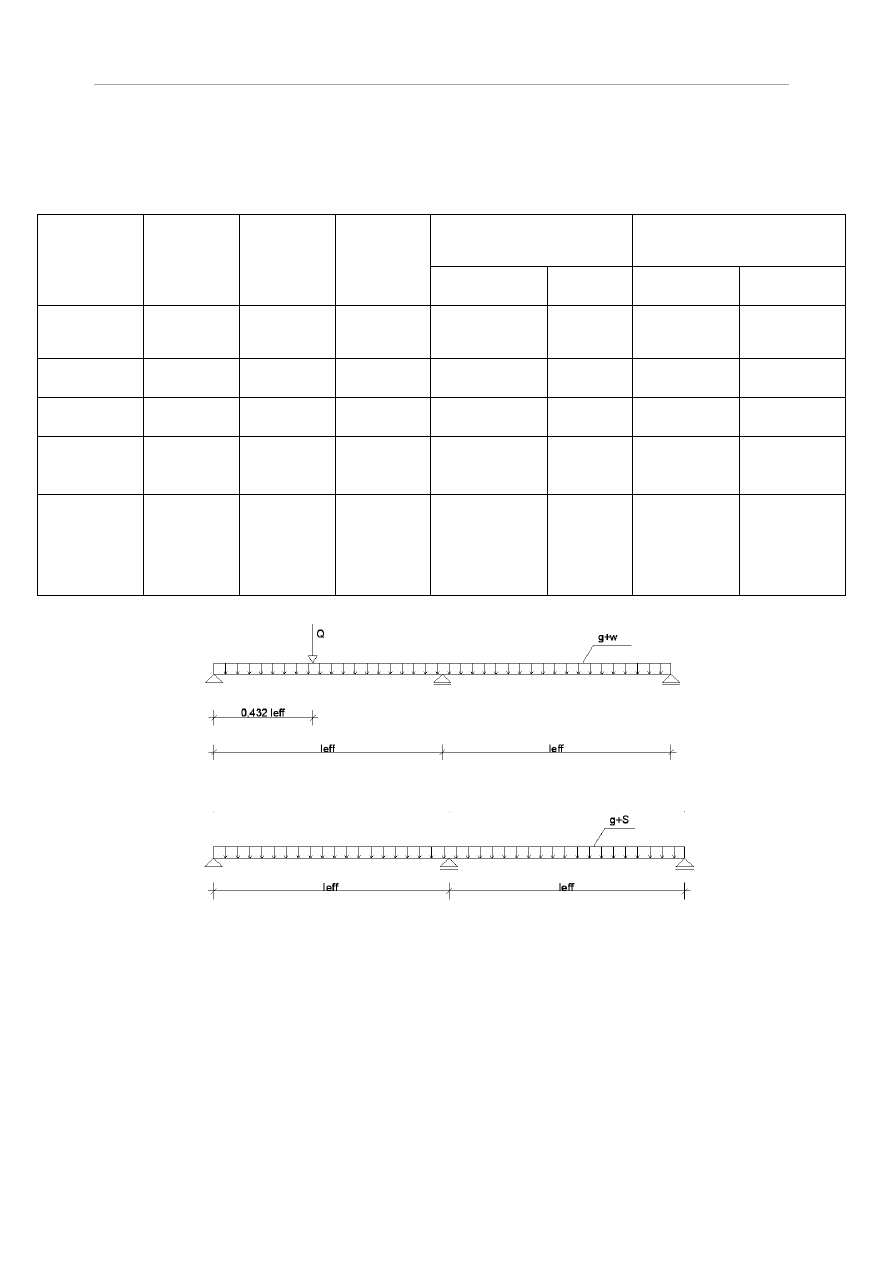
a)

b)

Rys.6.1 Schematy statyczne do obliczania łaty: a) wariant I obciążeń, b) wariant II obciążeń

Wymiarowanie łaty

Wariant I- obciążenie ciężarem własnym i pokryciem, wiatrem oraz siłą skupioną

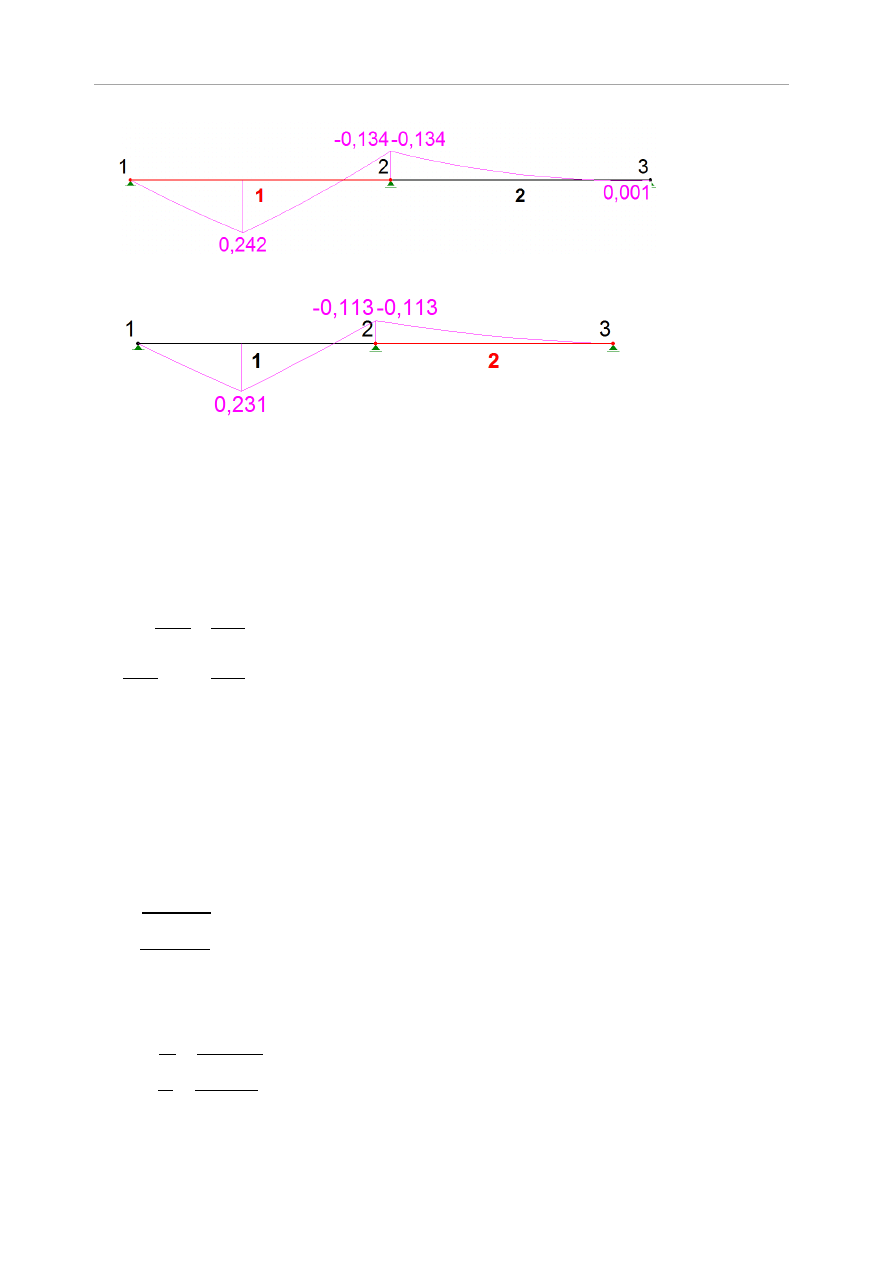
Schemat statyczny przedstawiono na rysunku 1.8 a). Obliczenia wykonano za pomocą
programu RM-WIN i otrzymano wykresy momentów zginających w kNm. Wykresy
sporządzono oddzielnie dla składowych prostopadłych oraz równoległych obciążenia.

Projekt Budownictwo Ogólne II

14

Wydział Budownictwa Wodnego i Lądowego

a)

b)

Rys.7.1 Wykresy momentów zginających od składowych obciążenia: a) prostopadłych, b)
równoległych

Sprawdzenie stanu granicznego nośności

Sprawdzenie warunku stanu granicznego nośności należy wykonywać według wzorów 6.11;
6.12, [14].

(5.8)

(5.9)

gdzie:

-współczynnik wyrażający możliwość redystrybucji naprężeń i niejednorodności materiału

w danym przekroju, dla przekroju prostokątnego, wg pkt.6.1.6, [ 14], k

m

=0,7

,

–obliczeniowe naprężenia zginające względem osi głównych

,

-wytrzymałości obliczeniowe na zginanie odpowiadające tym naprężeniom

Obliczenie wskaźników wytrzymałości łaty o wymiarach 45x45 mm:

Naprężenia obliczeniowe od zginania w stosunku do osi głównych:

Projekt Budownictwo Ogólne II

15

Wydział Budownictwa Wodnego i Lądowego

1

2

1

2

Dla klasy drewna C22 wytrzymałość charakterystyczna drewna na zginanie wynosi

22 MPa

Dach jest konstrukcją z drewna o wilgotności w przedziale 12-22%, co określa klasę
użytkowania jako 2. Decydujące znaczenie ma obciążenie chwilowe (człowiek), dlatego z
tablicy 3.1, [14] odczytano wartość współczynnika

=1,1. Częściowy współczynnik

bezpieczeństwa przyjęto wg tablicy 2.3, [14], dla drewna litego:

=1,3, stąd:

=

Ponieważ przekrój ma wysokość < 150 mm można zastosować współczynnik k

h

wg wzoru

(5.2):

{

}

k

h

=(

)

0,2

=1,25<1,3 więc:

=

Sprawdzenie warunku stanu granicznego nośności zgodne ze wzorami (5.8), (5.9):

Warunek SGN dla łaty został spełniony.

o

Sprawdzenie stanu granicznego użytkowalności

Według tab.7.2, [ 14] graniczna wartość ugięcia dla deskowania dachowego wynosi:

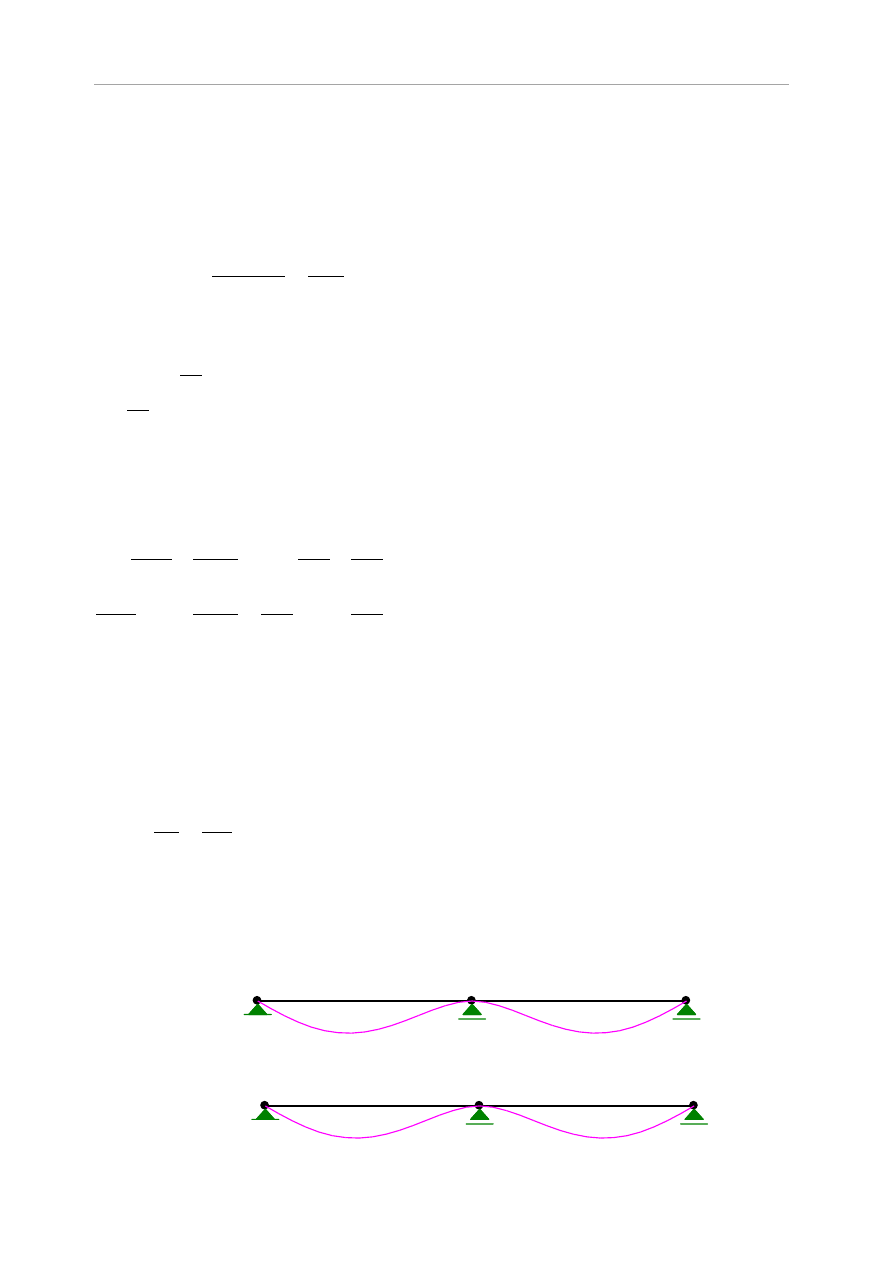
Obliczenie ugięcia wykonano za pomocą programu RM-WIN. Otrzymano wykresy ugięcia
doraźnego

od składowych charakterystycznych prostopadłych (rys. 5.10) i składowych

charakterystycznych równoległych obciążenia (rys.5.11).

a)

b)

Projekt Budownictwo Ogólne II

16

Wydział Budownictwa Wodnego i Lądowego

1

2

1

2

1

2

1

2

c)

Rys.5.10 Wykres ugięcia od składowych prostopadłych obciążenia: a) ciężarem własnym,

b) wiatrem, c) siłą skupioną

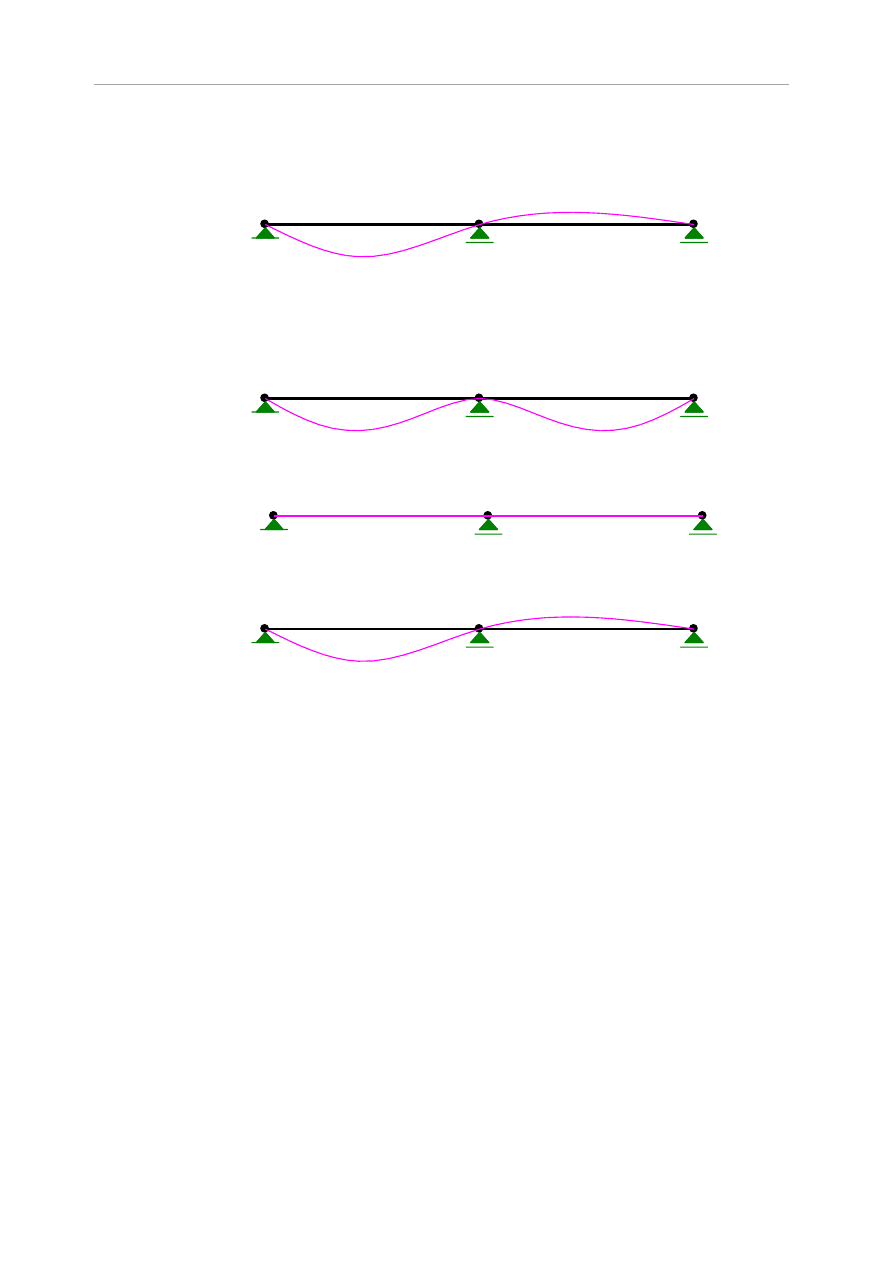
a)

b)

c)

Rys.5.11 Wykres ugięcia od składowych równoległych obciążenia: a) ciężarem własnym, b)

wiatrem, c) siłą skupioną

Końcowe przemieszczenie u

fin

oblicza się zgodnie ze wzorem 2.2, [14]:

(5.10)

gdzie:

-przemieszczenie od oddziaływania stałego

(5.11)

-przemieszczenie dla wiodącego oddziaływania zmiennego (siła skupiona)

(5.12)

-przemieszczenie od kolejnego oddziaływania zmiennego (wiatr)

(5.13)

–współczynnik odzwierciedlający wpływ pełzania, zależny od klasy użytkowania (wg

tablicy 3.2, [14] dla klasy użytkowania 2, dla drewna litego

=0,8)

,

–współczynnik dla wartości prawie stałej oddziaływania zmiennego

Projekt Budownictwo Ogólne II

17

Wydział Budownictwa Wodnego i Lądowego

-współczynnik dla wartości kombinacyjnej oddziaływania zmiennego

Zgodnie z tab.A1.1, [9]:

=0,0 (siła skupiona)

=0,6,

=0,0(wiatr)

Wartości ugięcia od poszczególnych składowych obciążenia przedstawiono w tabeli.

Tabela 5.14 Wartości ugięcia od poszczególnych składowych obciążenia

obciążenie

składowe prostopadłe [mm] składowe równoległe [mm]

u

inst,y

u

fin,y

u

inst, z

u

fin, z

1.ciężar własny

0,2

0,36

0,1

0,18

2.wiatr

0,18

0,14

0

0

3.siła skupiona

3,3

3,3

2,8

2,8

ugięcie sumaryczne
u

fin,y

=u

fin1,y

+u

fin2,y+

u

fin3,y

u

fin,z=

u

fin1,z+

u

fin2,z+

u

fin3,z

3,80

2,98

ugięcie całkowite u

fin

=(u

fin,y

2

+u

fin,z

2

)

0,5

4,83

u

fin

=4,83 mm < 6,77 mm

Warunek SGU dla łaty został spełniony.

Obliczenie krokwi

Przyjęto, że wiązar dachowy będzie wykonany z krokwi grubości 100mm. Przyjęto ocieplenie
połaci dachowych wełną mineralną 170mm oraz szczelinę nad wełną grubości 30mm.
Wysokość krokwi i jętki wynosi 200mm. Przyjęto, że na jętkach zostanie wykonany strop
ocieplony, a wyłaz rewizyjny umożliwi dostęp do przestrzeni nad jętką. Całość będzie
wykonana z drewna sosnowego klasy C22,



=

.

Maksymalny rozstaw krokwi wynosi l=1,0m

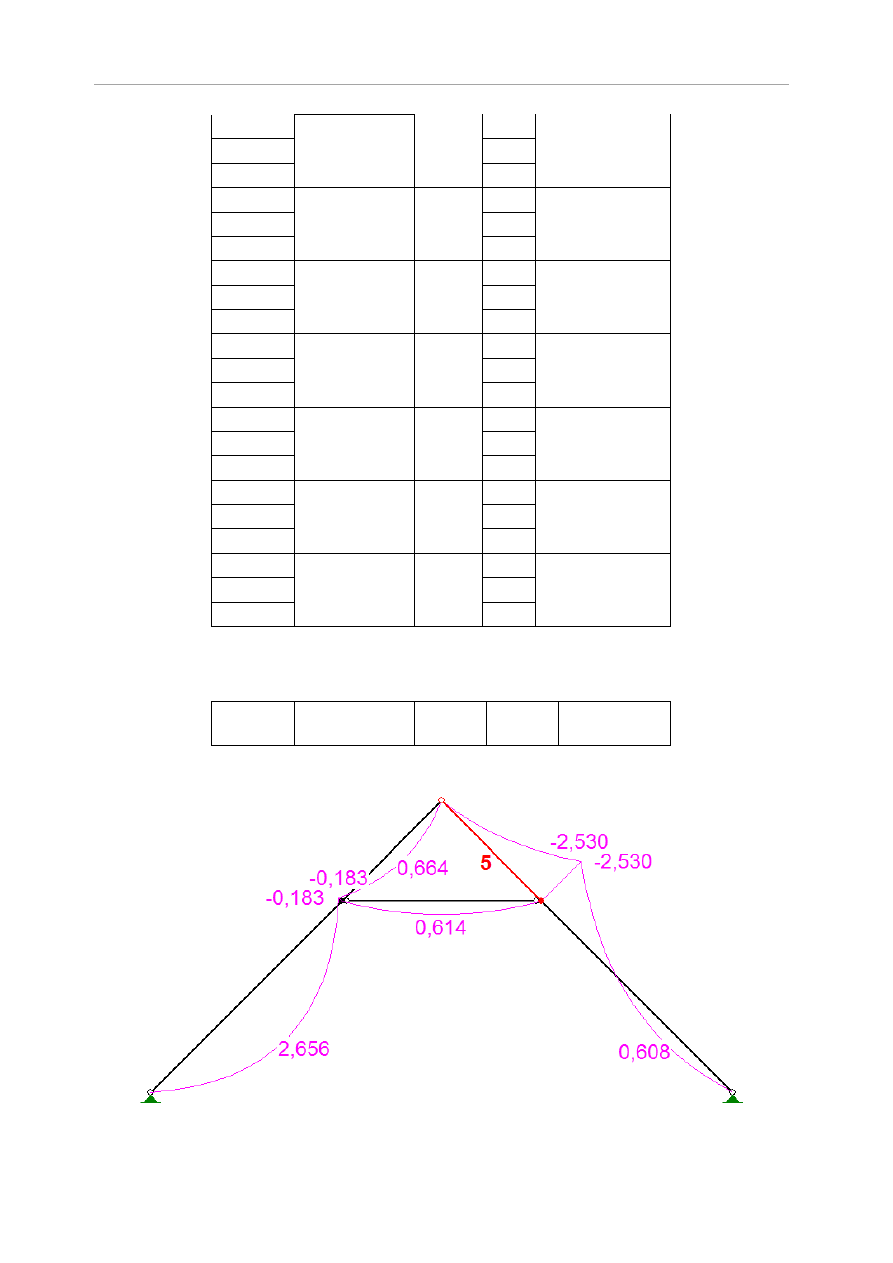
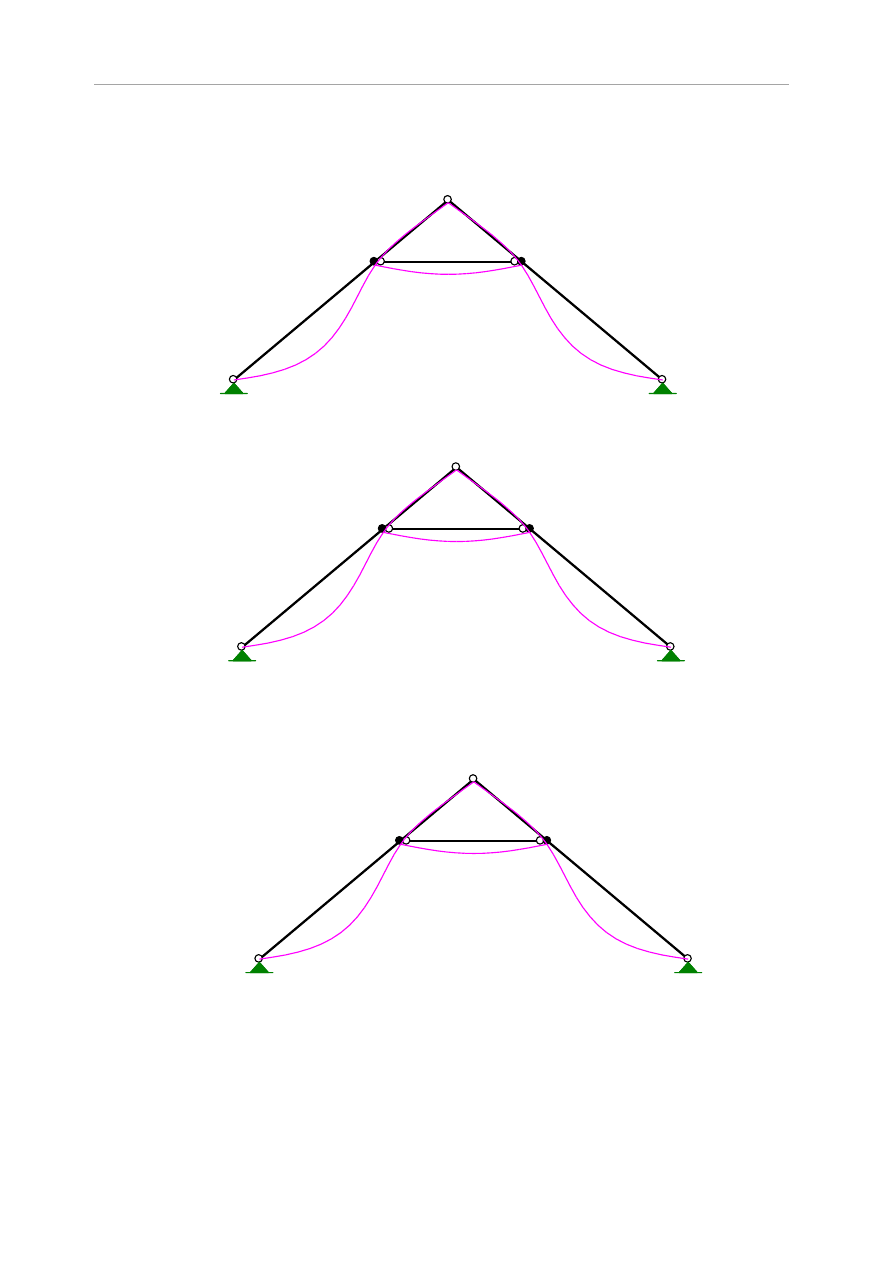
Rys.5.13 schemat statyczny wiązara jętkowego

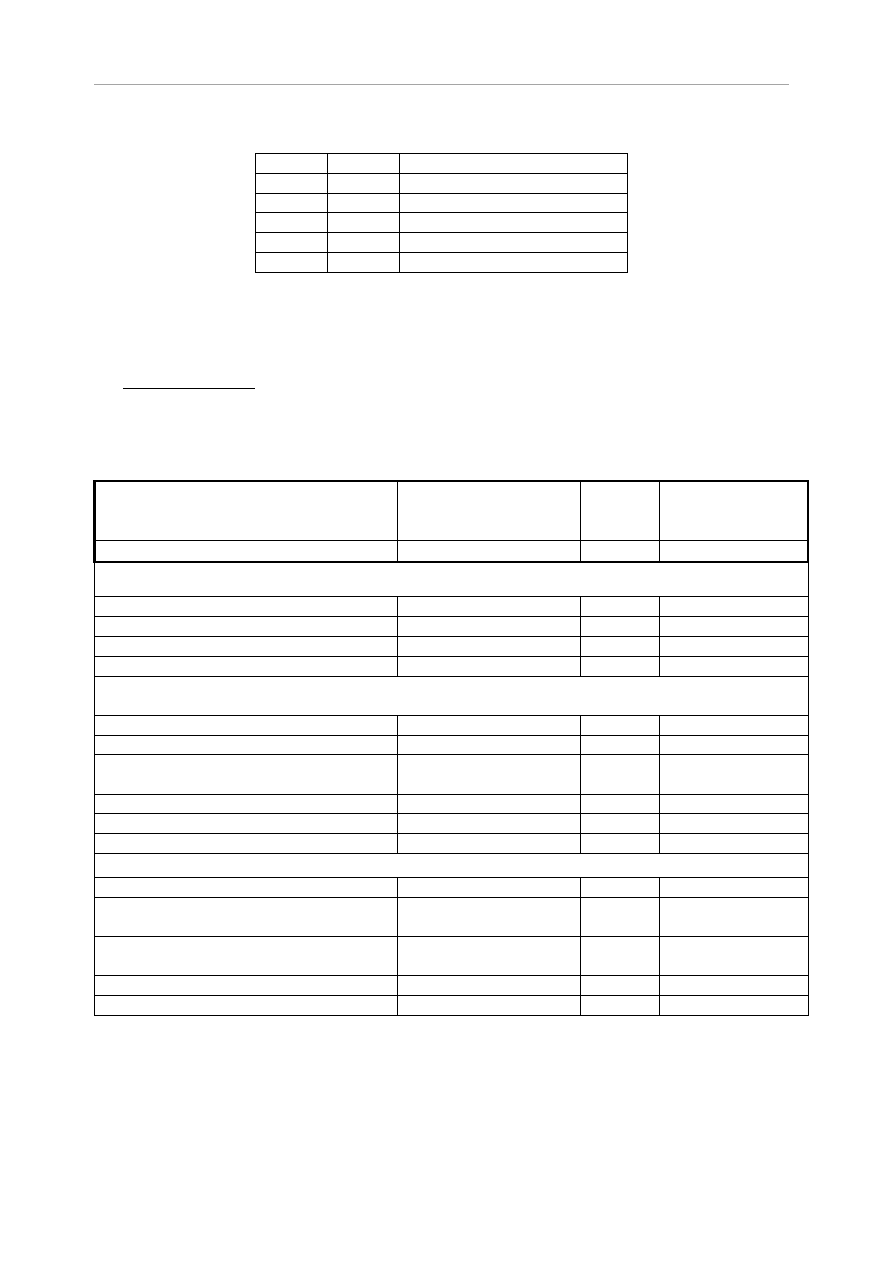
Projekt Budownictwo Ogólne II

18

Wydział Budownictwa Wodnego i Lądowego

Tabela 5.15 Pręty wiązara jętkowego

Nr

pręta

L [m]

typ

1

2,993

przegub-sztywny

2

1,568

sztywny-przegub

3

1,568

przegub-sztywny

4

2,993

sztywny-przegub

5

2,217

przegub-przegub



Zestawienie obciążeń

o

Obciążenie stałe g

Tabela 5.16 Zestawienie obciążeń stałych

obciążenie

wartość

charakterystyczna

[kN/m]

γ

f

wartość

obliczeniowa

[kN/m]

1

2

3

4

g

1

ciężar własny dachu z uwzględnieniem ciężaru krokwi nad jętką

ciężar łaty 0,009*(100/35)*1,0

0,026

1,35

0,035

ciężar własny dachówki 0,037*12*0,9

0,400

1,35

0,539

ciężar własny krokwi 0,08*0,2*4,1

0,066

1,35

0,089

RAZEM

0,492

0,664

g

2

ciężar własny dachu z uwzględnieniem ciężaru krokwi pod jętką

ciężar łaty 0,009*(100/35)*1,0

0,026

1,35

0,035

ciężar własny dachówki 0,037*12*0,9

0,400

1,35

0,539

ciężar ocieplenia (170mm wełny mineralnej)
0,17*0,024,0*0,9

0,153

1,35

0,207

ciężar własny krokwi 0,08*0,02*4,1

0,066

1,35

0,089

ciężar płyt g-k na ruszcie 0,0125*12*0,9

0,135

1,35

0,182

RAZEM

0,800

1,053

g

3

ciężar własny stropu ocieplonego

ciężar jętki 0,08*0,2*4,1

0,066

1,35

0,111

ciężar desek nad jętką (50% pow.)
(0,025*0,5)*4,1*1,0

0,049

1,35

0,067

ciężar ocieplenia (170mm wełny min.)
0,17*0,024*1,0

0,004

1,35

0,005

ciężar płyt g-k na ruszcie 0,0125*12*1,0

0,15

1,35

0,203

RAZEM

0,269

0,386

Projekt Budownictwo Ogólne II

19

Wydział Budownictwa Wodnego i Lądowego

o

Obciążenie zmienne – śnieg

Tabela 5.17 Zestawienie obciążeń od śniegu

o

Obciążenie zmienne-wiatr

760

3801

1567

2993

Po

le

H

Po

le

F

Po

le

J

Po

le I

Rys.5.14 podział na pola obliczeniowe przekroju wiązara dla kierunku wiatru Θ=0°

obciążenie

wartość

charakterystyczna

[kN/m]

γ

f

wartość

obliczeniowa

[kN/m]

1

2

3

4

S

1

-

równomierne obciążenie połaci

0,28*1,0

0,28

1,5

0,42

S

2

-

lewa połać bardziej obciążona niż prawa

lewa: 0,28*1,0
prawa: 0,5*0,28*1,0

0,28

1,5

0,42

0,14

0,21

S

3

-

prawa połać bardziej obciążona niż lewa

lewa: 0,5*0,28*1,0
prawa: 0,28*1,0

0,14

1,5

0,21

0,28

0,42

Projekt Budownictwo Ogólne II

20

Wydział Budownictwa Wodnego i Lądowego

4561

4561

P

ol

e H

P

ol

e H

Rys.5.15 podział na pola obliczeniowe przekroju wiązara dla kierunku wiatru Θ=90°

Tabela 5.18 Zestawienie obciążeń od wiatru na podstawie wcześniejszych obliczeń (pkt 5.1.1)

wartość

pole dla kierunku wiatru Θ=0°

wartości charakterystyczne

F

H

I

J

W1

w

net

*0,9

-0,0954

-0,0954

-0,1908

-0,2385

W2

-0,0954

-0,0954

-0,0954

-0,0954

W3

0,2385

0,1908

-0,1908

-0,2385

W4

0,2385

0,1908

-0,0954

-0,0954

W5

0,1431

0,1431

0,0477

0

W6

0,1431

0,1431

0,1431

0,1431

W7

0,477

0,4293

0,0477

0

W8

0,477

0,4293

0,1431

0,1431

wartości obliczeniowe

F

H

I

J

W1

w

d

,

net

*0,9

-0,1431

-0,1431

-0,2862

-0,3582

W2

-0,1431

-0,1431

-0,1431

-0,1431

W3

0,3582

0,2862

-0,2862

-0,3582

W4

0,3582

0,2862

-0,1431

-0,1431

W5

0,2151

0,2151

0,072

0

W6

0,2151

0,2151

0,2151

0,2151

W7

0,7155

0,6444

0,072

0

W8

0,7155

0,6444

0,2151

0,2151

wartość

pole dla kierunku wiatru Θ=90°

Projekt Budownictwo Ogólne II

21

Wydział Budownictwa Wodnego i Lądowego

wartości charakterystyczne

F

H

I

G

W9

w

net

*0,9

-0,6201

-0,5247

-0,3339

-0,7632

wartości obliczeniowe

F

H

I

G

W9

w

d,net

*0,9

-0,9306

-0,7875

-0,5013

-1,1448

o

Obciążenie użytkowe

Tabela 5.19 Zestawienie obciążeń użytkowych

obciążenie

wartość

charakterystyczna [kN/m]

γ

f

wartość

obliczeniowa

[kN/m]

1

2

3

4

U-

obciążenie użytkowe jętki

0,4*1,0

0,4

1,50

0,6

KOMBINACJE OBCIĄŻEŃ

Kombinacje sporządzono w oparciu o wzór 6.10, [9]:

∑

∑

(5.14)

gdzie:

–obciążenia stałe

– obciążenie zmienne dominujące

- obciążenie zmienne towarzyszące

– współczynniki częściowe dla obciążeń stałych i zmiennych (wg zał.A, [9])

– współczynniki dla wartości kombinacyjnej oddziaływania zmiennego ( tab.A1.1, [9])

I)

OBCIĄŻENIE ZMIENNE DOMINUJACE - OBCIĄŻENIE WIATREM

Gdy wiatr stanowi obciążenie dominujące, należy zastosować współczynniki dla wartości
kombinacyjnej oddziaływania zmiennego dla obciążenia śniegiem (

) oraz dla

obciążenia użytkowego (

).

Tabela 5.20 Możliwe kombinacje obciążeń

nr

kombinacji

obciążenia stałe

obciążenia zmienne

wiatr

śnieg

obc. użytkowe

1

g

1

+g

2

+g

3

W

1

S

1

*0,5

U*0,7

Projekt Budownictwo Ogólne II

22

Wydział Budownictwa Wodnego i Lądowego

2

S

2

*0,5

3

S

3

*0,5

4

g

1

+g

2

+g

3

W

2

S

1

*0,5

U*0,7

5

S

2

*0,5

6

S

3

*0,5

7

g

1

+g

2

+g

3

W

3

S

1

*0,5

U*0,7

8

S

2

*0,5

9

S

3

*0,5

10

g

1

+g

2

+g

3

W

4

S

1

*0,5

U*0,7

11

S

2

*0,5

12

S

3

*0,5

13

g

1

+g

2

+g

3

W

5

S

1

*0,5

U*0,7

14

S

2

*0,5

15

S

3

*0,5

16

g

1

+g

2

+g

3

W

6

S

1

*0,5

U*0,7

17

S

2

*0,5

18

S

3

*0,5

19

g

1

+g

2

+g

3

W

7

S

1

*0,5

U*0,7

20

S

2

*0,5

21

S

3

*0,5

22

g

1

+g

2

+g

3

W

8

S

1

*0,5

U*0,7

23

S

2

*0,5

24

S

3

*0,5

25

g

1

+g

2

+g

3

W

9

S

1

*0,5

U*0,7

26

S

2

*0,5

27

S

3

*0,5

II)

OBCIĄŻENIE ZMIENNE DOMINUJACE - OBCIĄŻENIE ŚNIEGIEM

Gdy śnieg stanowi obciążenie dominujące, należy zastosować współczynniki dla wartości
kombinacyjnej oddziaływania zmiennego dla obciążenia wiatrem (

) oraz dla

obciążenia użytkowego (

).

Tabela 5.21 Możliwe kombinacje obciążeń

nr

kombinacji

obciążenia stałe

obciążenia zmienne

wiatr

śnieg

obc. użytkowe

28

g

1

+g

2

+g

3

W

1

*0,6

S

1

U*0,7

29

S

2

30

S

3

31

g

1

+g

2

+g

3

W

2

*0,6

S

1

U*0,7

32

S

2

33

S

3

Projekt Budownictwo Ogólne II

23

Wydział Budownictwa Wodnego i Lądowego

34

g

1

+g

2

+g

3

W

3

*0,6

S

1

U*0,7

35

S

2

36

S

3

37

g

1

+g

2

+g

3

W

4

*0,6

S

1

U*0,7

38

S

2

39

S

3

40

g

1

+g

2

+g

3

W

5

*0,6

S

1

U*0,7

41

S

2

42

S

3

43

g

1

+g

2

+g

3

W

6

*0,6

S

1

U*0,7

44

S

2

45

S

3

46

g

1

+g

2

+g

3

W

7

*0,6

S

1

U*0,7

47

S

2

48

S

3

49

g

1

+g

2

+g

3

W

8

*0,6

S

1

U*0,7

50

S

2

51

S

3

52

g

1

+g

2

+g

3

W

9

*0,6

S

1

U*0,7

53

S

2

54

S

3

W wyniku wyboru losowego wybrałem kombinacje nr 20.

20

g

1

+g

2

+g

3

W

7

S

2

*0,5

U*0,7

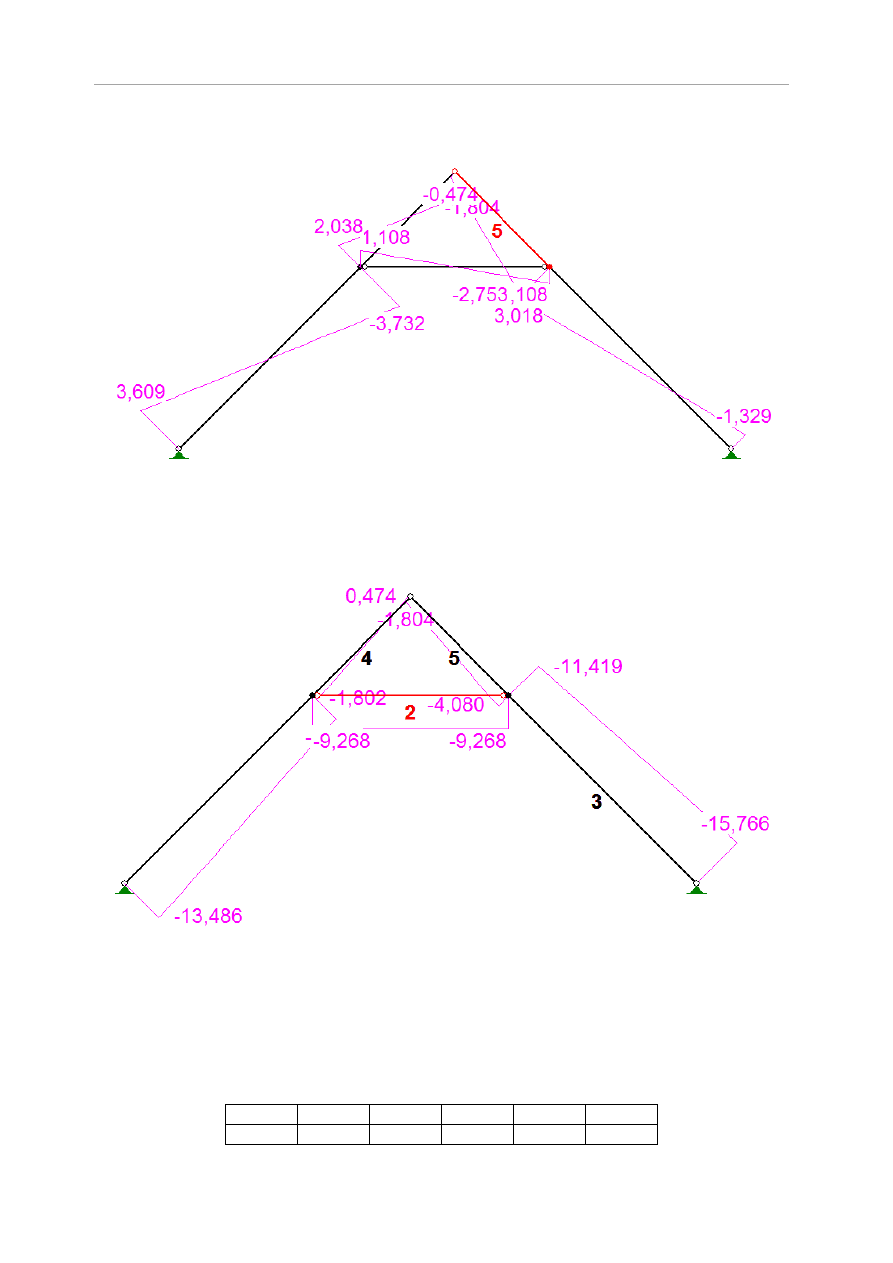
Otrzymane wykresy sił przekrojowych przedstawia rysunek 4.16.

a)

Projekt Budownictwo Ogólne II

24

Wydział Budownictwa Wodnego i Lądowego

b)

c)

Rys.5.16 Wykresy sił przekrojowych wiązara jętkowego: a) momenty, b) siły tnące, c) siły

osiowe

Tabela 5.22 Wartości sił przekrojowych na poszczególnych prętach wiązara

Pręt

x/L

x[m]

M [kNm]

V [kN]

N [kN]

1

0,00

0,000

0,000

3,609

-13,486

Projekt Budownictwo Ogólne II

25

Wydział Budownictwa Wodnego i Lądowego

0,48

1,966

3,155

-0,006

-10,931

1,00

4,095

-0,520

-3,447

-8,885

2

0,00

0,000

-0,520

1,657

-0,831

0,59

2,257

0,521

-0,001

-0,063

1,00

2,145

0,000

-1,172

0,695

3

0,00

0,000

0,000

-0,888

-1,034

1,00

2,145

-3,372

-2,256

-2,252

4

0,00

0,000

-3,372

2,848

-10,306

0,71

2,905

0,733

-0,027

-12,682

1,00

4,095

0,000

-1,206

-13,655

5

0,00

0,000

0,000

1,267

-9,451

0,50

1,643

1,040

0,000

-9,451

1,00

3,286

0,000

--3,732

-9,268

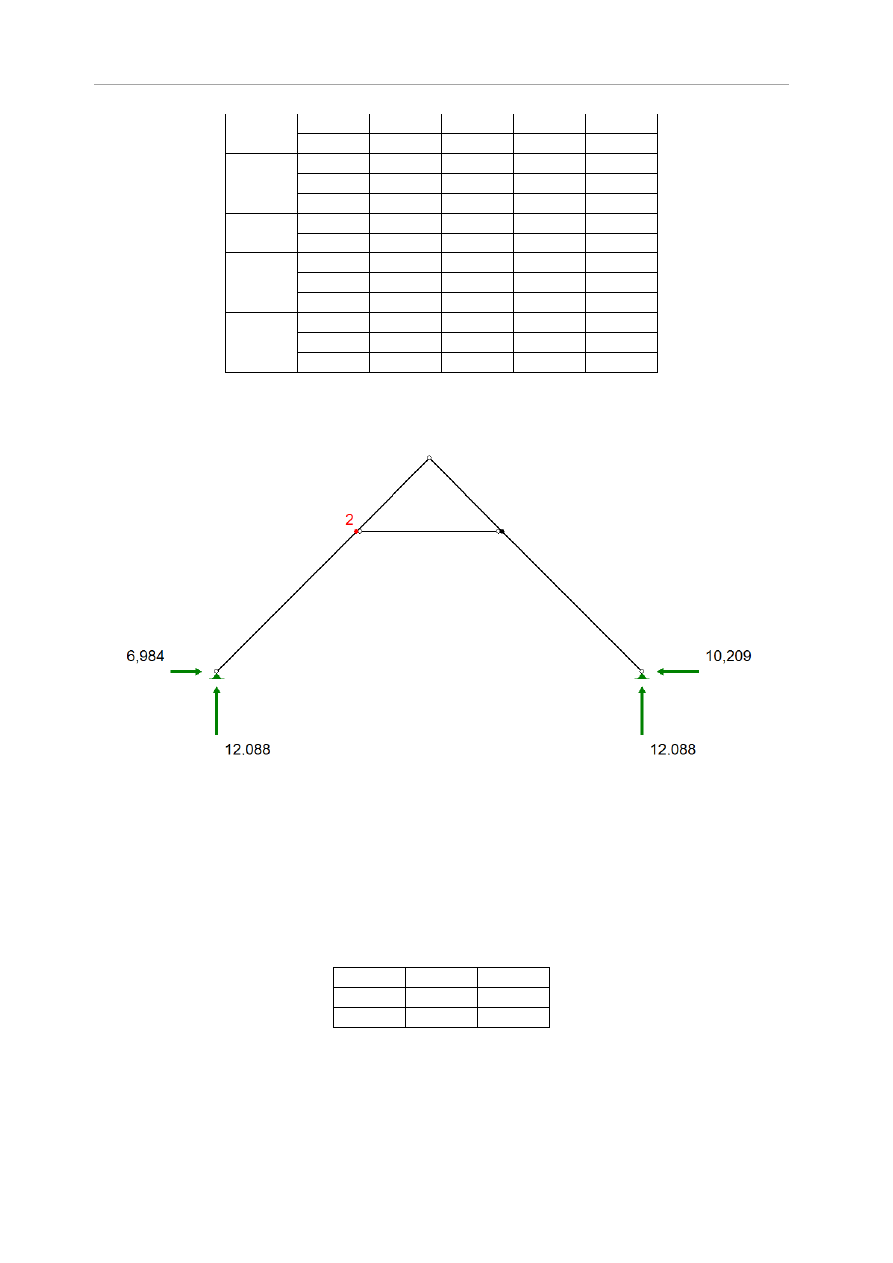
Rys.5.17 Wartości reakcji podporowych

Tabela 5.23 Wartości reakcji podporowych

węzeł

H [kN]

V [kN]

1

6,984

12,088

4

-10,209

12,088

Projekt Budownictwo Ogólne II

26

Wydział Budownictwa Wodnego i Lądowego



Wymiarowanie krokwi

o

Sprawdzenie stanu granicznego nośności

Maksymalny moment zginający i odpowiadająca mu siła osiowa wynoszą:
M

1

=2,659 kNm

N

1

= -11,377 kN (ściskanie)

Element jest najbardziej obciążony, gdy występuje zginanie oraz ściskanie osiowe, więc musi
spełniać nierówność podaną we wzorze 6.19, [14].

(5.15)

gdzie:

-współczynnik wyrażający możliwość redystrybucji naprężeń i niejednorodności materiału

w danym przekroju, dla przekroju prostokątnego, wg pkt.6.1.6, [ 14] k

m

=0,7

,

–obliczeniowe naprężenia zginające względem osi głównych

,

-wytrzymałości obliczeniowe na zginanie odpowiadające tym naprężeniom

–obliczeniowe naprężenia ściskające wzdłuż włókien

–obliczeniowa wytrzymałość na ściskanie wzdłuż włókien

Przyjęto przekrój krokwi 80x200mm , dla którego:
m

2

m

3

Naprężenia obliczeniowe ściskające w kierunku równoległym do włókien wynoszą:

Naprężenia obliczeniowe od zginania w stosunku do osi głównych wynoszą:

Zgodnie z tabelą 5.1 :

,

Decydujące znaczenie ma obciążenie wiatrem (krótkotrwałe), więc zgodnie z tabelą 5.2 :

Zgodnie ze wzorem 5.1 wyznaczono wartości obliczeniowe charakterystyk materiałowych.

Ponieważ przyjęty przekrój krokwi ma wysokość>150mm nie stosuje się współczynnika k

h

.

Projekt Budownictwo Ogólne II

27

Wydział Budownictwa Wodnego i Lądowego

Sprawdzenie SGN w oparciu o wzór 5.15:

Warunek stanu granicznego nośności został spełniony.

o

Sprawdzenie stateczności elementu

Element jest obciążony momentem zginającym oraz ściskającą siłą osiową, więc powinien
spełniać nierówność zgodną ze wzorem 6.35, [14].

(5.16)

gdzie:
σ

m,d

–obliczeniowe naprężenia zginające

σ

c,0,d

– obliczeniowe naprężenia ściskające wzdłuż włókien

f

m,d

–obliczeniowa wytrzymałość na zginanie

f

c,0,d

–obliczeniowa wytrzymałość na ściskanie wzdłuż włókien

k

crit

–współczynnik uwzględniający redukcję wytrzymałości ze względu na zwichrowanie

elementu
k

c,z

– współczynnik wyznaczany wg wzoru 6.26 [14]

√

(5.17)

gdzie:

-smukłość odpowiadająca zginaniu względem osi z obliczana ze wzoru 6.21, [14]

√

(5.18)

gdzie:
E

0,05

-5% kwantyl modułu sprężystości wzdłuż włókien, dla drewna C22, E

0,05

=6700 MPa

-charakterystyczna wytrzymałość na ściskanie wzdłuż włókien,

oblicza się wg wzoru 6.28, [14]

(5.19)

–

gdzie:

-współczynnik dotyczący prostoliniowości elementów, dla drewna litego

=0,2 (wg

pkt.6.3.2, [14])
λz – smukłość odpowiadająca zginaniu wzdłuż osi z, obliczona zgodnie ze wzorem:

(5.20)

gdzie:

–długość wyboczeniowa elementu w płaszczyźnie z-x

=4,56

=4,56m (belka swobodnie podparta, obciążenie rozłożone, tab. 6.1, [14])

-promień bezwładności względem osi z

i

z

= √

I

z

A

Projekt Budownictwo Ogólne II

28

Wydział Budownictwa Wodnego i Lądowego

I

z

=

h b

3

12

=

0,2 0,08

3

12

= 8,53 10

-6

m

4

A =b

0,016 m

2

i

z

= √

0,016

m

√

–

=6,77

√

Współczynnik k

crit

określa wzór 6.34, [14] :

{

(5.21)

gdzie:

-smukłość względna przy zginaniu wyznaczana ze wzoru 6.30, [95].

√

(5.22)

gdzie:

=22 MPa

-naprężenie krytyczne przy zginaniu wyznaczane w oparciu o wzór 6.32 normy [14]

(5.23)

=1,0

=1,0 (wg tab. 6.1, [14]) belka swobodnie podparta, obciążenie

rozłożone)

√

Dla

= 0,77,

=

= = 0,983

Sprawdzenie warunku stateczności:

Warunek stateczności spełniony.

Projekt Budownictwo Ogólne II

29

Wydział Budownictwa Wodnego i Lądowego

o

sprawdzenie stanu granicznego użytkowalności

Graniczne przemieszczenie dla konstrukcji ze stropem otynkowanym (na jętkach strop z płyt
gipsowo-kartonowych) wg.[14]:

=0,0152m=15,2 mm

Obliczenia ugięcia krokwi dokonano analogicznie do obliczenia ugięcia łaty. Końcowe
przemieszczenie u

fin

oblicza się zgodnie ze wzorem 2.2, [14]:

(5.10)

gdzie:

-przemieszczenie od oddziaływania stałego

(5.11)

-przemieszczenie dla wiodącego oddziaływania zmiennego (wiatr)

(5.12)

-przemieszczenie od kolejnego oddziaływania zmiennego (śnieg, obciążenie

użytkowe)

(5.13)

–współczynnik odzwierciedlający wpływ pełzania, zależny od klasy użytkowania (wg

tablicy 3.2, [14] dla klasy użytkowania 2, dla drewna litego

=0,8)

,

–współczynnik dla wartości prawie stałej oddziaływania zmiennego

-współczynnik dla wartości kombinacyjnej oddziaływania zmiennego

Zgodnie z tab.A1.1, [9]:

Dla wiatru:

= -,

=0,0

Dla śniegu:

= 0,5,

=0,2

Dla obciążenia użytkowego:

= 0,0,

=0,0

Obliczenia ugięcia krokwi przeprowadzono za pomocą programu RM-WIN. Otrzymane
wartości od poszczególnych składowych obciążenia przedstawiono w tabeli. Wykresy ugięć
przedstawiono na rysunku 1.18.

Tabela 5.24 Wartości ugięcia od poszczególnych składowych obciążenia

obciążenie

k

def

Ψ

0,i

Ψ

2,i

składowe obciążenia [mm]

u

inst

u

fin

1.ciężar własny

0,8

-

-

2,600

4,820

2.śnieg

0,8

0,5

0,2

4,100

2,504

3.wiatr

0,8

-

0

7,400

7,400

4.obciążenie
użytkowe

0,8

0

0

1,600

0,000

ugięcie sumaryczne

u

fin=

u

fin1+

u

fin

+u

fin,3

+u

fin,4

14,724

Projekt Budownictwo Ogólne II

30

Wydział Budownictwa Wodnego i Lądowego

1

2

3

4

5

1

2

3

4

5

1

2

3

4

5

a)

b)

c)

Rys.5.18 Wykresy ugięć krokwi od obciążenia: a) ciężarem własnym, b)śniegiem, c) wiatrem

u

fin

=14,724 mm < 15,2 mm

Projekt Budownictwo Ogólne II

31

Wydział Budownictwa Wodnego i Lądowego

Warunek SGU spełniony.

Przyjęto krokiew o wymiarach przekroju poprzecznego 80 x 200mm.
5.1.3 Obliczenie jętki



Wymiarowanie jętki

Założono, że jętka zostanie wykonana z drewna identycznego jak krokiew, dlatego
charakterystyczne właściwości materiałowe dla jętki są takie same jak dla krokwi.

o

Sprawdzenie stanu granicznego nośności

Sprawdzenie stanu granicznego nośności przeprowadzono, jak dla krokwi, w oparciu o wzór
5.15, ze względu na występowanie zginania oraz ściskania osiowego:

Maksymalny moment zginający i odpowiadająca mu siła osiowa wynoszą:

M

5

=0,614 kNm

N

5

=-9,268 kN (ściskanie)

Przyjęto przekrój jętki 80x200mm, dla którego:

m

2

m

3

Naprężenia obliczeniowe ściskające w kierunku równoległym do włókien wynoszą:

Naprężenia obliczeniowe od zginania w stosunku do osi głównych wynoszą:

Zgodnie z tabelą 5.1 :

,

Decydujące znaczenie ma obciążenie użytkowe (średniotrwałe), więc zgodnie z tabelą 5.2 :

Zgodnie ze wzorem 5.1 wyznaczono wartości obliczeniowe charakterystyk materiałowych.

Ponieważ przyjęty przekrój jętki ma wysokość>150mm nie stosuje się współczynnika k

h

.

Sprawdzenie SGN w oparciu o wzór 4.15:

Projekt Budownictwo Ogólne II

32

Wydział Budownictwa Wodnego i Lądowego

1

2

3

4

5

(5.15)

Przekrój jest przewymiarowany, jednak, ze względu na obecność izolacji termicznej na jętce
(warstwa wełny mineralnej grubości 170 mm), wymiary nie ulegaja zmianie.

Warunek stanu granicznego nośności został spełniony.

o Sprawdzenie stanu granicznego użytkowalności

Na jętce zostanie wykonany strop otynkowany (sufit z płyt g-k), więc wg [14]:

=0,0074m=7,4 mm

Końcowe ugięcie u

fin

obliczono się zgodnie ze wzorem 1,10 (2.2, [14]):

(5.10)

gdzie:

(5.11)

(5.12)

wg tablicy 3.2, [14] dla klasy użytkowania 2, dla drewna litego

=0,8

Zgodnie z tab.A1.1, [9]:

Dla obciążenia użytkowego:

=0,0

Obliczenia jętki krokwi przeprowadzono za pomocą programu RM-WIN. Otrzymane wartości
od poszczególnych składowych obciążenia przedstawiono w tabeli. Wykresy ugięć
przedstawiono na rysunku 5.19.

Tabela 5.25 Wartości ugięcia od poszczególnych składowych obciążenia

a)

obciążenie

k

def

Ψ

2,i

składowe

obciążenia [mm]

u

inst

u

fin

1.ciężar własny

0,8

-

1,000

1,800

2.obciążenie
użytkowe

0,8

0

1,600

1,600

ugięcie sumaryczne

u

fin=

u

fin1+

u

fin2

3,400

Projekt Budownictwo Ogólne II

33

Wydział Budownictwa Wodnego i Lądowego

1

2

3

4

5

b)

Rys.5.19 Wykresy ugięć jętki od obciążenia: a) ciężarem własnym, b)obciążeniem użytkowym

u

fin

=3,4 mm < 7,4 mm

Warunek SGU spełniony.

Przyjęto jętkę o wymiarach przekroju poprzecznego 80 x 200mm.

5.1.4 Obliczenie murłatu

Do zaprojektowania przewidziano murłat wykonany będzie z drewna klasy C22 o wymiarach
150x150 mm o polu przekroju poprzecznego A=0,0225 m

2

. Założono, iż zostanie

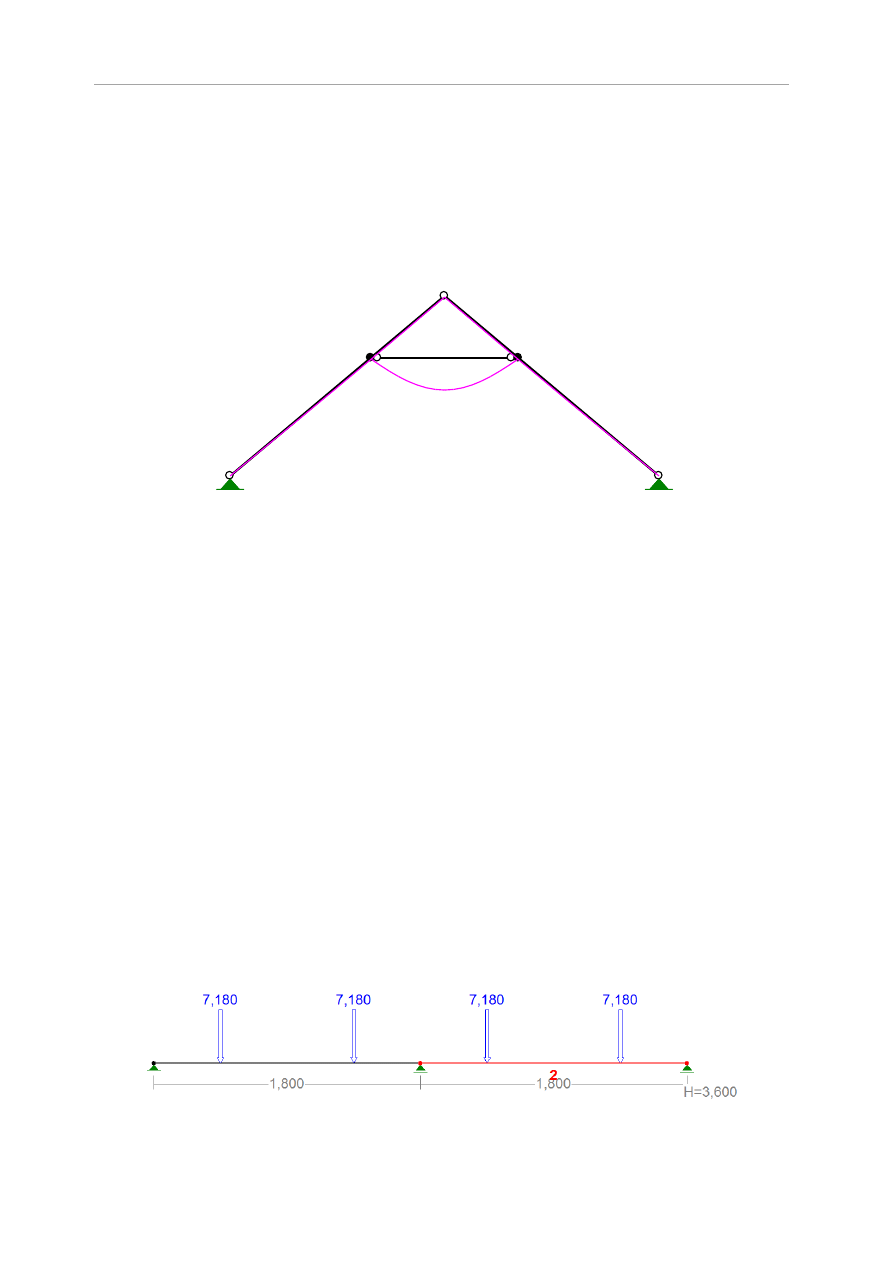
przymocowany bezpośrednio do wieńca żelbetowego śrubami co 1,8 m. Jako schemat
statyczny murłatu przyjęto belkę dwuprzęsłową obciążoną reakcjami poziomymi od wiązarów
dachowych.

Maksymalna reakcji poziomej od wiązarów, zgodnie z tabelą 5.23 wynosi H=

7,180

kN.

Obciążenia pionowe są przekazywane bezpośrednio na wieniec, więc pominięto je w
obliczeniach.

Rys.5.20 Schemat statyczny i obciążenie murłatu

Projekt Budownictwo Ogólne II

34

Wydział Budownictwa Wodnego i Lądowego

Obliczenia przeprowadzono przy pomocy programu RM-WIN i dla zadanego obciążenia
otrzymano wykres momentów zginających przedstawiony na rysunku.

Rys.5.21 Wykres momentów zginających dla murłatu



Sprawdzenie stanu granicznego nośności

Murłat jest elementem zginanym, więc sprawdzenie stanu granicznego nośności sporządzono w
oparciu o wzór 6.11, [14].

(5.8)

gdzie:

-współczynnik wyrażający możliwość redystrybucji naprężeń i niejednorodności materiału

w danym przekroju, dla przekroju prostokątnego, wg pkt.6.1.6, [ 14] k

m

=0,7

,

–obliczeniowe naprężenia zginające względem osi głównych

,

-wytrzymałości obliczeniowe na zginanie odpowiadające tym naprężeniom

Obliczenie wskaźnika wytrzymałości murłatu:

Moment maksymalny wynosi:
M=3,635 kNm

Naprężenia obliczeniowe od zginania w stosunku do osi głównych:

Dla klasy drewna C22 wytrzymałość charakterystyczna drewna na zginanie wynosi

22 MPa

Decydujące znaczenie ma obciążenie stałe, dlatego z tablicy 3.1, [14] odczytano wartość
współczynnika

=0,6 (2 klasa użytkowania konstrukcji). Częściowy współczynnik

bezpieczeństwa przyjęto wg tablicy 2.3, [14], dla drewna litego:

=1,3, stąd:

=

Projekt Budownictwo Ogólne II

35

Wydział Budownictwa Wodnego i Lądowego

1

2

Przekrój ma wysokość równą 150 mm, więc nie można zastosować współczynnika k

h

wg

wzoru (5.2).

Sprawdzenie warunku stanu granicznego nośności zgodne ze wzorem (5.8):

Warunek SGN spełniony.



Sprawdzenie stanu granicznego użytkowalności

Według [ 14] graniczna wartość ugięcia dla murłatu wynosi:

Obliczenie ugięcia u

inst

wykonano programem RM-WIN.

Końcowe przemieszczenie u

fin

oblicza się zgodnie ze wzorem 2.2, [14]:

(5.10)

gdzie:

-przemieszczenie od oddziaływania stałego

-przemieszczenie dla wiodącego oddziaływania zmiennego

-przemieszczenie od kolejnego oddziaływania zmiennego

W przypadku murłatu mamy do czynienia wyłącznie z obciążeniem stałym, więc wzór
przyjmuje postać:

=0,8 dla drewna litego (wg tab. 3.2, [14])

Tabela 5.26 Wartości ugięcia murłatu

obciążenie

k

def

składowe obciążenia [mm]

u

inst

u

fin

obciążenie stałe

0,8

1,600

2,880

Rys.5.22 Wykres ugięć murłatu

u

fin

=2,88 mm < 9,0 mm

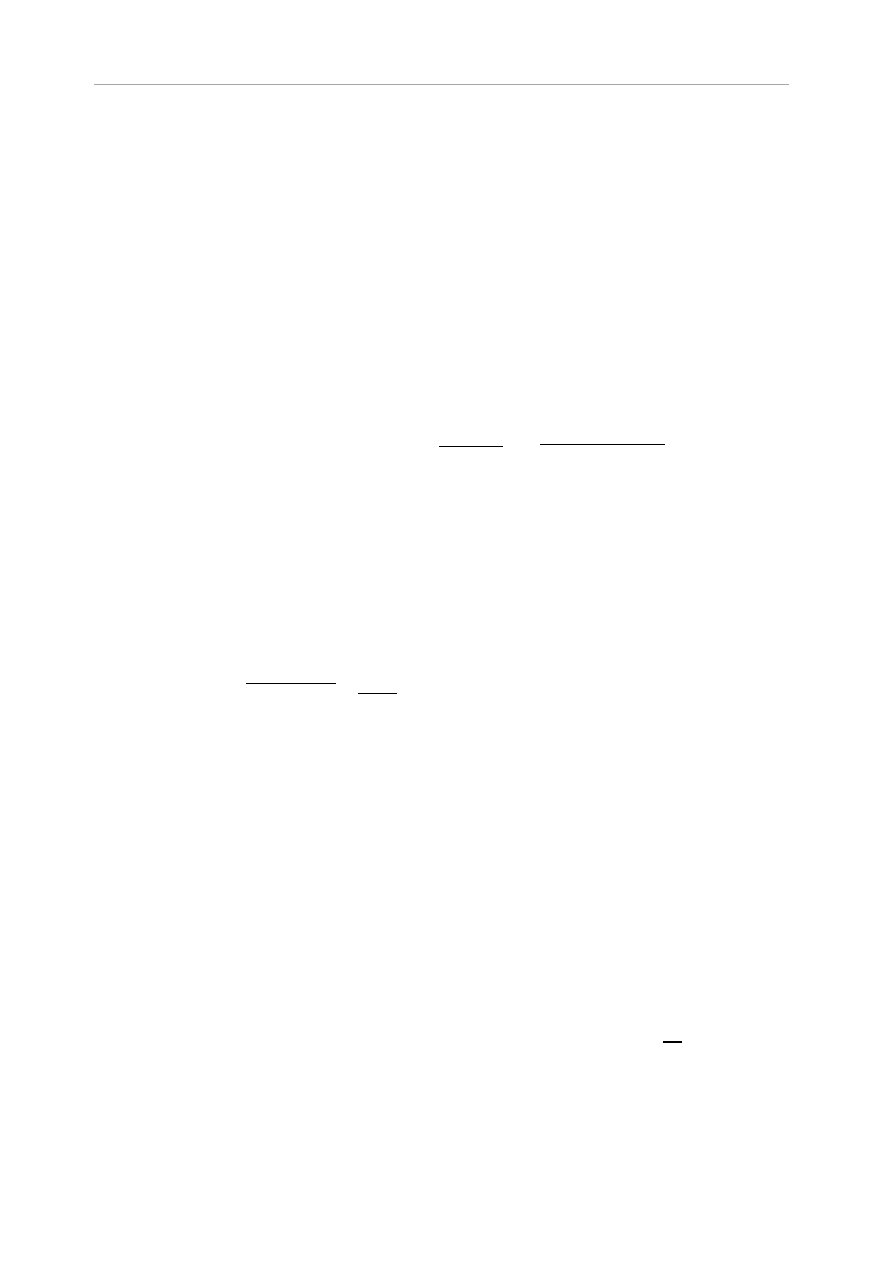
Projekt Budownictwo Ogólne II

36

Wydział Budownictwa Wodnego i Lądowego

Warunek SGU spełniony.

Przyjęto murłat o wymiarach przekroju poprzecznego 150 x 150mm.

5.1.5 Obliczenie połączenia krokwi z jętką

Przyjęto, że połączenie krokwi z jętką zostanie wykonane w formie dwustronnej nakładki z
płytki stalowej perforowanej grubości 2mm. Nakładka będzie przytwierdzona do wiązara
gwoździami 4,0 x 40 mm. Końcówki z ostrzem są jednocięte. Charakter złącza to stal-drewno.

Siły działające na złącze to siła pozioma w jętce (zgodnie z tab.5.23):

N=10,523kN oraz pionowa reakcja wyznaczona na podstawie obciążeń podanych w tabeli
5.16:
V=0,5(g

1

+g

3

)

= 0,5

2,217 = 1,16 kN

Wypadkowa sił działających na gwoździe: F=

√

√

Klasyfikacja blachy według punktu 8.2.3, [14]:

t=2,0 mm-grubość blachy
d=4,0 mm –średnica trzpienia gwoździa
t

2,0mm, więc płytka należy do płyt cieńkich

Nośność gwoździ dla płyt cieńkich określa wzór 8.9, [14]:

{

√

(5.16)

gdzie:
d - średnica trzpienia łącznika, d=4,0 mm

t

1

-długość zakotwienia łącznika

t

1

=40-2-1=37, 0 mm > 8d =8=32,0 mm

–nośność charakterystyczna nośnika na wyciąganie, wg pkt.8.2.2, [14] dla łączników

okrągłych jednociętych

=15%

– wytrzymałość charakterystyczna na docisk łącznika do elementu drewnianego, wg pkt.

8.3.1.1, [14] dla gwoździ o średnicy < 8,0 mm , bez uprzednio nawierconych otworów:

(5.17)

-gęstość charakterystyczna drewna , na podstawie tablicy 1, [9]:

Projekt Budownictwo Ogólne II

37

Wydział Budownictwa Wodnego i Lądowego

-moment charakterystyczny uplastycznienia łącznika, wg wzoru 8.14, [14]dla gwoździ

okrągłych:

=0,3

(5.18)

-wytrzymałość drutu stalowego na rozciąganie w MPa, przyjęto

=600 MPa

d - średnica trzpienia łącznika, d=4,0 mm

=0,3

=6616,5 N

mm

Wyznaczenie minimalnej nośności łącznika wg wzoru (5.16):

{

√

{

=1088,69 N

Potrzebna ilość gwoździ:

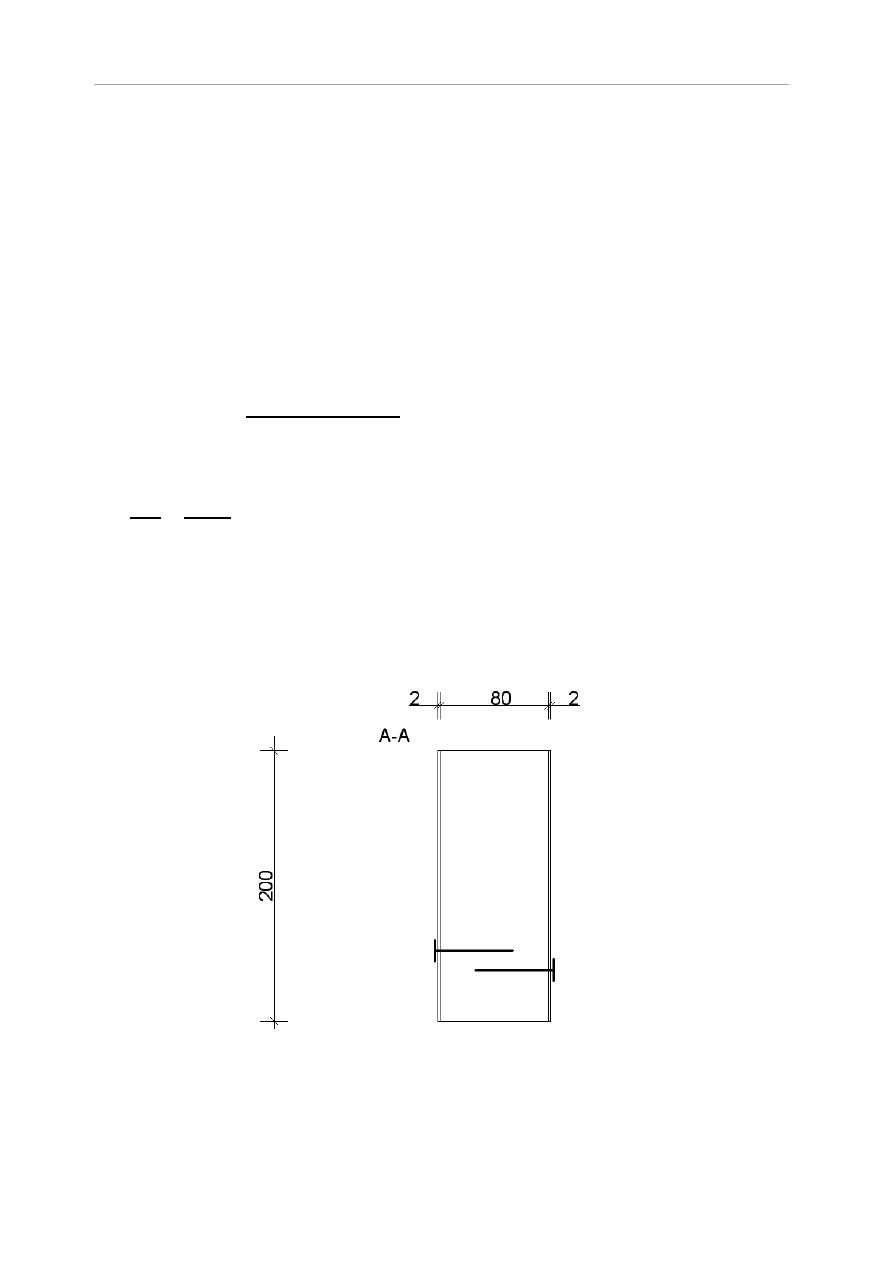
Przyjęto 10 gwoździ i wymiary płytki stalowej : 2 x 175 x 380mm.

Projekt Budownictwo Ogólne II

38

Wydział Budownictwa Wodnego i Lądowego

Rys. 5.23 Rozmieszczenie gwoździ w połączeniu krokwi z jętką

Projekt Budownictwo Ogólne II

39

Wydział Budownictwa Wodnego i Lądowego

6. Strop Ceram

Dla projektowanego budynku wybrano strop Ceram. Wysokość konstrukcyjna stropu wynosi
230mm. Rozpiętość modularna wynosi 300-360 cm ze stopniowaniem co 30 cm.
Sprawdzenie stanów granicznych wykonuje się poprzez porównanie momentu zginającego
obliczonego od obciążenia stropu oraz momentu od maksymalnej dopuszczalnej wartości
obciążenia podanej przez producenta.
Do obciążenia stropu przyjęto zgodnie z tablicą 6.2, [10] charakterystyczną wartość obciążenia
użytkowego dla stropu q

k

=1,5 kN/m

2

, obciążenie od ścianek działowych przyjęto wg punktu

6.3.1.2(8), [10]:

Tabela 5.27 Ciężar ścianki działowej na 1m długości

Obciązenie

Wartość

charakterystyczna

[kN/m]

γ

f

Wartość

obliczeniowa

[kN/m]

tynk gipsowy 10mm
0,01*3,135*12

0,376

1,35

0,508

gazobeton 100mm
0,1*3,135*4

1,254

1,35

1,693

tynk gipsowy
10mm0,01*3,135*12

0,376

1,35

0,508

RAZEM

2,006

2,709

q

k

=1,2 kN/m

2

, ponieważ ciężar ścianki działowej przekracza 2kN/m

Tabela 5.28 Zestawienie obciążeń na strop Ceram bez ciężaru własnego

Obciązenie

Wartość

charakterystyczna

[kN/m

2

]

γ

f

Wartość obliczeniowa

[kN/m

2

]

g-

obciążenie stałe

panele 10mm 0,08

0,080

1,35

0,108

gładź cementowa
35mm 0,035*21

0,735

1,35

0,992

folia PE

-

-

styropian 20mm
0,02*0,45

0,009

1,35

0,012

tynk gipsowy 10mm
0,01*12

0,120

1,35

0,162

RAZEM-

obc.stałe

0,944

1,620

p-

obciążenie zmienne

technologiczne

1,500

1,50

2,250

q-

obciążenie

zastępcze od ścianek
działowych 1,2

1,200

1,35

1,620

RAZEM g+q

2,144

3,240

Projekt Budownictwo Ogólne II

40

Wydział Budownictwa Wodnego i Lądowego

Tabela 5.29 Zestawienie obciążeń na strop Ceram z ciężarem własnym

Obciązenie

Wartość charakterystyczna

[kN/m

2

]

γ

f

Wartość obliczeniowa [kN/m

2

]

g-

obciążenie stałe

panele 10mm 0,08

0,080

1,35

0,108

gładź cementowa
35mm 0,035*21

0,735

1,35

0,992

folia PE

-

-

styropian 20mm
0,02*0,45

0,009

1,35

0,012

strop Teriva I

3,03

1,35

4,091

tynk gipsowy 10mm
0,01*12

0,120

1,35

0,162

RAZEM-

obc.stałe

3,974

5,365

p-

obciążenie zmienne

technologiczne

1,500

1,50

2,250

q-

obciążenie

zastępcze od ścianek
działowych 1,2

1,200

1,35

1,620

RAZEM g+q

5,174

6,985

Efektywną rozpiętość elementu l

eff

obliczono według wzoru 5.8, [13], przyjmując częściowo

utwierdzone podparcie:

l

eff

= l

n

+a

1

+a

2

l

n

- rozpiętość w świetle podpór, przyjęto 3,6m

a

1

i a

2

– odległość teoretycznych punktów podparcia elementu od krawędzi podpór

a

1,2

= min { 0,5h; 0,5t }= min{0,115m; 0,12m}=0,115m.

h- wysokość stropu
t- grubość ściany

l

eff

= 3,6+0,115+0,115=3,83m

Obliczona w tabeli 4.26. wartość obliczeniowa obciążenia całkowitego wynosi 3,24 kN/m

2

.

Rozstaw belek stropowych wynosi 0,45 m, wiec wartość obliczeniowa obciążenia stałego
przypadającego na belkę wynosi 3,24

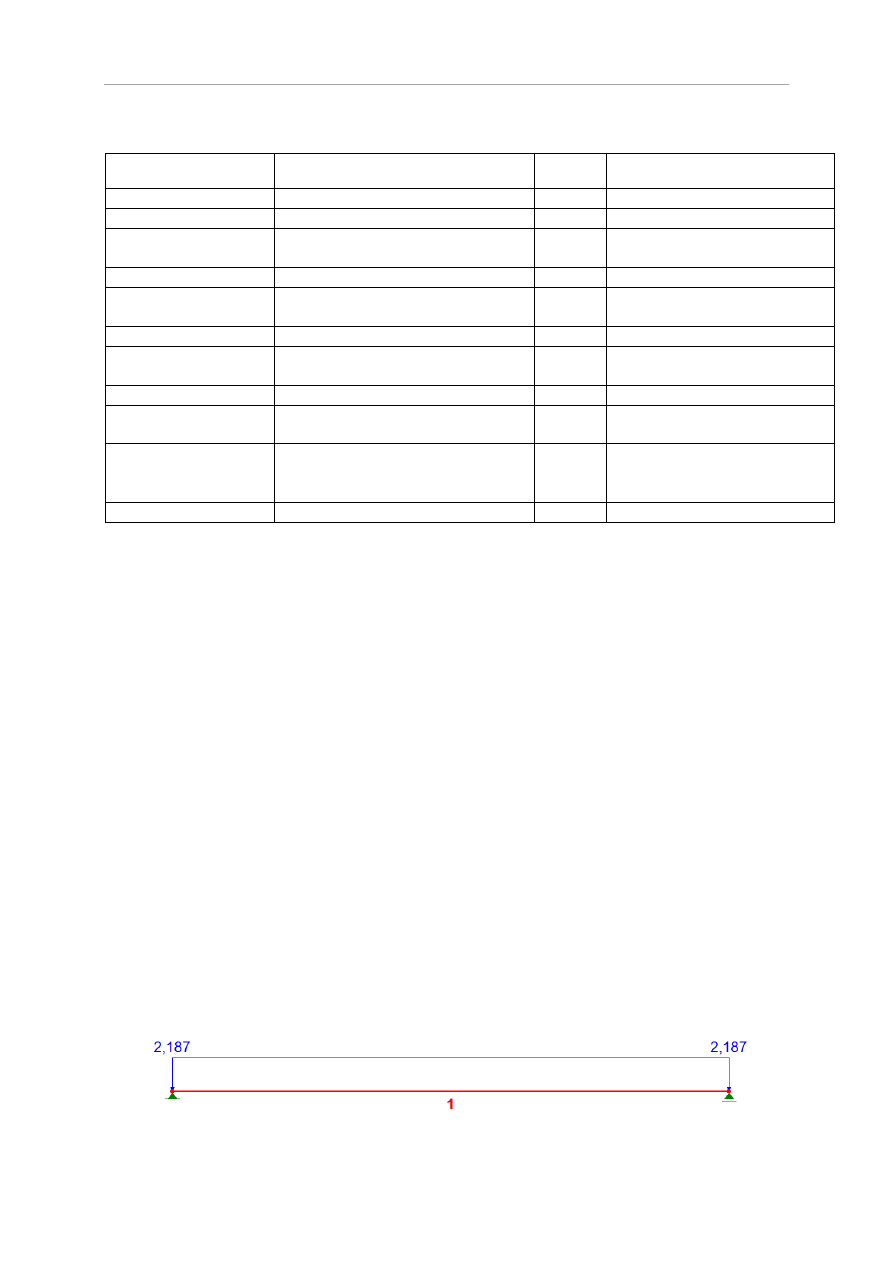
Wartość obliczeniowa obciążenia użytkowego przypadającego na belkę wynosi 1,62

Sumaryczna wartość obciążenia na belkę q=1,458+0,729=2,187 kN/m

Rys.5.24 Schemat statyczny belki stropu Ceram

Projekt Budownictwo Ogólne II

41

Wydział Budownictwa Wodnego i Lądowego

Dopuszczalna wartość obciążenia wg [18] wynosi q

2

=4,42 kN/m

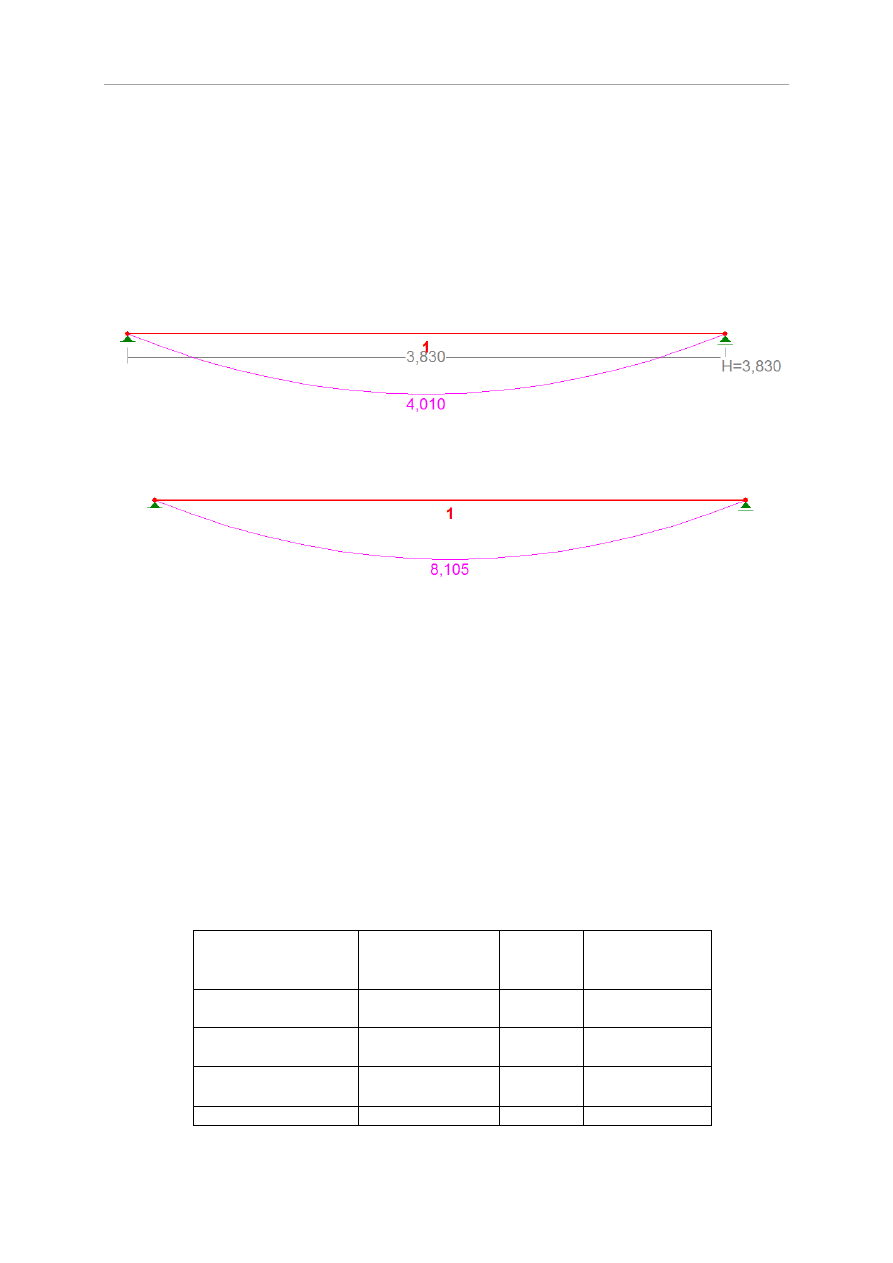
Obliczenia przeprowadzono w programie RM-WIN. Otrzymane wykresy momentów
przedstawia rysunek.
a)

b)

Rys.5.25 Wykresy momentów dla stropu: a) od obciążenia rzeczywistego, b) od obciążenia

dopuszczalnego.

Obliczona maksymalna wartość momentu zginającego 4,010 kNm nie przekracza wartości
dopuszczalnej wynoszącej 8,105 kNm. Wobec tego, belka stropowa Ceram spełnia
wymagania stanów granicznych.

Do obciążenia stropu przyjęto zgodnie z tablicą 6.2, [10] charakterystyczną wartość
obciążenia użytkowego dla stropu q

k

=1,5 kN/m

2

, obciążenie od ścianek działowych przyjęto

wg punktu 6.3.1.2(8), [10]:

Tabela 5.27 Ciężar ścianki działowej na 1m długości

Obciązenie

Wartość

charakterystyczna

[kN/m]

γ

f

Wartość

obliczeniowa

[kN/m]

tynk gipsowy 10mm
0,01*3,135*12

0,376

1,35

0,508

gazobeton 100mm
0,1*3,135*4

1,254

1,35

1,693

tynk gipsowy
10mm0,01*3,135*12

0,376

1,35

0,508

RAZEM

2,006

2,709

Projekt Budownictwo Ogólne II

42

Wydział Budownictwa Wodnego i Lądowego

q

k

=1,2 kN/m

2

, ponieważ ciężar ścianki działowej przekracza 2kN/m

Tabela 5.28 Zestawienie obciążeń na strop Ceram bez ciężaru własnego

Tabela 5.29 Zestawienie obciążeń na strop Ceram z ciężarem własnym

Obciązenie

Wartość charakterystyczna

[kN/m

2

]

γ

f

Wartość obliczeniowa [kN/m

2

]

g-

obciążenie stałe

panele 10mm 0,08

0,080

1,35

0,108

gładź cementowa
35mm 0,035*21

0,735

1,35

0,992

folia PE

-

-

styropian 20mm
0,02*0,45

0,009

1,35

0,012

strop Ceram

3,03

1,35

4,091

tynk gipsowy 10mm
0,01*12

0,120

1,35

0,162

RAZEM-

obc.stałe

3,974

5,365

p-

obciążenie zmienne

technologiczne

1,500

1,50

2,250

q-

obciążenie

zastępcze od ścianek
działowych 1,2

1,200

1,35

1,620

RAZEM g+q

5,174

6,985

Efektywną rozpiętość elementu l

eff

obliczono według wzoru 5.8, [13], przyjmując częściowo

utwierdzone podparcie:

l

eff

= l

n

+a

1

+a

2

l

n

- rozpiętość w świetle podpór, przyjęto 3,0m

Obciązenie

Wartość

charakterystyczna

[kN/m

2

]

γ

f

Wartość obliczeniowa

[kN/m

2

]

g-

obciążenie stałe

panele 10mm 0,08

0,080

1,35

0,108

gładź cementowa
35mm 0,035*21

0,735

1,35

0,992

folia PE

-

-

styropian 20mm
0,02*0,45

0,009

1,35

0,012

tynk gipsowy 10mm
0,01*12

0,120

1,35

0,162

RAZEM-

obc.stałe

0,944

1,620

p-

obciążenie zmienne

technologiczne

1,500

1,50

2,250

q-

obciążenie

zastępcze od ścianek
działowych 1,2

1,200

1,35

1,620

RAZEM g+q

2,144

3,240

Projekt Budownictwo Ogólne II

43

Wydział Budownictwa Wodnego i Lądowego

a

1

i a

2

– odległość teoretycznych punktów podparcia elementu od krawędzi podpór

a

1,2

= min { 0,5h; 0,5t }= min{0,115m; 0,12m}=0,115m.

h- wysokość stropu
t- grubość ściany

l

eff

= 3,0+0,115+0,115=3,23m

Obliczona w tabeli 4.26. wartość obliczeniowa obciążenia całkowitego wynosi 3,24 kN/m

2

.

Rozstaw belek stropowych wynosi 0,45 m, wiec wartość obliczeniowa obciążenia stałego
przypadającego na belkę wynosi 3,24

Wartość obliczeniowa obciążenia użytkowego przypadającego na belkę wynosi 1,62

Sumaryczna wartość obciążenia na belkę q=1,458+0,729=2,187 kN/m

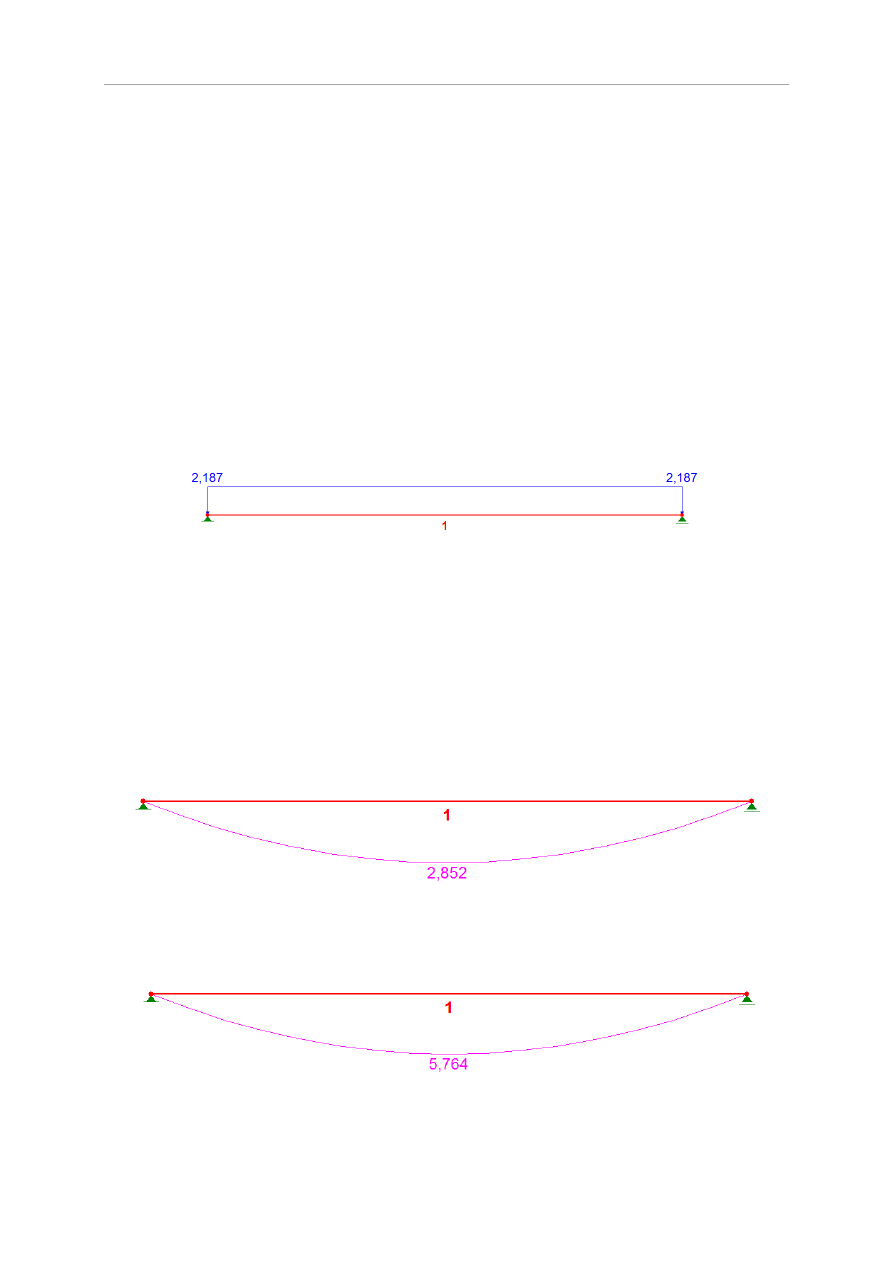
Rys.5.24 Schemat statyczny belki stropu Ceram

Dopuszczalna wartość obciążenia wg [18] wynosi q

2

=4,42 kN/m

Obliczenia przeprowadzono w programie RM-WIN. Otrzymane wykresy momentów
przedstawia rysunek.
a)

b)

Projekt Budownictwo Ogólne II

44

Wydział Budownictwa Wodnego i Lądowego

Rys.5.25 Wykresy momentów dla stropu: a) od obciążenia rzeczywistego, b) od obciążenia

dopuszczalnego.

Obliczona maksymalna wartość momentu zginającego 2,852 kNm nie przekracza wartości
dopuszczalnej wynoszącej 5,764 kNm. Wobec tego, belka stropowa Ceram spełnia
wymagania stanów granicznych.

5.3 Nadproże L 19

Przyjęto nadproża w formie belek prefabrykowanych żelbetowych L19.

Tabela 5.30 Zestawienie obciążeń dla nadproża

Obciązenie

Wartość

charakterystyczna

[kN/m

2

]

γ

f

Wartość

obliczeniowa

[kN/m

2

]

tynk cementowo-
wapienny 15mm
0,015*18,5

0,185

1,35

0,250

mur z gazobetonu
240mm 0,24*7

2,943

1,35

3,973

tynk gipsowy 10mm
0,01*12

0,120

1,35

0,162

styropian 120mm
0,12*0,4

0,048

1,35

0,065

obciążenie ze stropu

5,174

1,35

6,985

RAZEM

8,470

11,435

wieniec żelbetowy
0,25*0,25*25

1,563

1,35

2,110

ciężar nadproża
0,25*0,19*25

1,188

1,35

1,604

Rozpiętość efektywna nadproża :
l

eff

= 1,05 l

s

l

eff

= 1,05

m

a)

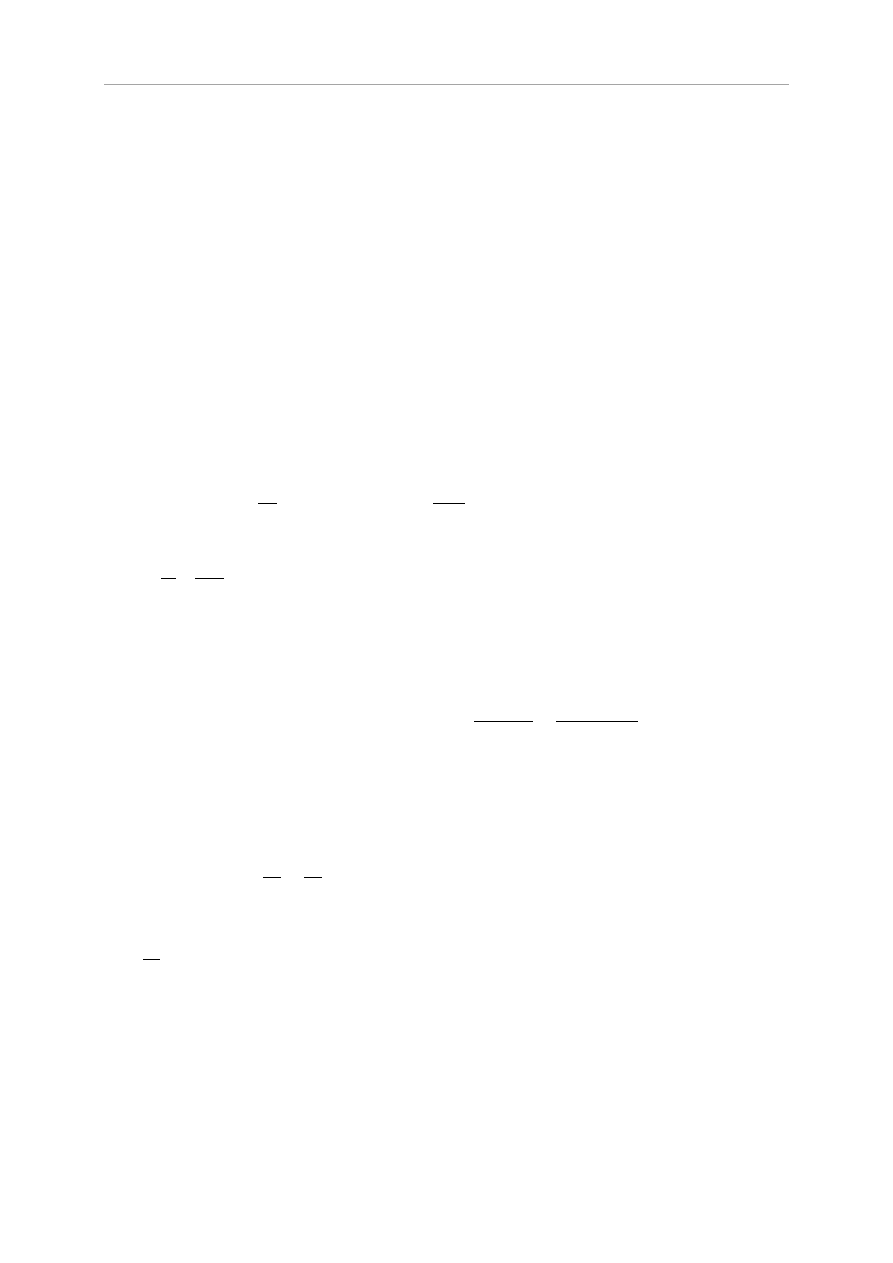
Projekt Budownictwo Ogólne II

45

Wydział Budownictwa Wodnego i Lądowego

Rys.5.26 Widok fragmentu rzutu z nadprożem

Powierzchnia obciążenia dla nadproża bez powierzchni wieńców wynosi:
A

obc

=1,0 m

2



Sprawdzenie stanu granicznego nośności

Obciążenie przypadające od muru N

1

=( 0,25+3,973+0,162+0,065)

1,0=4,45 kN

Według [9], obciążenie ze stropu należy przyjmować w postaci obciążenia równomiernie
rozłożonego q

s

‘ na całej efektywnej rozpiętości nadproża.

Obciążenie obliczeniowe ze stropu q

s

=6,985 kN/m

2

q

s

= 6,99 · 6,0 · 0,5

= 31,46 kN/m

q’

s

= (q

s

+ q

wieńca

) ·

= (31,455 + 2,110) ·

= 20,39 kN/m

Obciążenie zastępcze od ciężaru muru:
q

zast,1

=

N

1

l

eff

=

4,45

1,575

= 2,86 kN/m

Całkowite obciążenie zastępcze przypadające na nadproże:
q

zast

= q

zast,1

+ q

’

s

+ q

nadproża

= 2,86 + 20,39 + 1,604 = 24,854 kN/m

Nadproże traktujemy jako belkę swobodnie podpartą.

Maksymalny moment zginający wynosi:

Przyjęto 2 belki N/180.

Belka N/180 posiada zbrojenie w postaci 2 prętów o średnicy 6 mm, o polu przekroju As

1

=

1,01cm

2

= 1,01 · 10

-4

m

2

.

Beton:

C20/25,

f

cd

=

=

= 14,29MPa

gdzie:

f

cd

=

wytrzymałość obliczeniowa betonu na ściskanie

f

ck

= 20,0 MPa – wytrzymałość charakterystyczna betonu C20/25 na ściskanie (wg [13])

c

= 1,4 – współczynnik częściowy zastosowany do betonu, ( tab. NA. 2 [13] )

stal: RB500, f

y

=500MPa, f

yd

=500/1,15=435 MPa

Grubość otulenia zbrojenia dla klasy XC3( wg pkt.4.4.1 [13] ):
c

nom

= c

min

+ Δc

dev

= 25mm + 5mm = 30mm

Projekt Budownictwo Ogólne II

46

Wydział Budownictwa Wodnego i Lądowego

W belce L 19 mamy strzemiona Φ4,5mm.

b

w

= 60 mm

Wysokość użyteczna przekroju:
d = 190 – 30 – 4,5 – 0,5 · 8 = 153,5 mm

Stopień zbrojenia:
ρ =

=

= 0,0110 = 1,10 %

Na podstawie stopnia zbrojenia odczytano z tabeli 6, [2]:

=0,3218 153,5=49,40mm

M

Rd

=

M

Rd

=

=6,6 kNm

Ponieważ przyjęto 2 belki M

Rd

=13,2 kNm> 7,71 kNm

Stan graniczny nośności spełniony.

Przyjęto dwie belki N/180.

5.4 Mur z porothermu

5.4.1 Obliczenie filara w ścianie zewnętrznej

Ściana zewnętrzna wykonana będzie z porothermu 250mm o

Na zaprawie zwykłej, przepisanej, klasy M5.
Dane z katalogu producenta:

- masa bloczka 250mm: 18 kg,
- zużycie na 1m

2

muru: 10,7 szt.

- ciężar własny muru: 18 10,7 = 192,6 kg/m

2

= 1,93 kN/m

2

Wytrzymałość charakterystyczna muru na ściskanie obliczona wg wzoru 3.1, [15]:

(5.19)

gdzie:

K–stała podana w NA.5 [15], dla porothermu grupy1: K=0,45
f

b

- znormalizowana wytrzymałość średnia elementów murowych na ściskanie w kierunku

działania obciążenia, dla porothermu odmiany 700 producent podaje f

b

=5,3 MPa

f

m

– wytrzymałość zaprawy na ściskanie, dla zaprawy M5: f

m

=5 MPa

Projekt Budownictwo Ogólne II

47

Wydział Budownictwa Wodnego i Lądowego

Współczynnik bezpieczeństwa

określono wg tablicy NA.1, [15] dla zaprawy przepisanej,

elementów kat.I, klasa wykonania robót na budowie B:

Określenie wytrzymałości muru:

Pole przekroju poprzecznego konstrukcji murowej:
A=0,25

0,5=0,125 m

2

< 0,3m

2

,więc wytrzymałość obliczeniową zmniejszamy, zgodnie z tab.

NA.2, [15], przez współczynnik

=1,43

Wytrzymałość obliczeniowa muru wynosi:

0,74 MPa

Przyjęto następujące dane geometryczne:

-wymiary filara: 0,25 x 1 m
-szerokość pasma, z którego przekazywane jest obciążenie na filar:

0 m

-grubość muru

t=0,25m

- szerokość wieńca

-wysokość ściany w świetle stropów h=2,48 m
-rozpiętość stropu w świetle ścian l

s

=3,35 m

19

0

0

1673

Projekt Budownictwo Ogólne II

48

Wydział Budownictwa Wodnego i Lądowego

5.27. Rzut parteru i widok elewacji budynku z zaznaczonym obliczanym filarem w ścianie

zewnętrznej: a) rzut parteru, b) widok przekroju



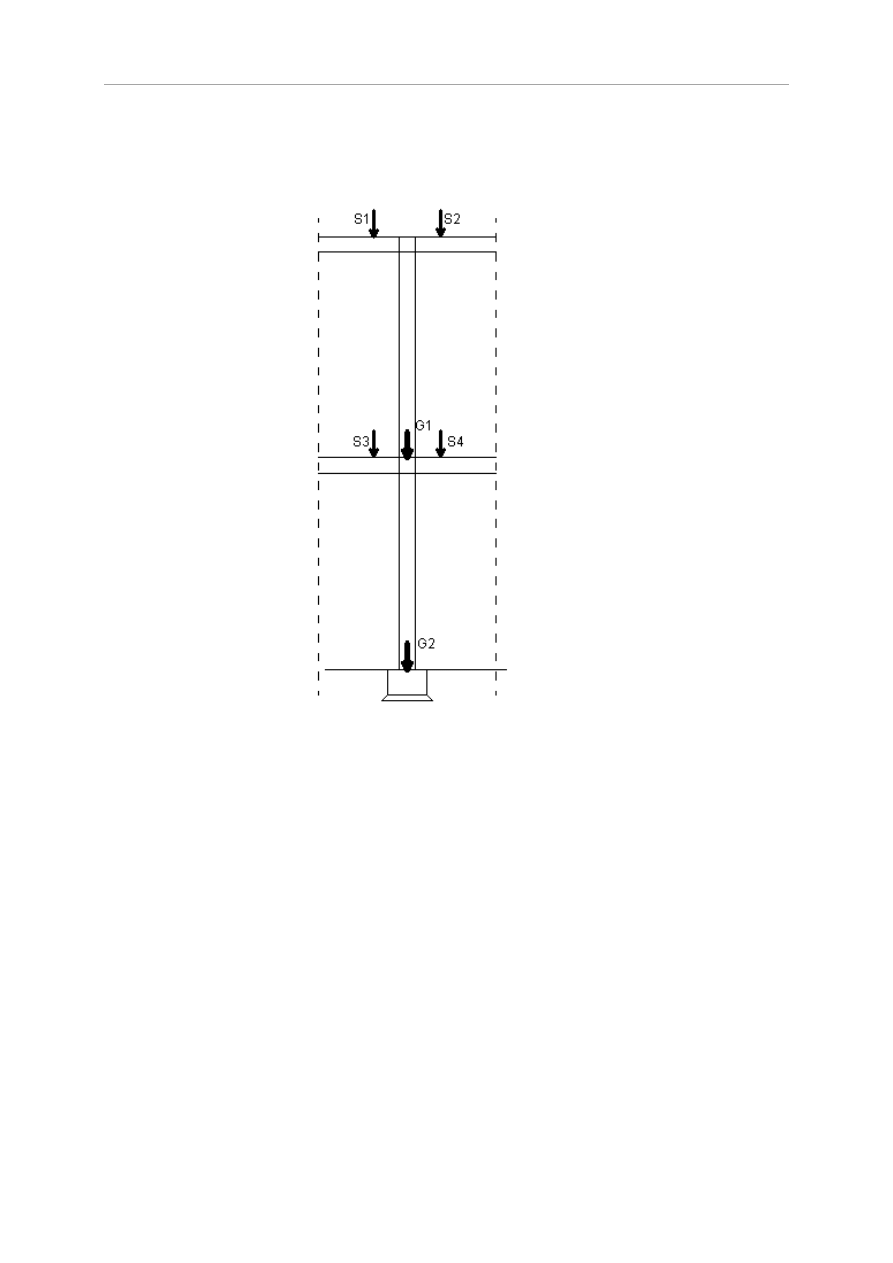
Zestawienie obciążeń na filar



ciężar ścian:

-

ciężar własny muru:

1,93

kN/m

2

-

ciężar tynku cem. – wap.:

0,015 18,5 1,35 = 0,37 kN/m

2

-

ciężar tynku gipsowego:

0,01 12 1,35 = 0,162 kN/m

2

-

ciężar styropianu: 0,12 0,4 1,35 = 0,065 kN/m

2

-

ciężar własny ściany wynosi:

q

s

= 2,606 + 0,37 + 0,162+0,065 = 3,203 kN/m

2



Obciążenie od stropów:

obciążenie od stropu:

6,985 kN/m

2

powierzchnia obciążenia stropu:

A

obc1

= 1,9 1,673 = 3,18 m

2

reakcja od stropu:

S

1

= S

2

= S = 6,985 3,18 = 22,21 kN

Powierzchnia obciążenia stolarką okienną i drzwiową na parterze:

2,1

2

Powierzchnia obciążającego muru (parter) skorygowana o powierzchnię stolarki okiennej:

2

Na poddaszu nie ma stolarki w obszarze zbierania obciążenia dla obliczanego filara.

8

00

3

46

2

454

3

50

Projekt Budownictwo Ogólne II

49

Wydział Budownictwa Wodnego i Lądowego

Powierzchnia obciążającego muru (poddasze) :

2

Obciążenie z dachu:

Stanowi je reakcja pionowa z krokwi. Zgodnie z tabelą (5.23) wynosi ona 12,09 kN. Brak
obciążenia od murłatu.

W obliczeniach przyjęto ciężar muru taki sam jak wieńca żelbetowego.
Przyjęto ciężar stolarki okiennej i drzwiowej 0,4 kN/m

2

Siły skupione od ciężaru ścian:



Obciążenie wiatrem

Wartość obciążenia wiatrem określono ze wzorów (5.4), (5.7) opisanych w punkcie
dotyczącym zbierania obciążeń dla wiązara dachowego:

pe

e

p

e

c

z

q

w





)

(

(5.7)

=

=0,3 kN/m

2

(wg NB.1, [12])

Wartość współczynnika ekspozycji wyznaczono na podstawie rysunku 4.4.

(5.6)

gdzie: z –wysokość odniesienia dla budynku wg rozdziału 7 [12]:

=1,36

Pola obciążenia ścian budynku wyznaczono z godnie z rysunkiem 7.5 [12].

Projekt Budownictwo Ogólne II

50

Wydział Budownictwa Wodnego i Lądowego

Rys.1.4

Rys. 5.29 Oznaczenie ścian pionowych przy obciążeniu wiatrem

Przy obliczaniu filara uwzględniono pola D oraz E. Współczynniki ciśnienia zewnętrznego
zostały wybrane z tab.7.1, [12] dla h/d=7,75/6,95=1,12.

Ciśnienie sumaryczne działające na dach jest różnicą algebraiczną ciśnień po dwóch stronach
przegrody. Dlatego należy wyznaczyć ciśnienie działające na stronę wewnętrzną konstrukcji,
a następnie odjąć je od ciśnienia po stronie zewnętrznej(wg pkt.5.2, [12]).

Współczynniki c

pi

dobiera się stosując bardziej niekorzystną z wartości: c

pi

=+0,2, c

pi

=-0,3.

Tabela 5.31 Obciążenie wiatrem działające na filar

Pole

c

pe

w

e

c

pi

w

i

w

e

-w

i

γ

f

w

d

– wartość

obliczeniowa

Szerokość

pasma

oddziaływania

Obciążenie

wiatrem

[kN/m

2

]

[m]

[kN/m]

A

-1,2

-0,492

-0,3

-0,123

-0,615

1,5

-0,923

0,7917

-0,731

B

-0,8

-0,328

0,2

0,082

-0,410

1,5

-0,615

1,1083

-0,682

Wybrano wartość charakteryzującą parcie wiatru: w

e

=-0,682 kN/m



Określenie smukłości filara.

Projekt Budownictwo Ogólne II

51

Wydział Budownictwa Wodnego i Lądowego

Wysokość efektywną filara przyjęto ze wzoru 5.2, [15]:

h

ef

= ρ

n

h

(5.20)

gdzie:
h = 2,48 m – wysokość kondygnacji w świetle,
ρ

n

= współczynnik redukcji

Według pkt. 5.5.1.2, [15] w ścianach utwierdzonych na górnej i dolnej krawędzi przez stropy
żelbetowe:
ρ

2

= 0,75

h

ef

= 0,75

=1,86m

Współczynnik smukłości ściany murowej :

λ =

=

= 7,44 < 27

(wg.5.5.1.4, [15])

(5.21)

t

ef

= t –grubość ściany



Sprawdzenie stanu granicznego nośności filara

Sprawdzenie nośności przeprowadzono w trzech miejscach: u góry, u dołu i w połowie
wysokości ściany (odpowiednio przekroje I-I, II-II, III-III).
Sprawdzenie stanu granicznego nośności sprawdza się z warunku określonego w pkt. 6.1,
[15]:

(5.22)

t-grubość ściany

-obliczeniowa wytrzymałość muru na ściskanie

-współczynnik redukcyjny nośności, u góry i u dołu ściany, wyznaczany ze wzoru 6.4,
[15]:

=

(5.23)

e

i

- odpowiednio mimośród u dołu, u góry ściany wyznaczany ze wzoru 6.5. [15]:

(5.24)

Projekt Budownictwo Ogólne II

52

Wydział Budownictwa Wodnego i Lądowego

-moment zginający wywołany działaniem obciążeń obliczeniowych u góry i u dołu

ściany

-siła pionowa wywołana działaniem obciążeń obliczeniowych u góry i u dołu ściany

-mimośród pochodzący od sił poziomych np. wiatru

-mimośród początkowy wyznaczany jako h

ef

/450

Dla połowy wysokości ściany wyznacza się mimośród e

mk.

(5.25)

-mimośród działania obciążenia

=

(5.26)

-obliczeniowy moment zginający w połowie wysokości ściany

-obliczeniowa siła pionowa w połowie wysokości ściany

-mimośród w połowie wysokości ściany

-mimośród wywołany przez pełzanie, obliczany ze wzoru:

√

(5.27)
t

ef

=t

-końcowy współczynnik pełzania

Wyznaczenie wartości momentów zginających przeprowadzono w oparciu o wzór C.1, [15]:

(5.28)

gdzie:

n

i

-współczynnik sztywności prętów równy 4 dla prętów utwierdzonych na obydwu końcach,

w przeciwnym wypadku 3
E

i

=1000f

k

=1000

I

i

-moment bezwładności pręta i

h

i

-wysokość w świetle pręta i

l

i

- rozpiętość w świetle pręta i

w

i

- obciążenie równomiernie rozłożone na prętach

Obliczone wg powyższego wzoru momenty redukuje się współczynnikiem redukcyjnym:
=

(5.29)

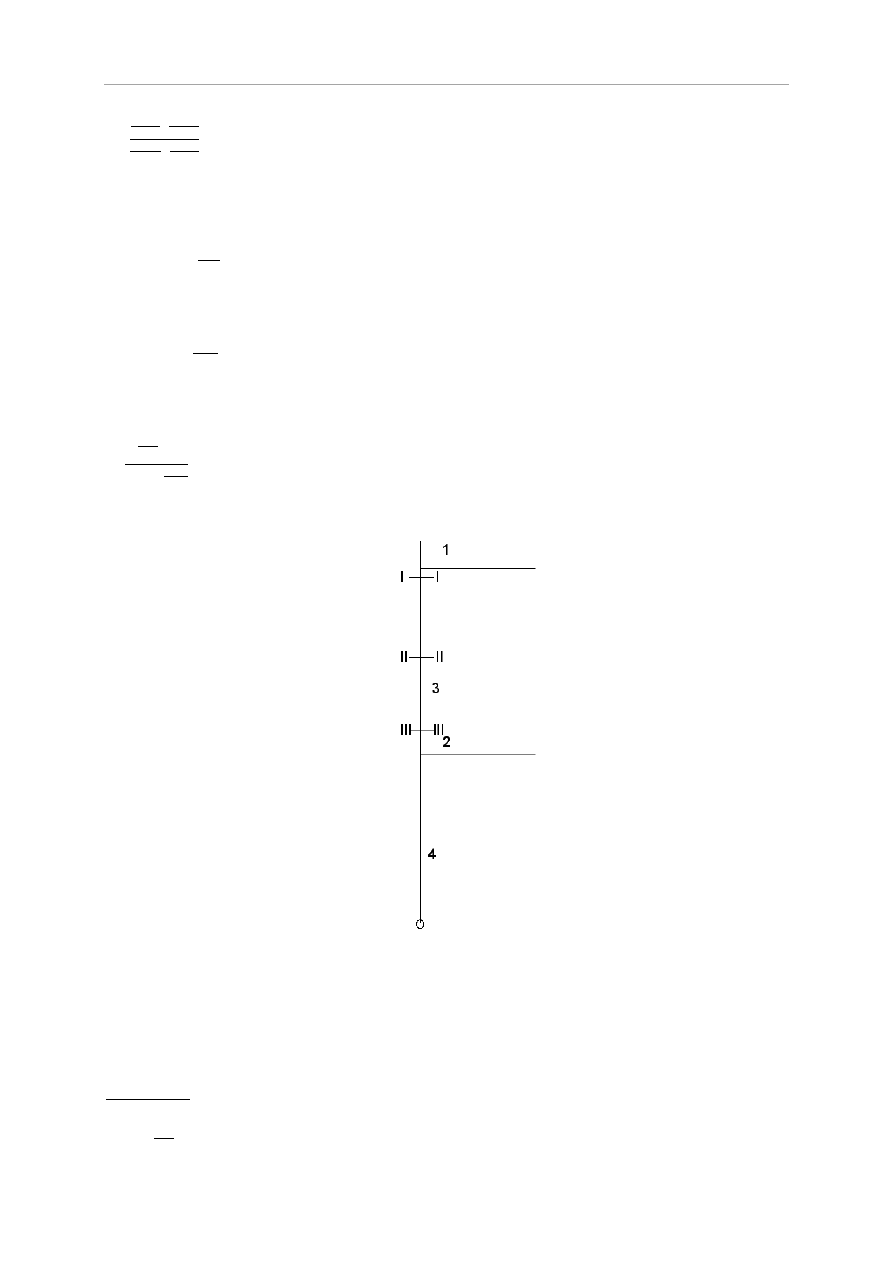
Projekt Budownictwo Ogólne II

53

Wydział Budownictwa Wodnego i Lądowego

k

m

=

(5.30)

Dla połowy wysokości ściany oblicza się współczynnik redukcyjny:

(5.31)

gdzie:

(5.32)

Dla muru o module sprężystości E=1000f

k

u=

(5.33)

Rys.5.30 Schemat obliczeniowy filara

Sprawdzenie nośności w poszczególnych przekrojach:

Przekrój I-I

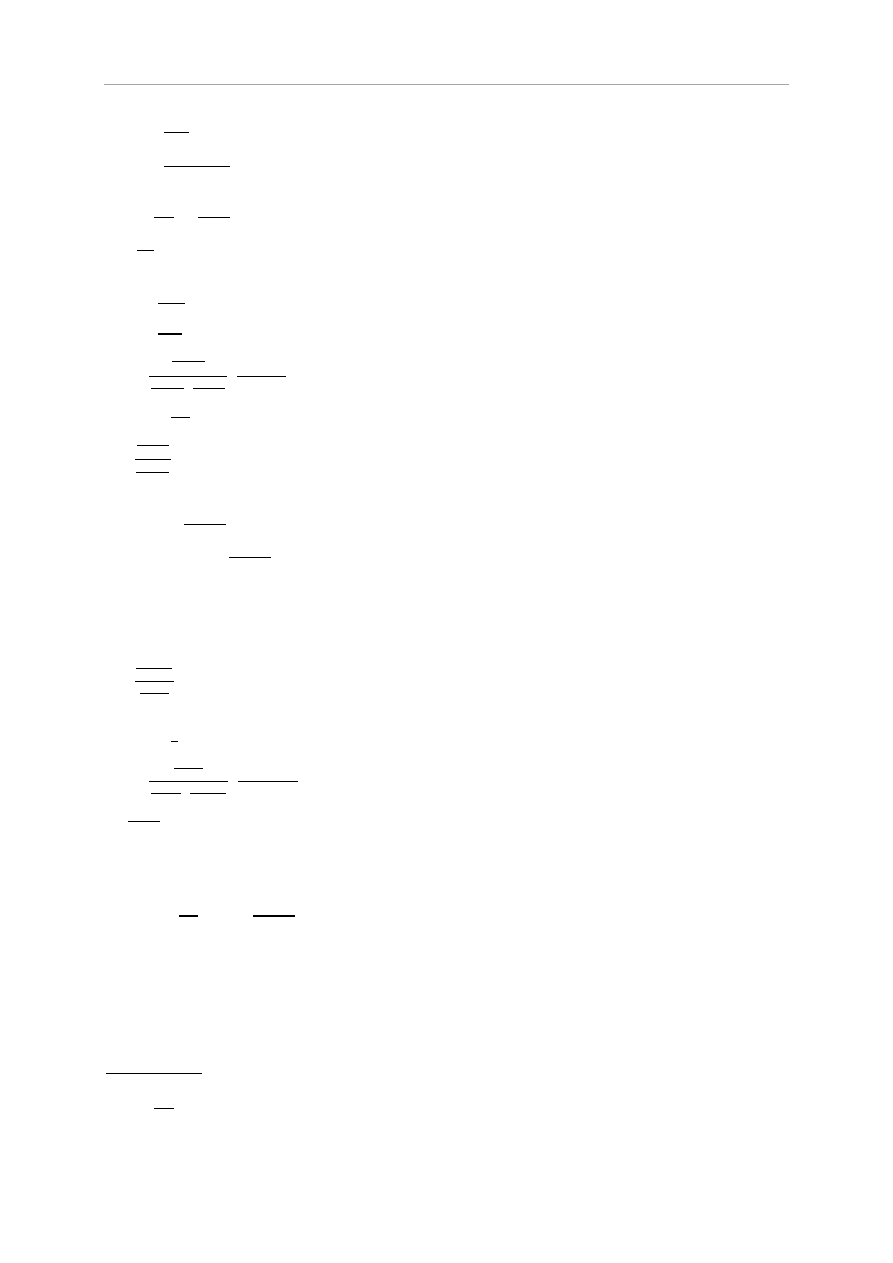
Projekt Budownictwo Ogólne II

54

Wydział Budownictwa Wodnego i Lądowego

= 54,83 kN

e

I

=

k

m

=

E

betonu C20/25

=30000 MPa

EI

3

=1710

2,23

N

EI

1

=0,33

30000

12,89

N

h

3

=2,48 m

l

1

=3,35 m

w

1

=6,985 kN/m

2

m= 13,27 kN/m

w

3

=-0,682kN/m

k

m

=

k

m

=2,0

[

]

e

I

=

=0,05 0,25=0,0125 m

W przekroju I-I współczynnik redukcyjny wynosi

W przekroju I-I nośność filara wynosi:

Stan graniczny nośności w przekroju I-I nie jest przekroczony.

Przekrój II-II

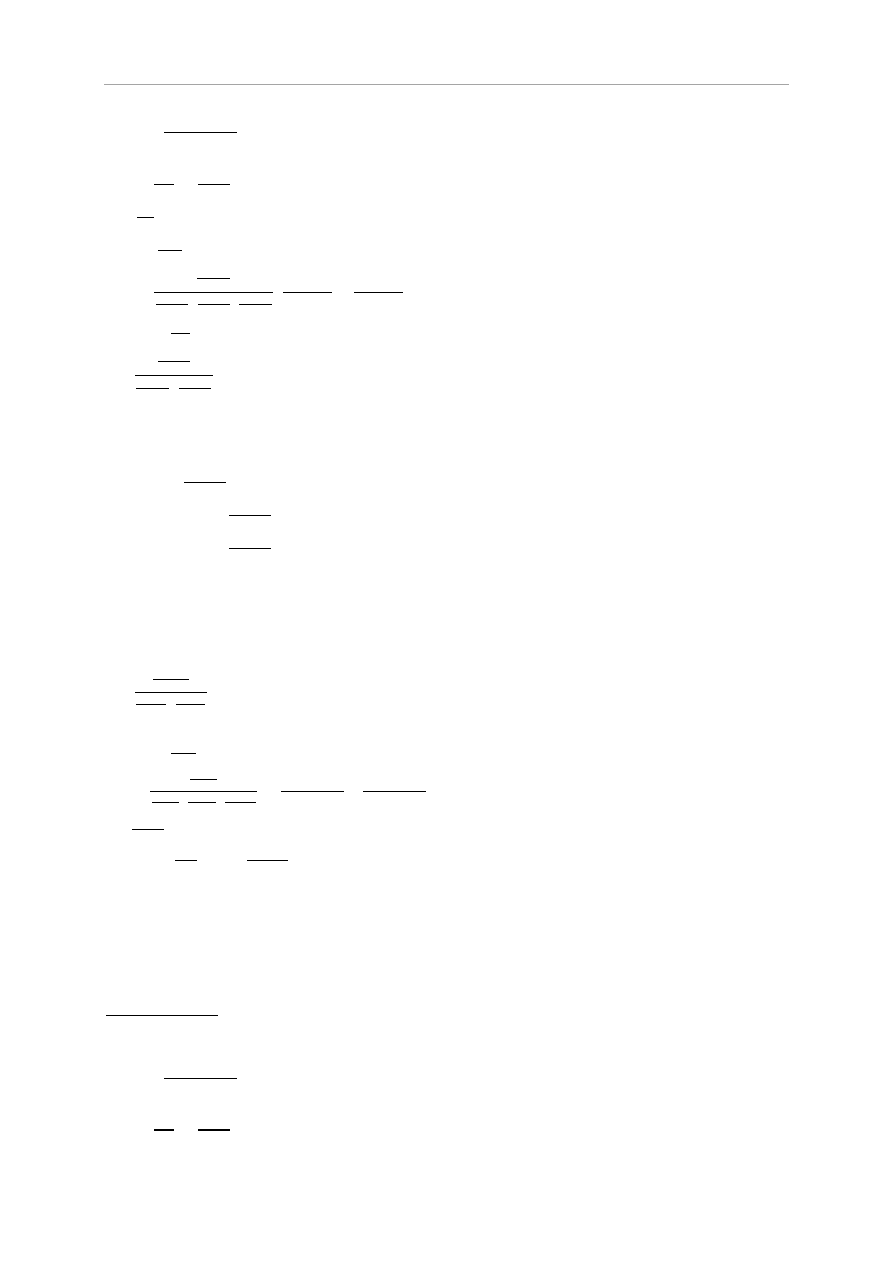
Projekt Budownictwo Ogólne II

55

Wydział Budownictwa Wodnego i Lądowego

65,15 kN

e

II

=

k

m

=

E

betonu C12/15

=27000 MPa (ściana piwnicy)

E

betonu C20/25

=30000 MPa (strop)

EI

3

=1710

2,23

N

EI

1

=0,33

30000

12,89

N

EI

4

=0,33

27000

11,60

N

h

3

=2,48 m

h

4

=2,45 m

l

2

=3,35 m

w

1

=6,985 kN/m

2

m= 13,27 kN/m

w

3

=0,682kN/m

k

m

=

k

m

=2,0

[

]

e

II

=

=0,05 0,24=0,012 m

W przekroju II-II nośność filara wynosi:

Stan graniczny nośności w przekroju II-II nie jest przekroczony.

Przekrój III-III

59,99 kN

65,15 kN

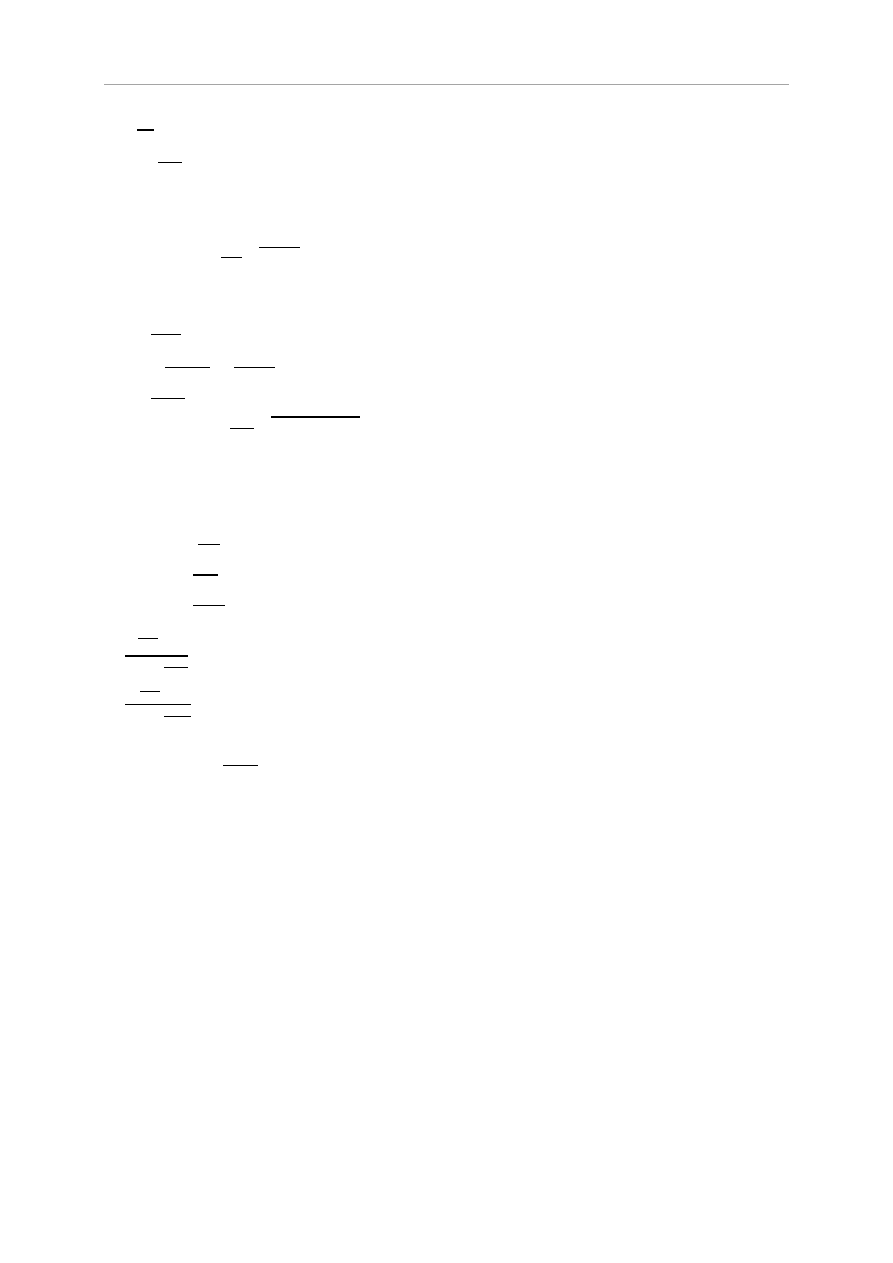
Projekt Budownictwo Ogólne II

56

Wydział Budownictwa Wodnego i Lądowego

e

II

=

Mimośród w połowie wysokości ściany wynosi

√

t

ef

=t

=0,5 (ceramika)

√

Założono cechę sprężystości zaprawy 1000.

u=

u=

W przekroju III-III nośność filara wynosi:

Stan graniczny nośności w przekroju III-III nie jest przekroczony.

5.4.2 Obliczenie ściany wewnętrznej

Ściana wewnętrzna piwnicy wykonana będzie z porothermu 25 P+W 250mm .Na zaprawie
zwykłej, przepisanej, klasy M5. Elementy murowe kategori I, klasa wykonania robót na
budowie B.

Dane z katalogu producenta:

- masa bloczka 250mm: 18 kg,
- zużycie na 1m

2

muru: 10,7 szt.

-ciężar własny muru: 18 10,7 = 193 kg/m

2

= 1,9 kN/m

2

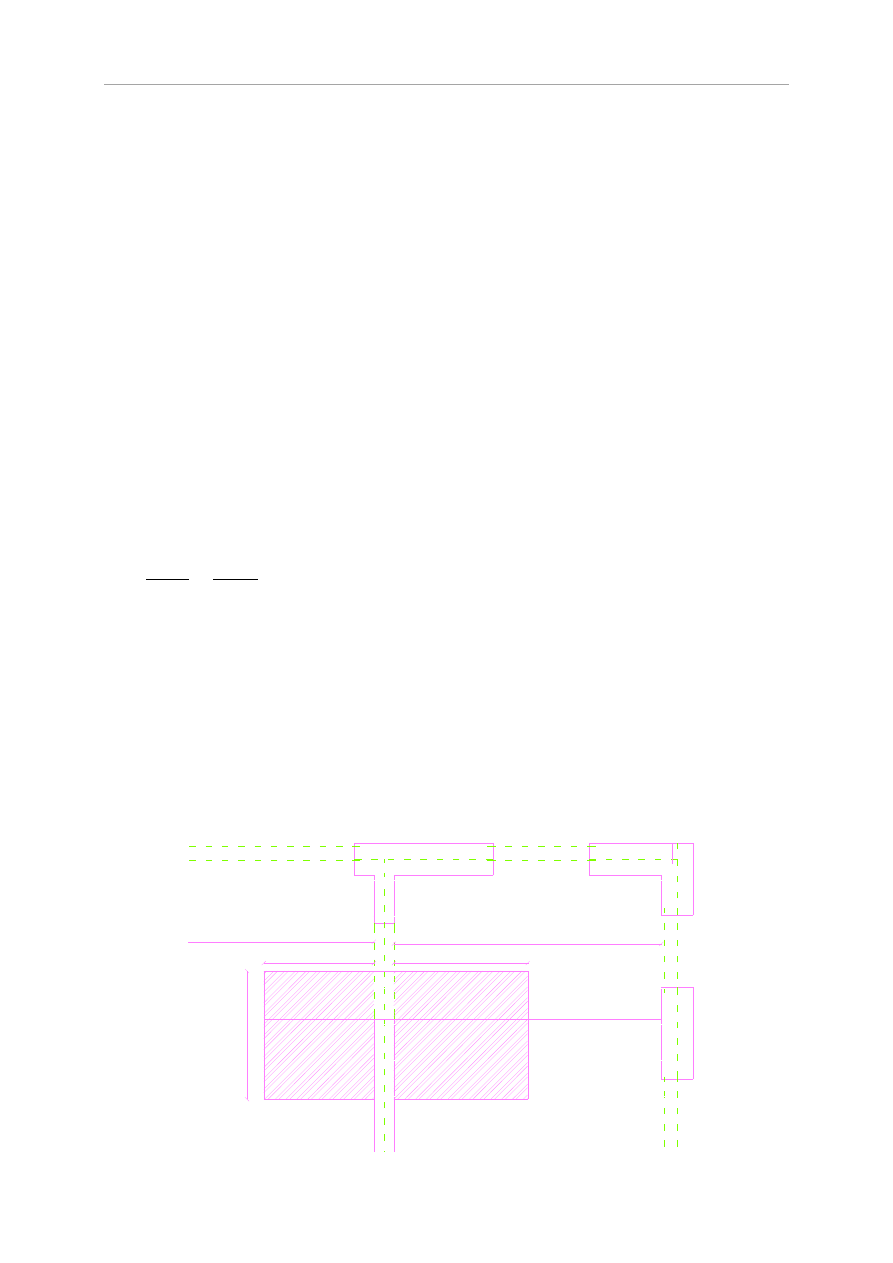
Projekt Budownictwo Ogólne II

57

Wydział Budownictwa Wodnego i Lądowego

Wytrzymałość charakterystyczną muru na ściskanie obliczono analogicznie do punktu 5.4.1 :

(5.19)

K=0,45
f

b

=5,3 MPa

f

m

=5 MPa

Określenie wytrzymałości muru:

Pole przekroju poprzecznego konstrukcji murowej:

A=0,25

1=0,25 m

2

< 0,3m

2

,więc wytrzymałość obliczeniową zmniejszamy, zgodnie z tab.

NA.2, [14], przez współczynnik

=1,43

Wytrzymałość obliczeniowa muru wynosi:

0,74 MPa

Przyjęto następujące dane geometryczne:

- wymiary: 0,25 x 1 m
-

szerokość pasma, z którego przekazywane jest obciążenie na filar:

1,60 m

-

grubość muru:

t=0,25m

-

szerokość wieńca:

-

wysokość ściany w świetle stropów: h=2,45 m

-

rozpiętość stropu w świetle ścian: l

s1

=2,75 m

l

s2

=3,445 m

1375

1673

1600

2750

3345

Projekt Budownictwo Ogólne II

58

Wydział Budownictwa Wodnego i Lądowego

Rys. 5.31. Rzut parteru z zaznaczonym obliczanym fragmentem ściany wewnętrznej

Rys. 5.32 Układ sił działających na ścianę wewnętrzną



Zestawienie obciążeń na filar



ciężar ścian:

-

ciężar własny muru:

1,9

kN/m

2

-

ciężar tynku gipsowego po obu stronach ściany:

3,2

0,01 12 1,35 = 0,518 kN/m

2

-

ciężar własny muru wynosi:

q

s

= 2,565+ 0,518 = 3,083 kN/m

2



Obciążenie od stropów:

-

obciążenie od stropu:

6,982 kN/m

2

-

powierzchnia obciążenia stropu:

A

obc1

= 1,6 1,375= 2,2 m

2

- reakcja od stropu:

S

1

= S

3

= 6,982 1,375 = 9,6 kN

S

2

=S

4

=6,982 1,673=11,68 kN

Projekt Budownictwo Ogólne II

59

Wydział Budownictwa Wodnego i Lądowego

Powierzchnia obciążającego muru (piwnica):

2

Powierzchnia obciążającego muru (parter):

2

Siły skupione od ciężaru ścian:

(ściana z porothermu)

(ściana z porothermu)



Określenie smukłości filara

Według pkt. 5.5.1.2, [15] w ścianach utwierdzonych na górnej i dolnej krawędzi przez stropy
żelbetowe:
ρ

2

= 0,75

h

ef

= 0,75

2,45=1,84m

Współczynnik smukłości ściany murowej :

λ =

=

= 7,36 < 27

(wg.5.5.1.4, [15])

t

ef

= t –grubość ściany

Rys.5.33 Schemat obliczeniowy ściany wewnętrznej

Projekt Budownictwo Ogólne II

60

Wydział Budownictwa Wodnego i Lądowego



Sprawdzenie stanu granicznego nośności filara

Sprawdzenie nośności przeprowadzono tak j w trzech miejscach: u góry, u dołu i w połowie
wysokości ściany (odpowiednio przekroje I-I, II-II, III-III).
Sprawdzenie stanu granicznego nośności sprawdzono analogicznie jak w punkcie 4.4.1. z
warunku określonego we wzorze (4.4) i zgodnie z pozostałymi wzorami z tego punktu.
Pominięto wzory dotyczące oddziaływania wiatru, gdyż mamy do czynienia ze ściana
wewnętrzną.

(5.22)

Sprawdzenie nośności w poszczególnych przekrojach:

Przekrój I-I

= 57,93 kN

e

I

=

k

m

=

E

betonu C20/25

=30000 MPa

E

betonu C12/15

=27000 MPa

EI

3

=1710

3,6

N

EI

4,5

=0,33

30000

20,6

N

EI

6

=2700

5,63

N

h

3

=2,48 m

h

6

=2,45 m

l

4

=2,75 m

l

5

=3,345

w

4

=w

5

= 6,982 kN/m

2

1,6m= 11,17 kN/m

Projekt Budownictwo Ogólne II

61

Wydział Budownictwa Wodnego i Lądowego

k

m

=

k

m

=2,0

[

]

e

1

=

=0,05 0,25=0,0125 m

e

1

=0,0125m

W przekroju I-I współczynnik redukcyjny wynosi

W przekroju I-I nośność filara wynosi:

Stan graniczny nośności w przekroju I-I nie jest przekroczony.

Przekrój II-II

kN

e

II

e

II

m, więc e

II

W przekroju II-II nośność filara wynosi:

Stan graniczny nośności w przekroju II-II nie jest przekroczony.

Przekrój III-III

Mimośród w połowie wysokości ściany wynosi

Projekt Budownictwo Ogólne II

62

Wydział Budownictwa Wodnego i Lądowego

√

t

ef

=t

=0,5 (ceramika)

√

, więc

Założono cechę sprężystości zaprawy 1000.

u=

u=

W przekroju III-III nośność filara wynosi:

Stan graniczny nośności w przekroju III-III nie jest przekroczony.

Projekt Budownictwo Ogólne II

63

Wydział Budownictwa Wodnego i Lądowego

BIBLOGRAFIA

Wykaz piśmiennictwa

[1]

Hoła J., Pietraszek P., Schabowicz K., Obliczanie konstrukcji budynków wznoszonych
tradycyjnie. Dolnośląskie Wydawnictwo Edukacyjne, Wrocław 2007.

[2]

Pędziwiatr J., Wstęp do projektowania konstrukcji żelbetowych wg PN-EN 1992-1-1.Dolnośląskie
wydawnictwo Edukacyjne, Wrocław 2010.

[3]

Puła O., Projektowanie fundamentów bezpośrednich według Eurokodu 7.Dolnośląskie wydawnictwo
Edukacyjne, Wrocław 2011.

[4]

Schabowicz K., Gorzelańczyk T., Materiały do ćwiczeń projektowych z budownictwa ogólnego.
Dolnośląskie wydawnictwo Edukacyjne, Wrocław 2009.

Wykaz przepisów i Norm

[5]

Rozporządzenie Ministra Infrastruktury z dnia 12 kwietnia 2002 roku w sprawie warunków
technicznych jakim powinny odpowiadać budynki i ich usytuowanie. Dz. U. nr 75 z dnia 15 czerwca
2002, poz. 690, z późniejszymi zmianami (ostatnia zmiana: Dz. U. nr 56 z dnia 10 grudnia 2010r.).

[6]

Rozporządzenia Ministra Edukacji Narodowej z dnia 10 stycznia 2008 r. w sprawie rodzajów innych
form wychowania przedszkolnego, warunków tworzenia i organizowania tych form oraz sposobu ich
działania. Dz. U. nr 7 z 2008 r., poz.38.

[7]

PN-81/B-03020. Grunty budowlane. Posadowienia bezpośrednie budowli. Obliczenia statyczne i
projektowanie.

[8]

PN-EN 338. Drewno Konstrukcyjne, Klasy wytrzymałości.

[9]

PN-EN 1990:2004 oraz zmiany A1:2008, AC:2008, Ap1:2004, Ap2:2010. Podstawy projektowania
konstrukcji.

[10]

PN-EN 1991-1-1:2004 oraz zmiany AC:2009, Ap1: 2010. Oddziaływania na konstrukcje. Część 1-1:
Oddziaływania ogólne – Ciężar objętościowy, ciężar własny, obciążenia użytkowe w budynkach.

[11]

PN-EN 1991-1-3:2005 oraz zmiany AC:2009, Ap1: 2010. Oddziaływania na konstrukcje. Część 1-3:
Oddziaływania ogólne - Obciążenie śniegiem.

[12]

PN-EN 1991-1-4:2008 oraz zmiany AC:2009, Ap1:2010, Ap2:2010. Oddziaływania na konstrukcje.
Część 1-4: Oddziaływania ogólne - Oddziaływania wiatru.

[13]

PN-EN 1992-1-1:2008 oraz zmiany Ap1:2010. Projektowanie konstrukcji z betonu. Część 1-1: Reguły
ogólne i reguły dla budynków.

[14]

PN-EN 1995-1-1:2005 oraz zmiany A1:2008. Projektowanie konstrukcji drewnianych. Część 1-1:
Zasady ogólne i zasady dla budynków.

[15]

PN-EN 1996-1-1:2010 oraz zmiany Ap1:2010. Projektowanie konstrukcji murowych. Część 1-1:
Reguły ogólne dla zbrojonych i niezbrojonych konstrukcji murowych.

[16]

PN-EN 1997-1:2008 + zmiany AC:2009, Ap1:2010. Projektowanie geotechniczne. Część 1: Zasady
ogólne.