Elektromagnetyzm

Fizyka sem II - ćwiczenia

Elektromagnetyzm

Zad. 1.

Ramka z 50 zwojami przewodnika o powierzchni 150 cm

2

, obraca się równomiernie w

jednorodnym polu magnetycznym o indukcyjności B = 0,8 Wb/m

2

. Ramka wykonuje n = 120

obr/min. Wyznaczyć maksymalną amplitudę siły elektromotorycznej indukcji.
Zad.2.

Solenoid zbudowany z n = 80 zwojów o średnicy d = 8 cm umieszczono w polu

magnetycznym o natężeniu H = 48000 A/m. Solenoid obraca się o 180

o

w przeciągu t = 0,2 s.

Wyznaczyć średnią wartość siły elektromotorycznej indukcji, która przy tym powstaje.
Zad.3.
Ciężar o masie m jest zawieszony na nici nawiniętej na osi prądnicy ze stałym magnesem i
zwartej oporem R. Ciężar jest opuszczany z prędkością v. Z jaką prędkością v

1

będzie unoszony

ten sam ciężar do góry, jeżeli prądnicę włączyć jako silnik do obwodu ze stałym prądem o sile
elektromotorycznej

εεεε

i o tym samym oporze R.

elektromotorycznej

εεεε

i o tym samym oporze R.

Zad.4.
Zamknięta cewka składająca się z n = 1000 zwojów jest umieszczona w polu magnetycznym
skierowanym wzdłuż osi cewki. Powierzchnia przekroju poprzecznego cewki wynosi S = 4 cm

2

,

opór jest równy R = 160

Ω

. Wyznaczyć moc traconą na nagrzewanie przewodów, jeżeli pole

magnetyczne zmienia się równomiernie z prędkością 8 A/m*s.
Zad.5.
W pole magnetyczne o indukcyjności B = 10

-2

Wb/m

2

wlatuje elektron, prostopadle do linii sił z

prędkością 10

6

m/s. Wyznaczyć wielkość siły, która działa na elektron w polu magnetycznym.

Zad.6.
W jednorodnym polu magnetycznym o natężeniu H znajduje się pierścień z nadprzewodnika. Linie
sił pola są prostopadłe do powierzchni pierścienia. Ile wynosi strumień magnetyczny, który
przechodzi przez pierścień po wyłączeniu pola zewnętrznego. Promień pierścienia wynosi R.

Zad.7.
W jednorodnym polu magnetycznym o indukcyjności
B = 0,05 Wb/m

2

obraca się pręt o długości 1 m ze stałą

prędkością kątową

ω

ωω

ω

= 20 s

-1

. Oś obrotu przechodzi przez

koniec pręta równolegle do linii sił pola magnetycznego.
Wyznaczyć siłę elektromotoryczną indukcji powstającą na
końcach pręta.

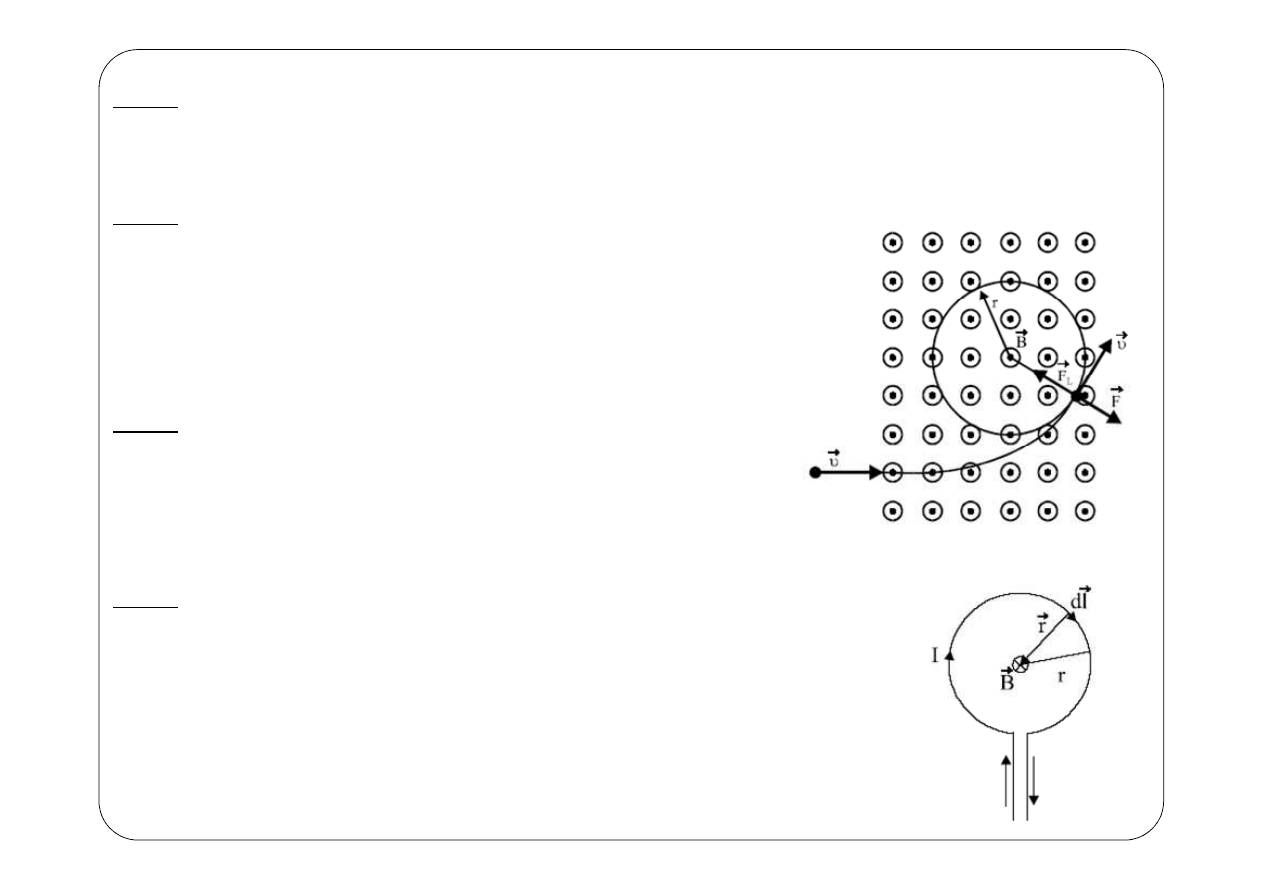
Zad.8.
Elektron (o masie m = 9,1*10

-31

kg i ładunku elektrycznym e

Elektron (o masie m = 9,1*10

-31

kg i ładunku elektrycznym e

= 1,6*10

-19

C) wpada z prędkością v = 10

7

m/s w obszar

jednorodnego pola magnetycznego o indukcji B = 10

-2

T

prostopadle do linii sił tego pola. Znaleźć tor ruchu elektronu
w polu magnetycznym.

Zad.9.
Wyznaczyć wartość indukcji magnetycznej B w środku obwodu
kołowego o promieniu r, w którym płynie prąd elektryczny o natężeniu I.

Zad.10.
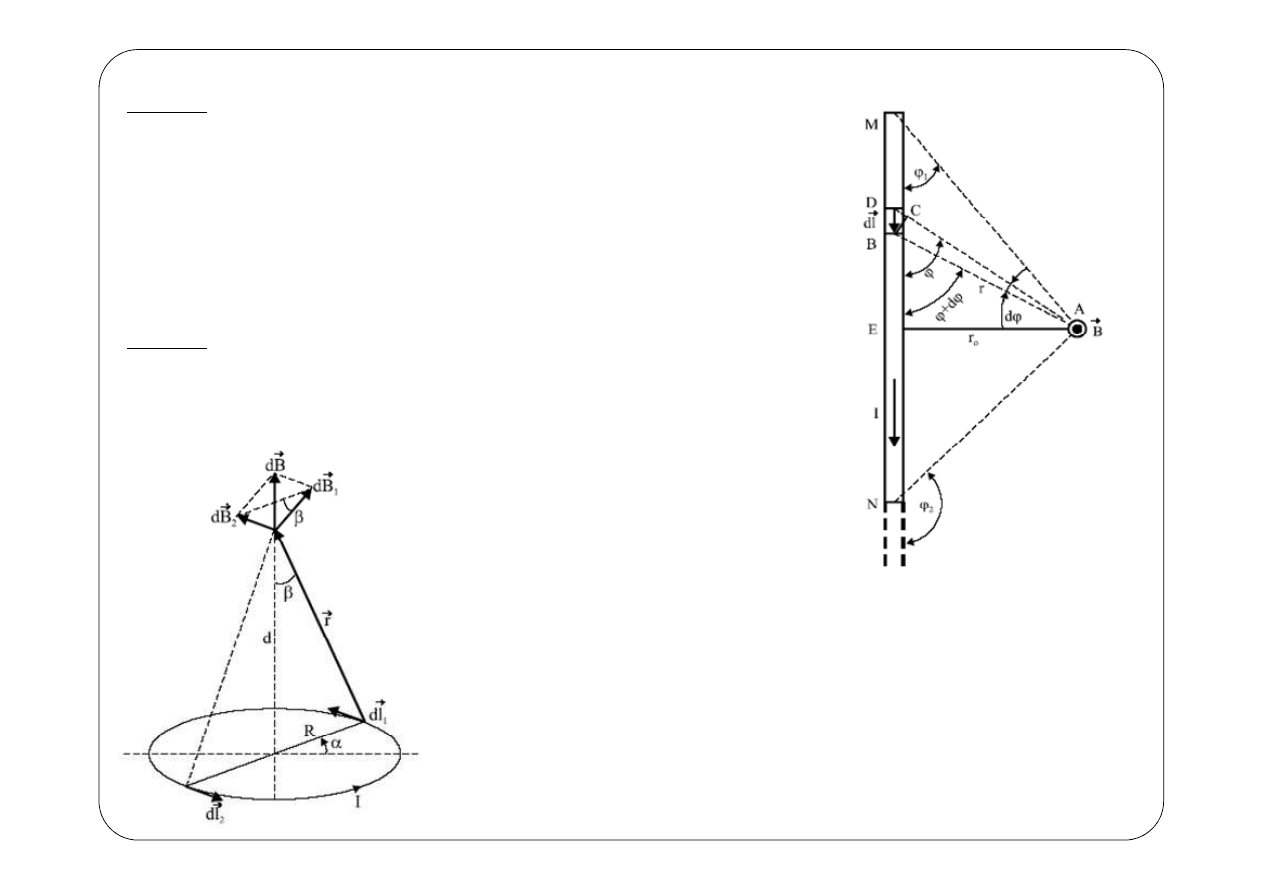
W prostoliniowym przewodniku o długości l płynie prąd o
natężeniu I. Wyznaczyć wartość indukcji magnetycznej B w
punkcie A odległym o r

o

od przewodnika. Punkt A jest tak

usytuowany w przestrzeni, że z tego punktu końce M i N

przewodnika widać odpowiednio pod kątami i

φφφφ

1

φφφφ

2

(patrz

rysunek).

Zad.11.
Obliczyć indukcję magnetyczną B na osi obwodu kołowego w
odległości d od środka obwodu. Natężenie prądu w obwodzie
wynosi I, a promień obwodu R.

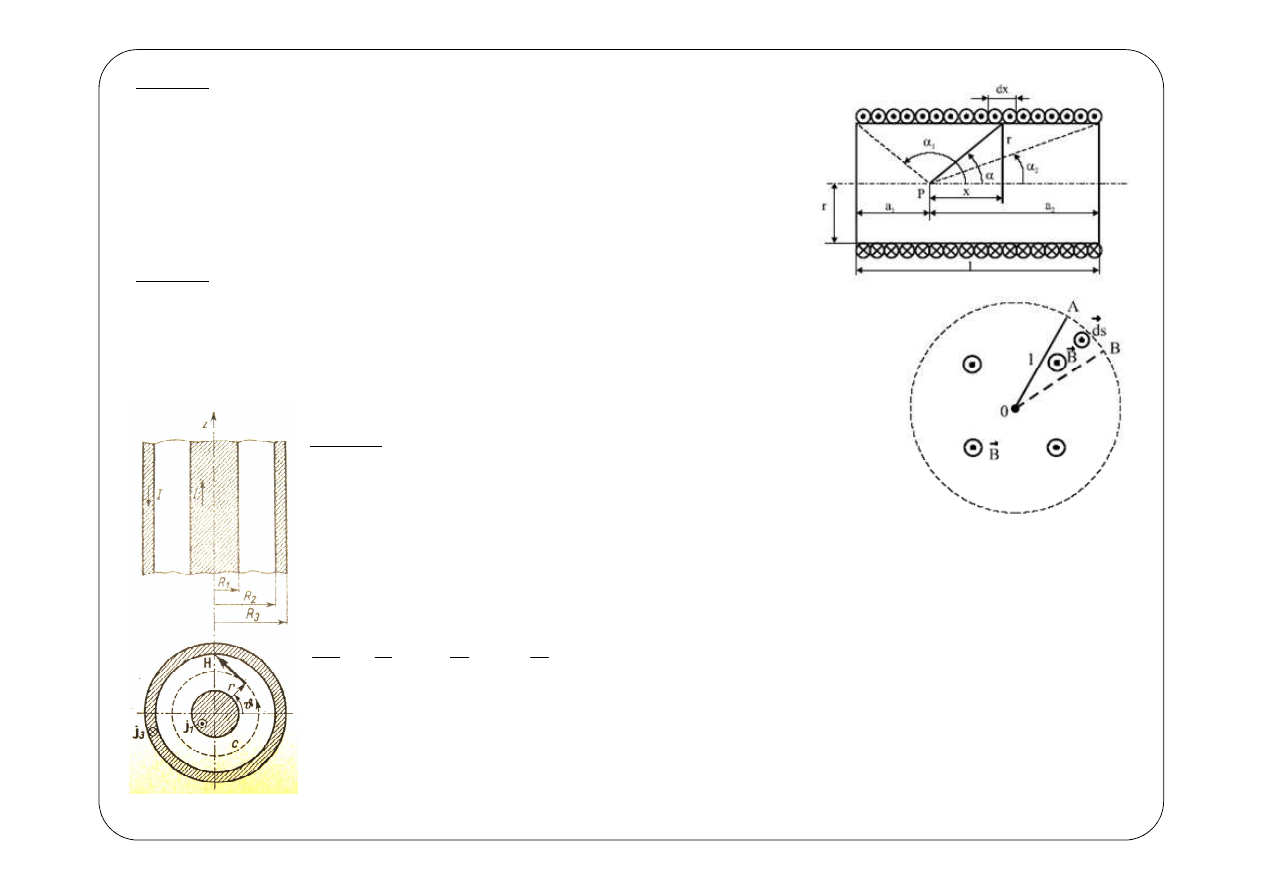
Zad.12.
Wyznaczyć natężenie H pola magnetycznego na osi cewki
cylindrycznej (solenoidu) z równomiernie i gęsto nawiniętymi
zwojami, przez które przepływa prąd o natężeniu I. Cewka ma n
zwojów, długość l i promień przekroju poprzecznego r. Położenie
punktu P, dla którego liczymy H, określają odcinki a

1

i a

2

mierzone

od końca cewki. Przedyskutować otrzymany wynik.
Zad.13.
Wyprowadź z prawa Faradaya wzór na siłę elektromotoryczną ε
indukowaną w pręcie o długości l, obracającym się w jednorodnym polu
magnetycznym o indukcji B ze stałą prędkością kątową ω wokół osi
przechodzącej przez jeden z końców pręta i prostopadłej do niego.

Płaszczyzna obrotu jest prostopadła do B.
Zad.14.

Zad.14.

Wyznaczyć

natężenie

pola

magnetycznego,

wytwarzanego przez prąd o natężeniu I, płynący
przez nieskończenie długi kabel koncentryczny jak na
rysunku obok o znanych wymiarach: R

1

, R

2

, R

3

. Rozwiązać zadanie

stosując prawo Ampere’a. Wyniki ostateczne przedstawić na wykresie
we współrzędnych znormalizowanych:













=

1

1

R

r

f

H

H

R

dla

5

,

2

1

2

=

R

R

i

3

1

3

=

R

R

.

Zad.15.

Znaleźć pole magnetyczne prądu, który wypływa z
jednego punktu i rozchodzi się radialnie po
nieskończonej płaszczyźnie.

Zad.16.

Z jednego punktu wypływają dwa prądy liniowe
skierowane w przeciwne strony. Natężenie każdego z
nich jest równe ½ I. Porównać wytworzone przez nie
pole magnetyczne z polem prądu opisanego w
zadaniu 15.