Model atomu wodoru Bohr’a

Fizyka sem II - ćwiczenia

Model atomu wodoru Bohr’a

Widmo promieniowania atomów i jonów (w przeciwieństwie do ciągłego widma

promieniowania ogrzanych ciał stałych) jest zawsze widmem liniowym składającym się z
promieniowania o dyskretnych długościach fal (częstości).

Ernest Rutherford (18711 - 1937) zaproponował jądrowy model atomu, który jest

podstawą teorii nam współczesnych. W modelu tym ładunek dodatni i prawie cała masa
atomu są uwięzione w jądrze (bardzo małej kulce o promieniu rzędu 10

-14

[m]). Elektrony

krążą

wokół

jądra

w

objętości

o

promieniu

rzędu

10

-10

[m].

Niels Bohr (1913) uniknął tej trudności zakładając, że atom wodoru, podobnie jak
oscylatory Plancka, może znajdować się jedynie w pewnych ściśle określonych stanach
stacjonarnych, w których nie wypromieniowuje energii. Wypromieniowanie następuje
tylko wtedy, gdy atom przechodzi z jednego stanu o energii E

w

, do innego stanu o niższej

energii E

n

. Można to zapisać w postaci:

n

w

E

E

h

−

=

ν

(1)

gdzie

ν

h

oznacza kwant energii uniesiony przez foton, który jest w czasie przejścia

wypromieniowany z atomu.

Powtórzmy jego rozważania. Załóżmy, że elektron w atomie wodoru porusza się po
kołowych orbitach o promieniu r ze środkiem w miejscu gdzie znajduje się jądro. Zakładamy,
ż

e jądro (które jest pojedynczym protonem) jest tak ciężkie, że środek masy układu pokrywa

się ze środkiem protonu. Obliczmy energię takiego atomu. Korzystając z II zasady Newtona
dla ruchu elektronu, gdzie siłę działającą na elektron wyznaczamy z prawa Coulomba, mamy
kolejno:

a

m

F

e

=

albo

v

Ze

2

2

r

v

m

r

Ze

e

o

2

2

2

4

=

πε

(2)

gdzie: e - ładunek elektronu (protonu), m - masa elektronu, v - jego prędkość liniowa w
jednostajnym ruchu po orbicie , a - przyspieszenie dośrodkowe, F - siła jaką jądro przyciąga

elektron,

ε

ο

- przenikalność elektryczna próżni:

[

]

o

o

k

C

m

N

=

=

2

2

9

/

*

10

*

0

,

9

4

1

πε

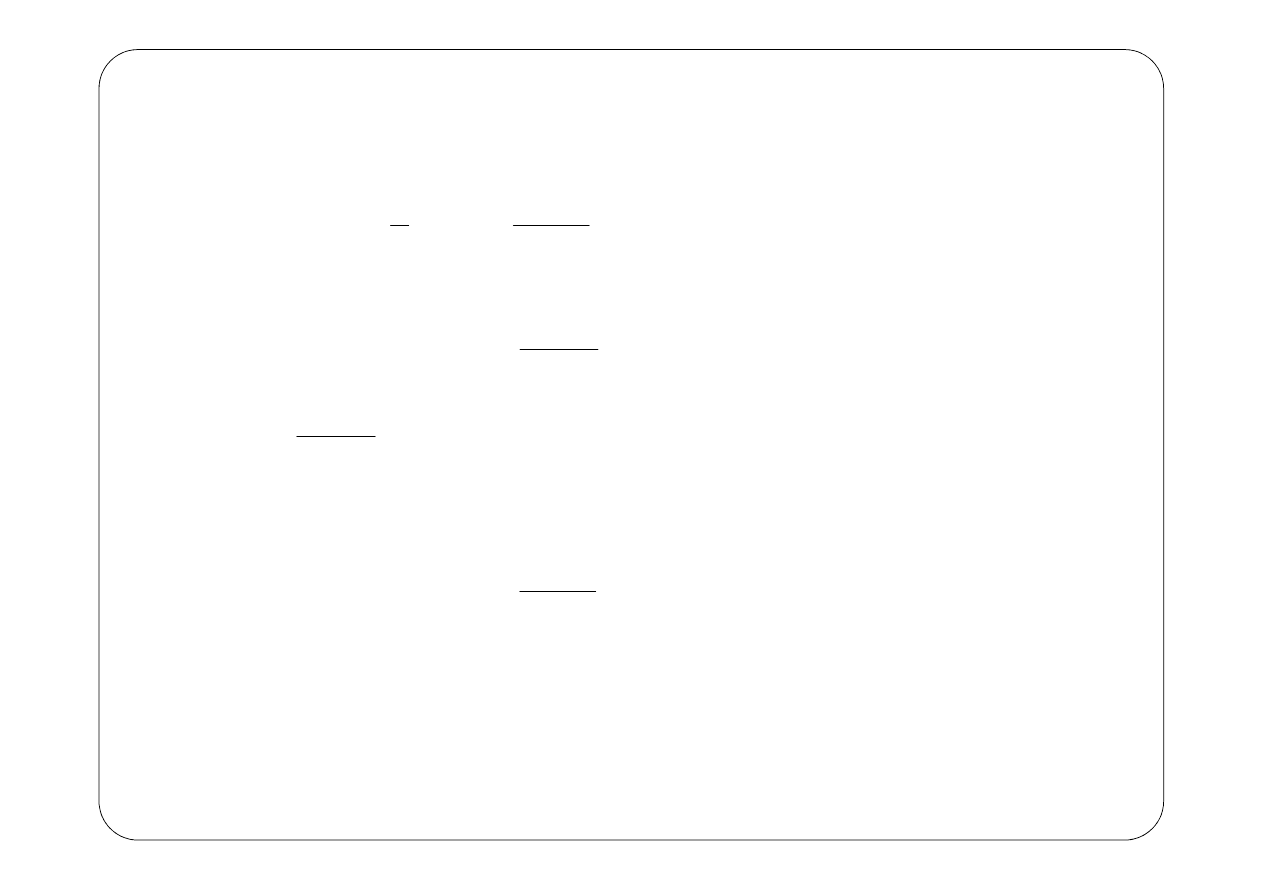
Na podstawie wyrażenia (2) łatwo wyliczyć energię kinetyczną elektronu

r

Ze

v

m

K

o

e

πε

8

2

1

2

2

=

=

(3)

Energia potencjalna układu proton - elektron dane jest równaniem

( )

r

Ze

e

V

U

o

πε

4

2

−

=

−

=

(4)

gdzie

r

Ze

V

πε

4

=

- oznacza potencjał pola elektrycznego wytworzonego przez proton

gdzie

r

V

o

πε

4

=

- oznacza potencjał pola elektrycznego wytworzonego przez proton

(ładunek punktowy) w odległości równej promieniowi orbity elektronu.
Całkowita energia elektronu jest równa:

r

Ze

U

K

E

o

πε

8

2

−

=

+

=

(5)

Stwierdzamy przede wszystkim, że całkowita energia elektronu związanego w

atomie przyjmuje wartości ujemne. Widać też, że energia jest funkcją promienia orbity.
Dlatego problem kwantowania energii sprowadza się do problemu kwantowania
promienia r.

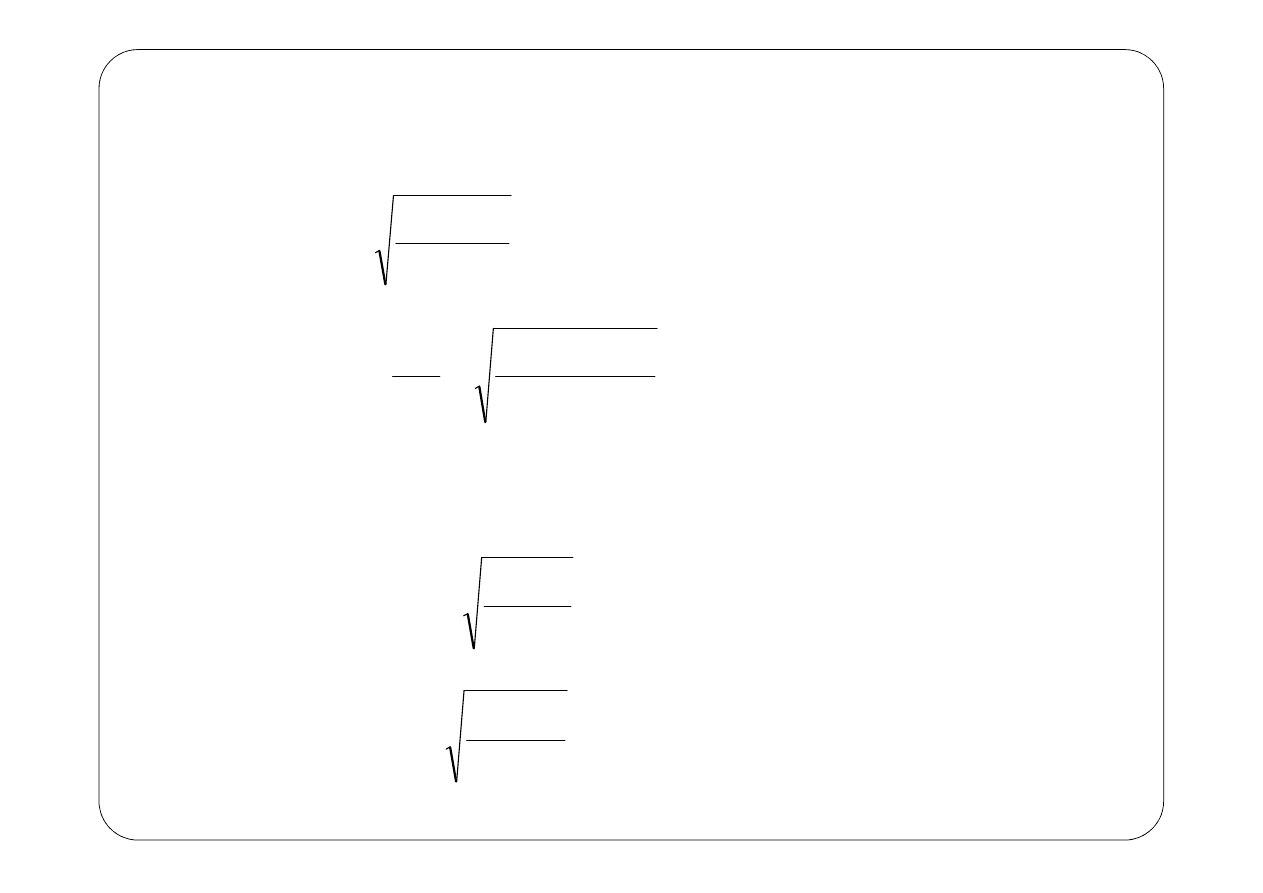
Znając promień można wyznaczyć wszystkie własności orbity:

-

prędkość liniowa elektronu:

r

m

Ze

v

e

o

πε

4

2

=

(6)

-

częstość obrotów

3

3

2

16

2

r

m

Ze

r

v

e

o

o

ε

π

π

ν

=

=

(7)

-

pęd elektronu

r

e

Zm

v

m

p

o

e

e

πε

4

2

=

=

(8)

-

moment pędu

o

e

r

e

Zm

pr

L

πε

4

2

=

=

(9)

Bohr wysunął hipotezę, że kwantyzacja parametrów orbitali jest najprostsza, jeżeli

zastosować ją do momentu pędu i założyć, że ta może przyjmować jedynie wartości
określone równaniem:

π

2

h

n

L

=

, n = 1, 2, 3, . . .

(10)

gdzie h oznacza stałą Plancka, n - liczbę kwantową.
Dla promienia otrzymuje się teraz wyrażenie

.

.

.

.

3,

2,

1,

,

*

2

2

2

=

=

n

h

n

r

o

π

ε

(11)

.

.

.

.

3,

2,

1,

,

*

2

=

=

n

e

m

n

r

e

π

(11)

a dla energii całkowitej elektronu w atomie wodoru

.

.

.

3,

2,

1,

,

8

2

2

4

2

=

−

=

n

n

h

e

m

Z

E

o

e

ε

(12)

Ostatni wzór dostarcza bezpośrednio wartości energii dozwolonych stanów
stacjonarnych.

Ze wzorów (1) i (12) otrzymujemy teoretyczny wzór dla częstości widmowych

wodoru















−

=

2

2

3

2

2

4

1

1

8

w

n

o

e

n

n

h

Z

e

m

ε

ν

(13)

Odpowiednie długości fali można łatwo znaleźć ze wzoru:

ν

λ

c

=

Można teraz sformułować wniosek:

Można teraz sformułować wniosek:

Energia elektronu związanego w atomie jest skwantowana

i przyjmuje ujemne wartości.

Poszczególne wartości liczby n w równaniu (12) określają poziomy lub inaczej

stany energetyczne elektronu w atomie. Na rysunku 1 przedstawiono wykres
poziomów energetycznych dla atomu wodoru:

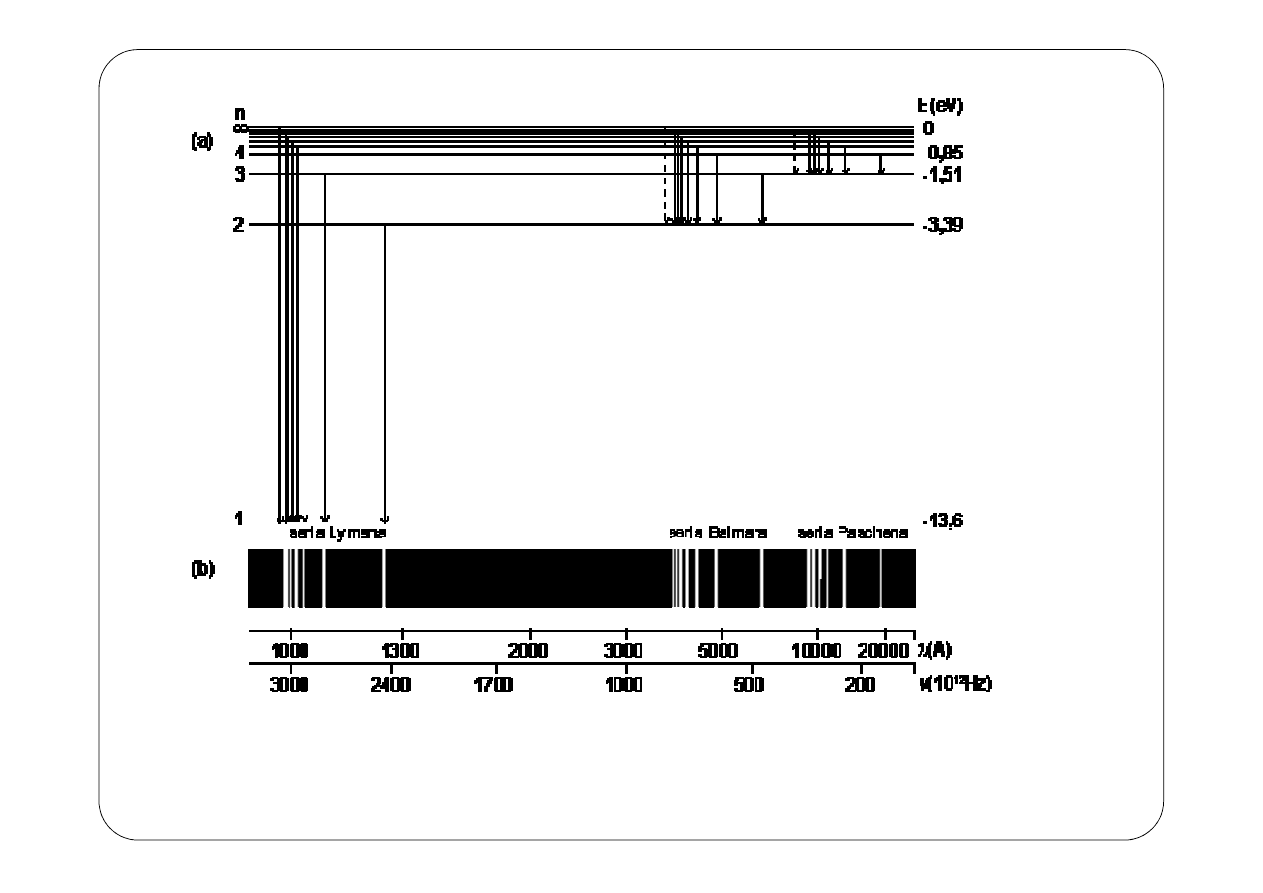
Rys. 1. Poziomy energetyczne dla atomu wodoru

Zad. 1.

Wzbudzony atom wodoru powraca do stanu podstawowego wypromieniowując

kolejno dwa kwanty promieniowania o długości fali

]

[

10

*

4051

9

1

m

−

=

λ

i

]

[

10

*

5

,

972

10

2

m

−

=

λ

. Określić energię stanu wzbudzonego i odpowiadającą mu

liczbę kwantową n.

Zad. 2.

Spoczywający atom wodoru wyemitował foton odpowiadający głównej linii serii

Lymana. Obliczyć prędkość jaką uzyskał atom w wyniku emisji.

Zad. 3.

Podczas jednego z przejść elektronu w atomie wodoru z jednego poziomu

stacjonarnego na drugi nastąpiło wypromieniowanie kwantu światła o częstotliwości

1

14

10

*

57

,

4

−

=

s

ν

. Wyznaczyć, o jaką wielkość zmieniła się energia elektronu w

atomie na koszt tego promieniowania.

Zad. 4.

Zgodnie z teorią Bohra promień pierwszej orbity elektronu w atomie wodoru

wynosi R = 0,53*10

-10

m. Wyznaczyć prędkość liniową i kątową ruchu elektronu po

orbicie.

Zad. 5.

Wyznaczyć promień a

o

pierwszej orbity borowskiej i prędkość v elektronu na tejże

orbicie. Jakie jest natężenie pola elektrycznego na tej orbicie?

Zad. 6.

Zgodnie z wyobrażeniami elektrodynamiki klasycznej moc promieniowania

wysyłanego przez elektron poruszający się z przyspieszeniem a wynosi:

2

2

2

4

2

c

a

e

N

o

πε

=

Oszacować czas życia jonu He

+

, przyjmując, że elektron porusza się jednostajnie po

orbicie kołowej o promieniu początkowym 10

-10

m.

orbicie kołowej o promieniu początkowym 10 m.

Zad. 7.

Wyznaczyć częstotliwość światła wysyłanego przez jon wodoropodobny przy

przejściu z poziomu o głównej liczbie kwantowej

µµµµ

do stanu, w którym promień orbity

jest k razy mniejszy.

Zad. 8.

Wyznaczyć długość fali odpowiadającej granicy Balmera.

Zad. 9.

Obliczyć pierwszy potencjał wzbudzenia wodoru.