Rozwa

Īamy równanie z funkcją niewiadomą

spe

ániającą równanie Laplace'a

z warunkiem brzegowym typu Dirichleta

dla

gdzie jest dan

ą funkcją ciągáą, która moĪe byü przedstawiona w postaci sumy trygonometrycznego

szeregu Fouriera.

Szkic rozwi

ązania

Przyk

áad obliczeniowy

Jedna z metod rozwi

ązania oparta jest na przedstawieniu niewiadomej funkcji harmonicznej w postaci

cz

ĊĞci rzeczywistej pewnej funkcji holomorficznej w kole

gdzie

Z warunku brzegowego otrzymujemy,

Īe dla

musi zachodzi

ü równoĞü

dla

Z w

áasnoĞci trygonometrycznych szeregów Fouriera wynika stąd, Īe

dla

Powrót

Rozwiązać zagadnienie Dirichleta dla

Rozwiązanie

Z podanych wzorów (patrz -

szkic rozwiązania

) wynika, że

zaś pozostałe współczynniki są równe zero.

W takim razie rozwiązanie zagadnienia wyraża się wzorem

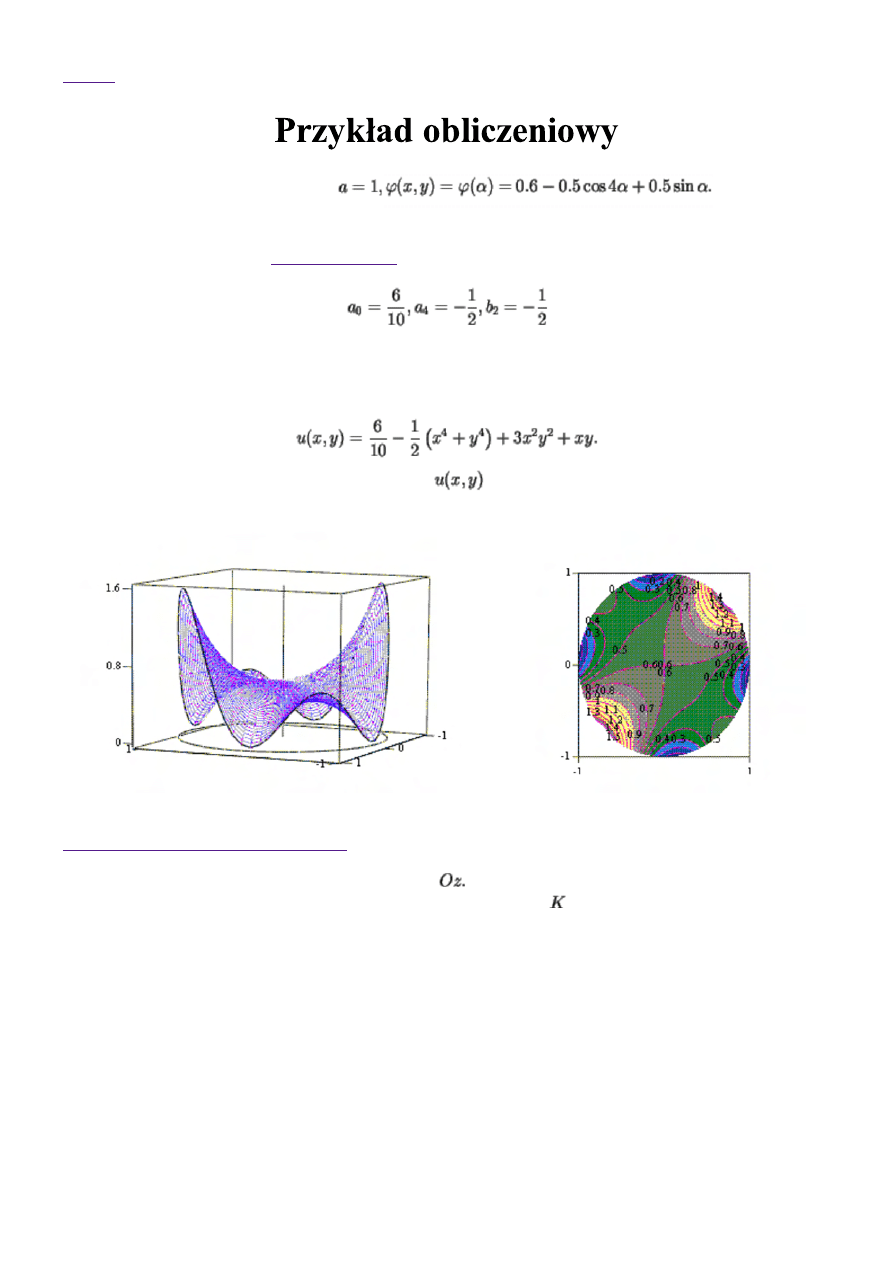
Poniższe rysunki przedstawiają wykres rozwiązania

oraz jego plan warstwicowy.

Na warstwicach jest zaznaczone odpowiadające im wychylenie, czyli wartość funkcji u.

Animacja - obrót powierzchni (331 kB)

Animacja przedstawia obrót rozwiązania dokoła osi

Zgodnie z zasadą maksimum dla funkcji

harmonicznych, rozwiązanie nie osiąga w żadnym punkcie obszaru swego kresu górnego i dolnego -
kresy te są przyjmowane na brzegu obszaru.

Przykład obliczeniowy

file:///C:/TMP/mm/RRCz/Elipt/Harm_1/Przyklad.html

1 of 1

5/22/2011 11:01 PM