1. Cele ćwiczenia:



Sporządzenie modelu przetwornika cylindrycznego cztero-uzwojeniowego o
liniowym obwodzie magnetycznym



Wykonanie obliczeń polowych



Wykreślenie linii pola magnetycznego

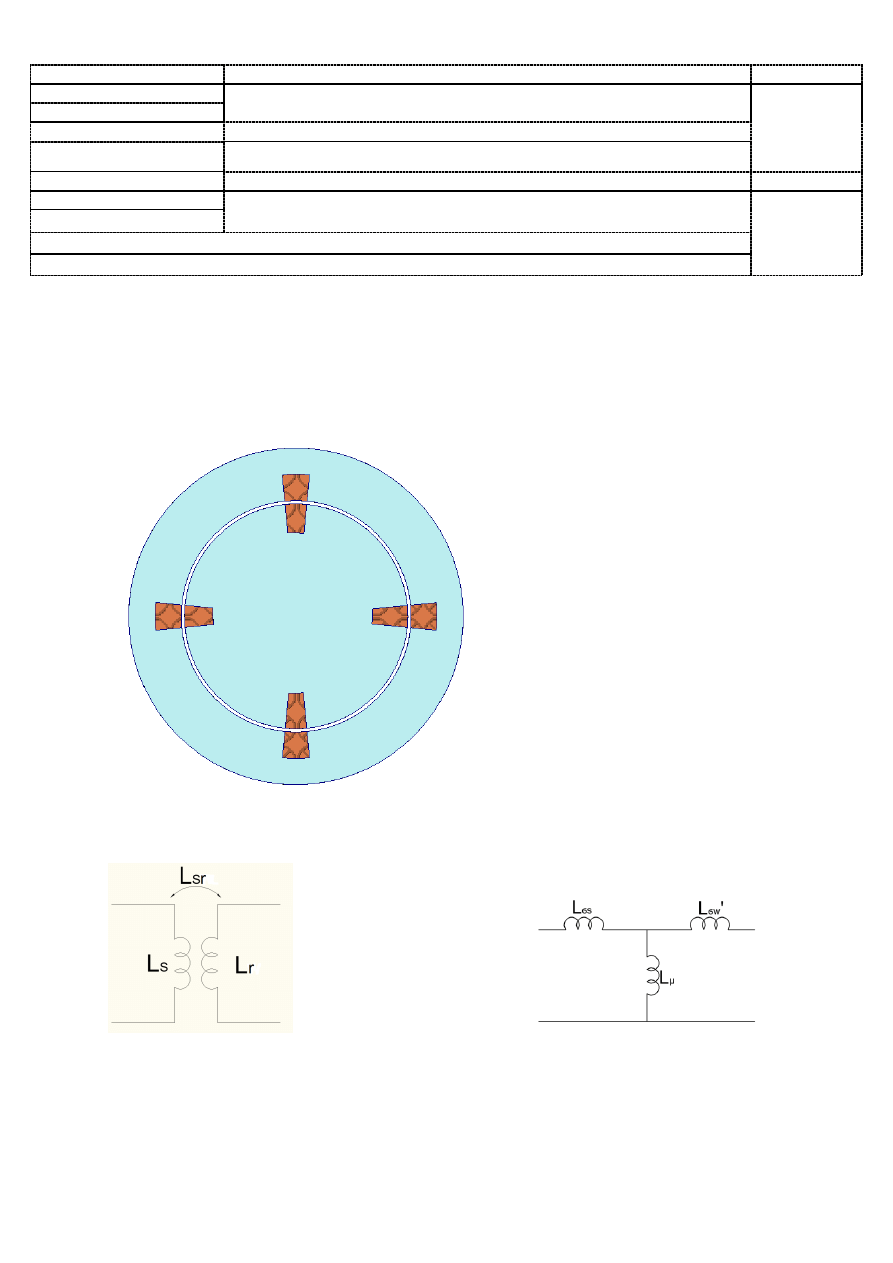
Rys.1 Model przetwornika cylindrycznego cztero-uzwojeniowego o liniowym obwodzie
magnetycznym

Rys.2 Schemat indukcyjności uzwojeń

Rys.3 Schemat zastępczy indukcyjności

stojana i wirnika

typu T

Numer ćw.:

Nazwa wydziału:

Ocena:

Ćw. 3

Wydział Inżynierii Elektrycznej i Komputerowej

Grupa stud. / grupa lab.

11M

Nazwa przedmiotu:

Data wykonania ćw.:

Polowe modelowanie układów elektromagnetycznych

23.05.2011

Temat ćw:

Podpis:

Data oddania sprawozdania:

Wyznaczanie indukcyjności własnych i wzajemnych

uzwojeń w przetworniku elektromechanicznym

06.06.2011

Skład zespołu:

Krzysztof Dziurda

Macierz indukcyjności własnych i wzajemnych

𝐿

𝑠1

𝐿

𝑠1𝑠2

𝐿

𝑠2𝑠1

𝐿

𝑠2

𝐿

𝑠1𝑟1

𝐿

𝑠1𝑟2

𝐿

𝑠2𝑟1

𝐿

𝑠2𝑟2

𝐿

𝑟1𝑠1

𝐿

𝑟1𝑠2

𝐿

𝑟2𝑠1

𝐿

𝑟2𝑠2

𝐿

𝑟1

𝐿

𝑟1𝑟2

𝐿

𝑟2𝑟1

𝐿

𝑟2

𝐿

𝑠1𝑠2

= 𝐿

𝑠2𝑠1

; 𝐿

𝑠1𝑟1

= 𝐿

𝑟1𝑠1

; 𝐿

𝑠1𝑟2

= 𝐿

𝑟2𝑠1

; 𝐿

𝑠2𝑟1

= 𝐿

𝑟1𝑠2

; 𝐿

𝑠2𝑟2

= 𝐿

𝑟2𝑠2

; 𝐿

𝑟1𝑟2

= 𝐿

𝑟2𝑟1

;

𝐿

𝑠

= 𝐿

𝑠1

= 𝐿

𝑠2

; 𝐿

𝑟

= 𝐿

𝑟1

= 𝐿

𝑟2

; 𝐿

𝑠𝑟

= 𝐿

𝑠1𝑟1

= 𝐿

𝑠2𝑟2

;

𝐿

𝑠1𝑠2

= 𝐿

𝑟1𝑟2

= 0; 𝐿

𝑠2𝑟1

= 𝐿

𝑠1𝑟2

= 0;

Macierz indukcyjności upraszcza się do postaci:

𝐿

𝑠

0

0

𝐿

𝑠

𝐿

𝑠𝑟

0

0

𝐿

𝑠𝑟

𝐿

𝑠𝑟

0

0

𝐿

𝑠𝑟

𝐿

𝑟

0

0

𝐿

𝑟

gdzie mamy 3 niewiadome:

𝐿

𝑠

- indukcyjność stojana

𝐿

𝑟

- indukcyjność wirnika

𝐿

𝑠𝑟

- indukcyjność wzajemna między stojanem, a wirnikiem

Prąd stojana na cewce 2-4:

𝑖

𝑠1

= 2 𝐴

Strumień stojana na cewce 2-4:

𝛹

𝑠1

= 0.1230931076116 𝑊𝑏

Indukcyjność stojana na cewce 2-4:

𝐿

𝑠

= 𝐿

𝑠1

=

𝛹

𝑠1

𝑖

𝑠1

=

0.1230931076116 𝑊𝑏

2 𝐴

= 61,54655 𝑚𝐻 ≈ 61,5 𝑚𝐻

Prąd wirnika na cewce 2-4:

𝑖

𝑟1

= 2 𝐴

Strumień wirnika na cewce 2-4:

𝛹

𝑠1𝑟1

= 0.01208068432805 𝑊𝑏

Strumień wirnika na cewce 2-4:

𝛹

𝑟1

= 0.001235737256668 𝑊𝑏

Indukcyjność wirnika:

𝐿

𝑟

= 𝐿

𝑟1

=

𝛹

𝑟1

𝑖

𝑟1

=

0.001235737256668 𝑊𝑏

2 𝐴

= 0,61787 𝑚𝐻 ≈ 0,62 𝑚𝐻

Indukcyjność wzajemna cewki 2-4:

𝐿

𝑠𝑟

= 𝐿

𝑠1𝑟1

=

𝛹

𝑠1𝑟1

𝑖

𝑟1

=

0.01208068432805 𝑊𝑏

2 𝐴

= 6,04 𝑚𝐻

Indukcyjność wzajemna cewki 2-4:

𝐿

𝑠𝑟

′

= n ∙ 𝐿

𝑠𝑟

= 60,4 𝑚𝐻

Indukcyjność wirnika po sprowadzeniu na stronę stojana:

𝐿

𝑟

′

= 𝐿

𝑟

∙ 𝑛

2

= 𝐿

𝑟1

∙ 𝑛

2

= 0,61787 𝑚𝐻 ∙ 100 ≈ 61,8 𝑚𝐻

Przekładnia zwojowa cewek:

𝑛 =

𝑁

1

𝑁

2

=

100

10

= 10

gdzie:

𝑁

1

– liczba zwojów stojana

𝑁

2

– liczba zwojów wirnika

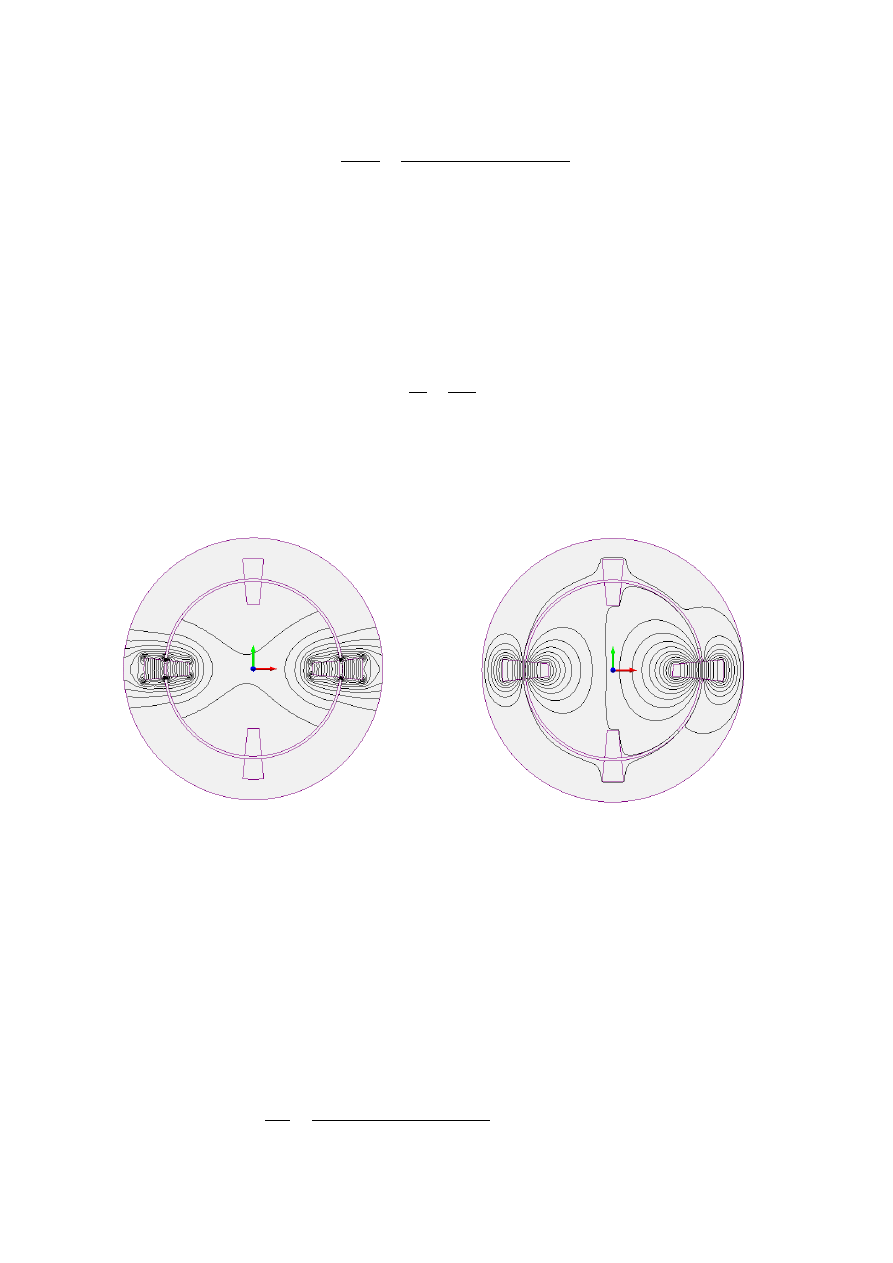
Rys.2 Natężenie pola indukcji

Rys. 3 Rozkład strumienia pola

magnetycznej B

magnetycznego przy

𝑖

𝑠1

= 2𝐴; 𝑖

𝑟1

= −20𝐴

Prądy stojana i wirnika na cewce 2-4:

𝑖

𝑠1

= 2𝐴; 𝑖

𝑟1

= −20𝐴

Strumień stojana na cewce 2-4

𝛹

𝑠1

= 0.002295171179649 𝑊𝑏

Strumień wirnika na cewce 2-4

𝛹

𝑟1

= −0.0002792016276969 𝑊𝑏

Obliczenie indukcyjności rozproszeń stojana i wirnika:

𝐿

𝜎𝑠

=

𝛹

𝑠1

𝑖

𝑠1

=

0.002295171179649 𝑊𝑏

2 𝐴

= 1,14759 𝑚𝐻 ≈ 1,1 𝑚𝐻

𝐿

𝜎𝑟

=

𝛹

𝑟1

𝑖

𝑟1

=

−0.0002792016276969 𝑊𝑏

−20 𝐴

= 0,01396 𝑚𝐻 ≈ 0,014 𝑚𝐻

Sprowadzenie indukcyjności rozproszenia wirnika na stronę stojana:

𝐿

𝜎𝑟

′

= 𝐿

𝜎𝑟

∙ 𝑛

2

= 0,014𝑚𝐻 ∙ 100 = 1,4 𝑚𝐻

Energia pola dla

𝑖

𝑟

= 𝑖

𝑠

∙ 𝑛

𝐸 𝑖

𝑠

, 𝑖

𝑟

= 𝑖

𝑠

𝑛 = 0.4883162783422 𝐽

Energia pola dla

𝑖

𝑟

= −𝑖

𝑠

∙ 𝑛

𝐸 𝑖

𝑠

, 𝑖

𝑟

= −𝑖

𝑠

𝑛 = 0.005087187492938 𝐽

Indukcyjność wzajemna wg wzoru:

𝐿

𝑠𝑟

=

𝐸 𝑖

𝑠

, 𝑖

𝑟

= 𝑖

𝑠

𝑛 − 𝐸 𝑖

𝑠

, 𝑖

𝑟

= −𝑖

𝑠

𝑛

2𝑖

𝑠

𝑖

𝑟

=

0.4883162783422 𝐽 − 0.005087187492938 𝐽

2 ∙ 2𝐴 ∙ 20𝐴

𝐿

𝑠𝑟

= 6,04𝑚𝐻

Macierz indukcyjności własnych i wzajemnych:

𝐿

𝑠

0

0

𝐿

𝑠

𝐿

𝑠𝑟

0

0

𝐿

𝑠𝑟

𝐿

𝑠𝑟

0

0

𝐿

𝑠𝑟

𝐿

𝑟

0

0

𝐿

𝑟

=

61,5

0

0

61,5

6,04

0

0

6,04

6,04

0

0

6,04

0,62

0

0

0,62

𝑚𝐻

Indukcyjność główna obliczona z 3 wzorów:

𝐿

𝑠

= 𝐿

𝜎𝑠

+ 𝐿

𝜇

⇒ 𝐿

𝜇

= 𝐿

𝑠

− 𝐿

𝜎𝑠

𝐿

𝑟

′

= 𝐿

𝜎𝑟

′

+ 𝐿

𝜇

⇒ 𝐿

𝜇

= 𝐿

𝑟

′

− 𝐿

𝜎𝑟

′

𝐿

𝜇

= 𝐿

𝑠𝑟

∙ 𝑛

𝐿

𝜇

= 𝐿

𝑠

− 𝐿

𝜎𝑠

= 61,54655 𝑚𝐻 − 1,14759 𝑚𝐻 = 60,39896 𝑚𝐻 ≈ 60,4 𝑚𝐻

𝐿

𝜇

= 𝐿

𝑟

′

− 𝐿

𝜎𝑟

′

= 61,8𝑚𝐻 − 1,4 𝑚𝐻 = 60,4 𝑚𝐻

𝐿

𝜇

= 𝐿

𝑠𝑟

∙ 𝑛 = 6,04𝑚𝐻 ∙ 10 = 60,4 𝑚𝐻

Z powyższych 3 wzorów obliczamy

𝐿

𝜇

i uśredniamy wyniki :

𝐿

𝜇ś𝑟

=

60,4 𝑚𝐻 + 60,4 𝑚𝐻 + 60,4 𝑚𝐻

3

= 60,4 𝑚𝐻

Macierz indukcyjności sprowadzonych na stronę stojana z podziałem na indukcyjność główną i
indukcyjności rozproszeń:

𝐿

𝜇

+ 𝐿

𝜎𝑠

0

0

𝐿

𝜇

+ 𝐿

𝜎𝑠

𝐿

𝜇

0

0

𝐿

𝜇

𝐿

𝜇

0

0

𝐿

𝜇

𝐿

𝜇

+ 𝐿

𝜎𝑟

′

0

0

𝐿

𝜇

+ 𝐿

𝜎𝑟

′

=

61,5

0

0

61,5

60,4

0

0

60,4

60,4

0

0

60,4

0,62

0

0

0,62

𝑚𝐻