2005-12-19
© Lesław ŁADNIAK
ROZWIĄZYWANIE OBWODÓW ZE SPRZĘŻENIAMI
MAGNETYCZNYMI..............................................................................2
1.1
U
WZGLĘDNIANIE SPRZĘŻEŃ MAGNETYCZNYCH
...............................2
1.1.1 Cewki sprzężone magnetycznie ................................................2
1.1.2 Przykład. Połączenie szeregowe cewek....................................3
1.1.3 Przykład. Połączenie równoległe cewek ..................................4
1.1.4 Rozprzęganie gałęzi o wspólnym węźle....................................5
1.1.5 Cewki sprzężone jako źródła sterowane...................................6
1.2
R
ÓWNANIA OBWODÓW ZE SPRZĘŻENIAMI
........................................7
1.2.1 Metoda równań Kirchhoffa......................................................8
1.2.2 Przykład. Metoda potencjałów węzłowych...............................9
1.2.3 Przykład. Źródła sterowane w metodzie potencjałów ............10
1.2.4 Przykład. Mostek ze sprzężeniami..........................................11
1.3
P
RZEKAZYWANIE ENERGII PRZEZ SPRZĘŻENIE
................................12
2
© Lesław ŁADNIAK
R
OZWIĄZYWANIE OBWODÓW ZE
SPRZĘŻENIAMI MAGNETYCZNYMI
1.1 Uwzględnianie sprzężeń magnetycznych
Występujące w obwodach elektrycznych sprzężenia
magnetyczne można w czasie analizy tych obwodów uwzględnić
na kilka sposobów.
Podstawowy sposób polega na wyrażeniu napięć na cewkach
sprzężonych jako sumy napięć indukcji własnej i indukcji
wzajemnej, a następnie uwzględnieniu tych napięć w równaniach
Kirchhoffa lub innych równaniach (równaniach prądów
oczkowych, potencjałów węzłowych) napięć wywołanych
sprzężeniami magnetycznymi.
Gdy cewki sprzężone przyłączone są do tego samego węzła to
można taki układ cewek zastąpić obwodem równoważnym. W
obwodach, w których działają sinusoidalnie zmienne wymuszenia
napięcia indukcji wzajemnej można przedstawić jako sterowane
prądem źródła napięcia.
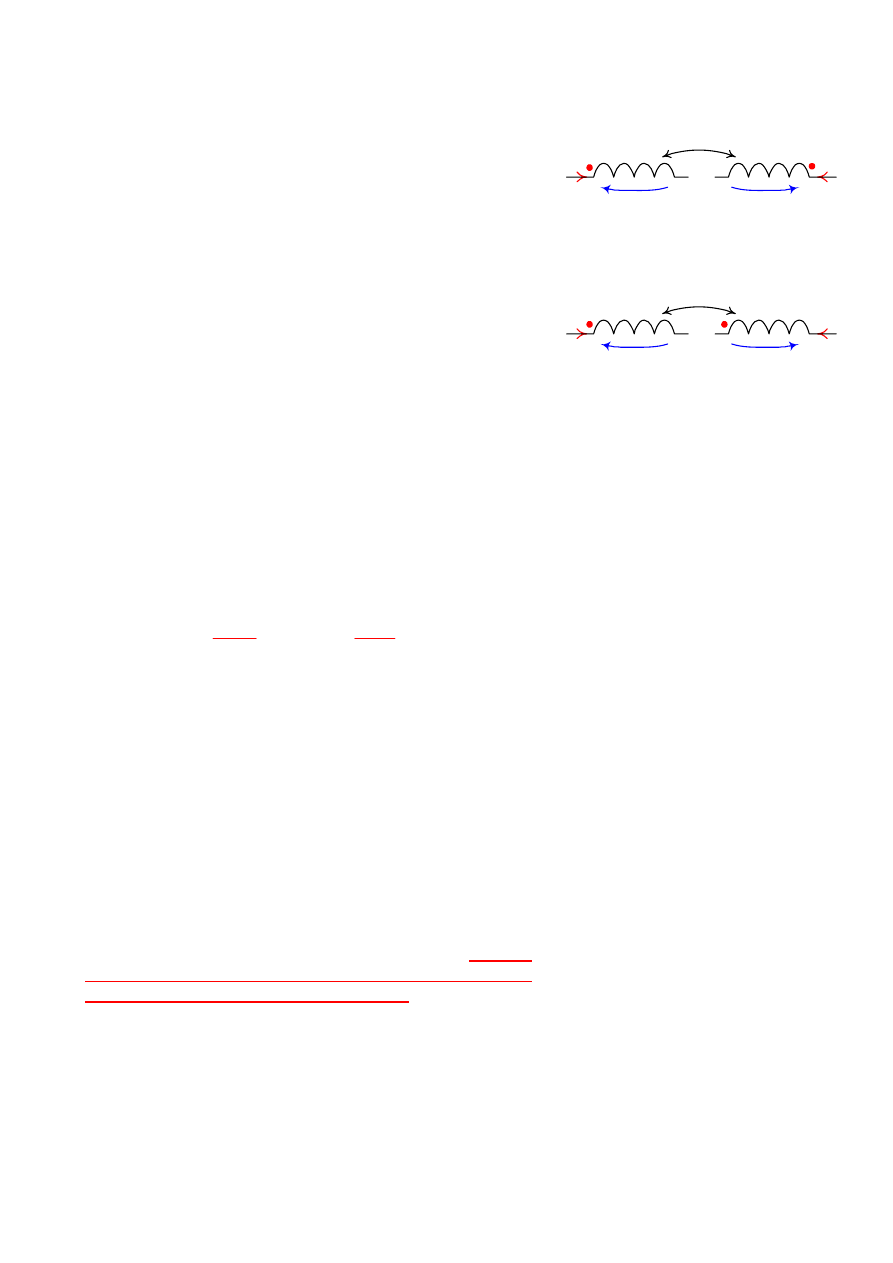
1.1.1 Cewki sprzężone magnetycznie
Napięcie na zaciskach cewki, która jest sprzężona magnetycznie
z innymi cewkami jest postać:
u
k
(t) = L
k
di
k
(t)
dt
+
∑
±
M
kl
di
l
(t)
dt
gdzie:
L
k
jest indukcyjnością własną cewki,
M
kl
jest indukcyjnością wzajemną cewki „k” z cewką ”l”.
W
powyższym równaniu znak stojący przy indukcyjności
wzajemnej zależy od rodzaju sprzężenia między rozpatrywanymi
cewkami. Znak „+" dotyczy przypadku, gdy sprzężenie
rozpatrywanych cewek jest zgodne, znak "
−
", gdy sprzężenie
cewek jest przeciwne.
Zapisując równania wynikające z napięciowego prawa
Kirchhoffa, kierunki napięć indukowanych w wyniku
sprzężeń magnetycznych najwygodniej jest określać
względem napięć samoindukcji pamiętając, że napięcie
indukowane dodajemy do napięcia samoindukcji, gdy
sprzężenie między cewkami jest zgodne, a odejmujemy
przy sprzężeniu przeciwnym.
i
k
L
k
+M
kl
L
l
i
l
u
ll
+
u
lk
u
kk
+
u
kl
Rys. 1. Cewki sprzężone zgodnie
i
k
L
k
- M
kl
L
l
i
l
u
ll
-
u
lk
u
kk
-
u
kl
Rys. 2. Cewki sprzężone przeciwnie
3
© Lesław ŁADNIAK
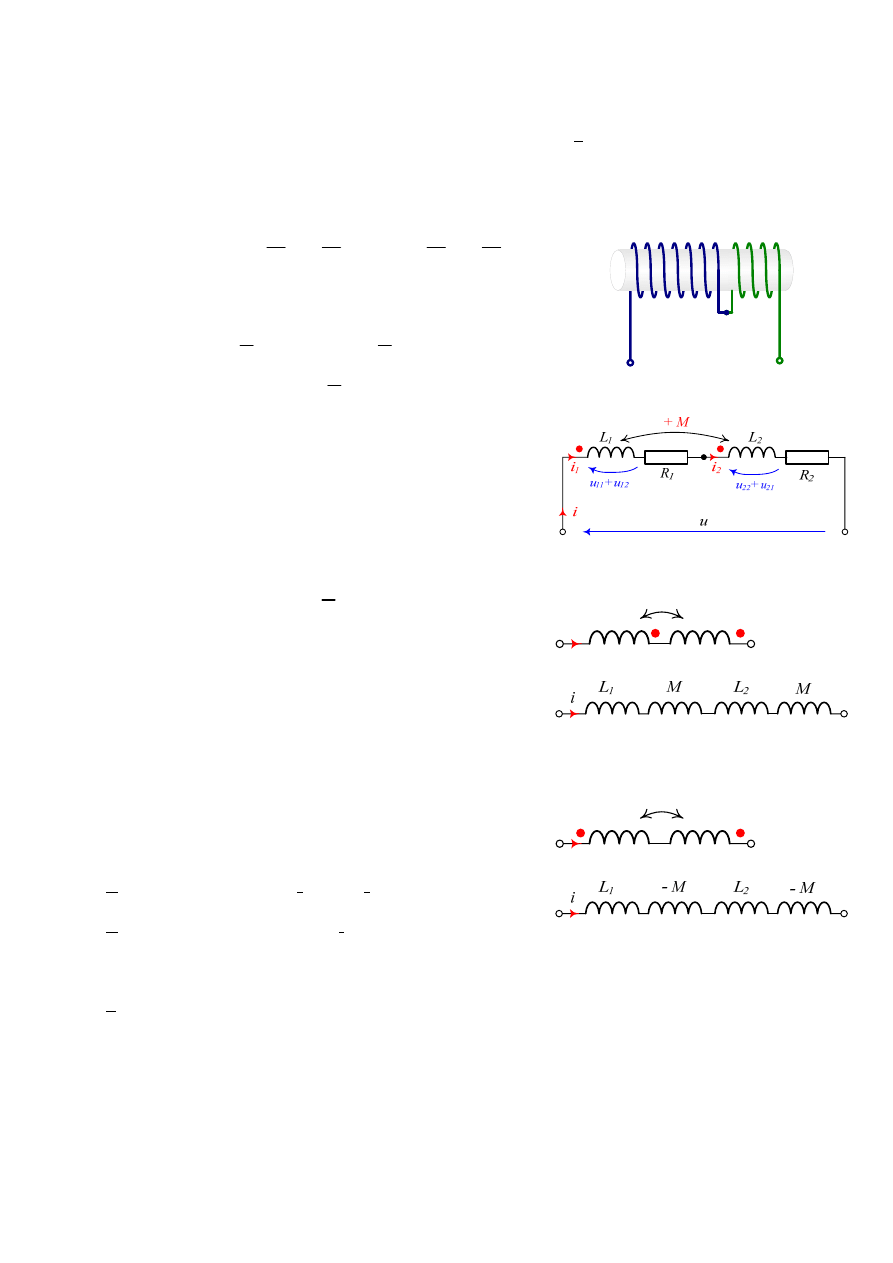
1.1.2 Przykład. Połączenie szeregowe cewek
Rozpatrzmy dwie cewki nawinięte na współnym redzeniu i
połączone tak jak pokazano na Rys. 3. Ponieważ sprzężenie
magnetycznie cewek jest zgodnie a cewki są połaczone szeregowo
to napięcię na zaciskach układu jest sumą napięć na
poszczególnych cewkach:
u = u
1
+ u
2
= R
1
i
1
+ L
1
di
1
dt + M
di
2
dt + R
2
i
2
+ L
2
di
2
dt + M
di
1
dt
Ponieważ prądy obu cewek są jednakowe, to można napisać:
u = R
1
i + (L
1
+ M)
di
dt + R
2
i + (L
2
+ M)
di
dt
u = (R
1
+ R
2
) i + (L
1
+ L
2
+ 2M)
di
dt
Indukcyjność zastępcza układu szeregowo połączonych cewek
sprzężonych magnetycznie zgodnie wynosi:
L
z
= L
1
+ L
2
+ 2M
Jeżeli szeregowo połaczone cewki są sprzężone ujemnie, to
napięcie na zaciskach układu jest opisane równaiem:
u = (R
1
+ R
2
) i + (L
1
+ L
2
- 2M)
di
dt
Indukcyjność zastępcza układu szeregowo połączonych cewek
sprzężonych magnetycznie przeciwnie jest mniesza i wynosi:
L
z
= L
1
+ L
2
+ 2M
Korzystając z pojecia indukcyjności zastępczej na Rys. 5 oraz
Rys.
6 przedstawiono obwody równoważne układu cewk
połaczonych szeregowo, gdy sprzężenie jest zgodne oraz
przeciwne.
W zapisie symbolicznym powyższe równania przyjmują postać:
U = (R
1
+ R
2
+ j
ω
(L
1
+ L
2
)) I + 2j
ω
M I
U = (R
1
+ R
2
+ j
ω
(L
1
+ L
2
+ 2M)) I
Wypadkowa impedancja układu wynosi:
Z = R
1
+ R
2
+ j
ω
(L
1
+ L
2
+ 2M)
W tym przypadku impedancja
wypadkowa układu jest mniejsza i wynosi:
Z = R
1
+ R
2
+ j
ω
(L
1
+ L
2
- 2M)
Wykorzystując ten fakt łatwo można
sprawdzić jakie jest sprzężenie magnetyczne
dwóch cewek połaczonych szeregowo.
Rys. 3. Cewki połaczone szeregowo
Rys. 4. Schemta układu
L
1
L
2
i
M
Rys. 5. Indukcyjność zastępcza układu cewek
sprzężonych zgodnie
L
1
L
2
i
M
Rys. 6. Indukcyjność zastępcza układu cewek
sprzężonych przeciwnie
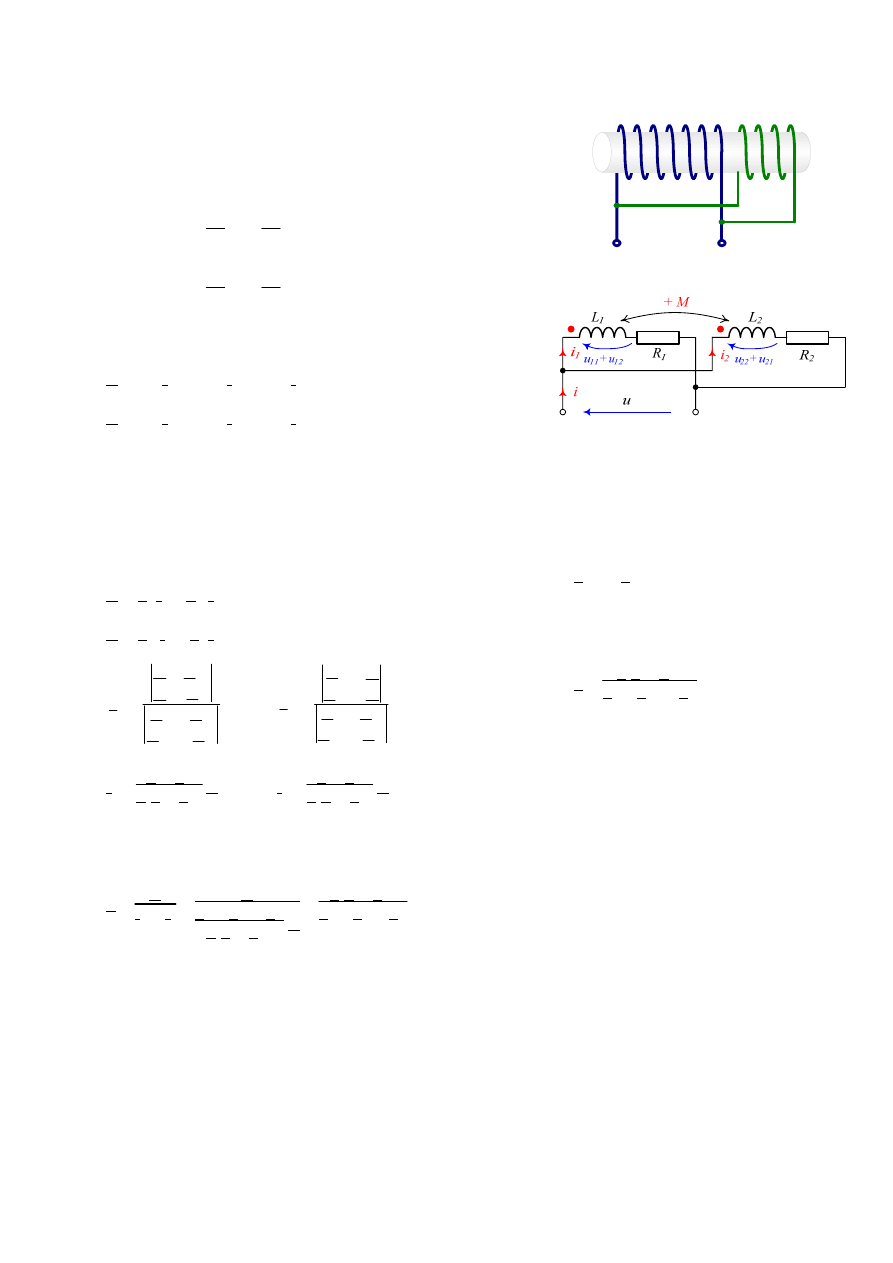
4
© Lesław ŁADNIAK
1.1.3 Przykład. Połączenie równoległe cewek
Rozpatrzmy cewki nawinięte na współnym redzeniu i
połaczone tak jak pokazano na Rys. 7. Ponieważ cewki są zgodnie
sprzężone magnetycznie i połaczone równolegle, to do dalszych
rozważań należy przyjąć przedstawiony na Rys. 8 schemat układu.
u
1
= R
1
i
1
+ L
1
di
1
dt + M
di
2
dt
u
2
= R
2
i
2
+ L
2
di
2
dt + M
di
1
dt
W zapisie symbolicznym:
U
1
= R
1
I
1
+ j
ω
L
1
I
1
+ j
ω
M I
2
U
2
= R
2
I
2
+ j
ω
L
2
I
2
+ j
ω
M I
1
gdzie:
ω
L
1
,
ω
L
2
- reaktancje własne gałęzi,
X
M
=
ω
M - reaktancja wzajemna gałęzi.
W celu wyznaczenia wypadkowej impedancji układu należy
rozwiązac następujący układ równań:
U = Z
1
I
1
+ Z
M
I
2
U = Z
M
I
1
+ Z
2
I
2
2
1
2
1
Z
Z
Z
Z
Z
U
Z
U
I
M
M
M
=
2
1
2
2
Z
Z
Z
Z
U
Z
U
Z
I
M
M
M
=
I
1
=
Z
2
- Z
M
Z
1
Z
2
- Z
M
2
U I
2
=
Z
1
- Z
M
Z
1
Z
2
- Z
M
2
U
Wypadkowa impedancja układu przy dodatnim sprzeżeniu
równolegle połaczonych cewek wynosi:
Z =
U
I
1
+ I
2
=
U
Z
1
+ Z
2
- 2Z
M
Z
1
Z
2
- Z
M
2
U
=
Z
1
Z
2
- Z
M
2
Z
1
+ Z
2
- 2Z
M
Rys. 7. Cewki połaczone równolegle
Rys. 8. Schemat układu
W przypadku cewek ujemnie
sprzężonych magnetycznie należy w
powyższych równaniach zmienić znak
impedancji wazjemnej:
Z
M
= - Z
M
Wypadkowa impedancja układu jest w
tym przypadku mniejsza i wynosi:
Z =
Z
1
Z
2
- Z
M
2
Z
1
+ Z
2
+ 2Z
M
5
© Lesław ŁADNIAK
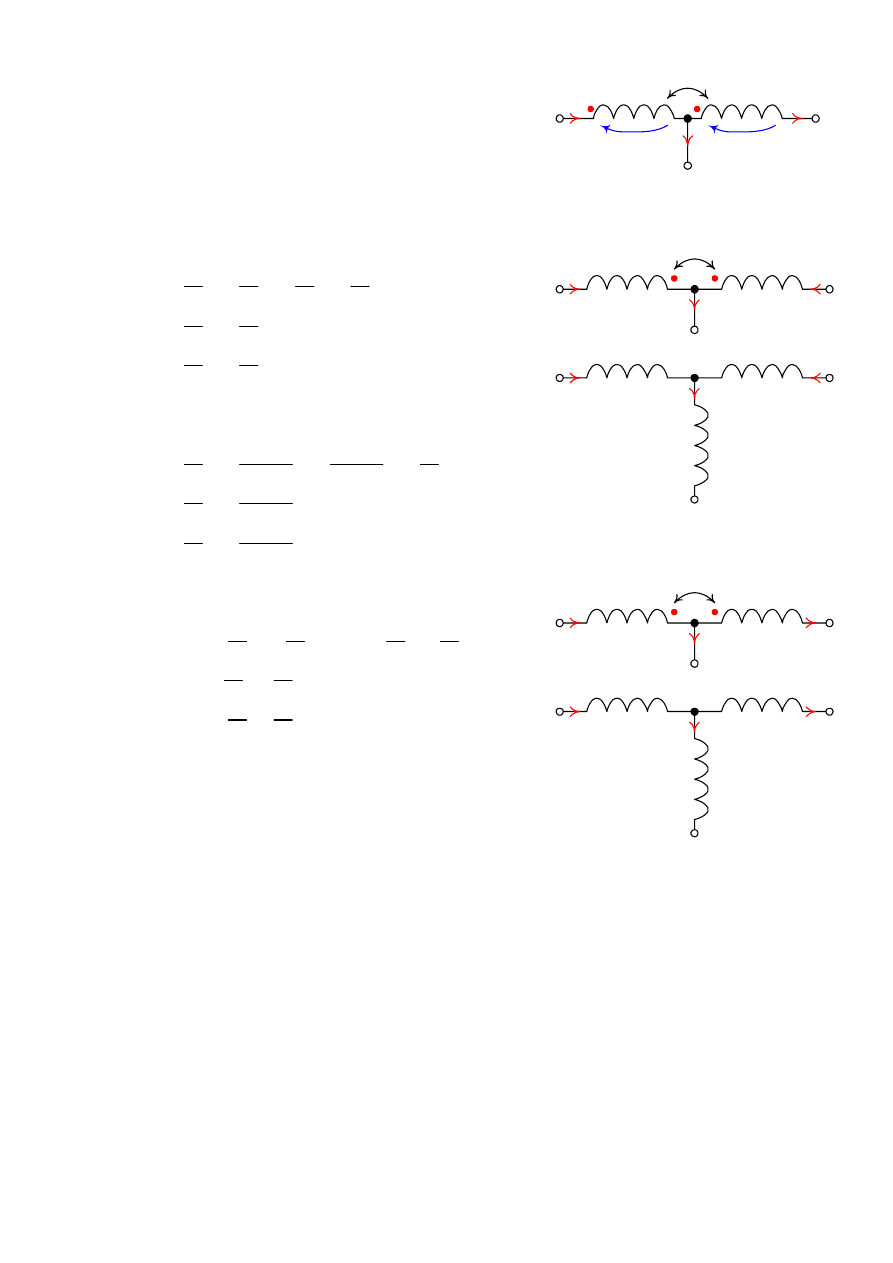
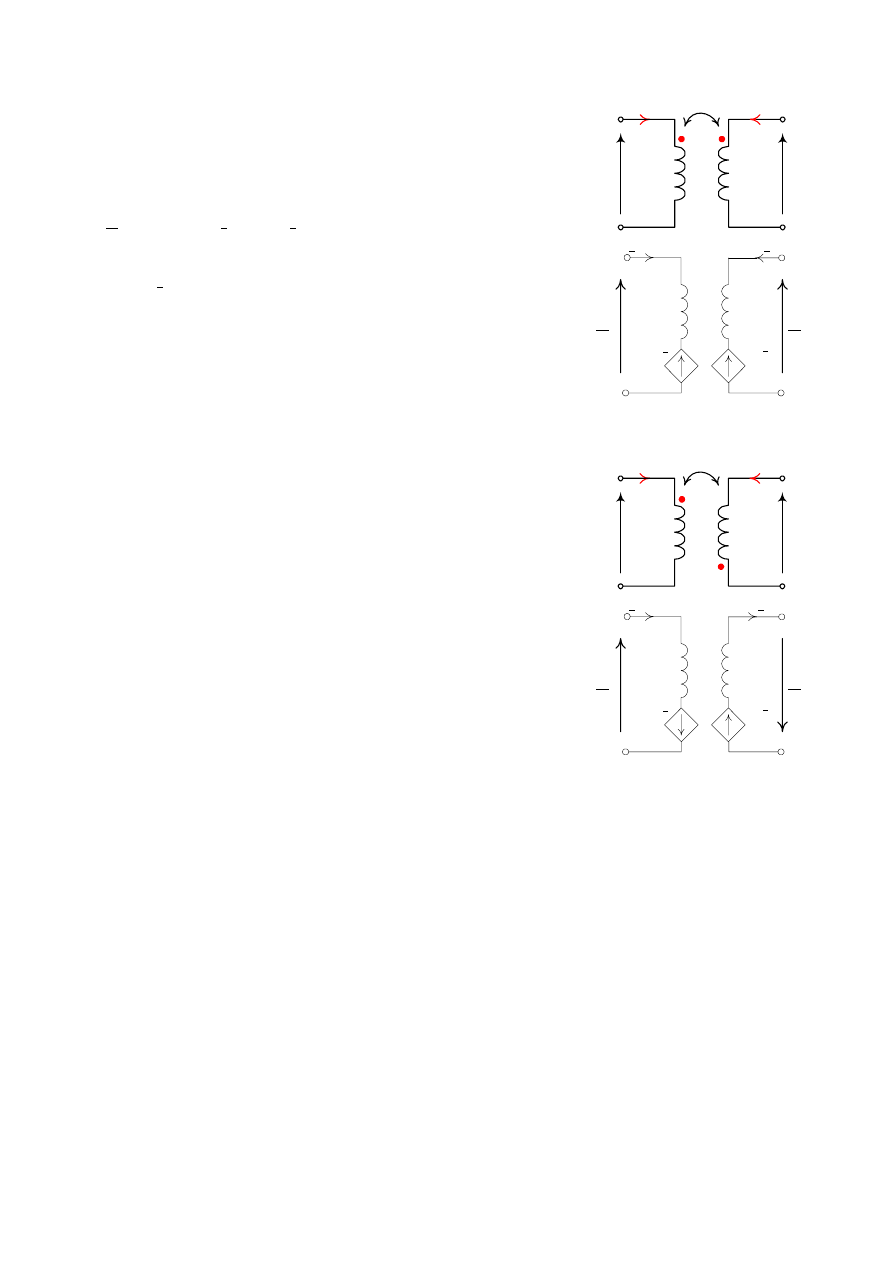
1.1.4 Rozprzęganie gałęzi o wspólnym węźle
Rozpatrzy fragment obwodu przedstawiony na Rys. 9, w
którym do wspólnego węzła dołączone są trzy gałęzie. Dwie z tych
trzech gałęzi są sprzężone magnetycznie.
Jeżeli do węzła 3 dołączona jest gałąź przez którą płynie prąd,
to napięcia między poszczególnymi węzłami są opisane
równaniami:
u
12
= L
1
di
1
dt + M
di
2
dt + L
2
di
2
dt + M
di
1
dt
u
13
= L
1
di
1
dt + M
di
2
dt
u
32
= L
2
di
2
dt + M
di
1
dt
Ponieważ i
1
= i
2
+ i
3
oraz i
2
= i
1
−
i
3
to
u
12
= L
1
di
1
dt + M
d(i
1
- i
3
)
dt
+ L
2
d(i
1
- i
3
)
dt
+ M
di
1
dt
u
13
= L
1
di
1
dt + M
d(i
1
- i
3
)
dt
u
32
= L
2
di
2
dt + M
d(i
2
- i
3
)
dt
czyli
u
12
= (L
1
+ M)
di
1
dt - 2M
di
1
dt + (L
1
+ M)
di
2
dt -2M
di
2
dt
u
13
= (L
1
+ M)
di
1
dt - M
di
3
dt
u
32
= (L
2
+ M)
di
2
dt - M
di
3
dt
Na Rys. 10 oraz Rys. 11 przedstawiono obwody równoważne,
gdy sprzężenie jest zgodne oraz przeciwne.
i
1
L
1
+M
L
2
i
2
i
3
1
2
u
22
+
u
21
u
11
+
u
12
3
Rys. 9. Gałęzie sprzężone posiadające wspólny
węzeł
i
1
L
1
+M
L
2
i
2
i
3
1
2
3
i
1
L
1
- M
+M
i
2
i
3
1
2
3
L
2
- M
Rys. 10.
Rozprzęganie gałęzi sprzężonych
zgodnie
i
1
L
1
-M
L
2
i
2
i
3
1
2
3
i
1
L
1
+ M
-M
i
2
i
3
1
2
3
L
2
+ M
Rys. 11.
Rozprzęganie gałęzi sprzężonych
przeciwnie
6
© Lesław ŁADNIAK
1.1.5 Cewki sprzężone jako źródła sterowane
W
przypadku,
gdy w obwodzie występują sinusoidalnie
zmieniające się wymuszenia, to postać równań opisujących
napięcie na zaciskach gałęzi sprzężonej jest następująca:
U
k
= (R
k
+ j
ω
L
k
) I
k
±
j
ω
M
kl
I
l
Występujące w równaniach dla gałęzi sprzężonych czynniki
typu j
ω
M I można traktować jak źródła napięciowe sterowane
prądowo. Włączając do sprzężonych gałęzi rozpatrywanego
obwodu takie źródła eliminujemy sprzężenia magnetyczne.
Jeżeli sprzężenie magnetyczne cewek jest zgodne, to
kierunek siły elektromotorycznej sterowanego źródła napięcia
jest taki sam, jak napięcia indukcji własnej wywołanego
przepływem prądu w rozpatrywanej gałęzi (Rys. 12).
Jeżeli sprzężenie magnetyczne cewek jest przeciwne, to
kierunek siły elektromotorycznej sterowanego źródła napięcia
jest skierowane przeciwnie do napięcia indukcji własnej
wywołanego przepływem prądu w rozpatrywanej gałęzi
(Rys. 13)
u
2
i
1
L
1
+ M
u
1
L
2
i
2
U
2
I
1
I
2
L
1
U
1
j
ωMI
2
L
2
j
ωMI
1
Rys. 12.
Sprzężenie zgodne
u
2
i
1
L
1
- M
u
1
L
2
i
2
U
2
I
1
I
2
L
1
U
1
j
ωMI
2
L
2
j
ωMI
1
Rys. 13.
Sprzężenie przeciwne
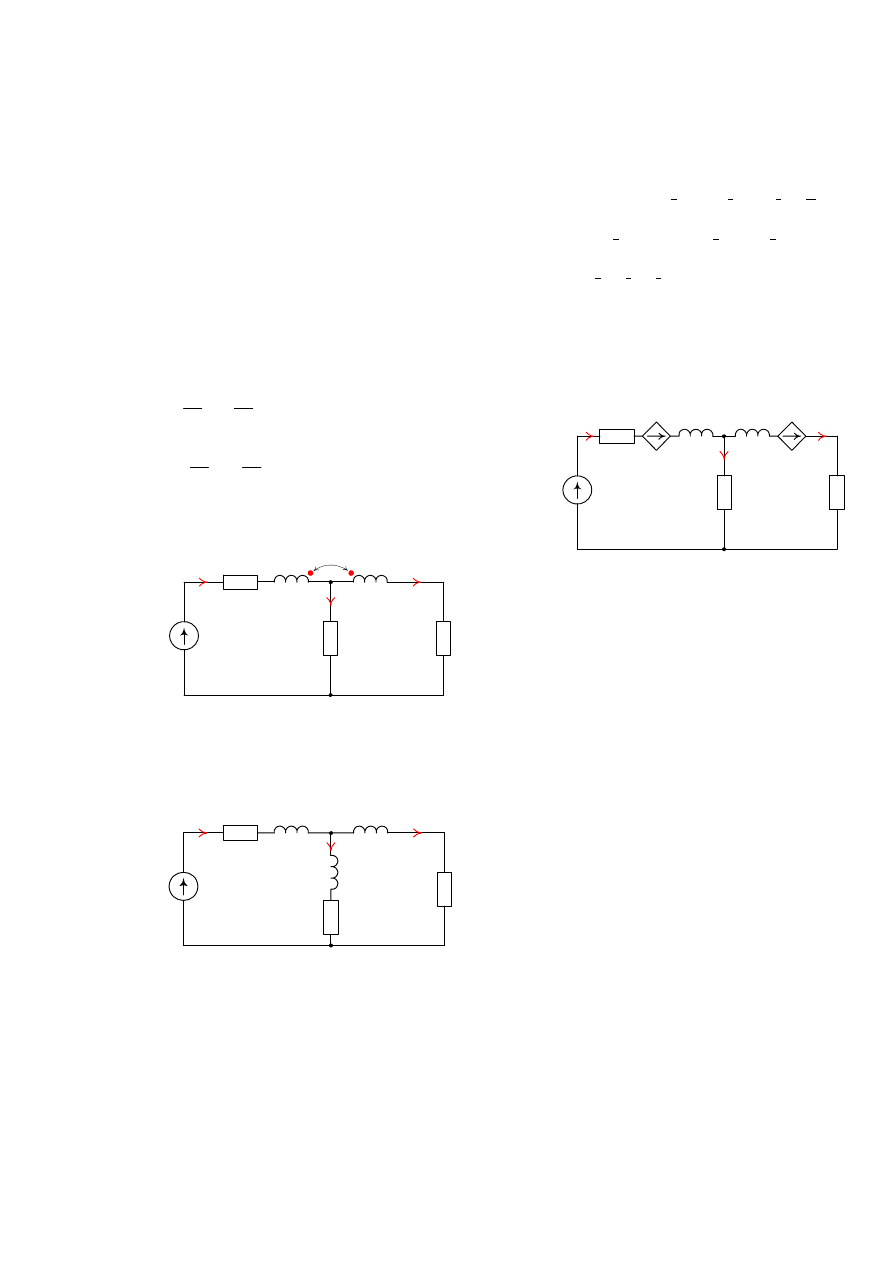
7
© Lesław ŁADNIAK
1.2 Równania obwodów ze sprzężeniami
Przystępując do rozwiązywania obwodów ze sprzężeniami
magnetycznymi należy przejść do obwodów równoważnych bez
sprzężeń magnetycznych.
Zasady tworzenia układów równoważnych bez sprzężeń
przedstawiono na Rys. 5, Rys. 6, Błąd! Nie można odnaleźć
źródła odwołania., Błąd! Nie można odnaleźć źródła
odwołania..
Rozpatrzmy obwód przedstawiony na Rys. 14, w którym
cewkami są sprzężone magnetycznie. Dla rozpatrywanego obwodu
równania Kirchhoffa przyjmują postać:
R
1
i
1
+L
1
di
1
dt - M
di
2
dt + R
3
i
3
= e(t)
R
3
i
3
+
L
2
di
2
dt - M
di
1
dt - R
2
i
2
= 0
i
1
= i
2
+ i
3
R
3
e(t)
R
2
R
1
i
1
L
1
L
2
i
2
i
3
M
Rys. 14.
Obwód ze sprzężeniem magnetycznym
Na Rys. 15 przedstawiono schemat zastępczy obwodu z Rys. 14
po eliminacji sprzężenia magnetycznego między cewkami L
1
i L
2
.
e(t)
R
2
R
1
i
1
i
2
L
1
+ M
L
2
+ M
R
3
i
3
- M
Rys. 15.
Schemat obwodu po eliminacji sprzężeń
Jeżeli działająca w obwodzie siła
elektromotoryczna e(t) jest sinusoidalnie
zmienna, to równania dla obwodu
przedstawionego na Rys.
14 przyjmują
postać:
(R
1
+
j
ω
L
1
)
I
1
- j
ω
M
I
2
+ R
3
I
3
= E
R
3
I
3
- (R
2
+
j
ω
L
2
)
I
2
- j
ω
M
I
1
= 0
I
1
= I
2
+ I
3
Zastępując napięcia indukcji wzajemnej
występujące w cewkach L
1
i L
2
sterowanymi
źródłami napięcia otrzymujemy schemat
obwodu przedstawiony na Rys. 16.
R
3
E
R
2
R
1
I
1
L
1
L
2
I
2
I
3
j
ωMI
1
j
ωMI
2
Rys. 16.
Schemat obwodu po eliminacji
sprzężeń magnetycznych
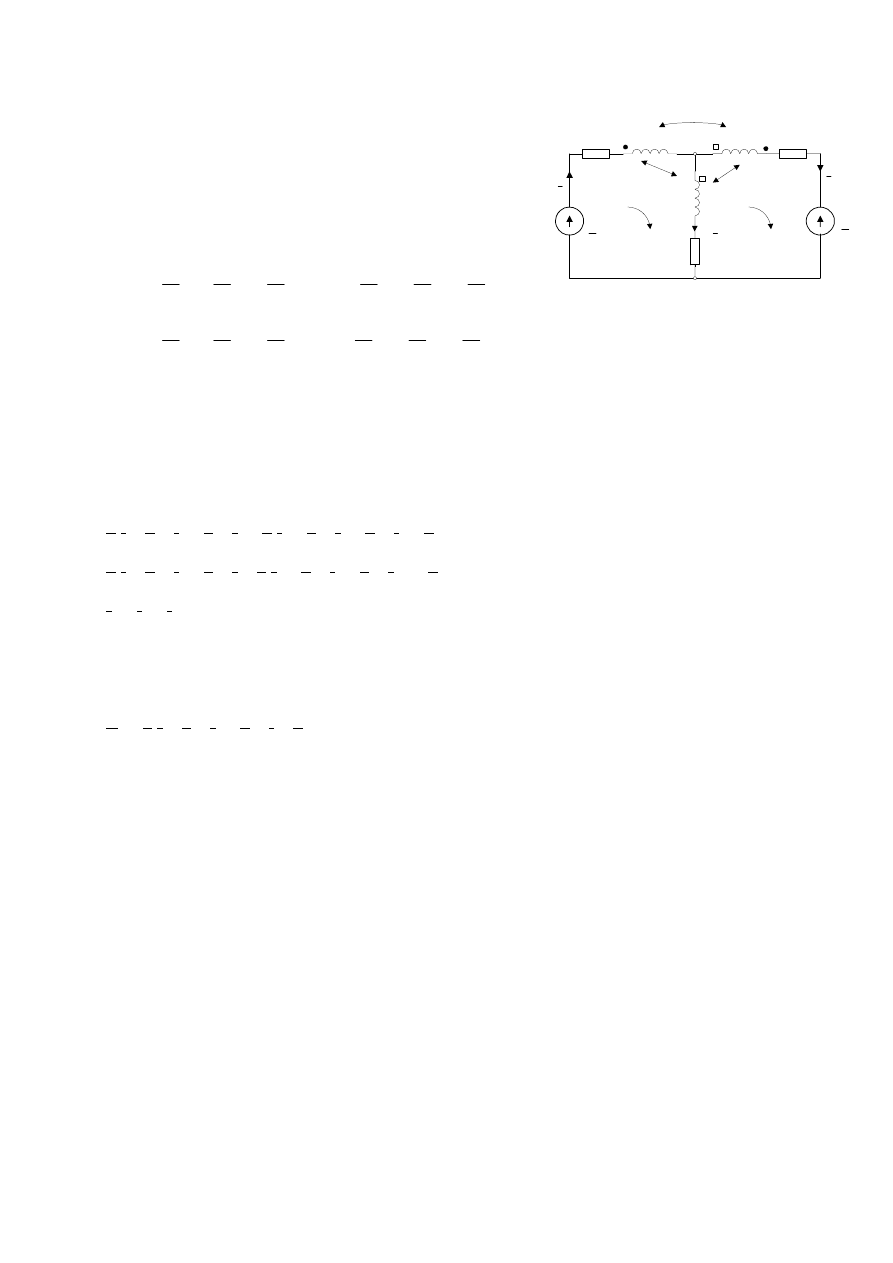
8
© Lesław ŁADNIAK
1.2.1 Metoda równań Kirchhoffa
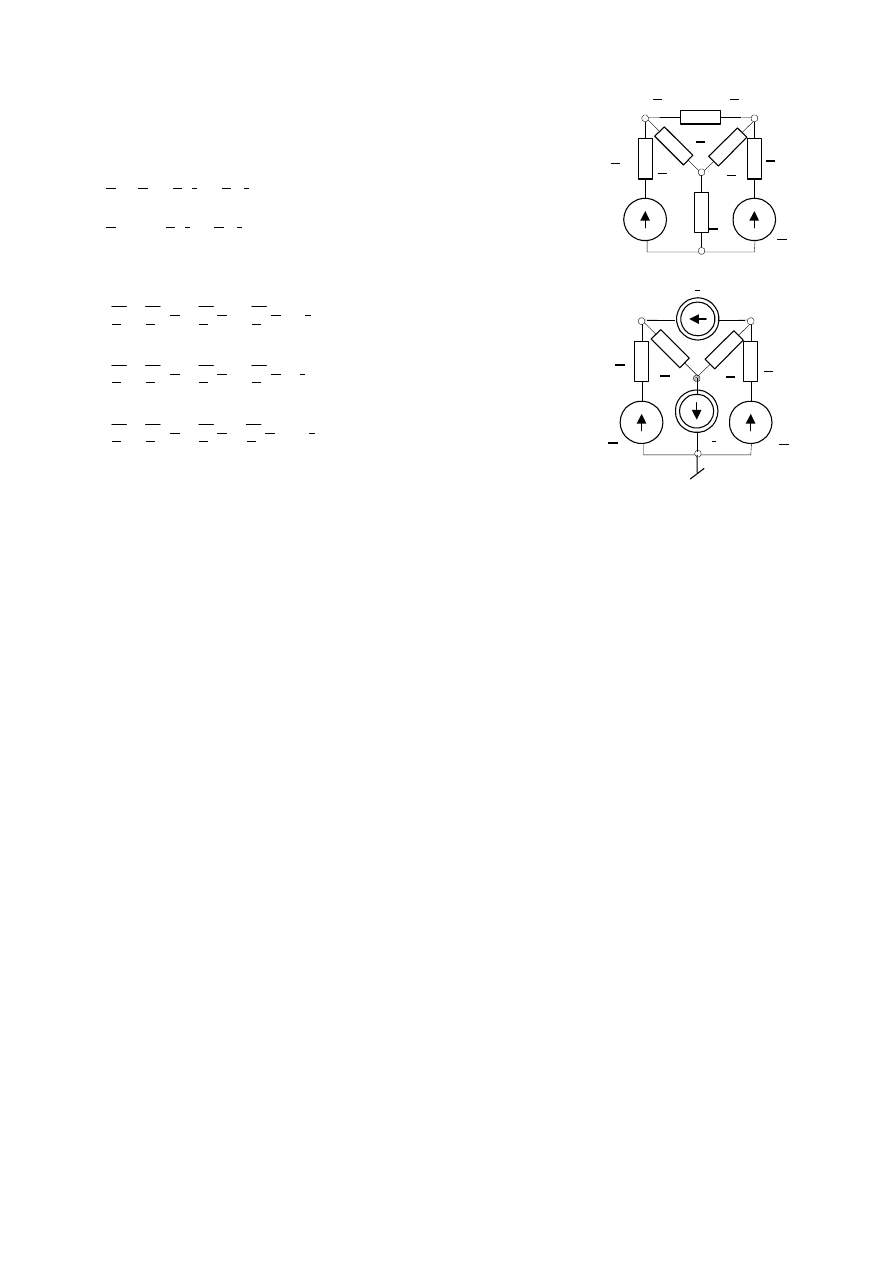
Na Rys.
17 przedstawiono obwód w którym występują
sprzężenia magnetyczne. Napiszmy równania wynikające z praw
Kirchhoffa dla rozpatrywanego obwodu.
Zgodnie
z
napięciowym prawem Kirchhoffa równania dla
oczka I oraz II przyjmują postać:
(R
1
i
1
+
L
1
di
1
dt
–
M
12
di
2
dt
+
M
13
di
3
dt )
+
(R
3
i
3
+
L
3
di
3
dt
+
M
13
di
1
dt
+
M
23
di
2
dt
=
e
1
(R
2
i
2
+
L
2
di
2
dt
–
M
12
di
1
dt
+
M
23
di
3
dt )
-
(R
3
i
3
+
L
3
di
3
dt
+
M
13
di
1
dt
+
M
23
di
2
dt
=
-
e
2
Korzystając z prądowego prawa Kirchhoffa otrzymujemy:
i
1
= i
2
+ i
3
Dla przebiegów sinusoidalnych równania powyższe przyjmują
postać:
Z
1
I
1
- Z
M12
I
2
+ Z
M13
I
3
+ Z
3
I
3
+ Z
M13
I
1
+ Z
M23
I
2
= E
1
Z
2
I
2
- Z
M12
I
1
+ Z
M23
I
3
- Z
3
I
3
+ Z
M13
I
1
+ Z
M23
I
2
= - E
2
I
1
= I
2
+ I
3
Jak wynika z przedstawionych równań napięcie w gałęzi
pierwszej jest w tym przypadku liniową kombinacją prądów we
wszystkich gałęziach ropztrywanego obwodu:
U
1
= Z
1
I
1
- Z
M12
I
2
+ Z
M13
I
3
- E
1
sprzężenie
sprzężenie
ujemne dodatnie
i
1
I
1
R
1
L
1
L
2
R
2
e
2
E
2
i
2
I
2
L
3
R
3
*
*
M
13
M
23
M
12
I
II
e
1
E
1
i
3
I
3
Rys. 17.
Obwód ze sprzężeniami
magnetycznymi
9
© Lesław ŁADNIAK
1.2.2 Przykład. Metoda potencjałów węzłowych
Dla gałęzi ze sprzężeniami:
V
2
– V
1
= Z
3
I
3
+ Z
M
I
5
V
3
– 0 = Z
5
I
5
+ Z
M
I
3
Równania dla metody potencjałów węzłowych:
(
1
Z
1
+
1
Z
2
) V
1
-
1
Z
2
V
3
=
1
Z
1
E
1
+ I
3
(
1
Z
4
+
1
Z
6
) V
2
-
1
Z
4
V
4
=
1
Z
6
E
6
- I
3
(
1
Z
2
+
1
Z
4
) V
3
-
1
Z
2
V
1
-
1
Z
4
V
2
= - I
5
Do dyspozycji mamy pięć równań, w których niewiadomymi są
trzy wartości potencjałów oraz dwa prądy.
Z
1
Z
2
Z
5
Z
3
Z
4
Z
6
E
6
*
Z
35
=j
ωM
35
=Z
M
*
Z
1
Z
2
Z
4
E
1
E
6
Z
6
V
1
V
2
V
3
I
5
I
3
Rys. 18.
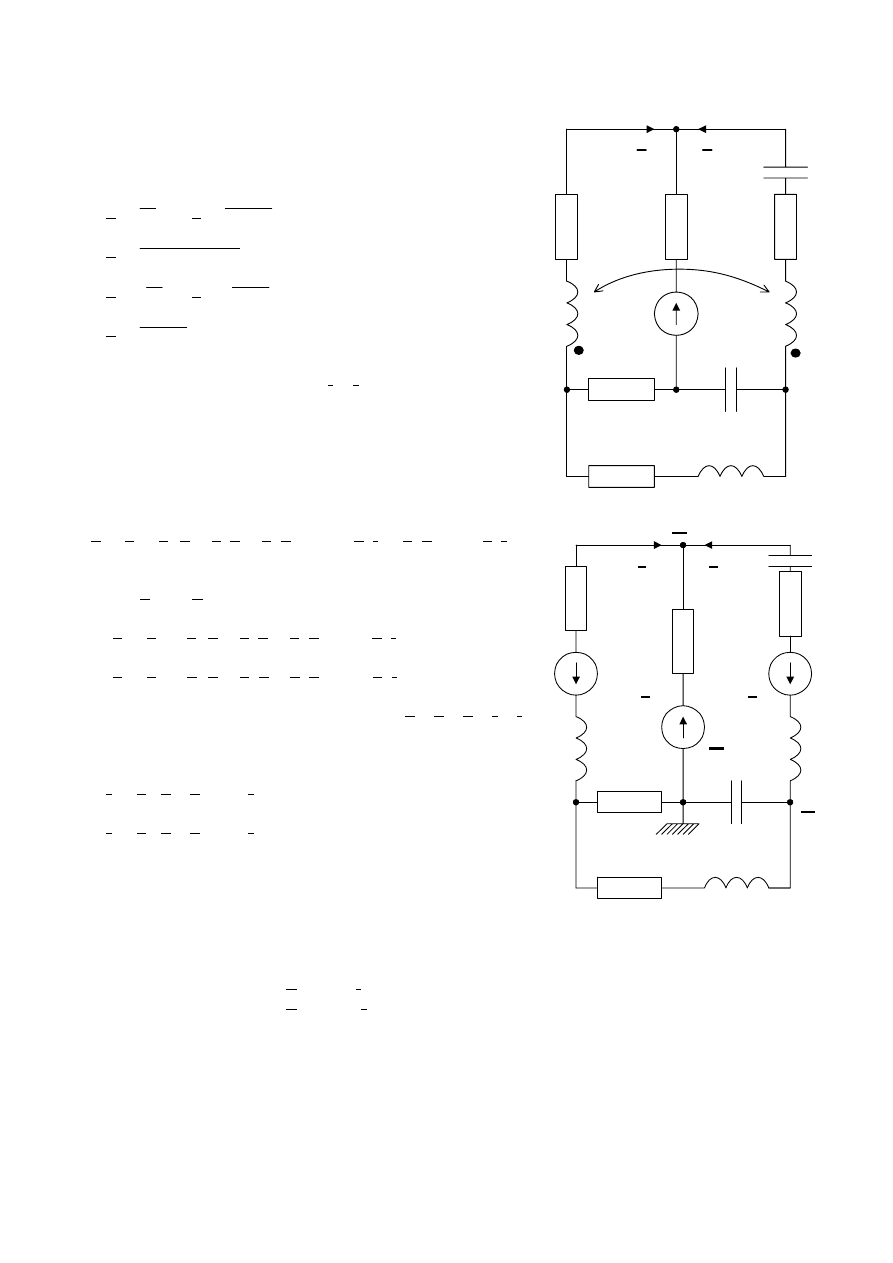
10
© Lesław ŁADNIAK
1.2.3 Przykład. Źródła sterowane w metodzie
potencjałów
Admitancje poszczególnych gałęzi obwodu wynoszą:
Y
0
=
1
R
0
Y
1
=
1
R
1
+jX
1
Y
2
=
1
R
2
+j(X
L2
- X
C2
)
Y
3R
=
1
R
3
Y
3C
=
1
- jX
3C
Y
4
=
1
R
4
+jX
4
Przyjęto, że kierunki prądów I
1
, I
2
płynących prze cewki
sprzężone są takie jak zaznaczono na rys. 1.
Istniejące w obwodzie sprzężenia można zastąpić sterowanymi
źródłami napięcia, co pokazano na rys. 2.
Równanie dla węzła pierwszego, o potencjale V
1
:
[Y
1
+ Y
0
+ Y
2
]V
1
– Y
1
V
2
– Y
2
V
3
= - jX
12
Y
1
I
2
+ Y
0
E
0
– jX
12
Y
2
I
1
Analogicznie równania dla pozostałych dwóch niezależnych
węzłów V
2
,oraz V
3
.
[Y
1
+ Y
3R
+ Y
4
]V
2
– Y
1
V
1
– Y
4
V
3
= jX
12
Y
1
I
2
[Y
1
+ Y
3C
+ Y
4
]V
3
– Y
2
V
1
– Y
4
V
2
= jX
12
Y
2
I
1
Liczba niewiadomych wzrosła do pięciu V
1
, V
2
, V
3
, I
1
, I
2
.
Brakujące dwa równania mają postać równań Ohma - dla gałęzi
sprzężonych magnetycznie:
I
1
= Y
1
(V
2
- V
1
- jX
12
I
2
)
I
2
= Y
2
(V
3
- V
1
- jX
12
I
2
)
Z
pięciu równań oblicza się pięć niewiadomych. Pozostałe
prądy oblicza się w znany sposób.
Uwaga:
Można przyjąć zasadę, że źródła sterowane strzałkujemy
przeciw prądom.
Przy
sprzężeniu dodatnim: E
kM
= jX
kl
I
l
Przy
sprzężeniu ujemnym: E
kM
= -jX
kl
I
l
R
1
R
0
R
2
R
3
R
4
I
1
I
2
M
12
C
2
C
3
L
1
L
2
L
4
e
0
Rys. 1
R
4
jX
L4
R
3
jX
L1
R
1
R
0
R
2
I
2
I
1
jX
12
I
2
V
1
-jX
C2
jX
12
I
1
V
3
-jX
C3
jX
L2
E
0
Rys. 2
11
© Lesław ŁADNIAK
1.2.4 Przykład. Mostek ze sprzężeniami
Wyznaczyć warunek równowagi mostka przedstawionego na
Rys. 19.
W warunkach równowagi mostka:
I
g
= 0 gdy V
1
- V
2
= 0
Z porównania napięć i prądów(przy zerowym prądzie
galwanometru):
U
1
= U
3
; U
2
= U
4
; I
2
= I
1
; I
4
= I
3
R
1
I
1
= (R
3
+ j
ω
L
3
) I
3
- j
ω
M I
1
R
4
I
3
= (R
2
+ j
ω
L
2
) I
1
- j
ω
M I
3
(R
1
+ j
ω
M) I
1
= (R
3
+ j
ω
L
3
) I
3
(R
4
+ j
ω
M) I
3
= (R
2
+ j
ω
L
2
) I
1
czyli
(R
1
+ j
ω
M) (R
4
+ j
ω
M) = (R
3
+ j
ω
L
3
) (R
2
+ j
ω
L
2
)
Po uporządkowaniu i porównaniu części rzeczywistych i
urojonych otrzymujemy następujące warunki równowagi:
ω
2
(L
2
L
3
- M
2
) = R
2
R
3
- R
1
R
4
(R
1
+ R
4
) M. = R
3
L
2
+ R
2
L
3
Z drugiego równania można obliczyć dowolną wielkość przy
założeniu, że pozostałe są znane. Z pierwszego równania można
pulsację
ω
.
Mostek
równoważy się wstępnie przy prądzie stałym
R
2
R
3
= R
1
R
4
,
a następnie przy prądzie sinusoidalnie zmiennym regulując jednym
z parametrów L
1
, L
2
lub M.
G
I
1
R
1
V
1
V
2
R
2
L
2
*
R
4
L
3
R
3
I
3
*
I
g
Rys. 19.
Mostek
12
© Lesław ŁADNIAK
1.3 Przekazywanie energii przez sprzężenie
Na Rys. 20 przestawiono dwie gałęzie sprzężone magnetycznie,
w których płyną prądy sinusoidalnie zmienne.
u
2
i
1
L
1
M
* *
u
1
L
2
i
2
W
W
P
w1
P
w2
Rys. 20.
Gałęzie sprzężone magnetycznie
W wyniku sprzężenia magnetycznego, przepływ prądu w gałęzi
pierwszej I
2
powoduje wyidukowanie się napięcia U
1M
w gałęzi
drugiej. Odpowiednio prąd I
1
wywołuje napięcie U
2M
.
U
1M
=
±
j
ω
M I
2
U
2M
=
±
j
ω
M I
1
Moc
pozorna
S
M
przekazywana między gałęziami poprzez
sprzężenie magnetyczne jest iloczynem napięcia wyidukowanego
w rozpatrywanej gałęzi oraz od prądu płynącego w rozpatrywanej
gałęzi:
S
M1
= U
1M
I
1
*
S
M2
= U
2M
I
2
*
Przy sprzężeniu dodatnim, napięcie wywołane przepływem prądu
w gałęzi sprzężonej jest równe:
U
1M
= j
ω
M I
2
Natomiast przy sprzężeniu ujemnym
U
1M
= - j
ω
M I
2
W rozpatrywanym przypadku występuje sprzężenie dodatnie, więc
S
M1
= (j
ω
MI
2
) I
1
*
= e
j
π
/2
ω
M I
2
e
j
ψ
2
I
1
e
-
j
ψ
1
S
M1
=
ω
M I
2
I
1
e
j(
π
/2 +
ψ
2 -
ψ
1)
Ponieważ
e
j
α
= cos
α
+ j sin
α
to moc czynna przekazywana przez
sprężenie wynosi:
P
M1
=
Re{S
M1
}
=
ω
M
I
2
I
1
cos(
π
2
+
ψ
2
-
ψ
1
)
Ostateczna
postać równania opisującego
ilość mocy czynnej przekazywanej przez
sprzężenie magnetyczne jest następująca:
P
M1
=
ω
M I
2
I
1
sin(
ψ
2
-
ψ
1
)
Wniosek:
Gdy przesunięcie fazowe między
prądami w
sprzężonych magnetycznie
gałęziach spełnia warunek:
0 <
ψ
2
-
ψ
1
<
π
to moc czynna P
M1
jest dodatnia, czyli
energia jest przekazywana z gałęzi drugiej
do pierwszej.
Przy sprzężeniu dodatnim energię
przekazuje ta gałąź, której prąd
wyprzedza w fazie przebieg drugiego
prądu.
Dla drugiej gałęzi możemy napisać, że
S
M2
=
ω
M I
1
I
2
e
j(
π
/2 +
ψ
1 -
ψ
2)
czyli
P
M2
=
ω
M I
1
I
2
sin(
ψ
1
-
ψ
2
) =
=
-
ω
M I
1
I
2
sin(
ψ
2
-
ψ
1
) = - P
M1
Wniosek:
Energia
jaką pobiera z sieci gałąź
pierwsza w
wyniku sprzężenia
magnetycznego jest oddawana do sieci
przez gałąź drugą.