1

K 03

1

ZADANIE 1

Zespolony wektor pola elektrycznego fali w próżni wyraża się
zależnością:
gdzie: E

x0

, E

y0

– stałe rzeczywiste.

a) Obliczyć zespolony i rzeczywisty wektor pola magnetycznego;
b) Dla jakich relacji między stałymi E

x0

, E

y0

, φ

x

, φ

y

polaryzacja fali

będzie: - liniowa,

- kołowa,
- eliptyczna?

0

0

0

0

y

x

j z j

j z j

x

x

y

y

E i E e

i E e

β

ϕ

β

ϕ

−

+

−

+

=

+

r r

r

0

1

H

n E

Z

=

×

r

r

r

a) Zespolony wektor natężenia pola magnetycznego:

0

0

0

0

0

0

y

x

j z j

y

j z j

x

x

y

E

E

H

i

e

i

e

Z

Z

β

ϕ

β

ϕ

−

+

−

+

= −

+

r

r

r

0

1

z

i

E

Z

=

× r

r

2

K 03

2

ZADANIE 1 (2)

• Rzeczywisty wektor natężenia pola magnetycznego:

0

0

0

0

0

0

H

cos(

)

cos(

)

y

x

x

y

y

x

E

E

i

t

z

i

t

z

Z

Z

ω β

ϕ

ω β

ϕ

= −

−

+

+

−

+

r

r

r

• Rzeczywisty wektor natężenia pola elektrycznego:

0

0

0

0

E

cos(

)

cos(

)

x

x

x

y

y

y

i E

t

z

i E

t

z

ω β

ϕ

ω β

ϕ

=

−

+

+

−

+

r r

r

b) Polaryzacja:

- liniowa:

0

0;

x

E

=

0

0;

y

E

=

0

0

0 i

0 i

albo

x

y

x

y

x

y

E

E

ϕ

ϕ

ϕ ϕ

π

≠

≠

=

−

= ±

- kołowa:

0

0

x

y

E

E

=

i

2

x

y

π

ϕ ϕ

−

= ±

- eliptyczna: pozostałe przypadki

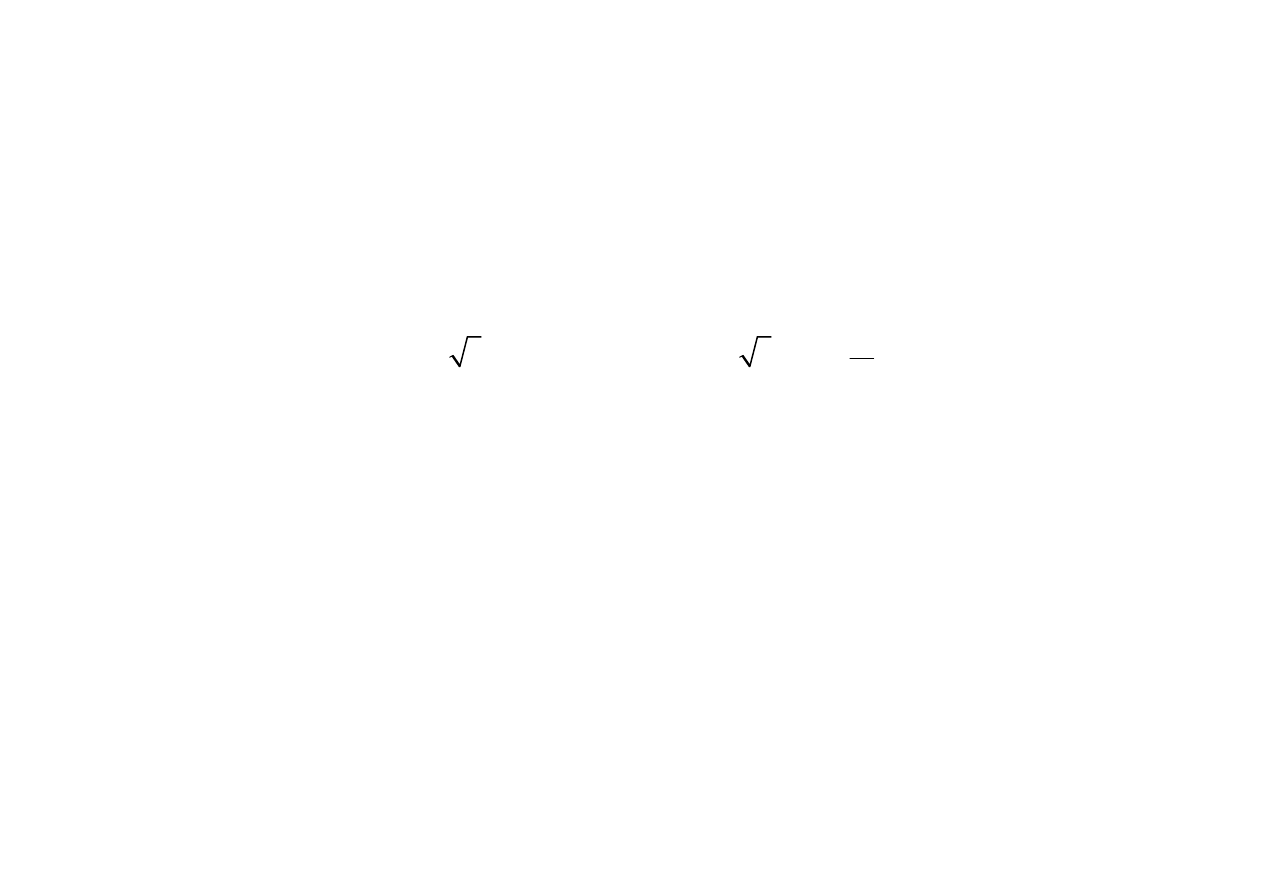
3

K 03

3

ZADANIE 2

Fala płaska o częstotliwości f = 9 GHz rozchodzi się w dielektryku.
Wektor natężenia pola magnetycznego fali wynosi:

(

)

(

)

A

( )

3

exp 30

3

.

m

x

y

H r

i

i

j

x

y

π

 





= −

+

+

 



  

r

r r

r

S( , ).

r t

r r

( , ), E( , )

E r t

r t

r

r

r

r

H( , )

r t

r r

Określić:
a) względną przenikalność elektryczną ε

r

dielektryka;

b) wektor natężenia pola magnetycznego:
c) wektory natężenia pola elektrycznego:
d) wektor Poyntinga:

4

K 03

4

Dane:

¾

Wyznaczenie przenikalności elektrycznej

ZADANIE 2 (2)

9 GHz

f

=

Ośrodek bezstratny

(

)

(

)

A

( )

3

exp 30

3

.

m

x

y

H r

i

i

j

x

y

π

 





= −

+

+

 



  

r

r r

r

• Współczynnik fazy:

• Wektor pola magnetycznego:

(

)

1

1

3

3

2

2

2

x

y

x

y

n

i

i

i

i

= −

+

= −

−

r

r

r

r

r

• Kierunek rozchodzenia się fali:

3

1

1

3

A

( ) 2

exp 60

2

2

2

2

m

x

y

H r

i

i

j

x

y

π













−

 

=

+

+













 

 













r

r

r

r

rd

60

m

β

π

=

• Względna przenikalność elektryczna:

2

0

r

β

ε

β





=

=









2

2

16

2

2

2

0

2

2

2

18

3 10

60

1

4

9 10

c

β

π

ω

π

⋅

=

=

⋅

⋅ ⋅

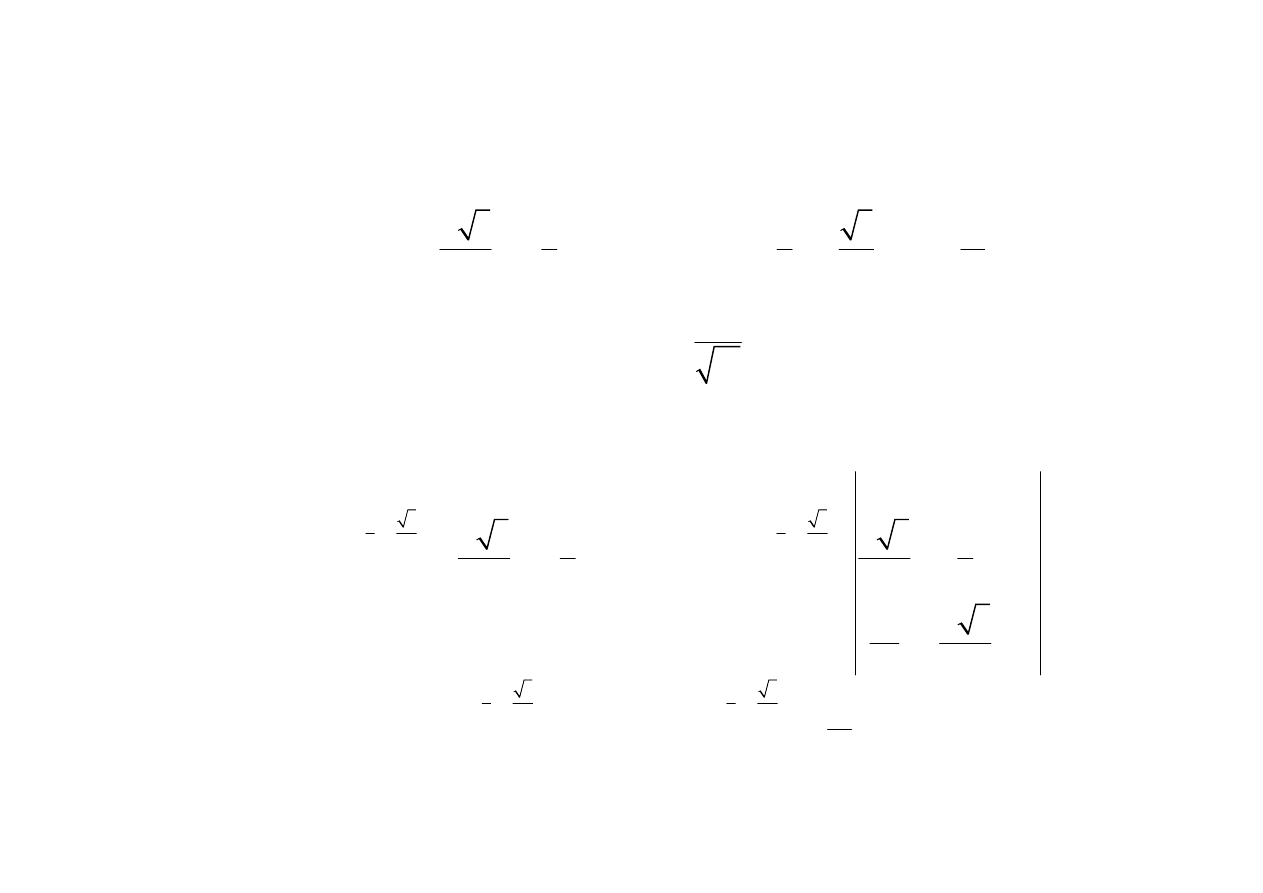
5

K 03

5

ZADANIE 2 (3)

• Wektor rzeczywisty natężenia pola magnetycznego:

E ZH n

=

×

r

r r

• Wektor natężenia pola elektrycznego:

1

3

1

3

2

2

2

2

0

0

3

1

3

1

0

2

2

2

2

1

3

0

2

2

x

y

z

j

x

y

j

x

y

x

y

i

i

i

E ZH e

i

i

n ZH e

β

β









+

+





















−

−

=

+

× =









−

−

r

r

r

r

r

r

r

3

1

1

3

A

H( , ) 2

cos

60

2

2

2

2

m

x

y

r t

i

i

t

x

y

ω

π













−

 

=

+

+

+













 

 













r

r

r

r

• Impedancja właściwa ośrodka:

0

120 [ ]

r

Z

Z

π

ε

=

=

Ω

1

3

1

3

60

2

2

2

2

0

V

240

m

j

x

y

j

x

y

z

z

E H Zi e

i e

β

π

π









+

+

















 

=

=

 

 

r

r

r

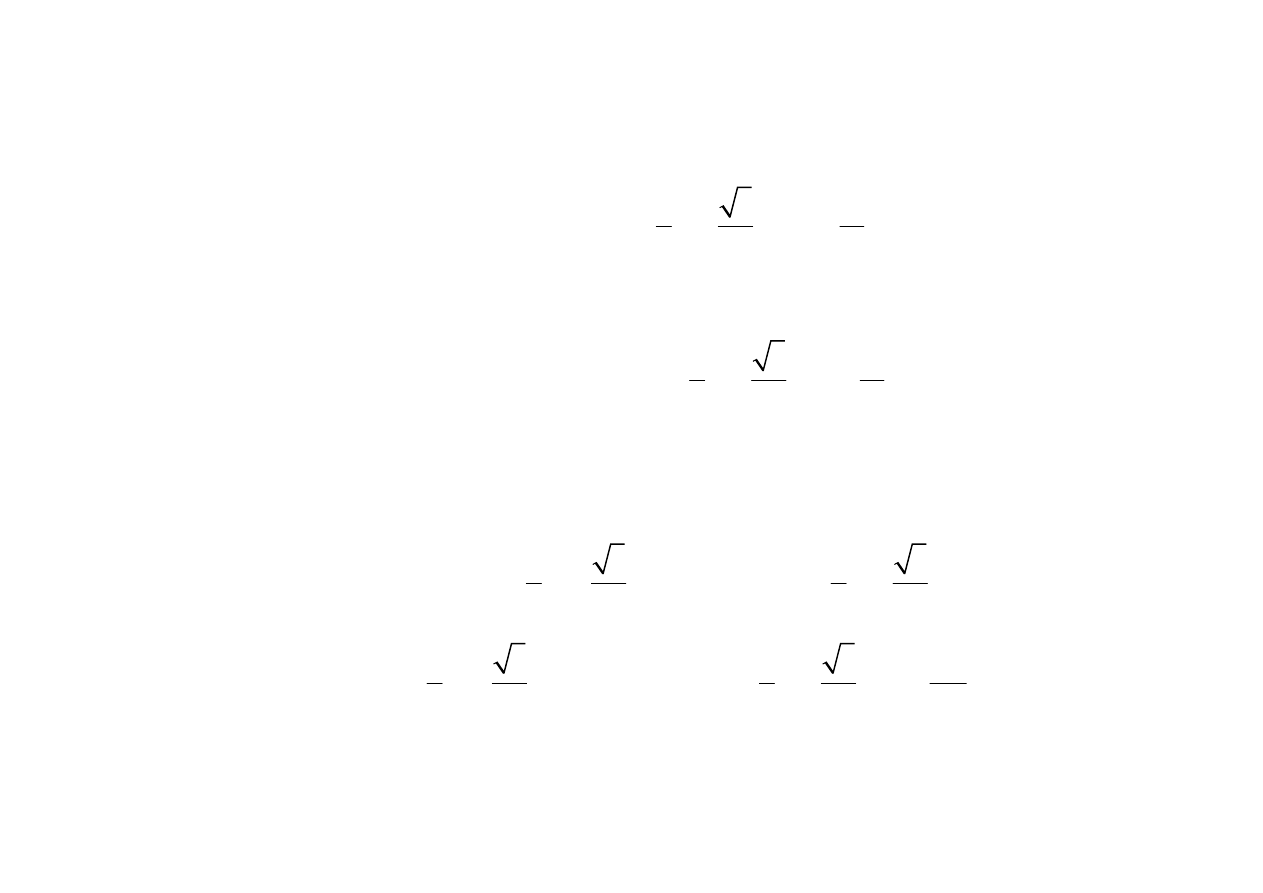
6

K 03

6

ZADANIE 2 (4)

• Wektor Poyntinga:

1

3

V

E( , ) 240

cos

60

2

2

m

z

r t

i

t

x

y

π

ω

π









=

+

+

















r

r

r

2

0

0

2

2

1

3

1

3

S E H

cos

2

2

2

2

1

3

1

3

W

480

cos

60

2

2

2

2

m

x

y

x

y

E H

i

i

t

x

y

i

i

t

x

y

ω β

π

ω

π













= × =

−

−

+

+





































=

−

−

+

+

























r r r

r

r

r

r

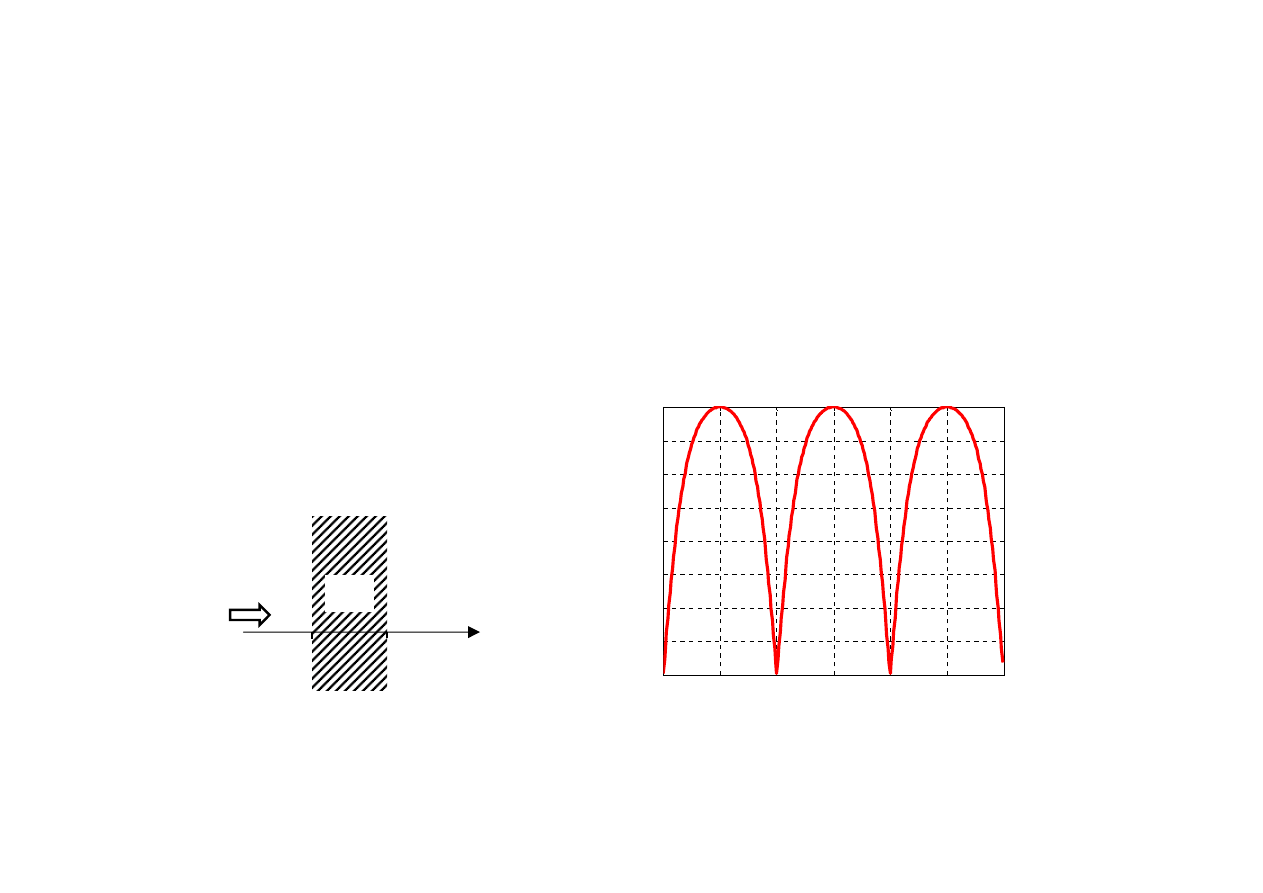
1

3

V

( ) 240

exp 60

2

2

m

z

E r

i

j

x

y

π

π









 

=

+









 

 









r

r

r

• Wektor rzeczywisty natężenia pola elektrycznego:

7

K 03

7

ZADANIE 3

Na umieszczoną w powietrzu warstwę bezstratnego dielektryka
o grubości d (Rys.1) pada prostopadle fala płaska o składowych

;

Ax

Ay

E

H

+

+

W oparciu o dane z Rys.2 obliczyć:

a) względną przenikalność elektryczną ε

r

dielektryka;

b) grubość warstwy d.

A

B

z

0

0

r

ε ε

d

−

0

ε

0

ε

C

;

Ax

Ay

E

H

+

+

Rys.1. Warstwa dielektryka

w powietrzu.

Rys.2. Częstotliwościowa charakterystyka

|Γ

A

| w obszarze A.

0

0.5

1

1.5

2

2.5

3

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

f [GHz]

|

Γ

A

|

8

K 03

8

ZADANIE 3 (2)

• Impedancja falowa „widziana” w drugim ośrodku w płaszczyźnie

granicznej z ośrodkiem pierwszym, tzn. dla z = –d :

2

tg(

)

(

)

tg(

)

C

B

B

Bf

B

B

C

Z

jZ

d

Z

d

Z

Z

jZ

d

β

β

+

− =

+

• Współczynnik odbicia na granicy ośrodków pierwszego i drugiego:

(

)

(

)

(

)

Bf

A

A

Bf

A

Z

d

Z

d

Z

d

Z

− −

Γ − =

− +

,

,

A

B

C

Z Z Z

- impedancje właściwe poszczególnych obszarów

• Można wykazać, że

osiąga maksymalną wartość dla:

A

Γ

2

B

d

n

π

β

π

= +

• Z warunków zadania:

[ ]

0

120

A

C

Z

Z

Z

π

=

=

=

Ω

9

K 03

9

ZADANIE 3 (3)

•

dla:

0

A

Γ =

B

d k

β

π

=

• Z Rys.2 wynika:

0

C

Z

Z

=

2

max

0.5 GHz

=

(

)

2

B

A

B

Bf

C

Z

f

d

Z

d

Z

π

β

=

⇒ Γ

Γ

⇒

=

⇒

− =

1 GHz

=0

(

)

A

B

Bf

C

f

d

Z

d

Z

β

π

=

⇒ Γ

⇒

=

⇒

− =

0

B

r

Z

Z

ε

=

2

0

(

)

B

Bf

C

r

Z

Z

Z

d

Z

ε

− =

=

0.5 GHz

(

)

1

(

)

(

)

1

Bf

A

r

A

f

Bf

A

r

Z

d

Z

d

Z

d

Z

ε
ε

=

− −

−

Γ −

=

=

− +

+

10

K 03

10

ZADANIE 3 (4)

• Należy pamiętać, że dla dielektryków:

• Zatem:

0

rd

20

m

B

r

β

ε β

π

 

=

=

 

 

max

0.5 GHz

1

(

)

0.8

9

1

r

A

A

r

f

r

d

ε

ε

ε

=

−

Γ

= Γ −

=

=

⇒

=

+

1

r

ε

≥

• Grubość warstwy dielektryka wyznacza się znając dla

określonej częstotliwości

B

d

β

gdy

1 GHz to

B

f

d

β

π

=

=

9

0

8

rd

2 10

20

rd

s

dla

1 GHz

=

m

3

m

3 10

s

f

c

π

ω

π

β

 

 

 

 

=

⇒

=

=

 

 

 

⋅

 

 

[ ] [ ]

1

m

5 cm

20

B

d

d

β

π

=

⇒

=

=