
Politechnika Wrocławska
Politechnika Wrocławska
Wydział Budownictwa
Wydział Budownictwa
Lądowego i Wodnego
Lądowego i Wodnego
Instytut Inżynierii Lądowej
Rok studiów II
Zakład Dynamiki Budowli
PROJEKT NR 1
Z PODSTAW STATYKI BUDOWLI
BELKA
Rok akademicki:
201_/201_
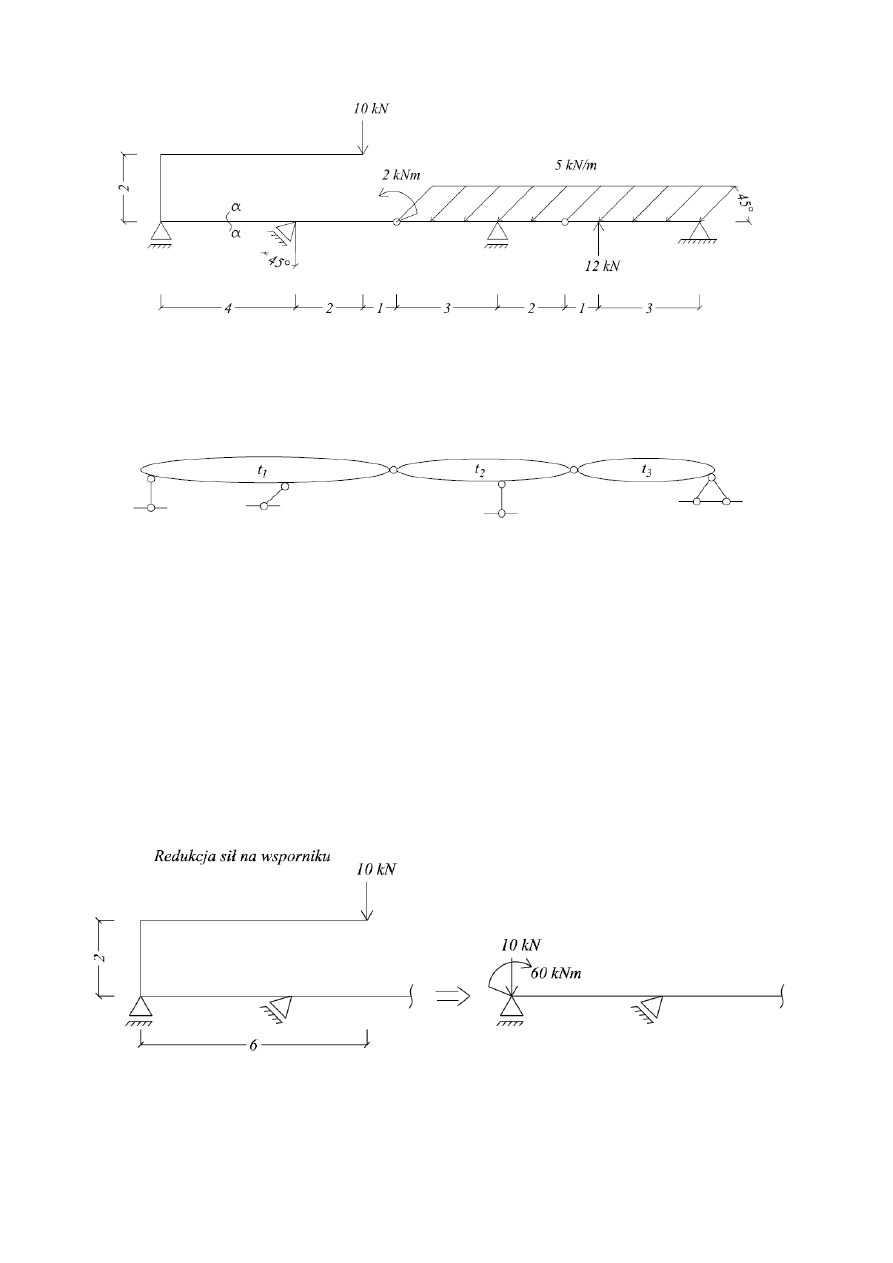
1.1 Sprawdzenie geometrycznej niezmienności i statycznej wyznaczalności
1.1.1. Warunek ilościowy
0
3
9
2
2
1
2
1
1
3
=
−
=
=
+
+
+
+
+
=
=
e
t
n
e
t
GN, SW – ilościowo
1.1.2. Warunek jakościowy
2
2
3
1
1
3
2
1
0
0
0
0
→
+
→
+
+
T
o
e
twierdzeni
T
o
e
twierdzeni
t
t
t
GN, SW – jakościowo
1.2. Wyznaczanie reakcji podporowych
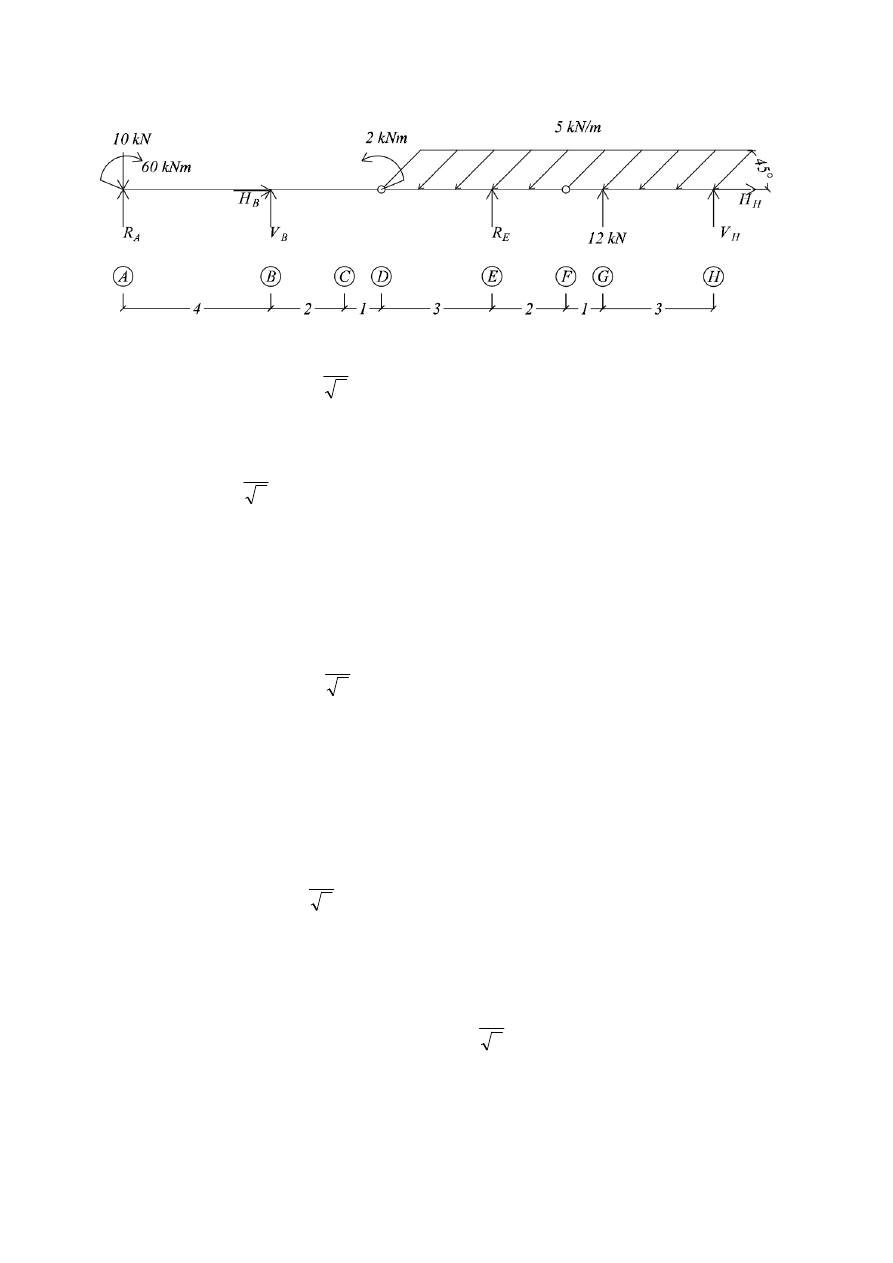
kN
H
H
H
X
kN
R
kN
H
kN
V
V
V
V
R
kN
V
R
V
R
V
R
Y
kN
V
R
V
R
M
kN
R
V
R
M
kN
V
V
M
H
H
B
A
B
B
B
B
B
A
B
A
H
E
B
A
B
A
B
A
L
D
E
H
E
P
D
H
H
P
F
29
,
8
0
9
2
5
:
0
67
,
8
57
,
23
57
,
23
10
3
)
9
,
14
(
7
9
,
14
9
,
14
0
12
9
2
5
10
:
0
10
3
7
0
3
7
7
10
60
:
0
85
,
10
0
9
6
12
3
5
,
4
9
2
5
2
:
0
07
,
4
0
2
4
2
5
4
1
12
:
0
=
=
⋅
−
+
=
−
=
=
→
=
=
⋅
+
−
⋅
−
=
=
+
=
+
+
+
⋅
−
+
−
=
=
⋅
+
⋅
=
⋅
+
⋅
+
⋅
−
=
=
=
⋅
+
⋅
+
⋅
+
⋅
⋅
−
=
=
=
⋅
⋅
−
⋅
+
⋅
=
∑
∑
∑
∑
∑
Sprawdzenie:
0
5
,
11
9
2
5
16
13
12
10
2
4
60
=
⋅
⋅
−
⋅
+
⋅
+
⋅
+
+
⋅
+
−
=
∑
H
E
B
A
V
R
V
M
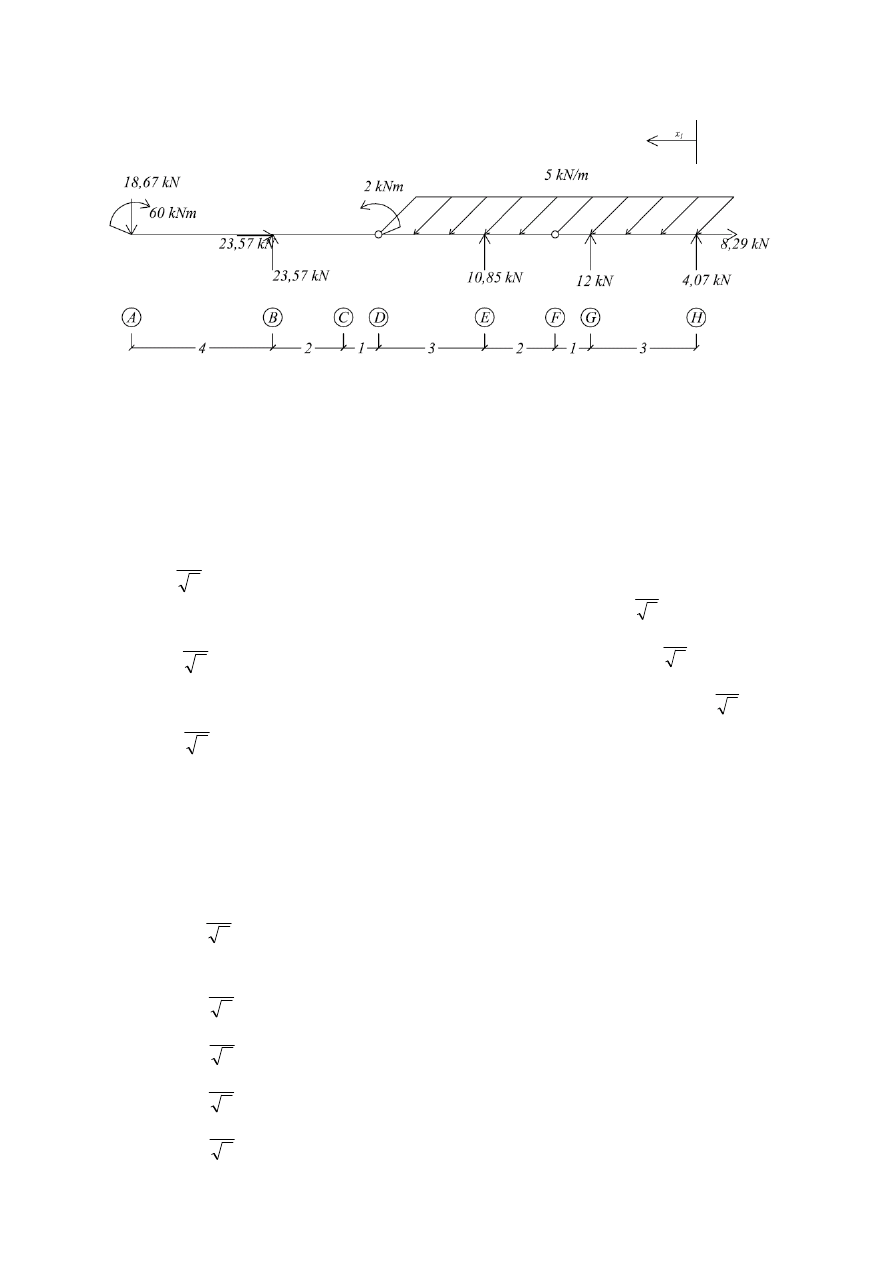
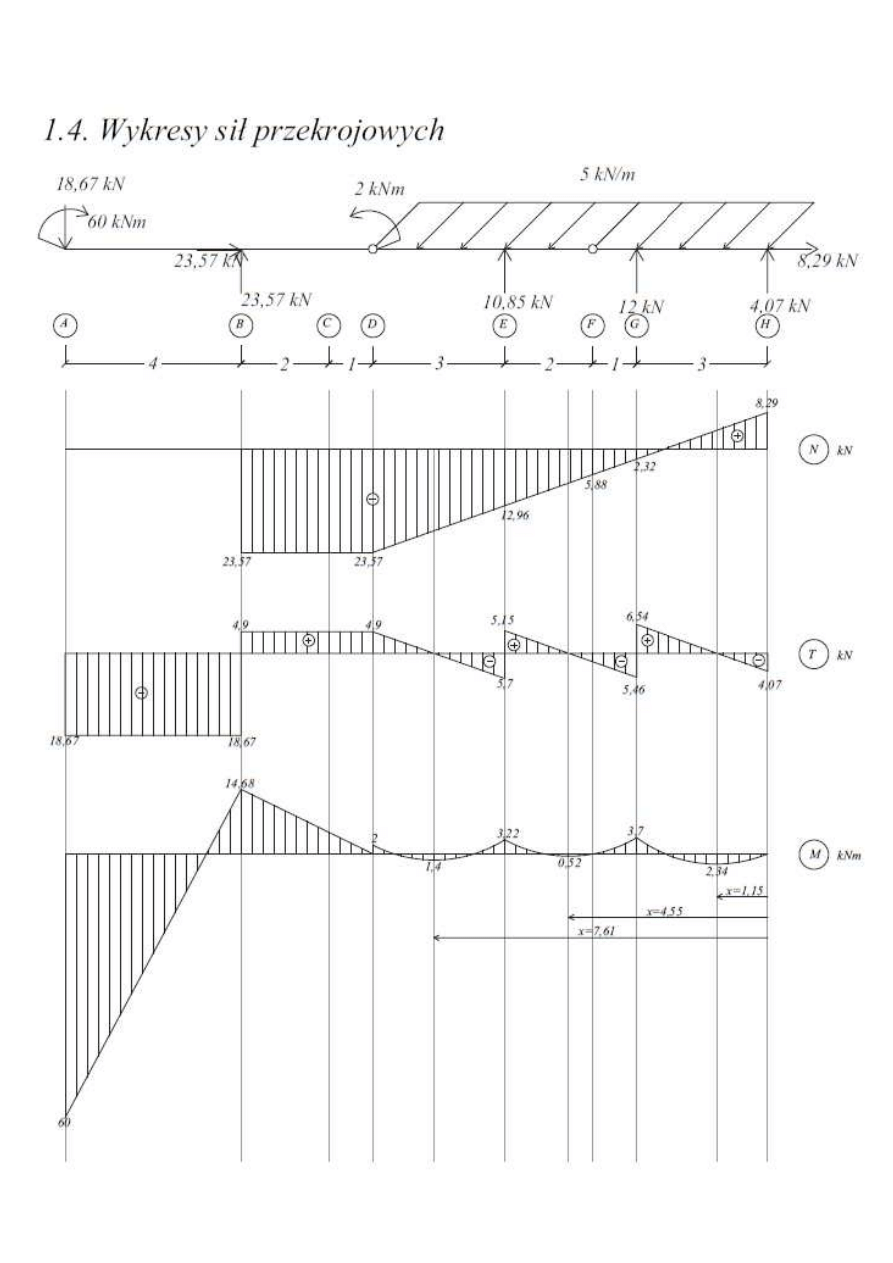
1.3 Wyznaczanie sił przekrojowych
1.3.1. Siły tnące
kN
T
kN
T
kN
T
kN
T
kN
T
kN
T
kN
T
kN
T
kN
T
H
P
G
L
G
P
E
L
E
D
P
B
L
B
A
07
,
4
3
2
5
54
,
6
54
,
6
12
46
,
5
46
,
5
6
2
5
15
,
5
15
,
5
85
,
10
7
,
5
7
,
5
3
2
5
9
,
4
9
,
4
9
,
4
57
,
23
67
,
18
67
,
18
67
,
18
−
=
⋅
−
=
=
+
−
=
−
=
⋅
−
=
=
+
−
=
−
=
⋅
−
=
=
=
+
−
=
−
=
−
=
1.3.2. Siły osiowe
kN
N
kN
N
N
D
B
A
57
,
23
57
,
23
0
−
=
−
=
=
Przedział H-D
kN
N
kN
N
kN
N
kN
N
kN
N
x
x
N
x
D
x
E
x
F
x
G
x
H
57
,
23
9
2
5
29
,
8
96
,
12
6
2
5
29
,
8
85
,
5
4
2
5
29
,
8
32
,
2
3
2
5
29
,
8
29
,
8
2
5
29
,
8
)
(
9
;
6
;
4
;
3
;
0
;
1
−
=
⋅
−
=
−
=
⋅
−
=
−
=
⋅
−
=
−
=
⋅
−
=
=
⋅
−
=
=
=
=
=
=
x
x
T
D
E
x
x
T
E
G
x
x
T
G
H
⋅
+
−
−
−
=
−
⋅
+
−
−
=
−
⋅
+
−
=
−
2
5
85
,
10
12
07
,
4
)
(
:
2
5
12
07
,
4
)
(
:
2
5
07
,
4
)
(
:
1
1
1
1.3.3. Momenty zginające
kNm
M
M
kNm
M
kNm
M
P
D
L
D
B
A
2
0
7
67
,
18
60
68
,
14
4
67
,
18
60
60
−
=
=
⋅
−
=
−
=
⋅
−
=
=
Przedział H-G
kNm
M
M
x
x
x
M
x
G
x
H
7
,
3
3
07
,
4
5
,
4
2
5
0
07
,
4
2
2
5
)
(
)
3
(
)
0
(
2
1
1
1
−
=
⋅
+
⋅
−
=
=
⋅
+
⋅
−
=
=
=
kNm
M
m
x
x
dx
x
dM
Ekstremum
x
34
,
2
15
,
1
0
07
,
4
2
5
)
(
)
15
,
1
(
=
=
=
+
⋅
−
=
=
Przedział G-E
kNm
M
M
x
x
x
x
M
x
E
x
F
22
,
3
36
6
07
,
4
18
2
5
0
12
4
07
,
4
8
2
5
)
3
(
12
07
,
4
2
2
5
)
(
)
6
(
)
4
(
2
1
1
1
−
=
+
⋅
+
⋅
−
=
=
+
⋅
+
⋅
−
=
−
+
⋅
+
⋅
−
=
=
=
kNm
M
m
x
x
dx
x
dM
Ekstremum
x
52
,
0
55
,
4
0
07
,
16
2
5
)
(
)
55
,
4
(
=
=
=
+
⋅
−
=
=
Przedział E-D
kNm
M
x
x
x
x
x
M
x
D
2
3
85
,
10
6
12
9
07
,
4
5
,
40
2
5
)
6
(
85
,
10
)
3
(
12
07
,
4
2
2
5
)
(
)
9
(
2
1
1
−
=
⋅
+
⋅
+
⋅
+
⋅
−
=
−
⋅
+
−
+
⋅
+
⋅
−
=
=
kNm
M
m
x
x
dx
x
dM
Ekstremum
x
4
,
1
61
,
7
0
92
,
26
2
5
)
(
)
61
,
7
(
=
=
=
+
⋅
−
=
=
1.5. Zasada prac przygotowanych
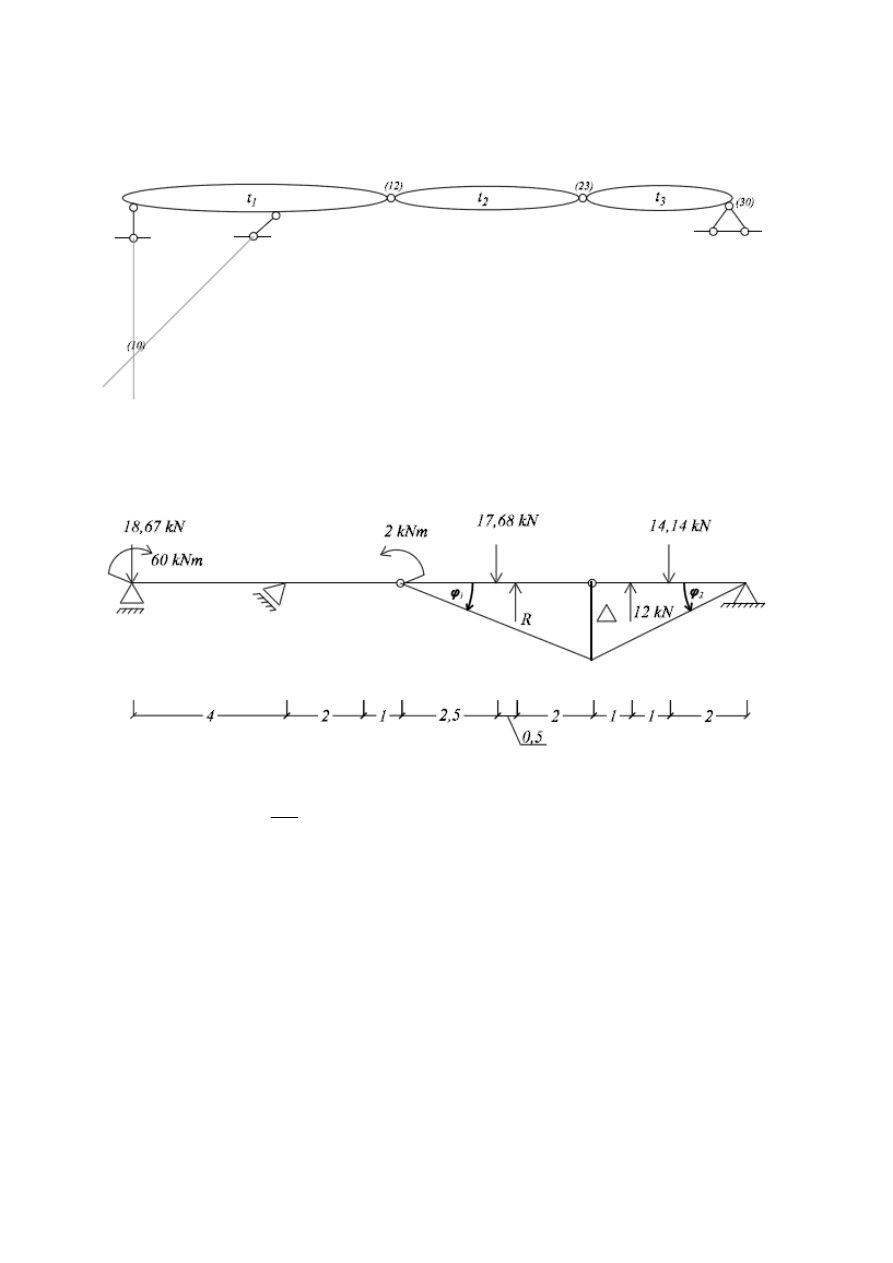
1.5.1. Mechanizm „R”
Warunek zgodności przesunięć:
2
1
4
5
ϕ
ϕ
=
kN
R
R
R
L
85
,
10
0
36
,
35
45
3
19
,
44
2
0
2
14
,
14
3
12
3
5
,
2
68
,
17
2
:
0
4
5
2
2
1
1
1
1
2
=
=
+
−
⋅
−
+
−
=
⋅
⋅
+
⋅
⋅
−
⋅
⋅
−
⋅
⋅
+
⋅
−
=
=
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
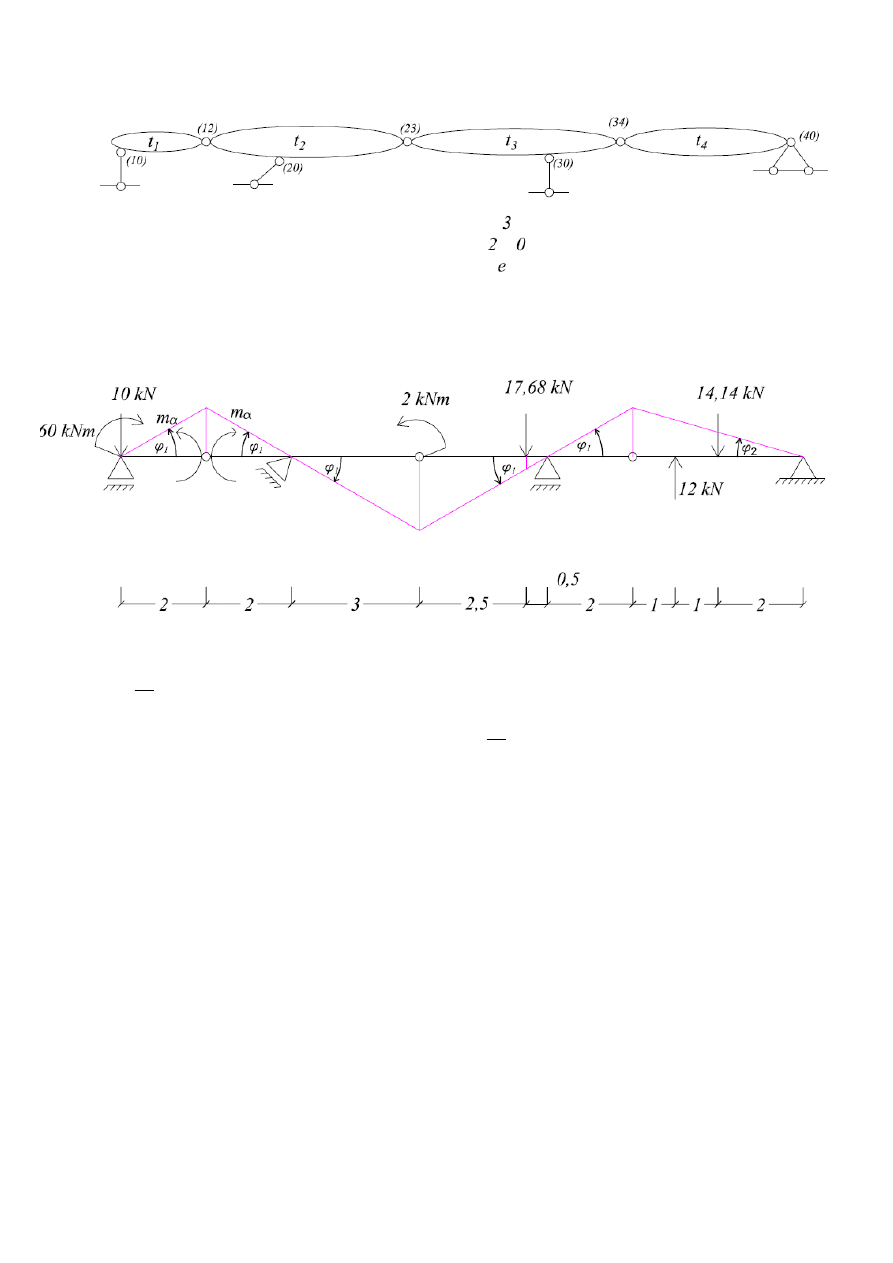
1.5.2. Mechanizm
α
m
warunek zgodności przesunięć:
2
1
4
2
ϕ
ϕ
⋅
=
⋅
0
14
,
14
18
84
,
8
2
2
60
0
2
14
,
14
3
12
2
68
,
17
2
60
:
0
2
2
2
1
1
1
1
1
1
2
=
−
+
+
+
⋅
+
−
=
⋅
⋅
−
⋅
⋅
+
⋅
+
⋅
+
⋅
+
⋅
+
⋅
−
=
=
α
α
α
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
m
m
m
L
kNm
m
kNm
m
65
,
22
3
,
45
2
=
=
⋅
α
α
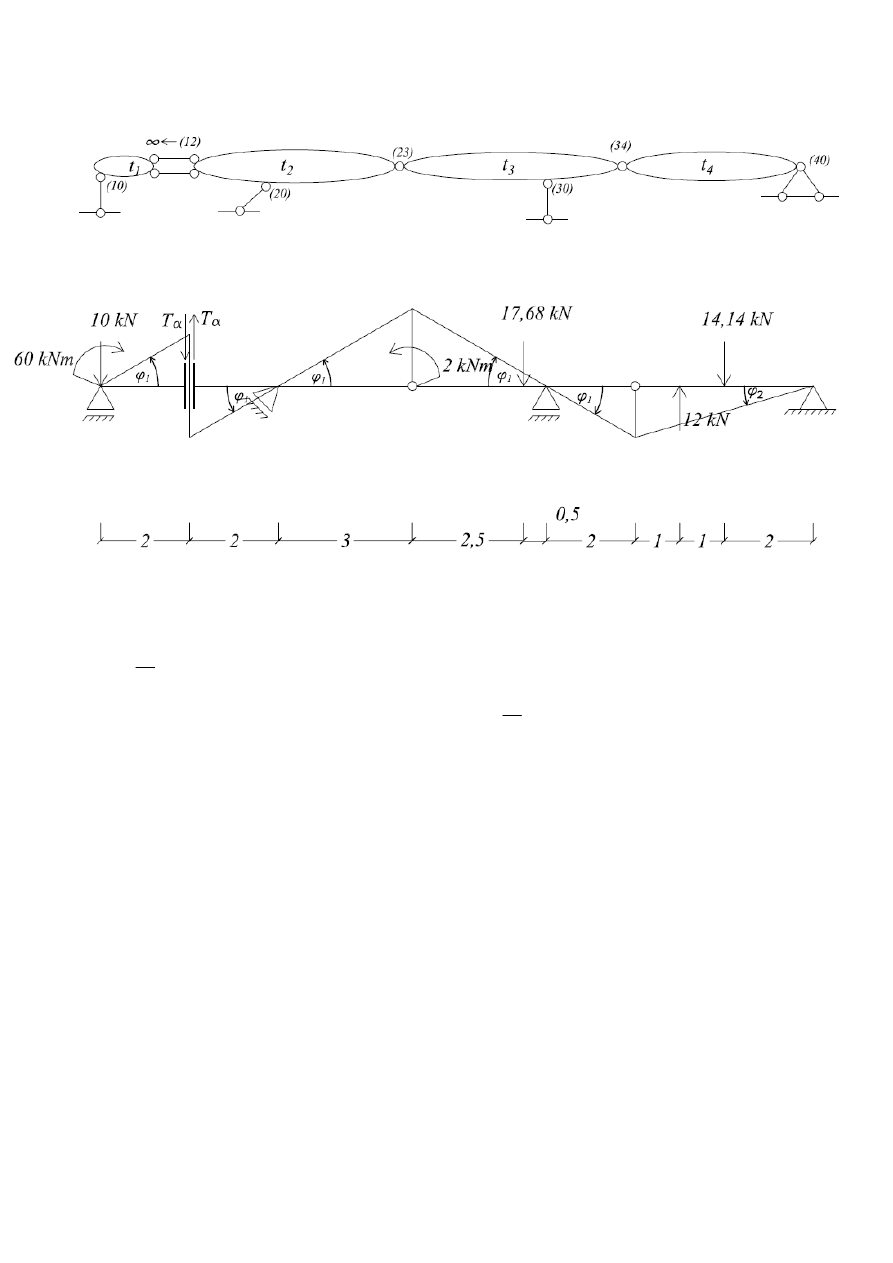
1.5.3. Mechanizm
α
T
warunek zgodności przesunięć:
2
1
4
2
ϕ
ϕ
⋅
=
⋅
0
14
,
14
18
84
,
8
2
4
60
0
2
14
,
14
3
12
2
68
,
17
2
2
60
:
0
2
2
2
1
1
1
1
1
1
2
=
+
−
−
−
⋅
−
−
=
⋅
⋅
+
⋅
⋅
−
⋅
−
⋅
−
⋅
−
⋅
⋅
−
⋅
−
=
=
α
α
α
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
T
T
T
L
kN
T
kN
T
67
,
18
7
,
74
4
−
=
−
=
⋅
α
α
Wyszukiwarka
Podobne podstrony:
Belka Projekt 2 Układ1
Belka Projekt 2
belka typu L, Budownictwo, PWSZ -BUDOWNICTWO, SEMESTR III, 2R, Technologia betonu, starsze roczniki,
Projekt belka met przemieszczen
belka stropowa, Projekt domku
belka 31, Inżynieria Środowiska [PW], sem 2, Wytrzymałość Materiałów i Mechanika Budowli, Grupa 10 p
PROJEKT Z WYT BELKA II, wytrzymałość materiałów
Metoda sił, projekt-belka
belka zespolona, projektowanie
projekt 2(BELKA)
Metoda sił projekt belka
projekt z drewna belka 10 (przy schodach)
projekt z drewna belka 10 (przy schodach)
projekt o narkomanii(1)
więcej podobnych podstron