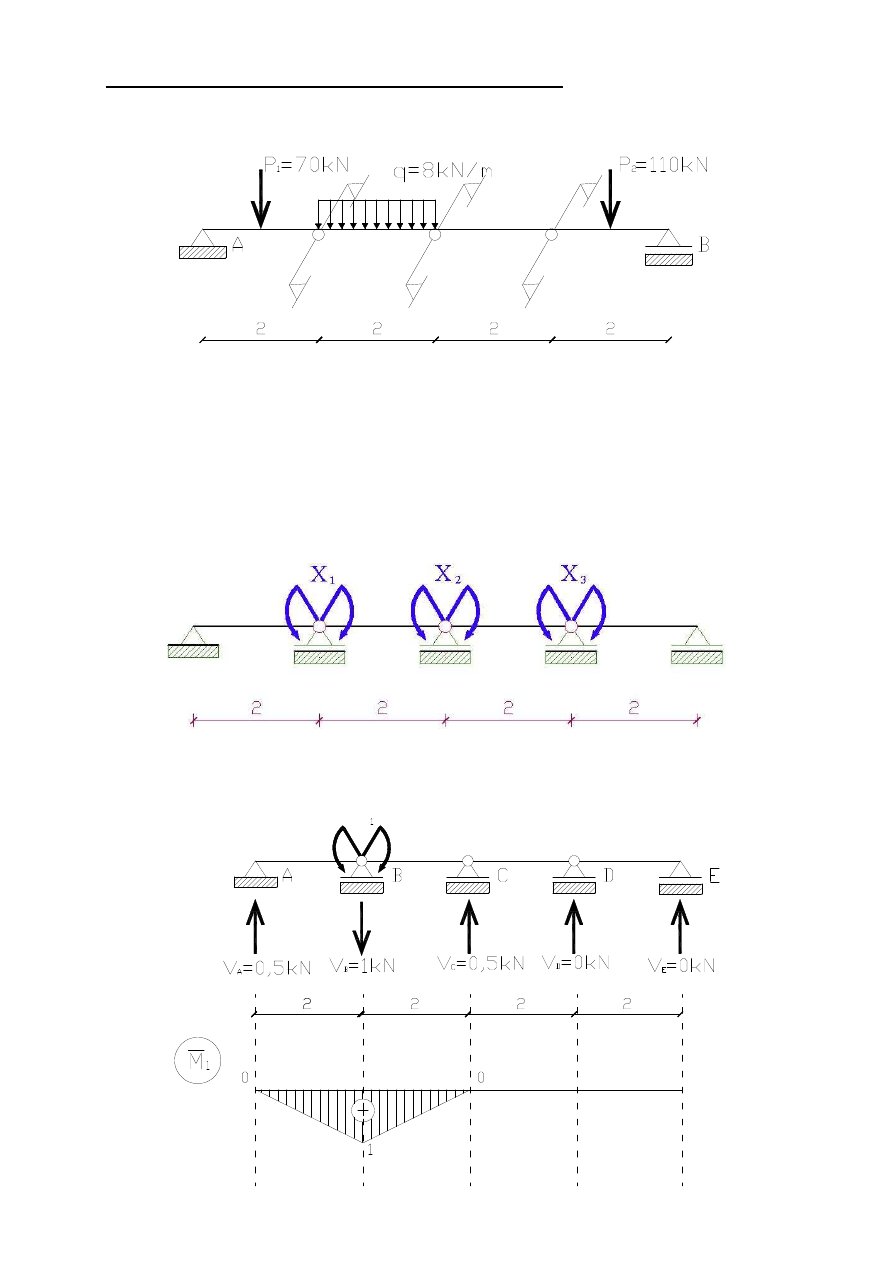
Zadanie 3. Belka wieloprzęsłowa na podporach sprężystych
q = 8 kN/m; P
1
= 70 kN P
2
= 110 kN
3.1. Określenie stopnia statycznej niewyznaczalności
3
3
1
1
1
1
2
n
h
=
−
+
+
+
+
=
3.2. Przyjęcie schematu podstawowego
3.3. Rozwiązanie ustroju podstawowego
3.1. Stan X
1
= 1
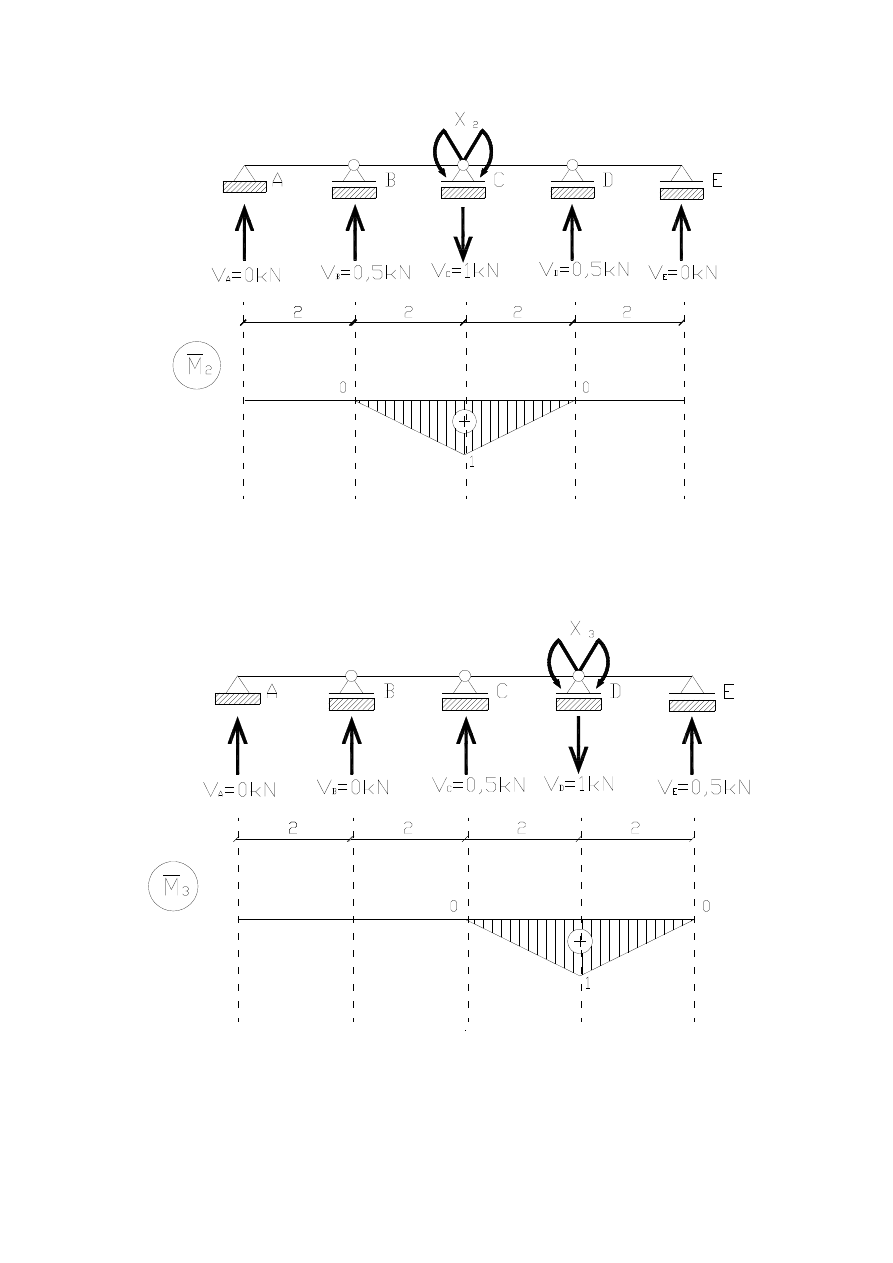
3.2. Stan X
2
= 1
3.3. Stan X
3
= 1
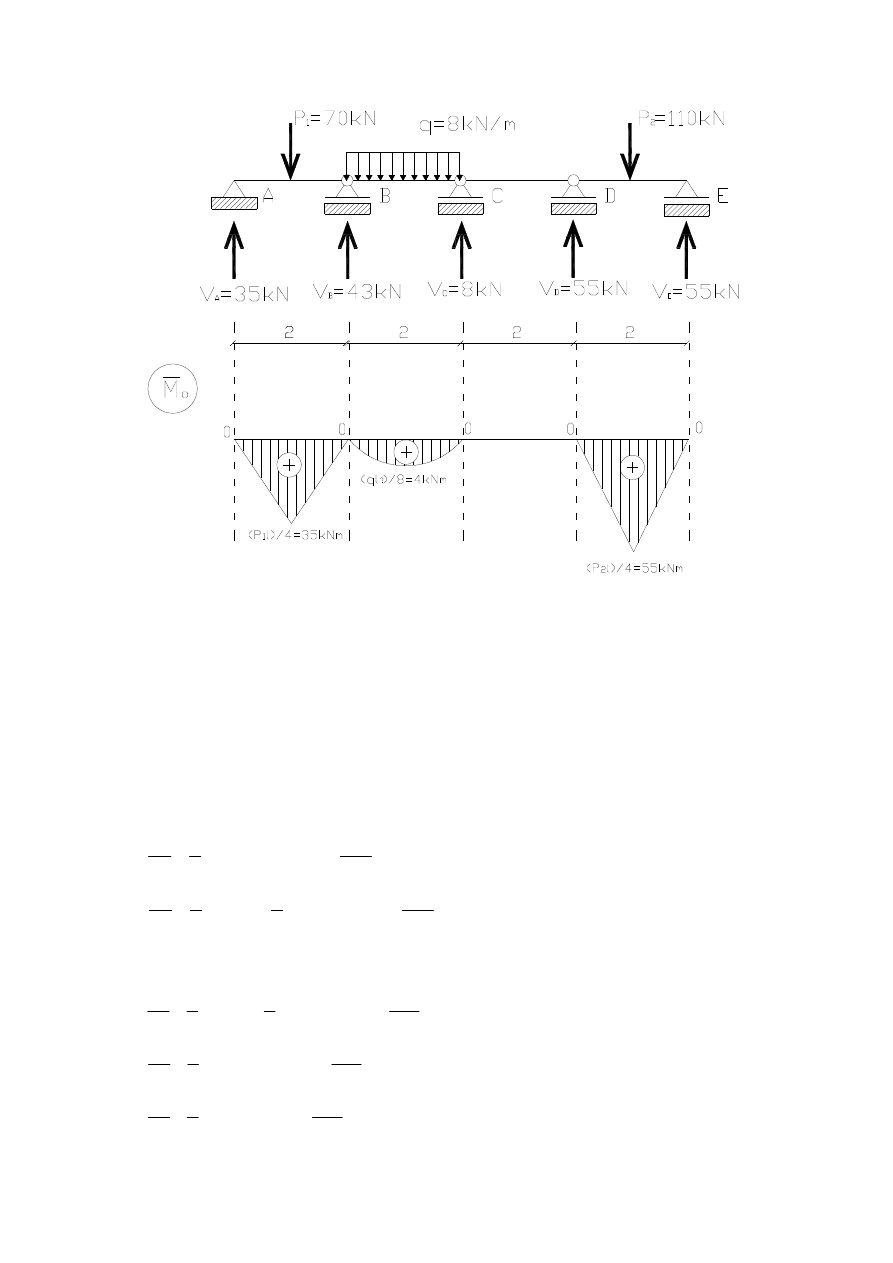
3.4. Stan obciążenia zewnętrznego
4. Układ równań zgodności przemieszczeń
=
+
+
+
=
+
+
+
=
+
+
+
0
X
X
X
0
X
X
X
0
X
X
X
30
30
33
20
32
10
31
20
30
23
20
22
10
21
10
30
13
20
12
10
11
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
δ
•
przemieszczenia w miejscach usuniętych więzów:
21
22
23
1
1
1
1
1 2 0
1 2 0, 33 1
2
2
3
1
1
4
1 2 2 0, 67 1
2
3
1
1
1
1 2 0, 33 1
2
3
EI
EI
EI
EI
EI
EI
δ
δ
δ
=
⋅
⋅ ⋅ ⋅ + ⋅ ⋅ ⋅
⋅ =
=
⋅
⋅ ⋅ ⋅ ⋅
⋅ =
=
⋅
⋅ ⋅ ⋅
⋅ =
11
12
13
1
1
4
1 2 2 0, 67 1
2
3
1
1
1
1
1 2 0
1 2 0, 33 1
2
2
3
0
EI
EI
EI
EI
δ
δ
δ
=
⋅
⋅ ⋅ ⋅ ⋅
⋅ =
=
⋅
⋅ ⋅ ⋅ + ⋅ ⋅ ⋅
⋅ =
=

31
32
33
0
1
1
1
1 2 0, 33 1
2
3
1
1
4
1 2 2 0, 67 1
2
3
EI
EI
EI
EI
δ
δ
δ
=
=
⋅
⋅ ⋅ ⋅
⋅ =
=
⋅
⋅ ⋅ ⋅ ⋅
⋅ =
•
wyrazy wolne:
[
]
[
]
[
]
1
2
3
1
20,18
0, 5 35 1 0, 33 0, 5 35 1 0, 67 0, 67 2 4 0, 5 1
1
2, 67
0, 67 2 4 0, 5 1
1
27, 5
0, 5 1 55 0, 67 1 0, 33 0, 5 55 1
O
O
O
EI
EI
EI
EI
EI
EI
δ
δ
δ
=
⋅
⋅ ⋅ ⋅
+
⋅ ⋅ ⋅
+
⋅ ⋅ ⋅
⋅ =
=
⋅
⋅ ⋅ ⋅
⋅ =
=
⋅
⋅ ⋅ ⋅
⋅ +
⋅
⋅ ⋅ =
10
20
30
10
20
30
10
20
30
4
1
20,18
X
X
0 X
0
3EI
3
1
4
1
2, 67
X
X
X
0
3
3EI
3
3
1
4
27, 5
0 X
X
X
0
3
3
EI
EI
EI
EI
EI
EI
EI
EI
EI
+
+ ⋅
+
=
+
+
+
=
⋅
⋅
+
+
+
=
10
20
30
10
20
30
10
20
30
4 X
1 X
0 X
60, 51 0
1 X
4 X
1 X
8, 01
0
0 X
1 X
4 X
82,5
0
⋅
+ ⋅
+ ⋅
+
=
⋅
+ ⋅
+ ⋅
+
=
⋅
+ ⋅
+ ⋅
+
=
•
układ równań zgodności przemieszczeń w ujęciu macierzowym
- zapis rozwinięty:
=
δ
δ
δ
+
⋅
δ
δ
δ
δ
δ
δ
δ
δ
δ
0
0
0
X
X
X
30
20
10
30
20
10
33
32
31
23
22
21
13
12
11
10
20
30
4
1
0
60,51
0
1
1
1
4
1
8, 01
0
3
3
0
1
4
82,5
0
X
X
EI
EI
X
⋅
+
=

- zapis zwinięty:
10
1
11
0
10
1
11
0
1
11
10
1
11
0
11
1
11
1
11
L
10
0
11
b
B
X
0
b
B
X
O
B
b
B
X
B
B
B
O
b
X
B
⋅
−
=
=
⋅
+
/
⋅
=
⋅
+
⋅
⋅
/
=
+
⋅
−
−
−
−
−
−
1
11
11
10
4
1
0
2, 43
0, 64
0,16
6, 66
1
1
1
4
1 ;
0, 64
2, 6
0, 64 ;
0,88
3
0
1
4
0,16
0, 64
2, 43
9,1
B
B
EI
b
EI
EI
−
−
=
=
−
−
=
−
10
0
20
30
2, 43
0, 64
0,16
6, 66
17, 25
0, 64
2, 6
0, 64
0,88
7,86
0,16
0, 64
2, 43
9,1
22, 64
X
X
X
EI
X
−
−
=
=
−
−
⋅
=
−
−
X
10
= -17,25 ; X
20
= 7,86 ; X
30
= -22,64;
5. Obliczenie reakcji i sił wewnętrznych w ustroju rzeczywistym
•
wyznaczenie reakcji:
1
2
3
0
10
20
30
0, 5 ( 17, 25) 35
26,375
A
A
A
A
A
A
V
V
X
V
X
V
X
V
V
kN
=
⋅
+
⋅
+
⋅
+
=
⋅ −
+
=
1
2
3
0
10
20
30
1 ( 17, 25) 0,5 7,86 43
64,18
B
B
B
B
B
B
V
V
X
V
X
V
X
V
V
kN
=
⋅
+
⋅
+
⋅
+
= − ⋅ −
+
⋅
+
=
1
2
3
0
10
20
30
0, 5 ( 17, 25) 1 (7,86) 0,5 ( 22, 64) 8
19,8
C
C
C
C
C
C
V
V
X
V
X
V
X
V
V
kN
=
⋅
+
⋅
+
⋅
+
=
⋅ −
− ⋅
+
⋅ −
+ = −
1
2
3
0
10
20
30
0,5 7,86 1 ( 22, 64) 55
81,57
D
D
D
D
D
D
V
V
X
V
X
V
X
V
V
kN
=
⋅
+
⋅
+
⋅
+
=
⋅
− ⋅ −
+
=
1
2
3
0
10
20
30
0,5 ( 22, 64) 55
43, 68
E
E
E
E
E
E
V
V
X
V
X
V
X
V
V
kN
=
⋅
+
⋅
+
⋅
+
=
⋅ −
+
=
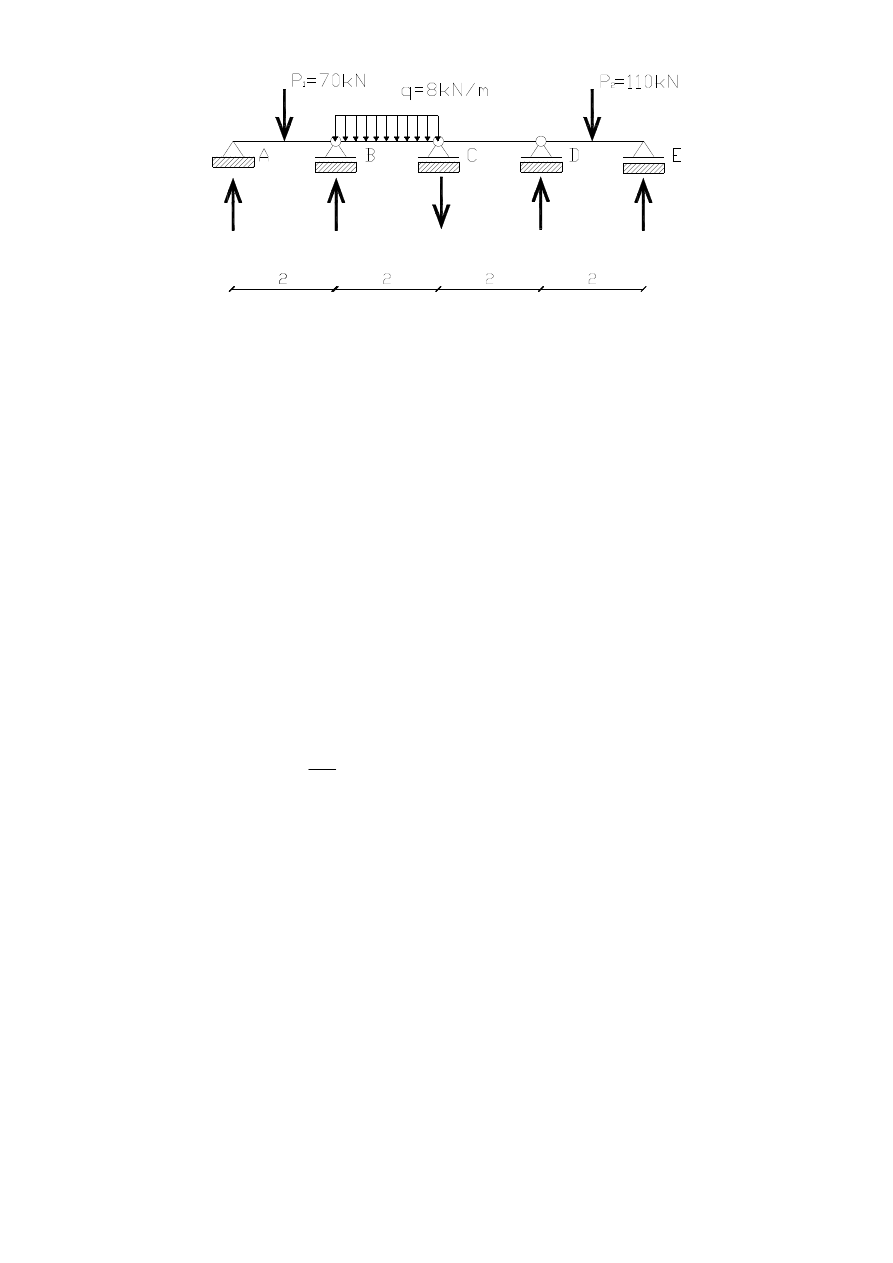
V
C
=19,8kN
V
B
=64,18kN
V
A
=26,375kN
V
D
=81,57kN V
E
=43,68kN
•
wyznaczenie sił wewnętrznych:
- momenty zginające:
10
20
30
0;
17, 25
;
7,86
;
22, 64
;
0
A
B
C
D
E
M
M
X
kNm
M
X
kNm
M
X
kNm
M
=
=
= −
=
=
=
= −
=
- wyznaczenie momentów ekstremalnych:
1
2
1
(0; 1)
( )
26, 375
;
(0)
0
(1)
26, 375
(0; 1)
( )
(
1)
26, 375
26, 375 70
26, 375 43, 625 ;
(0)
26, 375
(1)
17, 25
(0; 2)
( )
(
2)
(
1)
26, 3
2
A
A
A
B
przedzia I
x
M x
V x
kNm
M
M
kNm
przedzia II
x
M x
V x
P x
x
x
x
M
M
kNm
przedzia III
x
qx
M x
V x
P x
V x
∈
=
=
=
=
∈
=
+ −
=
+
−
=
−
=
= −
∈
=
+ −
+ +
−
=
2
2
2
75
52, 75 70 70
64,18
4
17, 25 20, 555
4
;
(0)
17, 25
(2)
7,86
(0; 2)
( )
(
2)
(
1)
43, 68
87, 36 110 110
81, 57
15, 25
22, 64;
(0)
22, 64
(2)
7,86
(0; 1)
( )
E
D
x
x
x
x
x
x
M
M
kNm
przedzia IV
x
M x
V x
P x
V x
x
x
x
x
M
kNm
M
kNm
przedzia V
x
M x
+
−
−
+
−
= −
+
−
= −
=
∈
=
+ −
+ +
=
+
−
−
+
=
−
= −
=
∈
2
(
1)
43, 68
43, 68 110
66, 32
43, 68;
(0)
43, 68
(1)
22, 64
E
V x
P x
x
x
x
M
kNm
M
kNm
=
+ −
=
+
−
= −
−
=
= −
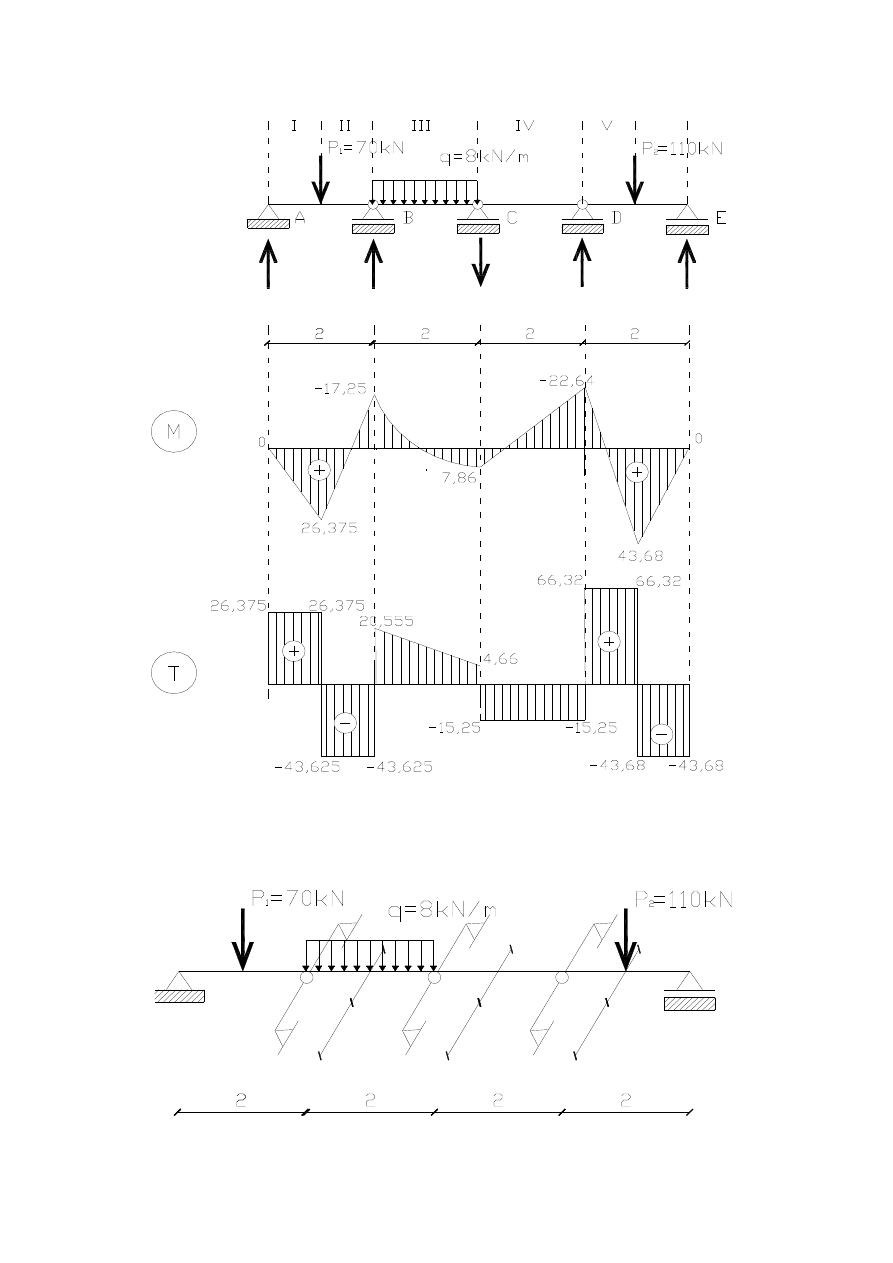
•
wykresy sił wewnętrznych:
V
C
=19,8kN
V
B
=64,18kN
V
A
=26,375kN
V
D
=81,57kN V
E
=43,68kN
6. Rozwiązanie belki na podporach sprężystych
l/
2
l/
2
l/
2
l/
2
l/
2
l/
2
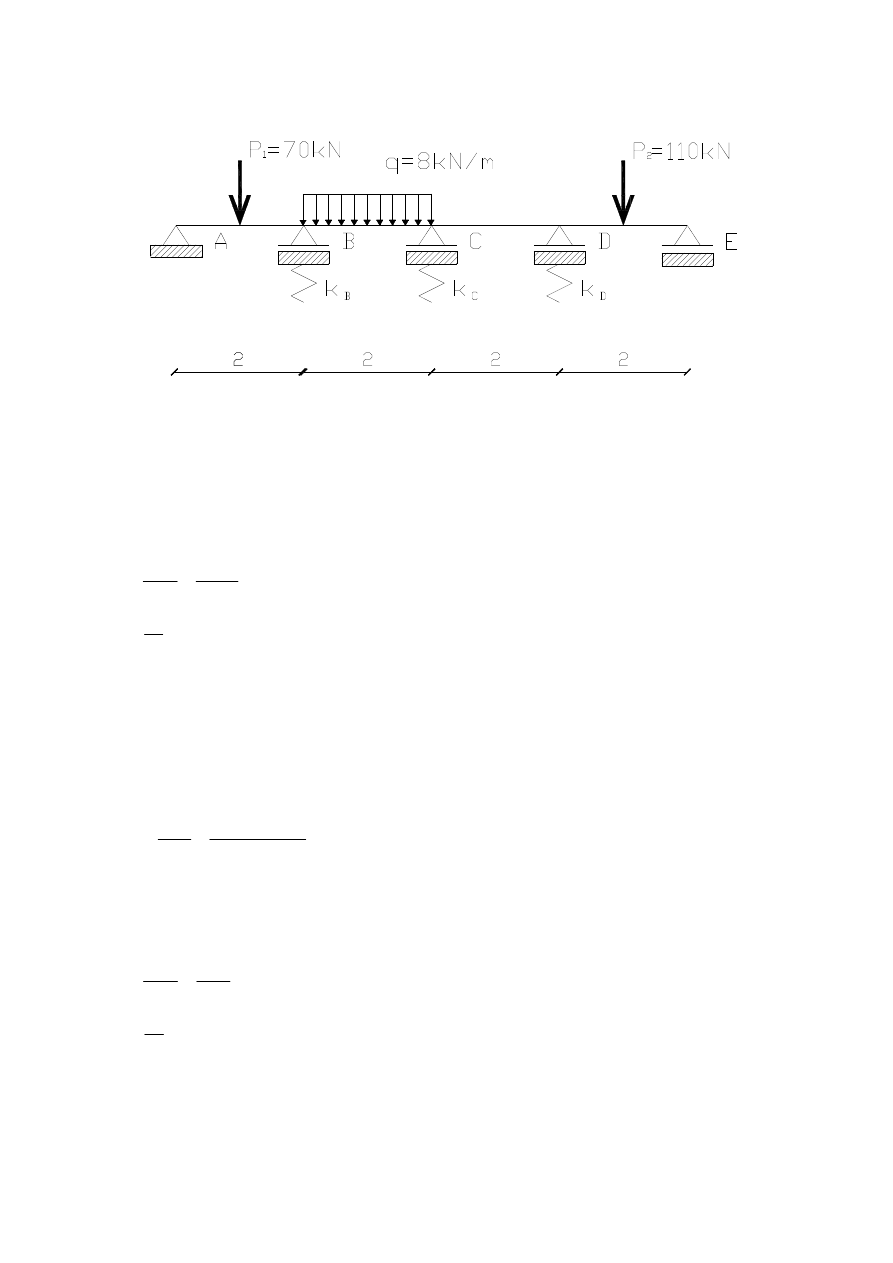
•
schemat obliczeniowy:
Ugięcie maksymalne:
∆
max
= 0,01 m
7. Obliczenie podatności podpór
•
podpora A:
max
max
4
max
0, 01
1, 56 10
/
64,18
1
6410, 2
/
B
B
B
B
B
B
b V
b
m kN
V
k
kN m
b
−
∆
= ⋅
≤ ∆
∆
≤
=
=
⋅
=
=
Przyjęto:
k
B
= 6500 kN/m
Dla l = 2 m:
3
3
1
4
1
2
1070
48
48 1, 56 10
p
l
EI
kN
b
−
≥
=
=
⋅
⋅
•
podpora C:
max
max
4
max
0, 01
5, 05 10
/
19,8
1
1998
/
C
C
C
C
C
C
b V
b
m kN
V
k
kN m
b
−
∆
= ⋅
≤ ∆
∆
≤
=
=
⋅
=
=
Przyjęto:
k
C
= 2000 kN/m
Dla l = 2 m:
3
3
2
4
1
2
330,1
48
48 5, 05 10
p
l
EI
kN
b
−
≥
=
=
⋅
⋅
•
podpora 3:
max
max
4
max
0, 01
1, 23 10
/
81, 57
1
8130,1
/
D
D
D
D
D
D
b
V
b
m kN
V
k
kN m
b
−
∆
=
⋅
≤ ∆
∆
≤
=
=
⋅
=
=
Przyjęto:
K
D
= 8150 kN/m
Dla l = 2 m:
3
3
3
4
3
2
1333
48
48 1, 23 10
p
l
EI
kN
b
−
≥
=
=
⋅
⋅
8. Obliczenie podatności wynikających z podparcia sprężystego
∑∫
∑
⋅
+
⋅
=
δ
k
R
R
ds
EI
M
M
j
i
j
i
ij
4
1
1
1
1
1
1
11
1 1
0, 5 0, 5
2, 79 10
6500
2000
k
C
C
B
B
D
D
B
C
D
V
V
V
V
V
V
k
k
k
δ
−
⋅
⋅
⋅
⋅
⋅
=
+
+
=
+
=
⋅
4
1
2
1
2
1
2
12
1 0, 5
0, 5 1
3, 27 10
6500
2000
k
C
C
B
B
D
D
B
C
D
V
V
V
V
V
V
k
k
k
δ
−
⋅
⋅
⋅
⋅
⋅
=
+
+
= −
−
= −
⋅
4
1
3
1
3
1
3
13
0, 5 0, 5
1, 25 10
2000
k
B
B
C
C
D
D
B
C
D
V
V
V
V
V
V
k
k
k
δ
−
⋅
⋅
⋅
⋅
=
+
+
=
=
⋅
4
21
12
3, 27 10
k
k
δ
δ
−
=
= −
⋅
4
2
2
2
2
2
2
22
0, 5 0, 5
1 1
0, 5 0, 5
5, 69 10
6500
2000
8150
k
C
C
B
B
D
D
B
C
D
V
V
V
V
V
V
k
k
k
δ
−
⋅
⋅
⋅
⋅
⋅
⋅
=
+
+
=
+
+
=
⋅
4
2
3
2
3
2
3
23
1 0, 5
0, 5 1
3,11 10
2000
8150
k
B
B
C
C
D
D
B
C
D
V
V
V
V
V
V
k
k
k
δ
−
⋅
⋅
⋅
⋅
⋅
=
+
+
= −
−
= −
⋅

4
31
13
1, 25 10
k
k
δ
δ
−
=
=
⋅
4
32
23
3,11 10
k
k
δ
δ
−
=
= −
⋅
4
3
3
3
3
3
3
33
0, 5 0, 5
1 1
2, 48 10
2000
8150
k
B
B
C
C
D
D
B
C
D
V
V
V
V
V
V
k
k
k
δ
−
⋅
⋅
⋅
⋅
⋅
=
+
+
=
+
=
⋅
•
wyrazy wolne:
4
1
0
1
0
1
0
10
1 43
8 0, 5
46,15 10
6500
2000
k
B
B
C
C
D
D
B
C
D
V
V
V
V
V
V
k
k
k
δ
−
⋅
⋅
⋅
⋅
⋅
=
+
+
= −
+
= −
⋅
4
2
0
2
0
2
0
20
0, 5 43
1 8
0, 5 55
26,84 10
6500
2000
8150
k
B
B
C
C
D
D
B
C
D
V
V
V
V
V
V
k
k
k
δ
−
⋅
⋅
⋅
⋅
⋅
⋅
=
+
+
=
−
+
=
⋅
4
3
0
3
0
3
0
30
0, 5 8
1 55
47, 5 10
2000
8150
k
B
B
C
C
D
D
B
C
D
V
V
V
V
V
V
k
k
k
δ
−
⋅
⋅
⋅
⋅
⋅
=
+
+
=
−
= −
⋅
;
;
k
0
i
0
i
s
0
i
k
ij
ij
s
ij
δ
+
δ
=
δ
δ
+
δ
=
δ
k
10
10
s
10
k
11
11
s
11
b
b
b
;
B
B
B
+
=
+
=
3
3
11
10
0, 279
0, 327
0,125
4, 615
10
0,327
0,569
0, 311 ;
10
2, 684
0,125
0, 311
0, 248
4, 75
k
k
B
b
−
−
−
−
=
−
−
=
−
−
11
10
4
1
0
60,51
1
1
1
4
1 ;
8, 01
3
3
0
1
4
82, 5
B
b
EI
EI
=
=
9. Zaprojektowanie przekroju belki
•
belka stalowa:
2
2
8
m
/
kN
000
220
R
;
m
/
kN
10
1
,
2
E
=
⋅
=
4
3
3
;
43, 68
43, 68
1, 98 10
198
220 000
M
R
M
kN
W
M
W
m
cm
R
σ
−
=
≤
=
≥
=
=
⋅
=
Przyjęto:
3
4
5
4
8
5
2
200
200
;
2000
2, 00 10
2,1 10 2, 00 10
4200
HEB
W
cm
I
cm
m
EI
kNm
−
−
Ι
→
=
=
=
⋅
=
⋅
⋅
⋅
=

3
3
11
10
4
1
0
0,32
0, 08
0
60, 51
4,8
1
1
1
4
1
10
0, 08
0,32
0, 08 ;
8, 01
10
0, 64
3 4200
3 4200
0
1
4
0
0, 08
0,32
82,5
6, 6
B
b
−
−
=
=
=
=
⋅
⋅
3
3
11
11
11
10
10
10
0, 599
0, 247
0,125
0,185
10
0, 247
0,889
0, 231 ;
10
3, 324
0,125
0, 231
0, 568
1,85
S
k
s
k
B
B
B
b
b
b
−
−
−
=
+
=
−
−
=
+
=
−
s
10
s
11
0
s
10
s
11
s
0
s
11
s
11
s
11
s
0
s
11
s
11
s
11
L
s
10
s
0
s
11
b
B
X
0
b
B
X
O
B
b
B
X
B
B
B
O
b
X
B
1
1
1
1
1
1
⋅
−
=
=
⋅
+
/
⋅
=
⋅
+
⋅
⋅
/
=
+
⋅
−
−
−
−
−
−
1
3
11
1,91
0, 47
0, 23
10
0, 47
1,37
0, 46
0, 23 0, 46
2
s
B
−
−
=
−
10
3
3
0
20
30
1, 91
0, 47
0, 23
0,185
1, 5
10
0, 47
1, 37
0, 46
10
3, 324
5, 5
0, 23
0, 46
2
1,85
5,16
s
s
s
s
X
X
X
X
−
−
−
= −
= −
⋅
= −
−
−
10
20
30
1, 5;
5, 5;
5,16
s
s
s
X
X
X
= −
= −
= −
10. Obliczenie reakcji i sił wewnętrznych w belce na podporach sprężystych
•
obliczenie reakcji:
1
2
3
0
10
20
30
0,5 ( 1,5) 35
0, 75 35
34, 25
S
S
S
S
A
A
A
A
A
S
A
V
V
X
V
X
V
X
V
V
kN
=
⋅
+
⋅
+
⋅
+
=
⋅ −
+
= −
+
=
1
2
3
0
10
10
30
1 ( 1, 5) 0, 5 ( 5,5)
43
41, 75
S
S
S
S
B
B
B
B
B
S
B
V
V
X
V
X
V
X
V
V
kN
=
⋅
+
⋅
+
⋅
+
= − ⋅ −
+
⋅ −
+
=
1
2
3
0
10
20
30
0,5 ( 1,5) 1 ( 5, 5) 0, 5 ( 5,16) 8 10,17
S
S
S
S
C
C
C
C
C
S
C
V
V
X
V
X
V
X
V
V
kN
=
⋅
+
⋅
+
⋅
+
=
⋅ −
− ⋅ −
+
⋅ −
+ =
1
2
3
0
10
20
30
0,5 ( 5,5) 1 ( 5,16) 55
57, 41
S
S
S
S
D
D
D
D
D
S
D
V
V
X
V
X
V
X
V
V
kN
=
⋅
+
⋅
+
⋅
+
=
⋅ −
− ⋅ −
+
=
1
2
3
0
10
20
30
0,5 ( 5,16) 55
52, 42
S
S
S
S
E
E
E
E
E
S
E
V
V
X
V
X
V
X
V
V
kN
=
⋅
+
⋅
+
⋅
+
=
⋅ −
+
=

•
siły wewnętrzne:
- momenty zginające:
10
20
30
0;
1, 5;
5, 5;
5,16;
0
s
s
s
A
B
C
D
E
M
M
X
M
X
M
X
M
=
=
= −
=
= −
=
= −
=
- wyznaczenie momentów ekstremalnych:
1
2
1
(0; 1)
( )
34, 25 ;
(0)
0
(1)
34, 25
(0; 1)
( )
(
1)
34, 25
34, 25 70
34, 25 35, 75 ;
(0)
34, 25
(1)
1, 5
(0; 2)
( )
(
2)
(
1)
34, 25
68, 5 70
2
A
A
A
B
przedzia I
x
M x
V x
x
M
M
kNm
przedzia II
x
M x
V x
P x
x
x
x
M
M
kNm
przedzia II I
x
qx
M x
V x
P x
V x
x
∈
=
=
=
=
∈
=
+ −
=
+
−
=
−
=
= −
∈
=
+ −
+ +
−
=
+
−
−
2
2
2
2
70
41, 75
4
1, 5 6
4
;
(0)
1, 5
(2)
5, 5
(0; 2)
( )
(
2)
(
1)
52, 42
104,84 110 110
57, 41
0,17
5,16;
(0)
5,16
(2)
5, 5
(0; 1)
( )
(
1)
52, 42
52,
E
D
E
x
x
x
x
x
M
M
kNm
przedzia IV
x
M x
V x
P x
V x
x
x
x
x
M
kNm
M
kNm
przedzia V
x
M x
V x
P x
x
+
−
= −
+
−
= −
= −
∈
=
+ −
+ +
=
+
−
−
+
= −
−
= −
= −
∈
=
+ −
=
+
42 110
57, 58
52, 42;
(0)
52, 42
(1)
5,16
x
x
M
kNm
M
kNm
−
= −
+
=
= −
•
sprawdzenie ugięć w punktach podparcia sprężystego:
- podpora 1:
max
1
41, 75
0, 0064
6500
s
B
B
B
b V
∆ = ⋅
=
⋅
=
≤ ∆
- podpora 2:
max
1
10,17
0, 0051
2000
s
C
C
C
b V
∆ = ⋅
=
⋅
=
≈ ∆
- podpora 3:
max
1
57, 41
0, 007
8150
s
D
D
D
b
V
∆ =
⋅
=
⋅
=
≤ ∆
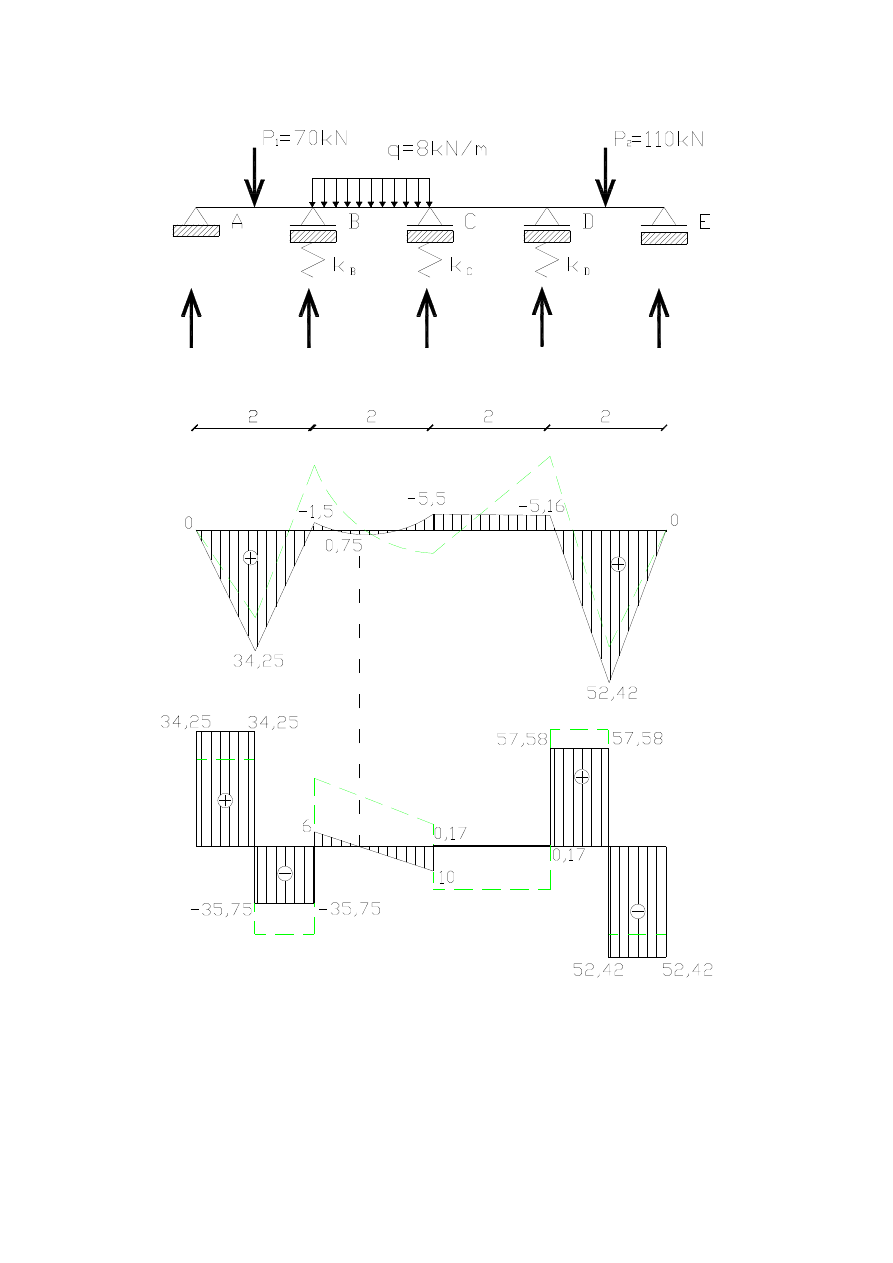
•
wykresy sił wewnętrznych
V
C
=10,17kN
V
B
=41,75kN
V
A
=34,25kN
V
D
=57,41kN V
E
=52,42kN
Wyszukiwarka
Podobne podstrony:
Metoda sił, projekt-belka
Metoda SI - notatka, metodyka pracy korekcyjno kompensacyjnej
Linie wpływu Metoda przemieszczeń mmp belka lw
[SI] projekt wizja
01 Metoda si
Metoda przemieszczen projekt4
Projekt belka met przemieszczen
Metoda SI(1), pomoce-logopedia
Metoda SI
Metoda SI, terapia zajęciowa
CAMatrix, SI Projekt Matrix
Metoda przemieszczen projekt
Metoda przemieszczen projekt3 i Nieznany
PPI Metoda I, Podstawy projektowania inżynierskiego
METODA WYBORU PROJEKTU INWESTYCJI BUDOWLANEJ
Metoda sił, projekt-rama
Metoda sił, projekt-kratownica
Metoda Paszkowskiego projektowanie betonu0001 (1)
więcej podobnych podstron