
Ćwiczenie nr 2:
Posadowienie na palach
wg PN-83 / B-02482

Ćwiczenie nr 3: Posadowienie na palach wg PN-84/B-02482 2
Dla warunków gruntowych przedstawionych na rys.1 zaprojektować posadowienie fundamentu
na palach pod słup obciążony siłami M,N oraz H.
Obciążenia obliczeniowe zestawione w poziomie terenu:
Nr
5210kN
:=
Hr
52kN
:=
Mr
1250kNm
:=
1. Wstępne założenia.
1.1. Wysokość płyty:
H
0.5m
:=
1.2. Przyjęto pale Franki o średnicy trzonu
Di
0.5m
:=
1.3. Minimalna długość zagłębienia pala w warstwie nośnej:
lmin
2.0m
:=
1.4. Długość pala:
Lp
zagl
5
lmin
+
H
−
:=
Lp 6.9 m
=
Niech:
Lp
8m
:=
Rzeczywiste zagłębienie w warstwę nośną:
l
3.1m
:=
Ćwiczenie nr 3: Posadowienie na palach wg PN-84/B-02482 3
2. Wyznaczenie nośności pala.
Nt.r Np.r Ns
+
=
Sp qr
⋅
Ap
⋅
i
Ss
i
tr
i
⋅
As
i
⋅
∑
+
=
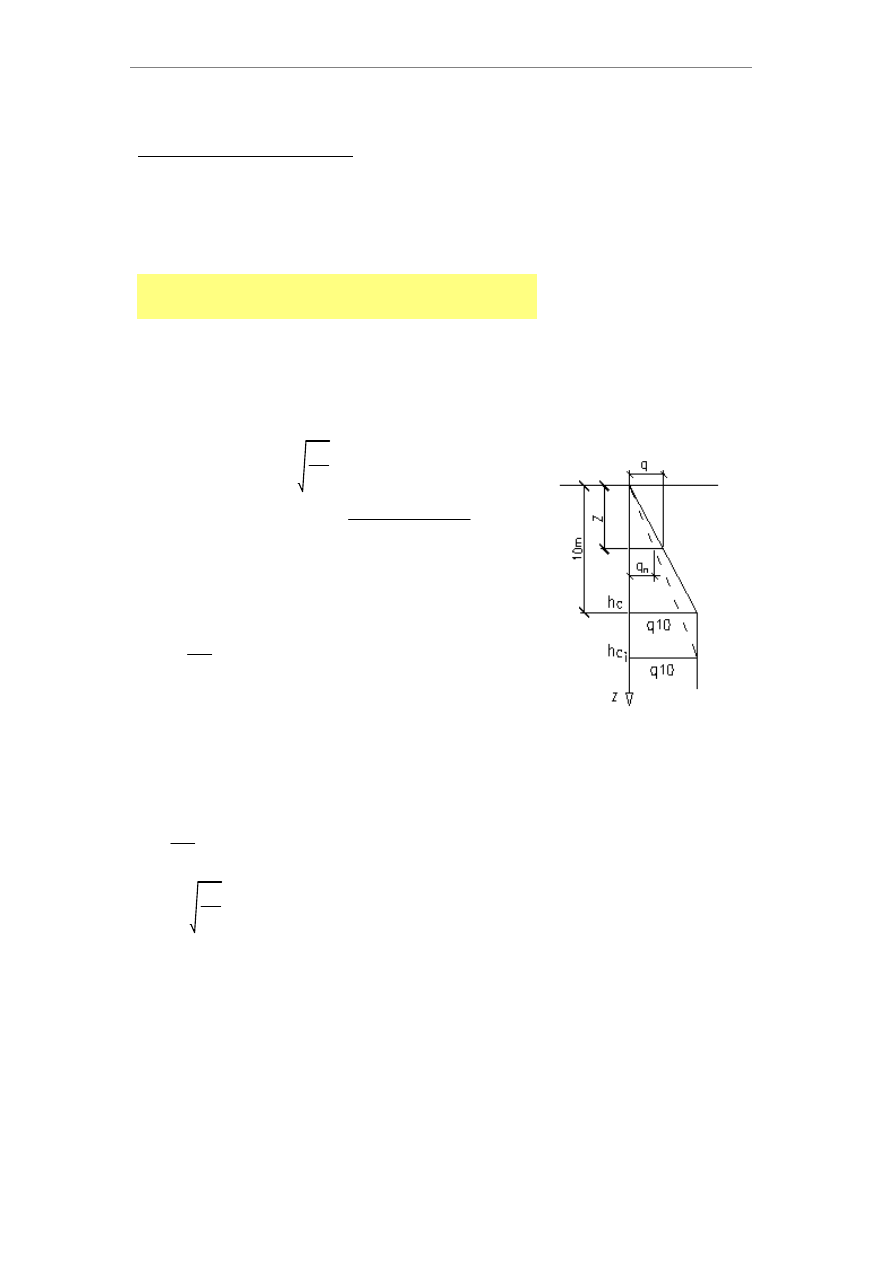
2.1. Jednostkowy graniczny opór gruntu pod podstawą pala:
Warstwa 6 - Po; I
D
=0,43 - średnio zagęszczony
--> q i h
c
zależą od średnicy
z
Lp H
+
zagl
1
−
:=
z
7.7 m
=
Di 0.5 m
=
> D0
0.4m
:=
hc
10m
:=
hci
hc
Di
D0
⋅
:=
hci 11.2 m
=
q10
3000kPa
0.43
0.33
−
(
)
5100kPa
3000kPa
−
0.67
0.33
−
⋅
+
:=
q10 3617.6 kPa
=
I sposób obliczenia qn:
z
7.7 m
=
qn
q10
hci
z
⋅
:=
qn 2491.5 kPa
=
qr
0.9 qn
⋅
:=
qr 2242.4 kPa
=
--------------------------------------------------------------------------------------------------------------------------------------
II sposób obliczenia qn - wzór (6) normy:
q
q10
hc
z
⋅
:=
q
2785.6 kPa
=
qn
q
D0
Di
⋅
:=
qn 2491.5 kPa
=
qr
0.9 qn
⋅
:=
qr 2242.4 kPa
=
--------------------------------------------------------------------------------------------------------------------------------------
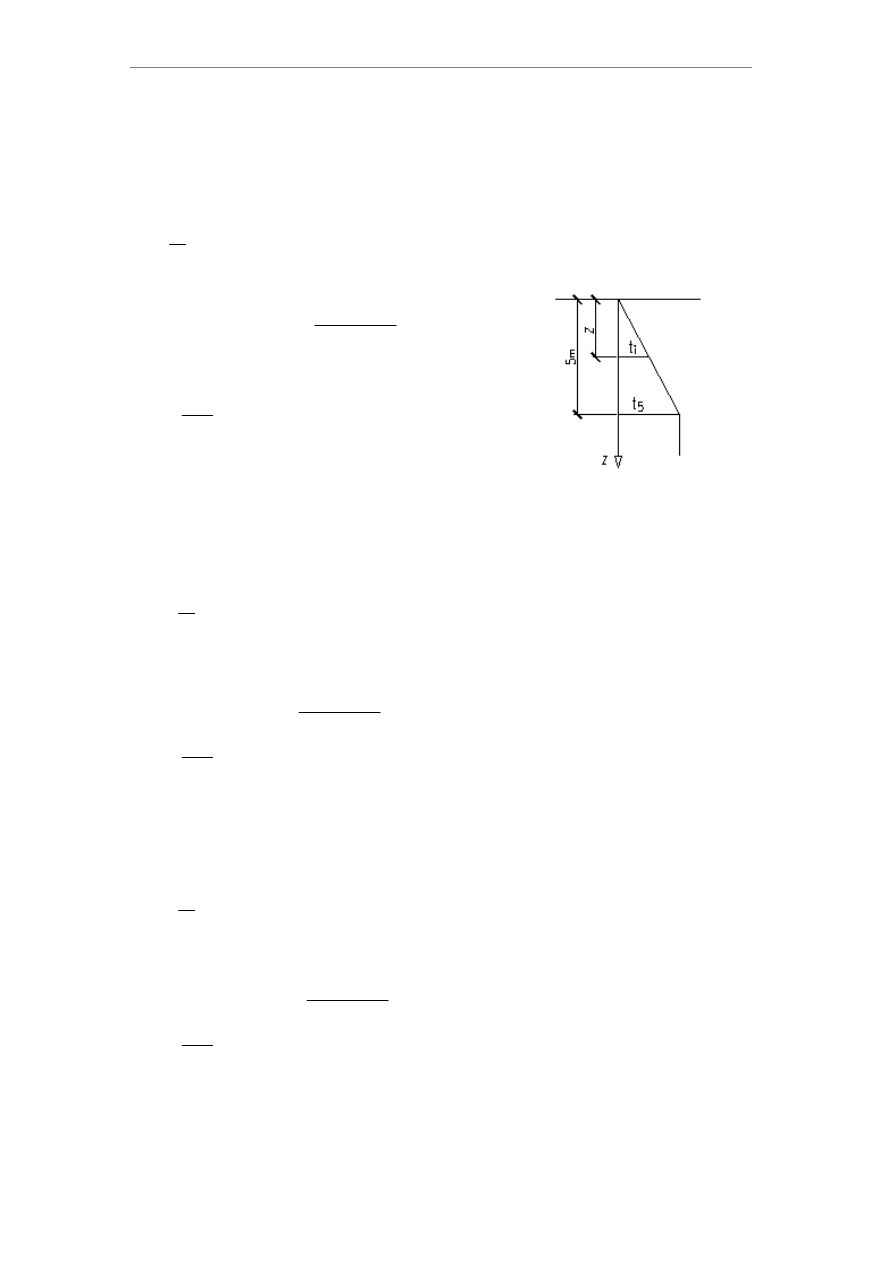
2.2. Jednostkowy graniczny opór gruntu wzdłuż pobocznicy pala:
Warstwa 1 -
Τ; I
L
=0,79 --> t
n1
= 0
PRZYPADEK --> Rys. 5 c) + d)
Ćwiczenie nr 3: Posadowienie na palach wg PN-84/B-02482 4
Warstwa 2 - Gπ; I
L
=0,57
h
2
zagl
2
zagl
1
−
:=
z
h
2
2
:=
z
0.65 m
=
t5
14kPa
0.75
0.57
−
(
)
31
14
−
(
)kPa
0.75
0.5
−
⋅
+
:=
t5 26.2 kPa
=
tn
2
z
5.0m
t5
⋅
:=
tn
2
3.4 kPa
=
tr
2
0.9 tn
2
⋅
:=
tr
2
3.1 kPa
=
Warstwa 3 -
Π
p
; I
L
=0,40
h
3
zagl
3
zagl
2
−
:=
z
h
3
2
h
2
+
:=
z
2.05 m
=
t5
16kPa
0.5
0.4
−
(
)
30
16
−
(
)kPa
0.5
⋅
+
:=
t5 18.80 kPa
=
tn
3
z
5.0m
t5
⋅
:=
tn
3
7.71 kPa
=
tr
3
0.9 tn
3
⋅
:=
tr
3
6.94 kPa
=
Warstwa 4 - P
g
; I
L
=0,35
h
4
zagl
4
zagl
3
−
:=
z
h
4
2
2
3
k
h
k
∑
=
+
:=
z
3.35 m
=
t5
31kPa
0.5
0.35
−
(
)
50
31
−
(
)kPa
0.5
⋅
+
:=
t5 36.7 kPa
=
tn
4
z
5.0m
t5
⋅
:=
tn
4
24.59 kPa
=
tr
4
0.9 tn
4
⋅
:=
tr
4
22.13 kPa
=

Ćwiczenie nr 3: Posadowienie na palach wg PN-84/B-02482 5
Warstwa 5 - P
π
; I
D
=0,24
h
5
zagl
5
zagl
4
−
:=
z
h
5
2
2
4
k
h
k
∑
=
+
:=
z
4.25 m
=
t5
16kPa
0.24
0.2
−
(
)
25
16
−
(
)kPa
0.33
0.20
−
⋅
+
:=
t5 18.77 kPa
=
tn
5
z
5.0m
t5
⋅
:=
tn
5
15.95 kPa
=
tr
5
0.9 tn
5
⋅
:=
tr
5
14.36 kPa
=
Warstwa 6 - Po; I
D
= 0,43
h
6
Lp H
+
zagl
5
−
:=
z
h
6
2
2
5
k
h
k
∑
=
+
:=
t5
74kPa
0.43
0.33
−
(
)
110
74
−
(
)kPa
0.67
0.33
−
⋅
+
:=
t5 84.59 kPa
=
z
6.15 m
=
> 5 m
tn
6
t5
:=
tn
6
84.59 kPa
=
tr
6
0.9 tn
6
⋅
:=
tr
6
76.13 kPa
=
--------------------------------------------------------------------------------------------------------------------------------------
Ponieważ strop warstwy 6-tej znajduje się na:
zagl
5
zagl
1
−
4.6 m
=
można ewentulanie podzielić ją na dwie pod warstwy:
A - sięgającą do 5,0 m (o zmiennym t)
B - sięgającą od 5,0 do końca pala (t = const = t
5
)
h6A
5.0m
zagl
1
+
zagl
5
−
:=
h6A 0.4 m
=
zA
h6A
2
2
5
k
h
k
∑
=
+
:=
zA 4.80 m
=
tn.6A
zA
5.0m
t5
⋅
:=
tn.6A 81.2 kPa
=
tr.6A
0.9 tn.6A
⋅
:=
tr.6A 73.08 kPa
=
h6B
h
6
h6A
−
:=
h6B 2.7 m
=
tn.6B
t5
:=
tn.6B 84.59 kPa
=
tr.6B
0.9 tn
6
⋅
:=
tr.6B 76.13 kPa
=
--------------------------------------------------------------------------------------------------------------------------------------

Ćwiczenie nr 3: Posadowienie na palach wg PN-84/B-02482 6
2.3. Wyznaczenie pola powierzchni podstawy i pobocznicy pala.
- pole podstawy pala Franki:
Ap
1.75π Di
2
⋅
4
:=
Ap 0.3 m
2
=
- pola powierzchni odcinków pobocznicy:
h
2
1.3 m
=
As
2
π D
i
⋅
h
2
⋅
:=
As
2
2 m
2
=
h
3
1.5 m
=
As
3
π D
i
⋅
h
3
⋅
:=
As
3
2.4 m
2
=
h
4
1.1 m
=
As
4
π D
i
⋅
h
4
⋅
:=
As
4
1.7 m
2
=
h
5
0.7 m
=
As
5
π D
i
⋅
h
5
⋅
:=
As
5
1.1 m
2
=
h
6
3.1 m
=
As
6
π D
i
⋅
h
6
⋅
:=
As
6
4.9 m
2
=
Sprawdzenie czy suma wszystkich h równa się długości pala Lp:
h
1
zagl
1
H
−
:=
h
1
0.3 m
=
1
6
i
h
i
∑
=
8 m
=
= L
p
2.4. Przyjęcie współczynników technologicznych.
Sp
1.8
:=
Ss
2
1.0
:=
Ss
3
1.0
:=
Ss
4
1.0
:=
Ss
5
1.6
:=
Ss
6
1.6
:=
2.4. Nośność pojedynczego pala.
Np
Sp qr
⋅
Ap
⋅
:=
Np 1386.9 kN
=
Ns
2
6
i
Ss
i
tr
i
⋅
As
i
⋅
∑
=
:=
Ns 679.2kN
=
Nt
Np Ns
+
:=
Nt 2066.1 kN
=
--------------------------------------------------------------------------------------------------------------------------------------
Lub w przypadku rozbicia warstwy 6-tej na dwie podwarstwy.
Ns
2
5
i
Ss
i
tr
i
⋅
As
i
⋅
∑
=
Ss
6
tr.6A
⋅
h6A
⋅
Ss
6
tr.6B
⋅
h6B
⋅
+
π
⋅ D
i
⋅
+
:=
Ns 676.2kN
=
Co daje tylko 3 kN różnicy!
--------------------------------------------------------------------------------------------------------------------------------------
Ćwiczenie nr 3: Posadowienie na palach wg PN-84/B-02482 7
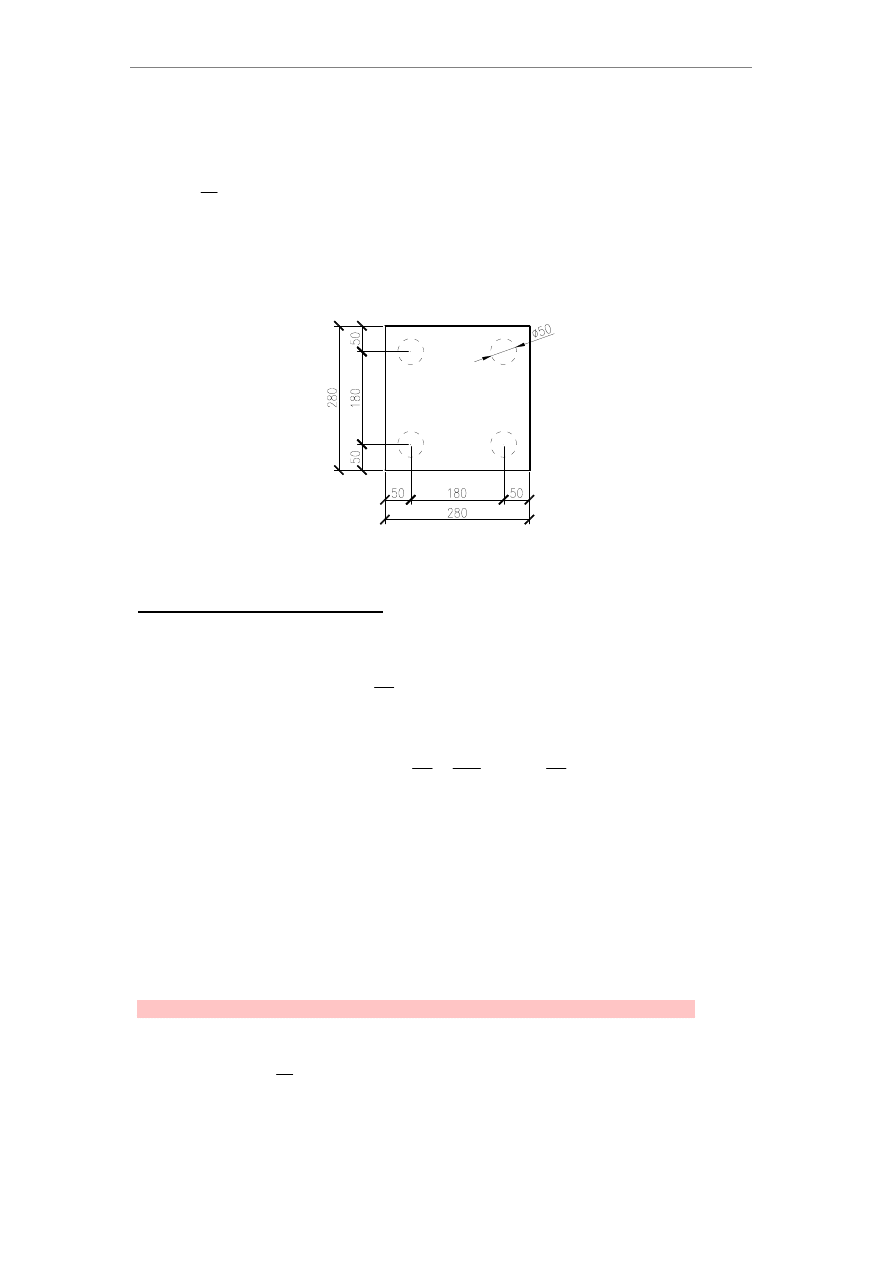
2.5. Przyjęcie liczby pali. Wymiary oczepu i rozstaw osiowy pali.
n
1.25
Nr
Nt
⋅
:=
n
3.2
=
przyjęto
n
4
:=
<
rozstaw -
3.5Di 1.8 m
=
< r
1.8m
:=
8Di 4 m
=
<
<
odległoć do krawędzi oczepu:
0.5Di 0.15m
+
0.4 m
=
a1
0.5m
:=
0.5Di 0.35m
+
0.6 m
=
B
2.8m
:=
L
2.8m
:=
H
0.5 m
=
Przyjęto 4 pale Franki o średnicy 0.5m rozmieszczonych jak na rys.
3. Sprawdzenie warunku nośności.
3.1. Warunku nośności dla pojedynczego prz y obciąż eniu siłą osiową i cziężarem
własnym fundamentu.
Ciężar płyty:
Go.r
1.1B L
⋅ H
⋅ 25
⋅
kN
m
3
:=
Go.r 107.8 kN
=
Ciężar pala:
Gp.r
1.1 Ap 0.3
⋅
Lp
⋅
25
⋅
kN
m
3
⋅
Ap
1.75
0.7
⋅
Lp 25
⋅
kN
m
3
⋅
+
⋅
:=
Gp.r 52.9 kN
=
Uwaga: Uwzględniam zwiększone zużycie betonu (potrzebnego do ukształtowania buławy), ale
tylko na 30% długości pala!
--------------------------------------------------------------------------------------------------------------------------------------
Siła pionowa wraz z ciężarem własnym całego fundamentu palowego:
Qr
Nr n Gp.r
⋅
+
Go.r
+
:=
Qr 5529.5 kN
=
Warunek nośności (sprawdzany tylko gdy fundament nie jest obciążony momentami):
m
0.9
:=
Qr
n
1382.4 kN
=
<
m Nt
⋅
1859.5 kN
=
--------------------------------------------------------------------------------------------------------------------------------------
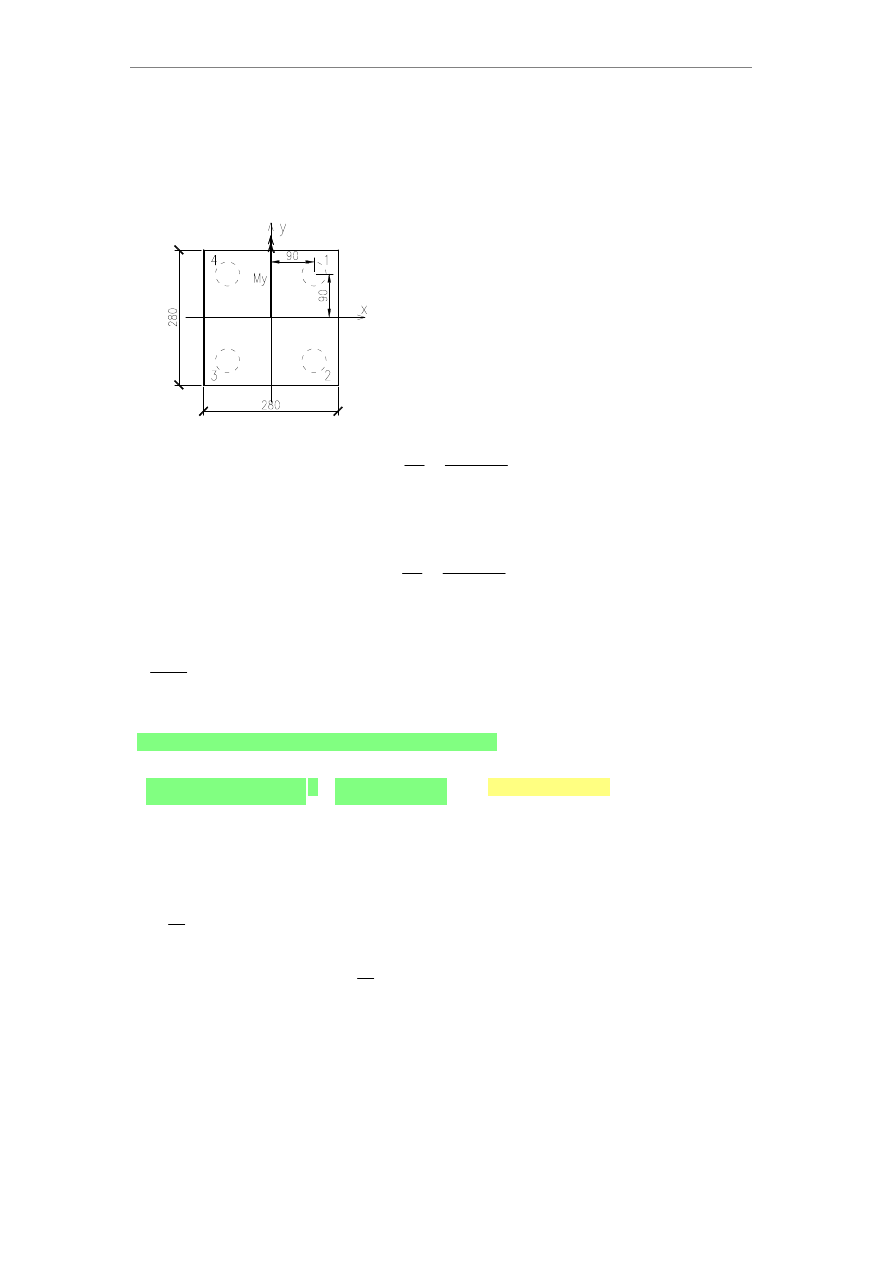
Ćwiczenie nr 3: Posadowienie na palach wg PN-84/B-02482 8
Zaś dla obciążeń z momentem postępujemy jak następuje:
3.2. Warunku nośności dla pala najniekorz ystniej obciążonego.
- zestawienie obciążeń:
Q'r
Nr Go.r
+
:=
Q'r 5317.8 kN
=
My.r
Mr Hr H
⋅
+
:=
My.r 1276 kNm
=
- współrzędne środków ciężkośći przekrojów
poprzecznych pali w poziomie posadowienia oczepu:
x
1
90cm
:=
x
2
90cm
:=
x
3
90
− cm
:=
x
4
90
− cm
:=
- maksymalna siła w palu:
Rmax
Q'r
n
My.r x
1
⋅
1
4
i
x
i
( )
2
∑
=
+
:=
Rmax 1683.9 kN
=
- minimalna siła w palu:
Rmin
Q'r
n
My.r x
3
⋅
1
4
i
x
i
( )
2
∑
=
+
:=
Rmin 975 kN
=
Rmax
Rmin
1.7
=
<
3
Warunek nośności dla pala obciążonego maksymalnie:
Rmax Gp.r
+
1736.8 kN
=
<
m Nt
⋅
1859.5 kN
=
warunek spełniony
--------------------------------------------------------------------------------------------------------------------------------------
Ale
Qr
n
mozna wykorzystac do sprawdzenia czy:
Rmax Gp.r
+
1736.8 kN
=
>
Qr
n
1382.4 kN
=
>
Rmin Gp.r
+
1027.9 kN
=
--------------------------------------------------------------------------------------------------------------------------------------
Ćwiczenie nr 3: Posadowienie na palach wg PN-84/B-02482 9
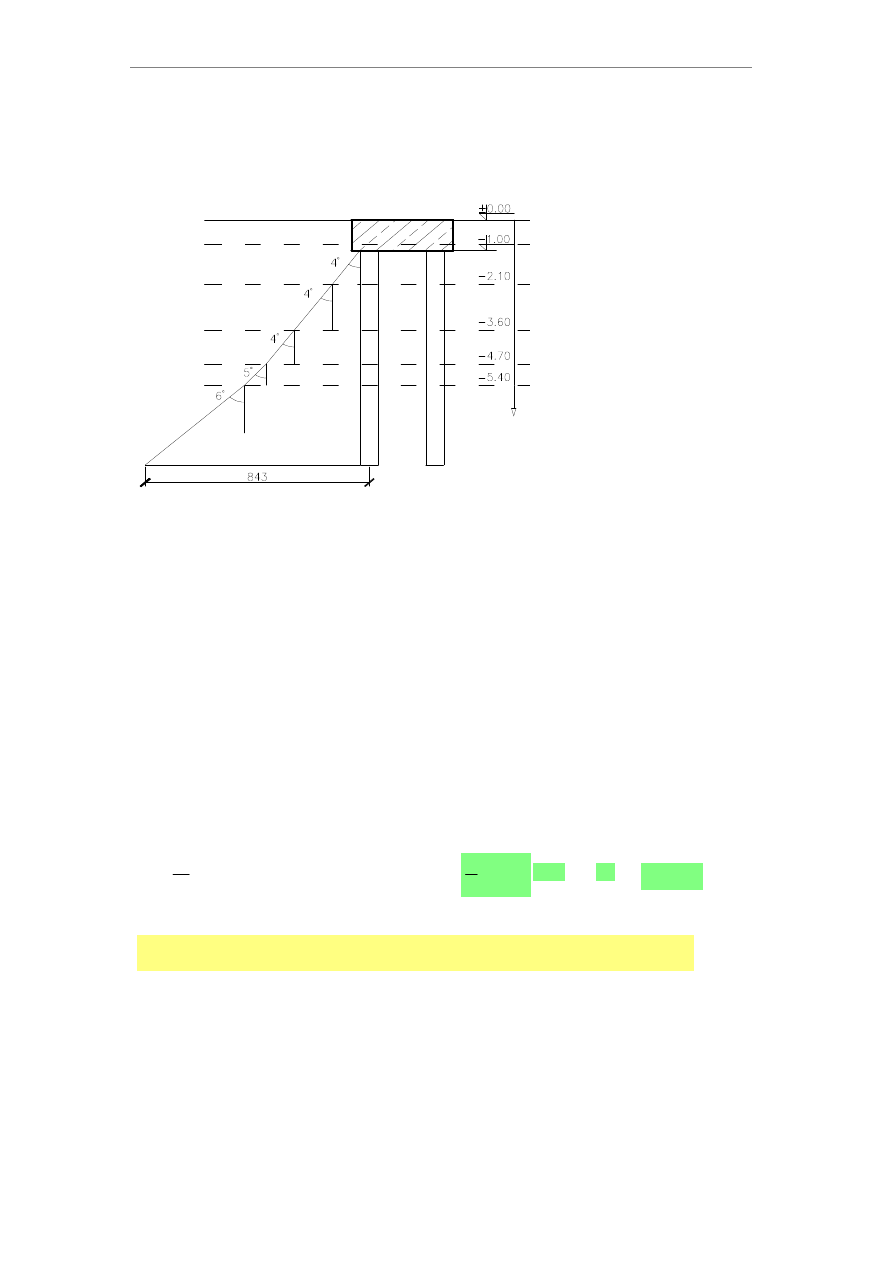
3.3. Nośność pali w grupie.
r
1.8 m
=
Di 0.5 m
=
miąższość
kąt a
tg
α
i
h
i
x
tg
α
i
warstwa 2
h
2
1.3 m
=
α
2
1deg
:=
tan α
2
( )
0.017
=
h
2
tan α
2
( )
⋅
0 m
=
warstwa 3
h
3
1.5 m
=
α
3
4deg
:=
tan α
3
( )
0.070
=
h
3
tan α
3
( )
⋅
0.1 m
=
warstwa 4
h
4
1.1 m
=
α
4
4deg
:=
tan α
4
( )
0.070
=
h
4
tan α
4
( )
⋅
0.1 m
=
warstwa 5
h
5
0.7 m
=
α
5
5deg
:=
tan α
5
( )
0.087
=
h
5
tan α
5
( )
⋅
0.1 m
=
warstwa 6
h
6
3.1 m
=
α
6
6deg
:=
tan α
6
( )
0.105
=
h
6
tan α
6
( )
⋅
0.3 m
=
===================
2
6
i
h
i
tan α
i
( )
⋅
(
)
∑
=
0.6 m
=
Promień strefy naprężeń:
R
Di
2
2
6
i
h
i
tan α
i
( )
⋅
(
)
∑
=
+
:=
R
0.84 m
=
r
R
2.14
=
> 2
=>
m1
1.0
:=
Strefy naprężeń poszczególnych pali nie zachodzą na siebie - nie ma potrzeby
redukowania nośności na pobocznicy
Wyszukiwarka
Podobne podstrony:
Pal tematy zima 2013
Podróże służbowe po zmianach przepisów od 1 marca 2013 r
10 maj 2013 zmiana ustawy o prawie prasowymid 10940
09 W sprawie warunków technicznych, jakim powinny odpowiadać budowle rolnicze i ich usytuowanie zmia
zmiana w ustawie pragmatycznej z X 2013
17 W sprawie warunków technicznych jakim powinny odpowiadać drogowe obiekty inżynierskie i ich usytu
wykłady NA TRD (7) 2013 F cz`
Pr UE Zródła prawa (IV 2013)
W WO 2013 technologia
TEORIE 6 2013 R
Wyk ECiUL#1 2013
Zarzadzanie zmianami GR3
więcej podobnych podstron