Ćwiczenie 5
Temat:
BADANIE LINII DŁUGIEJ
I. ZAGADNIENIA
1.
Badanie linii długiej w stanie jałowym, w stanie zwarcia oraz przy
obciążeniu impedancją falową.
2.
Badanie linii nieodkształcającej.
II. WIADOMOŚCI PODSTAWOWE
Parametry R
0
, L
0
, C
0
, G
0
w liniach elektrycznych rozłożone są w sposób
ciągły, co w liniach telekomunikacyjnych o większej długości (rzędu setek
i tysięcy kilometrów) wywiera duży wpływ na przebiegi prądów i napięć,
Parametry linii długiej zależą od rodzaju przewodów i ich rozmieszczenia,
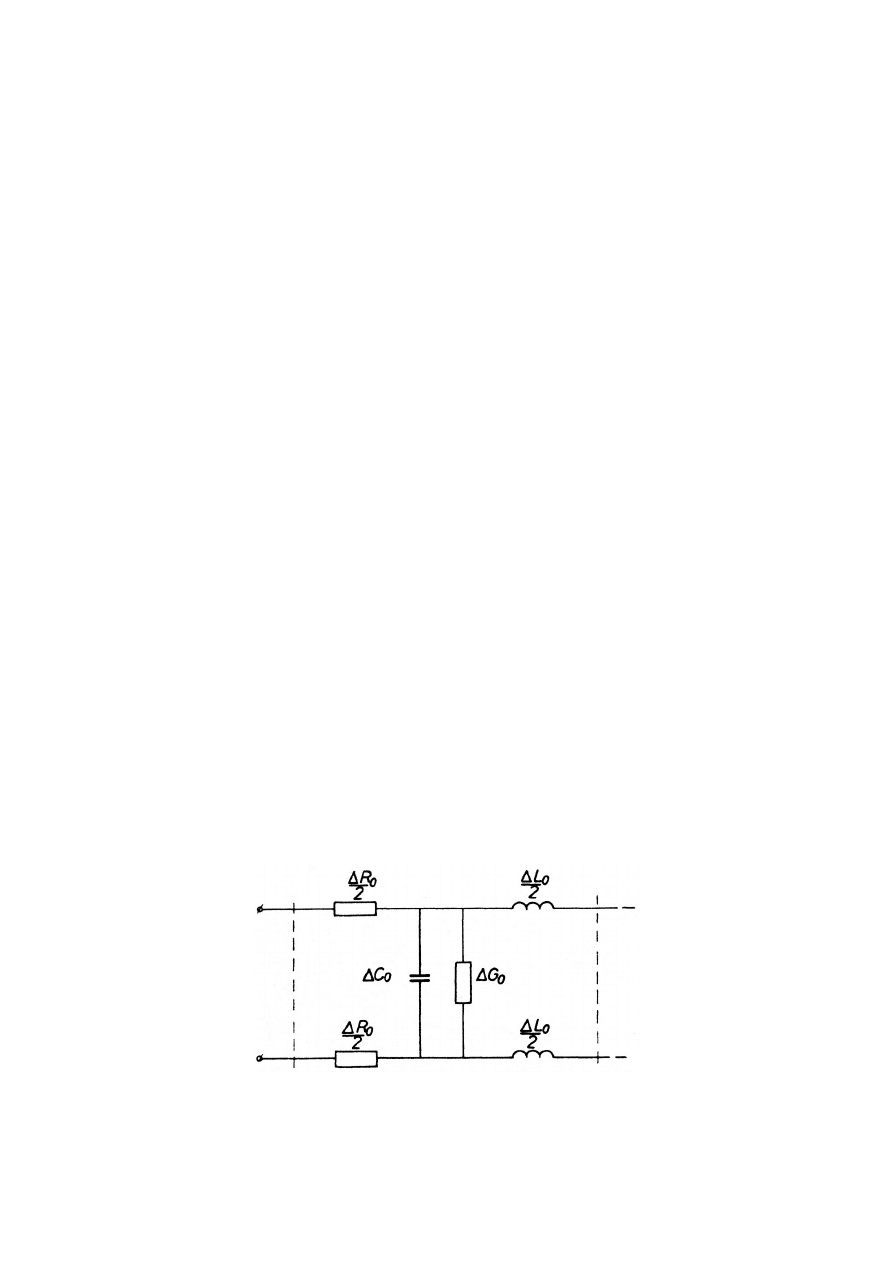
Linię długą należy rozpatrywać jako szereg łańcuchowo połączonych ze sobą
elementów, jak na rys, 5.1., gdzie: R- rezystancja przewodów, L- indukcyjność
pętli utworzonej przez przewody, lub przy uwzględnieniu ziemi - indukcyjność
robocza pętli, C
0
- pojemność międzyprzewodowa, lub też przy uwzględnieniu
pojemności przewodów względem ziemi - pojemność robocza
międzyprzewodowa, G - konduktancja (upływność) międzyprzewodowa,
występująca wskutek niedoskonałości środowiska izolacyjnego między
przewodami.
Rozważania dotyczę linii dwuprzewodowej w stanie ustalonym, przy czym
wielkości R
0
, L
0
, C
0
, G
0
oznaczają parametry linii na jednostkę długości (na 1
km)
Rys. 5.1
Przy zasilaniu sinusoidalnym powyższy obwód można opisać równaniami
U
C
j
G
dx
I
d
I
L
j
R
dx
U
d
)
(
)
(
0
0
0
0
ω
ω
+
=
+
=
(5.1)
0
0
0
L
j
R
Z
ω
+
=
- impedancja zespolona jednostkowa podłużna linii w Ω/km
0
0
0
C
j
G
G
ω
+
=
- admitancja zespolona jednostkowa podłużna linii w S/km
β
α
ω
ω
γ
γ
j
C
j
G
L
j
R
Y
Z
Y
Z
+
=
+
+
=
=
=
)
)(
(
0
0
0
0
0
0
2
0
0
(5.2)
γ
-
stała propagacji lub stała rozprzestrzeniania, zwana także tamownością
jednostkową
α - stała tłumienia, zwana tłumiennością jednostkową
β - stała fazowa, zwana przesuwnością jednostkową.
Równania hiperboliczne linii długiej maja postać:
x
Z
U
x
I
x
I
x
I
Z
x
U
x
U
C
C
γ
γ
γ
γ
sinh
cosh
)
(
sinh
cosh
)
(
2
2
2
2
+
=
+
=
przy x liczonym od końca linii, lub macierzowo:
=
2
2
cosh
sinh
sinh
cosh
)
(
)
(
I
Z
U
x
x
x
x
x
I
Z
x
U
C
C
γ
γ
γ
γ
(5.4)
Powyższe równania pozwalają uzależnić napięcie prąd na początku linii długiej
od napięcia i prądu na końcu linii:
l
Z
U
l
I
I
l
I
Z
l
U
U
C
C
γ
γ
γ
γ
sinh
cosh
sinh
cosh
2
2
1
2
2
1
+
=
+
=
(5.5)
gdzie:U
1
,I
1
– napięcie i prąd na początku linii,
U
2
,I
2
– napięcie i prąd na końcu linii,
L – długość linii,
Z
C
– impedancja charakterystyczna (falowa) linii
0
0
0
0
C
J
G
L
j
R
Z
C
⋅
+
⋅
+
=
ω
ω
(5.6)
(5.6)
Impedancja wejściowa linii długiej:
C
c
c
we
Z
l
Z
l
Z
l
Z
l
Z
I
U
Z
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
+
⋅
⋅
=
=
γ
γ
γ
γ
cosh
sinh
sinh
cosh
2
2
1
1
(5.7)
Jeżeli Z
2
= Z
C
– stan pracy linii nazywamy dopasowaniem falowym
Z
WE
= Z
C
(5.8)
Jeżeli Z
2
= ∞ – stan pracy linii nazywamy stanem jałowym
l
cth
Z
Z
C
we
⋅
=
γ
0
(5.9)
Jeżeli Z
2
= 0 – stan pracy linii nazywamy stanem zwarcia
l
th
Z
Z
C
z
we
⋅
=
γ
(5.10)
W zestawieniu powyższych wzorów otrzymujemy:
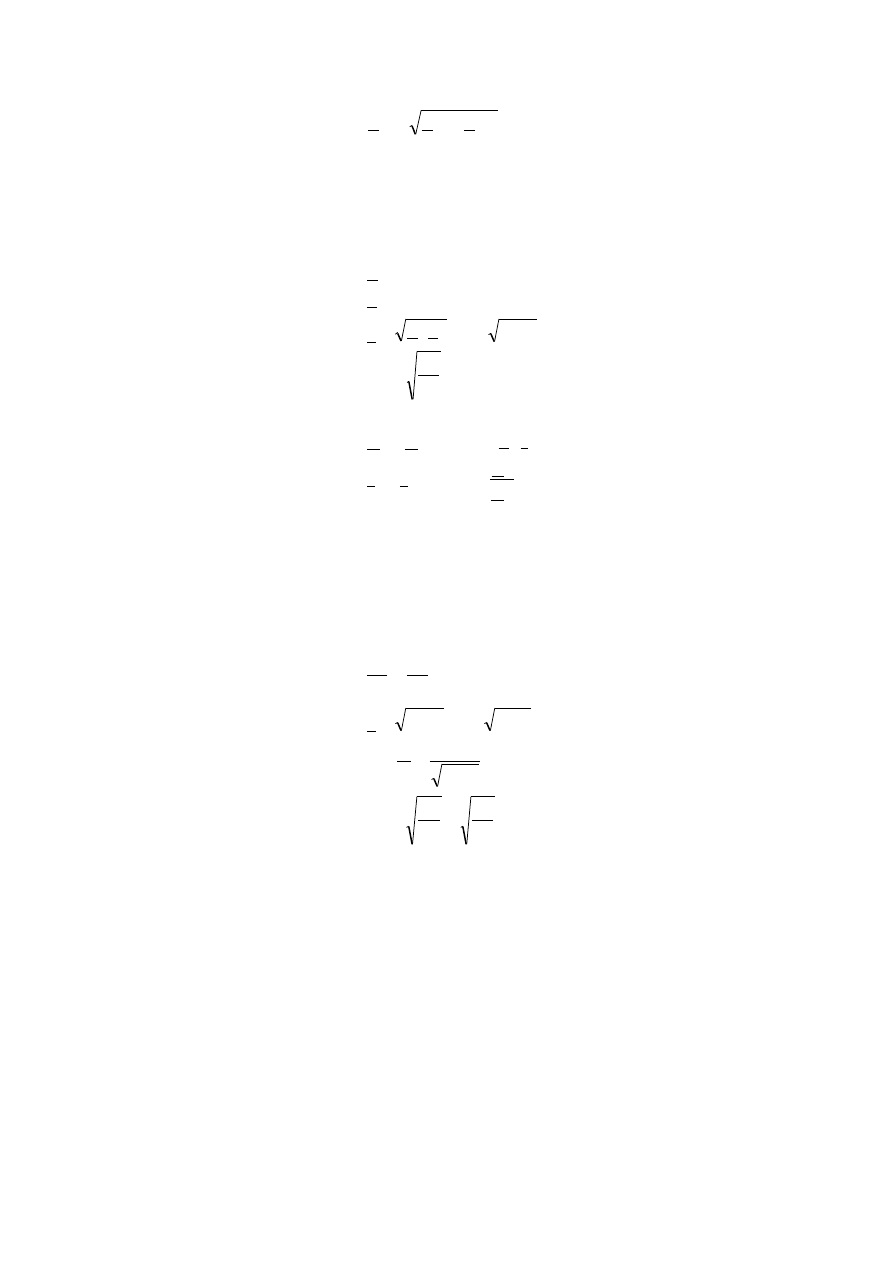
z
we
we
C
Z
Z
Z
⋅
=
0
(5.11)
Przy dopasowaniu falowym istnieje tylko fala pierwotna napięcia prądu, a nie
powstaję fale odbite. Linia długa ma własności linii nieskończenie długiej.
Linię bez strat nazywamy taką linię długą, w której R
0
=0 i G
0
=0.
W rzeczywistości linia bez strat nie istnieje, jednak w wielu przypadkach
z wystarczającą dla praktyki dokładnością, można pominąć R
0
i G
0
β
ω
γ
ω
ω
j
C
L
j
Y
Z
C
j
Y
L
j
Z
=
=
=
=
=
0
0
0
0
0
0
0
0
(5.12)
0
0
C
L
Z
C
=
(5.13)
Równania hiperboliczne linii bez strat przyjmują postać:
l
Z
U
j
l
I
I
l
I
Z
j
l
U
U
C
C
β
β
β
β
sin
cos
sin
cos
2
2
1
2
2
1
+
=
+
=
(5.14)
Linię długą nazywamy nieodkształcającą, jeżeli sygnały o różnej
częstotliwości rozchodzę się w linii z jednakową prędkością i są jednakowo
tłumione, tzn. prędkość fazowa w linii i stała tłumienia nie zależę od
częstotliwości.
Linia długa jest linią, nieodkształcającą, jeżeli parametry linii spełniają
proporcję:
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
C
L
G
R
Z
C
L
j
C
L
j
G
R
G
C
R
L
C
=
=
=
=
+
=
+
=
=
β
ω
ϑ
β
α
ω
γ
(5.15)
III. POMIARY
Pomiary napięć i prądów wszystkich analizowanych stanów pracy linii długiej
należy wykonać miernikami cyfrowymi.
1. Parametry linii długiej:
−
2647
,
0
0
=
R
Ω
km
;
−
85
,
1
0
=
L
km
mH
;
−
08
,
6
0
=
C
km
nF
;
−
068
,
0
0
=
G
km
S
µ
;
−
300
=
l
[ ]
km
;
−
314
=
ω
s
rad
;
−
1
max
=
I
[ ]
A
.
2. Stan jałowy linii długiej
(
)
∞
=
2
Z
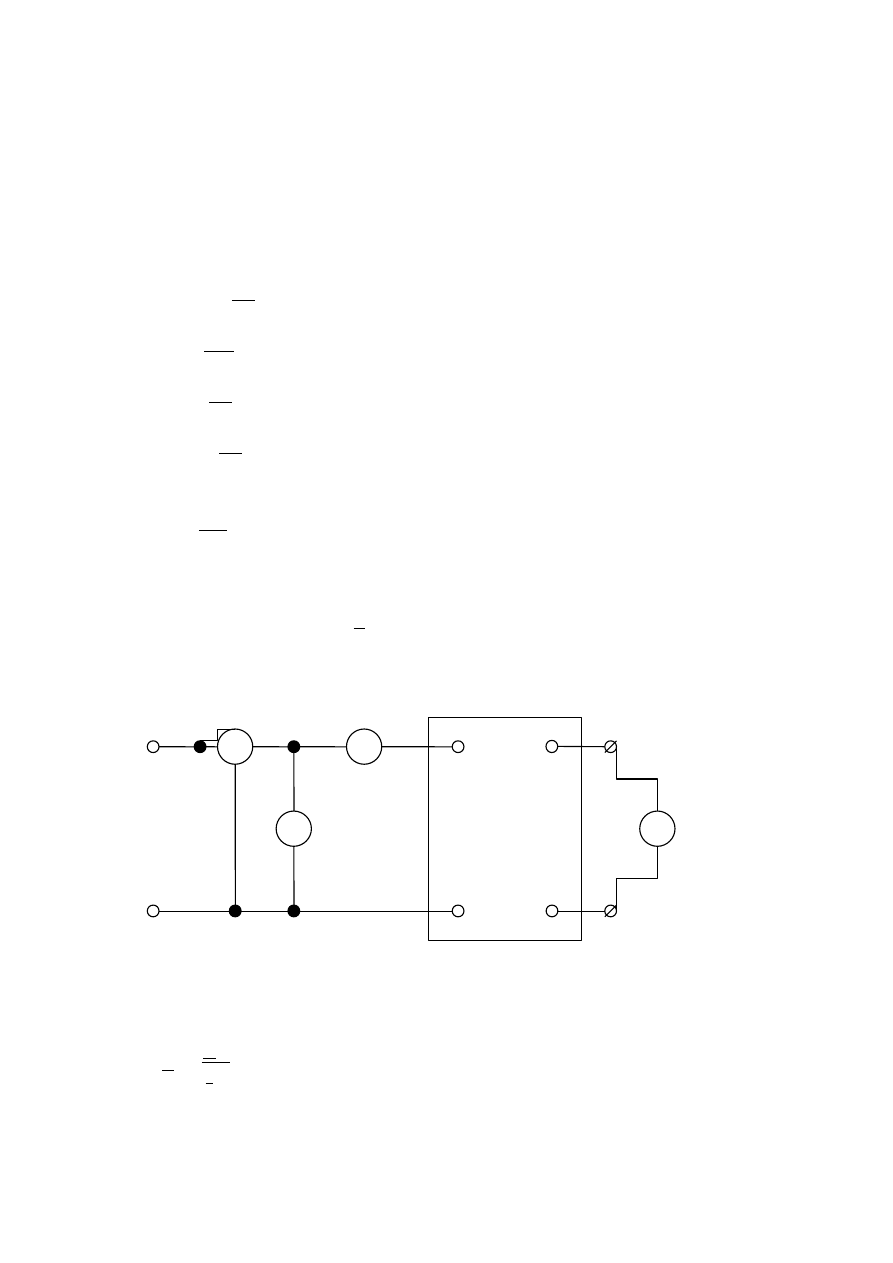
2.1 Badanie linii długiej w stanie jałowym należy przeprowadzić w układzie
pomiarowym przedstawionym na rysunku poniżej:
Rys.5.2. Układ pomiarowy do badania linii długiej w stanie jałowym.
2.2 Wyniki pomiarów umieścić w tabeli pomiarowej:
2.3 Obliczyć impedancję wejściową w stanie jałowym z poniższego wzoru:
10
10
I
U
o
Z
=
cos
ϕ
V
cyfr
A
cyfr
V
cyfr
Linia
długa
we
wy
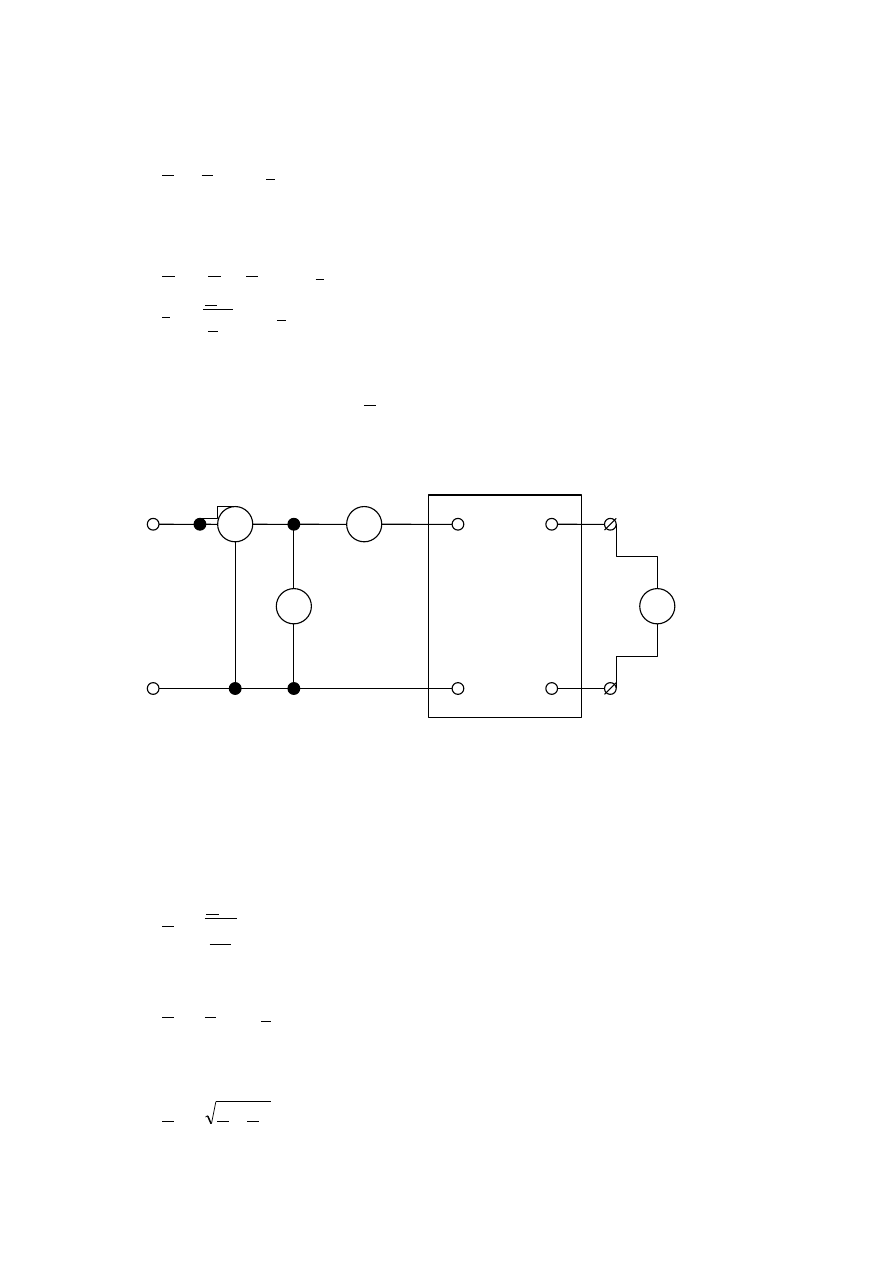
2.4 Obliczyć teoretycznie impedancję wejściową linii w stanie jałowym ze
wzoru:
l
ctgh
Z
o
Z
C
⋅
⋅
=
γ
i porównać ją z wartością otrzymaną z pomiarów.
2.5 Obliczyć napięcie oraz prąd na wejściu linii wykorzystując zmierzone
wartości napięć na wyjściu linii oraz wartość impedancji falowej:
l
Z
U
U
C
⋅
⋅
⋅
=
γ
cosh
20
10
l
Z
U
I
C
⋅
⋅
=
γ
sinh
20
10
3. Stan zwarcia linii długiej
(
)
0
2
=
Z
3.1 Badanie linii długiej w stanie zwarcia przeprowadzić w układzie
pomiarowym przedstawionym na rysunku poniżej:
Rys.5.3. Układ pomiarowy do badania linii długiej w stanie zwarcia.
Pomiary należy przeprowadzić przy prądzie nie przekraczającym 1 [A] (
1
=
dop
I
[ ]
A
).
3.2 Wyniki pomiarów umieścić w tabeli pomiarowej:
3.3 Obliczyć impedancję wejściową w stanie zwarcia:
Z
Z
Z
I
U
Z
1
1
=
3.4 Obliczyć teoretycznie impedancję wejściową linii w stanie zwarcia ze
wzoru:
l
tgh
Z
Z
C
Z
⋅
⋅
=
γ
i porównać z otrzymaną z pomiarów.
3.5 Na podstawie wyników obliczeń dla stanu jałowego oraz dla stanu
zwarcia dowieść, że:
Z
C
Z
o
Z
Z
⋅
=
cos
ϕ
V
cyfr
A
cyfr
Linia
długa
we
wy
A
cyfr
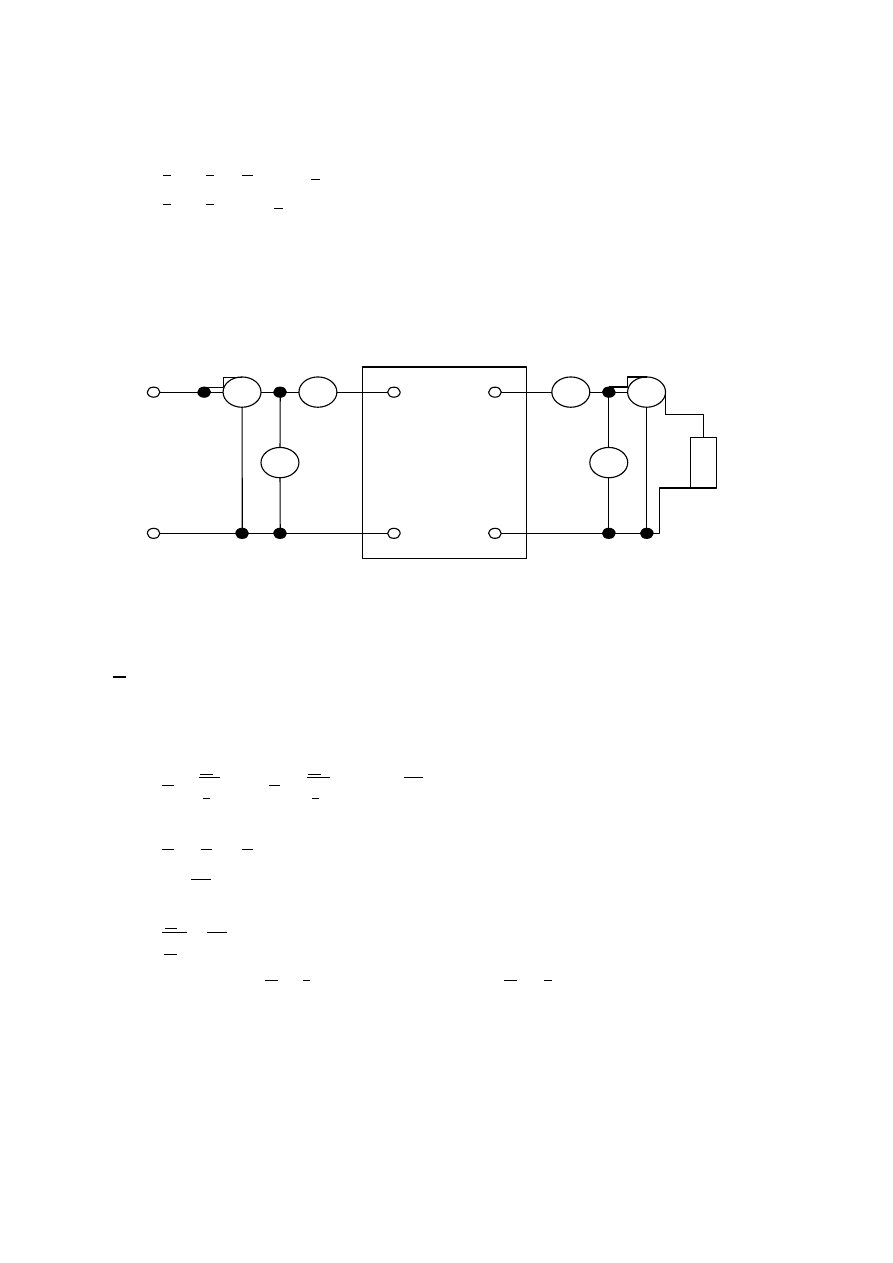
3.6 Obliczyć napięcie oraz prąd na wejściu linii wykorzystując zmierzone
wartości prądów na wyjściu linii oraz wartość impedancji falowej:
l
Z
I
I
C
Z
Z
⋅
⋅
⋅
=
γ
cosh
2
1
l
I
I
Z
Z
⋅
⋅
=
γ
sinh
2
1
4. Stan dopasowania falowego (Z
2
= Z
C
)
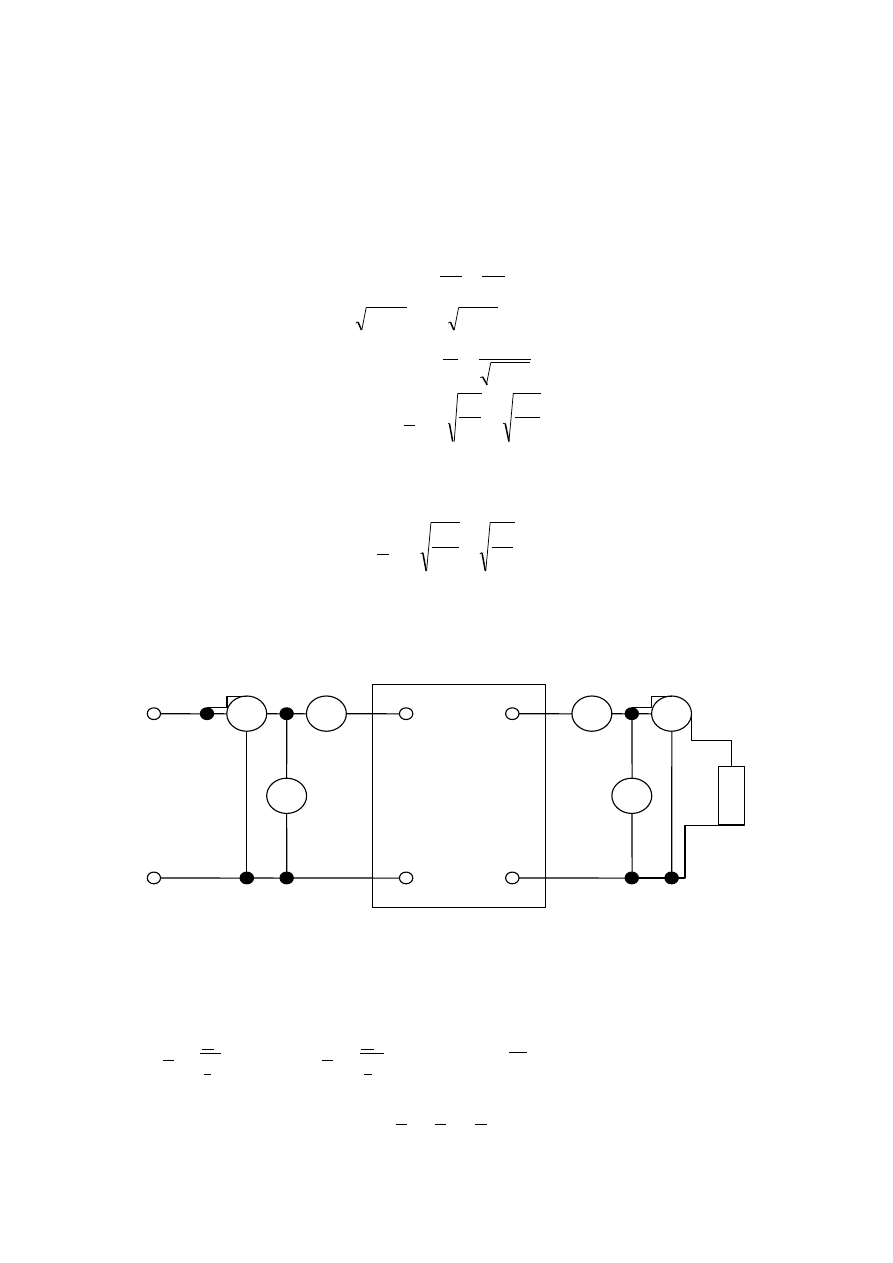
4.1 Badanie linii długiej w stanie dopasowania falowego przeprowadzić
w układzie pomiarowym przedstawionym na rysunku poniżej:
Rys.5.4. Układ pomiarowy do badania linii długiej w stanie dopasowania
falowego.
Pomiary przeprowadzić obciążając linie impedancją falową
(Z
C
= 567 – j112
) [Ω] dla kilku wartości napięcia zasilającego.
4.2 Wyniki pomiarów umieścić w tabeli pomiarowej:
4.3 Impedancję wejściową i wyjściową oraz sprawność obliczyć ze wzorów:
1
1
1
I
U
Z
=
;
1
2
2
I
U
Z
=
;
1
2
P
P
=
η
4.4 Sprawdzić czy:
C
Z
Z
Z
=
=
2
1
l
e
P
P
⋅
−
=
=
α
η
2
1
2
l
e
P
P
U
U
⋅
−
=
=
α
1
2
2
1
4.5 Mając dane
2
U
i
2
I
z pomiarów obliczyć
1
U
i
1
I
z równań hiperbolicznych
linii długiej.
cos
ϕ
cos
ϕ
A
cyfr
A
cyfr
V
cyfr
V
cyfr
Z
Linia
długa
we
wy
5. Linia nieodkształcająca obciążona impedancją falową (Z
2
= Z
C
)
Linię długą nazywamy nieodkształcającą, jeżeli sygnały o różnej częstotliwości
rozchodzą się w linii z jednakową prędkością i są jednakowo tłumione, tzn.
prędkość fazowa w linii i stała tłumienia nie zależą od częstotliwości.
Linia długa jest nieodkształcająca, jeżeli parametry linii spełniają proporcje:
0
0
0
0
G
R
C
L
=
β
α
ω
γ
j
C
L
j
G
R
+
=
+
=
0
0
0
0
0
0
1
C
L
=
=
β
ω
υ
'
0
0
0
0
G
R
C
L
Z
C
=
=
Aby były spełnione powyższe proporcje należy dołączyć w gałęziach
poprzecznych czwórników dodatkową rezystancje o wartości R = 40 [kΩ]
(przełączamy przełączniki na modelu linii). Wtedy G
0
= 0,88 [μS/km].
0
0
0
0
'
C
L
G
R
Z
C
≈
=
5.1 Badanie linii długiej niezniekształcającej obciążonej impedancją falową
przeprowadzimy w układzie pomiarowym przedstawionym na rysunku
poniżej:
Rys.5.5. Układ pomiarowy do badania linii niezniekształcającej obciążonej
impedancją falową
5.2 Wyniki pomiarów umieścić w tabeli pomiarowej:
5.3 Impedancję wejściową i wyjściową oraz sprawność obliczyć ze wzorów:
1
1
1
I
U
Z
=
;
2
2
2
I
U
Z
=
;
1
2
P
P
=
η
5.4 Sprawdzić czy:
C
Z
Z
Z
=
=
2
1
cos
ϕ
cos
ϕ
A
cyfr
A
cyfr
V
cyfr
V
cyfr
Z
Linia
długa
we
wy
l
e
P
P
⋅
−
=
=
α
η
2
1
2
l
e
P
P
U
U
⋅
−
=
=
α
1
2
2
1
5.5 Mając dane
2
U
i
2
I
z pomiarów obliczyć
1
U
i
1
I
z równań hiperbolicznych
linii długiej.
l
Z
I
l
U
U
c
⋅
⋅
+
⋅
=
γ
γ
cosh
cosh
2
2
1
l
Z
U
l
I
I
C
⋅
⋅
+
⋅
=
γ
γ
sinh
cosh
2
2
1
l
Z
l
Z
l
Z
l
Z
Z
Z
C
C
C
⋅
⋅
+
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
=
γ
γ
γ
γ
cosh
sinh
sinh
cosh
2
2
1
Po wykonaniu obliczeń należy porównać odpowiednie wyniki otrzymane z
pomiarów oraz z równań hiperbolicznych i na tej podstawie wyciągnąć
odpowiednie wnioski