© Lesław ŁADNIAK

!412_Obwod_Analiza_ObwodR 2009-12-17

1.1 Analiza obwód rezystancyjnych

Rozpatrzmy

najprostszy

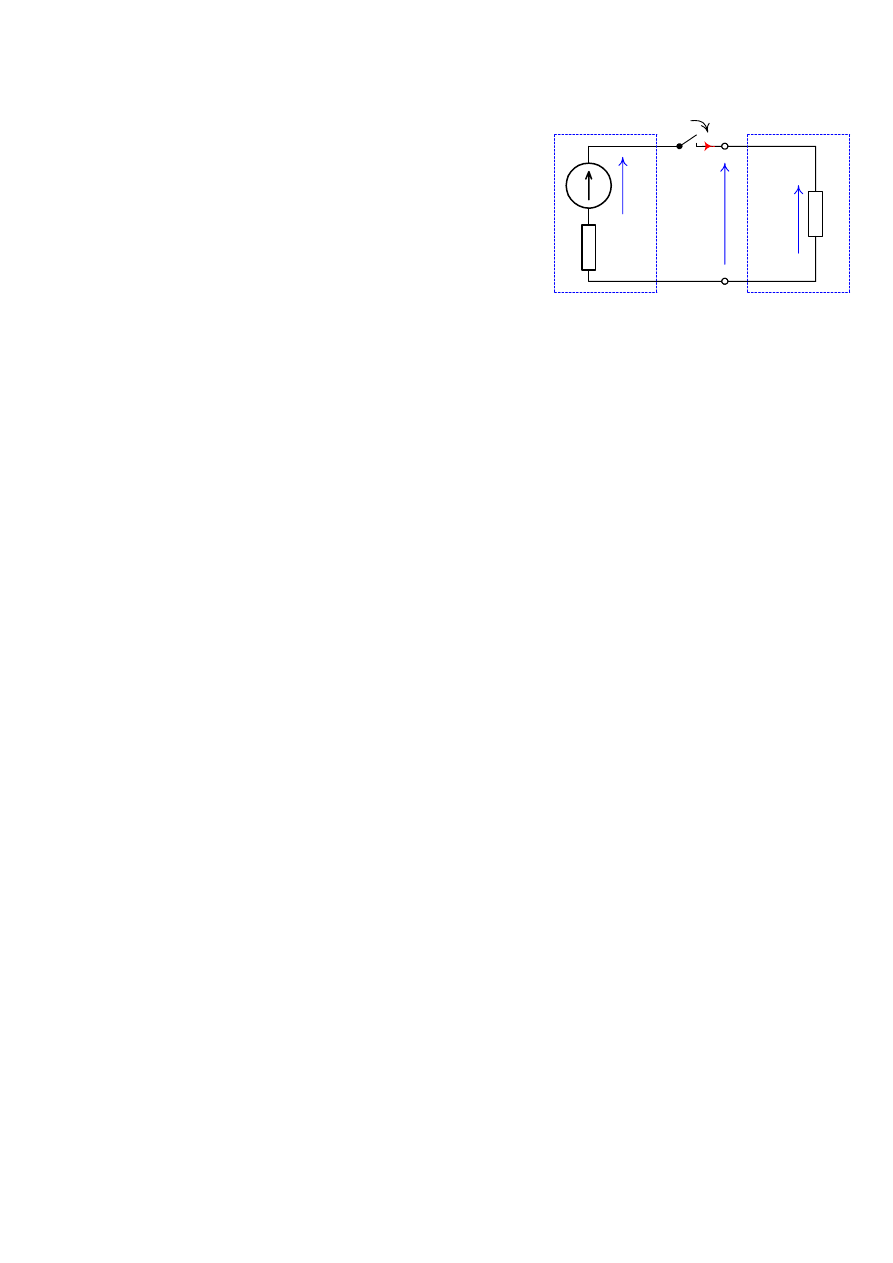
obwód elektryczny (Rys. 1) złożony z

odbiornika o rezystancji R

o

zasilanego ze źródła napięcia o sile

elektromotorycznej e(t) i rezystancji wewnętrznej R

w

.

Elementarna

ilość energii dostarczanej przez źródło zasilania o

sile elektromotorycznej e(t) oraz rezystancji wewnętrznej R

w

jest

opisana równaniem:

dW

E

= p

E

(t) dt = [e(t) i

E

(t) - R

w

i

E

2

(t)] dt

gdzie p

E

(t) jest ilością mocy dostarczanej przez źródło napięcia, a

R

w

i

E

2

(t) jest ilością energii rozpraszanej na rezystancji

wewnętrznej źródła zasilania w każdej chwili czasu.

Elementarna

ilość energii, jaka jest rozpraszana na rezystancji

obciążenia w każdej chwili czasu jest opisana wzorem:

dW

Ro

= p

Ro

(t) dt = u

Ro

(t) i

Ro

(t) dt

gdzie p

Ro

(t) jest wartością chwilową mocy odbiornika.

Korzystając z bilansu energii dla dowolnej chwili czasu
możemy napisać:

dW

E

(t) = dW

Ro

(t)

Zastępując bilans energii bilansem mocy otrzymujemy:

e(t) i

E

(t) - R

w

i

E

2

(t) = u

Ro

(t) i

Ro

(t)

lub

u

Ro

(t) i

Ro

(t) + R

w

i

E

2

(t) = e(t) i

E

(t)

Jeżeli uwzględnimy fakt, że w rozpatrywanym obwodzie przez
wszystkie elementy płynie ten sam prąd, to powyższe równanie
przyjmuje postać:

u

Ro

(t) + u

Rw

(t) = e(t)

Należy zauważyć, że powyższe równanie wynika bezpośrednio
z napięciowego prawa Kirchhoffa.

R

w

e(t)

i(t)

W

R

o

u

R

(t)

u(t)

A

B

Rys. 1. Obwód rezystancyjny

2

Sprawność obwodu rezystancyjnego

Sprawności najprostszego obwodu elektrycznego (Rys.

1)

złożonego ze źródła siły elektromotorycznej wartości E i
rezystancji wewnętrznej R

w

oraz odbiornika o rezystancji R

o

, jest

opisana wzorem:

η

=

W

R

W

D

=

R

o

i

o

dt

e i

E

dt

=

R

o

i

o

R

w

i

E

+ R

o

i

o

=

R

o

R

w

+ R

o

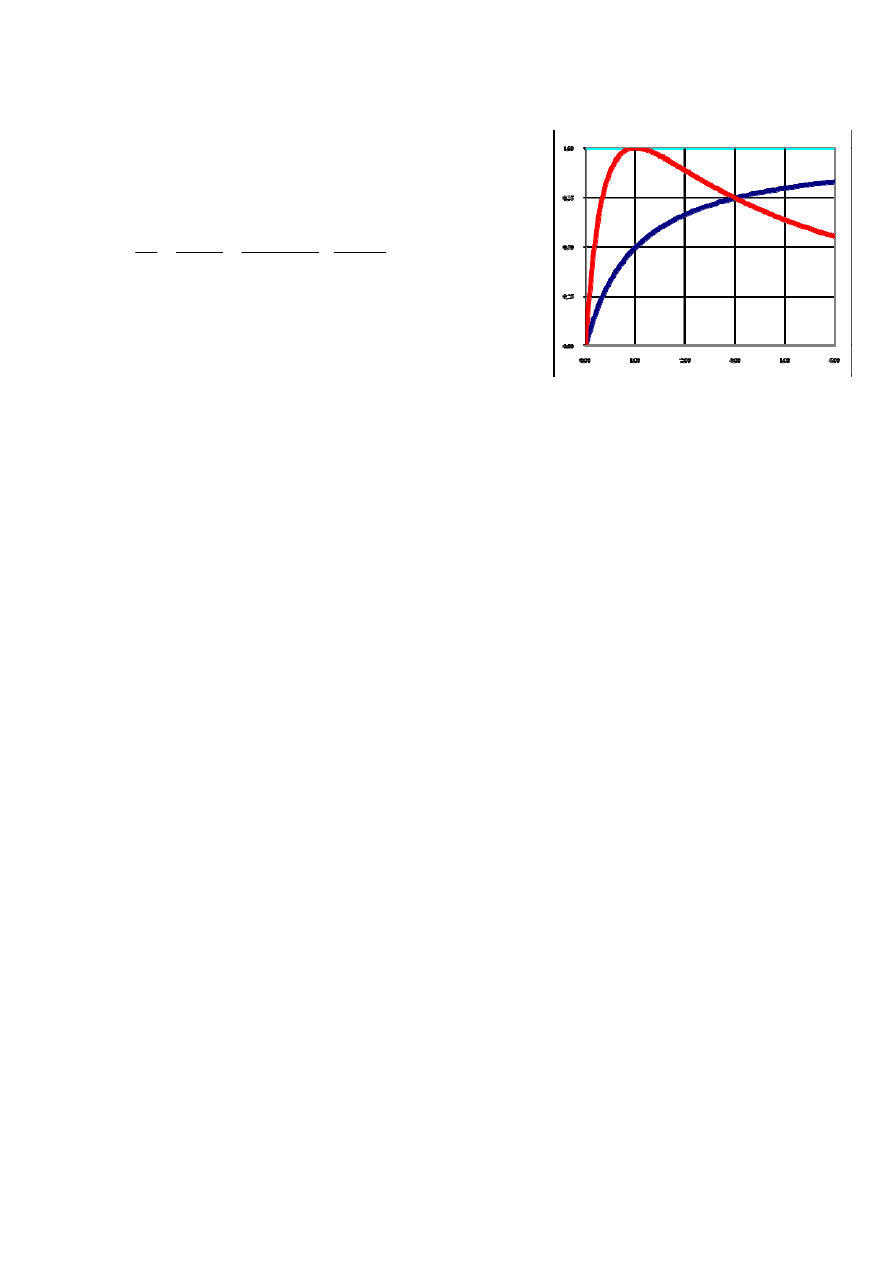
Jak wynika z przedstawionego na Rys. 2 wykresu sprawność
obwodu rośnie, gdy stosunek rezystancji odbiornika do rezystancji
źródła rośnie. Maksymalna szybkość przekazywania energii ze
źródła siły elektromotorycznej do obciążenia występuje, gdy
rezystancja obciążenia jest równa rezystancji źródła. W tym
przypadku sprawność obwodu elektrycznego wynosi tylko 50 %.
Sprawność obwodu elektrycznego rzędu 75 % uzyskamy, gdy
rezystancja obciążenia będzie trzy razy większa od rezystancji
źródła. Warto zwrócić uwagę na fakt, że w tym przypadku
szybkość przekazywania energii ze źródła do odbiornika będzie
tylko o 25 % mniejsza od wartości maksymalnej. Gdy sprawność
układu elektrycznego dąży do 100 %, to szybkość przekazywania
energii ze źródła sem do odbiornika dąży do 50 % mocy
maksymalnej.

Rys. 2. Moc i sprawność obwodu funkcji obciążenia

3

© Lesław ŁADNIAK

!412_Obwod_Analiza_ObwodR 17-12-2009

Prąd w obwodzie rezystancyjnym

Korzystając z bilansu energii lub bezpośrednio z napięciowego
prawa Kirchhoffa dla rozpatrywanego obwodu można napisać:

u

Ro

(t) + u

Rw

(t) = e(t)

Jeżeli występujące w obwodzie elementy rezystancyjne są
liniowe, to zgodnie z prawem Ohma, napięcie na zaciskach tych
elementów jest równe iloczynowi rezystancji R i wartości
natężenia prądu i(t) płynącego przez ten rezystor, czyli możemy
napisać:

R

o

i(t) + R

w

i(t) = e(t)

(*)

Wartość natężenia prądu płynącego rozpatrywanym obwodzie
obliczymy korzystając ze wzoru:

i(t) =

1

R

w

+ R

o

e(t)

W obwodzie rezystancyjnym wartość natężenia prądu w danej
chwili czasu jest równa wartości chwilowej napięcia zasilania
podzielonej przez wartość rezystancji zastępczej elementów
tworzących obwód, czyli

kształt zmian natężenia prądu jest taki

sam jak kształt zmian siły elektromotorycznej działającej w
tym obwodzie.

Wymuszenie stałe

Jeżeli w rozpatrywanym obwodzie siła elektromotoryczna ma
wartość stałą w czasie:

e(t) = E,

to po zamknięciu w chwili t = 0 wyłącznika W, w obwodzie
popłynie prąd i(t), którego wartość będzie też stała w czasie:

i(t) =

E

R

w

+ R

o

= I

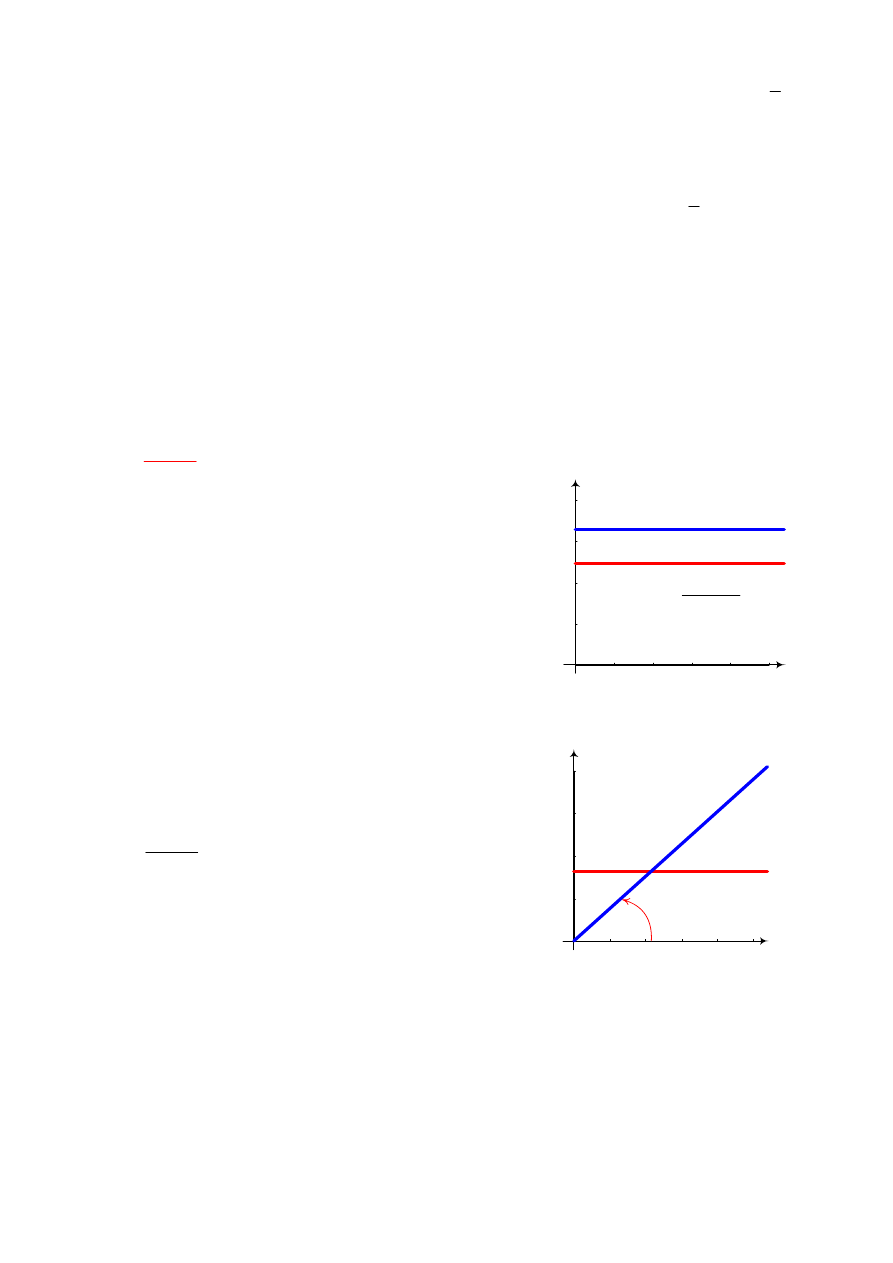
Na Rys. 3 przedstawiono wykres siły elektromotorycznej źródła
napięcia i wykres prądu płynącego w obwodzie rezystancyjnym.

Ponieważ zarówno napięcie na zaciskach odbiornika, jak i
natężenie prądu płynącego przez odbiornik mają wartość stałą w
czasie, to wartość chwilowa mocy odbiornika też nie ulega
zmianie:

p(t) = u(t) i(t) = U I = R I

2

=

1

R

U

2

czyli moc czynna odbiornika ma wartość
stałą i wynosi:

P = U I = R I

2

=

1

R

U

2

Ilość energii wydzielającej się w
odbiorniku jest proporcjonalna do czasu
przepływu prądu:

W(t) = R I

2

t

Na Rys. 4 przedstawiono wykres zmian
mocy i ilości energii dostarczanej do
odbiornika rezystancyjnego zasilanego ze
źródła siły elektromotorycznej o wartości
stałej w czasie.

0

2

3

4

t

e(t), i(t)

1

5

I

E

R

w

+ R

o

I =

E

Rys. 3. Prąd w obwodzie rezystancyjnym przy

wymuszeniu stałym

0

2

3

4

t

p(t), W(t)

1

5

RI

2

tg

α

= RI

2

Rys. 4. Moc i energia odbiornika rezystancyjnego

przy wymuszeniu stałym

4

Odpowiedź na sinusoidalnie wymuszenie

Jeżeli działająca w obwodzie siła elektromotoryczna zmienia
się sinusoidalnie:

e(t) = E

m

sin (

ω

t +

ψ

u

)

to prąd płynący w tym obwodzie jest opisany równaniem:

i(t) =

E

m

R

w

+ R

o

sin(

ω

t +

ψ

u

) = I

m

sin(

ω

t +

ψ

i

)

Jak wynika z powyższego równania wartość chwilowa prądu
zmienia się sinusoidalnie. Amplituda zmian natężenia prądu I

m

jest

proporcjonalna do amplitudy siły elektromotorycznej działającej w
obwodzie, a odwrotnie proporcjonalna do rezystancji obwodu.
Faza początkowa prądu

ψ

i

jest w tym przypadku taka sama jak faza

początkowa źródła napięcia

ψ

u

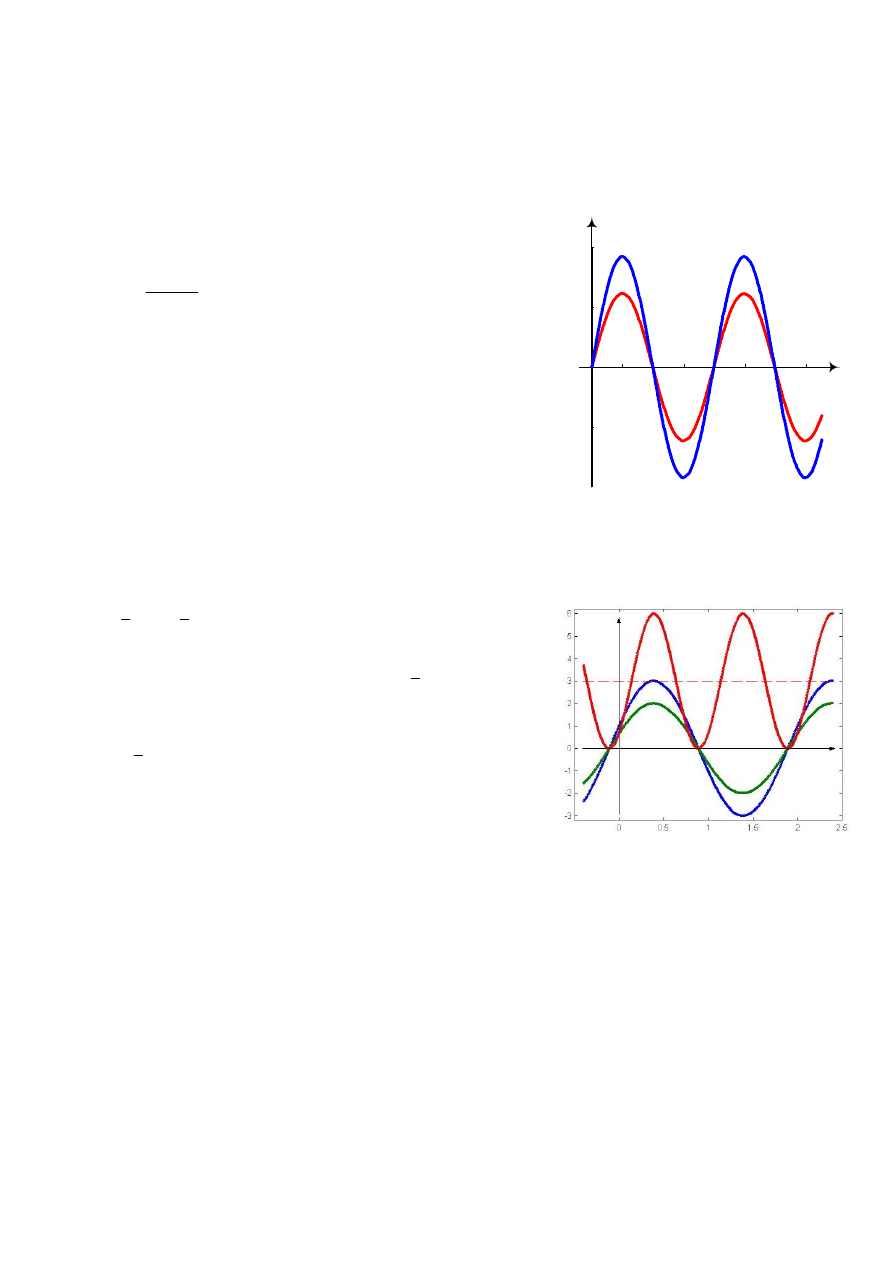
. Na (Rys. 5) przedstawiono wykres

zmian napięcia i prądu w rozpatrywanym obwodzie, gdy siła
elektromotoryczna źródła napięcia zmienia się sinusoidalnie.

Znając przebieg zmian napięcia i prądu w obwodzie
rezystancyjnym możemy wyznaczyć przebieg zmian wartości
chwilowej mocy na zaciskach odbiornika:

p

R

(t) = u

R

(t) i

R

(t) = R i

2

(t) = R I

m

2

sin

2

(

ω

t +

ψ

i

)

=

1
2

R I

m

2

-

1
2

R I

m

2

cos(2

ω

t + 2

ψ

i

) = R I

2

– R I

2

cos(2

ω

t + 2

ψ

i

)

Wartość średnia mocy chwilowej jest równa

1
2

R I

m

2

, czyli moc

czynna jest równa:

P =

1
2 R I

m

2

= R I

2

Energia, jaka wydzieliła się w rezystorze do chwili t wynosi:

W(t) =

⌡

⌠

0

t

p

R

(t) dt =

⌡

⌠

0

t

R I

m

2

sin

2

(

ω

t +

ψ

i

) dt =

=

⌡

⌠

0

t

{R I

2

– R I

2

cos(2

ω

t + 2

ψ

i

)} dt = R I

2

t

Na

Błąd! Nie można odnaleźć źródła

odwołania. przedstawiono zmiany
chwilowe mocy na elemencie
rezystancyjnym, gdy siła elektromotoryczna
źródła napięcia zmienia się sinusoidalnie.

e(t), i(t)

E

m

0

15

t

5

I

m

25

35

Rys. 5. Prąd w obwodzie rezystancyjnym przy

wymuszeniu sinusoidalnie

zmiennym

Rys. 6. Wartość chwilowa mocy na rezystancji

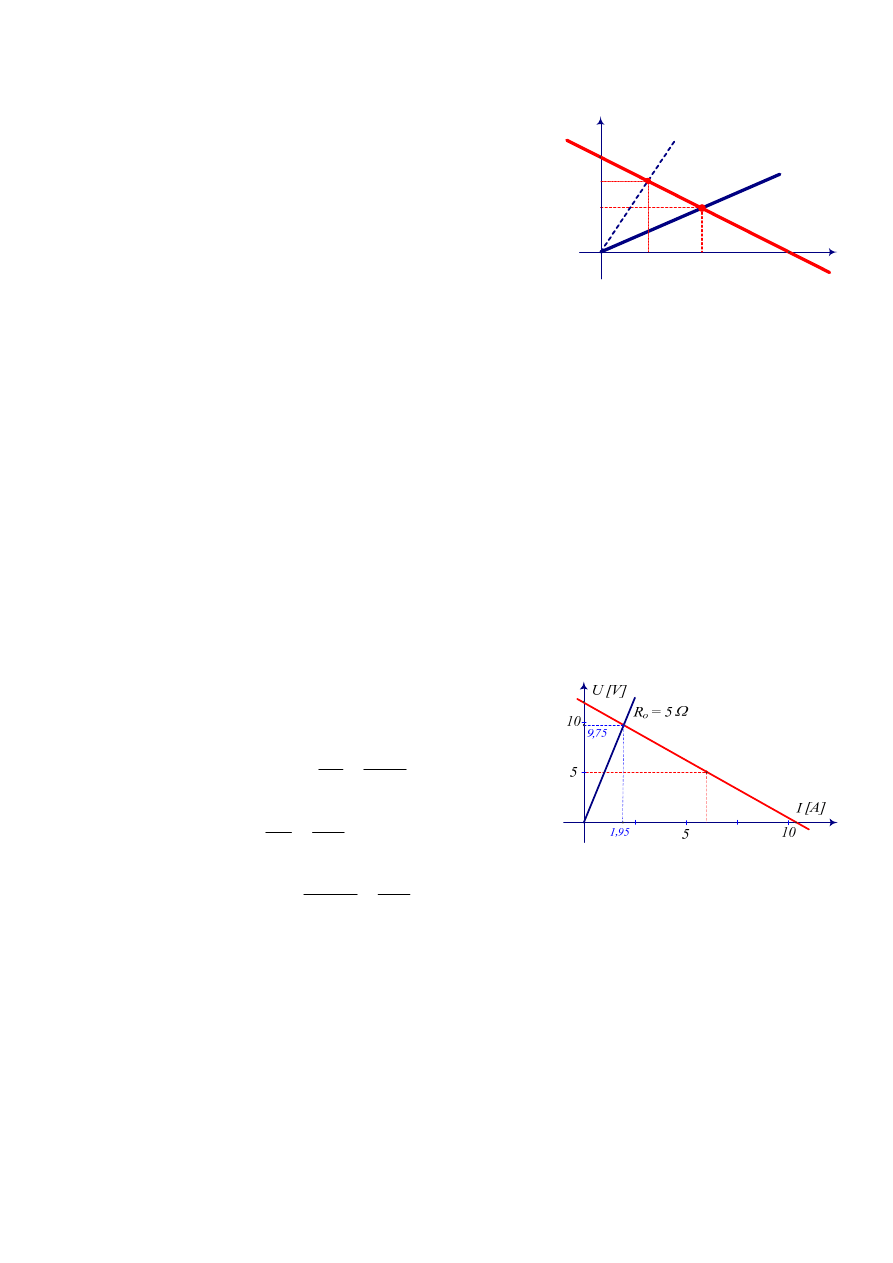
5

© Lesław ŁADNIAK

!412_Obwod_Analiza_ObwodR 17-12-2009

Graficzne rozwiązywanie obwodu

Równanie wiążące napięcie na zaciskach odbiornika o
rezystancji R

o

z napięciem na zaciskach źródła napięcia o sile

elektromotorycznej e(t) i rezystancji wewnętrznej R

w

jest postaci:

R

o

i(t) = e(t)

−

R

w

i(t)

Po prawej stronie równania jest zależność między napięciem na
zaciskach odbiornika, a prądem płynącym przez odbiornik. Po
lewej stronie równania jest zależność opisująca zmianę napięcia na
zaciskach źródła siły elektromotorycznej o wartości e(t) i
rezystancji wewnętrznej R

W

w zależności od wartości natężenia

prądu pobieranego ze źródła.

W celu graficznego wyznaczenia wartości napięcia i prądu
odbiornika należy wykreślić charakterystykę prądowo-napięciową
lub napięciowo-prądową źródła, a następnie na tym samym
wykresie narysować odpowiednią charakterystykę odbiornika.
Współrzędne punktu przecięcia się charakterystyki źródła z
charakterystyką odbiornika są szukanymi wartościami napięcia na
zaciskach obciążenia i prądu płynącego przez obciążenie (Rys. 7).

Graficzne

rozwiązanie powyższego równania jest szczególnie

łatwe, gdy działająca w obwodzie siła elektromotoryczna ma
wartość stałą w czasie lub sinusoidalnie zmienną.

Przykład. Graficzne rozwiązywanie obwodu

Jaką moc powinien posiadać odbiornik o rezystancji R = 5

Ω

zasilany ze źródła napięcia o sile elektromotorycznej E = 12 V,
jeżeli w czasie przepływu prądu o natężeniu I = 6 A napięcie na
zaciskach źródła wynosiło U

AB

= 5 V.

Rozwiązanie

Rezystancja źródła napięcia:

R

W

=

Δ

U

Δ

I

=

12 - 5

6 -0

= 1,16

Ω

Prąd zwarcia źródła:

I

z

=

E

R

W

=

12

1,16

= 10,34 A

Prąd płynący w obwodzie:

I

=

U

R

W

+ R

=

12

6,16

= 1,94 A

Napięcie na zaciskach rezystora: U = R

⋅

I = 5

⋅

1,94 = 9,74 V

Moc rezystora:

P = U

⋅

I = 9,74

⋅

2,35 = 22,88

W

E

I

U

I= E/R

w

U

o

I

o

R

o2

R

o

Rys. 7. Graficzne rozwiązywanie obwodu

Rys. 8. Graficzne wyznaczanie prądu

Z wykresu odczytano:

U = 9,75

V

I

= 1,9

5

A

6

Obwód z elementem nieliniowym

Graficzny sposób rozwiązywania obwodu można zastosować
nawet w tedy, gdy elementy tworzące układ są elementami nie
liniowymi.

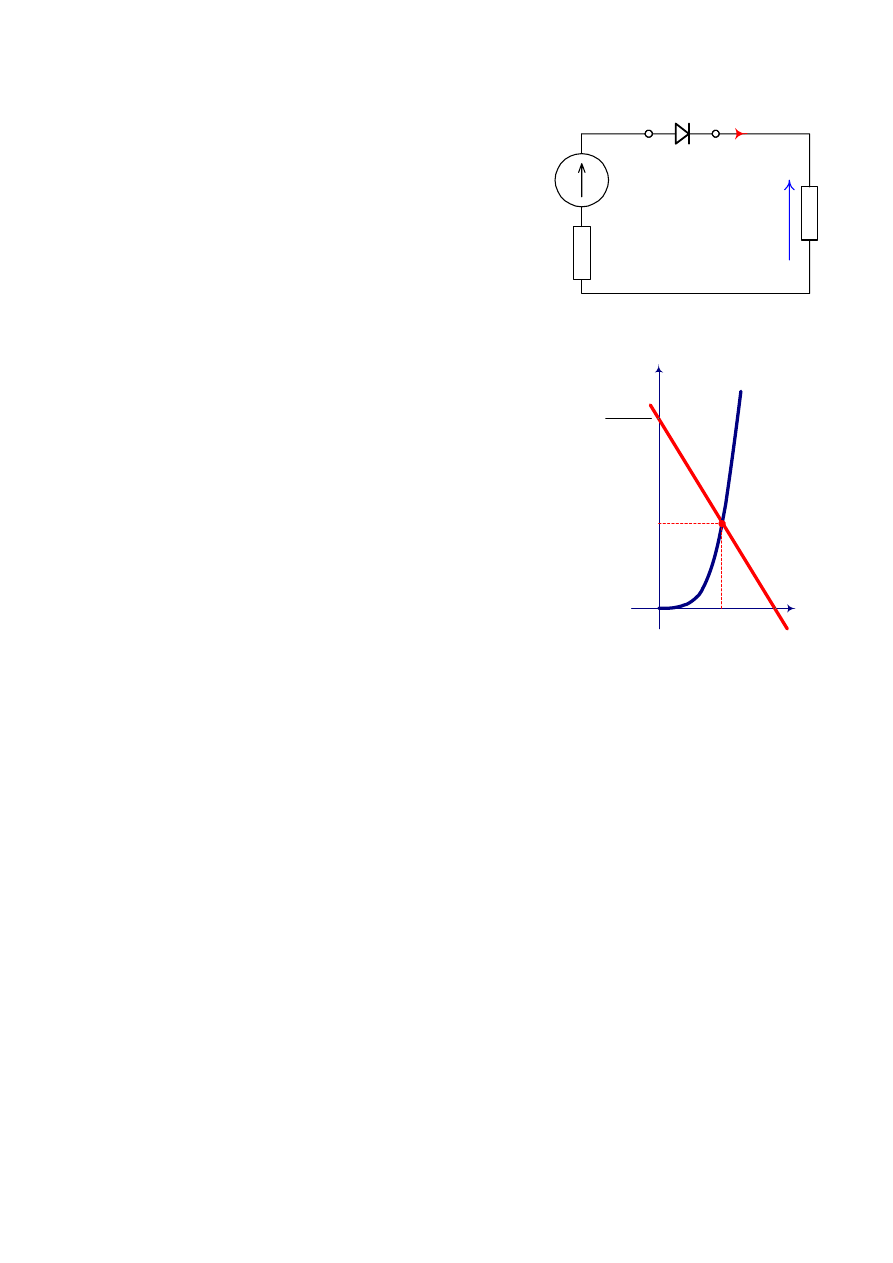
Rozpatrzmy w tym celu przedstawiony na Rys. 10 schemat
obwodu, w którym odbiornik rezystancyjny o rezystancji R

o

jest

zasilany poprzez diodę prostowniczą D ze źródła napięcia
sinusoidalnie zmiennego o wartości skutecznej E i rezystancji
wewnętrznej R

w

. Wartość prądu płynącego w obwodzie zależy

przede wszystkim od tego, jakie jest napięcie na zaciskach diody.
Jeżeli do potencjał punktu A jest wyższy do potencjał punktu B
(potencjał anody jest wyższy od potencjału katody), to dioda jest
spolaryzowana w kierunku przewodzenia. Znając charakterystykę
napięciowo-prądową diody w kierunku przewodzenia oraz
charakterystykę układu zasilającego tą diodę możemy wyznaczyć
wartość prądu płynącego przez diodę (Rys. 10).

Wyznaczone, tym przypadku, wartości napięcia na diodzie U

DF

i prądu płynącego przez diodę I

DF

są wartościami maksymalnymi.

Wykres zmian napięcia u

DF

(t), czyli napięcia między punktami A

oraz B, można uzyskać pamiętając, że siła elektromotoryczna
źródła napięcia zmienia się sinusoidalnie. Wykres zmian prądu
i

DF

(t) uzyskamy pamiętając, że przez diodę płynie prąd, gdy

potencjał punktu A jest wyższy od potencjału punktu B.

R

w

E

m

sin

ω

t

i(t)

D

R

o

u

R

(t)

A

B

Rys. 9. Obwód z diodą

E

m

I

U

I

DF

U

DF

E

m

R

w

+

R

o

Rys. 10. Graficzne rozwiązywanie obwodu z

diodą