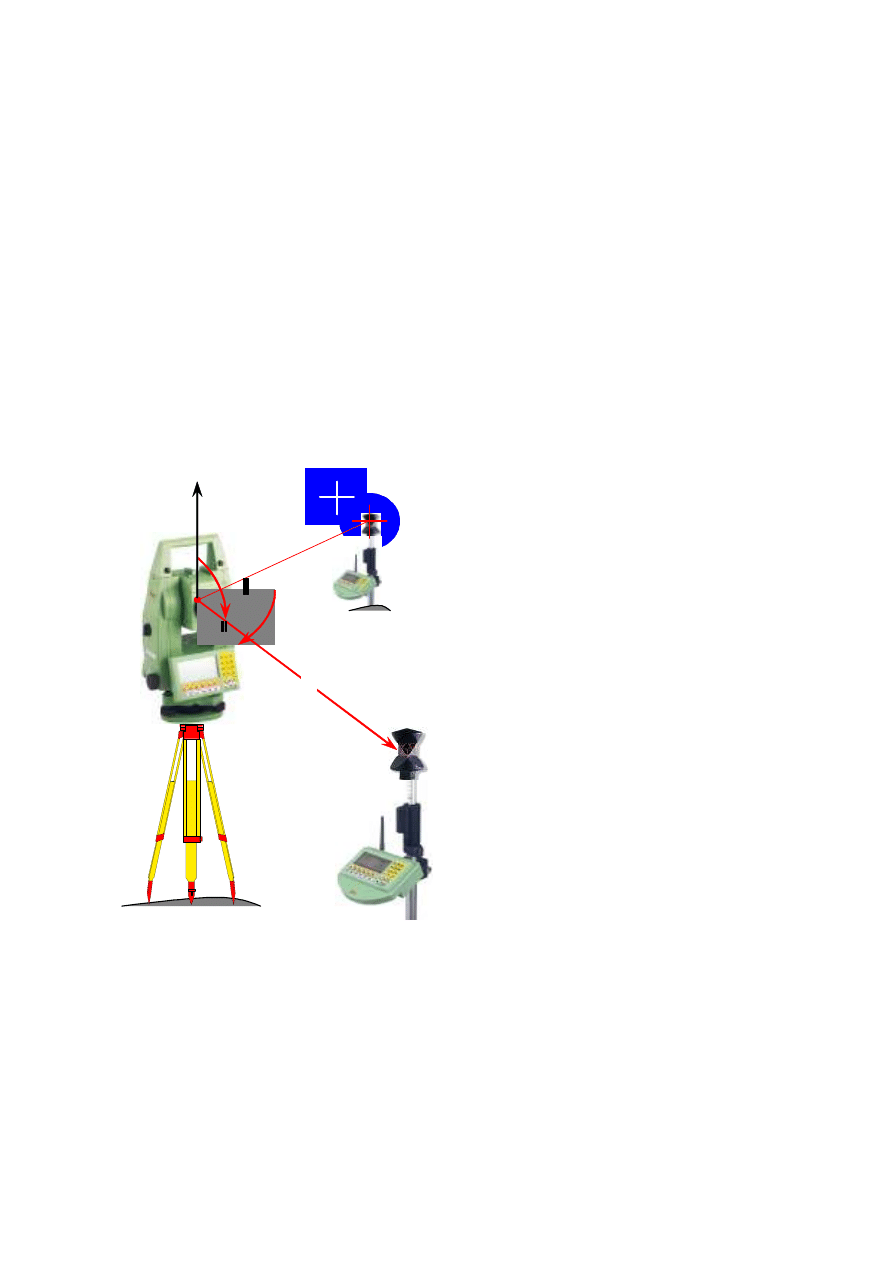
Pomiary sytuacyjno-wysokościowe

Pomiar sytuacyjno-wysokościowy x, y, H punktów szczegółów terenowych jest realizowany za pomocą
tachimetru (rozdz. 6.1, 6.4) lub odbiornika satelitarnego GPS. Wcięcia sytuacyjne punktów x, y są również
wykonywane za pomocą teodolitu, dalmierza lub taśmy. System kodowania i edycji atrybutów szczegółów
terenowych umożliwia automatyczne tworzenie numerycznych map, modeli terenu oraz przekrojów tras i rzek w
czasie pomiaru za pomocą tachimetru lub odbiornika GPS. Programy pomiarowe tachimetru i odbiornika GPS są
wyposażone w funkcje obliczania pól, objętości i długości linii mierzonych obiektów, tyczenia punktów
budowli, skarp, tras, DTM, warstwic i linii podziałowych katastru jak również sterowania

pracą koparek podczas

prac ziemnych na budowach.

1. Tachimetry

1.1 Pomiar sytuacyjno-wysokościowy

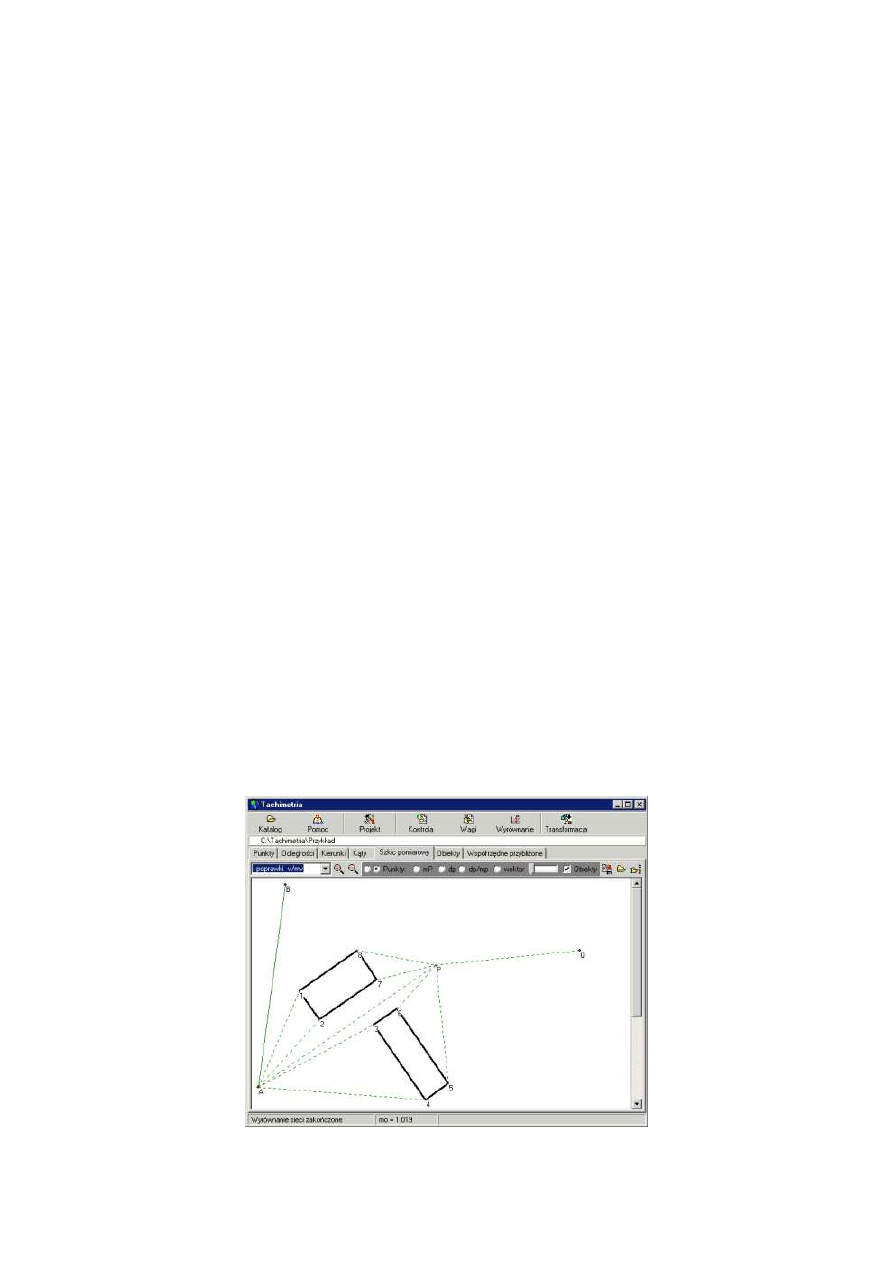
Tachimetr jest przeznaczony do wyznaczania położeń punktów na podstawie pomiaru kąta
poziomego

α, pionowego β i odległości s do stałego lub ruchomego pryzmatu (rys. 1.1).

Rys..1.1

Wyposażenie tachimetru:
a) sensor - do automatycznego
naprowadzenia lunety na stały
lub ruchomy pryzmat.
b) komputer z systemem DOS,
kartą pamięci PCMCIA,
ekranem graficznym i klawiaturą.
c) pryzmat i moduł radiowy
z ekranem graficznym
i klawiaturą do sterowania pracą

β

α

s

tachimetru z poziomu pryzmatu
d) programy pomiarowe:

- pomiar sytuacyjno-wysokościowy
(.............)
- pomiar czołówek (..........)
- pomiar niedostępnej wysokości
(...............0)
- wcięcie stanowiska tachimetru
(................)
- tworzenie mapy numerycznej
(................)
- transformacja współrzędnych
(...............)
- obliczanie pól, objętości i długości
linii (................)
- tyczenie projektu budowlanego
(....................)
- sterowanie pracą koparek

Błędy średnie pomiaru odległości i kątów są określone w charakterystyce tachimetru:

Leica TPS 1100

błąd średni pomiaru kąta poziomego i pionowego

mα,β = 1,5"

błąd średni pomiaru odległości

ms = 2 mm + 2 ppm, ppm=10

-6

s

zakres pomiaru odległości 5 km

czas pomiaru 1s

graficzny wyświetlacz: 8 linii po 32 znaki

klawisze funkcyjne i alfanumeryczne

wejście / wyjście: PCMCIA 2-84 MB, RS 232

waga 4.7 kg.

Program pomiar sytuacyjno-wysokościowy jest przeznaczony do pomiaru współrzędnych
poziomych x, y i wysokości punktów H szczegółów terenowych takich jak budynki, granice
działek ewidencyjnych, drogi, mosty, rzeki, linie energetryczne itp.
Pomiar rozpoczyna się zwykle po ustawieniu tachimetru na punkcie osnowy geodezyjnej
o znanych współrzędnych i wysokości A (rys. 1.2). Po nawiązaniu kierunkowym na
najbliższe punkty osnowy (np. B na rys. 1.2) wykonuje się pomiar kierunków i odległości
do punktów szczegółów terenowych 1, 2, 3, 4 oraz do wybranego punktu dla następnego
stanowiska tachimetru, utrwalonego palikiem lub bolcem metalowym P. Dla kontroli kierunki
i odległości - szczególnie do punktów osnowy oraz punktów będących stanowiskami
tachimetru, są mierzone dwukrotnie.

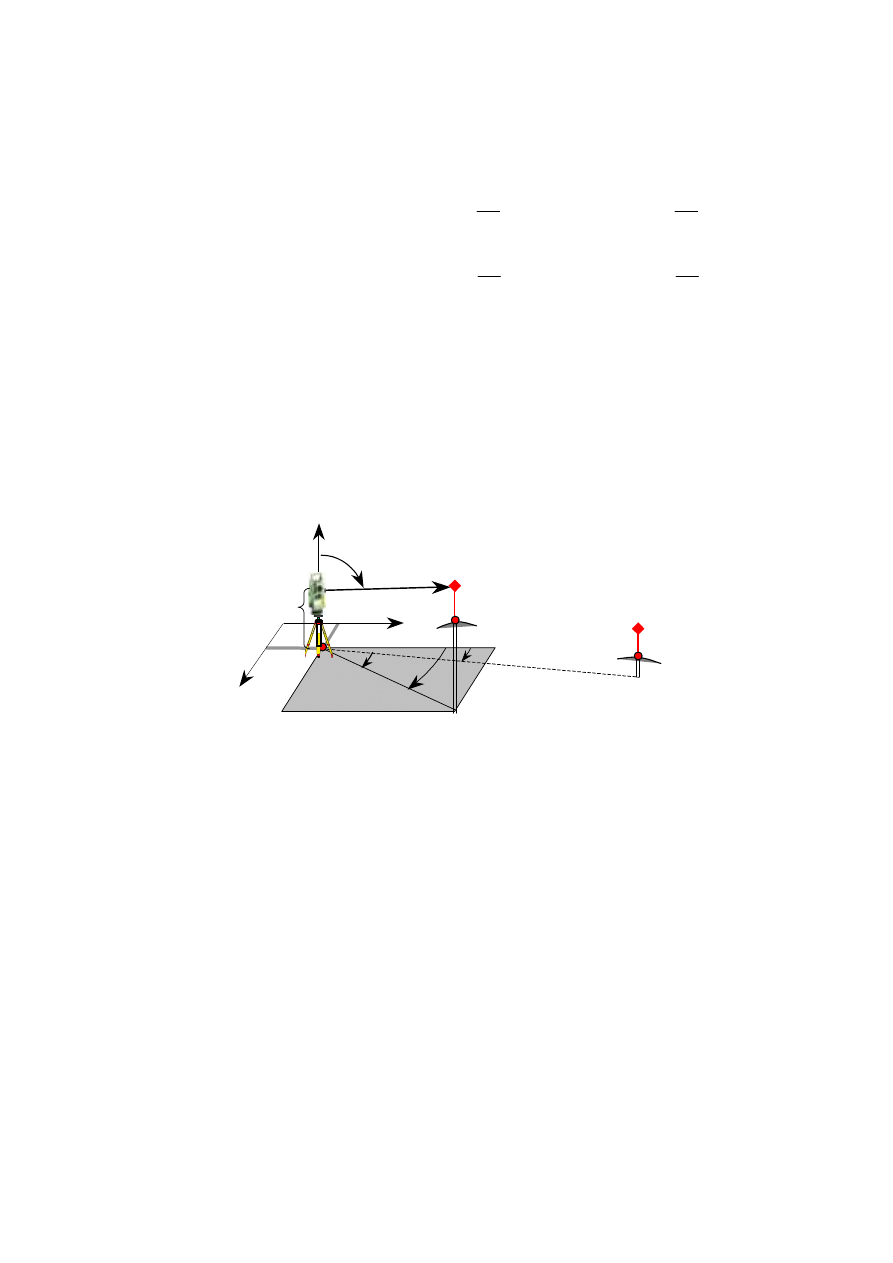
Rys. 1.2

Współrzędne poziome i wysokości mierzonych punktów, np. P, są obliczane na podstawie:

• odległości przestrzennej

s

100.5

:=

m

s

0.005

:=

• kąta pionowego

β

75

π

200

⋅

:=

m

β

0.0010

π

200

⋅

:=

• kąta poziomego

α

65

π

200

⋅

:=

m

α

0.0010

π

200

⋅

:=

• wysokości tachimetru

i

1.56

:=

m

i

0.005

:=

• wysokości pryzmatu

j

2.0

:=

m

j

0.005

:=

•

oraz wspólrzędnych i wysokości stanowiska A i punktu nawiązania B (rys. 1.2, 1.3):

układ 2000

X, Y,

kronsztad 86

H

z

s

j

β

α

A

y

P

B

A =A

0

+

α

∆x

∆y

∆z

x

i

A

0

x

A

y

A

- azymut kierunku nawiązania A-B [grad]

- odległość pozioma A-P

Dodając przyrosty współrzędnych

∆x, ∆y i przewyższenie trygonometryczne ∆z:

.........

do współrzędnych i wysokości stanowiska tachimetru A otrzymuje się współrzędne
i wysokość punktu P - odniesione do płaszczyzny poziomej i kierunku pionu na stanowisku
tachimetru A:

..............................

Po przeniesieniu tachimetru na stanowisko P i nawiązaniu kierunkowym na poprzednie
stanowisko A wykonywane są obserwacje kolejnych punktów mierzonych budynków 5, 6, 7,
8 oraz punktu następnego stanowiska tachimetru Q, utrwalonego palikiem lub bolcem. Dla
kontroli pomiary są wykonywane dwukrotnie. Ciąg tachimetryczny jest kontynuowany do
najbliższego punktu osnowy geodezyjnej - w rozpatrywanym przykładzie ciąg zawiera dwa
stanowiska pomiarowe szczegółów terenowych A i P, punkt Q jest punktem osnowy. Zwykle,
na punkcie osnowy (Q), w nawiązaniu kierunkowym do sąsiedniego punktu osnowy, jest
mierzony kierunek i odległość do poprzedniego stanowiska tachimetru (P).
W przypadku pomiaru za pomocą teodolitu wielkości s, j nie są mierzone, natomiast:
celowanie następuje bezpośrednio na znak naziemny mierzonego punktu, sygnalizowanego
tyczką mierniczą (j = 0),
obliczenie kątów poziomego

α i pionowego β jest prowadzone w dziennikach pomiaru kątów

(tabele 1.1 i 1.2),

odległość pozioma d jest mierzona dalmierzem nakładanym na lunetę teodolitu (celowanie
następuje na reflektor dalmierza) lub dalmierzem podręcznym np. DISTO, w ostateczności
taśmą mierniczą.

Tabela 1.1. Dziennik pomiaru kątów poziomych

POŁOŻENIE LUNETY

I

II

Kąt z I / II

położenia

Kąt poziomy

Stano

wisko

Cel

g c cc

Średnia

g c cc

Średnia

g c cc g c cc

B

115

40
41

50
50

41

00 315

42
43

00
00

42

50

A

P

145

87
87

50
00

87

25 345

87
88

50
00

87

75

30

46
45

25
25

30

45

75

Kierunki poziome pomierzone są w dwóch położeniach

lunety, wykonując po dwa naprowadzenia lunety na cel.

Tabela 1.2. Dziennik pomiaru kątów pionowych

POŁOŻENIE LUNETY

I - KL

II - KP

Błąd indeksu

2

400

−

+ KP

KL

Kąt pionowy

Stano

wisko

Cel

g c cc

Średnia

g c cc

Średnia

c cc

g c cc

A

P

101

40
40

00
00

40

00 298

58
58

00
00

58

00

-01

00

102

10

63

Kąty pionowe mierzone są w dwóch położeniach lunety:
I - koło pionowe teodolitu znajduje się po lewej stronie lunety
(KL), II - koło pionowe po prawej stronie lunety (KP);
wykonując po dwa naprowadzenia lunety na cel.

1.2. Poprawki wysokości

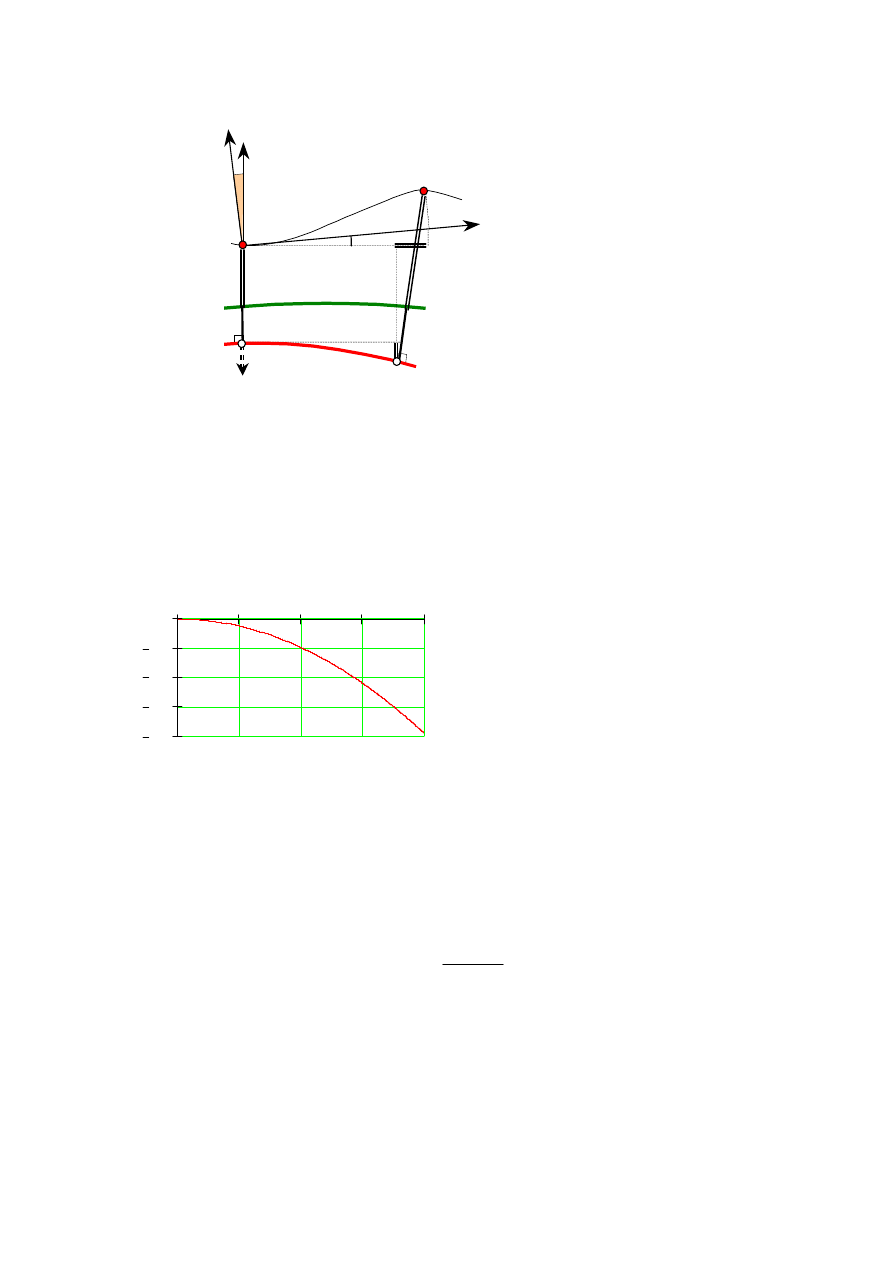
Dokładną wartość wysokości niwelacyjnej otrzymuje się dodając poprawki ze względu na
(rys. 1.4):

krzywiznę Ziemi - w przybliżeniu kuli o promieniu równym średniemu promieniowi elipsoidy

R

6383287

:=

- na szerokości 52

° (rys. 1.5):

nierównoległość geoidy i elipsoidy

∆N = NP - NA gdzie wysokości geoidy są obliczone przy

pomocy programu geoida niwelacyjna (rozdz. 2.5) na podstawie współrzędnych
geodezyjnych B, L (rys. 1.6) otrzymanych w wyniku przekształcenia x

2000

y

2000

→

→

→

→

B L

(..............):
odchylenie pionu - w azymucie mierzonego kierunku (...........):

Rys. 1.6

d

P

d - ∆d

H

A

N

A

R

∆z

A

δR

∆d δH

v

H

P

=H

A

+∆H

=H

A

+∆z+δR-∆N+δH

N

P

=N

A

+∆N

z

g

- prostopadła do elipsoidy

z

- oś obrotu tachimetru

v

A

- odchylenie pionu

w kierunku A-P

v

Geoida

Teren

Elipsoida

Rys. 1.4

0

250

500

750

1000

0.08

0.06

0.04

0.02

d [m]

P

o

p

raw

ka

[m

]

Elipsoida

Rys. .1.5

1.3. Poprawki współrzędnych

Dokładne wartości współrzędnych otrzymuje się obliczając przyrosty ∆x, ∆y na podstawie
zredukowanych odległości d i kąta α na płaszczyznę układu 2000:
redukcja odległości na elipsoidę (rys. 1.4):

d

h

d

H

P

N

P

+
R

⋅

:=

redukcja odległości z elipsoidy na płaszczyznę układu 2000 w strefie

c

6

:=

(.................):
redukcja kąta na elipsoidę

- redukcja kąta ze względu na odchylenie pionu v (. Redukcja kąta ze względu na wzniesienie celu jest zaniedbywalna na
terenach nizinnych -.

redukcja kąta z elipsoidy na płaszczyznę układu 2000 (..............):
Zatem, na podstawie zredukowanych odległości d i kąta α na płaszczyznę układu 2000:

są obliczane przyrosty

oraz współrzędne mierzonego punktu P:

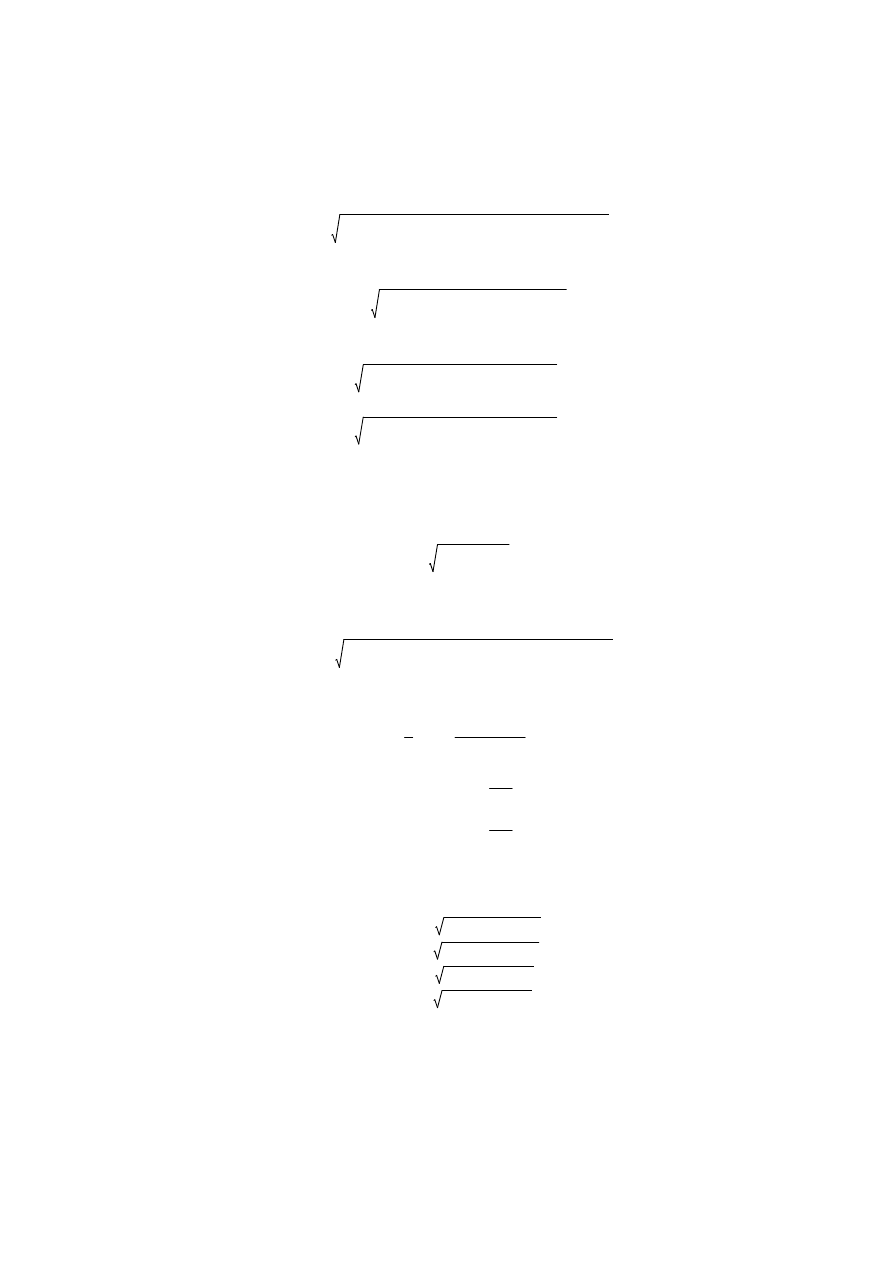
1.4. Błąd położenia punktu

Charakterystykami dokładności położenia pomierzonego punktu są:

• błąd wysokości H

m

H

cos

β

( )

2

m

s

2

⋅

s

2

sin

β

( )

2

⋅

m

β

2

⋅

+

m

i

2

+

m

j

2

+

:=

• błąd odległości poziomej d

m

d

sin

β

( )

2

m

s

2

⋅

s

2

cos

β

( )

2

⋅

m

β

2

⋅

+

:=

• błędy współrzędnych x, y:

m

x

cos A

( )

2

m

d

2

⋅

d

2

sin A

( )

2

⋅

m

α

2

⋅

+

10

3

⋅

:=

m

y

sin A

( )

2

m

d

2

⋅

d

2

cos A

( )

2

⋅

m

α

2

⋅

+

10

3

⋅

:=

m

xy

sin A

( ) cos A

( )

⋅

m

d

2

d

2

m

α

2

⋅

−

(

)

⋅

10

6

⋅

:=

• błąd położenia punktu m

P

, rys. 1.7:

m

P

m

x

2

m

y

2

+

:=

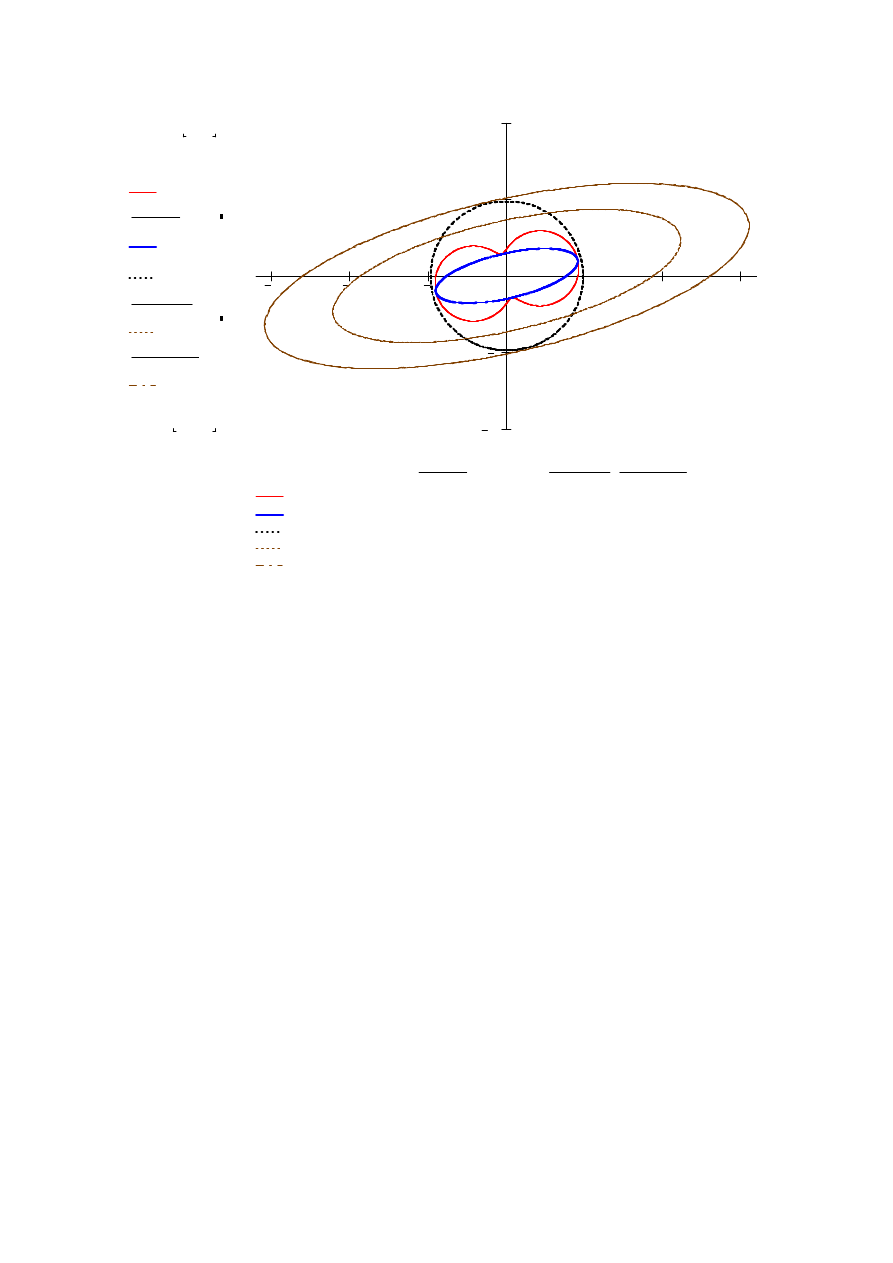
• błąd położenia punktu w zadanym kierunku α - krzywa błędu położenia punktu

(...........), rys. 1.7:

m

α

( )

m

x

2

cos

α

( )

2

⋅

m

xy

sin 2

α

⋅

( )

⋅

+

m

y

2

sin

α

( )

2

⋅

+

:=

• elipsa błędu położenia punktu o półosiach A, B i ich azymutach α

A

, α

B

, rys. 1.7:

α

A

1

2

atan

2 m

xy

⋅

m

x

2

m

y

2

−









⋅

:=

α

A

α

A

100

π

200

⋅

+

:=

α

B

α

A

100

π

200

⋅

+

:=

• elipsy na zadanych poziomach ufności ( ), rys. 1.7:

A

0.997

A

qchisq 0.997 2

,

(

)

⋅

:=

B

0.997

B

qchisq 0.997 2

,

(

)

⋅

:=

A

0.95

A

qchisq 0.95 2

,

(

)

⋅

:=

B

0.95

B

qchisq 0.95 2

,

(

)

⋅

:=

15

10

5

0

5

10

15

10

5

5

10

krzywa m(alfa)
elipsa A, B 39%
mP
elipsa 95%
elipsa 99.7%

6.055

6.055

−

m α

( )

cos α

( )

⋅

cos α

( )

m

el

α

( )

m

P

cos α

( )

⋅

cos α

( )

m

0.95

α

( )

cos α

( )

m

0.997

α

( )

16

16

−

m α

( )

sin α

( )

⋅

sin α

( )

m

el

α

( )

,

m

P

sin α

( )

⋅

,

sin α

( )

m

0.95

α

( )

,

sin α

( )

m

0.997

α

( )

,

.

Rys. 6.1.7