1
Imię i nazwisko
Data
…………………………………………..
……………………………….
Grupa
Podpis prowadzącego
………………………………………….
……………………………….
SPRAWOZDANIE
LABORATORIUM POFA/POFAT - ĆWICZENIE NR 1
Zadanie nr 1
(plik „strip.pro” ,nazwa ośrodka wypełniającego prowadnicę - "airlossy")
Rozważamy przypadek prowadnicy fali TEM, wypełnionej bezstratnym dielektrykiem o różnych
wartościach przenikalności elektrycznej
ε
r
i magnetycznej
µ
r
, w której rozchodzi się fala bieżąca.
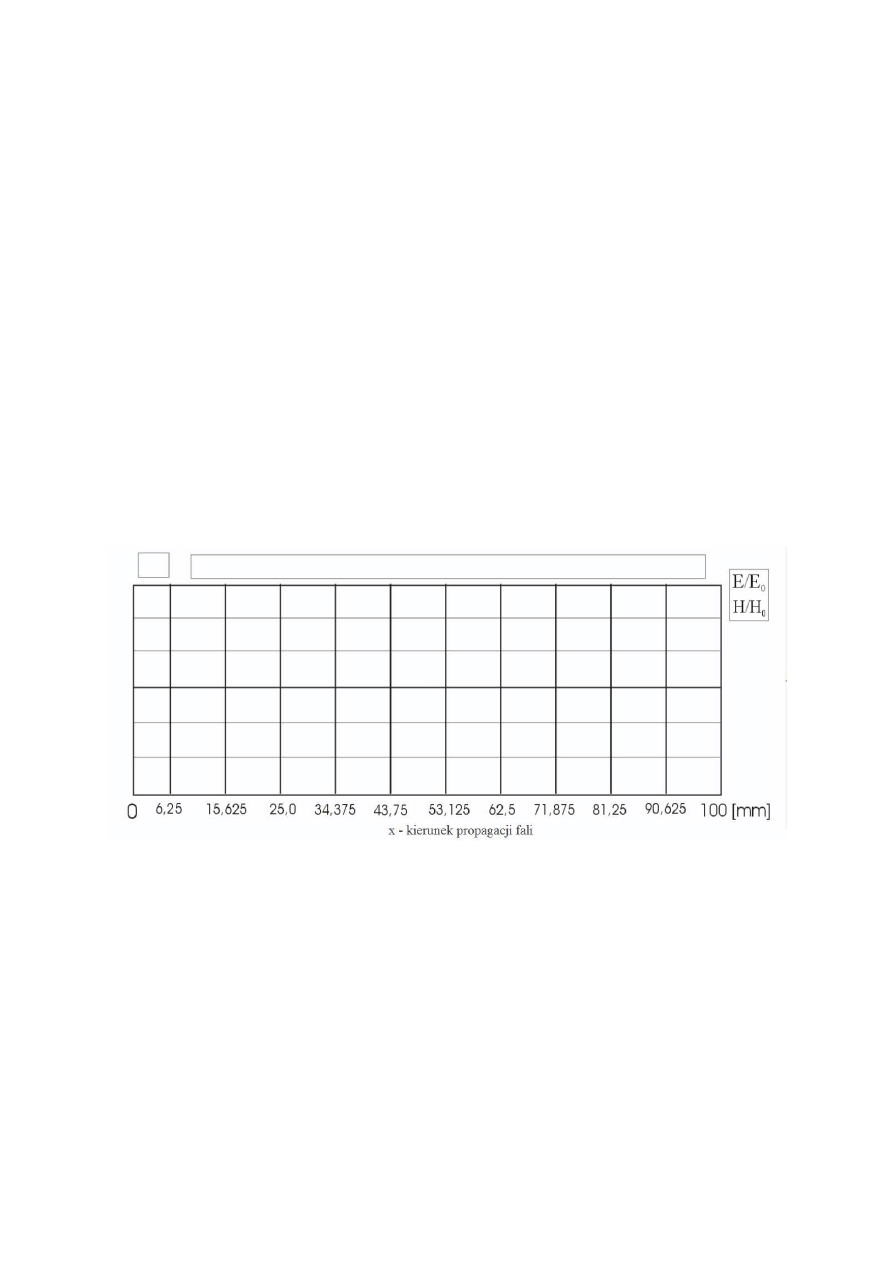
Narysować obwiednie oraz przykładowe rozkłady pól E(x)/E
0
i H(x)/H
0
dla jednego z
poniższych przypadków, wskazanego przez prowadzącego ćwiczenie ( pole E - kolor czerwony,
pole H - kolor niebieski):
a) f = 4 GHz
ε
r
= 1
µ
r
= 1
b) f = 8 GHz
ε
r
= 1
µ
r
= 1
c) f = 4 GHz
ε
r
= 4
µ
r
= 1
d) f = 4 GHz
ε
r
= 1
µ
r
= 4
Wyznaczyć wszystkie niżej podane parametry procesu falowego:
a)
α
=
λ
= Z = E/H = WFS =
β
=
b)
α
=
λ
= Z = E/H = WFS =
β
=
c)
α
=
λ
= Z = E/H = WFS =
β
=
d)
α
=
λ
= Z = E/H = WFS =
β
=
Uwaga!!! W trakcie wyznaczania wartości impedancji Z proszę zwrócić szczególną uwagę na
wartości amplitud pól E i H. Wartość WFS proszę wyznaczać w oparciu o kształt obwiedni
pola E oraz zależność WFS=E
max
/E
min
.
2
Wnioski:
Jak zmiana częstotliwości f fali TEM rozchodzącej się w ośrodku bezstratnym wpływa na
następujące parametry procesu falowego:
- długość fali λ -…………………………………………………………………………………
…………………………………………………………………………………………………
- współczynnik fazy β - ……………………………………………………………………….
…………………………………………………………………………………………………
- impedancję falową Z - ……………………………………………………………………….
…………………………………………………………………………………………………
Jak zmiana przenikalności elektrycznej ε
r
ośrodka bezstratnego wpływa na następujące
parametry procesu falowego:
- długość fali λ -…………………………………………………………………………………
…………………………………………………………………………………………………
- współczynnik fazy β - ……………………………………………………………………….
…………………………………………………………………………………………………
- impedancję falową Z - ……………………………………………………………………….
…………………………………………………………………………………………………
Jak zmiana przenikalności magnetycznej µ
r
ośrodka bezstratnego wpływa na następujące
parametry procesu falowego:
- długość fali λ -…………………………………………………………………………………
…………………………………………………………………………………………………
- współczynnik fazy β - ……………………………………………………………………….
…………………………………………………………………………………………………
- impedancję falową Z - ……………………………………………………………………….
…………………………………………………………………………………………………
Jaka funkcja matematyczna opisuje kształt obwiedni E(x)/E
0
gdzie x jest kierunkiem
propagacji fali?
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………...................................................................................................................................
Jakie wartości przyjmują składowe pola H
x
, H
z
, E
x
, E
y
i dlaczego?
…………………………………………………………………………………………………
…………………………………………………………………………………………………
………….....................................................................................................................................
………………………………………………………………………………………………....
3
Zadanie nr 2
(plik „stripm.pro” ,nazwa ośrodka wypełniającego prowadnicę- "dielektryk")
Rozważamy przypadek prowadnicy fali TEM, zakończonej metalową płytą i wypełnionej
bezstratnym dielektrykiem o różnych wartościach przenikalności elektrycznej
ε
r
i
magnetycznej
µ
r
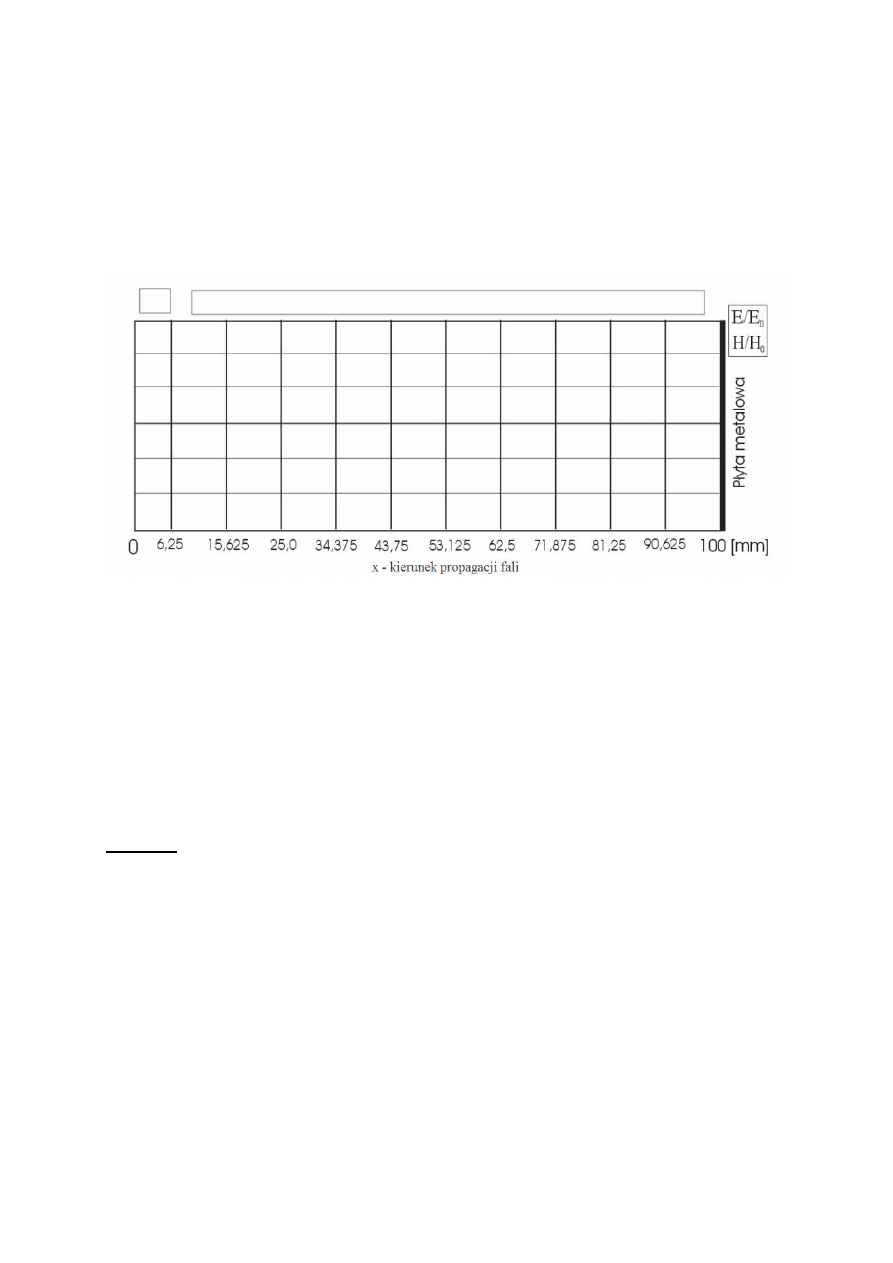
, w której generuje się fala stojąca. Narysować obwiednie pól E(x)/E
0
oraz
H(x)/H
0
dla jednego z poniższych przypadków, wskazanego przez prowadzącego ćwiczenie
(pole E - kolor czerwony, pole H - kolor niebieski).
a) f = 5 GHz
ε
r
= 1
µ
r
= 1
b) f = 10 GHz
ε
r
= 1
µ
r
= 1
c) f = 5 GHz
ε
r
= 4
µ
r
= 1
d) f = 5 GHz
ε
r
= 1
µ
r
= 4
Wyznaczyć wszystkie niżej wymienione parametry procesu falowego:
a)
α
=
λ
= Z = E/H = WFS =
β
=
b)
α
=
λ
= Z = E/H = WFS =
β
=
c)
α
=
λ
= Z = E/H = WFS =
β
=
d)
α
=
λ
= Z = E/H = WFS =
β
=
Uwaga!!! Proszę wyznaczać wartość impedancji falowej w miejscu, w którym wstawiona
została metalowa płyta. Wartość WFS proszę wyznaczać w oparciu o kształt obwiedni pola E
oraz zależność WFS=E
max
/E
min
.
Wnioski:
Jak zmiana częstotliwości f fali TEM rozchodzącej się w prowadnicy zakończonej metalową
płytą i wypełnionej materiałem bezstratnym wpływa na następujące parametry procesu
falowego:
- długość fali λ -…………………………………………………………………………………
…………………………………………………………………………………………………
Jaka funkcja matematyczna opisuje kształt obwiedni E(x)/E
0
gdzie x jest kierunkiem
propagacji?
…………………………………………………………………………………………………
Jaka jest odległość między węzłem a strzałką obwiedni?
…………………………………………………………………………………………………
4
Jaka jest wartość współczynnika odbicia
Γ
na granicy z płytą metalową?
…………………………………………………………………………………………………
Jakie wartości przyjmują całkowite pola E i H na granicy z płytą metalową w odniesieniu do
amplitud E
0
i H
0
?
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………....................................................................................................................................
Jaki jest sens fizyczny współczynnika fali stojącej WFS?
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………....................................................................................................................................
Zadanie nr 3
(plik „strip”, nazwa ośrodka wypełniającego prowadnice - "airlossy")
W dwóch prowadnicach fali TEM wypełnionych dielektrykiem stratnym o określonych
wartościach przenikalności elektrycznej
ε
r
i magnetycznej
µ
r
jest tłumiona fala płaska.
Wyznaczyć przewodność elektryczną
σ
tak, aby w jednej prowadnicy uzyskać:
a) f =1 GHz
ε
r
=4
µ
r
=1 tg
δ
=1
σ
= …
b) f =1 GHz
ε
r
=4
µ
r
=1 tg
δ
=0.1
σ
= …
Oszacować w trakcie symulacji wartość współczynnika tłumienia
α
w obu ośrodkach
korzystając z zależności:
)
(
)
(
)
(
ln
1
2
2
1
x
x
x
E
x
E
−
=
α
Porównać z pracą domową i skomentować.
a)
α
=
b)
α
=
......................................................................................................................................................
......................................................................................................................................................
.......................................................................................................................................................
5
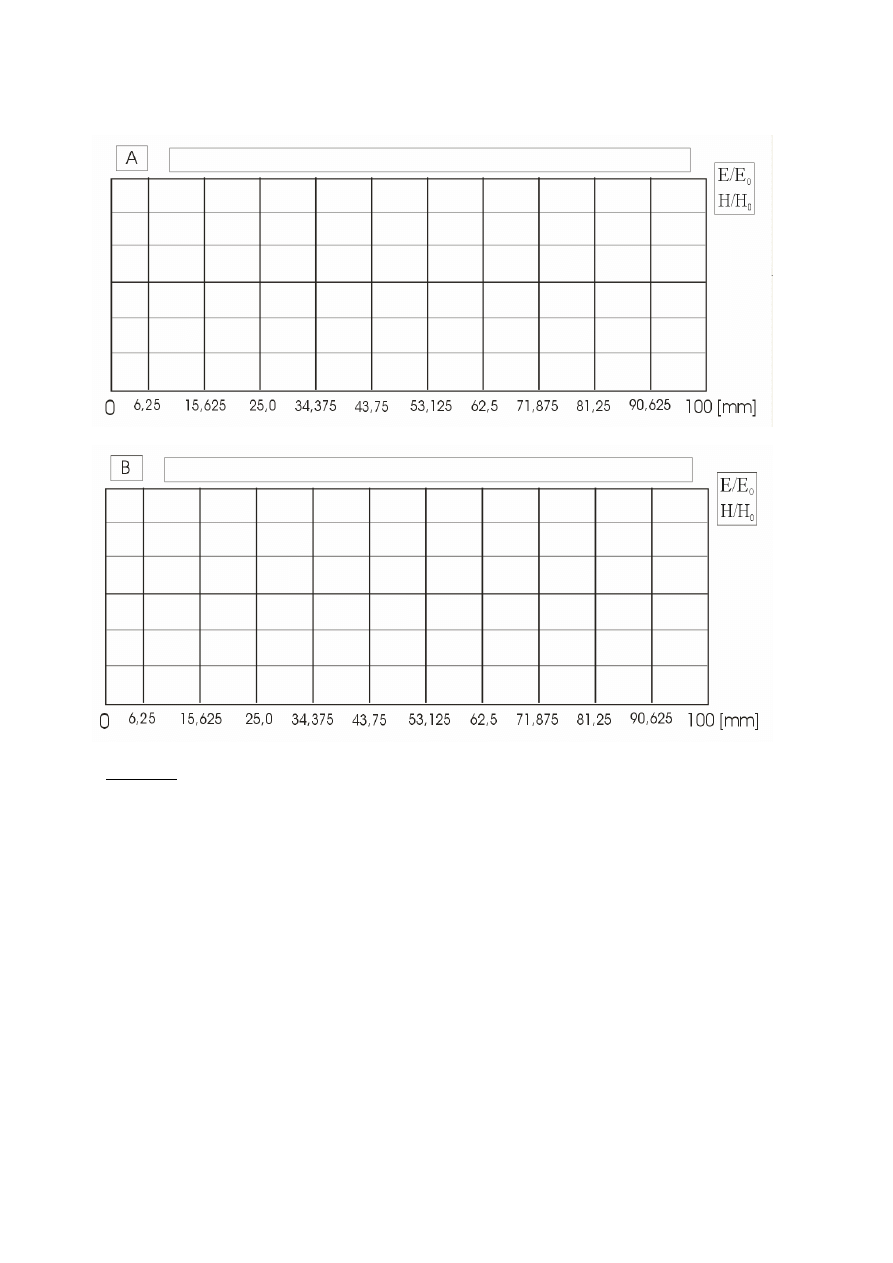
Narysować obwiednie pól E i H korzystając z poniższych wykresów (pole E - kolor
czerwony, pole H - kolor niebieski):
Wnioski:
Jaka funkcja matematyczna opisuje kształt obwiedni E(x)/E
0
gdzie x jest kierunkiem
propagacji?
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
Jak zmienia się wzajemne położenie pól E i H w porównaniu z ośrodkami bezstratnymi i
dlaczego?
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
Jaki jest sens fizyczny kąta impedancji?
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
6
Zadanie nr 4
(pliki „stripdi1”, „stripdi2”, nazwa ośrodków wypełniających prowadnice -"air" oraz
"dielektryk2")
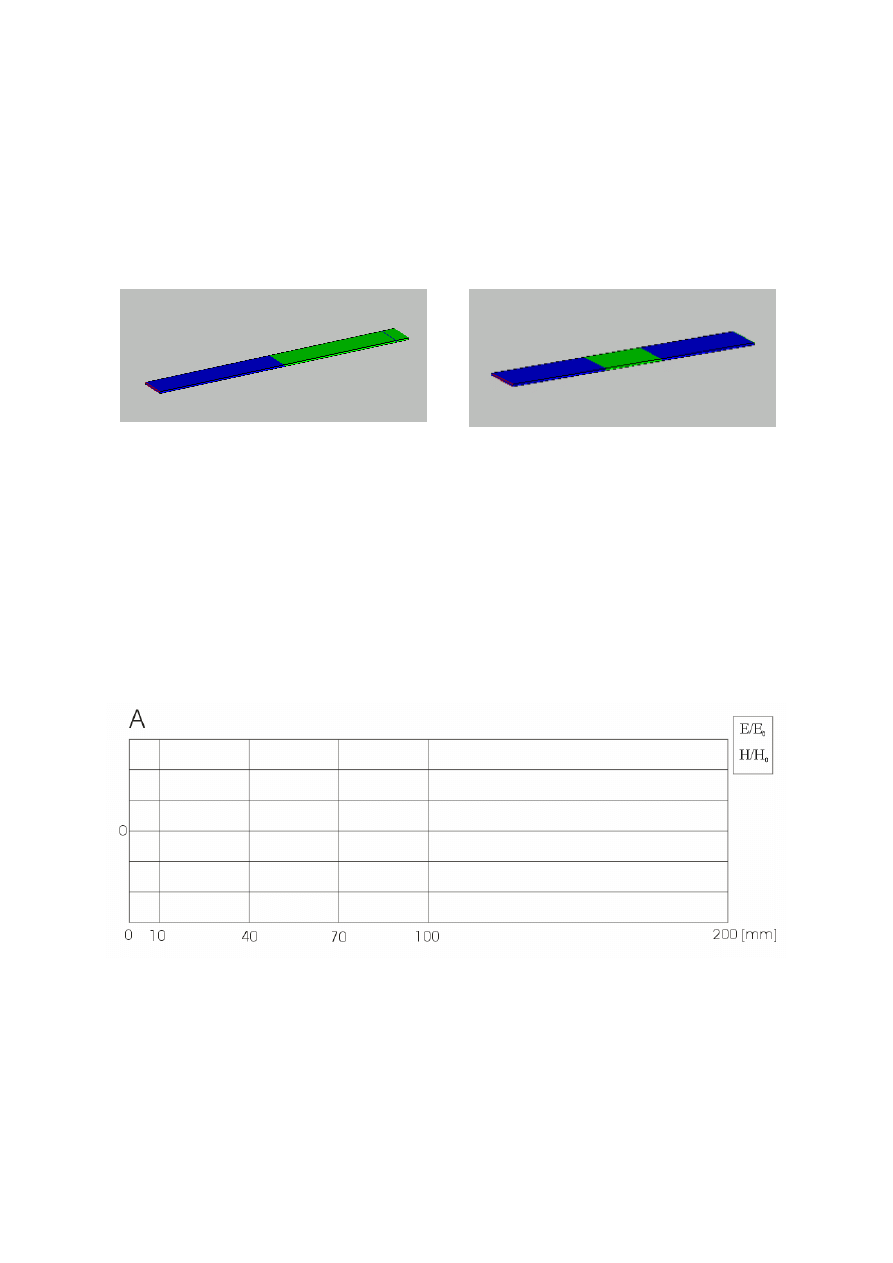
Rozważamy 2 przypadki:
a)
Padanie fali TEM (f=2.5 [GHz]) z powietrza, do bezstratnego (
σ
=0),
niemagnetycznego (
µ
r
=1) dielektryka o względnej przenikalności elektrycznej
ε
r
=4
(stripdi1.pro)
.
b)
Propagacja fali TEM (f=2.5 [GHz]) przez umieszczoną w powietrzu wkładkę
dielektryczną o długości d=30 mm i parametrach
ε
r
=4,
µ
r
=1,
σ
=0
(stripdi2.pro)
.
a)
b)
Rozmiary i własności ośrodków wypełniających prowadnice w modelu komputerowym:
a) powietrze 0-100 [mm] (
ε
r1
=1,
µ
r1
=1,
σ
1
=0), dielektryk 100-200 [mm] (
ε
r2
=4,
µ
r2
=1,
σ
2
=0)
b) powietrze 0-50 [mm] (
ε
r1
=1,
µ
r1
=1,
σ
1
=0), dielektryk 50-80 [mm] (
ε
r2
=4,
µ
r2
=1,
σ
2
=0),
powietrze 80-130 [mm] (
ε
r3
=1,
µ
r3
=1,
σ
3
=0)
Określić dla wszystkich przypadków:
a) f =2.5 GHz
WFS1 =
WFS2 =
b) f =2.5 GHz
WFS1 =
WFS2 =
WFS3=
Narysować obwiednie pól E i H na jednym rysunku, oddzielnie dla obydwu przypadków
(pole E - kolor czerwony, pole H - kolor niebieski):
7
Wnioski:
Jaki rodzaj fali obserwujemy w ośrodku pierwszym, a jaki w drugim w podpunkcie a) ?
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
Podać wzór i obliczyć długość fali TEM (f=2.5[GHz]) rozchodzącej się we wkładce
dielektrycznej z podpunktu b). Jaka jest grubość wkładki w stosunku do długości fali.
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
Jaką wartość ma współczynnik odbicia
Γ
na granicy ośrodków 1 i 2 z podpunktu b)?
Obliczenia przeprowadzić w oparciu o wyznaczoną wartość WFS.
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
Co to jest i do czego służy transformator półfalowy?
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
8
Zadanie nr 5
(pliki „layer1”, „layer2”, „layer3” nazwa ośrodków wypełniających prowadnice -"air" oraz
"dielektryk1" i "dielektryk2")
Rozważamy propagację fali TEM z powietrza do dielektryka ε
r3
=16, µ
r3
=1, σ
3
=0 przez
warstwę pośredniczącą o parametrach ε
r2
=4, µ
r2
=1, σ
2
=0.
Uruchomić symulacje dla następujących parametrów:
a) (layer1.pro) - d
2
=15mm f = 2.5 GHz
ε
1
= 1
ε
2
= 4
ε
3
= 16
b) (layer2.pro) - d
2
=15mm f = 5.0 GHz
ε
1
= 1
ε
2
= 4
ε
3
= 16
c) (layer3.pro) - d
2
=45mm f = 2.5 GHz
ε
1
= 1
ε
2
= 4
ε
3
= 16
Narysować obwiednie pól E i H na jednym rysunku oddzielnie dla wszystkich przypadków
(pole E - kolor czerwony, pole H - kolor niebieski):
9
Co to jest transformator ćwierćfalowy?
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
Jaki warunek na współczynnik odbicia
Γ
na granicy dwóch pierwszych ośrodków jest
spełniony dla transformatora ćwierćfalowego?
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
Przy jakiej liczbie ćwiartek fali odłożonych w ośrodku dopasowującym transformator
ćwierćfalowy działa poprawnie?
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………