Hubert

Skrzypulec

21.11.2008r.

ZiIP 3.2 Zabrze

POLITECHNIKA ŚLĄSKA W GLIWICACH

WYDZIAŁ ORGANIZACJI I ZARZĄDZANIA

Katedra Informatyki i Ekonometrii

BADANIA OPERACYJNE

Projekt nr 4

Metody programowania

dynamicznego

Strona 2 z 6

Treść zadania 

 

Przedsiębiorstwo  branży  spożywczej  „Frost”  jest  producentem  głęboko  mrożonych 

zestawów  obiadowych.  Chce  opracować  program  produkcji  na  najbliższe  3  miesiące  (od 

stycznia do marca). Wiadomo, że popyt na produkty tego przedsiębiorstwa jest stały i wynosi 

1200  szt.  zestawów  obiadowych.  Moce  wytwórcze  pozwalają  na  skierowanie  do  sprzedaży 

2000  sztuk  miesięcznie.  Koszt  produkcji  zależnie  od  ilości  wyprodukowanych  zestawów 

przedstawia tabela 1. 

 

Tabela 1

Ilość wyprodukowanych zestawów 

0

400

800

1200

1600 

2000

Koszt (zł)

0

2500

2900

3300

3700 

4100

 

 

Koszt  przechowywania  produktów  w  chłodni  wynosi  miesięcznie  150zł  od  400  sztuk. 

Chłodnia  jest  w  stanie  pomieścić  maksymalnie  1600  zestawów  obiadowych.  Obecnie  w 

magazynie znajduje się 800 sztuk. Na zakończenie planowanego okresu magazyn ma zostać 

pusty. Należy zminimalizować koszty. 

 

W trakcie rozwiązywania posługuję się ciągiem równań funkcyjnych Bellmana. 

 

Oznaczenia 

 

Dla  uporządkowania  procesu  rozwiązania  zagadnienia  dynamicznego  wprowadzam 

oznaczenia: 

x

1

 – ilość wyprodukowanych zestawów obiadowych w styczniu 

x

2

 – ilość wyprodukowanych zestawów obiadowych w lutym 

x

2

 – ilość wyprodukowanych zestawów obiadowych w marcu 

s

i

 – poziom zapasów na początku i‐tego miesiąca 

p – popyt 

Strona 3 z 6

k

i

(j) – koszty magazynowania j elementów (0 ≤ j ≤ 1600) w i‐tym miesiącu 

f

i

(x

i

,s

i

) – koszty produkcji i magazynowania w i‐tym miesiącu 

f

i

(x

i

,s

i

) = k

i

(x

i

) + k

i

(s

i+1

) 

łączne koszty produkcji i magazynowania z każdego miesiąca wynoszą: 

f

1

(x

1

,s

1

) + f

2

(x

2

,s

2

) + f

3

(x

3

,s

3

) 

 

 

W  tym  miejscu  warto  zauważyć  pewną  zależność  pomiędzy  produkcją,  stanem 

magazynowym i popytem, z której będę korzystał na dalszych etapach rozwiązania: 

0 ≤ s

i 

+ x

i

 – p ≤ 1600 

Wiemy,  że  na  początku  roku,  gdy  rozpoczynamy  planowanie  znany  jest  stan 

magazynowy, oraz założenie mówiące o pustym magazynie na koniec okresu planowania. 

Stąd: 

s

1 

= 800 

s

4 

= 0 

 

 

 

 

Rozwiązanie 

 

Sztucznie dzielę proces produkcji na 3 etapy: 

Etap 1 – wyprodukowanie x

1 

zestawów w styczniu. 

Etap 2 – wyprodukowanie x

2

 zestawów w lutym. 

Etap 3 – wyprodukowanie x

3

 zestawów w marcu. 

 

 

 

 

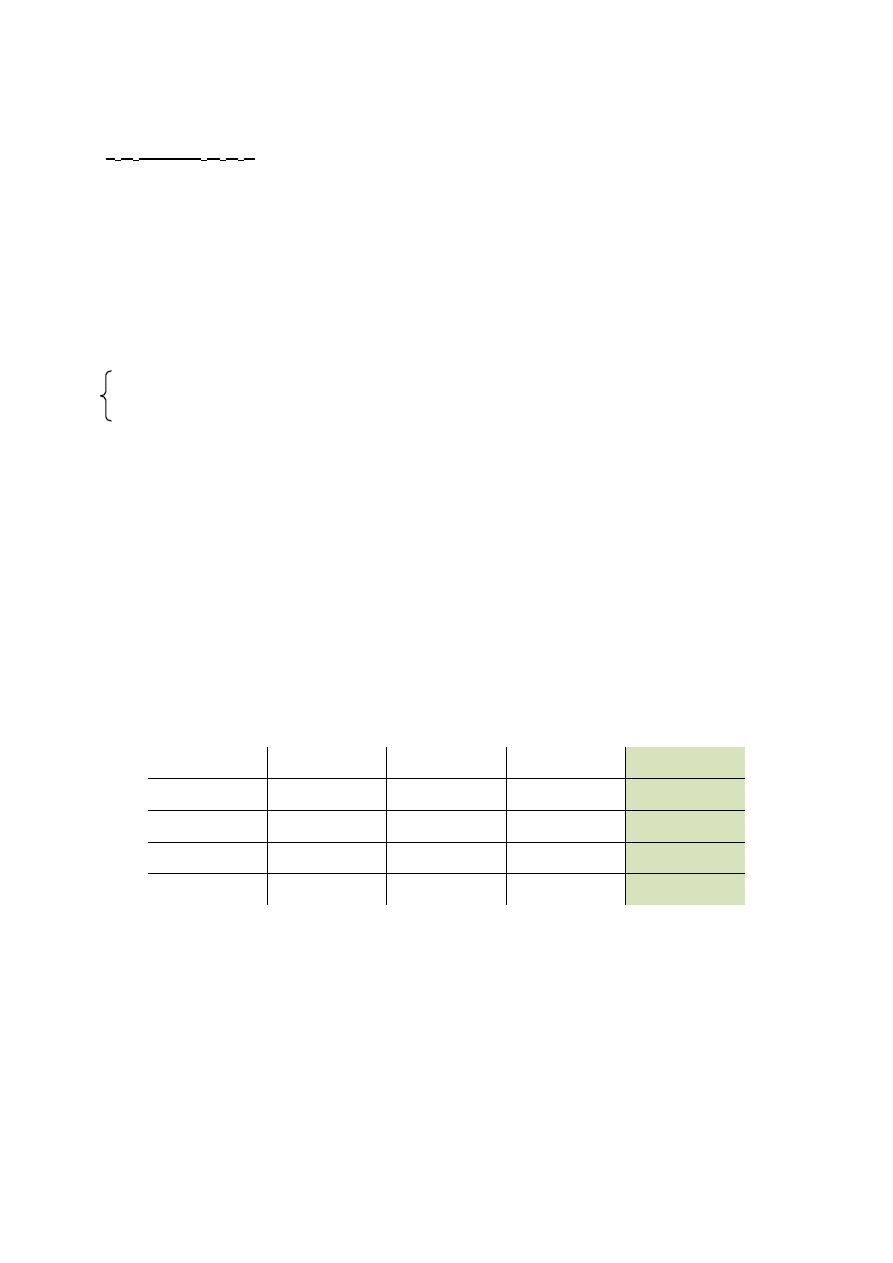
Strona 4 z 6

Krok 1 Etap 3 (Marzec) 

g

3

(s

3

) = min(f

3

(x

3

,s

3

)) 

funkcja  g

3

(s

3

)  mówi  nam  o  kosztach  ponoszonych  na  produkcje  i  magazynowanie. 

Założeniem zadania jest minimalizacja kosztów, stąd szukamy minimalnej wartości funkcji f

3

. 

Założenie  to  jest  obowiązujące  na  wszystkich  etapach  rozwiązywania  rozpatrywanego 

problemu dynamicznego. 

Wykorzystując zależność produkcji, stanów magazynowych i popytu otrzymuję: 

 

s

4 

= s

3 

+ x

3 

– p 

s

4

= 0 

s

3 

+ x

3 

– p = 0 

0 ≤ x

3

 = p ‐ s

3

 

0 ≤ s

3

 ≤ 1600 

0 ≤ s

3 

+ x

3

 – p ≤ 1600 

0 ≤ s

3 

+ x

3

 – 1200 ≤ 1600 

x

3

 ≤ 2800 ‐ s

3 

0 ≤ s

3

 ≤ 1600 

 

 

 

 

Wyznaczam minimalny koszt produkcji i utrzymania zapasów w marcu. 

Tabela 2

s

3

 

x

3

 

s

4

 

f

3

(x

3

,s

3

) 

g

3

(s

3

) 

0 

1200 

0 

3300+0 

3300 

400 

800 

0 

2900+0 

2900 

800 

400 

0 

2500+0 

2500 

1200 

0 

0 

0 

0 

 

 

 

 

 

 

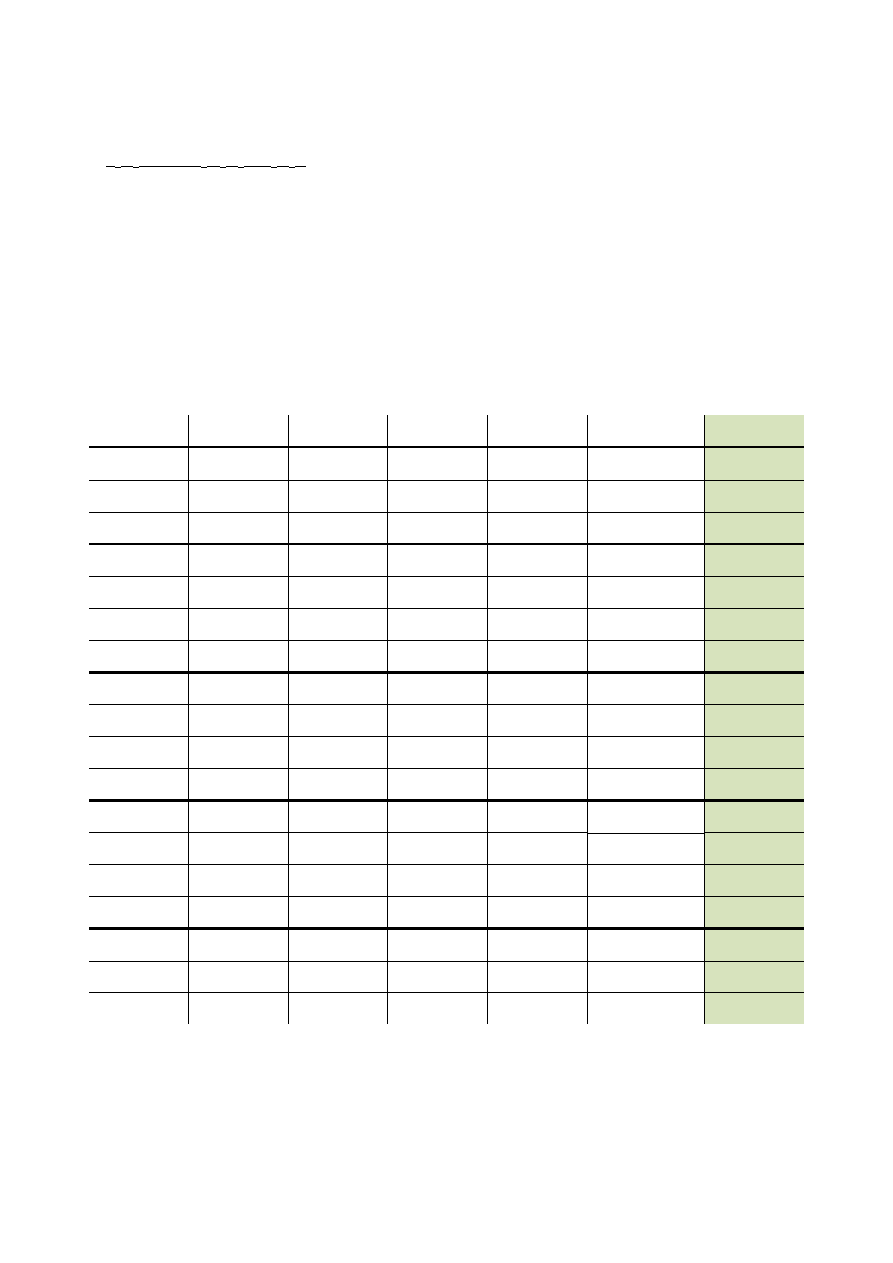
Strona 5 z 6

Krok 2 Etap 2 (Luty) 

g

2

(s

2

) = min(f

2

(x

2

,s

2

)+ g

3

(s

3

)) 

 

Wykorzystując zależność produkcji, stanów magazynowych i popytu otrzymuję: 

1200 ‐ s

2 

≤ x

2

 ≤ 2800 ‐ s

2 

0 ≤ s

2

 ≤ 1600 

0 ≤ s

2 

+ x

2

 – p ≤ 1600 

0 ≤ s

2 

+ x

2

 – 1200 ≤ 1600 

1200 ‐ s

2 

≤ x

2

 ≤ 2800 ‐ s

2

 

 

Tabela 3

s

2

 

x

2

 

s

3

 

f

2

(x

2

,s

2

) 

g

3

(s

3

) 

f

2

(x

2

,s

2

)+ g

3

(s

3

) 

g

2

(s

2

) 

0 

1200 

0 

3300 + 0 

3300 

6600 

6600 

0 

1600 

400 

3700 + 150 

2900 

6750 

 

0 

2000 

800 

4100 + 300 

2500 

6900 

 

400 

800 

0 

2900 + 0 

3300 

6200 

 

400 

1200 

400 

3300 + 150 

2900 

6350 

 

400 

1600 

800 

3700 + 300 

2500 

6500 

 

400 

2000 

1200 

4100 + 450 

0 

4450 

4450 

800 

400 

0 

2500 + 0 

3300 

5800 

 

800 

800 

400 

2900 + 150 

2900 

5950 

 

800 

1200 

800 

3300 + 300 

2500 

6100 

 

800 

1600 

1200 

3700 + 450 

0 

4150 

4150 

1200 

0 

0 

0 + 0 

3300 

3300 

3300 

1200 

400 

400 

2500 + 150 

2900 

5500 

 

1200 

800 

800 

2900 + 300 

2500 

5700 

 

1200 

1200 

1200 

3300 + 450 

0 

3750 

 

1600 

0 

400 

0 + 150 

2900 

3050 

3050 

1600 

400 

800 

2500 + 300 

2500 

5300 

 

1600 

800 

1200 

2900 + 450 

0 

3350 

 

 

 

 

Strona 6 z 6

Krok 3 Etap 1 (styczeń) 

g

1

(s

1

) = min(f

1

(x

1

,s

1

)+ g

2

(s

2

)) 

 

400 

 

≤ x

1

 ≤ 2000

 

s

1

 = 2 

0 ≤ s

1 

+ x

1

 – p ≤ 1600 

0 ≤ s

1 

+ x

1

 – 1200 ≤ 1600 

0 

 

≤ 2 + x

1

 – 1200 ≤ 1600 

 

Tabela 4

s

1

 

x

1

 

s

2

 

f

1

(x

1

,s

1

) 

g

2

(s

2

) 

f

1

(x

1

,s

1

) + g

2

(s

2

) 

g

1

(s

1

) 

2 

400 

0 

2500 + 0 

6600 

9100 

 

2 

800 

400 

2900 + 150 

4450 

7500 

 

2 

1200 

800 

3300 + 300 

4150 

7750 

 

2 

1600 

1200 

3700 + 450 

3300 

7450 

7450 

2 

2000 

1600 

4100 + 600 

3050 

7750 

 

 

 

 

 

 

Odpowiedź i interpretacja wyników. 

 

x

1 

= 1600 

x

2 

= 0 

x

3 

= 1200 

s

2 

= 1200 

s

3 

= 0 

 

Najniższy  koszt  wytwarzania  uzyskamy  produkując  w  styczniu  1600  sztuk  zestawów 

obiadowych.  W  tej  sytuacji  stan  magazynowy  na  początku  lutego  wyniesie  1200  sztuk.  W 

lutym najlepszym rozwiązaniem jest wstrzymanie produkcji na miesiąc. Dzięki temu magazyn 

na początku marca będzie pusty. W marcu, jako że mamy pusty magazyn, a popyt jest stały 

produkujemy  właśnie  tyle  ile  wynosi  wartość  popytu,  czyli  1200  sztuk.  Dzięki  temu 

osiągniemy najniższy z możliwych kosztów zorganizowania produkcji wynoszący 7450 zł