Von Bertalanffy Growth Function

Von Bertalanffy Growth Function (VBGF)

Updated technical summary based on

presentation

at the June 1995 AES meeting in Edmonton, Canada.

The von Bertalanffy growth function (VBGF) introduced by von Bertalanffy in 1938 predicts the

length of a shark as a function of its age, L = L(t): L(t) = Loo - (Loo - Lo) exp(-kt)

The VBGF has 3

parameters:

1. Lo (Lzero, y-axis
intercept) is the mean
length at birth (t = 0),

2. Loo (L infinity) is the
mean maximum length (t =
infinity),

3. k is a rate constant with
units of reciprocal time (e.
g. year-1).

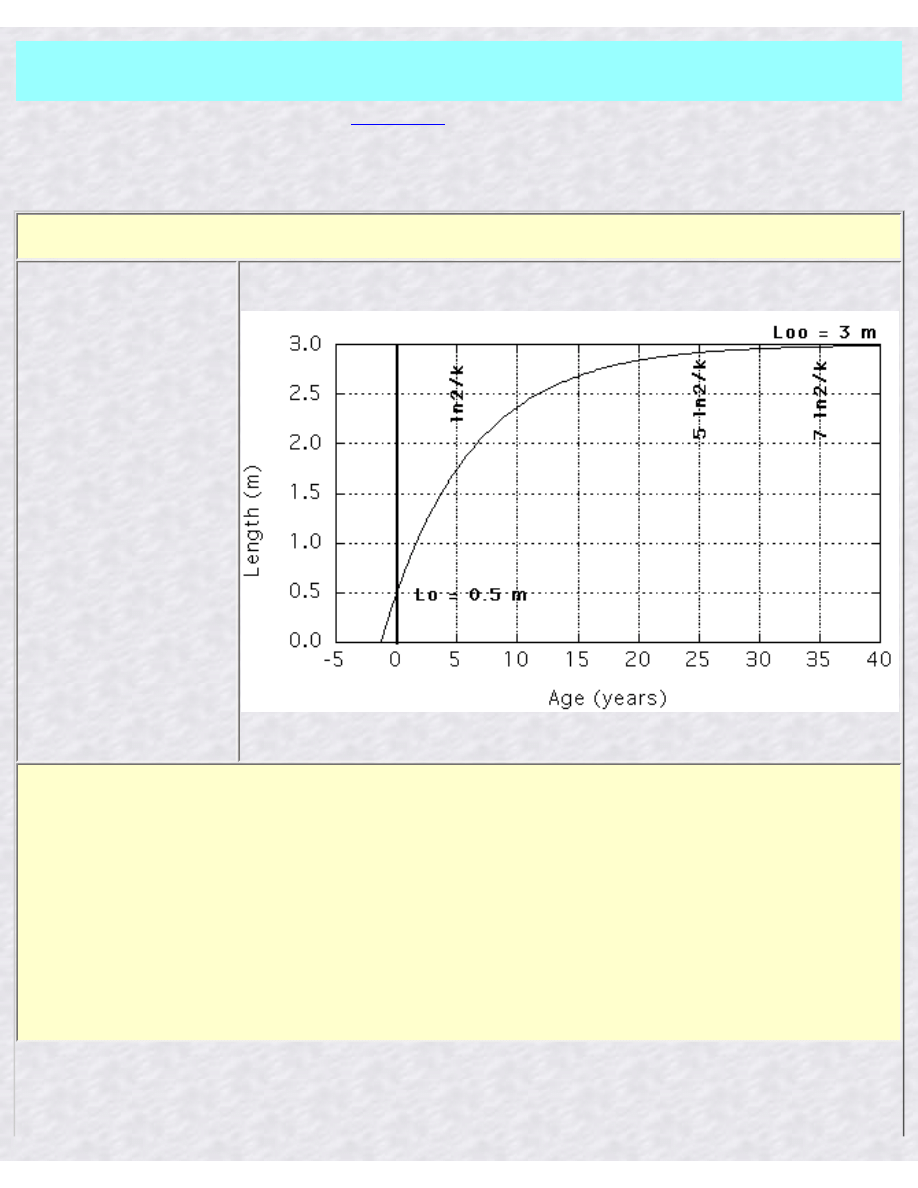
The graph on the left used
Lo = 0.5 m, Loo = 3 m,
k = 0.13863 year-1
(ln2/k = 5 years,
5 ln2/k = 25 years,
7 ln2/k = 35 years)

The difference between Loo and Lo diminishes ("decays") exponentially. Ln2/k is a half-life i.e. in

this time the shark will be halfway between Lo and Loo. 5ln2/k and 7ln2/k are good longevity

estimates. In this time the shark will have reached 95 and 99%, respectively, of the mean

maximum length Loo.

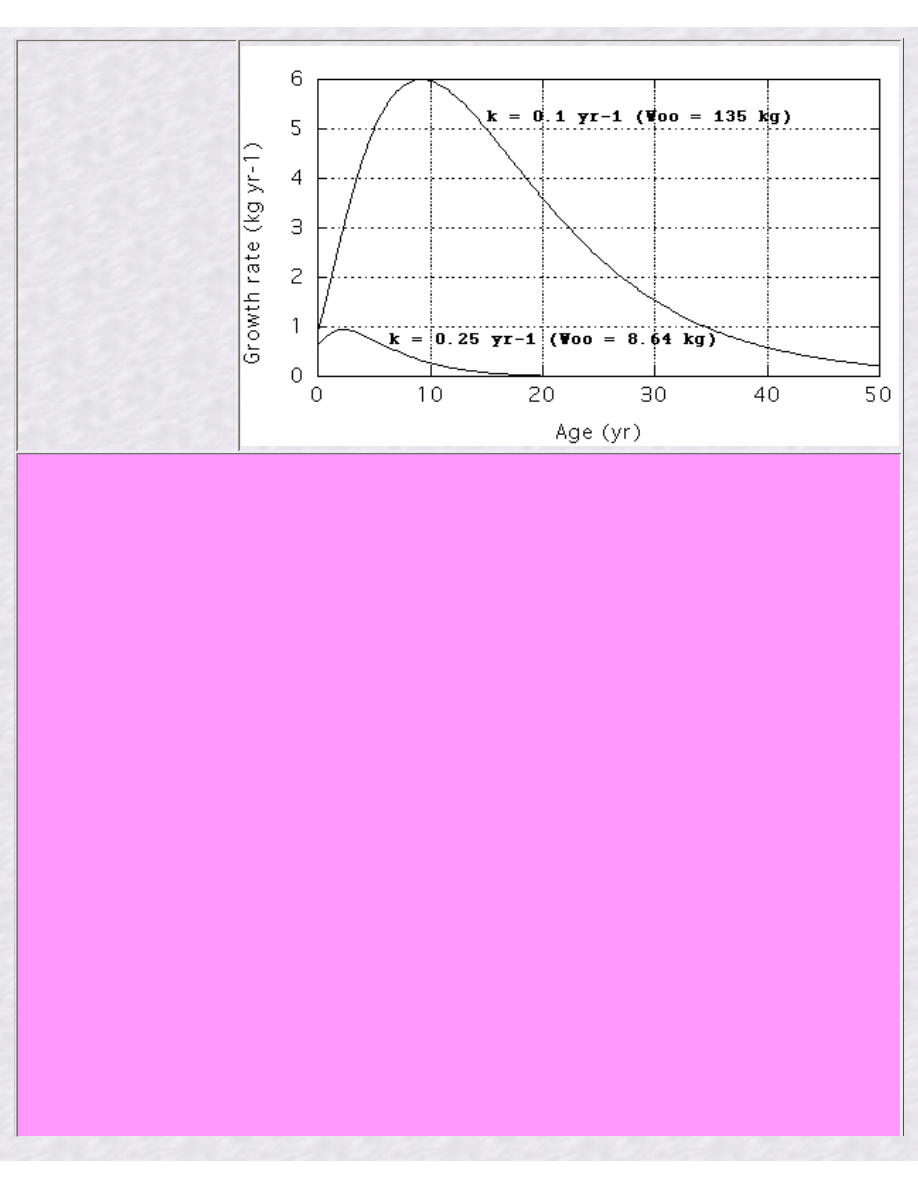
k has often been called a growth constant. In the demonstration plot below I used 2 pups with the

same length at birth (0.5 m) and weight (0.625 kg). I used the same anabolic constant a (usually

denoted as eta) and 2 different values for k (3k = catabolic constant, usually denoted as chi) and

calculated growth rates vs. age. A large k produces a mature adult shark of low mass (8.64 kg)

which is reached in a short time. This may look like fast growth, however, the corresponding growth

rates (with units of kg/yr or m/yr) are small. With a smaller k of 0.1, the maximum growth rates are

6 x as large and the shark reaches a considerably larger mass (135 kg), but it takes a lot longer to

reach the steady state.

file:///C|/Download/Texto/HTML/Von Bertalanffy Growth Function.htm (1 of 5)9/4/2005 19:13:17

Von Bertalanffy Growth Function

dM/dt = a M^(2/3) - 3k M

1. Mo = 0.625 kg;

2. a = 1.539 kg^0.333 yr-1;

3. k = 0.1 and 0.25 yr-1.

The anabolic constant a
was chosen to produce
Moo = 135 kg with k =
0.1, where 135 kg was the
estimated mass of a shark
of 3 m TL assuming M = 5
TL^3.0.

Miscellaneous items

●

As outlined above k is not a growth constant but apparently sharks with large growth rates

have large k. k (rate constant) and dL/dt (growth rate) are related as follows:

k = (dL/dt)/(Loo - L)

If "growth" is understood to be the growth rates of pups or juveniles (large adult sharks no

longer grow much) then we can replace L by Lo and now compare two shark of SIMILAR Loo.

Furthermore let's assume that Loo>>Lo, and we have k ~ (dL/dt)/Loo i.e. k is proportional to

dL/dt.

k in the VBGF is assumed to be a constant. However, Von Bertalanffy (1960) indicated that k

could change as a shark get older. Sevengill shark growth data indicated that indeed k is not

constant and becomes smaller as they get older.

The VBGF is a 3 parameter equation. In principle, three data points determine the

parameters. If adult males and females reach different maximum sizes, then the VBGF of

males and females must be different because size at birth and say first year growth of males

and females are the same.

Most statistical packages include a non-liner module which can be used to calculate the best

fitting parameters for the available length age data pairs. Most frequently least-squares are

used but a maximum likelihood loss function may produce more robust parameters.

The VBGF given here first, is the most suitable form for sharks which have a well

defined size at birth. The following theoretical publications and papers dealing with

elasmobranch research used this form:

Aasen, O. 1963. Length and growth of the porbeagle (Lamna nasus, Bonnaterre) in the

North West Atlantic. Rep. Norw. Fishery Mar. Invest. 13: 20-37.

file:///C|/Download/Texto/HTML/Von Bertalanffy Growth Function.htm (2 of 5)9/4/2005 19:13:17

Von Bertalanffy Growth Function

Bertalanffy, L. von 1938. A quantitative theory of organic growth (Inquiries on growth laws.

II). Human Biol. 10: 181-213.

Bertalanffy, L. von 1960. Principles and theory of growth, pp 137-259. In Fundamental

aspects of normal and malignant growth. W. W. Wowinski ed. Elseviers, Amsterdam.

Cailliet, G. M., H. F. Mollet, G. G. Pittenger, D. Bedford, and L. J. Natanson 1992.

Growth and demography of the pacific angel shark (Squatina californica), based upon tag

returns off California. Australian Journal of Marine and Freshwater Research 43: 1313-30.

Fabens, A. J. 1965. Properties and fitting of the von Bertalanffy growth curve. Growth 29:

265-289.

Van Dykhuizen, G. and H. F. Mollet 1992. Growth, age estimation, and feeding of captive

sevengill sharks, Notorynchus cepedianus, at the Monterey Bay Aquarium. In Sharks: Biology

and Fisheries. J. G. Pepperell ed. Australian Journal of Marine and Freshwater Research 43:

297-318.

●

The VBGF is more often presented in a different form which uses to (t zero, x-axis

intercept) as the 3rd parameter rather than Lo (L zero, y-axis intercept).

L(t) = Loo (1 - exp[-k(t-to)])

t zero was assumed to be the gestation time (time from fertilization to birth) by many (e.g.

Holden 1974) but this implies that embryonic growth follows the same growth law governing

post-natal growth. No data was ever produced to substantiate this, wheras available data of

embryonic growth suggests that it is different from post-natal growth and thus requires its

own growth curve. Indeed, it would be surprising if embryonic growth of elasmobranchs

featuring a large number of reproductive modes (ovipaity to placental vivipartiy) would follow/

determine) post-natal growth. Accordingly, t zero has little meaning and I suggest that

it is preferable to use Lo when reporting VBGF's of elasmobranchs. Lo can be

calculated from the parameters Loo, k, and t zero from the following equation Lo = Loo[1 -

exp(kto)]. The example in the graph has to = (1/k)ln[(Loo-Lo)/Loo] = 1.6 years.

●

The VBGF is sometimes used in yet another form involving as the third parameter b

= (Loo-Lo)/Loo = exp(kto)

L(t) = Loo [1 - b exp(-kt)]

●

Fabens' 1966 method allows determination of Loo and k

L(recapture) = L(tag) + (Loo - L(tag))(1 - exp(-kT)

where T = time-at-large. The age of the shark is not required.

●

Growth rate vs. age (explicit age dependence)

L'(t) = dL/dt = k(Loo - Lo) exp(-kt)

file:///C|/Download/Texto/HTML/Von Bertalanffy Growth Function.htm (3 of 5)9/4/2005 19:13:17

Von Bertalanffy Growth Function

Explicit expression of growth rate in units of length/time (e.g. m/year).

●

Growth rate vs. length (implicit age dependence, Gulland-Holt method)

L'(t) = dL/dt = kLoo - kL = k (Loo - L)

Age not required. Annualized growth rates are plotted vs. mean length at tagging and

recapture. Times-at-large don't have to be equal. If times-at large vary too much, a

correction factor can be used.

Fractional growth rate L'/L = k [(Loo/L) - 1]

Often k is misnamed as a growth constant although k has units of reciprocal time. The

Gulland-Holt equation shows how k and the growth rate are related: k = L'/(Loo - Lo) where

L' = L'(t)

●

Gulland method, L increment vs. L at tagging

L(increment) = Loo (1 - exp(-kT)

where T = time at large. Should be the same for all the data. Age is not required.

●

VBGF equations for mass, CRM = cube root mass

CRM(t) = CRMoo - (CRMoo - CRMo) exp(-kt)

M(t) = [CRMoo - (CRMoo - CRMo) exp(-kt)]3

M'(t) = dM/dt = 3k(CRMoo - CRMo) exp(-kt)[...]2

growth rate vs. age

M'(t)/M(t) = 3k(CRMoo - CRMo) exp(-kt)[...]-1

fractional growth rate vs. age, related to food intake

vs. age.

Back to previous page

GO

TO

Von Bertalanffy References

ElasMollet Home Page

Please send comments, corrections, and updates to

mailto:[e-mail]

Created August 1998; revised

file:///C|/Download/Texto/HTML/Von Bertalanffy Growth Function.htm (4 of 5)9/4/2005 19:13:17

Von Bertalanffy Growth Function

August 1998.

file:///C|/Download/Texto/HTML/Von Bertalanffy Growth Function.htm (5 of 5)9/4/2005 19:13:17