Dodawanie i odejmowanie

© Janusz Biernat, Dodawanie i odejmowanie, 14 pa

ździernika 2003

ADS–1

Dodawanie i odejmowanie w systemach naturalnych

β

β

}

,...,

,

,...,

{

,

}

,...,

,

,...,

{

0

1

1

0

1

1

m

k

m

k

y

y

y

y

x

x

x

x

−

−

−

−

=

=

Y

X

⇓ ⇓

1

+

±

=

±

±

i

i

i

i

i

c

s

c

y

x

β

⇓

0

=

−

m

c

β

}

,...,

,

,...,

{

0

1

1

m

k

s

s

s

s

−

−

=

S

})

1

,

0

{

}

1

,

0

{

(

}

1

,...,

1

,

0

{

,

,

1

∈

⇒

∈

⇒

−

∈

+

i

i

i

i

i

c

c

s

y

x

β

c

k

−2

x

1–m

s

1–m

c

2–m

y

1–m

Σ

s

k

−1

c

k

−1

c

k

y

k

−1

x

k

−1

Σ

x

–m

s

–m

c

–m

c

1–m

y

–m

Σ

s

k

−2

y

k

−2

x

k

−2

Σ

Schemat dodawania/odejmowania wielopozycyjnego

Dodawanie i odejmowanie

© Janusz Biernat, Dodawanie i odejmowanie, 14 pa

ździernika 2003

ADS–2

Poprawność dodawania i odejmowania w systemach naturalnych

β

β

}

,...,

,

,...,

{

,

}

,...,

,

,...,

{

0

1

1

0

1

1

m

k

m

k

y

y

y

y

Y

x

x

x

x

X

−

−

−

−

=

=

=

=

Y

X

⇓

1

+

±

=

±

±

i

i

i

i

i

c

s

c

y

x

β

⇓

|

}

,...,

,

,...,

{

|

0

1

1

β

m

k

s

s

s

s

Y

X

−

−

=

±

=

±

Y

X

!!

})

1

,

0

{

}

1

,

0

{

(

}

1

,...,

1

,

0

{

,

,

1

∈

⇒

∈

⇒

−

∈

+

i

i

i

i

i

c

c

s

y

x

β

Wynikiem dodawania lub odejmowania pozycyjnego (przy

0

=

−

m

c

) jest

∑

∑

−

−

=

+

−

−

=

−

±

=

±

=

±

1

1

1

)]

(

[

)

(

k

m

i

i

i

i

i

k

m

i

i

i

i

c

c

s

y

x

Y

X

β

β

β

,

k

k

k

k

k

m

i

i

i

k

m

i

i

i

i

i

k

m

i

i

i

c

S

c

s

c

c

s

Y

X

β

β

β

β

β

β

±

=

±

=

−

±

=

±

∑

∑

∑

−

−

=

−

−

=

+

+

−

−

=

1

1

1

1

1

)

(

poprawność dodawania

)

0

(

)

(

1

(

0

<

−

∧

>

+

⇒

=

⇒

<

≤

k

k

k

k

k

k

k

c

S

c

S

c

S

β

β

β

β

(

)

1

=

k

c

– nadmiar (wynik przekracza zakres)

Dodawanie i odejmowanie

© Janusz Biernat, Dodawanie i odejmowanie, 14 pa

ździernika 2003

ADS–3

Dodawanie i odejmowanie w systemach uzupełnieniowych

∑

−

−

=

−

−

+

−

−

+

−

=

1

1

1

1

)

(

}

,

,...,

{

k

m

i

i

i

k

m

m

k

x

R

x

x

x

x

β

ϕ

gdzie

)

)

1

2

(

sgn

1

(

)

(

1

2

1

1

+

−

+

=

−

−

β

ϕ

k

k

x

x

,

m

k

R

−

−

=

δβ

β

(

δ

= 1 lub 0)

U

U

Y

X

}

,...,

,

,...,

{

,

}

,...,

,

,...,

{

0

1

1

0

1

1

m

k

m

k

y

y

y

y

x

x

x

x

−

−

−

−

=

=

⇓ ⇓

1

+

±

=

±

±

i

i

i

i

i

c

s

c

y

x

β

⇓

0

=

−

m

c

Y

X

S

Y

X

S

U

±

=

⇔

±

=

=

−

−

}

,...,

,

,...,

{

0

1

1

m

k

s

s

s

s

Wynik działania powinien da

ć się zapisać w postaci

V

+

=

±

S

Y

X

gdzie

∑

−

−

=

−

−

−

+

−

=

=

1

1

0

1

1

)

(

}

,...,

,

,...,

{

|

|

k

m

i

i

i

k

m

k

s

R

s

s

s

s

s

β

ϕ

U

S

, V – nadmiar

Dodawanie i odejmowanie

© Janusz Biernat, Dodawanie i odejmowanie, 14 pa

ździernika 2003

ADS–4

Poprawność dodawania i odejmowania w systemach uzupełnieniowych

Skutkiem wykonania działa

ń zgodnie z regułą dodawania / odejmowania jest

∑

−

−

=

−

−

=

±

+

±

−

=

±

1

1

1

)

(

)]

(

)

(

[

|

|

|

|

k

m

i

i

i

i

k

k

y

x

R

y

x

β

ϕ

ϕ

Y

X

∑

−

−

=

+

−

−

−

±

+

±

−

=

1

1

1

1

)]

(

[

)]

(

)

(

[

k

m

i

i

i

i

i

k

k

c

c

s

R

y

x

β

β

ϕ

ϕ

,

sk

ąd przy

0

=

−

m

c

otrzymamy

k

k

k

m

i

i

i

k

k

c

s

R

y

x

β

β

ϕ

ϕ

±

+

±

−

=

±

∑

−

−

=

−

−

1

1

1

)]

(

)

(

[

|

|

|

|

Y

X

Z porównania wzorów wynika

)

(

))]

(

)

(

(

)

)

(

[(

|

|

|

|

|

|

1

1

1

R

c

R

y

x

c

s

k

k

k

k

k

k

−

±

±

−

±

+

=

±

−

−

−

β

ϕ

ϕ

ϕ

S

Y

X

))

(

)

(

(

)

)

(

(

1

1

1

−

−

−

±

−

±

=

k

k

k

k

y

x

c

s

v

ϕ

ϕ

ϕ

– wska

źnik nadmiaru

m

k

k

k

c

R

c

−

=

−

β

δ

β

)

(

– korekcja wyniku (przeniesienie okr

ężne)

•

w systemie pełnym zb

ędna, bo

δ

= 0,

•

w systemie niepełnym – c

k

na najni

ższej pozycji (

δ

= 1)

Dodawanie i odejmowanie

© Janusz Biernat, Dodawanie i odejmowanie, 14 pa

ździernika 2003

ADS–5

Nadmiar w dodawaniu w systemach uzupełnieniowych

)]

(

)

(

[

]

)

(

[

1

1

1

−

−

−

+

−

+

=

k

k

k

k

y

x

c

s

v

ϕ

ϕ

ϕ

– znaki operandów dodatnie

1

,

0

2

1

1

1

−

≤

≤

−

−

β

k

k

y

x

(

0

)

(

)

(

1

1

=

+

−

−

k

k

y

x

ϕ

ϕ

):

•

albo

1

0

2

1

1

1

1

−

≤

+

+

≤

−

−

−

β

k

k

k

c

y

x

⇒

0

=

k

c

,

0

)

(

1

=

−

k

s

ϕ

, ⇒ v = 0

•

albo

1

1

1

1

2

1

−

≤

+

+

≤

−

−

−

β

β

k

k

k

c

y

x

⇒

0

=

k

c

,

1

)

(

1

=

−

k

s

ϕ

⇒ v = 1

– znaki operandów ujemne

1

,

1

1

2

1

−

≤

≤

−

−

β

β

k

k

y

x

(

2

)

(

)

(

1

1

=

+

−

−

k

k

y

x

ϕ

ϕ

):

•

1

1

1

1

2

1

−

+

≤

+

+

≤

+

−

−

−

β

β

β

β

k

k

k

c

y

x

⇒

1

=

k

c

,

1

)

(

1

=

−

k

s

ϕ

⇒ v = 0

•

1

2

1

1

1

1

−

+

≤

+

+

≤

−

−

−

β

β

β

k

k

k

c

y

x

⇒

1

=

k

c

,

0

)

(

1

=

−

k

s

ϕ

⇒ v =

−

1

– znaki operandów ró

żne (

1

)

(

)

(

1

1

=

+

−

−

k

k

y

x

ϕ

ϕ

):

•

albo

)

1

(

2

1

1

1

1

−

+

≤

+

+

≤

−

−

−

β

β

β

k

k

k

c

y

x

⇒

1

=

k

c

,

0

)

(

1

=

−

k

s

ϕ

⇒ v = 0

•

albo

1

1

1

1

2

1

−

≤

+

+

≤

−

−

−

β

β

k

k

k

c

y

x

⇒

0

=

k

c

,

1

)

(

1

=

−

k

s

ϕ

⇒ v = 0

Dodawanie i odejmowanie

© Janusz Biernat, Dodawanie i odejmowanie, 14 pa

ździernika 2003

ADS–6

Nadmiar w odejmowaniu w systemach uzupełnieniowych

)]

(

)

(

[

]

)

(

[

1

1

1

−

−

−

−

−

−

=

k

k

k

k

y

x

c

s

v

ϕ

ϕ

ϕ

– znaki operandów s

ą identyczne (

0

)

(

)

(

1

1

=

−

−

−

k

k

y

x

ϕ

ϕ

),

•

k

k

c

s

=

−

)

(

1

ϕ

⇒ v = 0

– znaki operandów s

ą różne, a odjemna jest ujemna (

1

)

(

)

(

1

1

=

−

−

−

k

k

y

x

ϕ

ϕ

),

•

0

=

k

c

,

1

)

(

1

=

−

k

s

ϕ

⇒ v = 0

•

0

=

k

c

,

0

)

(

1

=

−

k

s

ϕ

⇒ v =

−

1

– znaki operandów s

ą różne, a odjemna jest dodatnia (

1

)

(

)

(

1

1

−

=

−

−

−

k

k

y

x

ϕ

ϕ

),

•

1

=

k

c

,

0

)

(

1

=

−

k

s

ϕ

⇒ v = 0

•

1

=

k

c

,

1

)

(

1

=

−

k

s

ϕ

⇒ v = 1

Dodawanie i odejmowanie

© Janusz Biernat, Dodawanie i odejmowanie, 14 pa

ździernika 2003

ADS–7

Inkrementacja i dekrementacja w systemach naturalnych

β

}

,

,...,

{

0

1

1

x

x

x

k

−

=

X

⇓ ⇓

1

+

±

=

±

i

i

i

i

c

s

c

x

β

⇓

1

0

±

=

c

β

}

,

,...,

{

0

1

1

s

s

s

k

−

=

±

1

X

})

1

,

0

{

}

1

,

0

{

(

}

1

,...,

1

,

0

{

,

1

∈

⇒

∈

⇒

−

∈

+

i

i

i

i

c

c

s

x

β

c

k

−2

x

1

s

1

c

2

s

k

−1

c

k

−1

c

k

x

k

−1

±

x

0

s

0

c

0

c

1

s

k

−2

x

k

−2

±

±

±

Schemat inkrementacji/dekrementacji

Dodawanie i odejmowanie

© Janusz Biernat, Dodawanie i odejmowanie, 14 pa

ździernika 2003

ADS–8

Zmiana znaku liczby w systemie uzupełnieniowym

W systemie pełnym

m

m

k

k

m

m

Y

Y

Y

−

−

−

−

−

−

+

−

−

+

+

+

−

=

+

−

−

=

−

β

β

β

β

β

β

β

β

]

)

1

)(

...

(

[

)

(

1

2

1

↓

m

k

m

i

i

i

k

k

k

m

i

i

k

y

y

Y

−

−

−

=

−

−

−

−

=

−

+

+

−

−

−

+

−

=

−

∑

∑

β

β

β

β

β

β

2

1

1

2

1

)

(

)

1

(

↓

ulp

Y

y

y

Y

m

k

m

i

i

i

k

k

+

=

+

+

−

=

−

−

−

−

=

−

−

∑

β

β

β

2

1

1

W ka

żdym systemie uzupełnieniowym

)

(

Q

R

Y

Y

0

−

+

=

−

, czyli

)

(

]

)

1

[(

)

(

)

(

1

1

1

1

m

k

k

m

i

i

i

k

k

m

i

i

i

k

y

R

y

y

R

y

−

−

−

=

−

−

−

=

−

−

−

−

−

+

=









+

−

−

∑

∑

β

β

β

β

ϕ

β

ϕ

gdzie

m

k

R

−

−

=

δβ

β

oraz

δ

= 0 w systemie pełnym, 1 – w niepełnym,

a poniewa

ż

)

(

1

)

(

1

1

−

−

−

=

k

k

y

y

ϕ

ϕ

m

k

m

i

i

i

k

y

R

y

Y

−

−

−

=

−

−

+

+

−

=

−

∑

β

δ

β

ϕ

)

1

(

)

(

1

1

Dodawanie i odejmowanie

© Janusz Biernat, Dodawanie i odejmowanie, 14 pa

ździernika 2003

ADS–9

Odejmowanie przez dodawanie

W systemie uzupełnieniowym

Y

X

Y

X

+

=

−

•

schemat uniwersalny, ale bardziej czasochłonny (dwukrotne dopełnianie)

albo, poniewa

ż

)

(

Q

R

Y

Y

0

−

+

=

−

,

ulp

Y

X

Q

Y

X

Y

X

δ

+

+

==

+

+

=

−

~

•

dodawanie ulp – na najni

ższej pozycji (zamiast przeniesienia c

–m

=0)

Odejmowanie liczb naturalnych przez dodanie uzupełnienia

β

β

U

1

1

1

1

}

,

,...,

,

0

{

}

,

,...,

{

m

m

k

m

m

k

x

x

x

x

x

x

−

+

−

−

−

+

−

−

=

m

m

m

k

m

m

k

y

y

y

y

y

y

−

−

+

−

−

−

+

−

−

+

−

=

−

δβ

β

β

β

U

1

1

1

1

}

,

,...,

,

1

{

}

,

,...,

{

Skoro

1

−

=

β

k

y

, x

k

= 0 i musi by

ć s

k

= 0, wi

ęc jeśli wynik jest poprawny, to

1

)]

(

)

(

[

]

)

(

[

1

1

−

=

+

−

+

=

+

+

k

k

k

k

k

c

y

x

c

s

v

ϕ

ϕ

ϕ

⇒ c

k+1

= 1 ⇒ c

k

= 1

Dodawanie i odejmowanie

© Janusz Biernat, Dodawanie i odejmowanie, 14 pa

ździernika 2003

ADS–10

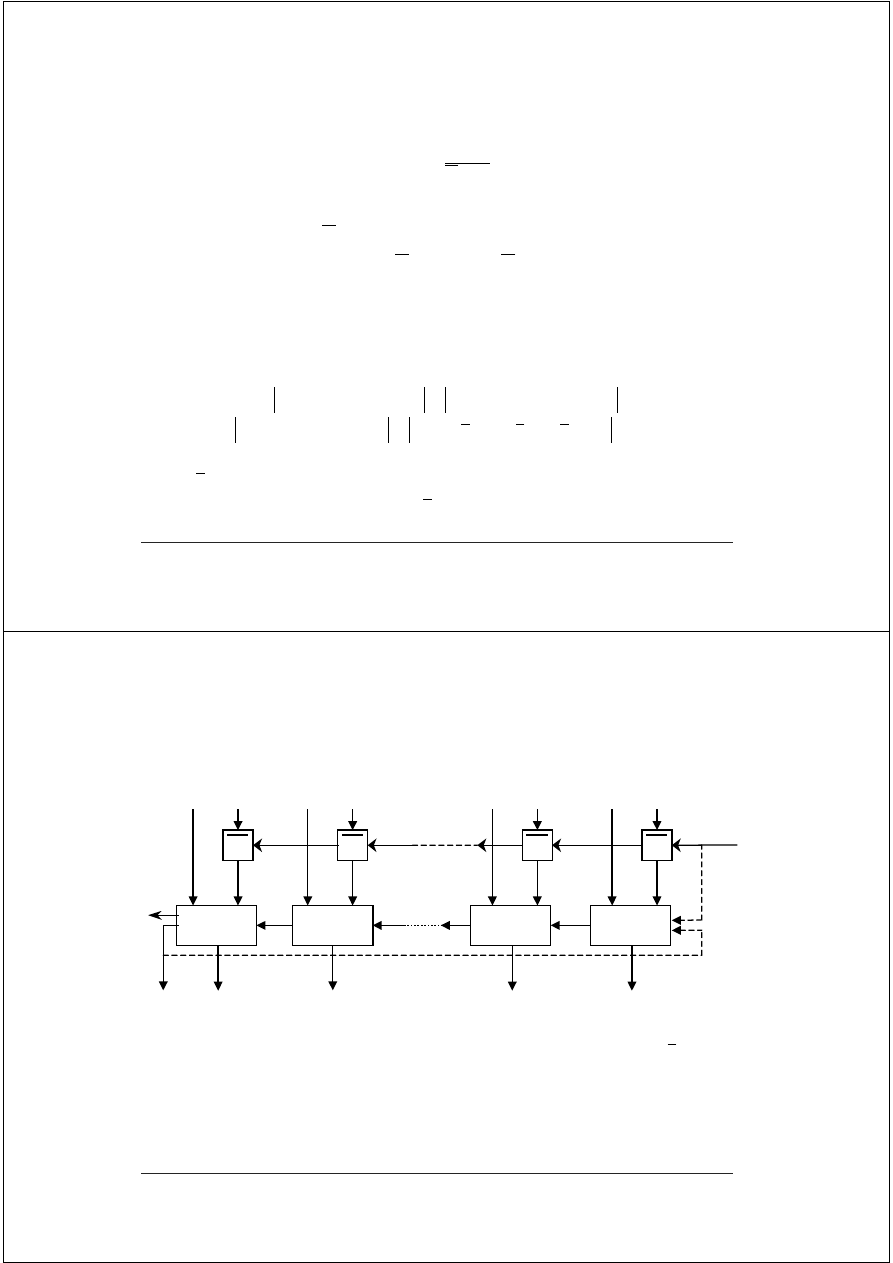
Uniwersalny schemat dodawania i odejmowania

δ

= 1

c

k

−2

x

1–m

s

1–m

c

2–m

y

1–m

Σ

s

k

−1

c

k

−1

c

k

y

k

−1

x

k

−1

Σ

x

–m

s

–m

c

1–m

y

–m

Σ

s

k

−2

y

k

−2

x

k

−2

Σ

v

( )

( )

( )

( )

M

δ

= 0

y

M

k

−1

y

M

k

−2

y

M

1−

m

y

M

−

m

Schemat dodawania i odejmowania w systemach uzupełnieniowych

)]

(

)

(

[

]

)

(

[

1

1

1

M

k

k

k

k

y

x

c

s

v

−

−

−

+

−

+

=

ϕ

ϕ

ϕ

,

1

1

1

)

1

(

−

−

−

+

−

=

k

k

M

k

y

M

y

M

y

Liczby naturalne:

•

dodawanie – wynik poprawny gdy c

k

= 0

•

odejmowanie – wynik poprawny gdy c

k

= 1

Dodawanie i odejmowanie

© Janusz Biernat, Dodawanie i odejmowanie, 14 pa

ździernika 2003

ADS–11

Dodawanie i odejmowanie w naturalnym systemie dwójkowym

i

i

i

i

i

s

c

c

y

x

+

±

=

±

±

+

1

2

sumator pełny (full adder, FA) – realizuje funkcje

•

sumy arytmetycznej

i

s

operandów dwójkowych

i

i

i

c

y

x

,

,

na pozycji i-tej

•

przeniesienia

1

+

i

c

na wy

ższą pozycję

i

i

i

i

c

y

x

s

⊕

⊕

=

,

i

i

i

i

i

i

i

i

i

i

i

c

y

x

y

x

c

y

x

y

x

c

)

(

)

(

1

+

+

=

⊕

+

=

+

subtraktor pełny (full subtracter, FS) – realizuje funkcje

•

ró

żnicy arytmetycznej

i

s

operandów dwójkowych

i

i

i

c

y

x

,

,

na pozycji i-tej

•

po

życzki

1

+

i

c

z wy

ższej pozycji

i

i

i

i

c

y

x

s

⊕

⊕

=

,

i

i

i

i

i

i

i

i

i

i

i

c

y

x

y

x

c

y

x

y

x

c

)

(

)

(

1

⊕

+

=

⊕

+

=

+

półsumator (half adder, HA) – realizuje funkcje

i

i

i

c

x

s

⊕

=

,

i

i

i

c

x

c

=

+

1

półsubtraktor (half subtracter, HS) – realizuje funkcje

i

i

i

c

x

s

⊕

=

,

i

i

i

c

x

c

=

+

1

Dodawanie i odejmowanie

© Janusz Biernat, Dodawanie i odejmowanie, 14 pa

ździernika 2003

ADS–12

Dodawanie i odejmowanie w dwójkowych systemach uzupełnieniowych

β

=2

⇒

1

1

)

(

−

−

=

k

k

x

x

ϕ

⇒

)

(

)

(

)

(

1

1

1

1

k

k

k

k

k

k

c

c

y

x

c

s

v

−

±

=

±

−

±

=

−

−

−

−

Mamy zatem (

m

k

R

−

−

=

2

2

δ

,

δ

=

0 w systemie U2 lub 1 w systemie U1)

m

k

k

k

k

m

i

i

i

k

c

R

c

c

s

R

s

S

−

−

−

−

=

−

±

−

±

+

−

=

∑

2

)

(

2

1

1

1

δ

Poprawny wynik mo

że być zawsze odtworzony w rozszerzeniu 1-pozycyjnym

•

w dodawaniu (liczb o jednakowych znakach)

v = 1 ⇒

1

1

−

−

=

k

k

c

s

⇒

}

,

,...,

,

{

1

1

e

m

m

k

k

s

s

s

c

−

+

−

−

=

S

•

w odejmowaniu (liczb o ró

żnych znakach),

v = 1 ⇒

1

1

−

−

≠

k

k

c

s

⇒

}

,

,...,

,

{

1

1

1

e

m

m

k

k

s

s

s

c

−

+

−

−

−

=

S

W systemie uzupełnieniowym do 2 (U2)

k

k

k

k

m

i

i

i

k

k

c

c

s

s

S

2

)

(

2

2

1

2

1

1

−

±

+

−

=

−

−

−

=

−

−

∑

Dodawanie i odejmowanie

© Janusz Biernat, Dodawanie i odejmowanie, 14 pa

ździernika 2003

ADS–13

Zmiana znaku liczby w kodzie uzupełnieniowym

X

X

X

m

m

−

+

−

=

−

=

−

−

−

2

2

0

↓

m

m

m

k

k

m

m

X

X

X

−

−

+

−

−

−

−

−

+

−

+

+

+

−

=

+

−

−

=

−

2

]

)

2

2

...

2

(

2

[

2

)

2

(

1

2

1

↓

m

k

m

i

i

i

k

k

k

m

i

i

k

x

x

X

−

−

−

=

−

−

−

−

=

−

+

+

−

−

+

−

=

−

∑

∑

2

]

)

2

2

(

)

2

2

[(

2

1

1

2

1

↓

m

m

k

m

i

i

i

k

k

X

x

x

X

−

−

−

−

=

−

−

+

=

+

−

+

−

−

=

−

∑

2

2

]

2

)

1

(

2

)

1

(

[

2

1

1

↓

algorytmy mnemotechniczne: („1”=ulp=2

–m

– jednostka na najni

ższej pozycji)

•

zaneguj wszystkie bity oryginału i do uzyskanego kodu dodaj pozycyjnie „1”

•

zaneguj wszystkie bity oryginału,

z wyj

ątkiem prawostronnego ciągu zer i poprzedzającej go „1”

(propagacja dodawanej „1” ko

ńczy się na pozycji najniższej „1” oryginału)

Dodawanie i odejmowanie

© Janusz Biernat, Dodawanie i odejmowanie, 14 pa

ździernika 2003

ADS–14

Dodawanie i odejmowanie liczb naturalnych jako rozszerze

ń w kodzie U2

U2

1

1

NB

1

1

}

,

,...,

,

0

{

}

,

,...,

{

m

m

k

m

m

k

x

x

x

x

x

x

−

+

−

−

−

+

−

−

=

↓

(s

k

=

c

k

),

ponadto w dodawaniu (c

k

+1

=

0

),

w odejmowaniu (c

k

+1

=

c

k

)

↓

k

k

k

m

i

i

i

k

m

i

i

i

i

k

c

s

y

x

S

2

2

2

)

(

2

)

0

0

(

1

1

±

=

±

+

±

−

=

∑

∑

−

−

=

−

−

=

Odejmowanie liczb naturalnych przez dodanie uzupełnienia

m

m

m

k

m

m

m

x

x

x

x

x

x

−

−

+

−

−

−

+

−

−

+

−

−

−

=

−

2

)}

1

(

),

1

(

),...,

1

(

,

1

{

}

,

,...,

{

U2

1

1

NB

1

1

↓

i

i

i

i

i

s

c

c

y

x

+

=

+

−

+

+

1

2

)

1

(

↓

k

k

k

m

i

i

i

m

k

m

i

i

i

i

k

c

s

y

x

S

2

)

1

(

2

2

2

))

1

(

(

2

)

1

0

(

1

1

−

−

=

+

−

+

+

+

−

=

∑

∑

−

−

=

−

−

−

=