Tytuł prezentacji:
Związki Fizyczne
( Równania konstytutywne )

Teoria Sprężystości i Plastyczności

Nazwa wydziału: IMiR

Nazwa katedry: KWMiK

Miejsce i data prezentacji: Kraków 26.11.2014r.

www.agh.edu.pl

Równania teorii sprężystości

3 Równania równowagi wewnętrznej (równania Naviera)

Gdzie: i,j = 1, 2, 3

oraz

i,k,r = 1, 2, 3

Równania teorii sprężystości

6 równań geometrycznych (równania Cauchy’ego)

Równania teorii sprężystości

6 równań fizycznych (równania Hooke’a)

Wprowadzając stałe:

gdzie: E - moduł Younga

- współczynnik Poissona

G- moduł Kirchhoffa

Równania teorii sprężystości

Podsumowując

:

W ten sposób otrzymujemy pełen komplet równań potrzebnych do opisu 15 niewiadomych!

Równania teorii sprężystości

Założenia do równań konstytutywnych:

-

związki fizyczne są niezależne od czasu i warunków

zewnętrznych, czyli zależności dla każdej chwili i temperatury są
takie same;
- zależność σ ( ε ) jest liniowa;
- ciała zachowują się sprężyście tzn. σ i ε zanikają po usunięciu
przyczyny.

Równania teorii sprężystości

Najogólniejszą postać związków fizycznych wiążących ze sobą
wartości tensorów naprężenia i odkształcenia, w przypadku
trójwymiarowym, w ciałach materialnych zarówno izotropowych
jak i anizotropowych liniowo sprężystych można przedstawić
następująco:

Wskaźnikowo:

Równania teorii sprężystości

Tensor C

ijkl

o walencji 4 nazywamy tensorem

sprężystości ( sztywności ) stałych materiałowych.
Tensor ten dla ciał izotropowych jest tensorem
izotropowym zatem można go zapisać w następującej
postaci:

Równania teorii sprężystości

Wykorzystując równanie otrzymamy:

Zatem:

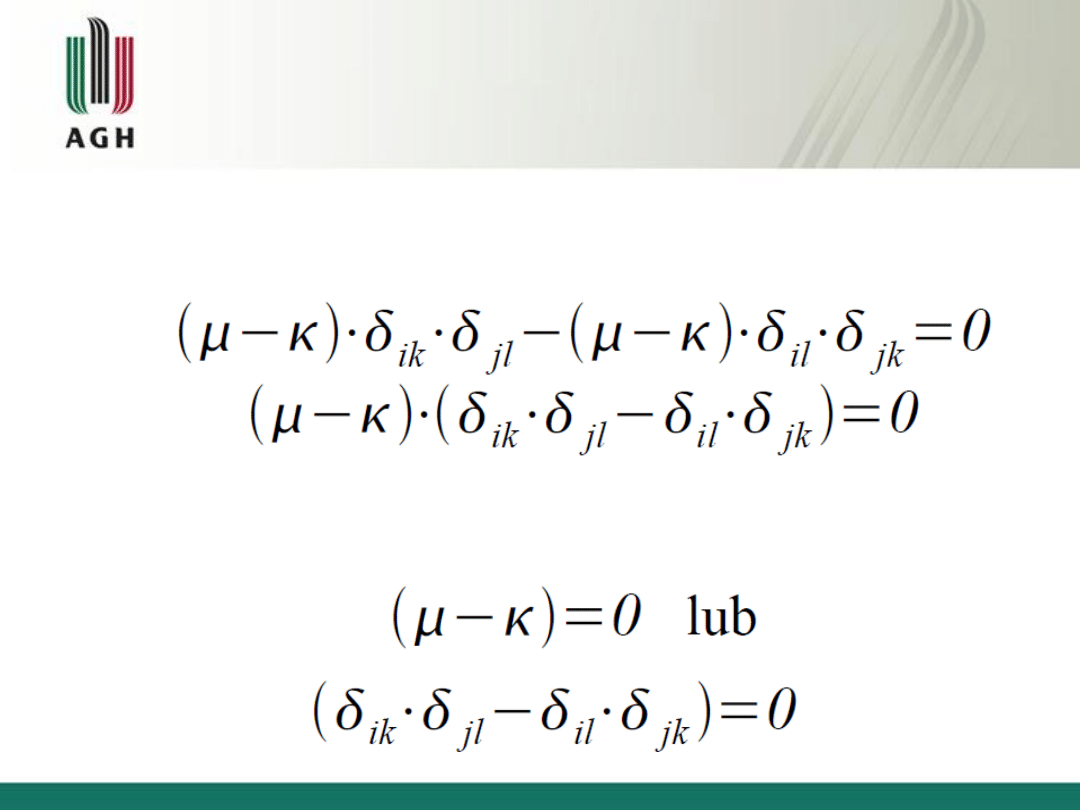
Równania teorii sprężystości

Po uporządkowaniu:

Równanie to jest spełnione, gdy:

Równania teorii sprężystości

Dla dowolnej kombinacji wskaźników
warunek drugi nie zawsze będzie spełniony
zatem:

Równania teorii sprężystości

Zauważmy, że:

Równania teorii sprężystości

Stąd po podstawieniu tych warunków otrzymamy:

Wzór przedstawia skrócony zapis równań fizycznych
wiążących ze sobą wartości tensorów naprężenia i
odkształcenia w przypadku trójwymiarowym ( dla
dowolnych osi ), w ciałach materialnych
izotropowych, liniowo – sprężystych bez
uwzględnienia temperatury i czasu.

Równania teorii sprężystości

W uzyskanym równaniu fizycznym naprężenia zostały
wyrażone przez odkształcenia. Doprowadźmy do
zależności odwrotnej.

Równania teorii sprężystości

Po przekształceniach

:

Przyjmując:

Równania teorii sprężystości

Równania teorii sprężystości

Po podstawieniu, uzyskamy związki fizyczne:

Równania teorii sprężystości

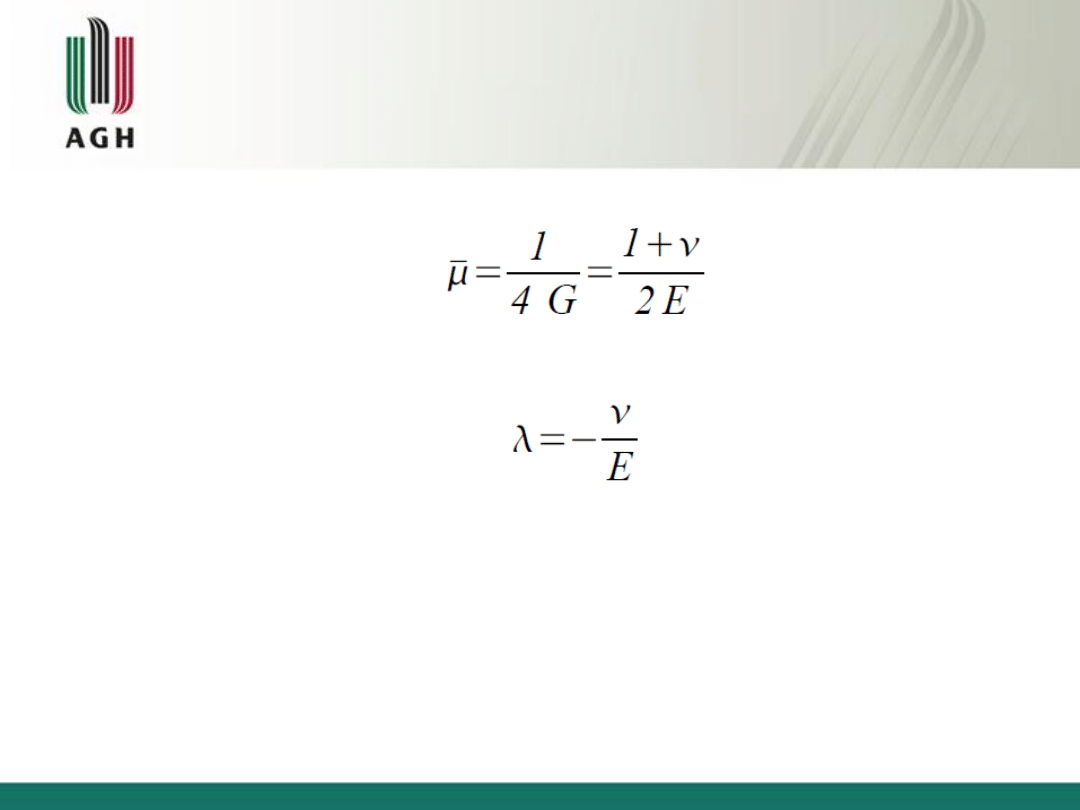
Równania teorii sprężystości

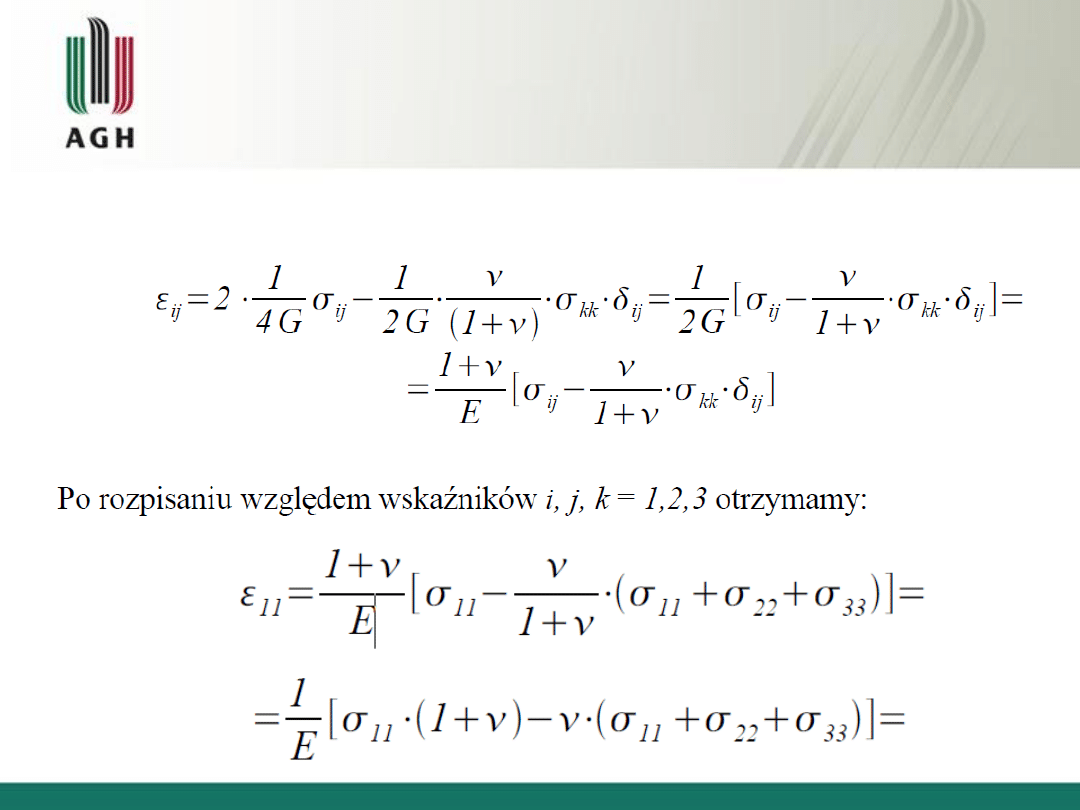
Równania teorii sprężystości

Uzyskujemy:

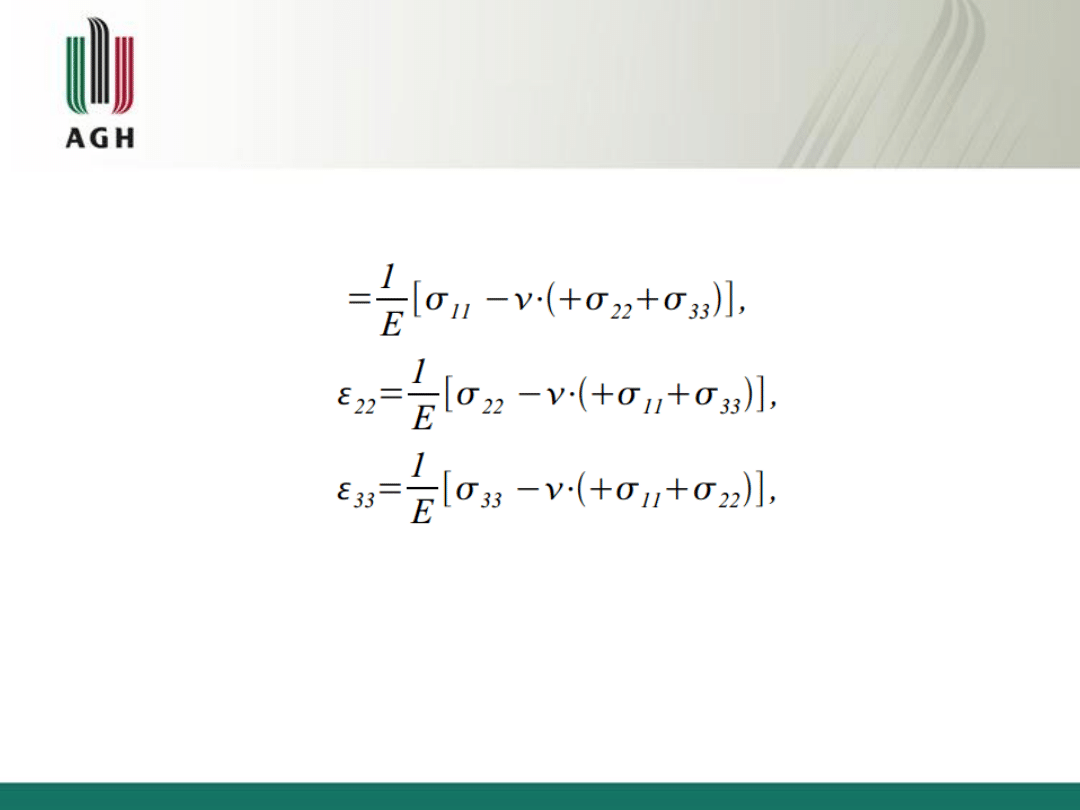
Równania teorii sprężystości

Równania teorii sprężystości

Równania teorii sprężystości

Zakończenie

Dziękujemy za uwagę.

Bibliografia

[1] A. Siemieniec, S. Wolny, Wytrzymałość Materiałów, cz. III, Kraków, 1995.

[2] Źródło pochodzące z Internetu:

http://www.ikb.poznan.pl/almamater/wyklady/teoria_sprezystosci_03-04/06.pdf