Pomiar strat miejscowych (lokalnych)

1

download: http://www.mech.pk.edu.pl/~m52/pdf/[12_opis].pdf

Ćwiczenie 12

POMIAR STRAT MIEJSCOWYCH (LOKALNYCH)

12.1. Określenie

strat

energetycznych

spowodowanych

przeszkodami

miejscowymi /lokalnymi/

Przy obliczeniach hydraulicznych: sieci, stacji pompowych, sprężarkowych, obok strat

ciśnienia wywołanych tarciem wewnętrznym płynu, konieczne jest uwzględnienie tzw.

miejscowych (lokalnych) strat ciśnienia. Występują one w tych elementach przewodu, gdzie

ulega zmianie wartość lub kierunek prędkości, a więc np. w krzywakach, zaworach,

zwężkach, siatkach, przyrządach mierniczych, przy przepływie przez kryzy, u wlotu ze

zbiornika do przewodu itp. Ogólną przyczyną tych strat są ruchy wirowe, którym zawsze

towarzyszy, w cieczy lepkiej, dyssypacja energii, zwiększona w porównaniu z przepływem

przez prostoosiowy odcinek przewodu o stałej średnicy, o długości tej samej co element,

w którym występuje strata miejscowa. Wobec trudności występujących przy określaniu

warunków brzegowych i początkowych, ograniczana jest możliwość wykorzystania równań

hydrodynamiki do obliczenia strat miejscowych ciśnienia. Dlatego też w praktyce korzystamy

ze wzorów, tabel i wykresów otrzymanych w drodze opracowania wyników badań

doświadczalnych nad stratami miejscowymi. Ciśnienie stracone na skutek miejscowych

przeszkód

∆

p

sm

obliczamy ze wzoru:

2

2

m

m

sm

m

m

v

v

p

2

2g

ρ⋅

γ ⋅

∆

= ξ

= ξ

(12.1)

Wysokość stracona h

sm

równa jest:

2

sm

m

sm

m

p

v

h

2g

∆

=

= ξ

γ

(12.2)

gdzie:

ρ

- gęstość cieczy,

γ

- ciężar właściwy cieczy,

v

m

- średnia prędkość przepływu,

g - przyśpieszenie ziemskie,

ξ

m

- bezwymiarowy współczynnik strat miejscowych.

2

Pomiar strat miejscowych (lokalnych)

download: http://www.mech.pk.edu.pl/~m52/pdf/[12_opis].pdf

Ze wzoru (12.1) wynika, że bezwymiarowy współczynnik strat miejscowych równy jest

stosunkowi ciśnienia straconego do ciśnienia dynamicznego:

sm

m

2
m

p

v

2

∆

ξ =

ρ⋅

(12.3)

Rozpatrując zależność (12.3) należy zwrócić uwagę, do jakiej prędkości średniej v

m

(przed czy za przekrojem, w którym występuje miejscowa strata ciśnienia) została odniesiona

wartość współczynnika

ξ

m

.

W tabelarycznych zestawieniach podaje się z reguły prędkości, do których odniesione

są wartości współczynników

ξ

m

. Warto tutaj podkreślić, że liczbowe wartości

współczynników

ξ

m

są zależne od liczby Reynoldsa. Znalezione doświadczalnie wartości

współczynników

ξ

m

, które podawane są w tablicach, odnoszą się do przepływów

turbulentnych

w

zakresie

odpowiadającym

prawie

ustalonym

wartościom

tych

współczynników. Często w praktyce wprowadza się pojęcie długości zastępczej L

z

danej

straty miejscowej. Porównując wzory Darcy-Weisbacha:

2

z

m

st

L

v

p

D

2g

γ ⋅

∆ = λ

oraz (12.1) otrzymamy:

2

2

z

m

m

m

L

v

v

D

2g

2g

γ ⋅

γ ⋅

λ

= ξ

Stąd długość zastępcza:

m

z

D

L

ξ ⋅

=

λ

(12.4)

gdzie: D - średnica przewodu,

λ

- współczynnik strat tarcia.

12.2. Straty energetyczne w konfuzorach

Przy przepływie cieczy przez stożkowe zwężające się w kierunku przepływu odcinki

przewodu (konfuzory) występują niewielkie straty energii wskutek tarcia. Wartość

współczynnika strat miejscowych zależy głównie od chropowatości i dla małych kątów

zbieżności /

α≈

5

°

/ wynosi:

0.06 0.005

ξ =

−

. Dla kątów

α

< 15° można przyjmować

m

0.1

ξ ≅

W obliczeniach dokładnych stosujemy wzór A. Fliegnera [2]:

2

2

2

2

sm

1

F

v

h

1

F

2g

8sin

2





 

λ 



∆

=

−  

α 



 





(12.5)

Pomiar strat miejscowych (lokalnych)

3

download: http://www.mech.pk.edu.pl/~m52/pdf/[12_opis].pdf

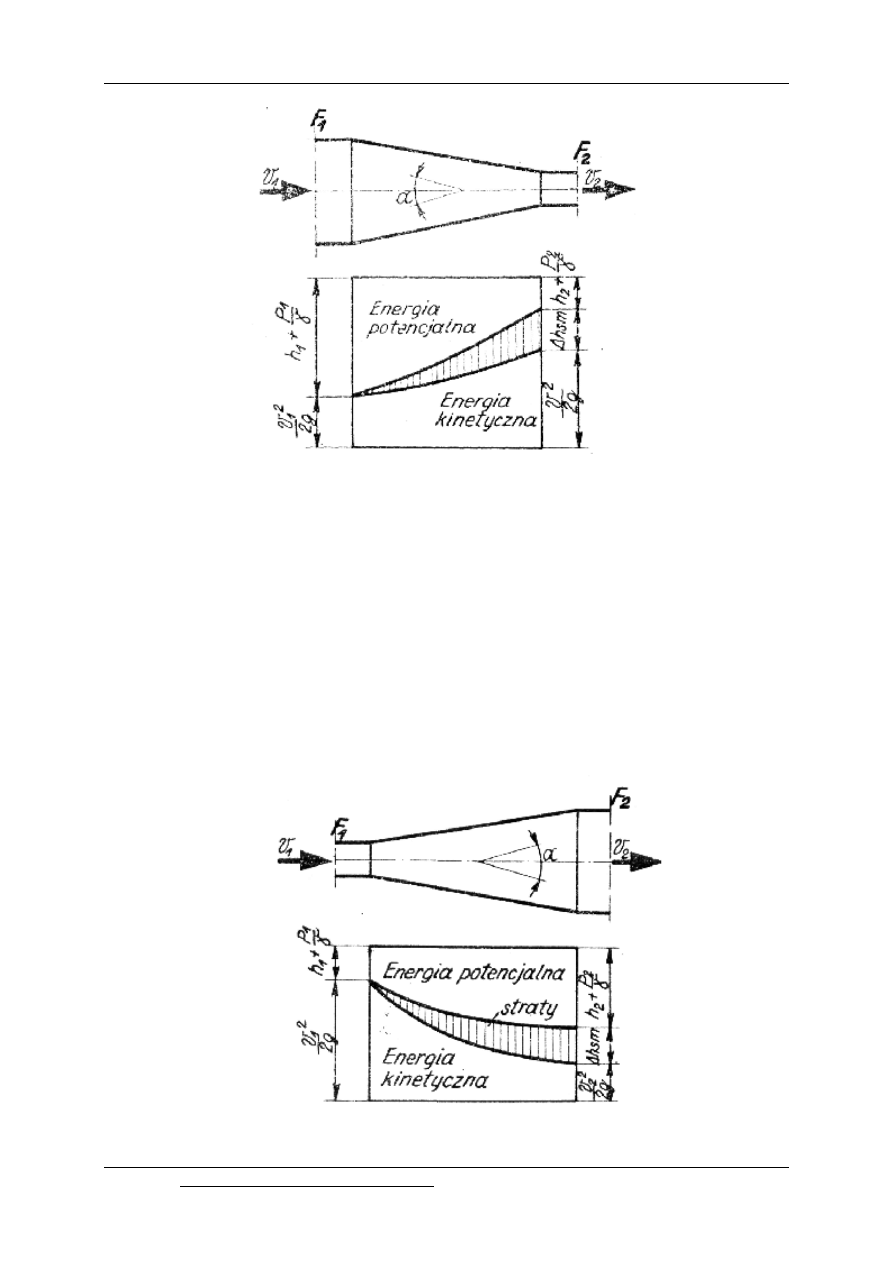
Rys. 12.1. Straty energetyczne w konfuzorach

12.3. Straty energetyczne w dyfuzorach

Straty energetyczne w przypadku stopniowego rozszerzenia przewodu /w dyfuzorze/ są

znacznie większe niż w konfuzorze. Na straty te składają się: straty wywołane tarciem i straty

spowodowane zmianą pędu.

Jak wynika z doświadczeń straty w dyfuzorze są tym większe, im większy jest kąt

rozwarcia. W miarę jednakże jak kąt

α

maleje, to przy stałym stosunku p

2

/p

1

Długość

dyfuzora wzrasta i straty wskutek tarcia rosną.

Rys. 12.1. Straty energetyczne w dyfuzorach

4

Pomiar strat miejscowych (lokalnych)

download: http://www.mech.pk.edu.pl/~m52/pdf/[12_opis].pdf

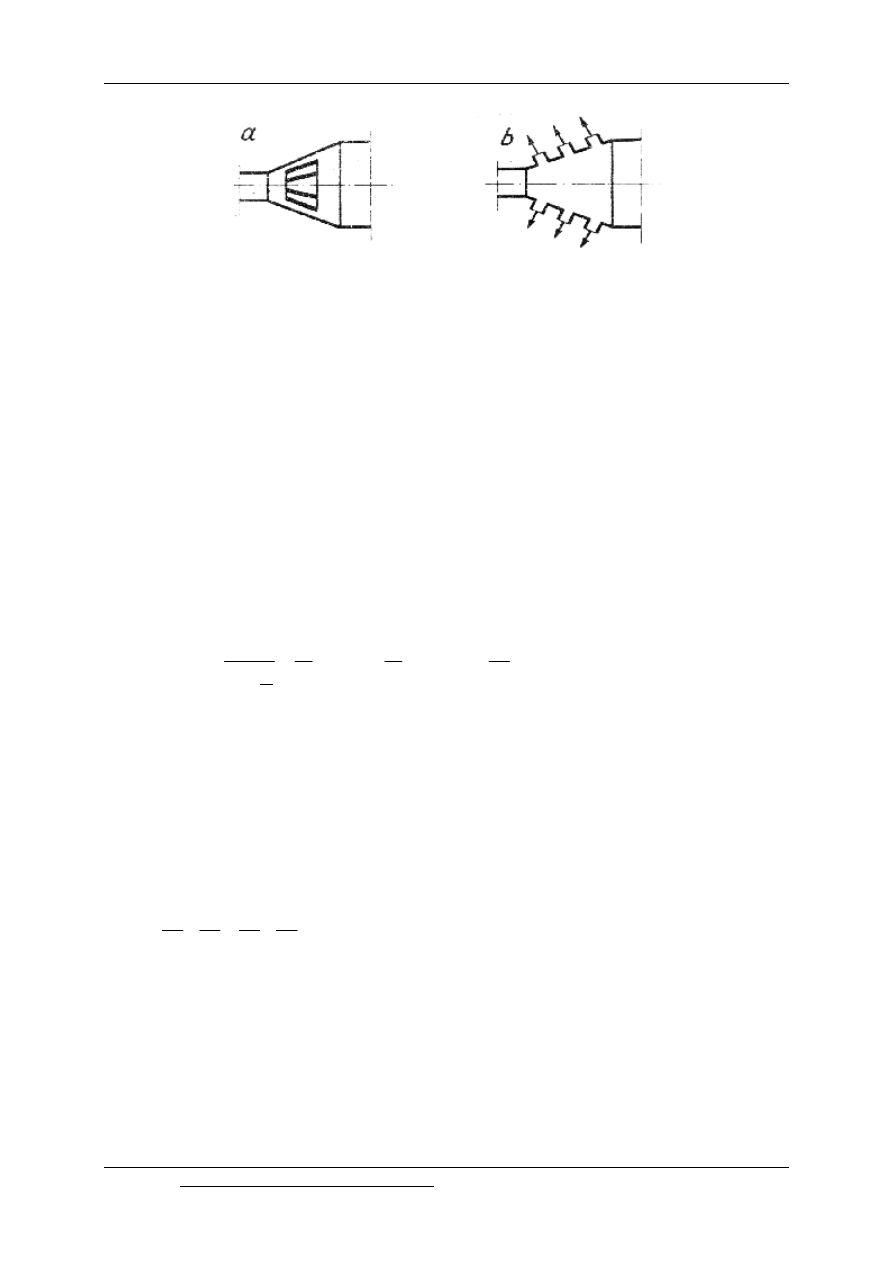
Rys. 12.3. Sposoby obniżania strat energetycznych w dyfuzorach

Z doświadczeń wynika, że najlepsze wyniki pod względem energetycznym osiąga się

przy

α

= 7

°÷

9°, przy czym dolna granica odnosi się do dyfuzorów o ścianach gładkich

/

λ

≅

0,02/, a górna granica - dla dyfuzorów o ścianach chropowatych /

λ

≅

0,04/.

W dyfuzorach, po przekroczeniu granicznej wartości

α

max

zależy od liczby Reynoldsa,

następuje oderwanie się strumienia cieczy od ścian przewodu, co wywołuje znaczny wzrost

oporów ruchu. W celu zapobieżenia odrywania się strumienia od ścian dyfuzora o dużych

kątach

α

stosuje się wkładki stożkowe rozchylające strumień /rys.12.3a/ lub odsysanie płynu

w dyfuzorze /rys.12.3b/. Dla kątów

α

< 10° całkowitą wysokość strat energetycznych można

wyliczyć ze wzoru A. Fliegnera [4]:

2

2

2

2

2

2

sm

1

1

F

F

v

h

1

1

sin

F

F

2g

8sin

2













 





λ 



∆

=

− +

−

α





 





α 



 

















(12.6)

12.4. Straty energetyczne przy skokowym zwiększaniu przekroju

Jednym z nielicznych przypadków, dla którego udaje się obliczyć wielkość strat

miejscowych w drodze teoretycznej, jest strata miejscowa występująca przy nagłym

rozszerzeniu przekroju.

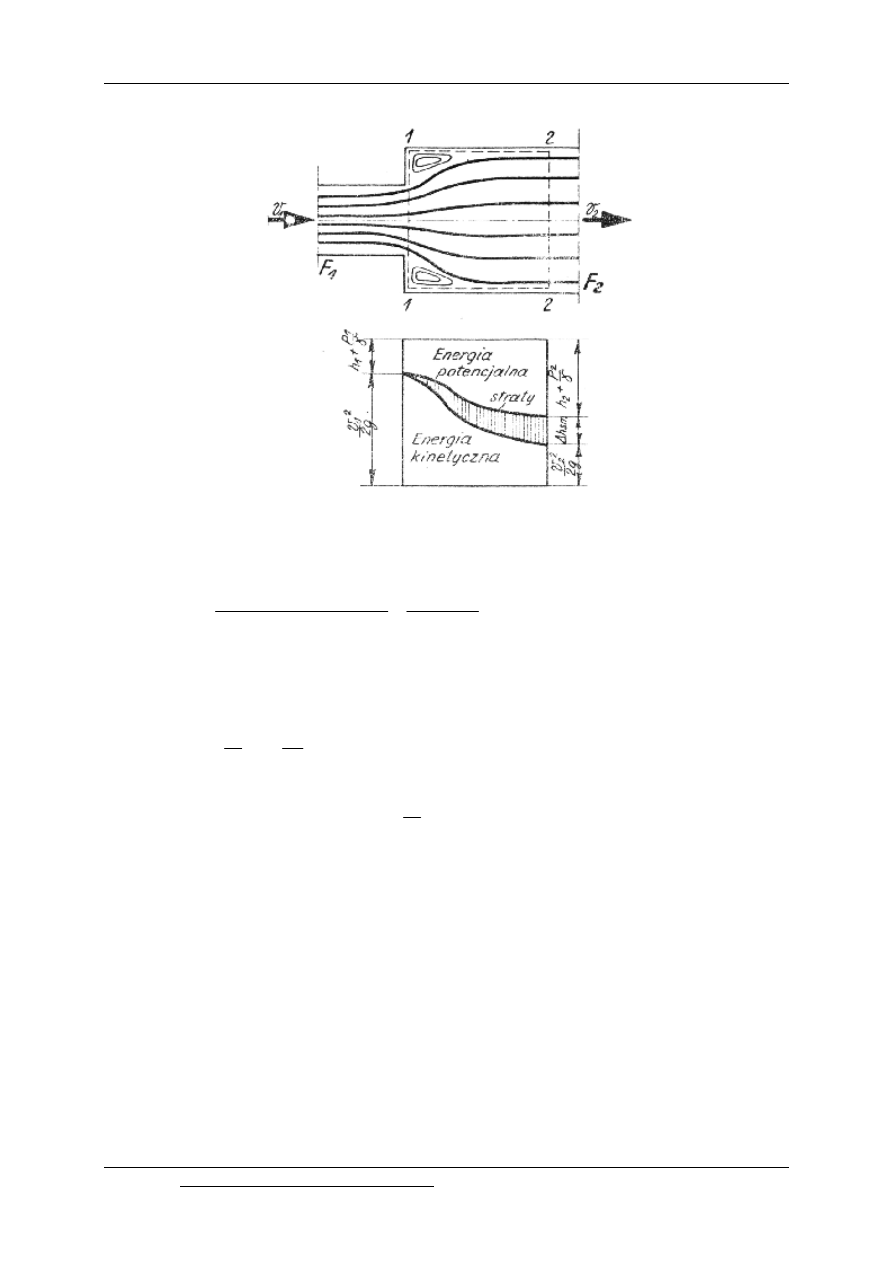
Równanie Bernoulliego dla przekrojów 1-1 i 2-2 na postać:

2

2

1

1

2

2

sm

v

p

v

p

h

2g

2g

2g

2g

+

=

+

+ ∆

(12.7)

Zasadę pędu dla powierzchni kontrolnej /przy pominięciu naprężeń stycznych/

zaznaczonej na rys.12.4 można zapisać następująco:

(

)

(

)

2

1

2

1

2

Q v

v

F p

p

ρ⋅

−

=

−

(12.8)

Uwzględniając, że Q = F

2

v

2

otrzymamy z równania (12.8)

(

)

2

1

1

2

2

p

p

v

v

v

− = ρ

−

(12.9)

Pomiar strat miejscowych (lokalnych)

5

download: http://www.mech.pk.edu.pl/~m52/pdf/[12_opis].pdf

Rys. 12.4. Straty energetyczne przy nagłym zwiększaniu się przekroju

Podstawiając (12.9) do równania (12.7) otrzymamy:

(

)

(

) (

)

2

2

2

1

2

2

1

2

1

2

sm

v

v

2v

v

v

v

v

h

2g

2g

−

−

−

−

∆

=

=

(12.10)

Powyższa zależność nosi nazwę wzoru Bordy-Carnota. Podstawiając do równania (12.10),

v

1

F

1

= v

2

F

2

otrzymujemy:

2

2

2

2

sm

1

F

v

h

1

F

2g





∆

=

−









(12.11)

gdzie współczynnik strat lokalnych

2

2

1

F

1

F





ξ =

−









Rzeczywista strata energii przy gwałtownym rozszerzeniu jest nieco większa.

12.5. Straty energetyczne przy skokowym zmniejszaniu przekroju

Przy przepływie cieczy przez nagłe zwężenie przewodu podstawowe znaczenie mają

straty występujące wskutek przewężenia /kontrakcji/ strumienia, a następnie wskutek jego

gwałtownego rozszerzenia.

Oznaczając przez v

0

średnią prędkość, w przekroju przewężenie –F

0

, a przez

β

- współczynnik zwężenia strugi, równanie ciągłości można zapisać w postaci:

0

0

2

0

2

2

F v

F v

F v

= β

=

(12.12)

6

Pomiar strat miejscowych (lokalnych)

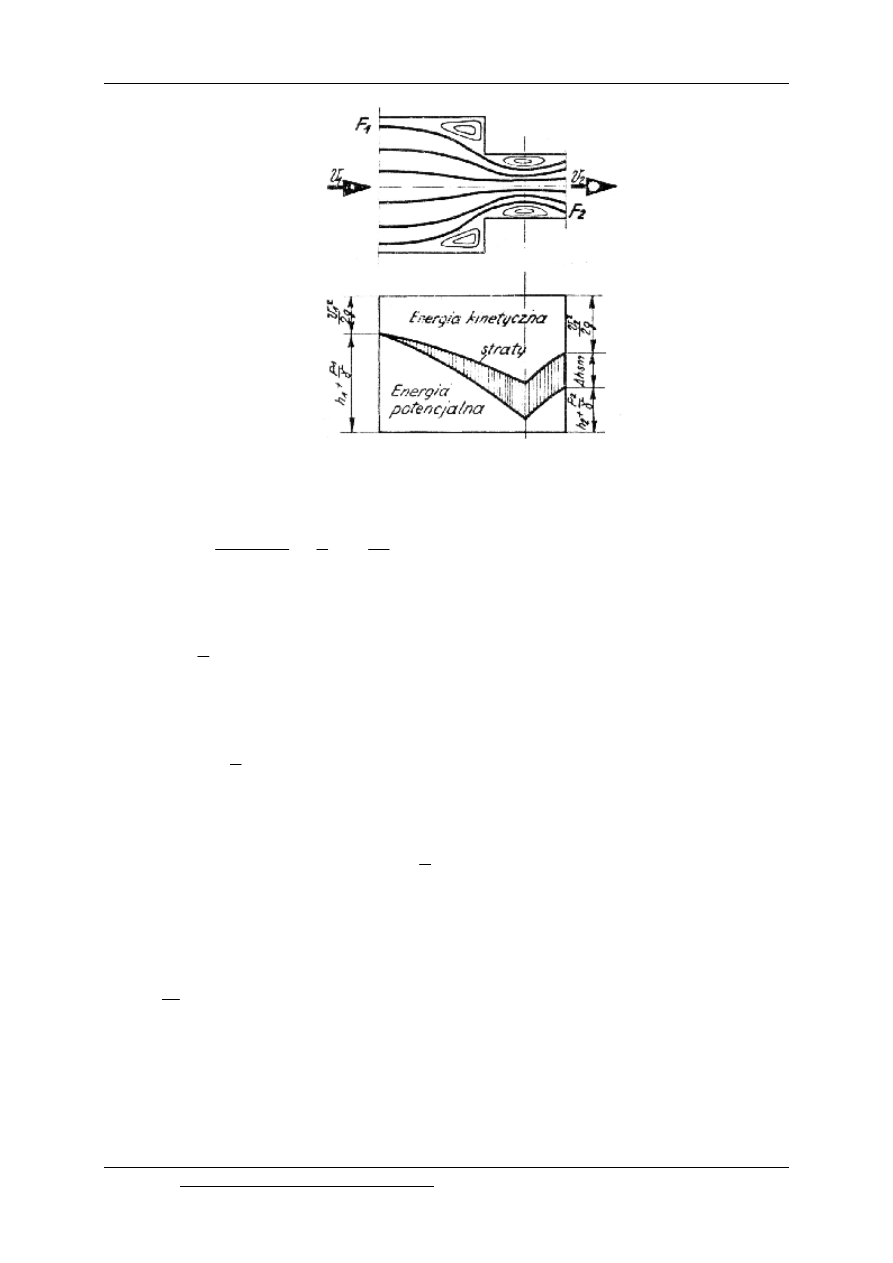
download: http://www.mech.pk.edu.pl/~m52/pdf/[12_opis].pdf

Rys. 12.5. Straty energetyczne przy nagłym zmniejszaniu się przekroju

Wysokość strat energetycznych przy przejściu z przekroju F

1

do przekroju F

2

wyniesie:

(

)

2

2

2

0

2

2

sm

v

v

v

1

h

1

2g

2g

−





∆

=

=

−





β





(12.13)

stąd współczynnik strat:

2

1

1





ξ =

−





β





(12.14)

W praktyce częściej stosuje się formułę Weisbacha [2]:

2

0

1

1





ξ = ξ +

+





β





(12.15)

Stała

ξ

0

= 0.04 odpowiada stratom spowodowanym oddziaływaniem krawędzi dławiącej na

masę płynącego płynu, natomiast człon

2

1

1





+





β





uwzględnia straty wywo2łane zwężeniem

i ponownym rozszerzeniem strugi. Współczynnik zwężenia

β

zależy od stosunku F

2

/F

1

.

W szczególności przy:

2

1

F

0.1

F

≤

β

= 0.61

÷

0.64 - przy krawędzi ostrej,

β

= 0,68

÷

0,8 - przy lekko sfazowanej krawędzi,

β

= 0,99 - przy zaokrąglonej i wygładzonej krawędzi.

Pomiar strat miejscowych (lokalnych)

7

download: http://www.mech.pk.edu.pl/~m52/pdf/[12_opis].pdf

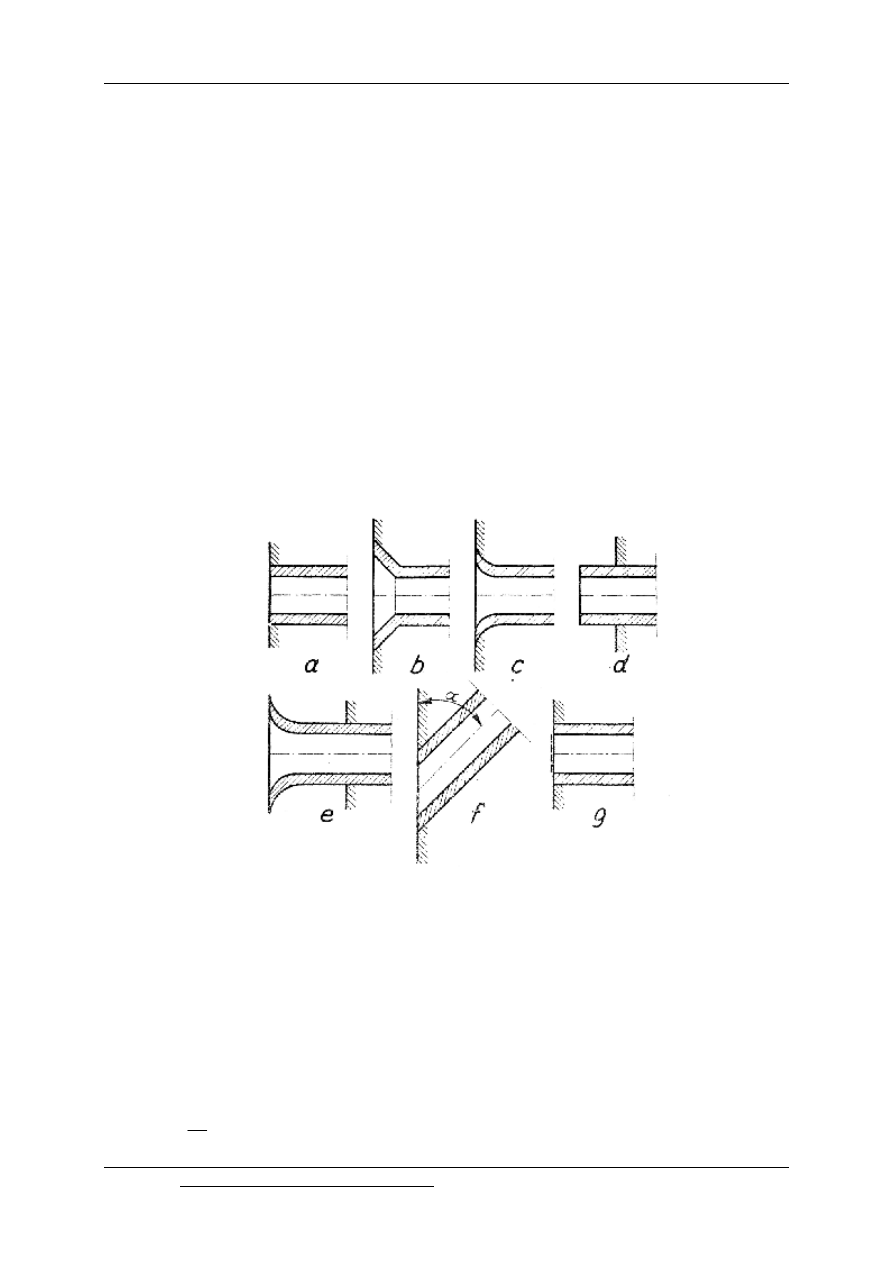
12.6. Straty energii na wlocie do przewodu

Na podstawie doświadczeń J. Weisbacha straty energii na wlocie do przewodu wynoszą

[2]:

a) dla wlotów o ostrych krawędziach -

ξ

= 0.3,

b) dla wlotów o ściętych krawędziach -

ξ

= 0,25,

c) dla wlotów o krawędziach łagodnie zaokrąglonych, zależnie od ukształtowania wlotu

i chropowatości ścian -

ξ

= 0.1

÷

0.005,

d) dla wlotu zatopionego o ostrych krawędziach -

ξ

= 3.0,

e) o zaokrąglonych krawędziach -

ξ

= 0.55,

f) pod kątem

α

o ostrych krawędziach:

2

0.5 0.3cos

0.2 cos

ξ =

+

α +

α

g) dla wlotu z siatką /wolny przekrój siatki 80 %/

ξ

= 0,4.

Rys. 12.6. Straty energii na wlocie do przewodu

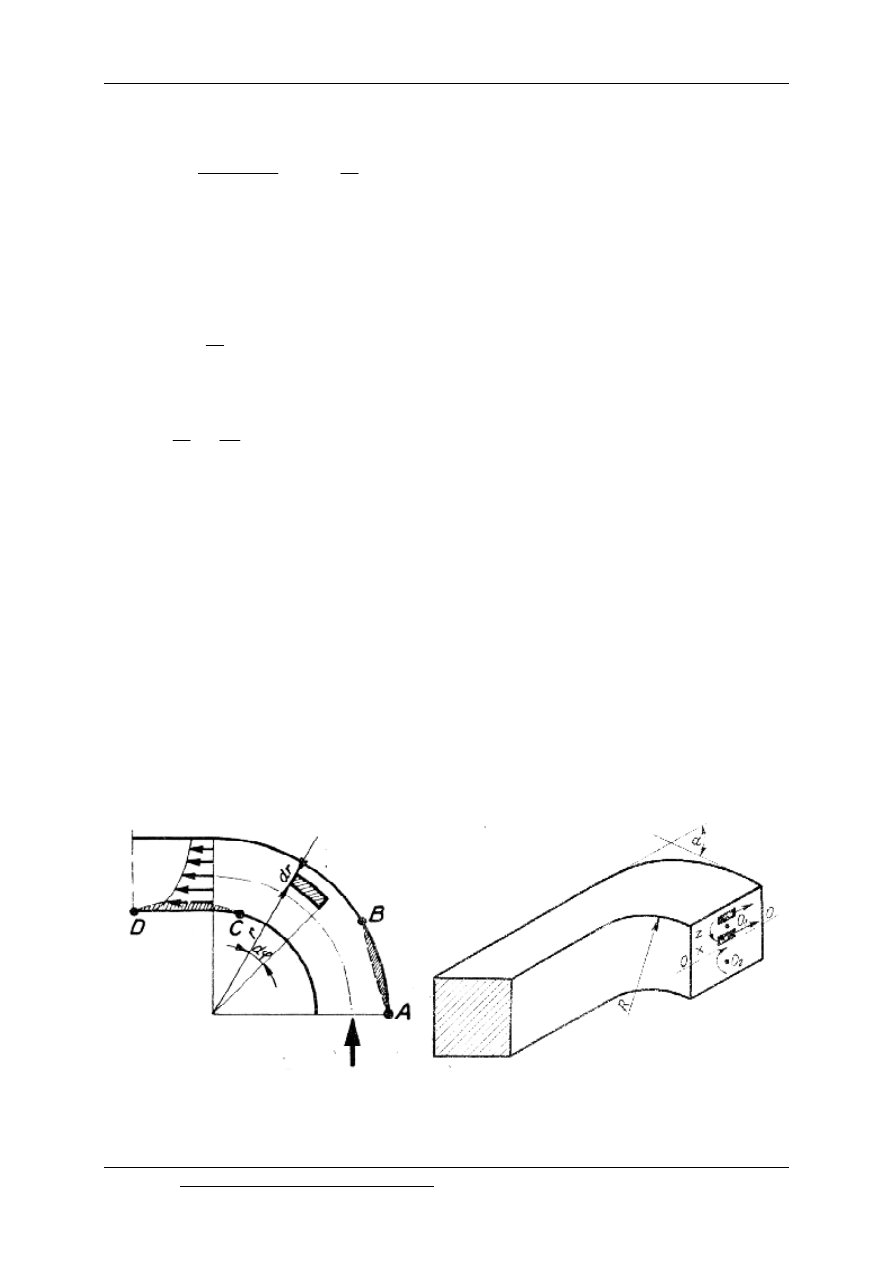
12.7. Straty energetyczne wywołane zakrzywieniem rury

Wyodrębnimy myślowo w płynie poruszającym się kolanie element o wymiarach rd

ϕ

,

dr i grubości jednostkowej. Masa tego elementu wyniesie

dm

r d

dr

= ρ⋅ ⋅ ϕ⋅

(12.16)

Siła odśrodkowa działająca na element ma wartość:

2

2

v

dm

v d

dr

r

= ρ⋅

ϕ⋅

8

Pomiar strat miejscowych (lokalnych)

download: http://www.mech.pk.edu.pl/~m52/pdf/[12_opis].pdf

Wartość ciśnienia spowodowana działaniem siły odśrodkowej wynosi:

2

2

v d

dr

dr

dp

v

r d

r

ρ⋅

ϕ⋅

=

= ρ⋅ ⋅

⋅ ϕ

(12.17)

Porównując równanie (12.16) i równanie Bernoulliego w postaci różniczkowej

dp

v dv

= −ρ⋅ ⋅

otrzymamy:

2

dr

v

v dv

r

ρ⋅ ⋅

= −ρ⋅ ⋅

Całkując to równanie:

dr

dv

const.

r

v

=

+

∫

∫

znajdziemy:

v r

const.

⋅ =

Wynika stąd, że prędkość w przekroju poprzecznym kolana cieczy doskonałej zmienia

się hiperbolicznie. Tarcie cieczy rzeczywistej bardziej zmniejsza prędkość elementów cieczy

poruszających się po zewnętrznym łuku kolana tak, że prędkość tych elementów spada do

zera, zmieniając następnie znak na przeciwny. Ten rozkład prędkości powoduje, że na ściance

kolana powstaje wzrost ciśnienia od niezakłóconej wartości p

0

w punkcie A aż do

podwyższonej wartości w punkcie B. Zatem w obszarze AB ciecz płynie naprzeciw

wzrastającemu ciśnieniu przy malejącej prędkości. Na stronie wewnętrznej kolana ciśnienie

zmniejsza się do punktu C i poczynając od niego znowu rośnie w kierunku D.

Rys. 12.7 a) Straty energetyczne wywołane zakrzywieniem rury, b) obrót płynu dookoła punktu O na
skutek różnicy sił odśrodkowych

a)

b)

Pomiar strat miejscowych (lokalnych)

9

download: http://www.mech.pk.edu.pl/~m52/pdf/[12_opis].pdf

W obszarze C-D, podobnie jak w obszarze AB, ciecz płynie przy wzrastającym

ciśnieniu /wskutek spadku prędkości w warstwie przyściennej/. Powstaje zjawisko podobne

jak przy przepływie cieczy przez rozszerzający się przewód, które powoduje oderwanie się

cieczy i straty energii strumienia.

Przy przepływie przez kolano mamy do czynienia jeszcze z jednym zjawiskiem, które

powoduje powstanie tzw. podwójnego wiru wewnątrz poszczególnych przekrojów

poprzecznych kolana. Podzielmy przekrój kanału kwadratowego prostą 0-0. Wskutek

zmiennego profilu prędkości /równanie (12.17)/ prędkość elementu z jest mniejsza niż

elementu x; siły odśrodkowe działająca na te elementy muszą być różne.

Różnica sił odśrodkowych powoduje obrót płynu dookoła punktu O. /rys.12.7b/. Taki

sam obrót, lecz w kierunku przeciwnym, występuje w drugiej części przekroju. Oprócz

prędkości podstawowej ruchu głównego postępowego istnieje jeszcze składowy ruch

obrotowy, więc wypadkowy ruch cieczy w kolanie odbywa się po linii śrubowej. Ilość energii

zużyta na wytworzenie wirów jest miarą strat energii przy przepływie przez kolano.

Całkowite straty energii przy przepływie przez kolano są sumą strat tarcia i strat

spowodowanych wytworzeniem poprzecznego wiru podwójnego.

Ze względu na złożoność zjawisk musimy polegać na formułach empirycznych, które

ujmują w sposób sumaryczny zjawiska energetyczne zachodzące przy przepływie cieczy

przez kolana.

Współczynnik oporu dla krzywaków o przekroju kołowym wynosi wg Weisbacha [2]:

0.131:

ξ =

3.5

o

D

0.163

R

90



 α

 





 





 





(12.18)

gdzie: D - średnica wewnętrzna przewodu, R - promień krzywizny.

Dla krzywaków o przekroju prostokątnym i stosunku boków

a

2

b

≤

, wg Weisbacha [2]:

0.124 :

ξ =

3.5

o

a

0.274

R

90



 α

 





 





 





(12.19)

gdzie: a - szerokość przekroju prostokąta mierzona po promieniu.

Współczynnik oporu

ξ

można wyznaczyć wg Richtera i Fritschego [4] dla przewodów

prostokątnych z zależności:

1

2

3

k k k

k

ξ = ⋅ ⋅ ⋅

(12.20)

gdzie: k = 0.73,

1

R

k

f

b

 

=  

 

,

( )

2

k

f

= α

,

3

h

k

f

b

 

=  

 

.

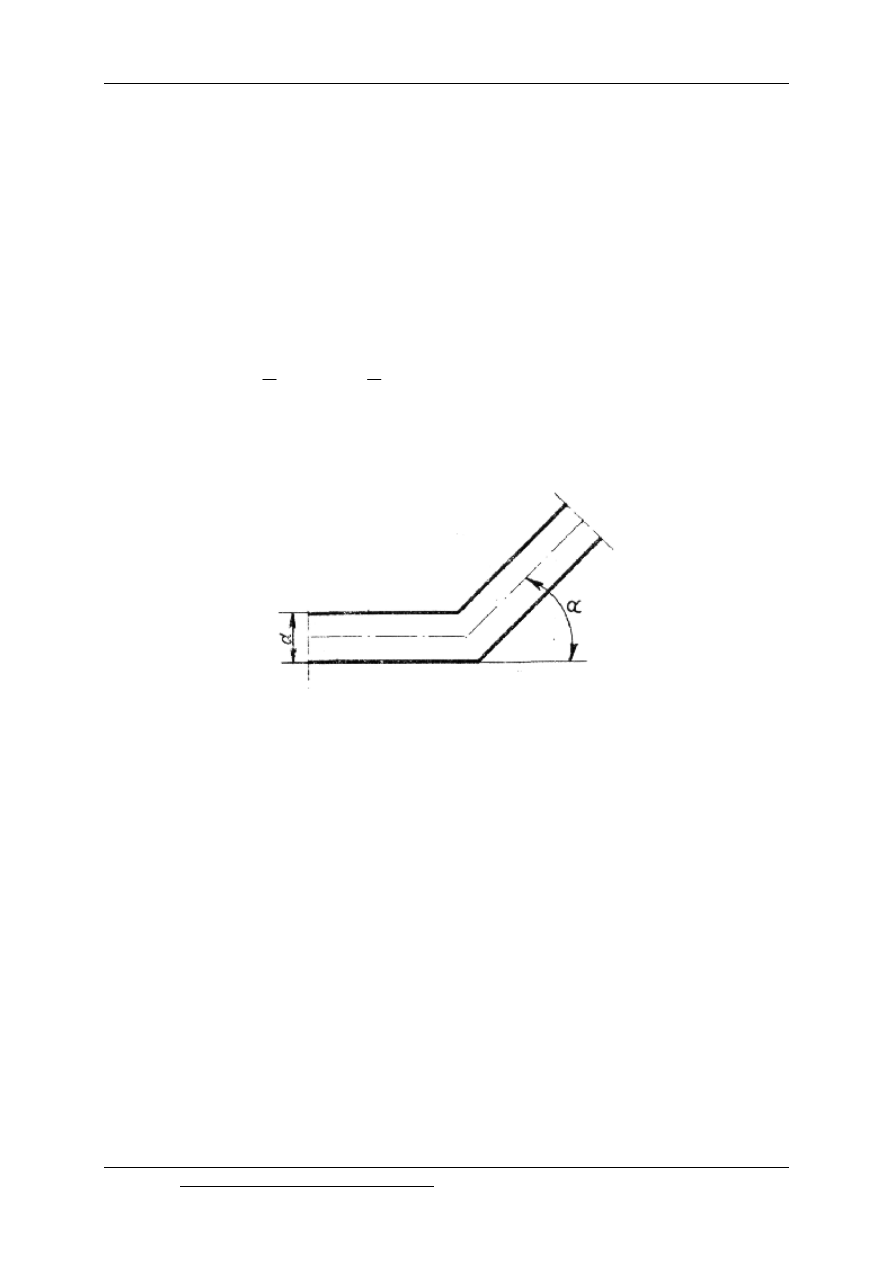
10

Pomiar strat miejscowych (lokalnych)

download: http://www.mech.pk.edu.pl/~m52/pdf/[12_opis].pdf

Badania Nipperta wykazały, że współczynnik strat jest zależny również od liczby

Reynoldsa, a na podstawie badań Hoffmana okazuje się, że wielkość współczynnika strat

zależy również od chropowatości kolana.

12.8. Straty energetyczne w załomie rury

Przepływ przez załamanie przebiega podobnie jak przez kolano z tyra, za strumień

odrywa się gwałtowniej, co powoduje większe straty miejscowe.

Wg badań Weisbacha [2]:

2

4

0.964sin

2.047 sin

2

2

α

α

ξ =

+

(12.21)

Wg badań Gibsona [4]:

6

2.17

67.6 10

−

ξ =

⋅

⋅α

(12.22)

Rys.12.8. Straty energetyczne w załomie rury

Współczynnik oporu wyznaczony w oparciu o badania Gibsona ma wartości wyższe

w porównaniu z wartościami wyliczonymi ze wzoru J. Weisbacha. Badania Zimmermanna

ustalające wpływ liczby Reynoldsa na wartość współczynnika oporu

ξ

wykazały jeszcze

większe wartości

ξ

.

12.9. Straty energii spowodowane zaworami

Wielkość strat energii w zaworach jest uzależniona od konstrukcji kanału przelotowego

w zaworze oraz od parametrów przepływającego płynu.

Przykładowo, dla zaworów grzybkowych przy pełnym otwarciu, w zależności od

konstrukcji zaworu mamy:

a) dla prostych -

ξ

= 3.9,

b) dla półprzelotowych -

ξ

= 2.5,

c) dla wolnoprzelotowych -

ξ

= 0,6.

Pomiar strat miejscowych (lokalnych)

11

download: http://www.mech.pk.edu.pl/~m52/pdf/[12_opis].pdf

Obecnie jednymi z częściej stosowanych elementów w rurociągach są zawory kulowe.

W przypadku zaworu kulowego wielkość strat lokalnych zależy od stopnia zamknięcia zaworu

ϕ.

Zależności te są opisane w normie PN-76/M-34034.

Tabela 1. Współczynnik strat lokalnych dla zaworu kulowego w funkcji kąta zamknięcia zaworu wg [1].

ϕ

[

°

]

5

10

20

30

40

45

50

60

70

83

ξ

0,05 0,29 1,56 5,17

17,3

31,2 52,6 206

486

∞

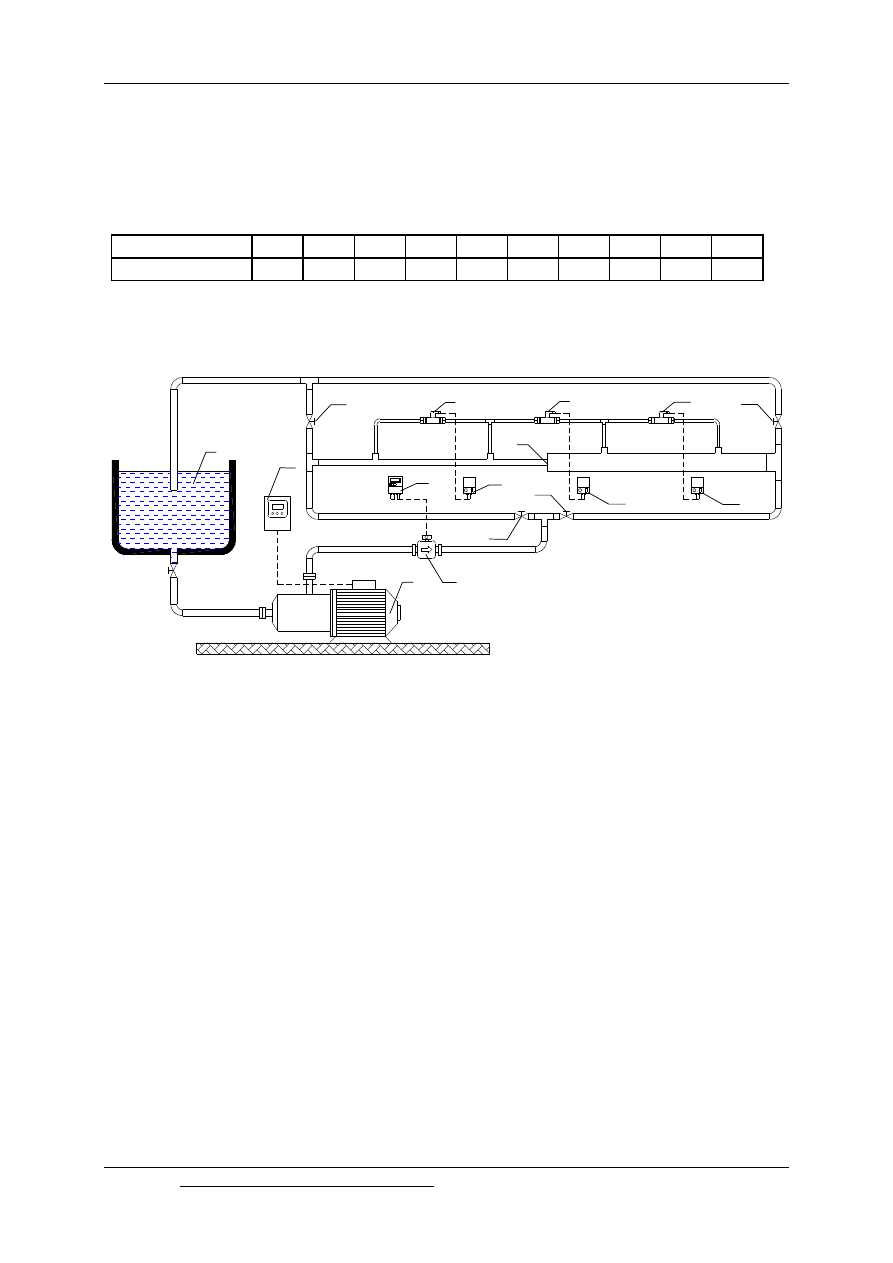
12.10. Stanowisko doświadczalne

L100

WILO

+

+

+

3

1

2

4

12

6

5

8

7

9

11

10

15

16

14

13

Rys. 12.9. Schemat stanowiska pomiarowego: 1 – zbiornik, 2 – pompa, 3 – skokowe rozszerzenie,

4 – miernik przepływu, 5 – sterownik przepływomierza, 6, 8, 10 – różnicowe czujniki

ciśnienia, 7, 9, 11 – przetworniki sygnału, 12 – – mikroprocesorowy przemiennik

częstotliwości, 13, 14, 15, 16 – zawory sterujące.

Przepływ cieczy w stanowisku doświadczalnym wymuszany jest za pomocą pompy (2),

która zasysa ciecz ze zbiornika (1). Prędkość obrotową silnika napędzającego pompę

i wynikające stąd objętościowe natężenie przepływu w stanowisku regulowane jest za pomocą

mikroprocesorowego przemiennika częstotliwości (12). Pomiaru wydatku objętościowego

dokonuje się za pomocą przepływomierza turbinowego. Do pomiaru strat ciśnienia

zastosowano 3 różnicowe przetworniki ciśnienia PTD firmy Peltron [6]. Elementem

pomiarowym czujnika jest wysokiej jakości piezorezystancyjny czujnik różnicy ciśnień

w postaci płytki krzemowej, na której umieszczono rezystory w postaci mostka Wheatstone’a.

Mierzone ciśnienie działa poprzez membrany separujące i olej silikonowy na czujnik,

powodując zmianę rezystancji mostka Wheatstone’a, na którego wyjściu pojawia się napięcie

o wartości proporcjonalnej do mierzonej różnicy ciśnień.

12

Pomiar strat miejscowych (lokalnych)

download: http://www.mech.pk.edu.pl/~m52/pdf/[12_opis].pdf

Napięcie wyjściowe z czujników doprowadzone jest do specjalnych wzmacniaczy

WP-01A (7, 9, 11). Przetwarzają one sygnał wyjściowy z czujników ciśnienia PTD na

standardowy sygnał prądowy (0÷20 mA) lub napięciowy (0÷10 V). Dodatkowo wartość

ciśnienia wyświetlana jest na wyświetlaczu.

12.11. Przebieg ćwiczenia

a) po włączeniu pompy i ustawieniu odpowiedniego kierunku przepływu cieczy, dla różnych

natężeń przepływu odczytać spadki ciśnienia na poszczególnych odcinkach,

b) określić współczynniki strat miejscowych dla poszczególnych liczb Reynoldsa.

Zapiszmy równanie Bernoulliego dla przekrojów, pomiędzy którymi mierzymy różnicę

ciśnień

∆

p = p

1

– p

2

2

2

1

1

1

2

2

2

1

2

st

sm

v

p

v

p

z

z

h

h

2g

2g

α ⋅

α ⋅

+

+ =

+

+ +

+

γ

γ

(12.23)

gdzie:

α

1

, α

2

−

współczynniki Coriolisa, dla ruchu turbulentnego

α

≈ 1,

h

st

- wysokość strat tarcia cieczy,

h

sm

- wysokość strat miejscowych.

Na wysokość strat tarcia

∆

h

st

będą się składać straty wywołane tarciem wewnętrznym

cieczy w przewodzie zarówno przed, jak i za przeszkodą miejscową, czyli:

2

2

1

1

2

2

st

1

1

1

2

L

v

L

v

h

d

2g

d

2g

= λ

⋅

+ λ

⋅

(12.24)

Wysokość tych strat może być policzona na podstawie pomiaru spadku ciśnienia na

dwukrotnie dłuższym odcinku pomiarowym przed i za przeszkodą:

1

2

1

2

st

p

p

p

p

1

1

h

2

2

2

∆

∆

∆ + ∆

=

+

=

γ

γ

γ

(12.25)

Po podstawieniu wyznaczonych wartości strat tarcia do równania Bernoulliego (12.23) można

wyznaczyć wysokość strat miejscowych na przeszkodzie:

2

2

1

2

1

2

sm

v

v

p

p

p

h

2g

2

−

∆ + ∆

∆

=

+

−

γ

γ

(12.26)

Znając wysokość strat miejscowych z równania (12.2) można wyznaczyć współczynnik strat

miejscowych z zależności:

Pomiar strat miejscowych (lokalnych)

13

download: http://www.mech.pk.edu.pl/~m52/pdf/[12_opis].pdf

sm

2

2 g

h

v

⋅

ξ =

dla danej wartości liczby Reynoldsa

d v

Re

⋅

=

ν

(12.27)

c/ wykonać wykres zależności współczynnika strat miejscowych

ξ

od liczby Reynoldsa.

12.12. Literatura

[1] PN-76/M-34034. Rurociągi. Zasady obliczeń strat ciśnienia.

[2] Troskolanski A., T.: Hydromechanika. WNT, Warszawa 1969, ss. 372-383.

[3] Bukowski J.: Mechanika płynów. PWN, Warszawa 1968, są.228-236.

[4] Walden H., Stasiak J.: Mechanika cieczy i gazów w inżynierii sanitarnej. Arkady,

Warszawa 1971 ss. 236-265.

[5] Daili D., Harlem D.: Miechanika żidkosti. Izd. Energija. ss. 329-345, Moskwa 1971.

[6] Przetworniki różnicy ciśnień seria PTD. Peltron LTD. http://www.peltron.home.pl/pub/ptd.pdf