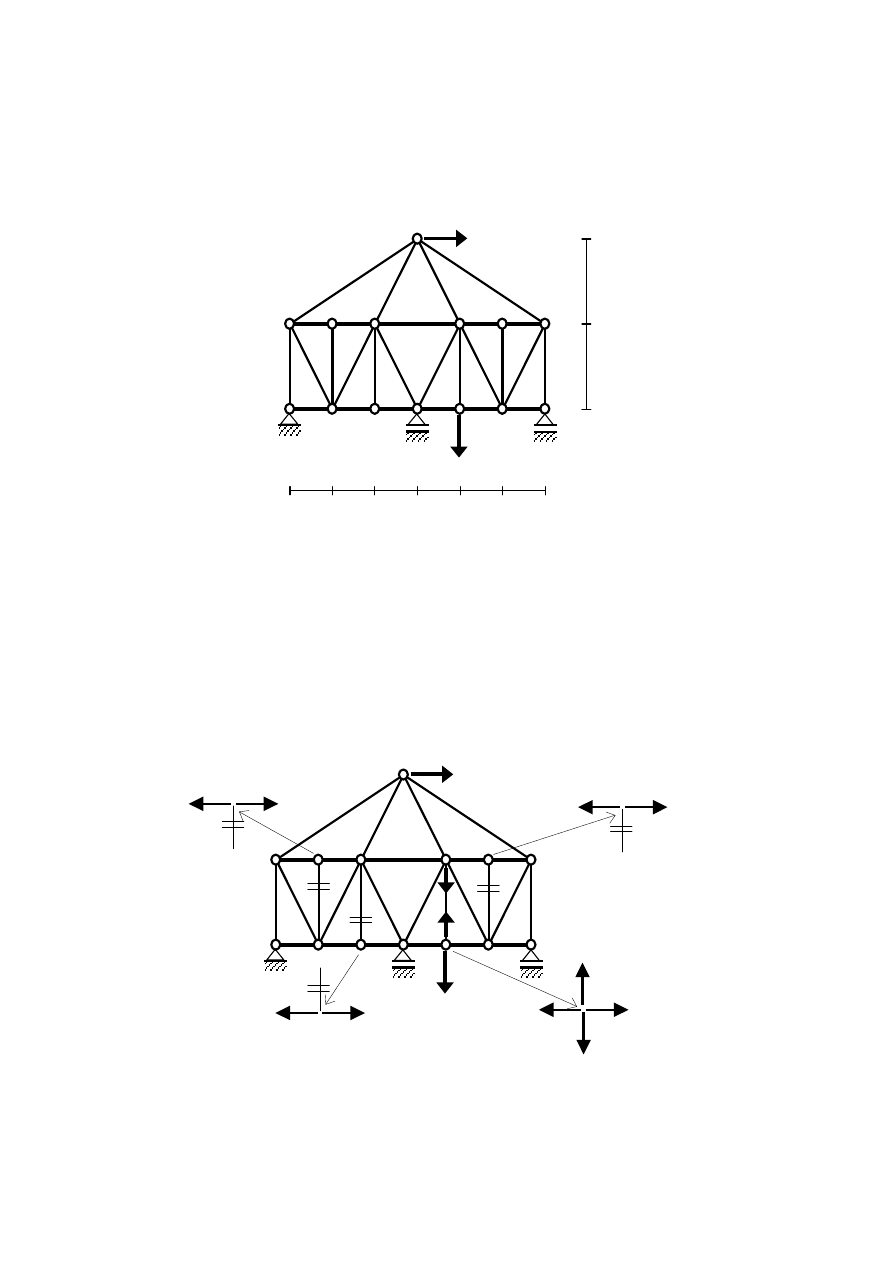
Przykład 5.2. Kratownica trzykrotnie statycznie niewyznaczalna
Polecenie: korzystając z metody sił wyznaczyć siły w prętach poniższej kratownicy. Przyjąć
sztywność ściskania dla słupków i krzyżulców równą EA, a dla prętów pasa dolnego i
górnego 2EA.
Rozwiązanie
zadania
rozpoczynamy
od
obliczenia
stopnia
statycznej
niewyznaczalności układu. W przypadku płaskiej kratownicy z węzłami przegubowymi
n = r + p − 2 · w
gdzie:
r
- liczba składowych reakcji podpór
p - liczba prętów kratownicy
w
- liczba węzłów kratownicy.
W rozpatrywanym układzie stopień statycznej niewyznaczalności wynosi
n = 4 + 27 − 2 · 14 = 3
Pomimo iż rozważana kratownica jest statycznie niewyznaczalna, to siły w czterech
słupkach można wyznaczyć z równań równowagi.
Uwzględniając ponadto jednakową sztywność ściskania dla prętów pasa dolnego i
górnego oraz równości:
2
1
G
G
=
,
5
4
G
G
=
,
3
2
D
D
=
,
5
4
D
D
=
możemy rozwiązać
przedstawiona poniżej kratownicę o mniejszej ilości prętów.
P
3P
2l
2l
l
l
l
l
l
l
D
3
= D
2
D
2
P
3P
3P
G
2
= G
1
G
1
G
5
= G
4
G
4
S=3P
3P
D
5
= D
4
D
4
2
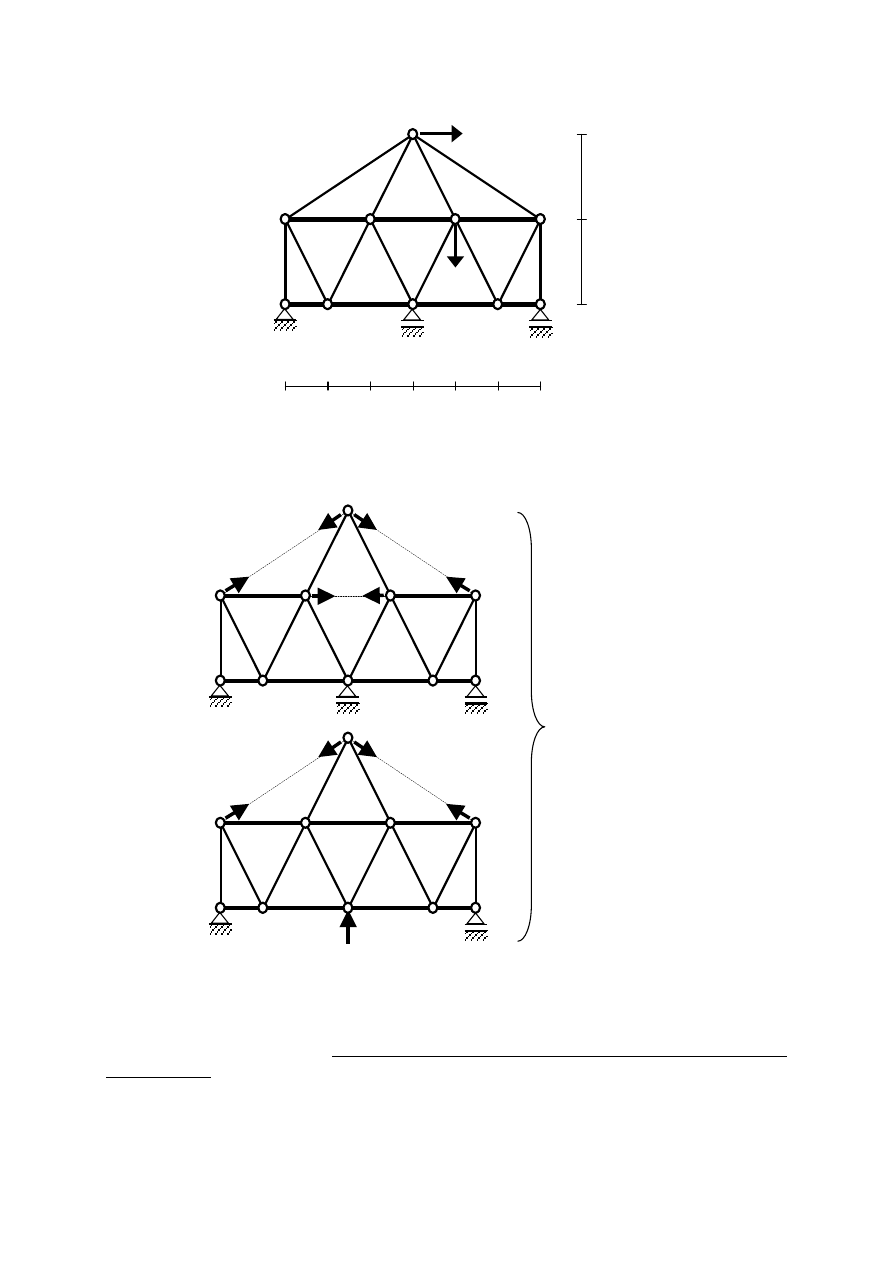
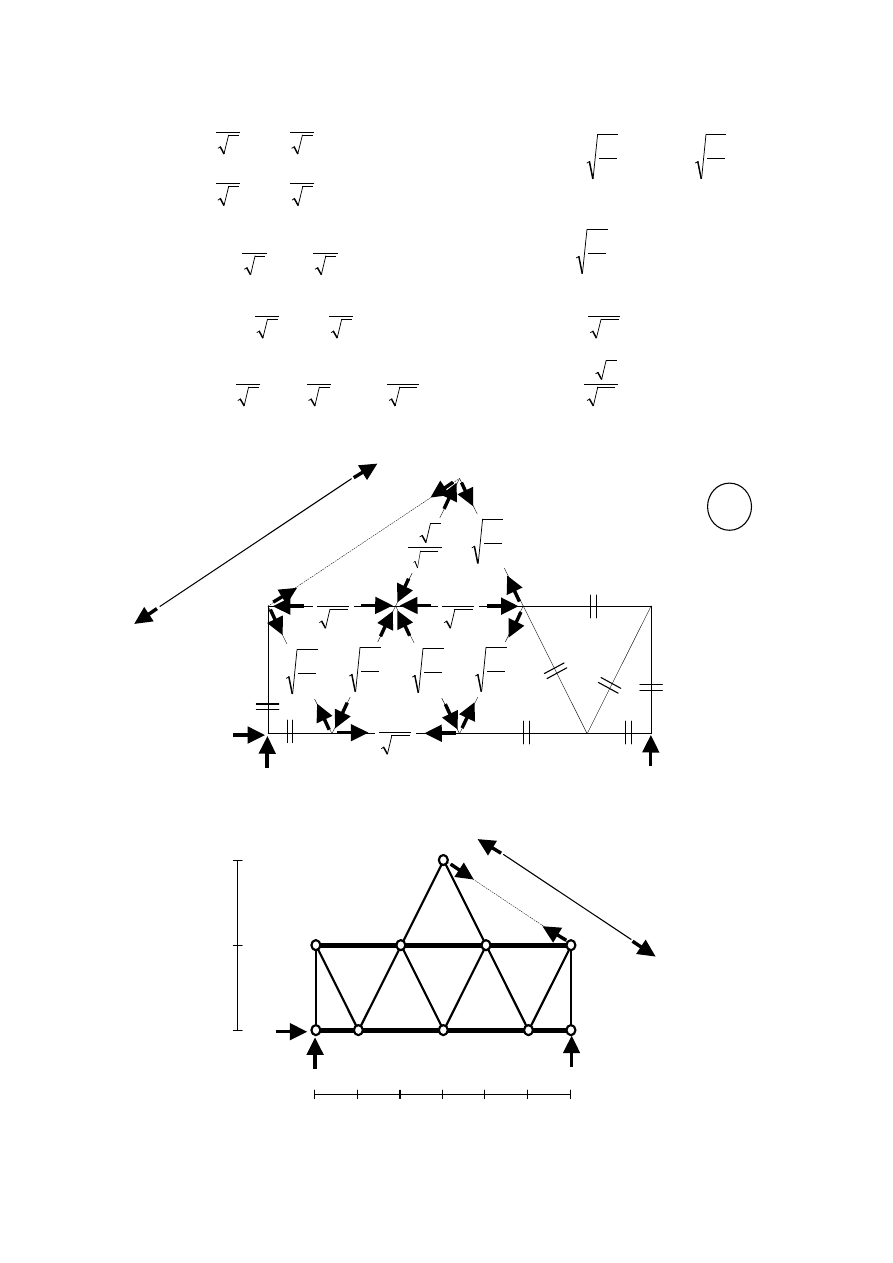
Układ jest trzykrotnie statycznie niewyznaczalny. Tworzymy układ podstawowy
statycznie wyznaczalny przez usunięcie trzech nadliczbowych więzów. Musi to być układ
geometrycznie niezmienny. Istnieje wiele takich schematów. Poniżej podano dwa przykłady.
Rozpatrywana kratownica jest układem zewnętrznie statycznie niewyznaczalnym.
Można, więc przyjąć jako jedną z trzech nadliczbowych reakcję podporową o kierunku
pionowym. Po usunięciu nadliczbowych więzów należy sprawdzić, czy otrzymany układ jest
geometrycznie niezmienny. Układ geometrycznie zmienny nie może być układem
podstawowym. Jako układ podstawowy przyjmiemy drugi spośród powyższych,
geometrycznie niezmiennych układów.
Poniżej pokazany jest układ geometrycznie zmienny otrzymany po usunięciu trzech
więzów w rozpatrywanej, trzykrotnie statycznie niewyznaczalnej kratownicy.
P
3P
2l
2l
l
l
l
l
l
l
Układy
geometrycznie
niezmienne
1
X
2
X
3
X
1
X
2
X
3
X
3
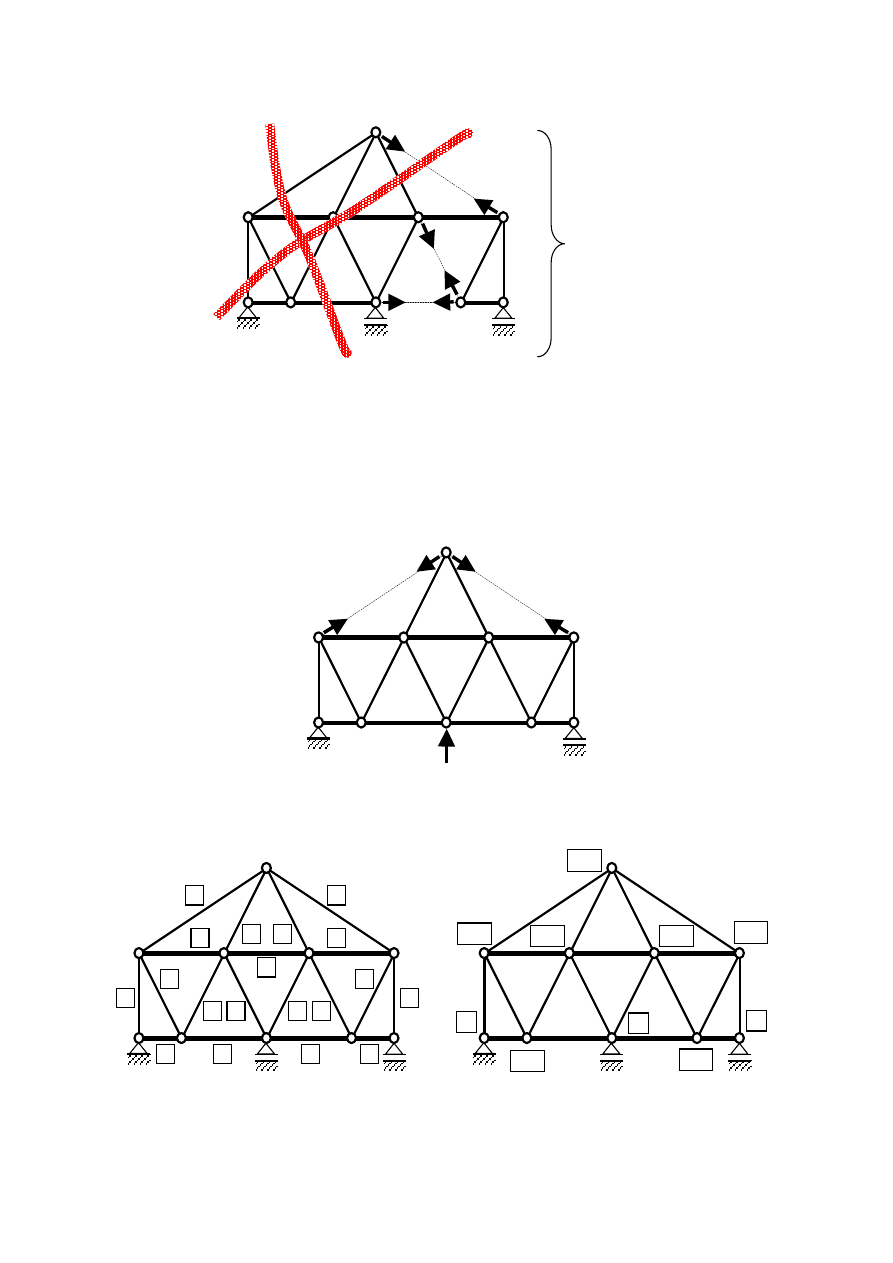
Siły w prętach nie zależą od przyjętego układu podstawowego. Wybór tego układu jest
jednak istotny, ponieważ od niego zależy, czy rozwiązanie zadania będzie mniej lub bardziej
pracochłonne. Poniższy rysunek przedstawia przyjęty do obliczeń układ podstawowy. W tak
przyjętym układzie podstawowym siły w prętach wyznaczone w stanie
1
1
=
X
możemy
wykorzystać również w stanie
1
2
=
X
ze względu na symetryczną budowę układu
podstawowego (składowa pozioma reakcji na podporze nieprzesuwnej jest równa zero w
stanach
1
,
1
,
1
3
2
1
=
=
=
X
X
X
).
Pzed przystąpieniem do obliczeń ponumerujemy pręty i węzły.
Wyznaczamy siły w prętach wywołane przez jednostkowe siły nadliczbowe i
obciążenie zewnętrzne w układzie podstawowym.
1
X
2
X
3
X
Układ
geometrycznie
zmienny
1
X
2
X
3
X
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
Oznaczenie prętów
Oznaczenie węzłów
W
6
W
5
W
1
W
4
W
3
W
2
W
7
A
B
C
4
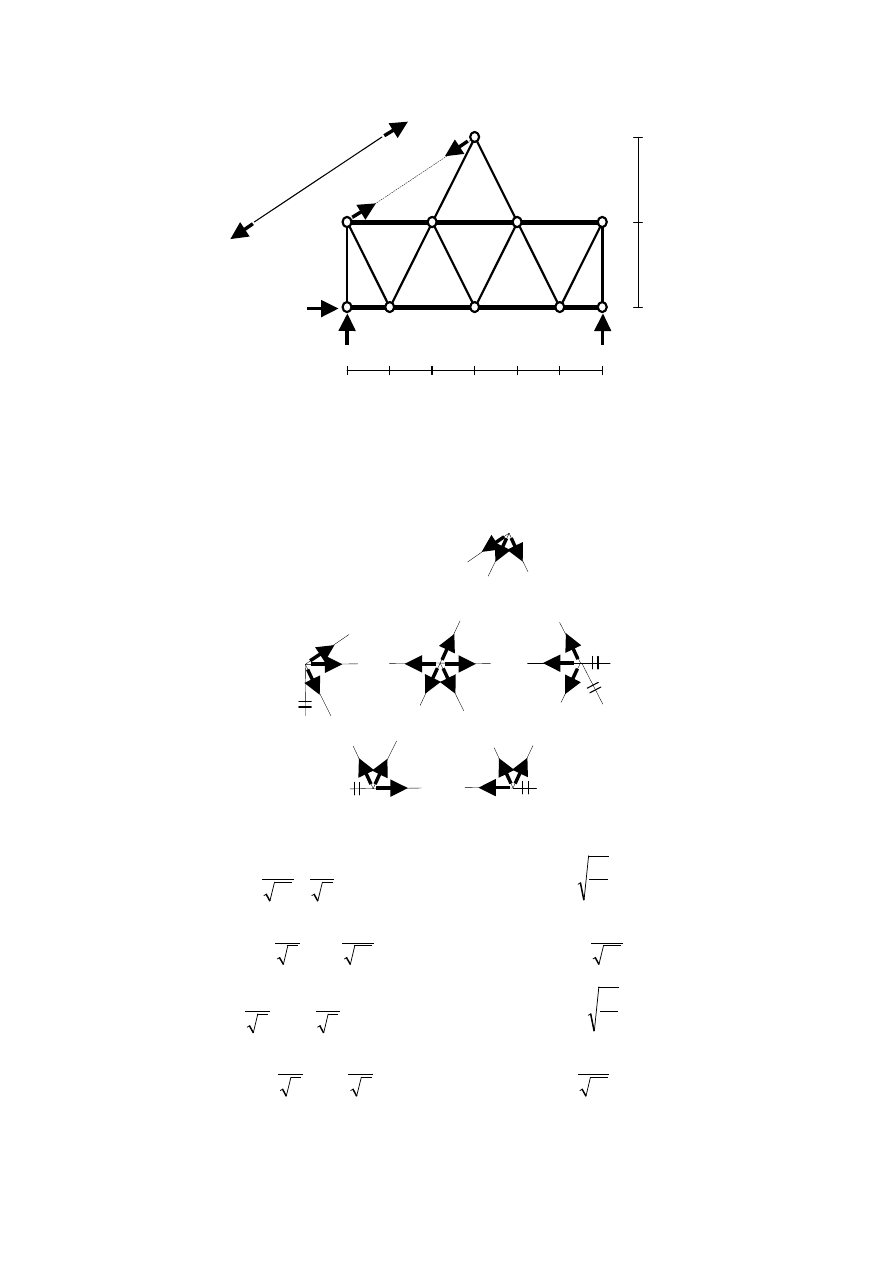
Stan X
1
= 1
W rozpatrywanym stanie obciążeniem są dwie jednostkowe siły o przeciwnych
zwrotach, mające wspólną linię działania (układ sił równoważących się). Otrzymamy, więc
wszystkie składowe reakcji podporowych zerowe. Siły S
1
, S
5
, S
11
, S
14
, S
15
, S
16
, S
17
, S
18
, S
19
są
równe zero. W celu wyznaczenia pozostałych sił w prętach kratownicy należy zapisać
równania równowagi dla węzłów W
1
, W
2
, W
3
, W
4
, W
6
oraz B.
13
5
0
5
2
13
2
1
0
4
4
2
=
⇒
=
⋅
−
⋅
=
∑
S
S
P
i
W
iy
13
4
0
1
13
3
5
1
0
3
4
3
2
−
=
⇒
=
⋅
+
⋅
+
=
∑
S
S
S
P
i
W
ix
13
5
0
5
2
5
2
0
6
6
4
6
−
=
⇒
=
⋅
+
⋅
=
∑
S
S
S
P
i
W
iy
13
2
0
5
1
5
1
0
7
6
4
7
6
=
⇒
=
⋅
+
⋅
−
=
∑
S
S
S
S
P
i
W
ix
Dla węzła B otrzymamy układ dwóch równań z dwiema niewiadomymi.
1
1
1
1
H
A
= 0
V
A
= 0
R
C
= 0
2l
2l
l
l
l
l
l
l
1
W
2
S
4
S
3
W
6
S
7
S
6
S
4
B
S
13
S
10
S
7
W
4
S
12
S
13
S
9
S
8
W
3
S
6
S
3
S
10
S
9
1
W
1
S
12
S
8
5
13
5
13
5
0
5
2
5
2
0
0
5
1
5
1
0
13
10
10
13
7
10
13
=
−
=
⇒
=
⋅
+
⋅
=
=
−
⋅
−
⋅
=
∑
∑
S
S
S
S
P
S
S
S
P
i
B
iy
i
B
ix
13
5
0
5
2
5
2
0
12
13
12
4
=
⇒
=
⋅
−
⋅
=
∑
S
S
S
P
i
W
iy
13
2
0
5
1
5
1
0
9
9
13
12
4
−
=
⇒
=
−
⋅
−
⋅
−
=
∑
S
S
S
S
P
i
W
ix
13
5
2
0
13
3
1
5
1
5
1
0
8
8
12
1
−
=
⇒
=
⋅
−
⋅
−
⋅
=
∑
S
S
S
P
i
W
ix
Pozostałe równania dla węzła W
1
i W
3
spełnione są tożsamościowo.
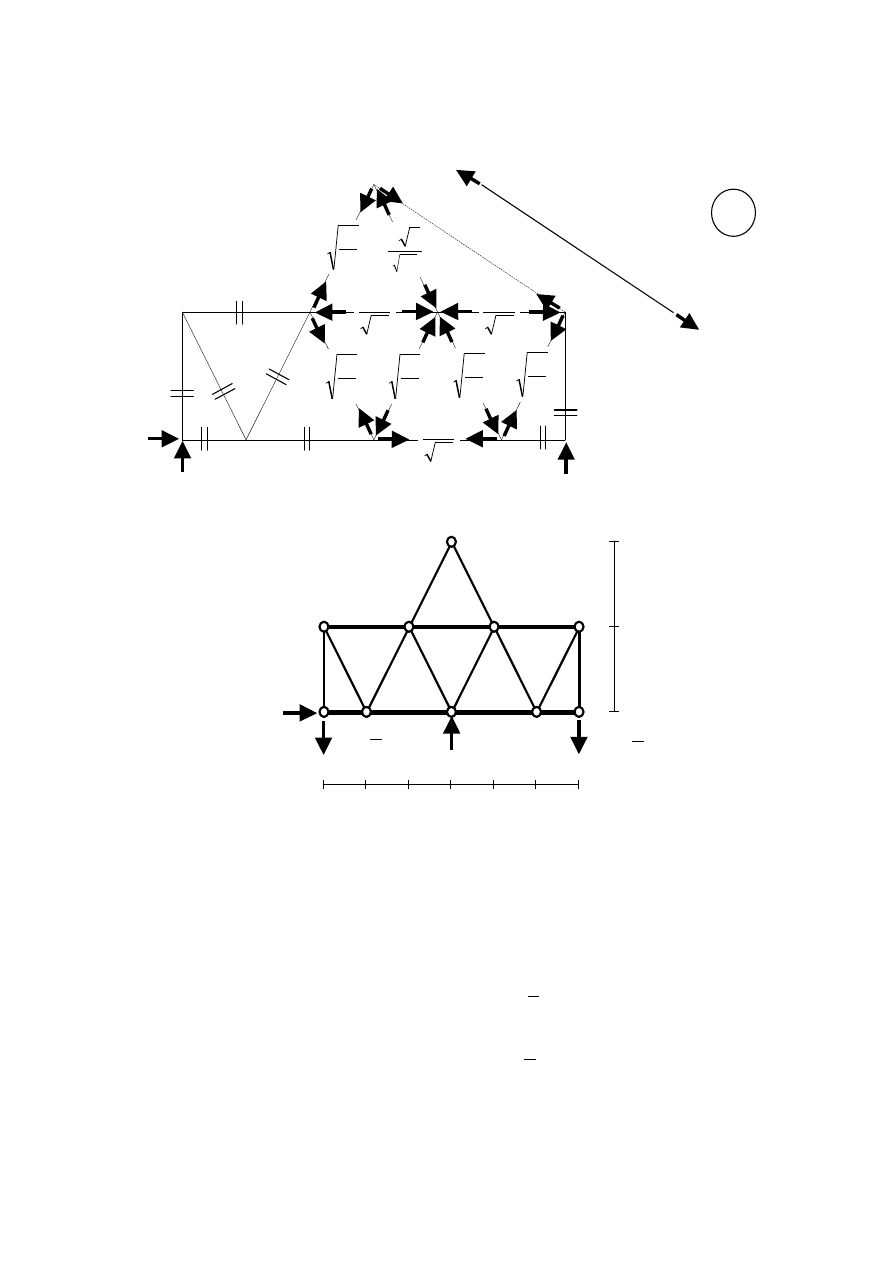
Stan X
2
= 1
)
(
1
i
N
i = 1, 2, …, 19
1
1
1
1
H
A
= 0
V
A
= 0
R
C
= 0
13
5
2
13
5
13
5
13
5
13
5
13
5
13
2
13
2
13
4
1
1
1
1
H
A
= 0
V
A
= 0
R
C
= 0
2l
2l
l
l
l
l
l
l
6
Możemy wykorzystać symetryczną budowę układu podstawowego. Rozkład sił w
prętach w stanie
1
2
=
X
jest „lustrzanym odbiciem” rozkładu sił w stanie
1
1
=
X
.
Stan X
3
= 1
Skoro składowa pozioma reakcji na podporze A jest równa zero, to rozkład sił w
prętach w stanie
1
3
=
X
ma charakter symetryczny. Możemy obliczyć siły dla prętów tylko
jednej połowy układu. Pozostałe siły wyznaczymy korzystając z symetrii.
Wyznaczamy reakcje podporowe:
0
0
=
⇒
=
∑
A
i
ix
H
P
2
1
0
3
1
6
:
0
=
⇒
=
⋅
+
⋅
−
=
∑
C
C
i
iA
R
l
l
R
M
2
1
0
1
0
=
⇒
=
−
−
=
∑
A
A
C
i
iy
V
V
R
P
Siły S
2
, S
5
, S
8
, S
11
, S
12
, S
18
są równe zero. Pozostałe siły w prętach kratownicy możemy
wyznaczyć z równań równowagi dla węzłów.
)
(
2
i
N
i=1, 2, …, 19
1
1
1
1
H
A
= 0
V
A
= 0
R
C
= 0
13
5
2
13
5
13
5
13
5
13
5
13
5
13
2
13
2
13
4
1
2l
2l
l
l
l
l
l
l
2
1
=
A
V
2
1
=
C
R
0
=
A
H
7
2
1
0
0
1
1
=
⇒
=
+
−
=
∑
S
S
V
P
A
i
A
iy
4
5
0
5
2
0
4
4
1
2
−
=
⇒
=
⋅
−
−
=
∑
S
S
S
P
i
W
iy
4
1
0
5
1
0
3
4
3
2
=
⇒
=
⋅
+
=
∑
S
S
S
P
i
W
ix
4
5
0
5
2
5
2
0
6
6
4
6
=
⇒
=
⋅
+
⋅
=
∑
S
S
S
P
i
W
iy
2
1
0
5
1
5
1
0
7
7
4
6
6
−
=
⇒
=
+
⋅
−
⋅
=
∑
S
S
S
S
P
i
W
ix
4
5
0
5
2
5
2
0
10
10
6
3
−
=
⇒
=
⋅
−
⋅
−
=
∑
S
S
S
P
i
W
iy
4
3
0
5
1
5
1
0
9
3
10
6
9
3
=
⇒
=
−
⋅
+
⋅
−
=
∑
S
S
S
S
S
P
i
W
ix
A
H
A
V
A
S
1
W
2
S
1
S
3
S
4
W
3
S
3
S
10
S
6
S
9
W
6
S
4
S
6
S
7
1
)
(
3
i
N
i = 1, 2, …, 19
2
1
2
1
2
1
2
1
2
1
2
1
4
1
4
1
4
3
4
5
4
5
4
5
4
5
4
5
4
5
0
8
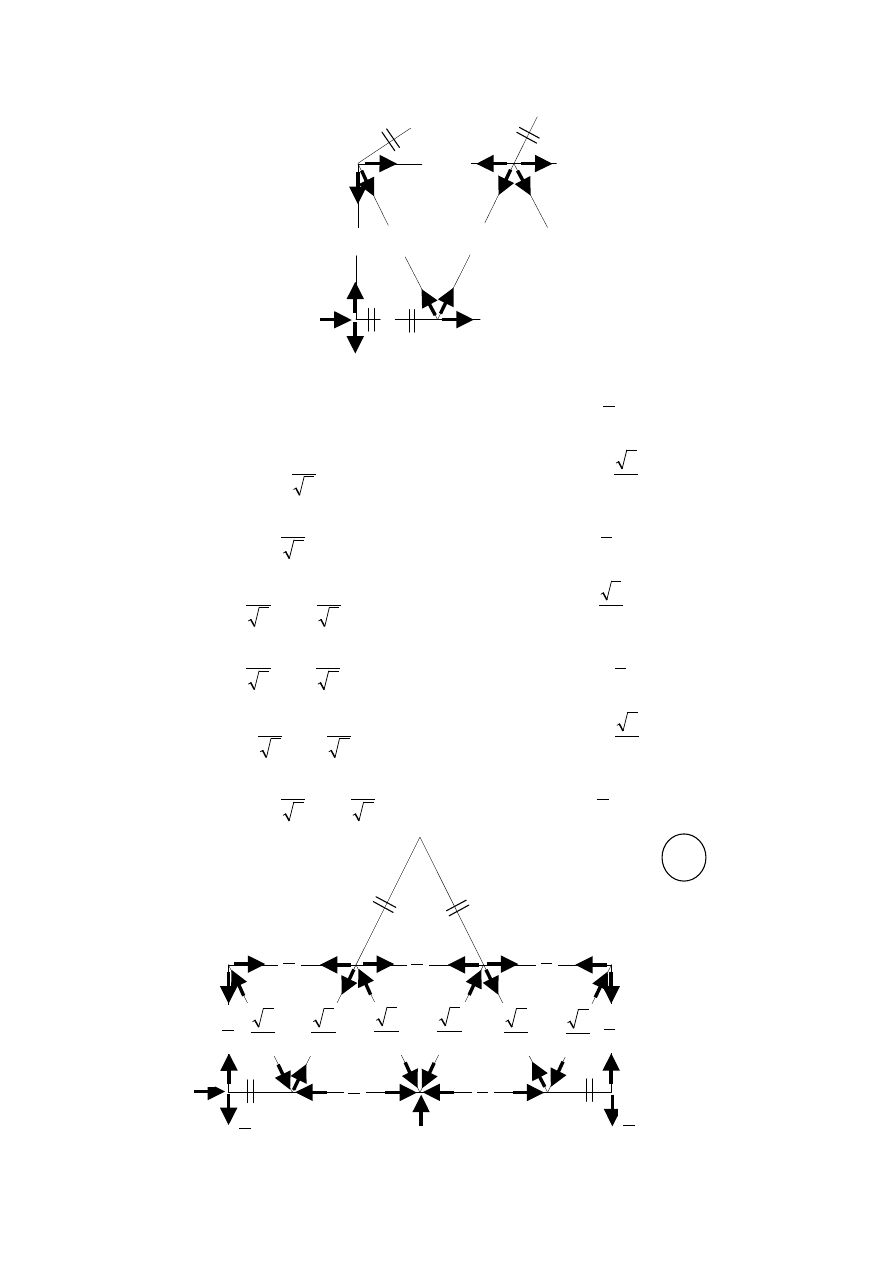
Stan zerowy (obciążenie zewnętrzne)
Wyznaczamy reakcje podporowe:
P
H
P
H
P
A
A
i
ix
=
⇒
=
+
−
=
∑
0
0
P
R
l
P
l
P
l
R
M
C
C
i
iA
3
8
0
4
3
4
6
:
0
=
⇒
=
⋅
−
⋅
−
⋅
=
∑
P
V
P
R
V
P
A
C
A
i
iy
3
1
0
3
0
=
⇒
=
−
+
=
∑
Siły S
2
, S
11
i S
18
są równe zero. W celu wyznaczenia pozostałych sił w prętach
kratownicy należy zapisać równania równowagi dla węzłów kratownicy.
P
S
S
P
P
i
A
ix
=
⇒
=
⋅
+
−
=
∑
5
5
0
0
P
3P
2l
2l
l
l
l
l
l
l
P
V
A
3
1
=
P
R
C
3
8
=
P
H
A
=
S
8
W
3
S
6
S
3
S
10
S
9
W
2
S
4
S
3
S
1
A
P
S
5
S
1
W
6
S
7
S
6
S
4
S
5
B
S
13
S
10
S
7
S
14
W
4
S
13
S
9
S
16
S
12
S
15
3P
P
W
1
S
12
S
8
S
4
S
3
S
19
W
5
W
7
S
17
S
16
S
14
C
S
19
P
3
1
P
3
8
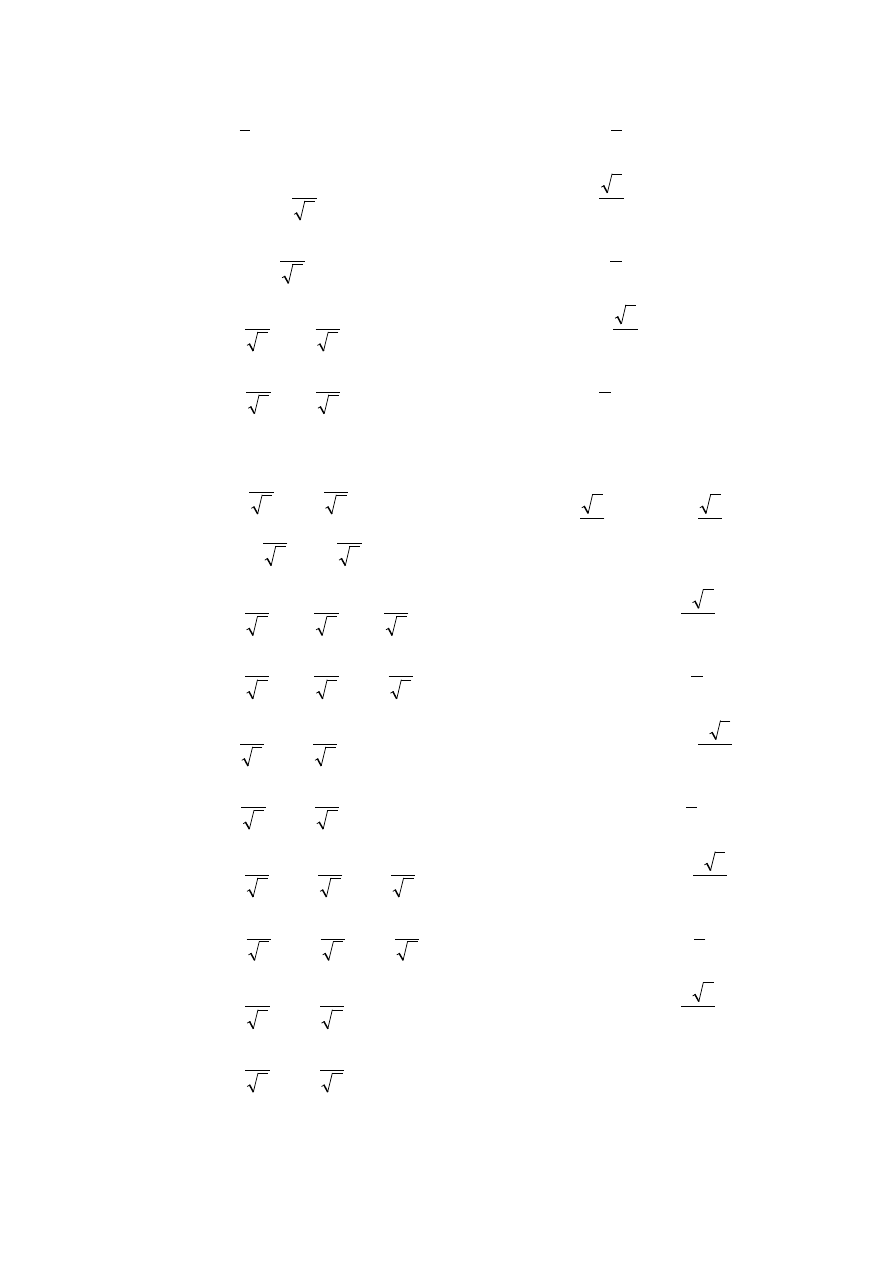
9
P
S
S
P
P
i
A
iy
3
1
0
3
1
0
1
1
−
=
⇒
=
⋅
+
=
∑
P
S
S
S
P
i
W
iy
6
5
0
5
2
0
4
4
1
2
=
⇒
=
⋅
−
−
=
∑
P
S
S
S
P
i
W
ix
6
1
0
5
1
0
3
4
3
2
−
=
⇒
=
⋅
+
=
∑
P
S
S
S
P
i
W
iy
6
5
0
5
2
5
2
0
6
6
4
6
−
=
⇒
=
⋅
+
⋅
=
∑
P
S
S
S
S
S
P
i
W
ix
3
4
0
5
1
5
1
0
7
5
7
4
6
6
=
⇒
=
−
+
⋅
−
⋅
=
∑
Dla węzła W
1
rozwiążemy układ dwu równań z dwiema niewiadomymi.
P
S
,
P
S
S
S
P
P
S
S
P
i
W
iy
i
W
ix
2
5
2
5
0
5
2
5
2
0
0
5
1
5
1
0
12
8
8
12
8
12
1
1
−
=
=
⇒
=
⋅
−
⋅
−
=
=
+
⋅
−
⋅
=
∑
∑
P
S
S
S
S
P
i
W
iy
3
5
2
0
5
2
5
2
5
2
0
10
10
6
8
3
=
⇒
=
⋅
−
⋅
−
⋅
=
∑
P
S
S
S
S
S
S
P
i
W
ix
2
3
0
5
1
5
1
5
1
0
9
3
9
6
10
8
3
−
=
⇒
=
−
+
⋅
−
⋅
+
⋅
=
∑
P
S
S
S
P
i
B
iy
3
5
2
0
5
2
5
2
0
13
13
10
−
=
⇒
=
⋅
+
⋅
=
∑
P
S
S
S
S
S
P
i
B
ix
3
8
0
5
1
5
1
0
14
7
14
10
13
=
⇒
=
−
+
⋅
−
⋅
=
∑
P
S
P
S
S
S
P
i
W
iy
3
5
4
0
3
5
2
5
2
5
2
0
16
16
13
12
4
−
=
⇒
=
−
⋅
−
⋅
−
⋅
=
∑
P
S
S
S
S
S
S
P
i
W
ix
3
4
0
5
1
5
1
5
1
0
15
15
9
13
12
16
4
−
=
⇒
=
+
−
⋅
−
⋅
−
⋅
=
∑
P
S
S
S
P
i
W
iy
3
5
4
0
5
2
5
2
0
17
17
16
7
=
⇒
=
⋅
+
⋅
=
∑
0
0
5
1
5
1
0
18
14
18
16
17
7
=
⇒
=
−
+
⋅
−
⋅
=
∑
S
S
S
S
S
P
i
W
ix
10
P
S
S
S
P
i
W
iy
3
8
0
5
2
0
19
19
17
5
−
=
⇒
=
−
⋅
−
=
∑
Pozostałe równania równowagi dla węzła W
5
i C spełnione są tożsamościowo.
Sztywność ściskania oraz siła podłużna na całej długości każdego pręta mają stałą
wartość. Uwzględniając to otrzymujemy
∑
∑∫
=
=
=
=
p
i
i
i
i
i
k
i
j
p
i
l
i
i
i
k
i
j
jk
A
E
l
N
N
s
A
E
N
N
i
1
)
(
)
(
1 0
)
(
)
(
d
δ
∑
∑∫
=
=
=
=
p
i
i
i
i
i
i
j
p
i
l
i
i
i
i
j
j
A
E
l
N
N
s
A
E
N
N
i
1
)
(
0
)
(
1 0
)
(
0
)
(
0
d
δ
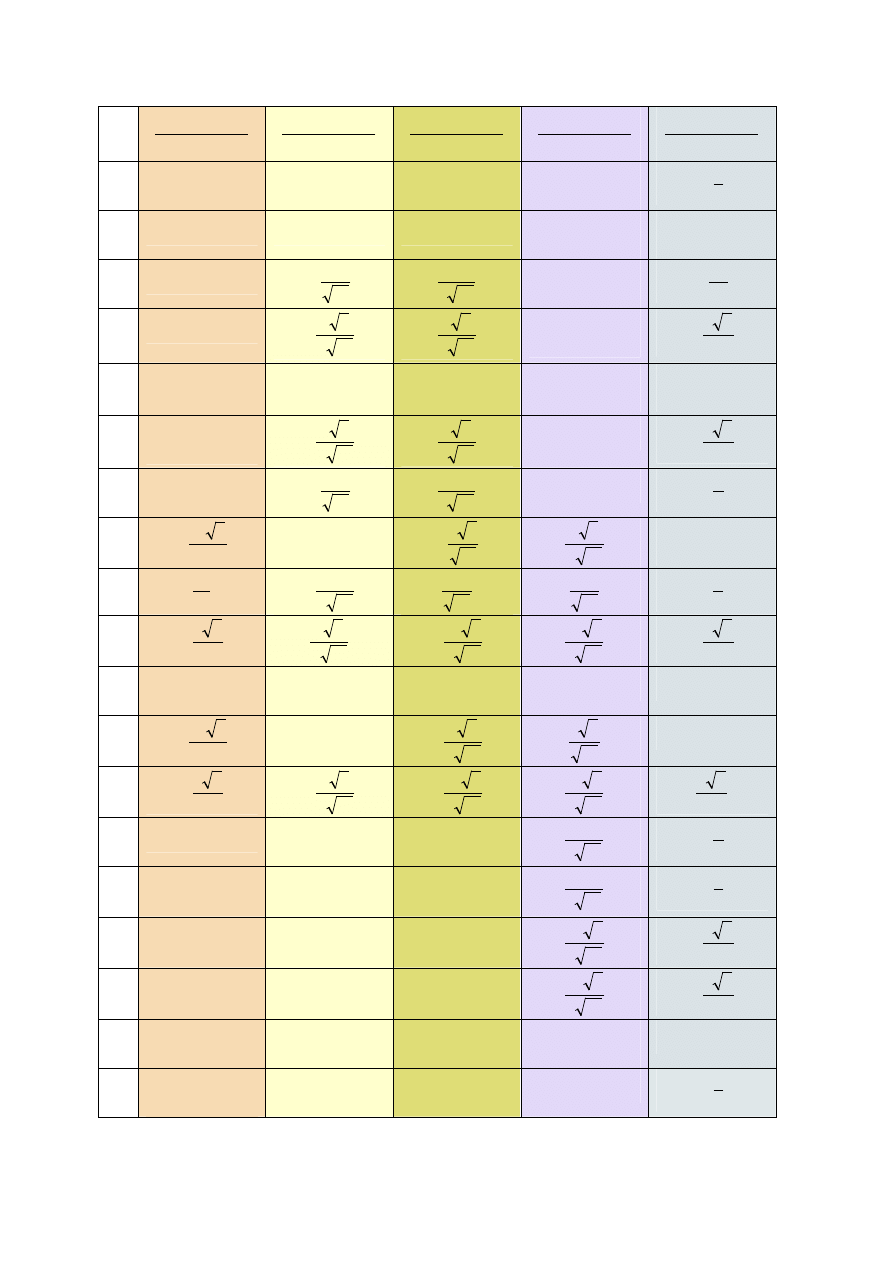
Wyznaczenie współczynników przy nadliczbowych i wyrazów wolnych układu
równań metody sił przeprowadzimy w tabeli.
Ze względu na symetryczną budowę układu podstawowego i taki dobór
nadliczbowych, że rozkład sił podłużnych w stanie
1
2
=
X
jest „lustrzanym odbiciem”
rozkładu sił w stanie
1
1
=
X
, a rozkład sił podłużnych w stanie
1
3
=
X
ma charakter
symetryczny otrzymamy
∑
∑
=
=
=
=
=
p
i
i
i
i
i
i
p
i
i
i
i
i
i
A
E
l
N
N
A
E
l
N
N
1
)
(
3
)
(
2
23
1
)
(
3
)
(
1
13
δ
δ
oraz
∑
∑
=
=
=
=
=
p
i
i
i
i
i
i
p
i
i
i
i
i
i
A
E
l
N
N
A
E
l
N
N
1
)
(
2
)
(
2
22
1
)
(
1
)
(
1
11
δ
δ
1
)
(
0
i
N
i = 1, 2, …, 19
mnożnik
P
2
1
3
8
3
1
3
8
3
4
3
8
3
4
6
1
2
3
6
5
6
5
3
5
2
3
5
2
3
5
4
3
5
4
1
3
2
5
2
5
1

11
i
i
i
i
A
E
l
)
(
1
i
N
)
(
2
i
N
)
(
3
i
N
)
(
0
i
N
i
i
i
i
i
A
E
l
N
N
⋅
⋅
)
(
1
)
(
1
i
i
i
i
i
A
E
l
N
N
⋅
⋅
)
(
3
)
(
3
1.
2
0
0
2
1
3
1
−
0
2
1
2.
13
1
0
0
0
13
0
3.
1
13
4
−
0
4
1
6
1
−
13
16
16
1
4.
5
13
5
0
4
5
−
6
5
13
5
5
16
5
5
5.
2
1
0
0
0
1
0
0
6.
5
13
5
−
0
4
5
6
5
−
13
5
5
16
5
5
7.
1
13
2
0
2
1
−
3
4
13
4
4
1
8.
5
13
5
2
−
13
5
0
2
5
13
5
20
0
9.
1
13
2
−
13
2
−
4
3
2
3
−
13
4
16
9
10.
5
13
5
−
13
5
4
5
−
3
5
2
13
5
5
16
5
5
11.
13
0
1
0
0
0
0
12.
5
13
5
13
5
2
−
0
2
5
−
13
5
5
0
13.
5
13
5
13
5
−
4
5
−
3
5
2
−
13
5
5
16
5
5
14.
1
0
13
2
2
1
−
3
8
0
4
1
15.
1
0
13
4
−
4
1
3
4
−
0
16
1
16.
5
0
13
5
−
4
5
3
5
4
−
0
16
5
5
17.
5
0
13
5
4
5
−
3
5
4
0
16
5
5
18.
2
1
0
0
0
0
0
0
19.
2
0
0
2
1
3
8
−
0
2
1
12
i
i
i
i
i
i
A
E
l
N
N
⋅
⋅
)
(
2
)
(
1
i
i
i
i
i
A
E
l
N
N
⋅
⋅
)
(
3
)
(
1
i
i
i
i
i
A
E
l
N
N
⋅
⋅
)
(
0
)
(
1
i
i
i
i
i
A
E
l
N
N
⋅
⋅
)
(
0
)
(
2
i
i
i
i
i
A
E
l
N
N
⋅
⋅
)
(
0
)
(
3
1.
0
0
0
0
3
1
−
2.
0
0
0
0
0
3.
0
13
1
−
13
3
2
0
24
1
−
4.
0
13
4
5
5
−
13
6
5
5
0
24
5
5
−
5.
0
0
0
0
0
6.
0
13
4
5
5
−
13
6
5
5
0
24
5
5
−
7.
0
13
1
−
13
3
8
0
3
2
−
8.
13
5
10
−
0
13
5
5
−
13
2
5
5
0
9.
13
4
13
2
3
−
13
3
13
3
8
9
−
10.
13
5
5
−
13
4
5
5
13
3
5
10
−
13
3
5
10
6
5
5
−
11.
0
0
0
0
0
12.
13
5
10
−
0
13
2
5
5
−
13
5
5
0
13.
13
5
5
−
13
4
5
5
−
13
3
5
10
−
13
3
5
10
6
5
5
14.
0
0
0
13
3
16
3
4
−
15.
0
0
0
13
3
16
3
1
−
16.
0
0
0
13
3
5
20
3
5
5
−
17.
0
0
0
13
3
5
20
3
5
5
−
18.
0
0
0
0
0
19.
0
0
0
0
3
8
−

13
EA
l
A
E
l
N
N
p
i
i
i
i
i
i
19194
,
13
1
)
(
1
)
(
1
22
11
=
=
=
∑
=
δ
δ
EA
l
A
E
l
N
N
p
i
i
i
i
i
i
38013
,
6
1
)
(
3
)
(
3
33
=
=
∑
=
δ
EA
l
A
E
l
N
N
p
i
i
i
i
i
i
85246
,
4
1
)
(
2
)
(
1
21
12
−
=
=
=
∑
=
δ
δ
EA
l
A
E
l
N
N
p
i
i
i
i
i
i
52116
,
2
1
)
(
3
)
(
1
32
23
31
13
−
=
=
=
=
=
∑
=
δ
δ
δ
δ
EA
l
A
E
l
N
N
p
i
i
i
i
i
i
99562
,
5
1
)
(
0
)
(
1
10
−
=
=
∑
=
δ
EA
l
A
E
l
N
N
p
i
i
i
i
i
i
84523
,
20
1
)
(
0
)
(
2
20
=
=
∑
=
δ
EA
l
A
E
l
N
N
p
i
i
i
i
i
i
88525
,
14
1
)
(
0
)
(
3
30
−
=
=
∑
=
δ
Układ równań metody sił ma postać
0
99562
5
52116
2
85246
4
19194
13
3
2
1
=
⋅
−
⋅
−
⋅
⋅
−
⋅
⋅
EA
Pl
,
X
EA
l
,
X
EA
l
,
X
EA
l
,
0
84523
20
52116
2
19194
13
85246
4
3
2
1
=
⋅
+
⋅
−
⋅
⋅
−
⋅
⋅
−
EA
Pl
,
X
EA
l
,
X
EA
l
,
X
EA
l
,
0
88525
14
38013
6
52116
2
52116
2
3
2
1
=
⋅
−
⋅
+
⋅
⋅
−
⋅
⋅
−
EA
Pl
,
X
EA
l
,
X
EA
l
,
X
EA
l
,
Rozwiązanie powyższego układu równań jest następujące
P
,
X
P
,
X
P
,
X
14096
2
98682
0
50067
0
3
2
1
=
−
=
=
.
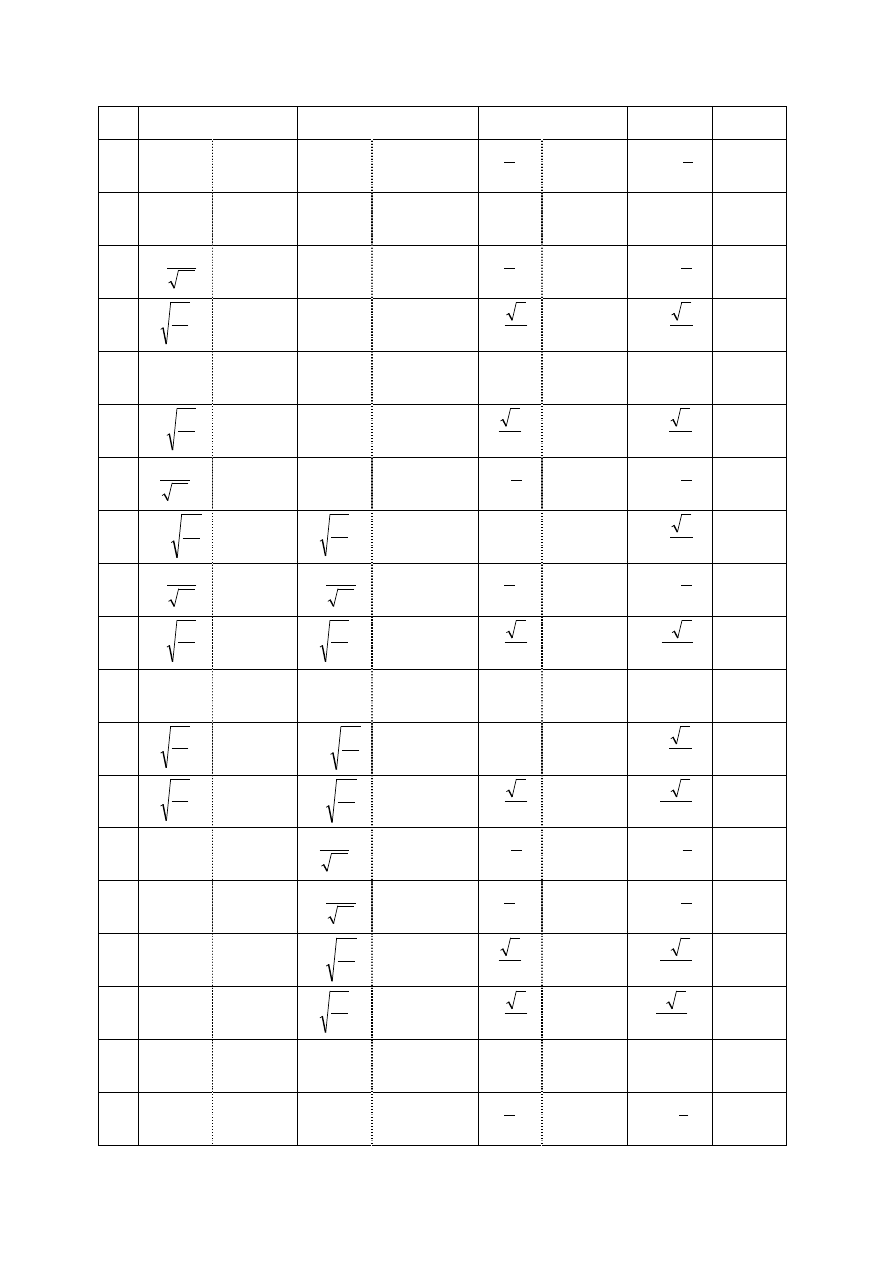
Po rozwiązaniu układu równań metody sił możemy wyznaczyć siły w prętach
)
(
0
3
)
(
3
2
)
(
2
1
)
(
1
)
(
i
i
i
i
i
N
X
N
X
N
X
N
N
+
⋅
+
⋅
+
⋅
=
Wartości sił w prętach kratownicy statycznie niewyznaczalnej obliczamy w ostatniej
kolumnie tabeli.
14
i
+
⋅
1
)
(
1
X
N
i
+
⋅
2
)
(
2
X
N
i
+
⋅
3
)
(
3
X
N
i
=
)
(
0
i
N
[ ]
P
N
i )
(
1.
0
·0,50067+
0
· (-0,98682)+
2
1
·2,14096+
3
1
−
=
0,73715
2.
1
·0,50067+
0
· (-0,98682)+
0
·2,14096+
0 =
0,50067
3.
13
4
−
·0,50067+
0
· (-0,98682)+
4
1
·2,14096+
6
1
−
=
−0,18687
4.
13
5
·0,50067+
0
· (-0,98682)+
4
5
−
·2,14096+
6
5
=
−0,51365
5.
0
·0,50067+
0
· (-0,98682)+
0
·2,14096+
1 =
1,00000
6.
13
5
−
·0,50067+
0
· (-0,98682)+
4
5
·2,14096+
6
5
−
=
0,51365
7.
13
2
·0,50067+
0
· (-0,98682)+
2
1
−
·2,14096+
3
4
=
0,54058
8.
13
5
2
−
·0,50067+
13
5
· (-0,98682)+
0
·2,14096+
2
5
=
−0,11125
9.
13
2
−
·0,50067+
13
2
−
· (-0,98682)+
4
3
·2,14096+
2
3
−
=
0,37206
10.
13
5
−
·0,50067+
13
5
· (-0,98682)+
4
5
−
·2,14096+
3
5
2
=
−0,62490
11.
0
·0,50067+
1
· (-0,98682)+
0
·2,14096+
0 =
−0,98082
12.
13
5
·0,50067+
13
5
2
−
· (-0,98682)+
0
·2,14096+
2
5
−
=
0,40903
13.
13
5
·0,50067+
13
5
−
· (-0,98682)+
4
5
−
·2,14096+
3
5
2
−
=
−1,76876
14.
0
·0,50067+
13
2
· (-0,98682)+
2
1
−
·2,14096+
3
8
=
1,05213
15.
0
·0,50067+
13
4
−
· (-0,98682)+
4
1
·2,14096+
3
4
−
=
0,29003
16.
0
·0,50067+
13
5
−
· (-0,98682)+
4
5
·2,14096+
3
5
4
−
=
−1,17631
17.
0
·0,50067+
13
5
· (-0,98682)+
4
5
−
·2,14096+
=
3
5
4
1,17631
18.
0
·0,50067+
0
· (-0,98682)+
0
·2,14096+
0 =
0,00000
19.
0
·0,50067+
0
· (-0,98682)+
2
1
·2,14096+
=
−
3
8
−1,59619
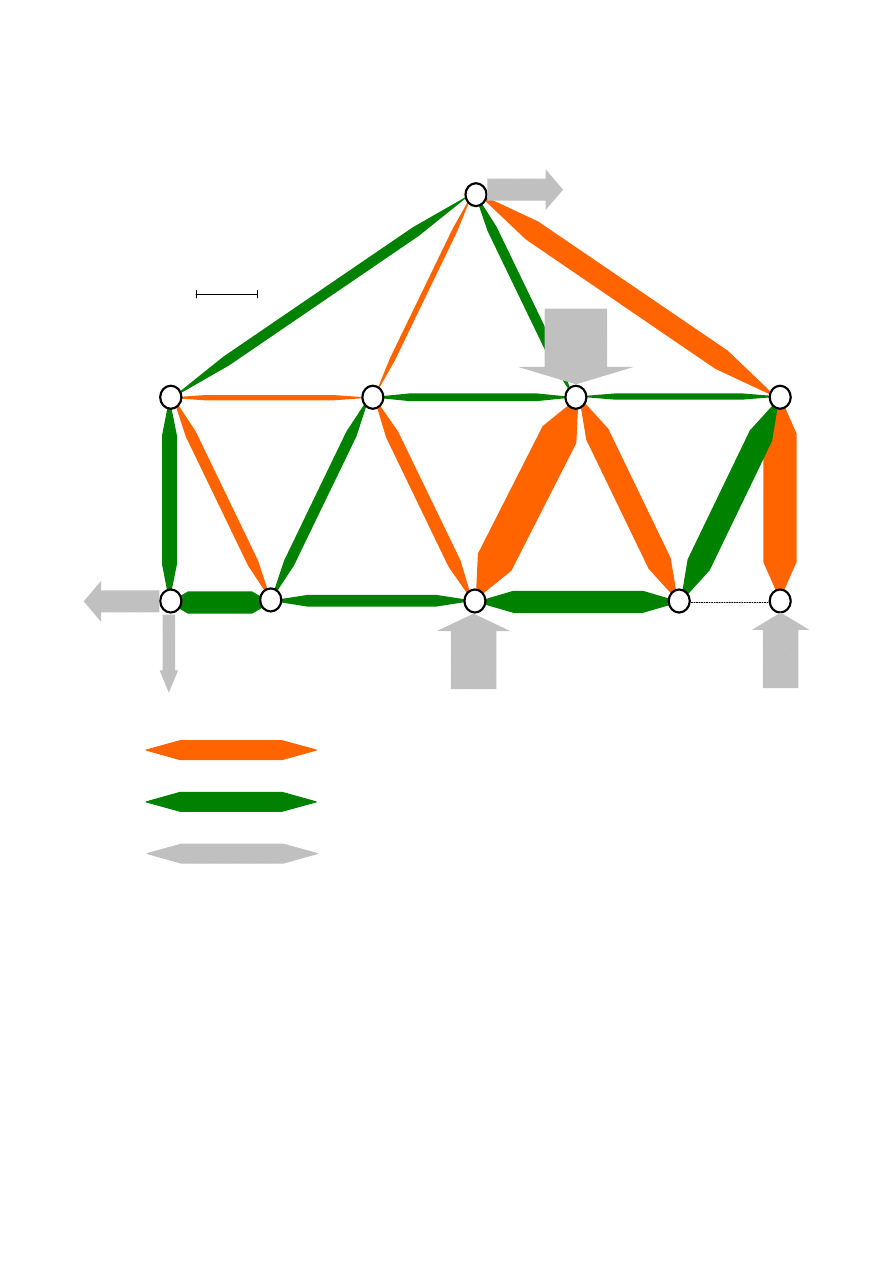
15
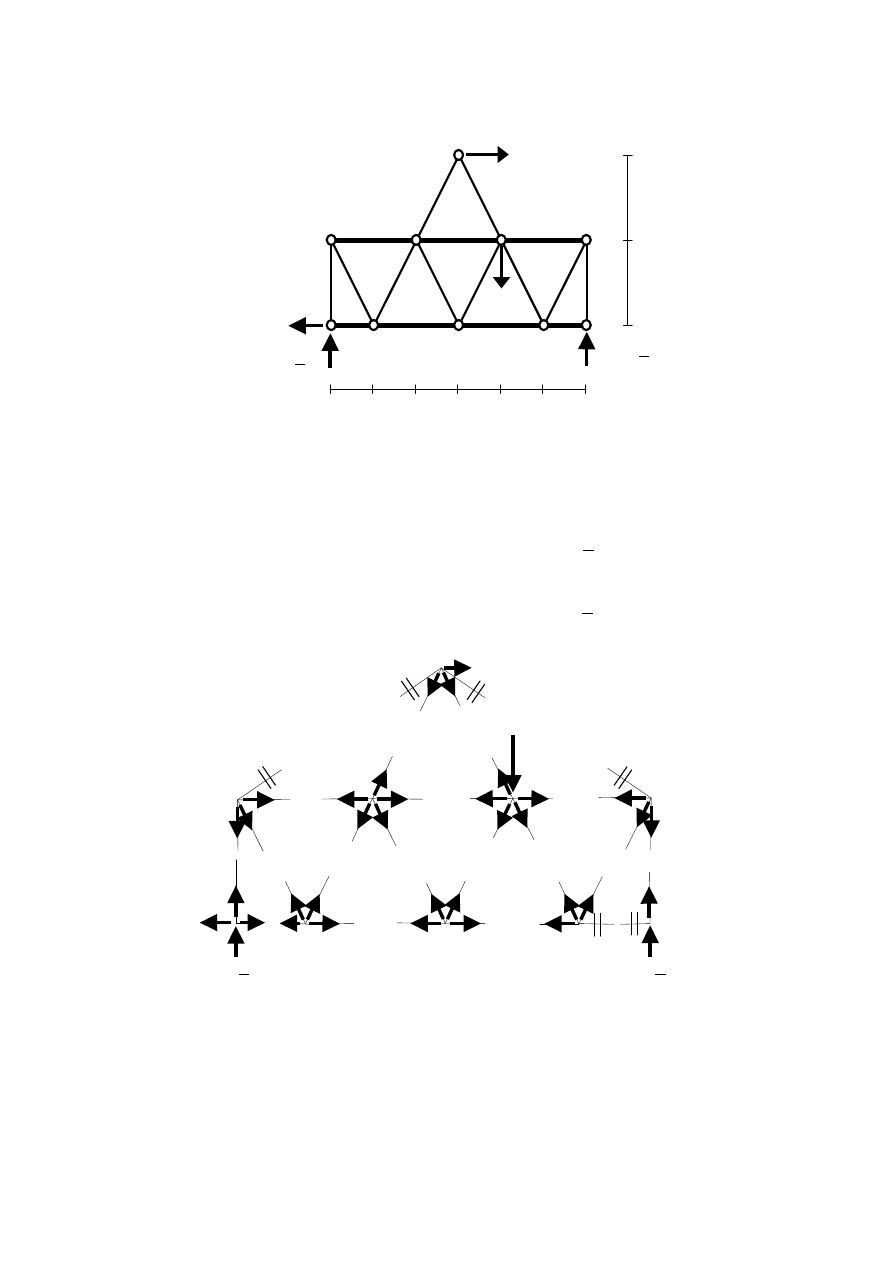
Otrzymane wyniki przedstawia poniższy rysunek, na którym grubości „prętów” są
proporcjonalne do wyznaczonych wartości sił (w przyjętej skali).
Ze względu na symetryczną budowę rozpatrywanej kratownicy powyższe zadanie
można rozwiązać stosując grupowe nadliczbowe. Układ trzech równań z trzema
niewiadomymi rozprzęga się wtedy na układ dwóch równań z dwiema niewiadomymi oraz
jedno równanie z jedną niewiadomą.
P
3P
H
A
= P
V
A
= 0,73715P
R
B
= 2,14096P
R
C
= 1,59619P
3P
0P
Pręty ściskane
Pręty rozciągane
Obciążenie zewnętrzne
i reakcje podporowe
Skala
Wyszukiwarka
Podobne podstrony:
Kratownica trzykrotnie statycznie niewyznaczalna
Metoda sił ćwiczenie nr 2 kratownica statycznie niewyznaczalna
cwicz mechanika budowli obliczanie ukladow statycznie niewyznaczalnych metoda sil krata
5 Analiza naprężeń i odkształceń w?lce statycznie niewyznaczalnej
Obciążenie termiczne w układzie statycznie niewyznaczalnym
Obliczanie układów statycznie niewyznaczalnych metoda sił z wykorzystaniem symetrii i antysymetrii
więcej podobnych podstron