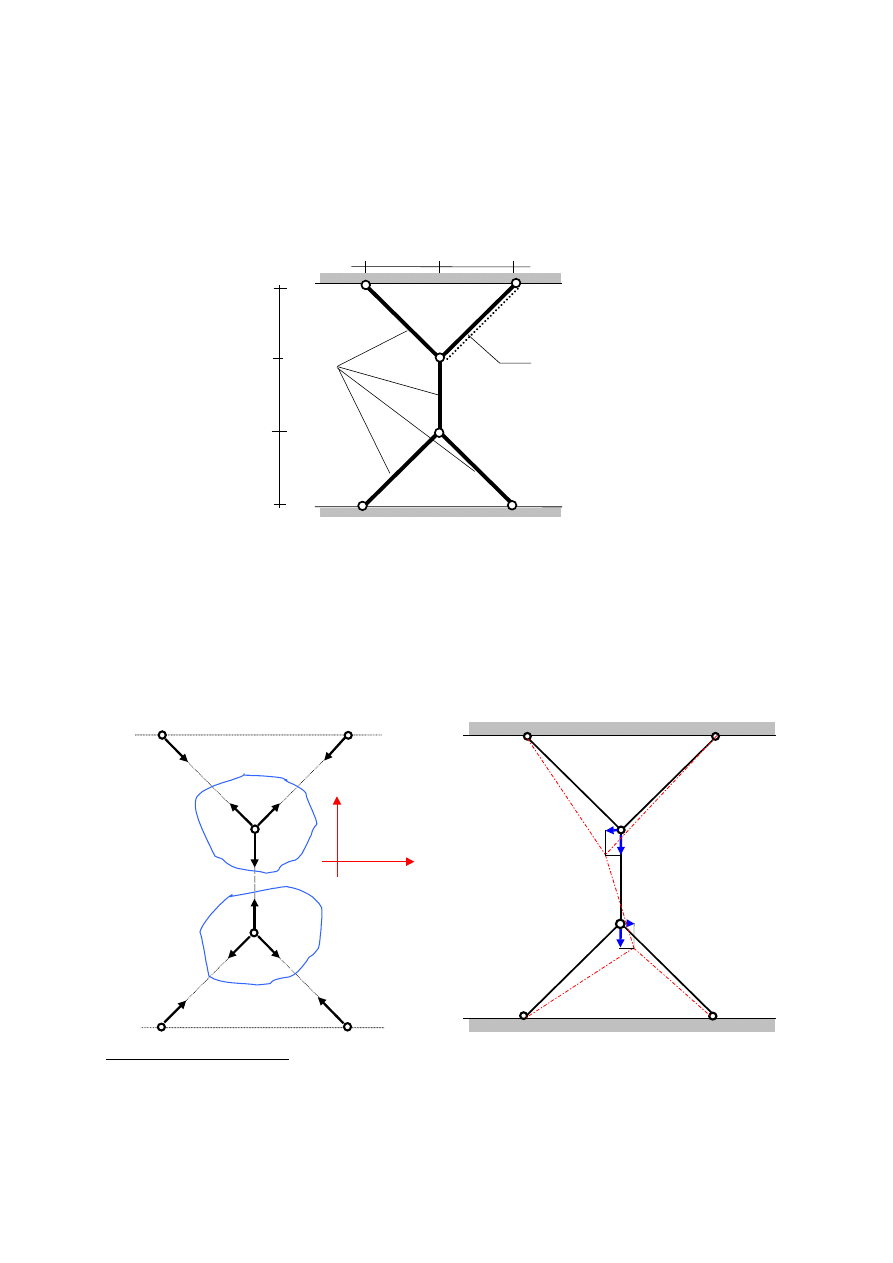
Przykład 1.6. Obciążenie termiczne

Wyznaczyć siły w prętach przedstawionego układu prętowego wywołane obciążeniem
termicznym ∆t [˚C] jednego pręta. Przekroje poprzeczne prętów są jednakowe i wynoszą
A [m

2

], długości l w [m], ich moduł Younga - E [N/m

2

] i współczynnik rozszerzalności

liniowej α

t

[1/˚C],

l

l

E,A

l

E,

A,

α

t

,

∆

t

l

l

Rozwiązanie

Obciążenie termiczne ∆t > 0 pręta wywołuje jego wydłużenie. Ponieważ jednak swoboda jego
odkształcania jest ograniczona, więc powstaje stan wstępnych naprężeń wywołany
niemożnością swobodnego odkształcenia ogrzanego pręta i odkształceniami pozostałych
prętów układu.
Wprowadźmy oznaczenia sił w prętach i

opiszmy przemieszczenia dwu swobodnych węzłów

1 i 2 składowymi wektorów ich przemieszczeń, odpowiednio u

1

, v

1

i u

2

, v

2

.

S

3

2

S

5

S

4

S

3

1

S

1

S

2

x

y

1

u

1

V

1

2

U

2

V

2

Równania geometryczne.
Równania geometryczne przyjmują postać

o

1

o

1

2

o

1

o

1

1

45

cos

v

45

cos

u

l

45

cos

v

45

cos

u

l

+

=

∆

+

−

=

∆

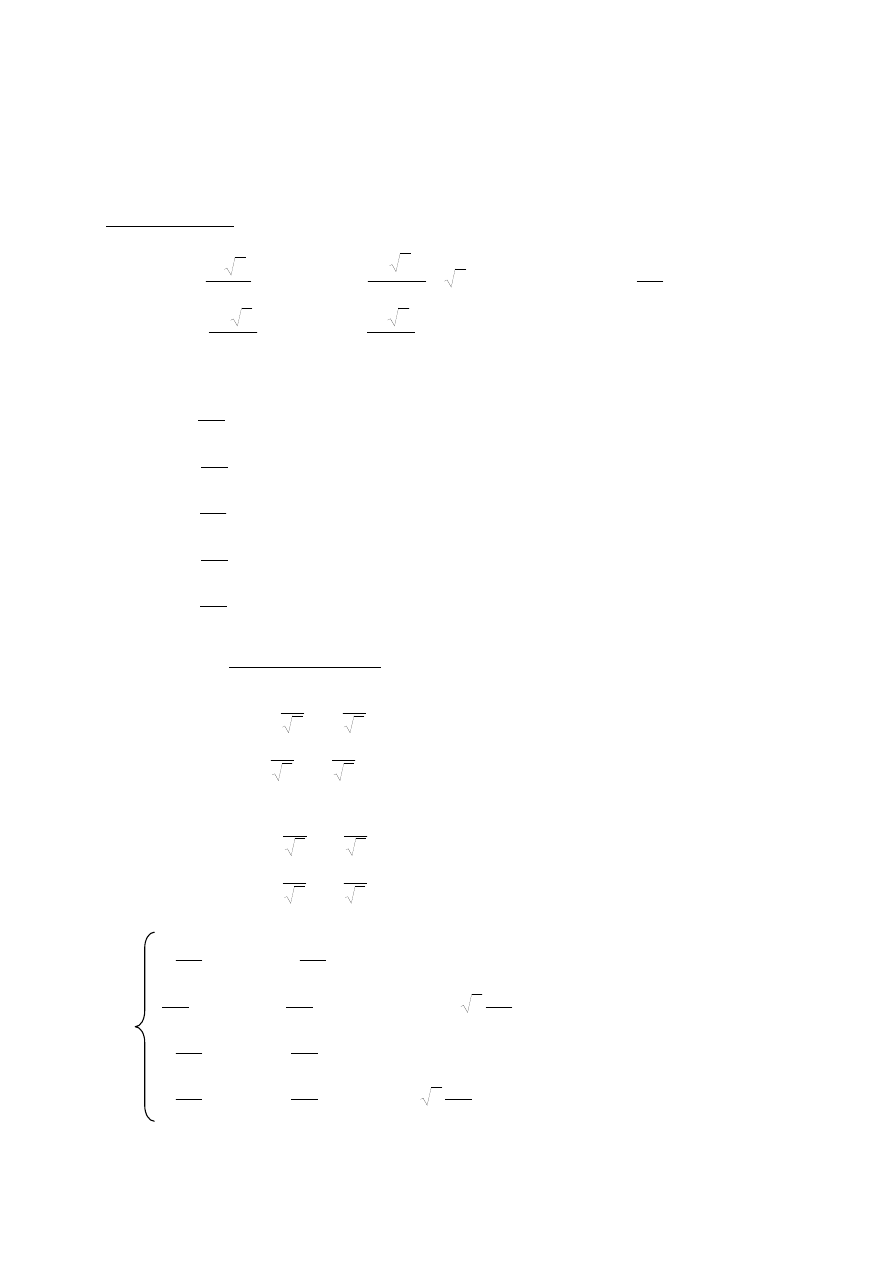
2

o

2

o

2

5

o

2

o

2

4

2

1

3

45

cos

v

45

cos

u

l

45

cos

v

45

cos

u

l

v

v

l

−

−

=

∆

−

=

∆

+

−

=

∆

(1-5)

Warunki fizyczne
Wydłużenia prętów wynoszą:

EA

l

2

S

l

1

1

=

∆

,

tl

α

2

EA

l

2

S

l

t

2

2

∆

+

=

∆

,

EA

l

S

l

3

3

=

∆

,

EA

l

2

S

l

4

4

=

∆

,

EA

l

2

S

l

5

5

=

∆

(6-10)

Wyznaczając siły z równań (6-10) i uwzględniając równania (1-4) otrzymujemy

(

)

1

1

1

v

u

l

2

EA

S

+

−

=

(

)

tl

α

2

v

u

l

2

EA

S

t

1

1

2

∆

−

+

=

(

)

2

1

3

v

v

l

EA

S

+

−

=

(6*-10*)

(

)

2

2

4

v

u

l

2

EA

S

−

=

(

)

2

2

5

v

u

l

2

EA

S

−

−

=

Zapiszemy teraz równania równowagi dla węzłów swobodnych 1 i 2.
Węzeł 1

∑

∑

=

−

+

⇒

=

=

+

−

⇒

=

0

S

2

1

S

2

1

S

0

P

0

2

1

S

2

1

S

0

P

3

2

1

iy

2

1

ix

(11,12)

Węzeł 2

∑

∑

=

+

−

−

⇒

=

=

+

−

⇒

=

0

S

2

1

S

2

1

S

0

P

0

2

1

S

2

1

S

0

P

3

5

4

iy

5

4

ix

(13,14)

Podstawiając wyrażenia (6*-10*) do równań (11-14) mamy układ 4 równań:

(

)

(

)

0

tl

α

2

v

u

l

2

EA

v

u

l

2

EA

t

1

1

1

1

=

∆

−

+

+

+

−

−

(

)

(

)

(

)

0

v

v

l

EA

2

tl

α

2

v

u

l

2

EA

v

u

l

2

EA

2

1

t

1

1

1

1

=

+

−

−

∆

−

+

+

+

−

(

)

(

)

0

v

u

l

2

EA

v

u

l

2

EA

2

2

2

2

=

−

−

+

−

−

(

)

(

)

(

)

0

v

v

l

EA

2

v

u

l

2

EA

v

u

l

2

EA

2

1

2

2

2

2

=

+

−

+

−

−

−

−

−

który po uporządkowaniu ma postać:

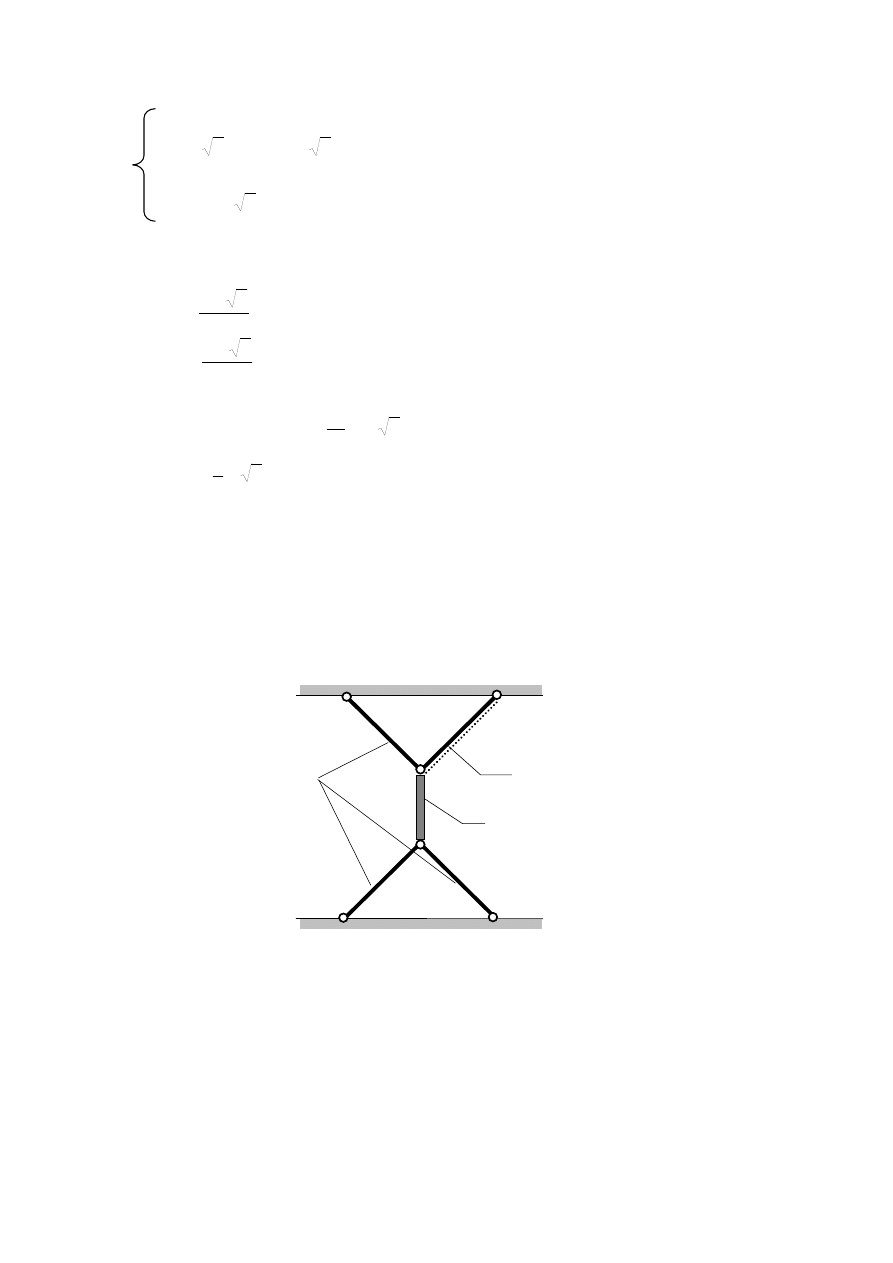
3

0

tl

α

u

t

1

=

∆

−

(

)

tl

α

2

v

2

v

2

2

2

t

2

1

∆

=

−

+

0

u

2

=

(

)

0

v

2

2

v

2

2

1

=

+

−

Z rozwiązania układu otrzymujemy

tl

α

u

t

1

∆

=

,

u

2

= 0 ,

tl

α

7

2

3

v

t

1

∆

+

=

,

tl

α

7

2

4

v

t

2

∆

−

=

.

Z równań (6*-10*) wyznaczamy siły w prętach

(

)

t

α

EA

1847

.

0

t

α

EA

2

4

14

1

S

S

S

S

t

t

5

4

2

1

∆

⋅

−

=

∆

−

−

=

=

=

=

,

(

)

t

α

EA

2612

.

0

t

α

EA

1

2

2

7

1

S

t

t

3

∆

⋅

−

=

∆

−

−

=

.

Wszystkie pręty są ściskane.

Ćwiczenie
Wykorzystując przedstawione rozwiązanie wyznacz siły w prętach tego układu, przy
założeniu, że pręt nr 2 jest nieodkształcalny (np. wykonany jest z materiału o dużo większym
module Younga, niż pozostałe pręty). Porównaj rozwiązania.

E,A

E,

A,

α

t

,

∆

t

E

1

A

E

1

A

→∞