
Zadania z rozwiązaniami
Projekt współfinansowany przez Unię Europejską w ramach Europejskiego Funduszu Społecznego
Wstęp do fizyki kwantowej

Zadanie 1
Widmo słoneczne jest bardzo zbliżone do widma ciała doskonale czarnego, dla którego maksymalna moc
promieniowania przypada na długość fali
a)
Znaleźć temperaturę Słońca i moc jego promieniowania
b)
Obliczyć czas po którym jego masa zmaleje o 1% wskutek emisji promieniowania
Masa Słońca , promień Słońca
Rozwiązanie
m
,
max
48
0
Skorzystamy z praw opisujących promieniowanie ciała doskonale czarnego:
•Prawa Stefana-Boltzmana gdzie - całkowita zdolność emisyjna (całkowita moc
promieniowania z jednostkowego obszaru powierzchni) [W/m
2
].
•Prawa przesunięć Wiena gdzie - długość fali odpowiadającej położeniu maksimum w widmie
promieniowania dla temperatury T
(najbardziej prawdopodobna długość fali).
4
T
T
c
T
c
T
b
max
4
2
8
10
67
5
K
m
W
,
max
mK
,
b
3
10
9
2
(a) Z wzoru Wiena wyznaczamy temperaturę powierzchni Słońca
K
K
,
m
,
mK
,
b
T
max
6000
10
06
6
10
48
0
10
9
2
3
6
3
Całkowita moc promieniowania:
W
,
R
T
S
T
P
c
c
26
2
4
10
5
4
4
powierzchnia Słońca:
kg
M
30
10
2
kg
R
8
10
7
(b) Energia wypromieniowana w czasie t
odpowiada utracie masy Słońca zgodnie ze wzorem Einsteina:
t
P
E
c
M
t
P
Mc
E
c
2
s
P
Mc
t
c
18
26
2
8
28
2
10
4
10
4
10
3
10
2
s
s
kgm
s
m
kg
W
s
m
kg
t
3
2
2
2
2
2
Jednostki:
Wyraźmy czas w latach:
lat
10
27
1
lat
10
16
3
10
4
11
7
18
,
,
t
s
,
7
10
16
3
rok
1
Otrzymaliśmy czas dłuższy od wieku Wszechświata, który wynosi
Słońce ma około 5 mld lat i paliwa w jego wnętrzu (wodoru) starczy na następne 5-6 mld lat.
Utrata masy na skutek promieniowania nie odgrywa więc żadnej roli w ewolucji Słońca.
lat
10
4
1
lat
mld
14
10
,
28
10
2
1
M
%
M
Zadanie 2
Obliczyć temperaturę, jaką uzyska czarna płyta izolowana termicznie od otoczenia, do której dochodzi prostopadle
światło słoneczne o natężeniu I = 1,4 kW/m
2
Rozwiązanie
Temperatura płyty ustali się, gdy energia wypromieniowana przez płytę zrówna się z energią absorbowaną.
Zakładamy, że płyta nie traci ciepła w procesie przewodzenia i konwekcji (izolacja termiczna) oraz, że płyta
promieniuje na obie strony. Pochłanianie promieniowania zachodzi tylko po stronie zwróconej do słońca.
IS
P
abs
S
T
P
prom
2
4
Moc absorbowana:
Moc wypromieniowana:
4
2
T
S
IS
S
– powierzchnia płyty
K
,
I
T
3
333
2
4
lub
C
,
t
0
3
60
Zadanie 3
Znaleźć gęstość strumienia fotonów w odległości 1m od punktowego źródła światła o mocy 1W, jeśli światło jest:
a)
monochromatyczne, o długości fali 0,5 μm;
b)
zawiera dwie linie widmowe o długościach fali 0,7 μm i 0,4 μm, których natężenia pozostają w stosunku 1:2.
Gęstość strumienia fotonów to liczba fotonów przechodzących przez jednostkową powierzchnię w jednostce czasu:
Ponieważ źródło jest punktowe, A jest powierzchnią kuli o promieniu R =1m:
Liczba fotonów to:
A
n
liczba fotonów wysyłanych ze źródła na sekundę
powierzchnia, na którą padają
2
4
R
A
f
E
P
n
moc źródła
energia fotonu:
hc
h
E
f
hc
P
n
2
4
R
hc
P
A
n
s
m
c
s
J
,
h
8
34
10
3
10
626
6
Rozwiązanie
a)
Jednostki:
b)
stosunek natężeń:
m
m
6
10
5
,
0
5
,
0
1
2
17
19
19
8
34
7
10
2
10
020
,
0
10
626
,
6
12
5
4
10
3
10
626
,
6
10
5
,
1
s
m
1
2
2
2
s
m
m
J
s
J
m
s
m
s
J
m
W
m
m
6
1
10
7
,
0
7
,
0
m
m
6
2
10
4
,
0
4
,
0
2
:
1
:
2
1
p
p
2
1
2
1
3
2
3
1
hc
P
n
n
n
2
1
2
1
3
2
3
1
hcA
P
m
hcA
P
m
hcA
P
m
hcA
P
6
6
6
10
5
,
0
10
5
,
1
3
1
10
4
,
0
3
2
7
,
0
3
1
Jest to wynik dokładnie taki sam jaki otrzymaliśmy w punkcie a).
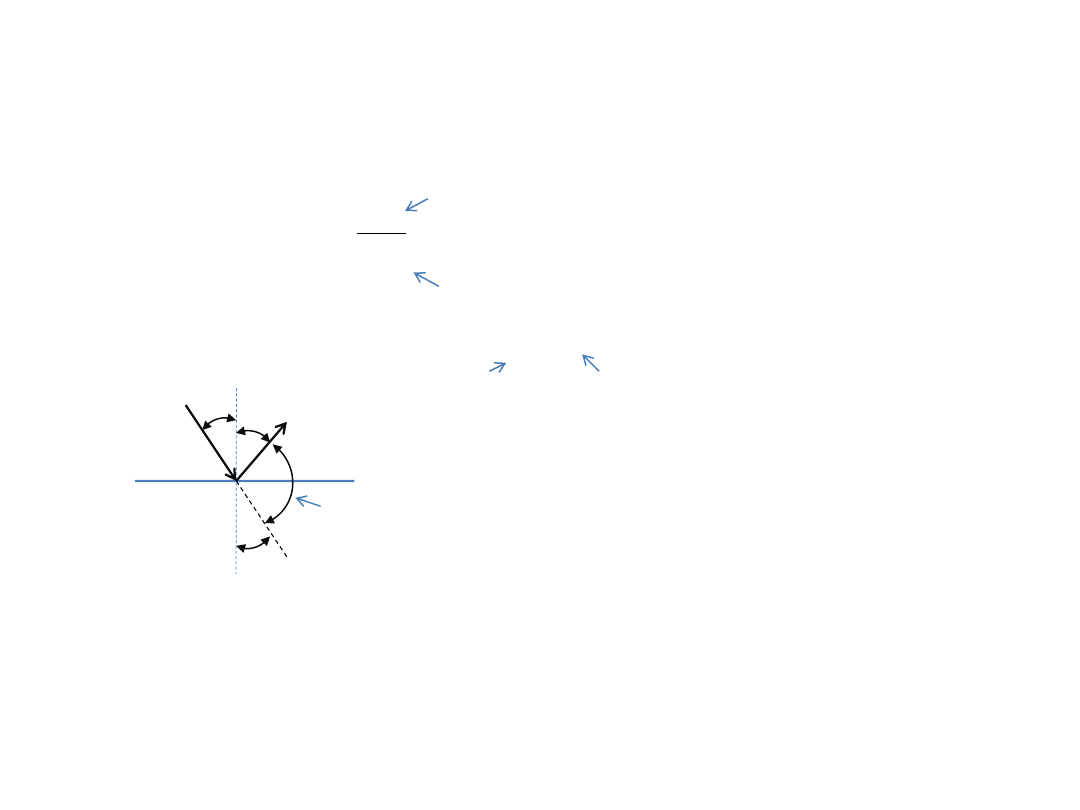
Zadanie 4
Krótki impuls światła o energii
pada w postaci wąskiej wiązki na powierzchnię zwierciadła o
współczynniku odbicia
. Kąt padania
. Znaleźć pęd przekazany powierzchni.
Dane:
Szukamy pędu przekazanego powierzchni:
Aby obliczyć wartość wektora pędu, obie strony równania podnosimy do kwadratu:
J
E
5
,
7
6
,
0
r
30
J
E
5
,
7
6
,
0
pad
odb
E
E
r
30
energia wiązki padającej
energia wiązki odbitej
odb
pad
p
p
p
pęd wiązki odbitej
pęd wiązki padającej
2
180
kąt między pędem wiązki padającej a pędem wiązki odbitej
pad
p
odb
p
odb
pad
odb
pad
p
p
p
p
p
2
2
2
2
2
cos
2
180
cos
odb
pad
odb
pad
odb
pad
p
p
p
p
p
p
)
2
cos(
2
2
2
2
odb
pad
odb
pad
p
p
p
p
p
Rozwiązanie
)
2
cos(
2
1
2
2
2
2
r
r
c
E
p
pad
c
E
p
c
E
p
pad
pad
pad
odb
odb
E
c
r
c
E
p
8
8
2
10
5
,
3
2
1
6
,
0
2
36
,
0
1
10
3
5
,
7
)
2
cos(
2
1
r
r
c
E
p
pad
s
m
kg
m
s
s
m
kg
p
2
2
Jednostki:
Odpowiedź:
s
m
kg
p
8
10
5
,
3

Zadanie 5
W impulsie trwającym
laser promieniuje wąską wiązkę światła o energii .
Znaleźć średnie (w czasie trwania impulsu) ciśnienie tej wiązki światła, jeśli skupić ją w plamkę o średnicy
na prostopadłej do wiązki powierzchni o współczynniku odbicia .
Dane:
Szukamy ciśnienia wiązki:
gdzie:
-
dla wiązki padającej prostopadle do powierzchni
, ponieważ:
ms
1
,
0
J
E
10
m
d
10
5
,
0
r
s
ms
3
10
1
,
0
1
,
0
m
m
d
6
10
10
10
5
,
0
r
J
E
E
pad
10
pad
odb
rE
E
S
F
P
m
d
10
2
4
1
d
S
p
F
powierzchnia plamki;
siła działająca na powierzchnię S
przekazany pęd
r
c
E
p
1
0
odb
pad
p
p
p
odb
pad
odb
pad
odb
pad
odb
pad
p
p
p
p
p
p
p
p
p
2
)
2
180
cos(
2
2
2
2
2
2
odb
pad
p
p
p
r
E
c
E
E
c
p
c
E
p
pad
odb
pad
1
1
1
Rozwiązanie

2
1
4
d
c
r
E
S
p
P
Ostatecznie:
Podstawiamy wartości:
Jednostki:
Odpowiedź:
6
7
6
10
4
8
10
4
6
10
2
10
3
5
1
10
4
10
10
10
3
5
0
1
10
4
,
,
,
P
Pa
m
N
mm
J
sm
J
P
s
m
2
2
2
Pa
P
6
10
4
,
6
Zadanie 6
Światło przejawia swoją korpuskularną naturę w tym, że ma pęd. Wykorzystując ten fakt, wykazać, że foton w próżni:
a)
nie może wytworzyć pary elektron-pozyton,
b)
w pojedynczym zderzeniu nie może oddać całej swej energii elektronowi swobodnemu (nie może zostać
pochłonięty przez swobodny elektron)
Przyjmujemy oznaczenia: energia fotonu: , pęd fotonu:
a)
Załóżmy, że foton wytworzy parę elektron-pozyton.
E
e
-
energia całkowita elektronu, E
p
-
energia całkowita pozytonu, p
e
– pęd elektronu, p
p
-
pęd pozytonu. Z zasady
zachowania energii mamy:
c
h
c
E
p
f
f
h
E
f
p
e
f
E
E
E
2
2
4
2
0
2
2
4
2
0
c
p
c
m
c
p
c
m
h
p
e
2
2
2
0
2
2
2
0
p
e
f
p
c
m
p
c
m
c
h
p
Pęd fotonu:
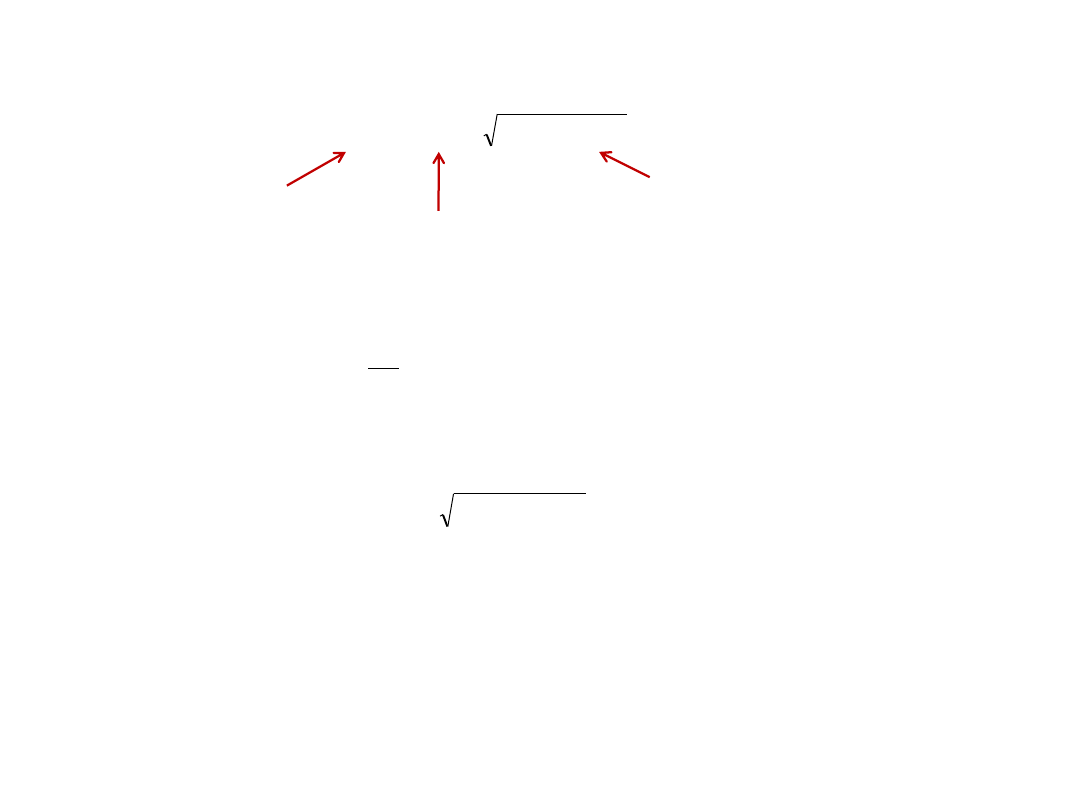
Korzystamy z zasady zachowania pędu:
p
e
f
p
p
p
Wektory pędów tworzą trójkąt i zachodzi
nierówność dla boków trójkąta:
e
p
p
p
f
p
f
p
e
p
p
p
1
p
e
f
p
p
p
2
p
e
f
p
p
p
Nierówności (1) i (2) są sprzeczne, więc założenie, że foton może wytworzyć parę elektron-pozyton jest fałszywe.
Rozwiązanie
b)
Załóżmy, że foton odda całą energię w zderzeniu ze swobodnym elektronem.
3
2
2
4
2
0
2
2
0
c
p
c
m
mc
c
m
E
e
f
energia spoczynkowa elektronu
energia elektronu po zderzeniu
pęd elektronu po zderzeniu
Zasada zachowania pędu:
e
f
p
p
4
e
f
p
c
h
p
Zasada zachowania energii:
Wstawiamy wyrażenie na pęd elektronu (4) do równania (3) i uwzględniamy, że:
h
E
f
2
4
2
0
2
0
h
c
m
c
m
h
Otrzymana równość jest fałszywa dla
i
0
0
m
0
h
Wniosek: założenie, że foton odda całą energię w zderzeniu ze swobodnym elektronem jest fałszywe.
Zadanie 7
Granica zjawiska fotoelektrycznego od strony fal długich wynosi dla rubidu
. Wyznaczyć
pracę wyjścia i maksymalną prędkość elektronów wybijanych z powierzchni metalu oświetlonego światłem
długości fali
.
to taka długość fali, która powoduje wybicie elektronu,
którego energia kinetyczna jest równa 0, więc
nm
gr
540
nm
400
k
E
W
h
maksymalna energia kinetyczna
wybitych elektronów
praca wyjścia
gr
gr
gr
hc
W
W
h
2
2
mv
E
k
maksymalna prędkość elektronów
gr
hc
W
h
mv
1
1
2
2
gr
m
hc
v
1
1
2
m
nm
gr
9
10
540
540
m
nm
9
10
400
400
s
J
h
34
10
63
,
6
s
eV
h
15
10
14
,
4
kg
m
31
10
11
,
9
s
m
c
8
10
3
J
eV
19
10
60
,
1
1
Rozwiązanie
Rachunek na jednostkach:
Podstawiamy wartości liczbowe:
s
m
kg
s
m
kg
kg
m
N
m
s
kg
s
m
J
v
2
1
2
1
2
1
2
2
eV
s
m
m
s
eV
W
3
,
2
10
4
,
5
10
3
10
14
,
4
7
8
15
W
J
eV
W
19
10
68
,
3
3
,
2
6
12
7
7
31
8
34
10
53
,
0
10
2830
,
0
10
4
,
5
1
10
4
1
10
11
,
9
10
3
10
63
,
6
2
kg
v
c
s
m
v
3
6
10
8
,
1
10
53
,
0
Zadanie 8
Światło o mocy P = 1mW i długości fali
pada na powierzchnię cezu. Jakie jest natężenie prądu
powstałego w zjawisku fotoelektrycznym oraz minimalny potencjał hamowania potrzebny do tego, aby prąd
przestał płynąć? Praca wyjścia dla cezu wynosi 1,93 eV. Założyć, że 50% fotonów wybija elektrony.
Bilans energii dla zjawiska fotoelektrycznego:
Minimalny potencjał hamowania to różnica potencjałów U potrzebna do zahamowania elektronów. Aby
zahamować przepływ prądu praca pola elektrycznego musi być równa lub większa od energii kinetycznej
elektronów.
nm
456
2
2
mv
W
h
eU
mv
2
2
eU
W
h
c
W
hc
e
U
1
m
nm
9
10
456
456
s
J
h
34
10
63
,
6
s
eV
h
15
10
14
,
4
s
m
c
8
10
3
V
U
79
,
0
Rozwiązanie
Natężenie prądu:
Natężenie prądu to liczba wybitych elektronów razy ładunek elektronu podzielona przez czas.
50% fotonów powoduje wybicie elektronu, czyli:
Jednostki:
t
eN
I
e
h
P
e
,
t
N
,
e
I
f
5
0
5
0
Moc światła:
t
N
h
t
E
P
f
f
Energia 1 fotonu
A
s
C
s
J
J
C
m
J
W
m
C
I
A
I
8
,
1
Energia N
f
fotonów
Zadanie 9
Początkowo próbowano opisywać zjawisko fotoelektryczne zgodnie z falową naturą światła. Sprawdźmy, do
jakich wniosków prowadzi taki opis.
W odległości od płytki cezowej znajduje się monochromatyczne źródło światła o mocy
.
Zakładając, że elektron może zaabsorbować energię z koła o promieniu równym promieniowi atomu
obliczyć, jakiego opóźnienia można się spodziewać między włączeniem światła a obserwacją fotoelektronu,
zgodnie z falową teorią światła. Praca wyjścia dla cezu
.
Źródło światła promieniuje jednakowo we wszystkich kierunkach. Energia wypromieniowana w
jednostce czasu na jednostkę powierzchni kuli o promieniu wynosi:
Elektron może gromadzić energię padającą na kołową powierzchnię płytki o promieniu
i środku w miejscu, w którym znajduje się elektron. Cała padająca energia jest absorbowana. Energia
absorbowana przez elektron w jednostce czasu:
m
l
1
W
P
30
m
r
o
10
10
eV
W
89
,
1
m
l
1
2
4
l
P
m
r
o
10
10
2
2
2
2
4
4
l
r
P
r
l
P
o
o
Rozwiązanie
Teraz musimy obliczyć, ile czasu potrzeba, aby elektron zgromadził energię wystarczającą do pokonania bariery
potencjału, czyli energię równą pracy wyjścia z metalu
.
J
eV
W
19
10
02
,
3
89
,
1
4
30
10
1
10
02
,
3
4
20
19
t
s
s
J
J
W
m
m
J
t
2
2
s
t
4
P
r
Wl
t
t
l
r
P
W
o
o
2
2
2
2
4
4
Otrzymany wynik jest sprzeczny z doświadczeniem, bo emisję elektronów obserwuje się niemal natychmiast po
włączeniu światła, a nie jak wynika z powyższych rachunków, po kilku sekundach. Sprzeczność tę wyjaśnił Einstein,
pokazując, że w zjawisku fotoelektrycznym przejawia się korpuskularna natura światła. Elektron wybity jest przez
pojedynczy foton, który natychmiast przekazuje mu całą swoją energię.
.
Zadanie 10
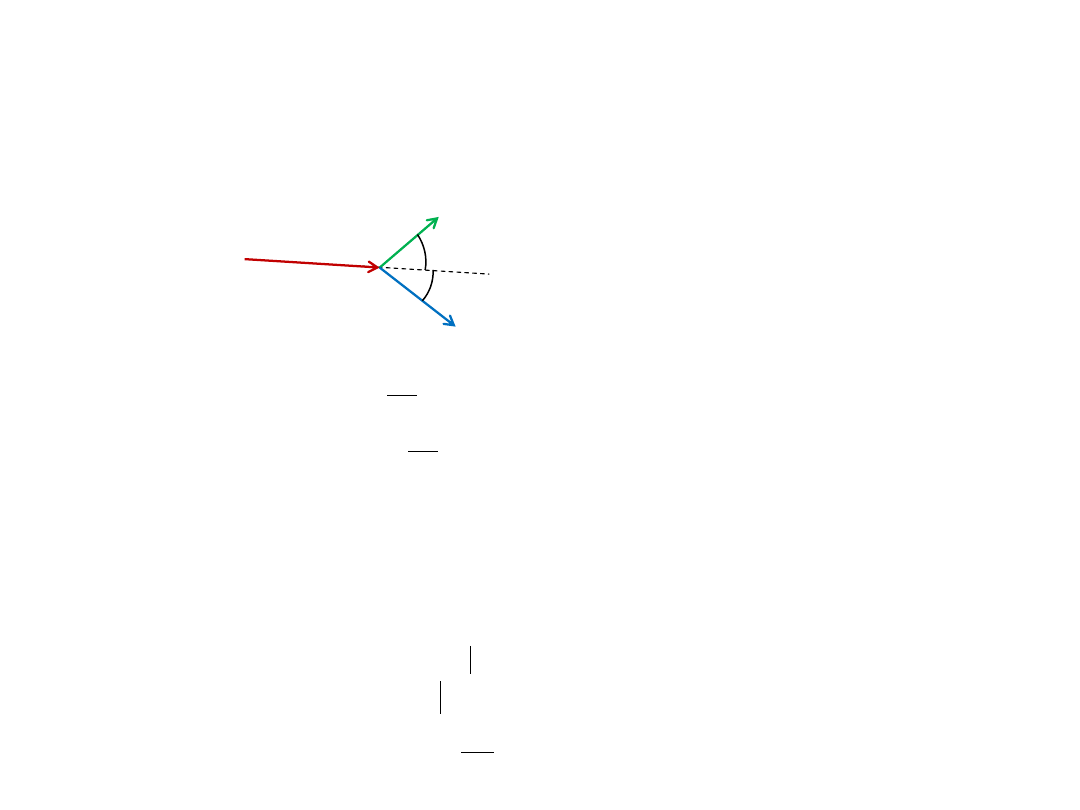
Efekt Comptona to rozproszenie fotonu na swobodnym elektronie, w wyniku którego foton oddaje część energii
elektronowi i zmienia kierunek ruchu. Oblicz zmianę długości fali fotonu rozproszonego pod kątem ϑ.
Rozwiązanie
keV
c
m
E
o
o
511
2
Energia spoczynkowa elektronu:
2
mc
E
e
Energia elektronu po rozproszeniu:
hc
h
E
f
Energia fotonu padającego:
Energia fotonu rozproszonego:
'
hc
'
h
'
E
f
f
'
p
e
p
f
p
Zasada zachowania energii:
1
2
2
mc
'
E
c
m
E
f
o
f
Zasada zachowania pędu:
2
f
e
f
'
p
p
p
Z równania (1) wyznaczamy kwadrat energii elektronu , wstawiając: i
4
2
2
c
m
E
e
c
mc
c
'
p
c
m
c
p
f
o
f
:
2
2
c
p
E
f
f
c
'
p
'
E
f
f
2
mc
c
m
'
p
p
o
f
f
2
2
2
2
2
c
E
c
m
c
m
'
p
p
e
o
f
f
Z równania (2) wyznaczamy kwadrat pędu elektronu:
Wykorzystując związek między energią a pędem elektronu:
otrzymujemy:
4
2
2
4
2
2
c
m
c
p
c
m
E
o
e
e
3
2
2
2
2
2
2
2
2
c
m
c
m
'
p
p
p
c
m
p
c
m
'
p
p
o
o
f
f
e
o
e
o
f
f
4
2
2
2
2
2
cos
'
p
p
'
p
p
'
p
p
p
f
f
f
f
f
f
e
Przyrównując prawe strony równania (3) i (4) otrzymujemy:
cos
'
p
p
'
p
p
c
m
c
m
'
p
p
f
f
f
f
o
o
f
f
2
2
2
2
2
2
cos
'
p
p
'
p
p
c
m
c
m
'
p
c
m
p
'
p
p
c
m
'
p
p
f
f
f
f
o
f
f
f
f
f
f
2
2
2
2
2
2
2
2
0
0
2
2
0
2
2
Z otrzymanego równania wyznaczamy pęd fotonu rozproszonego:
f
'
p
cos
c
m
p
p
cos
p
c
m
c
m
p
'
p
f
f
f
f
f
1
1
1
0
0
0
Wstawiamy: oraz
h
c
h
p
f
'
h
c
'
h
'
p
f
cos
c
m
h
'
cos
c
m
h
h
'
h
1
1
1
0
0
cos
c
m
h
'
1
0
Otrzymujemy przesunięcie Comptona: gdzie to comptonowska długość fali
c
m
h
0

Zadanie 11
Foton zderzył się z nieruchomym elektronem swobodnym i uległ rozproszeniu. Po zderzeniu energia fotonu i
energia kinetyczna elektronu są sobie równe. Kąt pomiędzy ich kierunkami po rozproszeniu wynosi
Wyznaczyć energię (pęd) padającego fotonu.
Energia spoczynkowa elektronu:
Korzystamy z zasady zachowania energii:
Nie znamy jeszcze pędu elektronu. Korzystamy z zasady zachowania pędu:
90
keV
c
m
E
o
o
511
2
2
2
'
mc
E
c
m
E
f
o
f
Energia padającego fotonu
Energia rozproszonego fotonu
Energia elektronu po zderzeniu
ke
f
o
f
f
E
E
c
m
mc
E
E
'
'
2
2
Energia kinetyczna elektronu po zderzeniu równa energii
fotonu po zderzeniu, więc:
2
4
2
2
2
2
2
2
2
c
m
c
m
c
p
c
m
mc
E
o
o
e
o
f
4
2
2
2
4
2
2
c
m
c
p
c
m
E
o
e
e
'
f
e
f
p
p
p
2
2
2
2
2
2
2
2
'
'
cos
'
2
'
f
f
e
f
e
e
f
f
e
f
p
p
p
p
p
p
p
p
p
p
c
E
p
f
f
c
E
c
E
p
f
f
f
2
1
'
'
Rozwiązanie

c
E
p
c
E
c
E
c
E
p
f
e
f
f
f
e
2
3
4
3
4
1
2
2
2
2
2
2
2
2
4
2
2
2
2
4
3
2
c
m
c
m
c
c
E
E
o
o
f
f
4
2
2
2
4
3
2
c
m
E
c
m
E
o
f
o
f
Obie strony równania podnosimy do kwadratu:
4
2
2
2
4
2
2
4
3
4
c
m
E
c
m
E
c
m
E
o
f
o
f
o
f
2
2
2
1
f
o
f
E
c
m
E
MeV
,
keV
keV
c
m
E
o
f
022
1
1022
511
2
2
2

Zadanie 12
Foton o energii E
f
= 400 keV został rozproszony na nieruchomym, swobodnym elektronie. Znaleźć energię
kinetyczną i pęd elektronu po zderzeniu, jeśli komptonowskie przesunięcie długości fali
nm
,
0012
0
Rozwiązanie
m
,
nm
,
12
10
2
1
0012
0
eV
keV
E
f
5
10
4
400
ke
f
f
E
'
E
E
Energia padającego fotonu
Energia rozproszonego fotonu
Energia kinetyczna elektronu po zderzeniu
f
f
ke
'
E
E
E
hc
'
hc
'
E
f
m
,
E
hc
hc
E
f
f
12
10
1
3
eV
,
hc
hc
hc
E
ke
5
10
11
1
Energia kinetyczna elektronu porównywalna z energią
spoczynkową - w celu obliczenia
pędu stosujemy wzory relatywistyczne.
eV
c
m
5
2
0
10
5
2
2
0
4
2
2
2
2
ke
o
e
E
c
m
c
m
c
p
E
c
keV
,
E
c
m
E
c
p
ke
ke
e
7
355
2
1
2
0
2
Zadanie 13
W zjawisku Comptona foton o energii E
f
= 100 keV
został rozproszony pod kątem ϑ = 90
0
. Wyznaczyć:
a)
Energię fotonu po zderzeniu,
b)
Energię kinetyczną elektronu,
c) Kierunek odrzutu elektronu.
Rozwiązanie
a) Zasada zachowania energii:
f
'
p
e
p
f
p
e
f
o
f
E
'
E
c
m
E
2
4
2
0
2
2
2
c
m
c
p
E
e
e
Energię elektronu wyrażamy przez pęd:
2
1
4
2
0
2
2
2
c
m
c
p
c
m
E
'
E
e
o
f
f
Pęd elektronu obliczamy z zasady zachowania pędu
e
f
f
p
'
p
p
wektory i są prostopadłe, więc:
2
2
2
f
f
e
p
'
p
p
f
p
f
'
p
c
E
p
f
f
2
2
2
2
1
f
f
e
E
'
E
c
p
2
1
4
2
0
2
2
2
c
m
'
E
E
c
m
E
'
E
f
f
o
f
f
Podnosimy obie strony równania do kwadratu i otrzymujemy:
keV
,
E
c
m
c
m
E
'
E
f
f
f
6
83
2
0
2
0
b) Energia kinetyczna elektronu równa jest stracie energii fotonu:
keV
,
'
E
E
E
f
f
ke
4
16
c) Kąt wyznaczamy z trójkąta, jaki tworzą
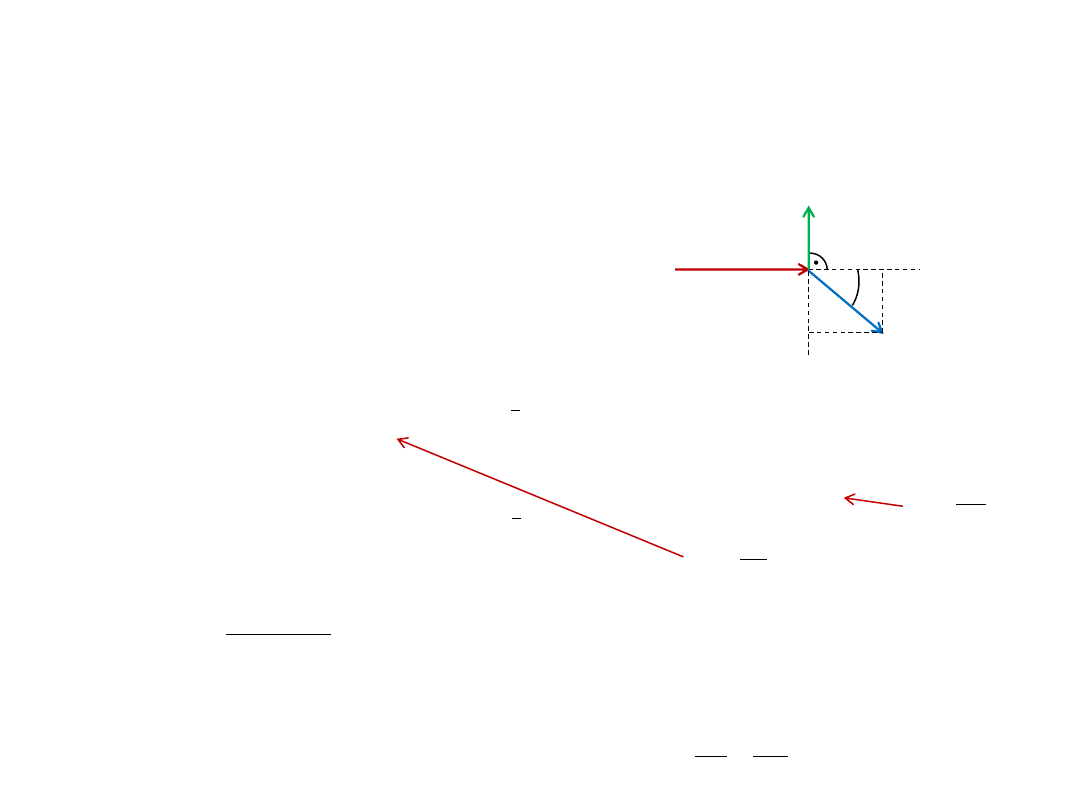
wektory pędów.
0
40
836
0
,
E
'
E
p
'
p
tg
f
f
f
f
Zadanie 14
Stosując postulaty Bohra, wyznacz energię elektronu na n-tej orbicie atomu wodoru.
Rozwiązanie
Postulat Bohra:
Elektron znajdujący się na stacjonarnej orbicie posiada moment pędu spełniający warunek
n
h
n
mvr
2
Energia elektronu jest sumą energii potencjalnej pola elektrycznego wytwarzanego przez proton o
ładunku +e oraz energii kinetycznej.
2
4
2
0
2
mv
r
e
E
Na elektron działa siła elektrostatyczna, która spełnia rolę siły dośrodkowej.
n
– liczba całkowita, h – stała Plancka
r
mv
r
e
2
2
0
2
4
Równanie to wraz z postulatem Bohra tworzą układ 2 równań, z których można wyznaczyć prędkość
i promień n-tej orbity
n
n
n
r
mv
r
e
2
2
0
2
4
2
h
n
r
mv
n
n
n
v
n
r
hn
e
v
n
0
2
2
2
2
0
2
me
n
h
r
n
Po wstawieniu tych wyrażeń do wzoru na energię, otrzymujemy:
2
2
2
0
4
1
59
13
1
8
n
eV
,
n
h
me
E
n
3
2
,
Energie emitowanych fotonów:
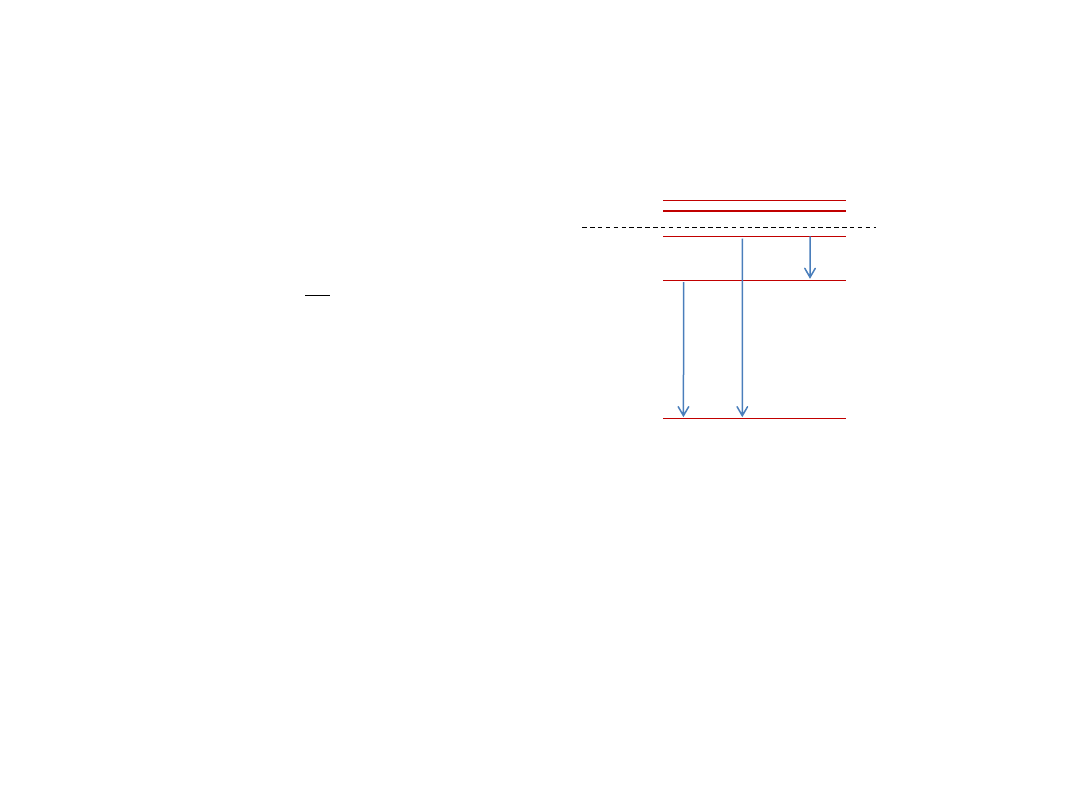
Zadanie 15
Jakie linie widmowe wystąpią przy wzbudzeniu atomu wodoru elektronami o energii 12,5 eV.
Rozwiązanie
eV
eV
E
E
E
08
,
12
59
,
13
51
,
1
1
3
3
,
1
Energie elektronu na kolejnych orbitach:
eV
,
E
59
13
1
eV
,
E
51
1
3
eV
,
E
84
0
4
eV
,
E
54
0
5
eV
,
E
39
3
2
2
1
59
13
n
eV
,
E
n
1
n
2
n
3
n
4
n
5
n
Przy wzbudzaniu atomu wodoru elektronami o energii 12,5 eV
elektron z pierwszej orbity może zwiększyć energię maksymalnie
do E
max
=(-13,59+12,5)eV = -
1,09eV, czyli może przeskoczyć na
orbitę drugą lub trzecią.
Wystąpią 3 linie widmowe:
eV
,
E
max
09
1
3
1
,
2
1
,
3
2
,
3
1
,
2
1
,
eV
,
eV
,
,
E
E
E
,
2
10
59
13
39
3
1
2
2
1
eV
,
eV
,
,
E
E
E
,
88
1
39
3
51
1
2
3
3
2

Długości fal emitowanych fotonów wygodnie
obliczyć z empirycznego wzoru Rydberga
m
,
R
R
,
,
7
3
2
3
2
10
563
6
36
5
9
1
4
1
1
2
2
2
0
4
1
1
8
n
k
h
me
E
E
c
h
E
k
n
f
2
2
2
2
3
0
4
1
1
1
1
8
1
n
k
R
n
k
c
h
me
k
n
1
7
10
097
1
m
,
R
Stała Rydberga
m
,
R
R
,
,
7
2
1
2
1
10
215
1
4
3
4
1
1
1
m
,
R
R
,
,
7
2
1
3
1
10
026
1
9
8
9
1
1
1
Seria Lymana (nadfiolet)
Seria Balmera (światło widzialne)

Zadanie 16
Obliczyć długości fal pierwszych trzech linii w serii Balmera oraz granicę tej linii. W jakiej części widma leżą te linie?
Rozwiązanie
Seria Balmera powstaje, gdy elektron w atomie wodoru przeskakuje na drugą orbitę: k = 2, n = 3, 4, 5…
Korzystamy z wzoru Rydberga
1
1
1
1
2
2
n
k
R
1
7
10
097
1
m
,
R
3
n
4
n
5
n
R
R
36
5
9
1
4
1
1
1
R
R
16
3
16
1
4
1
1
2
R
R
100
21
25
1
4
1
1
3
nm
m
,
R
656
10
56
6
5
36
7
1
nm
m
,
R
486
10
86
4
3
16
7
2
H
H
H
nm
m
,
R
434
10
34
4
21
100
7
3
Granicę serii znajdziemy, licząc granicę wyrażenia (1) dla
n
nm
nm
,
R
R
gr
gr
365
6
364
4
4
1
1
Linie serii Balmera leżą w widzialnej części widma (380nm – 780nm). Granica serii leży już w nadfiolecie.
Zadanie 17
Wyznaczyć najmniejszą energię niezbędną do wzbudzenia całego widma dwukrotnie zjonizowanego atomu litu.
Rozwiązanie
Dwukrotnie zjonizowany atomu litu (Z = 3) ma jeden elektron. Taki atom o jednym elektronie nazywamy atomem
wodoropodobnym. Energię elektronu na n-tej orbicie wyznaczamy podobnie jak dla atomu wodoru (Zad. 12) z tym,
że ładunek jądra jest równy Ze.
2
4
2
0
2
mv
r
Ze
E
n
n
n
r
mv
r
Ze
2
2
0
2
4
2
h
n
r
mv
n
n
hn
Ze
v
n
0
2
2
2
2
0
2
mZe
n
h
r
n
2
2
2
2
0
4
2
1
59
13
1
8
n
Z
eV
,
n
h
e
mZ
E
n
Energia fotonu, który może spowodować przeskok elektronu na wyższą orbitę wynosi
2
2
2
1
1
59
13
n
k
Z
eV
,
E
E
E
k
n
f
k
n
Najmniejsza energia do wzbudzenia całego widma to energia graniczna dla k = 1;
eV
,
Z
eV
,
E
f
3
122
59
13
2
n

Zadanie 18
O ile zmieni się długość fali de Broglie’a elektronu przy wyrzuceniu go przez foton o energii E
f
= 14,5 eV z pierwszej
orbity bohrowskiej w atomie wodoru.
Rozwiązanie
Zgodnie z korpuskulano-
falową teorią materii poruszająca się cząstka jest jednocześnie falą o długości ,
gdzie p
jest pędem cząstki.
Aby obliczyć długość fali elektronu na orbicie w atomie wodoru, skorzystamy z postulatu Bohra
p
h
2
h
n
pr
n
– liczba całkowita, h – stała Plancka, p – pęd elektronu
n
r
r
n
h
p
n
n
2
2
1
dla n =1
m
,
r
10
1
1
10
3
3
2
2
2
0
2
me
n
h
r
n
gdzie
Energia fotonu, który wybił elektron z atomu jest większa od energii jonizacji W = 13,59 eV.
Elektron uzyska energię kinetyczną E
k
, którą obliczymy z równania:
eV
,
E
E
W
E
k
k
f
91
0
Energia kinetyczna elektronu jest dużo mniejsza od jego energii spoczynkowej
Możemy więc użyć nierelatywistycznego związku między energią kinetyczną i pędem.
keV
c
m
E
o
o
511
2
s
kgm
,
mE
p
k
25
10
15
5
2
s
J
h
34
10
63
,
6
kg
m
31
10
11
,
9
J
eV
19
10
60
,
1
1
m
,
p
h
10
2
10
8
12
m
,
10
1
2
10
5
9
długość fali elektronu zwiększy się o:

Zadania do samodzielnego rozwiązania

Zadanie 1
Źródło monochromatyczne o mocy wysyła fotonów na sekundę. Obliczyć długość fali
wysyłanych fotonów.
Odp:
Zadanie 2
Temperatura ciała doskonale czarnego wynosiła 2000 K. O ile stopni zmieniła się temperatura, gdy najbardziej
prawdopodobna długość fali w jego widmie wzrosła o 500 nm.
Odp: zmalała o 510 K.
Zadanie 3
Maksimum promieniowania ciała doskonale czarnego przypada dla długości fali . Wyznaczyć
całkowitą moc wysyłanego promieniowania, jeżeli pole powierzchni ciała wynosi
Odp:
Zadanie 5
Graniczna długość fali dla pewnego metalu jest równa . Obliczyć prędkość elektronów wybitych w
zjawisku fotoelektrycznym zewnętrznym, jeśli metal oświetlimy światłem nadfioletowym o długości fali
Odp: v = 603 379 m/s
W
P
2
10
13
10
n
nm
,
2
0
nm
max
580
2
8
m
S
W
,
P
4
10
84
2
nm
gr
400
gr
4
3
Zadanie 4
Ciało doskonale czarne podgrzano tak, że najbardziej prawdopodobna długość fali zmieniła się od
do
. Ile razy wzrośnie moc wypromieniowana przez ciało?
Odp.: Moc wzrośnie 81-krotnie.
m
,
6
0
1
m
,
2
0
2

Zadanie 6
Dla powierzchni oświetlonej promieniowaniem o długości fali
, potencjał hamowania U jest
równy 1,47V . Wyznaczyć graniczną długość fali promieniowania dla zjawiska fotoelektrycznego.
Odp:
nm
360
nm
eU
hc
hc
gr
628
Zadanie 7
Obliczyć długości fal pierwszych dwóch linii w serii Paschena (przeskok elektronu w atomie wodoru na 3 orbitę) oraz
granicę tej linii. W jakiej części widma leżą te linie?
Odp
Linie te leżą w podczerwieni.
Zadanie 8
Wyznaczyć długość fali w widmie zjonizowanego helu, odpowiadającą przejściu elektronu z orbity trzeciej na drugą.
Odp:
nm
164
nm
1875
1
nm
1282
2
Zadanie 9
Przy wzroście energii elektronu o , długość fali de Broglie’a zmalała dwa razy. Znaleźć początkową
długość fali elektronu.
Odp:
eV
E
200
m
,
10
10
5
1

Zadanie 10
Na atom wodoru pada foton i wybija z niego elektron o energii kinetycznej . Obliczyć energię
padającego fotonu, jeśli atom znajdował się w stanie wzbudzonym o liczbie kwantowej n = 2.
Odp:
eV
E
k
5
eV
,
E
f
4
8
Zadanie 11
Wyznaczyć najmniejszy potencjał hamujący konieczny do zahamowania elektronów wysyłanych przez fotokatodę,
jeśli pada na nią promieniowanie o długości fali , a granica zjawiska fotoelektrycznego odpowiada
długości fali
Odp
Zadanie 12
O ile zmieni się długość fali de Broglie’a elektronu przy przejściu z drugiej orbity stacjonarnej na pierwszą
a) w atomie wodoru
b) w jednokrotnie zjonizowanym atomie helu
Odp: a) b)
Zadanie 13
Oszacować, ile razy zwiększy się promień orbity elektronu w atomie wodoru znajdującym się w stanie
podstawowym przy wzbudzeniu go fotonem o energii 12,08 eV.
Odp: Promień wzrośnie 9-krotnie.
nm
490
nm
gr
670
V
,
U
h
68
0
m
,
10
10
3
3
m
,
10
10
65
1

Zadanie 14
Gaz składający się z atomów wodoru w stanie podstawowym jest naświetlany światłem monochromatycznym, w
wyniku czego zaczyna on emitować dokładnie trzy linie widmowe. Wyznaczyć długość fali światła wzbudzającego.
Odp.:
Zadanie 15
Napięcie hamujące ruch fotoelektronów w fotokomórce próżniowej, oświetlonej światłem o długości fali ,
wynosi . Oblicz wartość pracy wyjścia materiału fotokatody i częstotliwość graniczną zjawiska
fotoelektrycznego
Odp.:
Zadanie16
W atomie wodoru elektron przeskakuje z trzeciej orbity na pierwszą. Oblicz zmianę pędu i energii kinetycznej
elektronu. Dane: masa elektronu m
, ładunek elektronu e, stała Plancka h, przenikalność elektryczna próżni
0
.
Odp.:
nm
400
Hz
,
gr
14
10
244
7
0
2
6
me
p
m
,
8
10
7
9
mV
U
106
eV
W
3
2
2
0
2
4
32
16
15
me
E
k
Zadanie17
Na powierzchnię metalu pada strumień fotonów o częstości n = 3 razy większej niż częstość graniczna . Oblicz
długość fali de Broglie’a elektronów o maksymalnej energii kinetycznej
Dane: masa elektronu m
, ładunek elektronu e, stała Plancka h, prędkość światła c.
Odp.:
gr
gr
m
k
h
1
2

Zadanie18
Maksymalna wartość energii kinetycznej elektronów w efekcie Comptona jest równa energii spoczynkowej
elektronu . Oblicz energię padających fotonów.
Odp.:
MeV
,
c
m
E
o
o
5
0
2
MeV
,
E
f
7
0
Zadanie19
Kwant o energii zderzył się centralnie ze swobodnym elektronem, a następnie wywołał efekt
fotoelektryczny wewnętrzny. Oblicz energie kinetyczne obu elektronów. Energia spoczynkowa elektronu
Odp.:
MeV
E
1
MeV
,
c
m
E
o
o
5
0
2
MeV
,
E
k
8
0
1
MeV
,
E
k
2
0
2
Wyszukiwarka
Podobne podstrony:
Fiz kwantowa
Wykład 4 Elementarne zagadnienia kwantowe
Wykład Chemia kwantowa 11
mechanika kwantowa
5 3 FIZJOLOGIA W FIZ
mat fiz 2008 10 06
9, dokumentacja pracy fiz, diagnostyka fizj, problemy i ich rozwiazywane zwiazane z plananem
Zestaw Fiz.wsp, AGH, ROK I, fizyka, Fizyka
Lab fiz 43 2, Studia, Semestr 1, Fizyka, Sprawozdania
Nr ćwiczenia5 moje, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
Fiz 10 P, Studia, Ogólne, Fiyzka, od romka, studia materiały, Fizyka lab, Termopary
fiz odp na pyt grA i B, Politechnika Poznańska, ZiIP, Semestr I, Fizyka
więcej podobnych podstron