
Cztery podstawowe podprzestrzenie
Paulina Wróbel
Marianna Piechowicz
Politechnika Poznańska
Wydział Informatyki
Automatyka i Robotyka
19 grudnia 2012r.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
1 / 32

Spis treści :
1
Znajdowanie bazy przestrzeni wektorowej
2
Cztery podstawowe podprzestrzenie
Przestrzeń kolumnowa
Przestrzeń zerowa
Przestrzeń wierszowa
Przestrzeń zerowa macierzy transponowanej
Powiązania między czterema podstawowymi przestrzeniami
Przykład
3
Jeszcze jedna przestrzeń wektorowa
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
2 / 32
Definicja bazy
Definicja
Baza przestrzeni wektorowej to niezależne wektory, które rozpinają całą
przestrzeń.
Każdy wektor będący w danej przestrzeni da się zapisać jako kombinacja
wektorów bazowych. Żeby określić, czy dane wektory są bazą, wystarczy
tylko sprawdzić, czy mają tyle samo współrzędnych oraz czy są niezależne.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
3 / 32
Definicja bazy
Definicja
Baza przestrzeni wektorowej to niezależne wektory, które rozpinają całą
przestrzeń.
Każdy wektor będący w danej przestrzeni da się zapisać jako kombinacja
wektorów bazowych. Żeby określić, czy dane wektory są bazą, wystarczy
tylko sprawdzić, czy mają tyle samo współrzędnych oraz czy są niezależne.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
3 / 32
Definicja bazy
Definicja
Baza przestrzeni wektorowej to niezależne wektory, które rozpinają całą
przestrzeń.
Każdy wektor będący w danej przestrzeni da się zapisać jako kombinacja
wektorów bazowych. Żeby określić, czy dane wektory są bazą, wystarczy
tylko sprawdzić, czy mają
tyle samo współrzędnych
oraz czy są niezależne.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
3 / 32
Definicja bazy
Definicja
Baza przestrzeni wektorowej to niezależne wektory, które rozpinają całą
przestrzeń.
Każdy wektor będący w danej przestrzeni da się zapisać jako kombinacja
wektorów bazowych. Żeby określić, czy dane wektory są bazą, wystarczy
tylko sprawdzić, czy mają tyle samo współrzędnych oraz czy są
niezależne
.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
3 / 32

Przykład
Czy następujące wektory tworzą bazę?
1
1
2
,
2
2
5
,
3
3
8
NIE , chociaż na pierwszy rzut oka wydaje się, że tak.
Jeżeli utworzymy z nich macierz, otrzymamy:
1
2
3
1
2
3
2
5
8
Ta macierz nie jest odwracalna!
Od razu widać, że dwa wiersze są takie same.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
4 / 32

Przykład
Czy następujące wektory tworzą bazę?
1
1
2
,
2
2
5
,
3
3
8
NIE
, chociaż na pierwszy rzut oka wydaje się, że tak.
Jeżeli utworzymy z nich macierz, otrzymamy:
1
2
3
1
2
3
2
5
8
Ta macierz nie jest odwracalna!
Od razu widać, że dwa wiersze są takie same.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
4 / 32

Przykład
Czy następujące wektory tworzą bazę?
1
1
2
,
2
2
5
,
3
3
8
NIE , chociaż na pierwszy rzut oka wydaje się, że tak.
Jeżeli utworzymy z nich macierz, otrzymamy:
1
2
3
1
2
3
2
5
8
Ta macierz nie jest odwracalna!
Od razu widać, że dwa wiersze są takie same.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
4 / 32

Przykład
Czy następujące wektory tworzą bazę?
1
1
2
,
2
2
5
,
3
3
8
NIE , chociaż na pierwszy rzut oka wydaje się, że tak.
Jeżeli utworzymy z nich macierz, otrzymamy:
1
2
3
1
2
3
2
5
8
Ta macierz nie jest odwracalna!
Od razu widać, że dwa wiersze są takie same.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
4 / 32

Przykład
Czy następujące wektory tworzą bazę?
1
1
2
,
2
2
5
,
3
3
8
NIE , chociaż na pierwszy rzut oka wydaje się, że tak.
Jeżeli utworzymy z nich macierz, otrzymamy:
1
2
3
1
2
3
2
5
8
Ta macierz
nie jest odwracalna
!
Od razu widać, że dwa wiersze są takie same.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
4 / 32
Co robić?
Jak sprawdzić, czy dane wektory są bazą?
•
Utworzyć macierz z danych wierszy.
•
Sprawdzić, czy macierz jest odwracalna.
MACIERZ
ODWRACALNA
Dane wektory są bazą.
NIEODWRACALNA
Dane wektory nie są bazą.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
5 / 32
Co robić?
Jak sprawdzić, czy dane wektory są bazą?
•
Utworzyć macierz z danych wierszy.
•
Sprawdzić, czy macierz jest odwracalna.
MACIERZ
ODWRACALNA
Dane wektory są bazą.
NIEODWRACALNA
Dane wektory nie są bazą.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
5 / 32
Co robić?
Jak sprawdzić, czy dane wektory są bazą?
•
Utworzyć macierz z danych wierszy.
•
Sprawdzić, czy macierz jest odwracalna.
MACIERZ
ODWRACALNA
Dane wektory są bazą.
NIEODWRACALNA
Dane wektory nie są bazą.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
5 / 32
Co robić?
Jak sprawdzić, czy dane wektory są bazą?
•
Utworzyć macierz z danych wierszy.
•
Sprawdzić, czy macierz jest odwracalna.
MACIERZ
ODWRACALNA
Dane wektory są bazą.
NIEODWRACALNA
Dane wektory nie są bazą.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
5 / 32
Podstawowe podprzestrzenie
Uwaga
Cztery podstawowe podprzestrzenie są badzo ważnym pojęciem dla
algebry! Ważne jest też zobaczenie, jak są ze sobą powiązane.
Podprzestrzenie macierzy A:
•
Przestrzeń kolumnowa C(A)
•
Przestrzeń zerowa N (A)
•
Przestrzeń wierszowa C(A
T
)
•
Przestrzeń zerowa macierzy transponowanej N (A
T
)
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
6 / 32
Podstawowe podprzestrzenie
Uwaga
Cztery podstawowe podprzestrzenie są badzo ważnym pojęciem dla
algebry! Ważne jest też zobaczenie, jak są ze sobą powiązane.
Podprzestrzenie macierzy A:
•
Przestrzeń kolumnowa C(A)
•
Przestrzeń zerowa N (A)
•
Przestrzeń wierszowa C(A
T
)
•
Przestrzeń zerowa macierzy transponowanej N (A
T
)
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
6 / 32

W dalczej części prezentacji będziemy określać przestrzenie dla macierzy A:
A =
1
2
3
1
1
1
2
1
1
2
3
1
Będzie nam też potrzebna jej zredukowana wierszowa postać
schodkowa R. Możemy wyrożnić w niej kilka charakterycznych części:
•
macierz identycznościowa I
•
kolumny ze zmiennymi wolnymi F
•
wiersze z zerami
R =
1
0
1
1
0
1
1
0
0
0
0
0
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
7 / 32

W dalczej części prezentacji będziemy określać przestrzenie dla macierzy A:
A =
1
2
3
1
1
1
2
1
1
2
3
1
Będzie nam też potrzebna jej zredukowana wierszowa postać
schodkowa R. Możemy wyrożnić w niej kilka charakterycznych części:
•
macierz identycznościowa I
•
kolumny ze zmiennymi wolnymi F
•
wiersze z zerami
R =
1
0
1
1
0
1
1
0
0
0
0
0
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
7 / 32

W dalczej części prezentacji będziemy określać przestrzenie dla macierzy A:
A =
1
2
3
1
1
1
2
1
1
2
3
1
Będzie nam też potrzebna jej zredukowana wierszowa postać
schodkowa R. Możemy wyrożnić w niej kilka charakterycznych części:
•
macierz identycznościowa I
•
kolumny ze zmiennymi wolnymi F
•
wiersze z zerami
R =
1
0
1
1
0
1
1
0
0
0
0
0
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
7 / 32

W dalczej części prezentacji będziemy określać przestrzenie dla macierzy A:
A =
1
2
3
1
1
1
2
1
1
2
3
1
Będzie nam też potrzebna jej zredukowana wierszowa postać
schodkowa R. Możemy wyrożnić w niej kilka charakterycznych części:
•
macierz identycznościowa I
•
kolumny ze zmiennymi wolnymi F
•
wiersze z zerami
R =
1
0
1
1
0
1
1
0
0
0
0
0
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
7 / 32
Przestrzeń kolumnowa
Macierz A ma m wierszy, n kolumn i ma rząd r
Wymiar przestrzeni kolumnowej wynosi r .
Bazą tej przestrzeni są kolumny osiowe.
Ta przestrzeń jest podprzestrzenią przestrzeni R
m
.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
8 / 32
Przestrzeń kolumnowa
Macierz A ma m wierszy, n kolumn i ma rząd r
Wymiar przestrzeni kolumnowej wynosi r .
Bazą tej przestrzeni są kolumny osiowe.
Ta przestrzeń jest podprzestrzenią przestrzeni R
m
.
Przestrzeń kolumnowa C(A) zawiera wszystkie kombinacje
kolumn macierzy A.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
8 / 32
Przestrzeń kolumnowa
Macierz A ma m wierszy, n kolumn i ma rząd r
Wymiar przestrzeni kolumnowej wynosi r .
Bazą tej przestrzeni są kolumny osiowe.
Ta przestrzeń jest podprzestrzenią przestrzeni R
m
.
Przestrzeń kolumnowa C(A) zawiera wszystkie kombinacje
kolumn macierzy A.
Te kolumny mają m współrzędnych, więc przestrzeń
kolumnowa jest podprzestrzenią przestrzeni R
m
.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
8 / 32

Przestrzeń kolumnowa
Znaleźć przestrzeń kolumnową macierzy A
Spójrzmy na kolumny osiowe
macierzy R:
R =
1
0
1
1
0
1
1
0
0
0
0
0
Te kolumny tworzą bazę
dla C(R):
C(R) = c
1
1
0
0
+ c
2
0
1
0
To wskazuje na to, że bazą
przestrzeni kolumnowej
macierzy A też będzie jej
pierwsza i druga kolumna.
A =
1
2
3
1
1
1
2
1
1
2
3
1
C(A) = c
1
1
1
1
+ c
2
2
1
2
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
9 / 32

Przestrzeń kolumnowa
Znaleźć przestrzeń kolumnową macierzy A
Spójrzmy na
kolumny osiowe
macierzy R:
R =
1
0
1
1
0
1
1
0
0
0
0
0
Te kolumny tworzą bazę
dla C(R):
C(R) = c
1
1
0
0
+ c
2
0
1
0
To wskazuje na to, że bazą
przestrzeni kolumnowej
macierzy A też będzie jej
pierwsza i druga kolumna.
A =
1
2
3
1
1
1
2
1
1
2
3
1
C(A) = c
1
1
1
1
+ c
2
2
1
2
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
9 / 32

Przestrzeń kolumnowa
Znaleźć przestrzeń kolumnową macierzy A
Spójrzmy na kolumny osiowe
macierzy R:
R =
1
0
1
1
0
1
1
0
0
0
0
0
Te kolumny tworzą bazę
dla C(R):
C(R) = c
1
1
0
0
+ c
2
0
1
0
To wskazuje na to, że bazą
przestrzeni kolumnowej
macierzy A też będzie jej
pierwsza i druga kolumna.
A =
1
2
3
1
1
1
2
1
1
2
3
1
C(A) = c
1
1
1
1
+ c
2
2
1
2
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
9 / 32

Przestrzeń kolumnowa
Znaleźć przestrzeń kolumnową macierzy A
Spójrzmy na kolumny osiowe
macierzy R:
R =
1
0
1
1
0
1
1
0
0
0
0
0
Te kolumny tworzą bazę
dla C(R):
C(R) = c
1
1
0
0
+ c
2
0
1
0
To wskazuje na to, że bazą
przestrzeni kolumnowej
macierzy A też będzie jej
pierwsza i druga kolumna.
A =
1
2
3
1
1
1
2
1
1
2
3
1
C(A) = c
1
1
1
1
+ c
2
2
1
2
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
9 / 32

Przestrzeń kolumnowa
Znaleźć przestrzeń kolumnową macierzy A
Spójrzmy na kolumny osiowe
macierzy R:
R =
1
0
1
1
0
1
1
0
0
0
0
0
Te kolumny tworzą bazę
dla C(R):
C(R) = c
1
1
0
0
+ c
2
0
1
0
To wskazuje na to, że bazą
przestrzeni kolumnowej
macierzy A też będzie jej
pierwsza i druga kolumna.
A =
1
2
3
1
1
1
2
1
1
2
3
1
C(A) = c
1
1
1
1
+ c
2
2
1
2
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
9 / 32

Przestrzeń kolumnowa
Łatwo zauważyć, że C(R) i C(A) mają wymiar równy 2. Rzędy tych
macierzy też są równe 2.
dim(C(A)) = dim(C(R)) = r
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
10 / 32

Przestrzeń kolumnowa
Łatwo zauważyć, że C(R) i C(A) mają wymiar równy 2. Rzędy tych
macierzy też są równe 2.
dim(C(A)) = dim(C(R)) = r
Wyznaczyliśmy aż dwie przestrzenie kolumnowe: macierzy A i macierzy R.
Te podprzestrzenie
nie są równe
!
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
10 / 32

Przestrzeń kolumnowa
Łatwo zauważyć, że C(R) i C(A) mają wymiar równy 2. Rzędy tych
macierzy też są równe 2.
dim(C(A)) = dim(C(R)) = r
Wyznaczyliśmy aż dwie przestrzenie kolumnowe: macierzy A i macierzy R.
Te podprzestrzenie nie są równe!
Zauważmy, że wektor
h
1
1
1
i
, który na pewno jest w C(A), nie jest w C(R).
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
10 / 32

Przestrzeń kolumnowa
Łatwo zauważyć, że C(R) i C(A) mają wymiar równy 2. Rzędy tych
macierzy też są równe 2.
dim(C(A)) = dim(C(R)) = r
Wyznaczyliśmy aż dwie przestrzenie kolumnowe: macierzy A i macierzy R.
Te podprzestrzenie nie są równe!
Zauważmy, że wektor
h
1
1
1
i
, który na pewno jest w C(A), nie jest w C(R).
C(A) 6= C(R)
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
10 / 32
Przestrzeń zerowa
Macierz A ma m wierszy, n kolumn i ma rząd r
Wymiar przestrzeni zerowej wynosi n − r .
Bazą tej przestrzeni są rozwiązania specjalne.
Ta przestrzeń jest podprzestrzenią przestrzeni R
n
.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
11 / 32
Przestrzeń zerowa
Macierz A ma m wierszy, n kolumn i ma rząd r
Wymiar przestrzeni zerowej wynosi n − r .
Bazą tej przestrzeni są rozwiązania specjalne.
Ta przestrzeń jest podprzestrzenią przestrzeni R
n
.
Przestrzeń zerowa N (A) zawiera wszystkie rozwiązania
równania Ax = 0.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
11 / 32
Przestrzeń zerowa
Macierz A ma m wierszy, n kolumn i ma rząd r
Wymiar przestrzeni zerowej wynosi n − r .
Bazą tej przestrzeni są rozwiązania specjalne.
Ta przestrzeń jest podprzestrzenią przestrzeni R
n
.
Przestrzeń zerowa N (A) zawiera wszystkie rozwiązania
równania Ax = 0.
Wektor x ma n współrzędnych, więc przestrzeń zerowa jest
podprzestrzenią przestrzeni R
n
.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
11 / 32
Przestrzeń zerowa
Znaleźć przestrzeń zerową macierzy A
Najpierw trzeba znaleźć
rozwiązania specjalne.
Są kolumnami poniższej
macierzy:
"
−F
I
#
=
− 1
− 1
− 1
0
1
0
0
1
Dzięki temu wiemy, jak
wygląda przestrzeń zerowa
macierzy A:
N (A) = c
1
−1
−1
1
0
+ c
2
−1
0
0
1
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
12 / 32
Przestrzeń zerowa
Znaleźć przestrzeń zerową macierzy A
Najpierw trzeba znaleźć
rozwiązania specjalne.
Są kolumnami poniższej
macierzy:
"
−F
I
#
=
− 1
− 1
− 1
0
1
0
0
1
Dzięki temu wiemy, jak
wygląda przestrzeń zerowa
macierzy A:
N (A) = c
1
−1
−1
1
0
+ c
2
−1
0
0
1
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
12 / 32
Przestrzeń zerowa
Znaleźć przestrzeń zerową macierzy A
Najpierw trzeba znaleźć
rozwiązania specjalne.
Są kolumnami poniższej
macierzy:
"
−F
I
#
=
− 1
− 1
− 1
0
1
0
0
1
Dzięki temu wiemy, jak
wygląda przestrzeń zerowa
macierzy A:
N (A) = c
1
−1
−1
1
0
+ c
2
−1
0
0
1
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
12 / 32

Przestrzeń zerowa
Dzięki
zredukowanej wierszowej postaci schodkowej macierzy
łatwiej jest
znaleźć rozwiązania specjalne.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
13 / 32

Przestrzeń zerowa
Dzięki
zredukowanej wierszowej postaci schodkowej macierzy
łatwiej jest
znaleźć rozwiązania specjalne.
W macierzy R wyraźnie widać, że ich liczba to liczba kolumn macierzy
minus jej rząd.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
13 / 32

Przestrzeń zerowa
Dzięki zredukowanej wierszowej postaci schodkowej macierzy łatwiej jest
znaleźć rozwiązania specjalne.
W macierzy R wyraźnie widać, że ich liczba to liczba kolumn macierzy
minus jej rząd.
Dlatego prawdziwa jest równość:
dim(N (A)) = n − r
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
13 / 32
Przestrzeń wierszowa
Macierz A ma m wierszy, n kolumn i ma rząd r
Wymiar przestrzeni wierszowej wynosi r .
Bazą tej przestrzeni jest pierwsze r wierszy macierzy R.
Ta przestrzeń jest podprzestrzenią przestrzeni R
n
.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
14 / 32
Przestrzeń wierszowa
Macierz A ma m wierszy, n kolumn i ma rząd r
Wymiar przestrzeni wierszowej wynosi r .
Bazą tej przestrzeni jest pierwsze r wierszy macierzy R.
Ta przestrzeń jest podprzestrzenią przestrzeni R
n
.
Przestrzeń wierszowa C(A
T
) zawiera wszystkie liniowe
kombinacje wierszy macierzy A.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
14 / 32
Przestrzeń wierszowa
Macierz A ma m wierszy, n kolumn i ma rząd r
Wymiar przestrzeni wierszowej wynosi r .
Bazą tej przestrzeni jest pierwsze r wierszy macierzy R.
Ta przestrzeń jest podprzestrzenią przestrzeni R
n
.
Przestrzeń wierszowa C(A
T
) zawiera wszystkie liniowe
kombinacje wierszy macierzy A.
Te wiersze mają n współrzędnych, więc przestrzeń zerowa
jest podprzestrzenią przestrzeni R
n
.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
14 / 32
Przestrzeń wierszowa
Macierz A ma m wierszy, n kolumn i ma rząd r
Wymiar przestrzeni wierszowej wynosi r .
Bazą tej przestrzeni jest pierwsze r wierszy macierzy R.
Ta przestrzeń jest podprzestrzenią przestrzeni R
n
.
Minusem jest tutaj operowanie na wierszach, wygodniej
byłoby operować na kolumnach.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
14 / 32
Przestrzeń wierszowa
Macierz A ma m wierszy, n kolumn i ma rząd r
Wymiar przestrzeni wierszowej wynosi r .
Bazą tej przestrzeni jest pierwsze r wierszy macierzy R.
Ta przestrzeń jest podprzestrzenią przestrzeni R
n
.
Minusem jest tutaj operowanie na wierszach, wygodniej
byłoby operować na kolumnach.
Jak można otrzymać kolumny z wierszy?
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
14 / 32
Przestrzeń wierszowa
Macierz A ma m wierszy, n kolumn i ma rząd r
Wymiar przestrzeni wierszowej wynosi r .
Bazą tej przestrzeni jest pierwsze r wierszy macierzy R.
Ta przestrzeń jest podprzestrzenią przestrzeni R
n
.
Minusem jest tutaj operowanie na wierszach, wygodniej
byłoby operować na kolumnach.
Jak można otrzymać kolumny z wierszy?
Wystarczy przetransponować macierz. Dzięki temu
poprawny bedzie zapis C(A
T
).
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
14 / 32
Przestrzeń wierszowa
Znaleźć przestrzeń wierszową macierzy A
Macierz R ma dwa elementy osiowe i występują one w pierwszym i drugim
wierszu tej macierzy.
R =
1
0
1
1
0
1
1
0
0
0
0
0
Wykonując operacje na wierszach, przestrzeń wierszowa nie będzie się
zmieniać.
Zatem:
C(A
T
) = C(R
T
)
= c
1
h
1
0
1
1
i
+ c
2
h
0
1
1
0
i
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
15 / 32
Przestrzeń wierszowa
Znaleźć przestrzeń wierszową macierzy A
Macierz R ma dwa elementy osiowe i występują one w pierwszym i drugim
wierszu tej macierzy.
R =
1
0
1
1
0
1
1
0
0
0
0
0
Wykonując operacje na wierszach, przestrzeń wierszowa nie będzie się
zmieniać.
Zatem:
C(A
T
) = C(R
T
)
= c
1
h
1
0
1
1
i
+ c
2
h
0
1
1
0
i
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
15 / 32
Przestrzeń wierszowa
Znaleźć przestrzeń wierszową macierzy A
Macierz R ma dwa elementy osiowe i występują one w pierwszym i drugim
wierszu tej macierzy.
R =
1
0
1
1
0
1
1
0
0
0
0
0
Wykonując operacje na wierszach, przestrzeń wierszowa nie będzie się
zmieniać.
Zatem:
C(A
T
) = C(R
T
)
= c
1
h
1
0
1
1
i
+ c
2
h
0
1
1
0
i
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
15 / 32
Przestrzeń wierszowa
Znaleźć przestrzeń wierszową macierzy A
Macierz R ma dwa elementy osiowe i występują one w pierwszym i drugim
wierszu tej macierzy.
R =
1
0
1
1
0
1
1
0
0
0
0
0
Wykonując operacje na wierszach, przestrzeń wierszowa nie będzie się
zmieniać.
Zatem:
C(A
T
) = C(R
T
) = c
1
h
1
0
1
1
i
+ c
2
h
0
1
1
0
i
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
15 / 32

Przestrzeń wierszowa
Dlaczego poniższa równość jest prawdziwa?
C(A
T
) = C(R
T
)
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
16 / 32

Przestrzeń wierszowa
Dlaczego poniższa równość jest prawdziwa?
C(A
T
) = C(R
T
)
Ponieważ mnożyliśmy wiersz przez liczbę lub dodawaliśmy do niego inny
wiersz, a te operacje
nie zmieniają przestrzeni wierszowej
.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
16 / 32

Przestrzeń wierszowa
Dlaczego poniższa równość jest prawdziwa?
C(A
T
) = C(R
T
)
Ponieważ mnożyliśmy wiersz przez liczbę lub dodawaliśmy do niego inny
wiersz, a te operacje nie zmieniają przestrzeni wierszowej.
Łatwo jeszcze zauważyć, że C(A
T
) ma wymiar równy 2. Rząd macierzy też
równa się 2. Ogólnie:
dim(C(A
T
)) = r
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
16 / 32
Lewa przestrzeń zerowa
Macierz A ma m wierszy, n kolumn i ma rząd r
Wymiar lewej przestrzeni zerowej wynosi m − r .
Bazą tej przestrzeni jest ostatnie m − r wierszy macierzy E.
Ta przestrzeń jest podprzestrzenią przestrzeni R
m
.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
17 / 32
Lewa przestrzeń zerowa
Macierz A ma m wierszy, n kolumn i ma rząd r
Wymiar lewej przestrzeni zerowej wynosi m − r .
Bazą tej przestrzeni jest ostatnie m − r wierszy macierzy E.
Ta przestrzeń jest podprzestrzenią przestrzeni R
m
.
Dlaczego przestrzeń zerową macierzy
transponowanej N (A
T
) można nazywać lewą przestrzenią
zerową?
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
17 / 32
Lewa przestrzeń zerowa
Macierz A ma m wierszy, n kolumn i ma rząd r
Wymiar lewej przestrzeni zerowej wynosi m − r .
Bazą tej przestrzeni jest ostatnie m − r wierszy macierzy E.
Ta przestrzeń jest podprzestrzenią przestrzeni R
m
.
Dlaczego przestrzeń zerową macierzy
transponowanej N (A
T
) można nazywać lewą przestrzenią
zerową?
Oznaczmy: y – wektory będące w tej podprzestrzeni.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
17 / 32
Lewa przestrzeń zerowa
Macierz A ma m wierszy, n kolumn i ma rząd r
Wymiar lewej przestrzeni zerowej wynosi m − r .
Bazą tej przestrzeni jest ostatnie m − r wierszy macierzy E.
Ta przestrzeń jest podprzestrzenią przestrzeni R
m
.
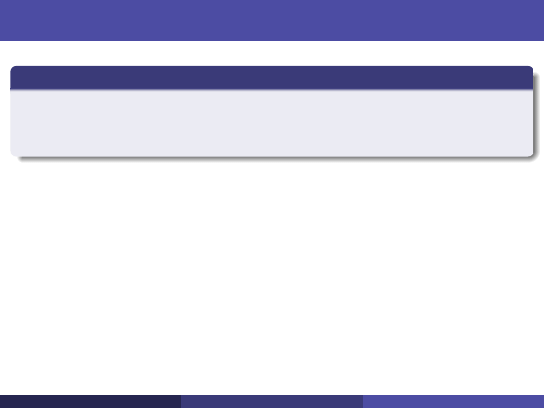
Zachodzi:
A
T
y = 0
transponujemy równanie
(A
T
y)
T
= 0
T
po prawej stronie otrzymuje-
my wierszowy wektor zerowy
y
T
A = 0
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
17 / 32
Lewa przestrzeń zerowa
Macierz A ma m wierszy, n kolumn i ma rząd r
Wymiar lewej przestrzeni zerowej wynosi m − r .
Bazą tej przestrzeni jest ostatnie m − r wierszy macierzy E.
Ta przestrzeń jest podprzestrzenią przestrzeni R
m
.
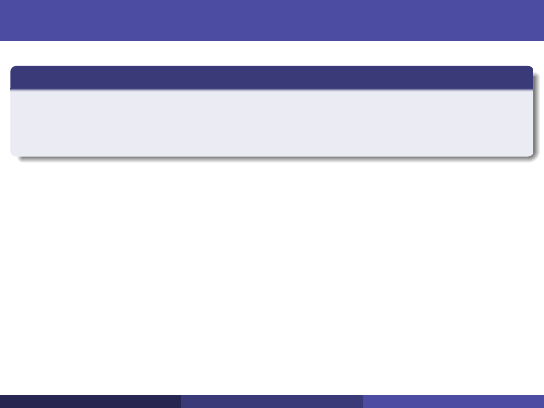
Zachodzi:
A
T
y = 0
transponujemy równanie
(A
T
y)
T
= 0
T
po prawej stronie otrzymuje-
my wierszowy wektor zerowy
y
T
A = 0
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
17 / 32
Lewa przestrzeń zerowa
Macierz A ma m wierszy, n kolumn i ma rząd r
Wymiar lewej przestrzeni zerowej wynosi m − r .
Bazą tej przestrzeni jest ostatnie m − r wierszy macierzy E.
Ta przestrzeń jest podprzestrzenią przestrzeni R
m
.
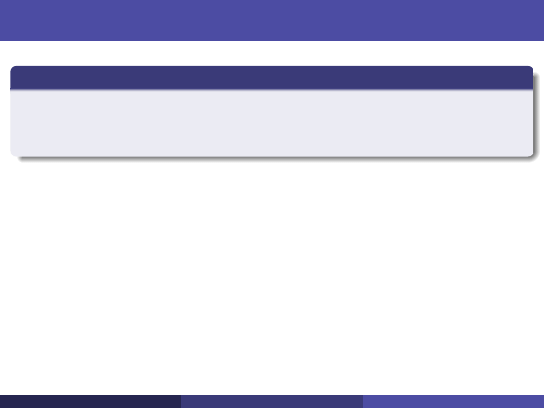
Zachodzi:
A
T
y = 0
transponujemy równanie
(A
T
y)
T
= 0
T
po prawej stronie otrzymuje-
my wierszowy wektor zerowy
y
T
A = 0
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
17 / 32
Lewa przestrzeń zerowa
Macierz A ma m wierszy, n kolumn i ma rząd r
Wymiar lewej przestrzeni zerowej wynosi m − r .
Bazą tej przestrzeni jest ostatnie m − r wierszy macierzy E.
Ta przestrzeń jest podprzestrzenią przestrzeni R
m
.
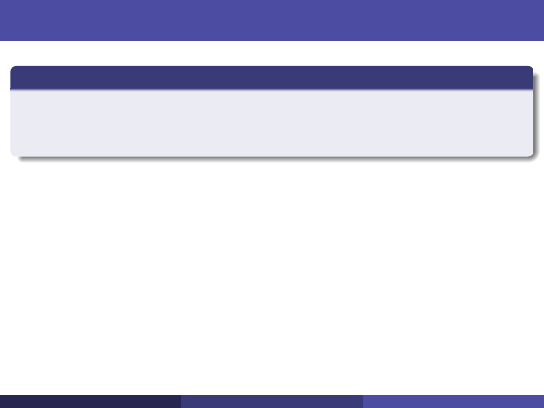
Zachodzi:
A
T
y = 0
transponujemy równanie
(A
T
y)
T
= 0
T
po prawej stronie otrzymuje-
my wierszowy wektor zerowy
y
T
A = 0
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
17 / 32
Lewa przestrzeń zerowa
Macierz A ma m wierszy, n kolumn i ma rząd r
Wymiar lewej przestrzeni zerowej wynosi m − r .
Bazą tej przestrzeni jest ostatnie m − r wierszy macierzy E.
Ta przestrzeń jest podprzestrzenią przestrzeni R
m
.
Zachodzi:
A
T
y = 0
transponujemy równanie
(A
T
y)
T
= 0
T
po prawej stronie otrzymuje-
my wierszowy wektor zerowy
y
T
A = 0
Wektor y występuje po lewej stronie macierzy A i właśnie
stąd wzięła się nazwa lewa przestrzeń zerowa.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
17 / 32

Lewa przestrzeń zerowa
Ta przestrzeń nie jest już tak oczywista jak wcześniejsze. Aby ją określić,
mamy dwie opcje.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
18 / 32

Lewa przestrzeń zerowa
Ta przestrzeń nie jest już tak oczywista jak wcześniejsze. Aby ją określić,
mamy dwie opcje.
Jedną opcją jest przetransportowanie macierzy A i wykonanie wszystkich
operacji od początku.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
18 / 32

Lewa przestrzeń zerowa
Ta przestrzeń nie jest już tak oczywista jak wcześniejsze. Aby ją określić,
mamy dwie opcje.
Drugą opcją jest wykorzystanie zredukowanej wierszowej postaci
schodkowej macierzy.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
18 / 32

Lewa przestrzeń zerowa
Ta przestrzeń nie jest już tak oczywista jak wcześniejsze. Aby ją określić,
mamy dwie opcje.
Drugą opcją jest wykorzystanie zredukowanej wierszowej postaci
schodkowej macierzy.
Będzie potrzebna macierz, która przekształci macierz A w macierz R.
Skorzystamy z czegoś podobnego do metody Gaussa-Jordana i dopiszemy
do macierzy A macierz identycznościową o rozmiarze m×m.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
18 / 32

Lewa przestrzeń zerowa
Ta przestrzeń nie jest już tak oczywista jak wcześniejsze. Aby ją określić,
mamy dwie opcje.
Drugą opcją jest wykorzystanie zredukowanej wierszowej postaci
schodkowej macierzy.
Będzie potrzebna macierz, która przekształci macierz A w macierz R.
Skorzystamy z czegoś podobnego do metody Gaussa-Jordana i dopiszemy
do macierzy A macierz identycznościową o rozmiarze m×m.
Przekształcanie macierzy A w macierz R będzie również przekształcało
macierz identycznościową w macierz E.
h
A
I
i
→
h
R
E
i
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
18 / 32

Lewa przestrzeń zerowa
Ta przestrzeń nie jest już tak oczywista jak wcześniejsze. Aby ją określić,
mamy dwie opcje.
Drugą opcją jest wykorzystanie zredukowanej wierszowej postaci
schodkowej macierzy.
Będzie potrzebna macierz, która przekształci macierz A w macierz R.
Skorzystamy z czegoś podobnego do metody Gaussa-Jordana i dopiszemy
do macierzy A macierz identycznościową o rozmiarze m×m.
Przekształcanie macierzy A w macierz R będzie również przekształcało
macierz identycznościową w macierz E.
h
A
I
i
→
h
R
E
i
Szukaną macierzą, która przekształci macierz identycznościową
w macierz E, jest macierz E.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
18 / 32

Lewa przestrzeń zerowa
Ta przestrzeń nie jest już tak oczywista jak wcześniejsze. Aby ją określić,
mamy dwie opcje.
Drugą opcją jest wykorzystanie zredukowanej wierszowej postaci
schodkowej macierzy.
Będzie potrzebna macierz, która przekształci macierz A w macierz R.
Skorzystamy z czegoś podobnego do metody Gaussa-Jordana i dopiszemy
do macierzy A macierz identycznościową o rozmiarze m×m.
Przekształcanie macierzy A w macierz R będzie również przekształcało
macierz identycznościową w macierz E.
h
A
I
i
→
h
R
E
i
Szukaną macierzą, która przekształci macierz identycznościową
w macierz E, jest macierz E.
Prawdziwe będzie równanie:
EA = R
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
18 / 32
Lewa przestrzeń zerowa
Znaleźć lewą przestrzeń zerową macierzy A
Najpierw musimy mieć macierz E.
Wykonujemy wszystkie kroki, jakie robiliśmy przy przekształceniu
macierzy A w macierz R, na macierzy identycznościowej.
Otrzymujemy:
E =
−1
2
0
1
−1 0
− 1
0
1
Biorąc ostatnie m − r = 3 − 2 = 1 wierszy macierzy E, otrzymujamy bazę
lewej przestrzeni zerowej
N (A
T
) = c
h
−1 0 1
i
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
19 / 32
Lewa przestrzeń zerowa
Znaleźć lewą przestrzeń zerową macierzy A
Najpierw musimy mieć macierz E.
Wykonujemy wszystkie kroki, jakie robiliśmy przy przekształceniu
macierzy A w macierz R, na macierzy identycznościowej.
Otrzymujemy:
E =
−1
2
0
1
−1 0
− 1
0
1
Biorąc ostatnie m − r = 3 − 2 = 1 wierszy macierzy E, otrzymujamy bazę
lewej przestrzeni zerowej
N (A
T
) = c
h
−1 0 1
i
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
19 / 32
Lewa przestrzeń zerowa
Znaleźć lewą przestrzeń zerową macierzy A
Najpierw musimy mieć macierz E.
Wykonujemy wszystkie kroki, jakie robiliśmy przy przekształceniu
macierzy A w macierz R, na macierzy identycznościowej.
Otrzymujemy:
E =
−1
2
0
1
−1 0
− 1
0
1
Biorąc ostatnie m − r = 3 − 2 = 1 wierszy macierzy E, otrzymujamy bazę
lewej przestrzeni zerowej
N (A
T
) = c
h
−1 0 1
i
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
19 / 32
Lewa przestrzeń zerowa
Znaleźć lewą przestrzeń zerową macierzy A
Najpierw musimy mieć macierz E.
Wykonujemy wszystkie kroki, jakie robiliśmy przy przekształceniu
macierzy A w macierz R, na macierzy identycznościowej.
Otrzymujemy:
E =
−1
2
0
1
−1 0
− 1
0
1
Biorąc ostatnie m − r = 3 − 2 = 1 wierszy macierzy E, otrzymujamy bazę
lewej przestrzeni zerowej
N (A
T
) = c
h
−1 0 1
i
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
19 / 32
Lewa przestrzeń zerowa
Znaleźć lewą przestrzeń zerową macierzy A
Najpierw musimy mieć macierz E.
Wykonujemy wszystkie kroki, jakie robiliśmy przy przekształceniu
macierzy A w macierz R, na macierzy identycznościowej.
Otrzymujemy:
E =
−1
2
0
1
−1 0
− 1
0
1
Biorąc ostatnie m − r = 3 − 2 = 1 wierszy macierzy E, otrzymujamy bazę
lewej przestrzeni zerowej
N (A
T
) = c
h
−1 0 1
i
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
19 / 32

Lewa przestrzeń zerowa
Dlaczego mogliśmy skorzystać z tego, że wymiar lewej przestrzeni zerowej
to m − r ?
Poniaważ macierz transponowana A
T
jest równie dobrą macierzą jak A,
tylko ma rozmiar n×m.
Taka macierz ma m kolumn, więc będzie m zmiennych, z czego tylko r
będzie zmiennymi osiowymi, czyli zostaje się m − r zmiennych wolnych.
Zachodzi równość:
dim(N (A
T
)) = m − r
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
20 / 32

Lewa przestrzeń zerowa
Dlaczego mogliśmy skorzystać z tego, że wymiar lewej przestrzeni zerowej
to m − r ?
Poniaważ macierz transponowana A
T
jest równie dobrą macierzą jak A,
tylko ma rozmiar n×m.
Taka macierz ma m kolumn, więc będzie
m zmiennych
, z czego tylko
r
będzie zmiennymi osiowymi
, czyli zostaje się
m − r zmiennych wolnych
.
Zachodzi równość:
dim(N (A
T
)) = m − r
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
20 / 32

Lewa przestrzeń zerowa
Dlaczego mogliśmy skorzystać z tego, że wymiar lewej przestrzeni zerowej
to m − r ?
Poniaważ macierz transponowana A
T
jest równie dobrą macierzą jak A,
tylko ma rozmiar n×m.
Taka macierz ma m kolumn, więc będzie m zmiennych, z czego tylko r
będzie zmiennymi osiowymi, czyli zostaje się m − r zmiennych wolnych.
Zachodzi równość:
dim(N (A
T
)) = m − r
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
20 / 32

Lewa przestrzeń zerowa
Dlaczego mogliśmy skorzystać z tego, że wymiar lewej przestrzeni zerowej
to m − r ?
Poniaważ macierz transponowana A
T
jest równie dobrą macierzą jak A,
tylko ma rozmiar n×m.
Taka macierz ma m kolumn, więc będzie m zmiennych, z czego tylko r
będzie zmiennymi osiowymi, czyli zostaje się m − r zmiennych wolnych.
Zachodzi równość:
dim(N (A
T
)) = m − r
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
20 / 32

Jak powiązać podprzestrzenie?
Co łączy przestrzenie, które poznaliśmy?
Przestrzeń wierszowa i przestrzeń zerowa są w R
n
, a ich wymiary sumują
się do n. Wynika to stąd, że mamy n zmiennych, r z nich to zmienne
osiowe, a n − r to zmienne wolne, czyli razem n.
Podobnie przestrzeń kolumnowa i lewa przestrzeń zerowa są w R
m
, a ich
wymiary sumują się do m.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
21 / 32

Jak powiązać podprzestrzenie?
Co łączy przestrzenie, które poznaliśmy?
Przestrzeń wierszowa i przestrzeń zerowa są w R
n
, a ich wymiary sumują
się do n. Wynika to stąd, że mamy n zmiennych, r z nich to zmienne
osiowe, a n − r to zmienne wolne, czyli razem n.
Podobnie przestrzeń kolumnowa i lewa przestrzeń zerowa są w R
m
, a ich
wymiary sumują się do m.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
21 / 32

Jak powiązać podprzestrzenie?
Co łączy przestrzenie, które poznaliśmy?
Przestrzeń wierszowa i przestrzeń zerowa są w R
n
, a ich wymiary sumują
się do n. Wynika to stąd, że mamy n zmiennych, r z nich to zmienne
osiowe, a n − r to zmienne wolne, czyli razem n.
Podobnie przestrzeń kolumnowa i lewa przestrzeń zerowa są w R
m
, a ich
wymiary sumują się do m.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
21 / 32
Jak powiązać podprzestrzenie?
Podsumowanie
Co zrobiliśmy?
•
wyróżniliśmy cztery podstawowe podprzestrzenie
•
określiliśmy, w jakiej są przestrzeni
•
określiliśmy, jaki mają wymiar
•
stworzyliśmy dla nich bazy
Cztery podstawowe podprzestrzenie przedstawia schematycznie
nastepujacy rysunek:
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
22 / 32
Jak powiązać podprzestrzenie?
Podsumowanie
Co zrobiliśmy?
•
wyróżniliśmy cztery podstawowe podprzestrzenie
•
określiliśmy, w jakiej są przestrzeni
•
określiliśmy, jaki mają wymiar
•
stworzyliśmy dla nich bazy
Cztery podstawowe podprzestrzenie przedstawia schematycznie
nastepujacy rysunek:
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
22 / 32
Jak powiązać podprzestrzenie?
Podsumowanie
Co zrobiliśmy?
•
wyróżniliśmy cztery podstawowe podprzestrzenie
•
określiliśmy, w jakiej są przestrzeni
•
określiliśmy, jaki mają wymiar
•
stworzyliśmy dla nich bazy
Cztery podstawowe podprzestrzenie przedstawia schematycznie
nastepujacy rysunek:
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
22 / 32
Jak powiązać podprzestrzenie?
Podsumowanie
Co zrobiliśmy?
•
wyróżniliśmy cztery podstawowe podprzestrzenie
•
określiliśmy, w jakiej są przestrzeni
•
określiliśmy, jaki mają wymiar
•
stworzyliśmy dla nich bazy
Cztery podstawowe podprzestrzenie przedstawia schematycznie
nastepujacy rysunek:
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
22 / 32
Jak powiązać podprzestrzenie?
Podsumowanie
Co zrobiliśmy?
•
wyróżniliśmy cztery podstawowe podprzestrzenie
•
określiliśmy, w jakiej są przestrzeni
•
określiliśmy, jaki mają wymiar
•
stworzyliśmy dla nich bazy
Cztery podstawowe podprzestrzenie przedstawia schematycznie
nastepujacy rysunek:
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
22 / 32
Jak powiązać podprzestrzenie?
Podsumowanie
Co zrobiliśmy?
•
wyróżniliśmy cztery podstawowe podprzestrzenie
•
określiliśmy, w jakiej są przestrzeni
•
określiliśmy, jaki mają wymiar
•
stworzyliśmy dla nich bazy
Cztery podstawowe podprzestrzenie przedstawia schematycznie
nastepujacy rysunek:
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
22 / 32

Jak powiązać podprzestrzenie?
Cztery
podstawowe
podprzestrzenie
Lewa
przestrzeń
zerowa
N (A
T
)
wymiar: m − r
Przestrzeń
zerowa N (A)
wymiar: n − r
Przestrzeń
wierszowa
C(A
T
)
wymiar: r
Przestrzeń
kolumnowa
C(A)
wymiar: r
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
23 / 32

Jak powiązać podprzestrzenie?
Cztery
podstawowe
podprzestrzenie
Lewa
przestrzeń
zerowa
N (A
T
)
wymiar: m − r
Przestrzeń
zerowa N (A)
wymiar: n − r
Przestrzeń
wierszowa
C(A
T
)
wymiar: r
Przestrzeń
kolumnowa
C(A)
wymiar: r
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
23 / 32
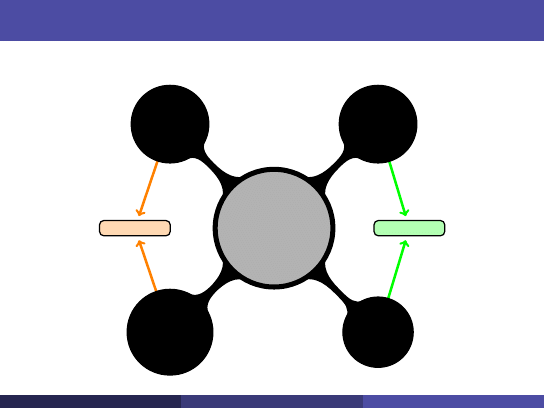
Jak powiązać podprzestrzenie?
Cztery
podstawowe
podprzestrzenie
Lewa
przestrzeń
zerowa
N (A
T
)
wymiar: m − r
Przestrzeń
zerowa N (A)
wymiar: n − r
Przestrzeń
wierszowa
C(A
T
)
wymiar: r
Przestrzeń
kolumnowa
C(A)
wymiar: r
r + (n − r ) = n
r + (m − r ) = m
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
23 / 32
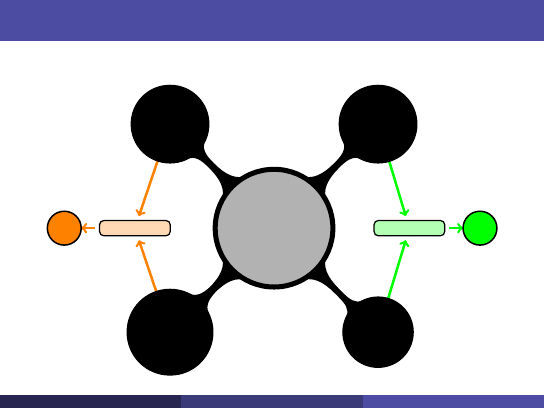
Jak powiązać podprzestrzenie?
Cztery
podstawowe
podprzestrzenie
Lewa
przestrzeń
zerowa
N (A
T
)
wymiar: m − r
Przestrzeń
zerowa N (A)
wymiar: n − r
Przestrzeń
wierszowa
C(A
T
)
wymiar: r
Przestrzeń
kolumnowa
C(A)
wymiar: r
R
m
R
n
r + (n − r ) = n
r + (m − r ) = m
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
23 / 32

To jeszcze nie koniec! Jeszcze przykład!
Zajmiemy się zbadaniem podprzestrzeni dla pewnej macierzy B:
B =
1
4
5
0
2
6
8
1
3
6
7
0
Najpierw sprowadzimy ją do zredukowanej wierszowej postaci schodkowej,
a przy okazji obliczymy macierz E.
h
B
I
i
=
1
4
5
0
1
0
0
2
6
8
1
0
1
0
3
6
7
0
0
0
1
→
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
24 / 32

To jeszcze nie koniec! Jeszcze przykład!
Zajmiemy się zbadaniem podprzestrzeni dla pewnej macierzy B:
B =
1
4
5
0
2
6
8
1
3
6
7
0
Najpierw sprowadzimy ją do zredukowanej wierszowej postaci schodkowej,
a przy okazji obliczymy macierz E.
h
B
I
i
=
1
4
5
0
1
0
0
2
6
8
1
0
1
0
3
6
7
0
0
0
1
→
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
24 / 32

To jeszcze nie koniec! Jeszcze przykład!
Zajmiemy się zbadaniem podprzestrzeni dla pewnej macierzy B:
B =
1
4
5
0
2
6
8
1
3
6
7
0
Najpierw sprowadzimy ją do zredukowanej wierszowej postaci schodkowej,
a przy okazji obliczymy macierz E.
h
B
I
i
=
1
4
5
0
1
0
0
2
6
8
1
0
1
0
3
6
7
0
0
0
1
→
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
24 / 32

To jeszcze nie koniec! Jeszcze przykład!
Zajmiemy się zbadaniem podprzestrzeni dla pewnej macierzy B:
B =
1
4
5
0
2
6
8
1
3
6
7
0
Najpierw sprowadzimy ją do zredukowanej wierszowej postaci schodkowej,
a przy okazji obliczymy macierz E.
h
B
I
i
=
1
4
5
0
1
0
0
2
6
8
1
0
1
0
3
6
7
0
0
0
1
→
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
24 / 32

→
1
4
5
0
1
0
0
0
−2 −2 1 −2 1 0
0
−6 −6 0 −3 0 1
→
1
4
5
0
1
0
0
0
−2 −2
1
−2
1
0
0
0
0
−3
3
−3 1
→
→
1
0
1
0
−3
2
0
0
−2 −2
1
−2
1
0
0
0
0
−3
3
−3 1
→
1
0
1
0
−3
2
0
0
1
1
−
1
2
1
−
1
2
0
0
0
0
1
−1
1
−
1
3
Otrzymujemy:
R =
1
0
1
0
0
1
1
−
1
2
0
0
0
1
,
E =
−3
2
0
1
−
1
2
0
−1
1
−
1
3
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
25 / 32

→
1
4
5
0
1
0
0
0
−2 −2 1 −2 1 0
0
−6 −6 0 −3 0 1
→
1
4
5
0
1
0
0
0
−2 −2
1
−2
1
0
0
0
0
−3
3
−3 1
→
→
1
0
1
0
−3
2
0
0
−2 −2
1
−2
1
0
0
0
0
−3
3
−3 1
→
1
0
1
0
−3
2
0
0
1
1
−
1
2
1
−
1
2
0
0
0
0
1
−1
1
−
1
3
Otrzymujemy:
R =
1
0
1
0
0
1
1
−
1
2
0
0
0
1
,
E =
−3
2
0
1
−
1
2
0
−1
1
−
1
3
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
25 / 32

→
1
4
5
0
1
0
0
0
−2 −2 1 −2 1 0
0
−6 −6 0 −3 0 1
→
1
4
5
0
1
0
0
0
−2 −2
1
−2
1
0
0
0
0
−3
3
−3 1
→
→
1
0
1
0
−3
2
0
0
−2 −2
1
−2
1
0
0
0
0
−3
3
−3 1
→
1
0
1
0
−3
2
0
0
1
1
−
1
2
1
−
1
2
0
0
0
0
1
−1
1
−
1
3
Otrzymujemy:
R =
1
0
1
0
0
1
1
−
1
2
0
0
0
1
,
E =
−3
2
0
1
−
1
2
0
−1
1
−
1
3
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
25 / 32

→
1
4
5
0
1
0
0
0
−2 −2 1 −2 1 0
0
−6 −6 0 −3 0 1
→
1
4
5
0
1
0
0
0
−2 −2
1
−2
1
0
0
0
0
−3
3
−3 1
→
→
1
0
1
0
−3
2
0
0
−2 −2
1
−2
1
0
0
0
0
−3
3
−3 1
→
1
0
1
0
−3
2
0
0
1
1
−
1
2
1
−
1
2
0
0
0
0
1
−1
1
−
1
3
Otrzymujemy:
R =
1
0
1
0
0
1
1
−
1
2
0
0
0
1
,
E =
−3
2
0
1
−
1
2
0
−1
1
−
1
3
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
25 / 32

→
1
4
5
0
1
0
0
0
−2 −2 1 −2 1 0
0
−6 −6 0 −3 0 1
→
1
4
5
0
1
0
0
0
−2 −2
1
−2
1
0
0
0
0
−3
3
−3 1
→
→
1
0
1
0
−3
2
0
0
−2 −2
1
−2
1
0
0
0
0
−3
3
−3 1
→
1
0
1
0
−3
2
0
0
1
1
−
1
2
1
−
1
2
0
0
0
0
1
−1
1
−
1
3
Otrzymujemy:
R =
1
0
1
0
0
1
1
−
1
2
0
0
0
1
,
E =
−3
2
0
1
−
1
2
0
−1
1
−
1
3
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
25 / 32

Przykładu ciąg dalszy
Przestrzeń kolumnowa C(B)
Kolumny osiowe macierzy R to kolumna pierwsza, trzecia i czwarta.
R =
1
0
1
0
0
1
1
−
1
2
0
0
0
1
, B =
1
4
5
0
2
6
8
1
3
6
7
0
Dlatego bazą przestrzeni kolumnowej macierzy B będzie również pierwsza,
trzecia i czwarta kolumna.
Stąd przestrzeń kolumnowa:
C(B) = c
1
1
2
3
+ c
2
4
6
6
+ c
3
0
1
0
Wymiar dim(C(A)) = 3
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
26 / 32

Przykładu ciąg dalszy
Przestrzeń kolumnowa C(B)
Kolumny osiowe macierzy R to kolumna pierwsza, trzecia i czwarta.
R =
1
0
1
0
0
1
1
−
1
2
0
0
0
1
, B =
1
4
5
0
2
6
8
1
3
6
7
0
Dlatego bazą przestrzeni kolumnowej macierzy B będzie również pierwsza,
trzecia i czwarta kolumna.
Stąd przestrzeń kolumnowa:
C(B) = c
1
1
2
3
+ c
2
4
6
6
+ c
3
0
1
0
Wymiar dim(C(A)) = 3
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
26 / 32

Przykładu ciąg dalszy
Przestrzeń kolumnowa C(B)
Kolumny osiowe macierzy R to kolumna pierwsza, trzecia i czwarta.
R =
1
0
1
0
0
1
1
−
1
2
0
0
0
1
, B =
1
4
5
0
2
6
8
1
3
6
7
0
Dlatego bazą przestrzeni kolumnowej macierzy B będzie również pierwsza,
trzecia i czwarta kolumna.
Stąd przestrzeń kolumnowa:
C(B) = c
1
1
2
3
+ c
2
4
6
6
+ c
3
0
1
0
Wymiar dim(C(A)) = 3
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
26 / 32
Przykładu ciąg dalszy
Przestrzeń zerowa N (B)
Potrzebujemy:
"
−F
I
#
=
−1
−1
1
0
Zatem jest tylko jedne rozwiązanie specjalne, a przestrzeń zerowa wygląda:
N (B) = c
−1
−1
1
0
Wymiar dim(N (B)) = 1
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
26 / 32
Przykładu ciąg dalszy
Przestrzeń zerowa N (B)
Potrzebujemy:
"
−F
I
#
=
−1
−1
1
0
Zatem jest tylko jedne rozwiązanie specjalne, a przestrzeń zerowa wygląda:
N (B) = c
−1
−1
1
0
Wymiar dim(N (B)) = 1
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
26 / 32
Przykładu ciąg dalszy
Przestrzeń wierszowa C(B
T
)
Wszystkie wiersze macierzy B zawierają elementy osiowe.
Przestrzeń
wierszowa będzie więc kombinacją wszystkich trzech:
C(B
T
) = c
1
h
1
4
5
0
i
+ c
2
h
3
6
7
0
i
+ c
3
h
3
6
7
0
i
Wymiar dim(C(B
T
)) = 3
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
26 / 32
Przykładu ciąg dalszy
Przestrzeń wierszowa C(B
T
)
Wszystkie wiersze macierzy B zawierają elementy osiowe. Przestrzeń
wierszowa będzie więc kombinacją wszystkich trzech:
C(B
T
) = c
1
h
1
4
5
0
i
+ c
2
h
3
6
7
0
i
+ c
3
h
3
6
7
0
i
Wymiar dim(C(B
T
)) = 3
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
26 / 32

Przykładu ciąg dalszy
Przestrzeń wierszowa C(B
T
)
Wszystkie wiersze macierzy B zawierają elementy osiowe. Przestrzeń
wierszowa będzie więc kombinacją wszystkich trzech:
C(B
T
) = c
1
h
1
4
5
0
i
+ c
2
h
3
6
7
0
i
+ c
3
h
3
6
7
0
i
Wymiar dim(C(B
T
)) = 3
Przestrzeń zerowa macierzy transponowanej N (B
T
)
Wymiar tej przestrzemi to dim(N (B
T
)) = 3 − 3 = 0
Oznacza to, że jedynym wektorem będącym w tej przestrzeni jest:
N (B
T
) =
h
0
0
0
i
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
26 / 32

Przykładu ciąg dalszy
Przestrzeń wierszowa C(B
T
)
Wszystkie wiersze macierzy B zawierają elementy osiowe. Przestrzeń
wierszowa będzie więc kombinacją wszystkich trzech:
C(B
T
) = c
1
h
1
4
5
0
i
+ c
2
h
3
6
7
0
i
+ c
3
h
3
6
7
0
i
Wymiar dim(C(B
T
)) = 3
Przestrzeń zerowa macierzy transponowanej N (B
T
)
Wymiar tej przestrzemi to dim(N (B
T
)) = 3 − 3 = 0
Oznacza to, że jedynym wektorem będącym w tej przestrzeni jest:
N (B
T
) =
h
0
0
0
i
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
26 / 32

Przestrzeń macierzowa M
Okazuje się, że nie musimy zawsze brać pojęcie wektora „na poważnie”.
Weźmiemy wszystkie
macerze 3×3
i każda z nich będzie „wektorem”.
Dlaczego można je tak nazywać? Ponieważ stosują się do reguł.
Między innymi:
•
Można je dodawać.
•
Można mnożyć je przez skalar.
•
Znajduje się wśród nich macierz zerowa (dodając ją do innej macierzy,
wynik się nie zmieni).
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
27 / 32

Przestrzeń macierzowa M
Okazuje się, że nie musimy zawsze brać pojęcie wektora „na poważnie”.
Weźmiemy wszystkie
macerze 3×3
i każda z nich będzie „wektorem”.
Dlaczego można je tak nazywać? Ponieważ stosują się do reguł.
Między innymi:
•
Można je dodawać.
•
Można mnożyć je przez skalar.
•
Znajduje się wśród nich macierz zerowa (dodając ją do innej macierzy,
wynik się nie zmieni).
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
27 / 32

Przestrzeń macierzowa M
Okazuje się, że nie musimy zawsze brać pojęcie wektora „na poważnie”.
Weźmiemy wszystkie
macerze 3×3
i każda z nich będzie „wektorem”.
Dlaczego można je tak nazywać?
Ponieważ stosują się do reguł.
Między innymi:
•
Można je dodawać.
•
Można mnożyć je przez skalar.
•
Znajduje się wśród nich macierz zerowa (dodając ją do innej macierzy,
wynik się nie zmieni).
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
27 / 32

Przestrzeń macierzowa M
Okazuje się, że nie musimy zawsze brać pojęcie wektora „na poważnie”.
Weźmiemy wszystkie
macerze 3×3
i każda z nich będzie „wektorem”.
Dlaczego można je tak nazywać?
Ponieważ stosują się do reguł.
Między innymi:
•
Można je dodawać.
•
Można mnożyć je przez skalar.
•
Znajduje się wśród nich macierz zerowa (dodając ją do innej macierzy,
wynik się nie zmieni).
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
27 / 32
Przestrzeń macierzowa M
Okazuje się, że nie musimy zawsze brać pojęcie wektora „na poważnie”.
Weźmiemy wszystkie
macerze 3×3
i każda z nich będzie „wektorem”.
Dlaczego można je tak nazywać? Ponieważ stosują się do reguł.
Między innymi:
•
Można je dodawać.
•
Można mnożyć je przez skalar.
•
Znajduje się wśród nich macierz zerowa (dodając ją do innej macierzy,
wynik się nie zmieni).
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
27 / 32
Przestrzeń macierzowa M
Okazuje się, że nie musimy zawsze brać pojęcie wektora „na poważnie”.
Weźmiemy wszystkie
macerze 3×3
i każda z nich będzie „wektorem”.
Dlaczego można je tak nazywać? Ponieważ stosują się do reguł.
Między innymi:
•
Można je dodawać.
•
Można mnożyć je przez skalar.
•
Znajduje się wśród nich macierz zerowa (dodając ją do innej macierzy,
wynik się nie zmieni).
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
27 / 32
Przestrzeń macierzowa M
Okazuje się, że nie musimy zawsze brać pojęcie wektora „na poważnie”.
Weźmiemy wszystkie
macerze 3×3
i każda z nich będzie „wektorem”.
Dlaczego można je tak nazywać? Ponieważ stosują się do reguł.
Między innymi:
•
Można je dodawać.
•
Można mnożyć je przez skalar.
•
Znajduje się wśród nich macierz zerowa (dodając ją do innej macierzy,
wynik się nie zmieni).
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
27 / 32

Co z podprzestrzeniami M?
Jeżeli ta przestrzeń jest przestrzenią wektorową, to będzie można wyróżnić
jej podprzestrzenie.
Czy macierze górnotrójkątne będą podprzestrzenią?
Sprawdźmy to.
•
Suma macierzy górnotrójkątnych jest macierzą górnotrójkątną.
•
Mnożąc macierz górnotrójkątną razy skalar również otrzymamy
macierz górnotrójkątną.
•
Macierz zerowa jest macierzą górnotrójkątną.
Wszystko się zgadza. Macierze górnotrójkątne 3×3 są podprzestrzenią
macierzy 3×3.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
28 / 32
Co z podprzestrzeniami M?
Jeżeli ta przestrzeń jest przestrzenią wektorową, to będzie można wyróżnić
jej podprzestrzenie.
Czy macierze górnotrójkątne będą podprzestrzenią?
Sprawdźmy to.
•
Suma macierzy górnotrójkątnych jest macierzą górnotrójkątną.
•
Mnożąc macierz górnotrójkątną razy skalar również otrzymamy
macierz górnotrójkątną.
•
Macierz zerowa jest macierzą górnotrójkątną.
Wszystko się zgadza. Macierze górnotrójkątne 3×3 są podprzestrzenią
macierzy 3×3.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
28 / 32
Co z podprzestrzeniami M?
Jeżeli ta przestrzeń jest przestrzenią wektorową, to będzie można wyróżnić
jej podprzestrzenie.
Czy macierze górnotrójkątne będą podprzestrzenią?
Sprawdźmy to.
•
Suma macierzy górnotrójkątnych jest macierzą górnotrójkątną.
•
Mnożąc macierz górnotrójkątną razy skalar również otrzymamy
macierz górnotrójkątną.
•
Macierz zerowa jest macierzą górnotrójkątną.
Wszystko się zgadza. Macierze górnotrójkątne 3×3 są podprzestrzenią
macierzy 3×3.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
28 / 32
Co z podprzestrzeniami M?
Jeżeli ta przestrzeń jest przestrzenią wektorową, to będzie można wyróżnić
jej podprzestrzenie.
Czy macierze górnotrójkątne będą podprzestrzenią?
Sprawdźmy to.
•
Suma macierzy górnotrójkątnych jest macierzą górnotrójkątną.
•
Mnożąc macierz górnotrójkątną razy skalar również otrzymamy
macierz górnotrójkątną.
•
Macierz zerowa jest macierzą górnotrójkątną.
Wszystko się zgadza. Macierze górnotrójkątne 3×3 są podprzestrzenią
macierzy 3×3.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
28 / 32
Co z podprzestrzeniami M?
Jeżeli ta przestrzeń jest przestrzenią wektorową, to będzie można wyróżnić
jej podprzestrzenie.
Czy macierze górnotrójkątne będą podprzestrzenią?
Sprawdźmy to.
•
Suma macierzy górnotrójkątnych jest macierzą górnotrójkątną.
•
Mnożąc macierz górnotrójkątną razy skalar również otrzymamy
macierz górnotrójkątną.
•
Macierz zerowa jest macierzą górnotrójkątną.
Wszystko się zgadza. Macierze górnotrójkątne 3×3 są podprzestrzenią
macierzy 3×3.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
28 / 32
Co z podprzestrzeniami M?
Jeżeli ta przestrzeń jest przestrzenią wektorową, to będzie można wyróżnić
jej podprzestrzenie.
Czy macierze górnotrójkątne będą podprzestrzenią?
Sprawdźmy to.
•
Suma macierzy górnotrójkątnych jest macierzą górnotrójkątną.
•
Mnożąc macierz górnotrójkątną razy skalar również otrzymamy
macierz górnotrójkątną.
•
Macierz zerowa jest macierzą górnotrójkątną.
Wszystko się zgadza. Macierze górnotrójkątne 3×3 są podprzestrzenią
macierzy 3×3.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
28 / 32
Co z podprzestrzeniami M?
Jeżeli ta przestrzeń jest przestrzenią wektorową, to będzie można wyróżnić
jej podprzestrzenie.
Czy macierze górnotrójkątne będą podprzestrzenią?
Sprawdźmy to.
•
Suma macierzy górnotrójkątnych jest macierzą górnotrójkątną.
•
Mnożąc macierz górnotrójkątną razy skalar również otrzymamy
macierz górnotrójkątną.
•
Macierz zerowa jest macierzą górnotrójkątną.
Wszystko się zgadza. Macierze górnotrójkątne 3×3 są podprzestrzenią
macierzy 3×3.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
28 / 32

Co z podprzestrzeniami M?
Musi być spełniony jeszcze warunek:
Przecięcie dwóch podprzestrzeni też musi być podprzestrzenią.
Potrzebujemy jeszcze jednej podprzestrzeni.
Sprawdźmy macierze symertycze:
•
Suma macierzy symetrycznych jest macierzą symetryczną.
•
Mnożąc macierz symetryczną razy skalar również otrzymamy macierz
symetryczną.
•
Macierz zerowa jest macierzą symetryczną.
Wszystko się zgadza.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
29 / 32

Co z podprzestrzeniami M?
Musi być spełniony jeszcze warunek:
Przecięcie dwóch podprzestrzeni też musi być podprzestrzenią.
Potrzebujemy jeszcze jednej podprzestrzeni.
Sprawdźmy macierze symertycze:
•
Suma macierzy symetrycznych jest macierzą symetryczną.
•
Mnożąc macierz symetryczną razy skalar również otrzymamy macierz
symetryczną.
•
Macierz zerowa jest macierzą symetryczną.
Wszystko się zgadza.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
29 / 32

Co z podprzestrzeniami M?
Musi być spełniony jeszcze warunek:
Przecięcie dwóch podprzestrzeni też musi być podprzestrzenią.
Potrzebujemy jeszcze jednej podprzestrzeni.
Sprawdźmy macierze symertycze:
•
Suma macierzy symetrycznych jest macierzą symetryczną.
•
Mnożąc macierz symetryczną razy skalar również otrzymamy macierz
symetryczną.
•
Macierz zerowa jest macierzą symetryczną.
Wszystko się zgadza.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
29 / 32

Co z podprzestrzeniami M?
Musi być spełniony jeszcze warunek:
Przecięcie dwóch podprzestrzeni też musi być podprzestrzenią.
Potrzebujemy jeszcze jednej podprzestrzeni.
Sprawdźmy macierze symertycze:
•
Suma macierzy symetrycznych jest macierzą symetryczną.
•
Mnożąc macierz symetryczną razy skalar również otrzymamy macierz
symetryczną.
•
Macierz zerowa jest macierzą symetryczną.
Wszystko się zgadza.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
29 / 32

Co z podprzestrzeniami M?
Musi być spełniony jeszcze warunek:
Przecięcie dwóch podprzestrzeni też musi być podprzestrzenią.
Potrzebujemy jeszcze jednej podprzestrzeni.
Sprawdźmy macierze symertycze:
•
Suma macierzy symetrycznych jest macierzą symetryczną.
•
Mnożąc macierz symetryczną razy skalar również otrzymamy macierz
symetryczną.
•
Macierz zerowa jest macierzą symetryczną.
Wszystko się zgadza.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
29 / 32

Co z podprzestrzeniami M?
Musi być spełniony jeszcze warunek:
Przecięcie dwóch podprzestrzeni też musi być podprzestrzenią.
Potrzebujemy jeszcze jednej podprzestrzeni.
Sprawdźmy macierze symertycze:
•
Suma macierzy symetrycznych jest macierzą symetryczną.
•
Mnożąc macierz symetryczną razy skalar również otrzymamy macierz
symetryczną.
•
Macierz zerowa jest macierzą symetryczną.
Wszystko się zgadza.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
29 / 32

Co z podprzestrzeniami M?
Musi być spełniony jeszcze warunek:
Przecięcie dwóch podprzestrzeni też musi być podprzestrzenią.
Potrzebujemy jeszcze jednej podprzestrzeni.
Sprawdźmy macierze symertycze:
•
Suma macierzy symetrycznych jest macierzą symetryczną.
•
Mnożąc macierz symetryczną razy skalar również otrzymamy macierz
symetryczną.
•
Macierz zerowa jest macierzą symetryczną.
Wszystko się zgadza.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
29 / 32

Co z podprzestrzeniami M?
Musi być spełniony jeszcze warunek:
Przecięcie dwóch podprzestrzeni też musi być podprzestrzenią.
Potrzebujemy jeszcze jednej podprzestrzeni.
Sprawdźmy macierze symertycze:
•
Suma macierzy symetrycznych jest macierzą symetryczną.
•
Mnożąc macierz symetryczną razy skalar również otrzymamy macierz
symetryczną.
•
Macierz zerowa jest macierzą symetryczną.
Wszystko się zgadza.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
29 / 32

Co z podprzestrzeniami M?
Jakie będzie przecięcie macierzy górnotrójkątnych i symetrycznych?
Będą to macierze diagonalne.
Czy macierze diagonalne są podprzestrzenią?
•
Suma macierzy diagonalnych jest macierzą diagonalną.
•
Mnożąc macierz diagonalną razy skalar również otrzymamy macierz
diagonalną.
•
Macierz zerowa jest macierzą diagonalną.
Również wszystko się zgadza.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
30 / 32

Co z podprzestrzeniami M?
Jakie będzie przecięcie macierzy górnotrójkątnych i symetrycznych?
Będą to macierze diagonalne
.
Czy macierze diagonalne są podprzestrzenią?
•
Suma macierzy diagonalnych jest macierzą diagonalną.
•
Mnożąc macierz diagonalną razy skalar również otrzymamy macierz
diagonalną.
•
Macierz zerowa jest macierzą diagonalną.
Również wszystko się zgadza.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
30 / 32
Co z podprzestrzeniami M?
Jakie będzie przecięcie macierzy górnotrójkątnych i symetrycznych?
Będą to macierze diagonalne.
Czy macierze diagonalne są podprzestrzenią?
•
Suma macierzy diagonalnych jest macierzą diagonalną.
•
Mnożąc macierz diagonalną razy skalar również otrzymamy macierz
diagonalną.
•
Macierz zerowa jest macierzą diagonalną.
Również wszystko się zgadza.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
30 / 32
Co z podprzestrzeniami M?
Jakie będzie przecięcie macierzy górnotrójkątnych i symetrycznych?
Będą to macierze diagonalne.
Czy macierze diagonalne są podprzestrzenią?
•
Suma macierzy diagonalnych jest macierzą diagonalną.
•
Mnożąc macierz diagonalną razy skalar również otrzymamy macierz
diagonalną.
•
Macierz zerowa jest macierzą diagonalną.
Również wszystko się zgadza.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
30 / 32
Co z podprzestrzeniami M?
Jakie będzie przecięcie macierzy górnotrójkątnych i symetrycznych?
Będą to macierze diagonalne.
Czy macierze diagonalne są podprzestrzenią?
•
Suma macierzy diagonalnych jest macierzą diagonalną.
•
Mnożąc macierz diagonalną razy skalar również otrzymamy macierz
diagonalną.
•
Macierz zerowa jest macierzą diagonalną.
Również wszystko się zgadza.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
30 / 32
Co z podprzestrzeniami M?
Jakie będzie przecięcie macierzy górnotrójkątnych i symetrycznych?
Będą to macierze diagonalne.
Czy macierze diagonalne są podprzestrzenią?
•
Suma macierzy diagonalnych jest macierzą diagonalną.
•
Mnożąc macierz diagonalną razy skalar również otrzymamy macierz
diagonalną.
•
Macierz zerowa jest macierzą diagonalną.
Również wszystko się zgadza.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
30 / 32
Co z podprzestrzeniami M?
Jakie będzie przecięcie macierzy górnotrójkątnych i symetrycznych?
Będą to macierze diagonalne.
Czy macierze diagonalne są podprzestrzenią?
•
Suma macierzy diagonalnych jest macierzą diagonalną.
•
Mnożąc macierz diagonalną razy skalar również otrzymamy macierz
diagonalną.
•
Macierz zerowa jest macierzą diagonalną.
Również wszystko się zgadza.
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
30 / 32

Baza i wymiar
Chcemy dowiedzieć się więcej o przestrzeni macierzy diagonalnych.
Chcemy poznać jej bazę i wymiar.
Co należy zrobić?
Wystarczy znaleźć odpowiednią liczbę
niezależnych macierzy
.
Na pewno warunki będą spełniać następujące macierze:
1
0
0
0
0
0
0
0
0
,
1
0
0
0
3
0
0
0
0
,
0
0
0
0
0
0
0
0
7
Oczywiście ta baza nie jest najpiękniejszą bazą, jest jedną z wielu
możliwych. Inną możliwą i jaśniejszą dla nas bazą mogłoby być:
1
0
0
0
0
0
0
0
0
,
0
0
0
0
1
0
0
0
0
,
0
0
0
0
0
0
0
0
1
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
31 / 32

Baza i wymiar
Chcemy dowiedzieć się więcej o przestrzeni macierzy diagonalnych.
Chcemy poznać jej bazę i wymiar.
Co należy zrobić?
Wystarczy znaleźć odpowiednią liczbę
niezależnych macierzy
.
Na pewno warunki będą spełniać następujące macierze:
1
0
0
0
0
0
0
0
0
,
1
0
0
0
3
0
0
0
0
,
0
0
0
0
0
0
0
0
7
Oczywiście ta baza nie jest najpiękniejszą bazą, jest jedną z wielu
możliwych. Inną możliwą i jaśniejszą dla nas bazą mogłoby być:
1
0
0
0
0
0
0
0
0
,
0
0
0
0
1
0
0
0
0
,
0
0
0
0
0
0
0
0
1
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
31 / 32
Baza i wymiar
Chcemy dowiedzieć się więcej o przestrzeni macierzy diagonalnych.
Chcemy poznać jej bazę i wymiar.
Co należy zrobić?
Wystarczy znaleźć odpowiednią liczbę
niezależnych macierzy
.
Na pewno warunki będą spełniać następujące macierze:
1
0
0
0
0
0
0
0
0
,
1
0
0
0
3
0
0
0
0
,
0
0
0
0
0
0
0
0
7
Oczywiście ta baza nie jest najpiękniejszą bazą, jest jedną z wielu
możliwych. Inną możliwą i jaśniejszą dla nas bazą mogłoby być:
1
0
0
0
0
0
0
0
0
,
0
0
0
0
1
0
0
0
0
,
0
0
0
0
0
0
0
0
1
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
31 / 32
Baza i wymiar
Chcemy dowiedzieć się więcej o przestrzeni macierzy diagonalnych.
Chcemy poznać jej bazę i wymiar.
Co należy zrobić?
Wystarczy znaleźć odpowiednią liczbę
niezależnych macierzy
.
Na pewno warunki będą spełniać następujące macierze:
1
0
0
0
0
0
0
0
0
,
1
0
0
0
3
0
0
0
0
,
0
0
0
0
0
0
0
0
7
Oczywiście ta baza nie jest najpiękniejszą bazą, jest jedną z wielu
możliwych. Inną możliwą i jaśniejszą dla nas bazą mogłoby być:
1
0
0
0
0
0
0
0
0
,
0
0
0
0
1
0
0
0
0
,
0
0
0
0
0
0
0
0
1
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
31 / 32
Baza i wymiar
Chcemy dowiedzieć się więcej o przestrzeni macierzy diagonalnych.
Chcemy poznać jej bazę i wymiar.
Co należy zrobić?
Wystarczy znaleźć odpowiednią liczbę
niezależnych macierzy
.
Na pewno warunki będą spełniać następujące macierze:
1
0
0
0
0
0
0
0
0
,
1
0
0
0
3
0
0
0
0
,
0
0
0
0
0
0
0
0
7
Oczywiście ta baza nie jest najpiękniejszą bazą, jest jedną z wielu
możliwych. Inną możliwą i jaśniejszą dla nas bazą mogłoby być:
1
0
0
0
0
0
0
0
0
,
0
0
0
0
1
0
0
0
0
,
0
0
0
0
0
0
0
0
1
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
31 / 32
Baza i wymiar
Chcemy dowiedzieć się więcej o przestrzeni macierzy diagonalnych.
Chcemy poznać jej bazę i wymiar.
Co należy zrobić?
Wystarczy znaleźć odpowiednią liczbę
niezależnych macierzy
.
Na pewno warunki będą spełniać następujące macierze:
1
0
0
0
0
0
0
0
0
,
1
0
0
0
3
0
0
0
0
,
0
0
0
0
0
0
0
0
7
Okazuje się, że dowolną macierz diagonalną 3×3 da się zapisać za pomocą
trzech powyższych. Wobec tego są one bazą tej przestrzeni macierzowej, a
jej wymiar to 3.
Oczywiście ta baza nie jest najpiękniejszą bazą, jest jedną z wielu
możliwych. Inną możliwą i jaśniejszą dla nas bazą mogłoby być:
1
0
0
0
0
0
0
0
0
,
0
0
0
0
1
0
0
0
0
,
0
0
0
0
0
0
0
0
1
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
31 / 32
Baza i wymiar
Chcemy dowiedzieć się więcej o przestrzeni macierzy diagonalnych.
Chcemy poznać jej bazę i wymiar.
Co należy zrobić?
Wystarczy znaleźć odpowiednią liczbę
niezależnych macierzy
.
Na pewno warunki będą spełniać następujące macierze:
1
0
0
0
0
0
0
0
0
,
1
0
0
0
3
0
0
0
0
,
0
0
0
0
0
0
0
0
7
Oczywiście ta baza nie jest najpiękniejszą bazą, jest jedną z wielu
możliwych. Inną możliwą i jaśniejszą dla nas bazą mogłoby być:
1
0
0
0
0
0
0
0
0
,
0
0
0
0
1
0
0
0
0
,
0
0
0
0
0
0
0
0
1
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
31 / 32

Prezentacja powstała na podstawie wykładu prof. Gilberta Stranga
„Four fundamental subspaces”.
Wykład jest dostępny na stronie internetowej [dostęp 1 grudnia 2012r.]:
http://ocw.mit.edu/courses/mathematics/18-06sc-linear-algebra-fall-
2011/ax-b-and-the-four-subspaces/the-four-fundamental-subspaces/
P. Wróbel, M. Piechowicz (PP, WI, AiR)
Cztery podstawowe podprzestrzenie
19 grudnia 2012r.
32 / 32
Document Outline
- Znajdowanie bazy przestrzeni wektorowej
- Cztery podstawowe podprzestrzenie
- Jeszcze jedna przestrzen wektorowa
Wyszukiwarka
Podobne podstrony:
Prez 10 08 00 ppt
MP 10 Z inz dz s3 cw Z1 prez Nieznany
Morze Bałtyckie prez na 31 10
Adonis prez 22 02 10
10 Metody otrzymywania zwierzat transgenicznychid 10950 ppt
10 dźwigniaid 10541 ppt
wyklad 10 MNE
Kosci, kregoslup 28[1][1][1] 10 06 dla studentow
10 budowa i rozwój OUN
10 Hist BNid 10866 ppt
POKREWIEŃSTWO I INBRED 22 4 10
Prezentacja JMichalska PSP w obliczu zagrozen cywilizacyjn 10 2007
więcej podobnych podstron