
2009-02-03
1
FUNDAMENTOWANIE 1
Część 2b
Ś
cianki szczelne
WYCIĄG Z MATERIAŁÓW
Rodzaje ścianek szczelnych
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/2
Ś
cianka szczelna – konstrukcja składająca się z podłużnych elementów
zagłębionych w grunt, ściśle do siebie przylegających lub połączonych.
Zadaniem ścianki szczelnej jest podtrzymanie uskoku naziomu i/lub
zapobieganie przenikaniu wody gruntowej. Może stanowić element
konstrukcyjny np. nabrzeża portowe, przyczółki mostowe. Konstrukcja
relatywnie podatna.
Inna nazwa: grodzice. Pojedynczy element: brus, grodzica.
Ze względu na rodzaj materiału ścianki szczelne można podzielić na:
- drewniane,
- żelbetowe,
- stalowe.
Ze względu na ich przeznaczenie można podzielić na:
- tymczasowe,
- stałe.
Rodzaje ścianek szczelnych
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/3
Ze względu na schemat pracy ścianki szczelne można podzielić na:
- wspornikowe,
- jednokrotnie kotwione
- utwierdzona w gruncie,
- swobodnie podparta;
- dwukrotnie kotwione
- utwierdzona w gruncie,
- swobodnie podparta,
- podpory ścianki szczelnej przesuwne;
- wielokrotnie kotwione
Ś
cianki szczelne drewniane
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/4
Ś
cianka szczelne drewniane – współcześnie
rzadko stosowane – do budowli
podrzędnych. Najczęściej z drewna
sosnowego. Grubość brusów zależy od
głębokości ich wbicia.
a) z wpustem kątowym, b) z zakładką, c) z wpustem pełnym
prostokątnym, d) z wpustem trapezowym, e) z żeberkiem obcym,
f) z żeberkiem obcym przybijanym
Ś
cianki szczelne żelbetowe
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/5
Ś
cianka szczelne żelbetowe – współcześnie rzadko stosowane –
z prefabrykowanych brusów żelbetowych oraz z betonu sprężonego.
Szerokość 50-60 cm, grubość 12-50 cm, długość do 20 m.
Ś
cianki szczelne stalowe
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/6
Ś
cianka szczelne stalowe – współeczśnie najczęściej stosowane różnią się
kształtem profilu (brusa), wskaźnikiem wytrzymałości oraz szczelnością.
Ze względu na kształt można wyróżnić:
- płaskie,
- korytkowe,
- zetowe,
- dwuteowe,
- skrzynkowe.

2009-02-03
2
Ś
cianki szczelne stalowe - rodzaje
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/7
Ś
cianki szczelne stalowe – rodzaje
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/8
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/9
Ś
cianki szczelne stalowe – rodzaje
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/10
Ś
cianki szczelne stalowe – rodzaje
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/11
Ś
cianki szczelne stalowe – rodzaje
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/12
Ś
cianki szczelne stalowe – rodzaje
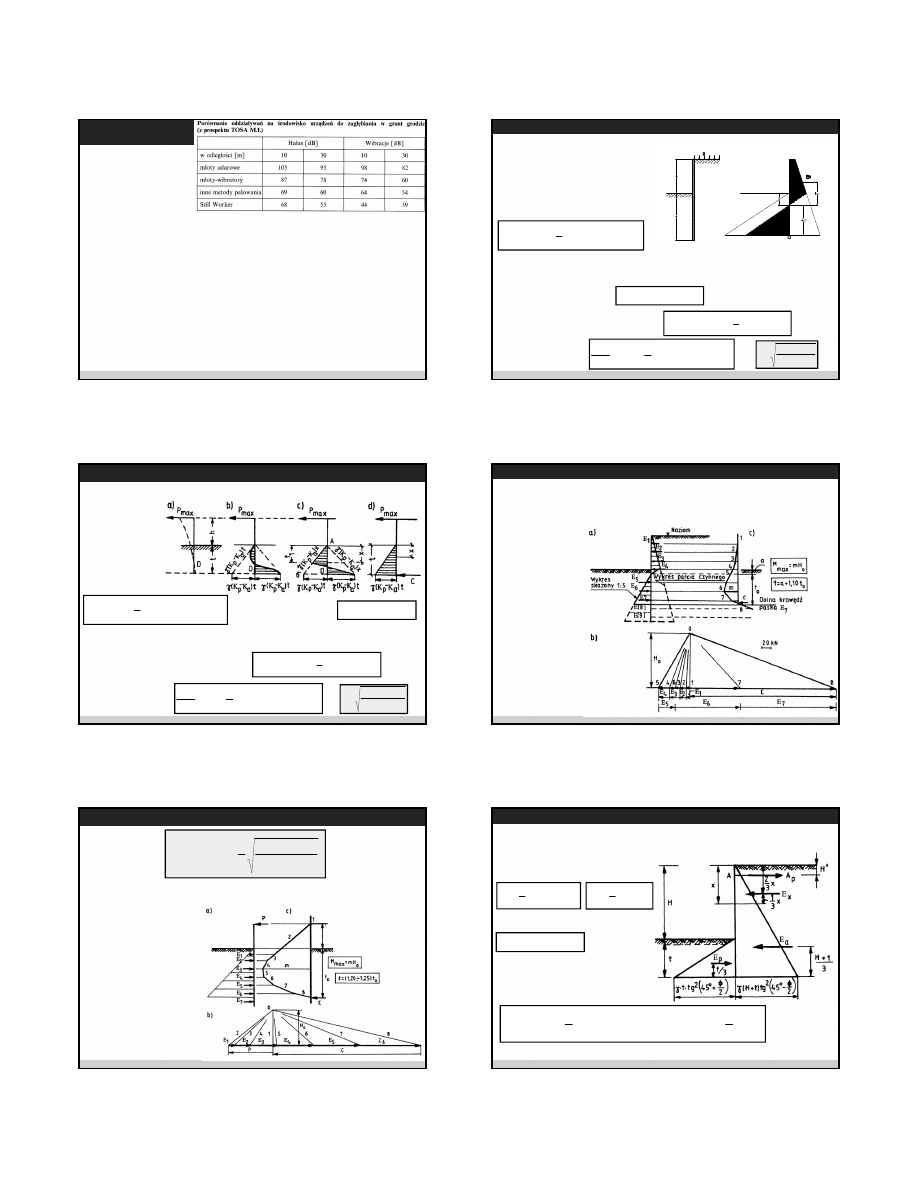
2009-02-03
3
Ś
cianki szczelne stalowe –
metody pogrążania
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/13
a)
wbijanie
b)
wwibrowywanie
c)
wpłukiwane
d)
wciskanie
ad. a) wbijanie kafarami stosuje się coraz rzadziej (w terenie otwartym daleko od innych
obiektów, w nabrzeżach)
ad. b) wwibrowywanie – najczęstszy sposób pogrążania ścianek szczelnych. Podstawowe
parametry młotów wibracyjnych – ze względu na oddziaływanie na środowisko – to:
częstotliwość oraz amplituda drgań.
ad c) wpłukiwanie – w przypadku trudności z pogrążeniem ścianki innymi metodami,
ad d) wciskanie – coraz częstszy sposób zagłębiania ścianki ze względu na brak drgań i
hałasu.
Ś
cianki szczelne stalowe - obliczanie
Ś
cianka szczelna nie zakotwiona, dołem utwierdzona, obciążona siła skupioną
poziomą P
Metoda analityczna
t
0
wyznaczamy z warunku
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/14
gdzie:
b - szerokość ścianki (1 m),
K
a
i K
p
- odpowiednio współczynniki parcia i odporu,
(
)
(
)
b
x
K
K
x
h
P
M
a
p
x
3
6
1
−
−
+
=
γ
(
)
(
)
0
6
1
3
0
0
=
−
−
+
b
t
K
K
t
h
P
a
p
γ
Praktycznie przyjmujemy
(
)
0
25
,
1
2
,
1
t
t
÷
=
Maksymalny moment zginający obliczamy z równania:
(
)
0
2
1
2
=
−
−
=
b
x
K
K
P
dx
dM
a
p
γ
(
)
b
K
K
P
x
a
p
−
=
γ
2
Ś
cianki szczelne stalowe - obliczanie
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/15
(
)
−
+
=
b
K
K
P
h
P
M
a
p
γ
2
3
2
max
Metoda graficzna
Sumaryczny wykres z lewej strony
(parcie bierne minus czynne) dzieli się
na paski i każdy z pasków zastępuje
siła skupioną Z
i
. Biegun O obiera się
na prostopadłej przechodzącej przez
początek siły P, wtedy zamykająca
wielobok sznurowy będzie pionowa, a
punkt przecięcia wieloboku
sznurowego z tą pionową wyznacza
głębokość wbicia ścianki.
a) rozkład obciążeń,
b) wielobok sił, c) wielobok
sznurowy (wykres momentów
zginających)
Ś
cianki szczelne stalowe - obliczanie
Ś
cianka szczelna nie zakotwiona, dołem utwierdzona, obciążona
obciążeniem ciągłym
Metoda analityczna
Z równania równowagi momentów
względem punktu D wyznaczamy
głębokość wbicia t
0
+ a
gdzie: E
a
– wypadkowe parcie, po stronie parcia czynnego; h
0
– położenie wypadkowej
E
a
względem punktu równoważenia się jednostkowego parcia i odporu
granicznego.
Głębokość wbicia przyjmujemy
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/16
(
)
(
)
0
6
1
3
0
0
0
=
−
−
+
t
K
K
t
h
E
a
p
a
γ
(
)
0
5
,
1
2
,
1
t
a
t
÷
+
=
(
)
(
)
3
0
6
1
x
K
K
x
h
E
M
a
p
a
x
−
−
+
=
γ
(
)
0
2
1
2
=
−
−
=
x
K
K
E
dx
dM
a
p
a
γ
(
)
a
p
a
K
K
E
x
−
=
γ
2
Maksymalny moment zginający obliczamy z równania:
Ś
cianki szczelne stalowe - obliczanie
Ś
cianka szczelna nie zakotwiona, dołem utwierdzona,
Metoda graficzna
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/17
Ś
cianki szczelne stalowe - obliczanie
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/18
Ś
cianka szczelna górą zakotwiona, dołem wolnopodparta
Metoda analityczna
Sumaryczne parcie wynosi:
(
)
a
a
K
t
H
E
2
2
1
+
=
γ
p
p
K
t
E
⋅
⋅
=
2
2
1
γ
Suma rzutów na oś poziomą:
0
=
−
+
a
p
p
E
E
A
Z tego równania określa się siłę w kotwie A
p.
Suma momentów względem punktu A:
(
)
0
3
2
3
2
=
+
′
−
−
′
−
+
=
∑
t
H
H
E
H
t
H
E
M
p
a
A
Z tego równania określa się metoda prób i błędów głębokość wbicia ścianki t
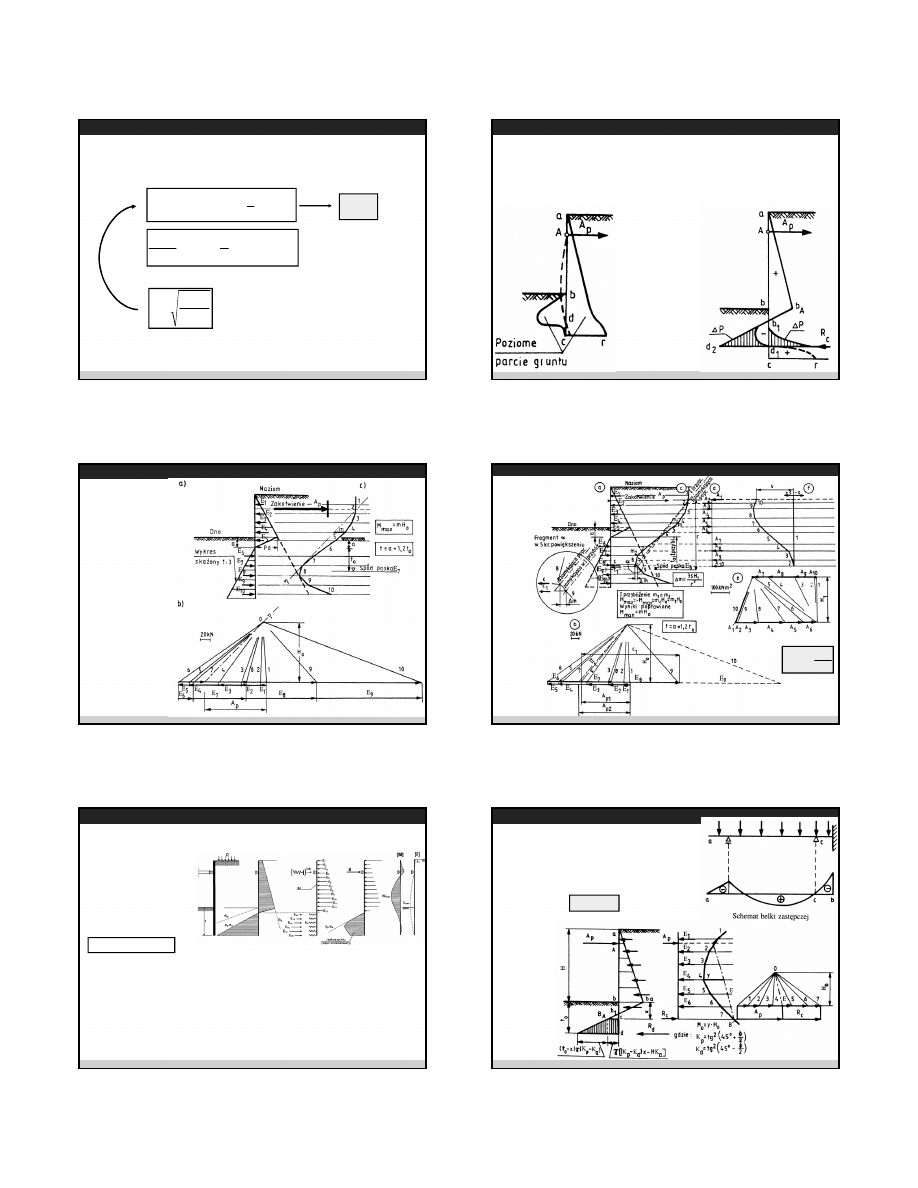
2009-02-03
4
Ś
cianki szczelne stalowe - obliczanie
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/19
0
2
1
2
=
⋅
−
=
a
p
x
K
x
A
dx
dM
γ
Moment zginający działający na odcinku 0 < x < H
a
p
K
A
x
⋅
=
γ
2
W tym punkcie wartość momentu
osiąga wartość maksymalną
(
)
a
p
x
K
x
H
x
A
M
⋅
−
′
−
=
γ
3
6
1
max
M
Ś
cianki szczelne stalowe - obliczanie
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/20
Metoda graficzna
Układ obciążeń jak w
metodzie analitycznej.
Z otrzymanych sił
rysuje się wielobok sił,
obiera (dowolnie)
biegun O i wykreśla
wielobok sznurowy.
Zamykająca prowadzi
się z punktu przecięcia
pierwszego promienia z
linia siły w zakotwieniu,
stycznie do wygiętej
linii wieloboku
sznurowego.
Ś
cianki szczelne stalowe - obliczanie
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/21
Metoda współpracy ścianki z sprężysto-plastycznym ośrodkiem
gruntowym
Reakcję gruntu poniżej niższego
naziomu modeluje się za pomocą
sprężysto-plastycznych podpór,
prostopadłych do ścianki w
rozstawie ok. ai = 0,5 m o
sztywności kxi
m
a
E
φ
S
k
i
n
xi
1
0
⋅
⋅
⋅
⋅
=
gdzie: Sn – wsp. technologiczny,
ϕ - wsp. uwzględniający długotrwałość obciążenia.
Obliczenia iteracyjne dowolnym programem do analizy statycznej ram płaskich. W trakcie obliczeń kontrola czy
reakcje w podporach nie przekroczyły reakcji granicznych, jeżeli tak – wyłączamy sprężynkę zastępując ją siłą
skupioną odpowiadającą reakcji granicznej (odpór). Przekroczenie reakcji granicznych we wszystkich
podporach oznacza że należy zwiększyć zagłębienie ścianki. W wyniku obliczeń uzyskuje się: wykres
momentów, przemieszczeń ścianki oraz wartość siły w ściągu oraz rozkład odporu.
Ś
cianki szczelne stalowe - obliczanie
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/22
Ś
cianka szczelna górą zakotwiona, dołem utwierdzona
Metoda graficzna – metoda linii ugięcia
Wykres parć i odkształceń
Wykres sumaryczny parć
Ś
cianki szczelne stalowe – obliczanie
Metoda graficzna – metoda linii ugięcia
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/23
Wielobok sił
i wielobok
sznurowy
jak
poprzednio.
Zamykającą
należy
poprowadzić
tak, aby były
spełnione
następujące
warunki:
a)
największy
moment nie
różnił się
więcej niż 5
– 10% od
największeg
o momentu
ujemnego.
b) linia
ugięcia była
styczna do
osi
pionowej.
s (+) – ścianka wbita za głęboko,
S (-) – ścinka wbita za płytko.
2
1
3
r
H
s
m
=
∆
Ś
cianki szczelne stalowe - obliczanie
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/24
W celu znalezienia wykresu momentów na odcinku a-c
wystarczy rozpatrywać belkę przegubowo-przesuwną,
odrzucając odcinek c-b. Taką belkę nazywa się belką zastępczą.
Położenie punktu c czyli odcinek x zakłada się według wzoru.
H
x
⋅
=
β
β=0,025 dla φ =20°,
β=0,08 dla φ =30°,
β=0,0 dla φ =40°,
Metoda graficzna – metoda belki zastępczej
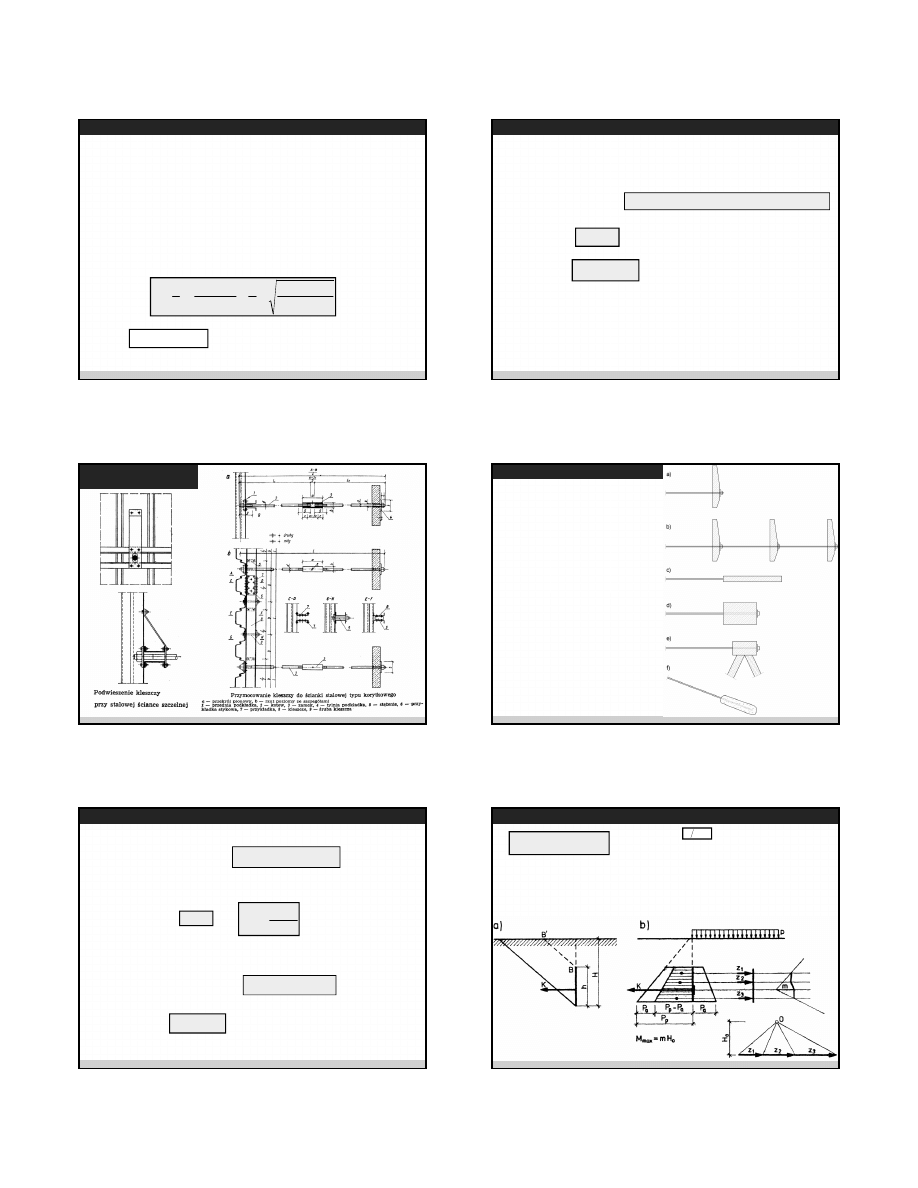
2009-02-03
5
Ś
cianki szczelne stalowe - obliczanie
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/25
Metoda belki zastępczej
Z warunku równowagi (suma momentów względem punktu zamocowania jest równa 0), po
odrzuceniu małych drugiego rzędu uzyskuje się:
(
)
a
p
c
a
p
a
K
K
R
x
K
K
K
H
t
−
+
−
−
=
γ
6
2
2
3
0
Zakłada się
(
)
0
25
,
1
2
,
1
t
t
÷
=
Dla tak określonej belki na dwóch podporach wyznacza się wykreślnie największy moment
zginający (rys. powyżej). A
p
– siła w kotwie, R
c
wielkość służąca do wyznaczenia potrzebnego
zagłębienia ścianki. Zakłada się, że dolna część ścianki jest utwierdzona w gruncie, obciążona siłą
skupiona R
c
na końcu wspornika oraz parciem (zakreskowany wykres parcia).
Ś
cianki szczelne stalowe –
ś
ciągi, kleszcze
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/26
Ś
cianki szczelne stalowe - wymiarowanie
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/27
Warunki nośności
zgodnie z normą stalową
1.
Elementy stalowe zginane:
brusy ścianki, kleszcze
W – wskaźnik wytrzymałości przekroju na zginanie;
f
d
– obliczeniowa wytrzymałość stali
Kleszcze
Rozstaw ściągów
S’’ – siła w ściągu na mb
b – szerokość brusa
2.
Elementy rozciągane osiowo
ś
ciągi – na siłę w kotwie
A
ѱ
– pole przekroju netto elementu;
N
t
– obliczeniowa siła w osi elementu.
Siła w ściągu
b
n
l
x
⋅
=
10
2
x
r
l
S
M
⋅
′′
=
x
r
l
S
P
⋅
′′
=
d
R
r
f
W
M
M
⋅
=
≤
d
Rt
t
f
A
N
N
⋅
=
≤
ψ
Ś
cianki szczelne stalowe - wymiarowanie
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/28
Warunki nośności
zgodnie z normą stalową
3.
Połączenia spawane:
o ile występują
4.
Połączenia śrubowe:
ś
ruby łączące ściankę z kleszczami
Rozstaw śrub
siła w śrubie
b
b
o
⋅
= 2
o
rs
b
S
P
⋅
′′
=
)
085
;
65
,
0
min(
s
e
s
m
Rt
Rt
t
A
R
A
R
S
N
N
⋅
⋅
=
=
≤
Zakotwienia ścianek szczelnych
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/29
Rodzaje zakotwień:
- elementy pionowe
- płyty pojedyncze (a), ciągłe,
- zespoły płyt (b);
- elementy poziome (płyty, kraty) (c);
- bloki kotwiące (d);
- kozły palowe (e);
- zakotwienia iniekcyjne (f).
- zakotwienie ścianką
Zakotwienia ścianek szczelnych – ściana kotwiąca ciągła
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/30
(
)
p
a
E
E
K
F
≤
+
F – przyjęty współczynnik bezpieczeństwa
E
a
– parcie czynne na 1 m długości ściany
E
p
– odpór graniczny gruntu na 1 m długości ściany
K – siła w ściągu działająca na płytę kotwiącą
Przy przyjmuje się w obliczeniach, że
ś
ciana sięga do powierzchni terenu
Ś
ciąg powinien być zamocowany w środku
ciężkości obciążenia wypadkowego
5
≤
h
H
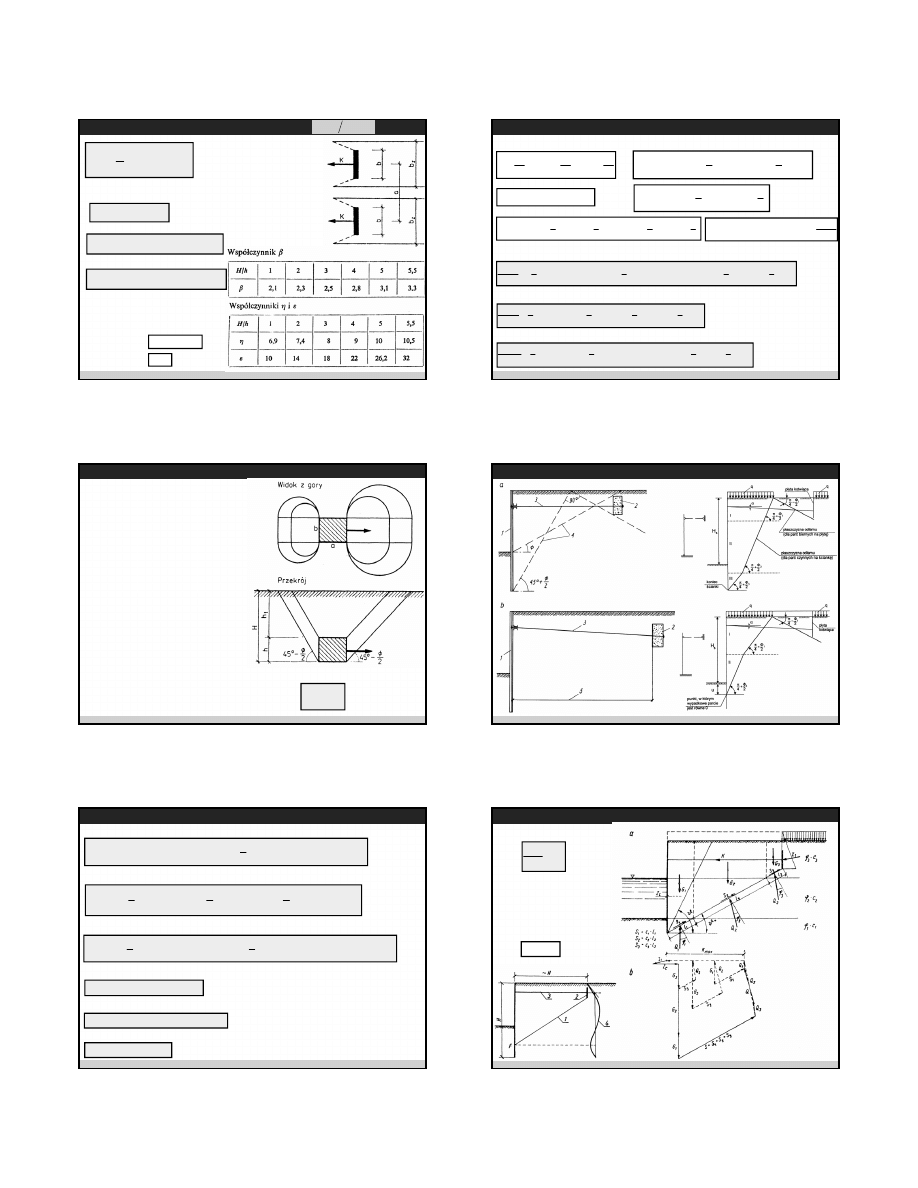
2009-02-03
6
Zakotwienia ścianek szczelnych – metoda Buchholza
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/31
2
2
1
H
b
E
p
⋅
⋅
⋅
⋅
=
η
γ
γ – ciężar objętościowy gruntu
η – współczynnik doświadczalny wg tabl.
b – szerokość płyty
H – zagłębienie dolnej krawędzi płyty
W przypadku gruntów spoistych odpór można zwiększyć o wartość:
H
b
c
E
p
⋅
⋅
⋅
=
′
ε
c – spójność gruntu
ε – współczynnik poprawkowy wg tabl.
5
,
5
1
≤
≤
h
H
(
)
b
E
a
K
a
E
a
p
⋅
+
⋅
⋅
≥
⋅
2
lub
a – rozstaw ściągów
b
z
– szerokość zastępcza płyty
Płytę można rozpatrywać jako element:
pojedynczy przy
ciągły przy
b
b
a
z
⋅
=
>
β
z
b
a
<
b
E
b
E
a
K
a
z
p
⋅
−
⋅
⋅
≤
⋅
5
,
0
Zakotwienia ścianek szczelnych – metoda Odrobińskiego – bloki i płyty kotwiące
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/32
Metoda dotyczy gruntów niespoistych.
Nośność graniczna pojedynczego elementu
kotwiącego jest sumą sił równoległych do linii
działania obciążenia na wszystkich ściankach
bloku. Siły te pochodzą od:
1) odporu na powierzchni czołowej,
2) parcia na powierzchni tylnej,
3) odporu spowodowanego przez boczne strefy
gruntu przed ściana czołową,
4) parcia spowodowanego przez boczne strefy
gruntu za ścianą tylną,
5) parcia od wpływu części strefy „martwej”
ponad zasadniczą bryłą odporu,
6) parcia od wpływu części strefy „martwej”
ponad zasadniczą bryłą parcia,
7) tarcia na powierzchniach bocznych bloku,
8) tarcia na powierzchni dolnej bloku,
9) tarcia na powierzchni górnej bloku,
Łączna graniczna siła odporu (zdolność graniczna):
∑
=
=
=
9
1
i
i
i
Q
Q
Zakotwienia ścianek szczelnych – metoda Odrobińskiego – bloki i płyty kotwiące
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/33
1) odpór i parcie na powierzchni czołowej i tylnej
(
)
(
)(
)
δ
γ
δ
γ
cos
2
1
cos
2
1
2
2
1
h
H
K
K
b
dz
z
K
K
b
Q
Q
a
p
H
h
a
p
−
−
⋅
=
−
⋅
=
+
∫
2) wpływ stref bocznych
(
)
δ
φ
φ
γ
cos
2
45
cot
2
45
cot
9
2
3
1
3
4
3
h
H
K
K
Q
Q
a
p
−
+
−
−
⋅
=
+
o
o
3) wpływ stref „martwych” ponad zasadniczymi bryłami odporu i parcia
(
)
(
)
θ
θ
θ
θ
γ
θ
θ
γ
′
′
−
⋅
⋅
+
′
−
⋅
⋅
⋅
=
+
cot
cos
cot
cos
6
1
cos
cos
2
1
2
2
3
1
2
2
2
1
6
5
h
h
b
Q
Q
4) wpływ tarcia na powierzchniach bocznych bloku
(
)
2
1
2
7
sin
h
H
K
a
Q
a
−
⋅
⋅
=
δ
γ
5) wpływ tarcia na powierzchni dolnej bloku
(
)
[
]
δ
γ
γ
tan
1
1
8
h
H
h
b
a
Q
bet
−
+
⋅
⋅
=
6) wpływ tarcia na powierzchni górnej bloku
δ
γ
tan
1
9
h
b
a
Q
⋅
⋅
⋅
=
Zakotwienia ścianek szczelnych – metoda Odrobińskiego – bloki i płyty kotwiące
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/34
Wprowadzając oznaczenia:
H
b
H
a
H
h
=
=
=
β
α
ξ
,
,
1
δ
φ
φ
cos
2
45
cot
2
45
cot
+
−
−
=
o
o
a
p
K
K
N
Nośność graniczna bloku
(
)
(
)
(
)
3
2
2
1
3
2
3
6
1
2
1
1
1
9
2
1
2
1
ξ
ξ
β
ξ
β
α
ξ
ξ
α
β
γ
⋅
+
⋅
⋅
+
+
⋅
⋅
+
−
+
−
⋅
+
⋅
=
⋅
R
R
f
N
K
K
H
Q
r
r
Nośność graniczna płyty poziomej
(
)
δ
cos
a
p
r
K
K
K
−
=
+
−
−
=
2
45
cos
2
45
cos
2
2
1
φ
φ
o
o
R
+
+
−
−
−
=
2
45
cot
2
45
cos
2
45
cot
2
45
cos
2
2
2
φ
φ
φ
φ
o
o
o
o
R
3
,
sin
,
tan
H
Q
Q
K
K
f
a
⋅
=
′
=
=
γ
δ
δ
(
)
(
)
(
)
3
2
2
1
3
2
3
6
1
2
1
1
1
3
2
1
2
1
ξ
ξ
ξ
β
α
ξ
ξ
β
γ
⋅
+
⋅
+
+
⋅
⋅
+
−
+
−
⋅
=
⋅
R
R
f
N
K
H
Q
r
c
Nośność graniczna płyty pionowej (poniżej powierzchni terenu)
(
)
(
)
3
2
2
1
3
2
3
6
1
2
1
1
9
2
1
2
1
ξ
ξ
β
ξ
ξ
β
γ
⋅
+
⋅
⋅
+
−
+
−
⋅
=
⋅
R
R
N
K
H
Q
r
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/35
Zakotwienia ścianek szczelnych – określanie długości ściągu
grunt niespoisty
1 – ś. szczelna
2 – blok lub płyta k.
3 – ściąg
4 – potencjalne linie odłamu
5 – szerokość masywu gruntowego na której opór
ś
cinania powinien być co najmniej równy nośności
granicznej zakotwienia
grunt spoisty
G.Horodecki – Fundamentowanie 1
Katedra Geotechniki, Geologii i Budownictwa Morskiego
2/36
Zakotwienia ścianek szczelnych – sprawdzenie stateczności metodą Kranza
Powinien być spełniony warunek
5
,
1
max
≥
obl
K
K
W przypadku utwierdzenia ścianki
dołem miarodajna dolna przechodzi
przez punkt odpowiadający
położeniu największego momentu
utwierdzenia,
i
i
i
l
c
S
⋅
≥
Wyszukiwarka
Podobne podstrony:
Japońskie techniki inwestycyjne, Analiza techniczna i fundamentalna, Analiza techniczna i fundamenta
FUNDAMENTOWANIE 6 materia y
FUNDAMENTOWANIE 2 c materia
Fundamenty materialy z wykladow
Fundamenty, materialy budowlane
FUNDAMENTOWANIE 2 a materia
FUNDAMENTOWANIE 3 materia y
Newsletter Johna Bollingera, Analiza techniczna i fundamentalna, Analiza techniczna i fundamentalna,
Notatki z materiaw, Budownictwo, IV semestr, Mechanika Gruntów, MGF Mechanika gruntó i fundamentowan
FutureRevisions, Courseware, IBM Tivoli Network Manager IP Edition 3.7 Fundamentals, materials
AT-folie2, Analiza techniczna i fundamentalna, Analiza techniczna i fundamentalna, materialy
FUNDAMENTOWANIE 4 materia y
Gann, Analiza techniczna i fundamentalna, Analiza techniczna i fundamentalna, materialy
Tabele z materiw, Budownictwo, IV semestr, Mechanika Gruntów, MGF Mechanika gruntó i fundamentowanie
FUNDAMENTOWANIE 5 materia y
FUNDAMENTOWANIE 1 materia y
ANALIZA FUNDAMENTALNA I JEJ ZWIAZKI Z ANALIZA TECHNICZNA, Analiza techniczna i fundamentalna, Analiz
Japońskie techniki inwestycyjne, Analiza techniczna i fundamentalna, Analiza techniczna i fundamenta
więcej podobnych podstron