POLITECHNIKA

CZĘSTOCHOWSKA

WYDZIAŁ

BUDOWNICTWA

SAMODZIELNY ZAKŁAD

WYTRZYMAŁOŚCI MATERIAŁÓW

L

ABORATORIUM

S

PRAWOZDANIE

N

R

VIII

T

EMAT

:

E

LASTOOPTYKA

Krzysztof Komisarczuk

Rok II, Grupa dziekańska II

Rok akademicki 2011/2012

Studia stacjonarne

1.Teoria

Pomiary punktowe w układzie z jedną ćwierćfalówką.

Do pomiaru wykorzystuje się polaryskop liniowy o ciemnym polu widzenia z wprowadzoną

dodatkowo (pomiędzy model i analizator) ćwierćfalówką. Metoda ta bazuje na pomyśle szczególnego
ustawienia filtrów względem kierunków głównych odkształcenia w badanym punkcie modelu – tak,
że kierunki główne odkształcenia (naprężenia) w punkcie pomiarowym modelu muszą tworzyć kąt
π/4 z osią optyczną polaryzatora.

Układ osi polaryzatora powoduje, że promień padając na tarczę ulegnie rozszczepieniu na

dwa drgania składowe o równych amplitudach -> płaszczyzny tych drgań pokrywają się z kierunkami
głównymi odkształcenia.

Następnie promienie padają na ćwierćfalówkę która przepuszcza drgania świetlne w dwóch

kierunkach wzajemnie prostopadłych przesuwając je jednocześnie w fazie o kąt π/2. Przesuniecie
względne składowych drgań promienia wynosi wtedy δ=λ/4

Składowe drgań po wyjściu z ćwierćfalówki:

Oba równania mają tę samą fazę -> wypadkowa obu drgań W:
- stanowi drganie spolaryzowane liniowo
- tworzy z osią optyczną analizatora kąt γ -> jeśli obrócimy analizator o ten kąt to:

- w punkcie pomiarowym będziemy obserwowali wygaszenie światła

- obrotowi w tym kierunku będzie towarzyszyło nasuwanie się sąsiedniej izochromy na ten

punkt

Pomiar rzędu izochromy w konkretnym punkcie należy przeprowadzić następująco:
- ustawić filtry tak by przez punkt przechodziła izoklina ( osie ćwierćfalówki pokrywające się z osiami
polaryzacji polaroidów)
- obrócić filtry i ćwierćfalówkę o λ/4
- obracać analizatorem tak by najbliższą izochromą najechać na badany punkt i wyznaczyć kąt γ
- obliczyć rząd izochromy w danym punkcie ze wzoru:

gdzie: m

c

– rząd izochromy całkowitej naprowadzonej

(+) – gdy naprowadzana izochroma jest o niższym rzędzie
(-) – gdy naprowadzana izochroma jest o wyższym rzędzie

Izokliny – miejsca punktów o jednakowych kierunkach głównych odkształcenia, określana jest
wartością kąta fi (parametr izokliny)

Izochromy – miejsca punktów w których różnice odkształceń mają jednakową wartość
Metoda różnic naprężeń stycznych
Znając w danym punkcie x wartość różnicy naprężeń głównych m(x) oraz parametr izokliny φ(x),
możemy znaleźć współrzędną σ

12

(x):

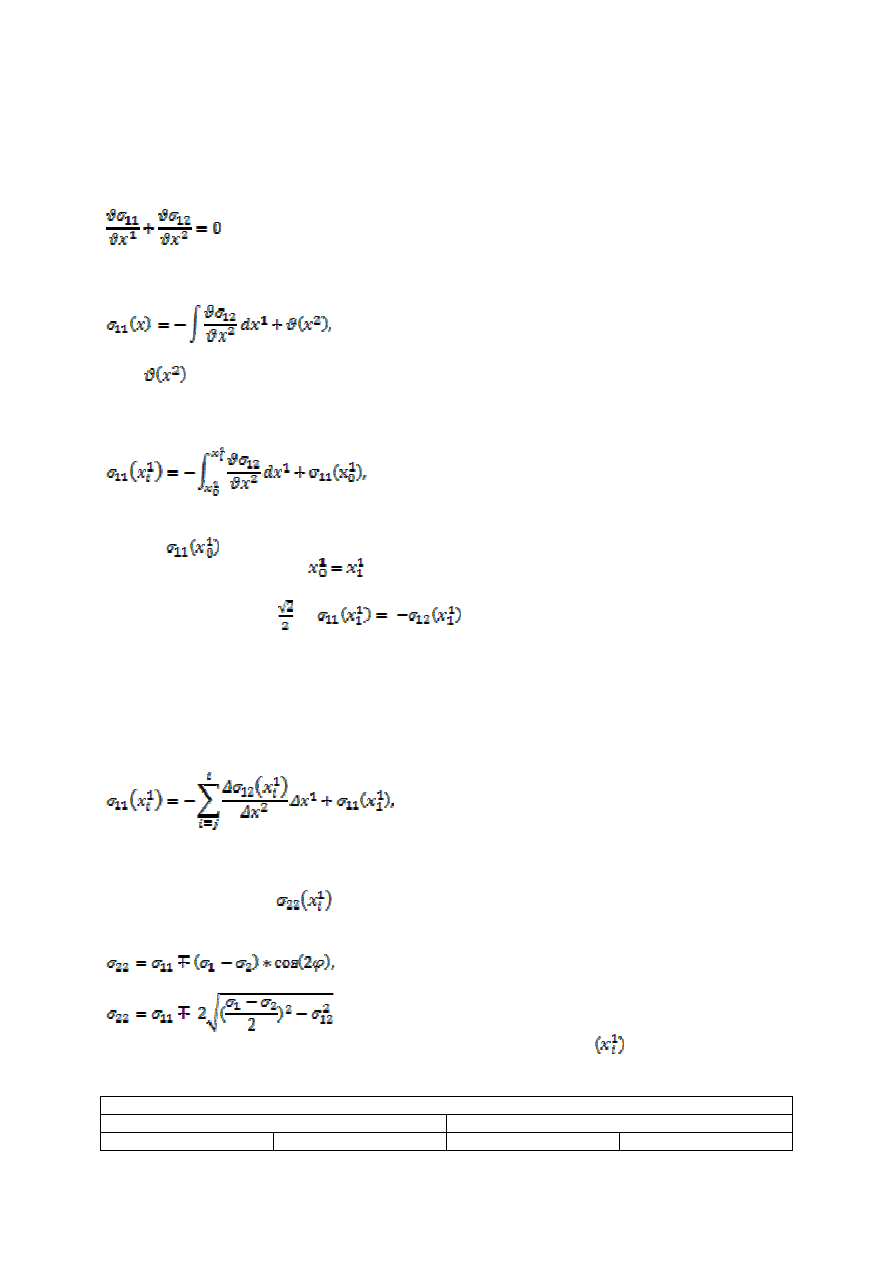
Znaki naprężeń σ

12

można łatwo określić tylko w punktach leżących na brzegu modelu. Aby ustalić

znaki w innych punktach należy wykonać dodatkowe analizy na podstawie warunków wynikających z
ogólnej teorii stanów płaskich.
Dla wyznaczenia σ

11

(x) wykorzystamy jedno z równań równowagi, na przykład:

Całkując powyższe równanie względem x

1

otrzymamy:

gdzie

jest funkcją, którą należy wyznaczyć z warunków brzegowych.

W rozpatrywanym zadaniu należy znaleźć σ

11

(x) dla x

2

= const, to znaczy funkcję σ

11

(x

1

,x

2

=const).

Równość przyjmie zatem postać:

gdzie: i = 4,7,10,13,16,19

Wartość

najprościej jest wyznaczyć zauważając, że punkt pomiarowy ‘1’ leży na brzegu

swobodnym. Otrzymamy tam

; k,l = 1,2:

p

k

= σ

kl

n

l

= 0 oraz n

1

= n

2

= =>

gdzie:
n – wektor jednostkowy, normalny do brzegu S,
p – wektor naprężenia.

Równanie całkujemy zmieniając zawarte tam operatory różniczkowe. Dochodzimy w ten sposób do
formuły:

i = 4, 7, 10, 13, 16, 19; j = 4,
gdzie: Δσ

12

(x

i

) = σ

12

(x

i-1

) – σ

12

(x

i+1

).

Współrzędne naprężenia

możemy wyznaczyć z ogólnie znanych zależności wynikających z

geometrii kół Mohra, np.>

Podstawiamy tu odpowiednio wielkości określone w kolejnych punktach

.

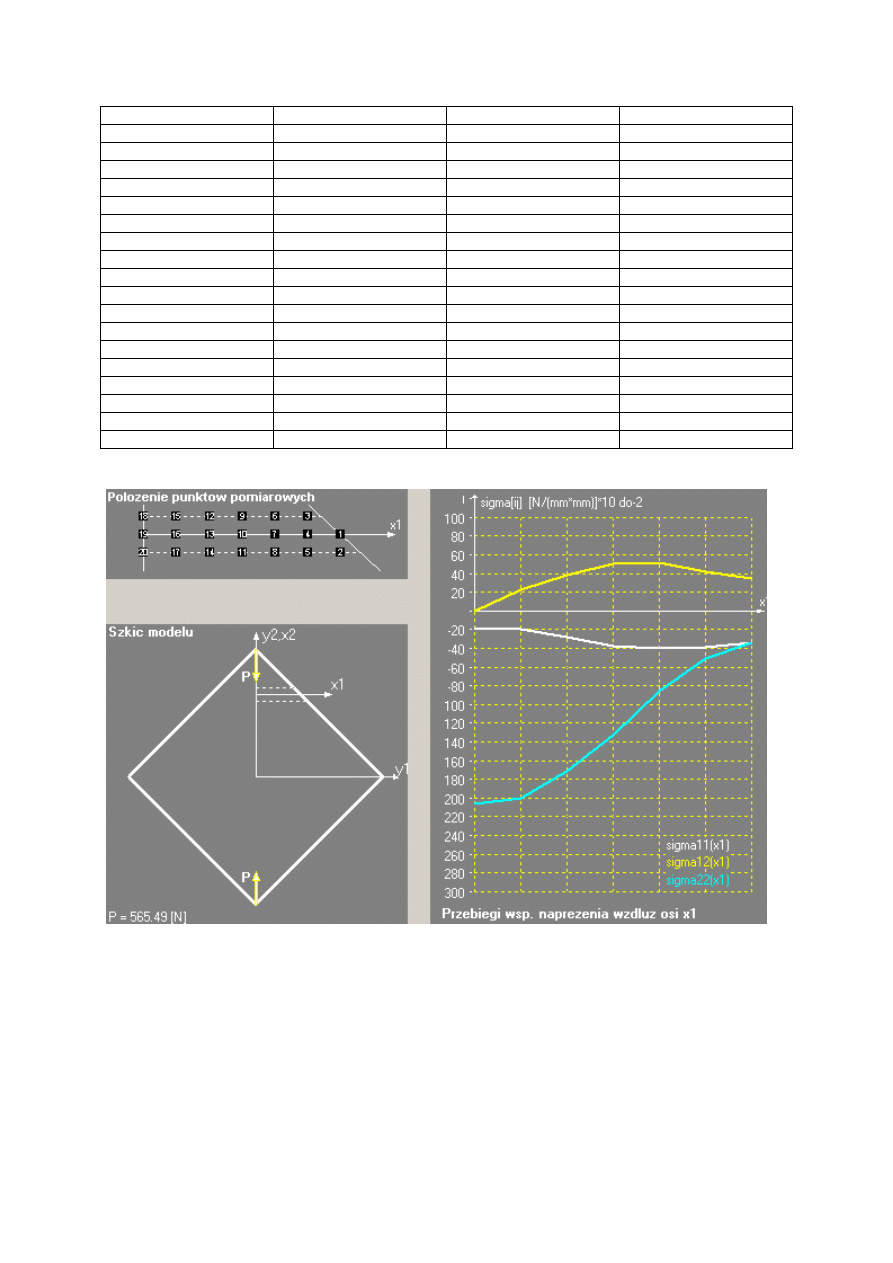
2. Tabela pomiarowa i wykresy

Dane pomiarowe

Rzędy izochrom

Parametry izoklin (ST)

m[1]

0,56667

Fi[1]

45

m[2]

0,59444

Fi[2]

44

m[3]

0,65556

Fi[3]

43

m[4]

0,70555

Fi[4]

41

m[5]

0,75000

Fi[5]

39

m[6]

0,85000

Fi[6]

38

m[7]

0,92778

Fi[7]

33

m[8]

0,95000

Fi[8]

29

m[9]

1,08889

Fi[9]

27

m[10]

1,15000

Fi[10]

23,5

m[11]

1,21000

Fi[11]

21

m[12]

1,33333

Fi[12]

18

m[13]

1,34444

Fi[13]

14

m[14]

1,44444

Fi[14]

11

m[15]

1,45556

Fi[15]

8

m[16]

1,54444

Fi[16]

7

m[17]

1,70556

Fi[17]

6

m[18]

1,46667

Fi[18]

0

m[19]

1,55556

Fi[19]

0

m[20]

1,68333

Fi[20]

0

3.Wnioski
Po przeprowadzeniu ćwiczenia otrzymaliśmy rozkład naprężeń w określonej części badanej
tarczy. Ułamkowe rzędy izochrom w wybranym punkcie posłużyły nam do obliczeń.
Ćwiczenie było przeprowadzane przy małym obciążeniu tak by obraz izochrom nie utrudniał
nam odczytania obrazu izoklin. Źródłem pewnej niedokładności mógł być błąd paralaksy,
który wynikał z błędnego odczytu wskazań parametrów rzędu izoklin.