Sekcja: 1 Wtorek, P, 830
Grupa: 3
Kierunek: Automatyka i Robotyka
Wydział: Mechaniczny Technologiczny
rok akademicki: 2000/2001
semestr: letni
Katedra Wytrzymałości Materiałów
i Metod Komputerowych Mechaniki
LABORATORIUM
WYTRZYMAŁOŚCI MATERIAŁÓW
Temat ćwiczenia:
ANALIZA STANU NAPRĘŻENIA METODĄ ELASTOOPTYCZNĄ
Skład sekcji:
1 |
Bańka Marek |
2 |
Dusza Tomasz |
3 |
Florek Paweł |
4 |
Hanus Andrzej |
5 |
Jendrysik Sebastian |
6 |
Karp Maciej |
7 |
Kauch Tomasz |
8 |
Koźlak Marek |
9 |
Krawczyk Dariusz |
10 |
Król Adrian |
11 |
Markiewicz Adam |
12 |
Osiecki Tomasz |
13 |
Trepka Krzysztof |
Wstęp teoretyczny:
Polaryzacja liniowa - polega na sprowadzeniu drgań promieni świetlnych do jednej płaszczyzny.
Polaryzacja kołowa - ma ten sam cel co polaryzacja liniowa z tą różnicą, że w wyniku użycia ćwierćfalówek zostają wyeliminowane izokliny co ułatwia analizę obrazu.
Izochromy - prążki będące miejscami geometrycznymi punktów o jednakowych naprężeniach stycznych.
Izokliny - (tylko w polaryzacji liniowej) prążki będące miejscami geometrycznymi punktów, w których kierunki naprężeń głównych pokrywają się z osiami analizatora i polaryzatora.
Cel ćwiczenia:
Zapoznanie się z budową polaroskopu elastooptycznego.
Zapoznanie się z elastooptyczna metodą badan modelowych na przykładzie płaskownika poddanego rozciąganiu.
Okreslenie elastooptycznej stałej modelowej.
Schemat rozciągarki.
Wyznaczenie y = f (P, l, I, E)
a) Moment bezwładności belki (I):
b) Siły i momenty bezwładności w belce stalowej
Równania reakcji i momentów:
(1)
(2)
(3)
Równanie różniczkowe osi ugiętej belki:
(4)
(5)
(6)
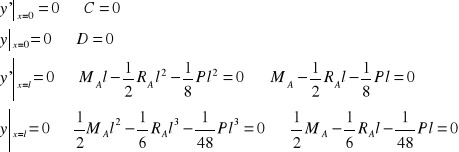
Warunki brzegowe:
(7)
(8)
(9)
(10)
Rozwiązujemy układ równań (9) i (10):
Wyliczamy strzałkę ugiecia (y) podstawiając powyższe wyniki do równania (6):
(11)
Przekształcamy równanie (11):
![]()
(12)
Elastoplastyczna stała modelowa:
BELKA |
PŁASKOWNIK |
||
Długośc (l) [m] |
214,52.10-3 |
Szerokośc (a) [m] |
21,1.10-3 |
Wysokość (h) [m] |
4,74.10-3 |
Grubośc (b) [m] |
5,0.10-3 |
Szerokość (b) [m] |
17,0.10-3 |
|
|
Moduł Younga (E) [MPa] |
2.105 |
|
|
Moment bezwładnosci (I) [m4] |
1,5.10-10 |
|
|
Z równania (12) obliczamy Pi:
![]()
, gdzie:![]()
,![]()
i=1..5
Rząd izochromy (mi) |
Strzałka ugięcia belki yi [m] |
Wartość siły P [kN] |
1 |
0,85.10-3 |
0,49 |
2 |
1,15.10-3 |
0,67 |
3 |
1,60.10-3 |
0,93 |
4 |
2,10.10-3 |
1,22 |
5 |
2,35.10-3 |
1,37 |
Wyznaczamy elastooptyczną stałą modelową (kg) i naprężenia (σi):
σi = kg . mi
![]()
[Pa], gdzie A - przekrój poprzeczny modelu
A= a.b= 105,5.10-6 [m2],
n = 1..5
Pi [kN] |
mi |
kgi [MPa] |
σi [MPa] |
0,49 |
1 |
4,64 |
4,64 |
0,67 |
2 |
3,17 |
6,34 |
0,93 |
3 |
2,93 |
8,79 |
1,22 |
4 |
2,89 |
11,56 |
1,37 |
5 |
2,59 |
12,95 |
kg = 3,24 [MPa]
Elastooptyczna stała materiałowa (k):
k = kg . g [N/m], gdzie: g - grubość płaskownika
k = 3,24 . 5 . 10-3 = 16,2 [kN/m]
Naprężenia w okreslonych punktach modelu
σi = kg . mi gdzie: i = 1..3
kg = 3,24 [MPa]
Pkt. |
mi |
σi [MPa] |
1 |
8 |
25,92 |
2 |
22 |
71,28 |
3 |
0 |
0 |
Uwagi i wnioski:
punkt 3 leży na osi obojętnej badanego modelu i dlatego nie występują w nim naprężenia.
ze wzrostem wartości siły Pi , maleje wartość kgi
naprężenia zachowują się zgodnie z prawem Hooke'a.
najwieksze naprezenia powstają w punkcie nr 2, i dlatego jest on najbardziej narazony na odkształcenie
na niedokładnośc pomiarów mogly mieć wpływ: błędy przyrzadów pomiarowych, niedokładny montaż i stan elementów układu pomiarowego
b) Siły i momenty bezwładności w belce stalowej
Równania reakcji i momentów:
(1)
(2)
(3)
Równanie różniczkowe osi ugiętej belki:
(4)
(5)
(6)
Warunki brzegowe:
(7)
(8)
(9)
(10)
0,5 l 0,5 l
MB
MA
P
y
RA RB
A B
y
y
x
b
h
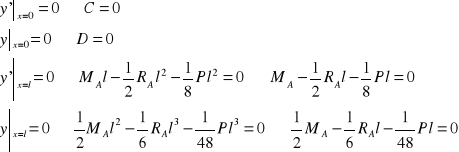
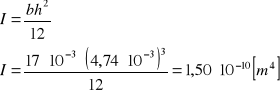
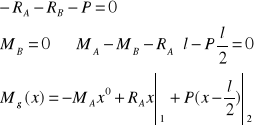
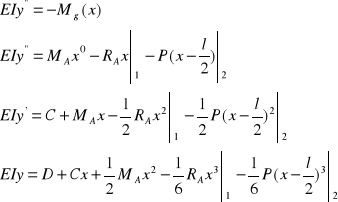
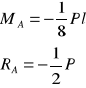
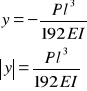
0,5 l 0,5 l
MB
MA
P
y
RA RB
A B
y
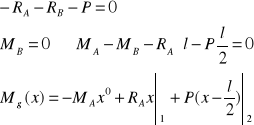
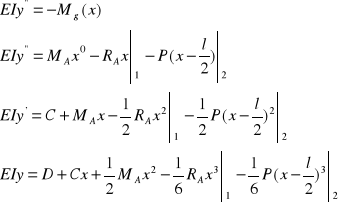
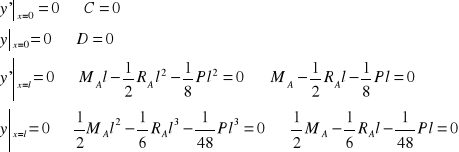
Wyszukiwarka
Podobne podstrony:
Analiza stanu naprężenia metodą elastoptyczną
3 laborka -analiza stanu naprężenia Elastooptyka, Wytrzymałość materiałów(1)
2 Analiza stanu naprezenia i odksztalcenia w punkcie
Analiza stanu naprężenia i odkształcenia
ANALIZA STANU NAPRĘŻENIA I ODKSZTAŁCENIA
10 Analiza stanu naprężenia pojęcia podstawowe
stan naprezen, Budownictwo PK, Wytrzymałość materiałów, semestr 1
analiza stanu naprezen
2 Analiza stanu naprężenia i odkształcenia w punkcie
ANALIZA STANU NAPRĘŻENIA I ODKSZTAŁCENIA, Budownictwo, semestr 4, Mechanika Budowli
2 Analiza stanu naprężenia i odkształcenia w punkcie (1)
Badania zmeczeniowe metali w zakresie jednoosiowego stanu naprezenia (2), Uczelniane, Wytrzymałość m
wydyma elastooptyka, Laboratorium wytrzyma˙o˙ci materia˙˙w
Wytrzymałość materiałów, Pomiar odkształceń - metoda elektrycznych tensometrów, Badanie odkształceń
więcej podobnych podstron