Analiza stanu naprężeń

i odkształceń w punkcie

.

Seminarium dyplomowe

10 grudzień 2013r.

Teoria stanu naprężenia

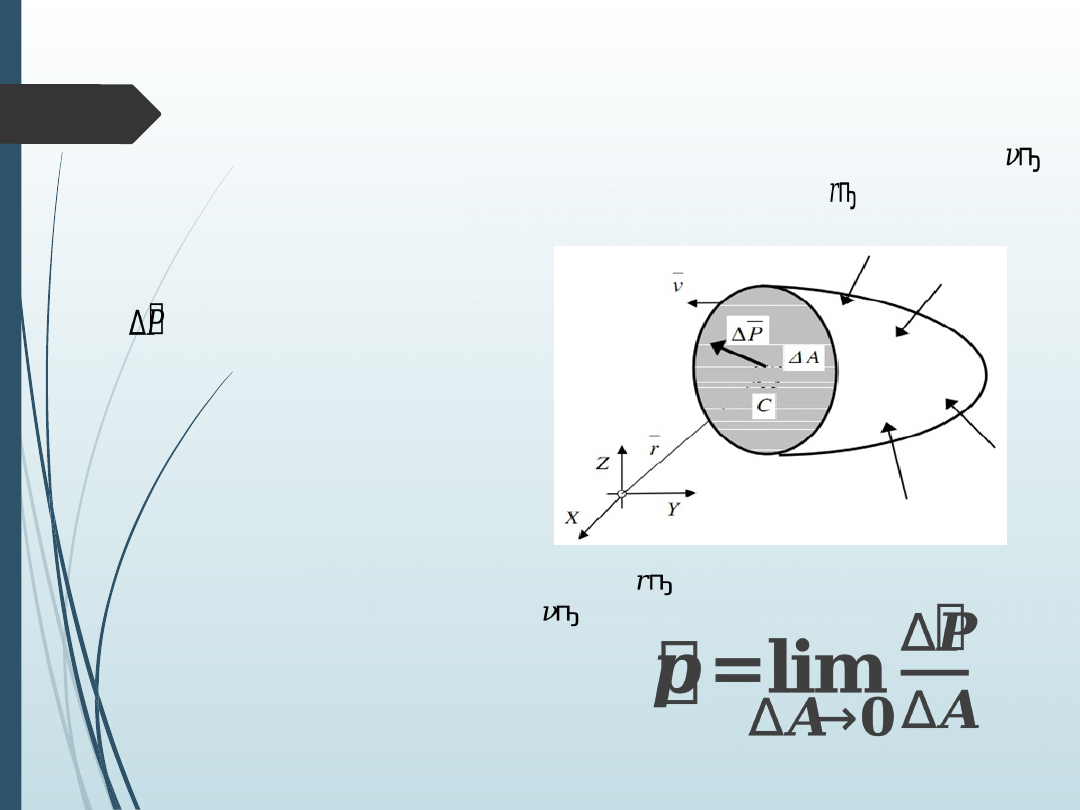
Definicja naprężenia

Rozważamy dowolny przekrój bryły płaszczyzną o
wersorze normalnym przechodzącą przez dowolny pkt. C o
wektorze wodzącym . Do każdego punktu płaszczyzny
przekroju przyłożona jest siła wewnętrzna.

- suma sił wewnętrznych
przyłożonych do punktów
powierzchni ΔA

Naprężeniem w punkcie o wektorze
wodzącym
na powierzchni przekroju o normalnej
nazywamy wektor:

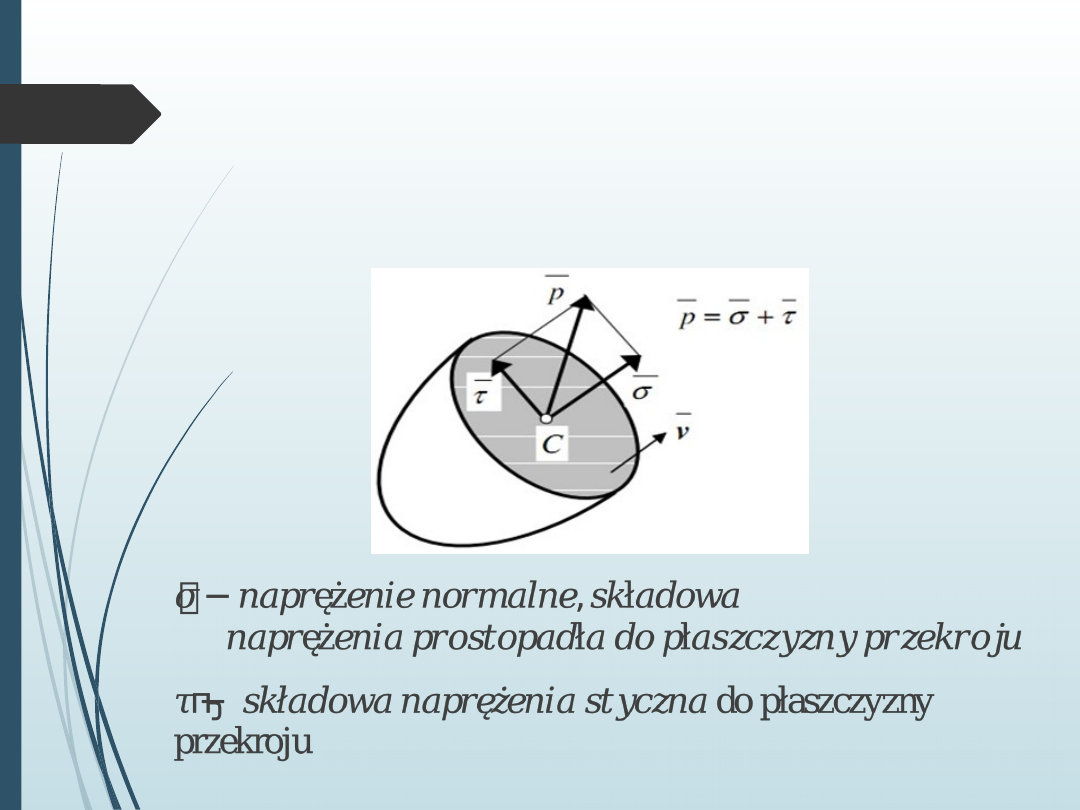
Kierunek wektora naprężenia jest dowolny w
odniesieniu do płaszczyzny na której występuje. Można
go rozłożyć na dwie składowe których kierunki są
normalne i styczne do przekroju .

Definicja naprężenia

Stan naprężenia w punkcie

Stan naprężenia w punkcie to nieskończony zbiór

wektorów naprężeń przyporządkowanych
wszystkim płaszczyznom przecięcia bryły,

przechodzące przez ten punkt.

Stan naprężenia w punkcie

Wyróżniamy trzy możliwe stany naprężenia:



Jednoosiowy

–

występuje gdy wektory naprężeń przyporządkowane

dowolnym płaszczyznom cięcia bryły w danym punkcie mają ten sam

kierunek



Płaski

– występuje gdy wektory naprężeń przyporządkowane

dowolnym płaszczyznom cięcia bryły w danym punkcie leżą w jednej

płaszczyźnie



Przestrzenny

– występuje gdy wektory naprężeń przyporządkowane

dowolnym płaszczyznom cięcia bryły w danym punkcie są w ogólności

różne (mają różne długości, kierunki i zwroty)

.

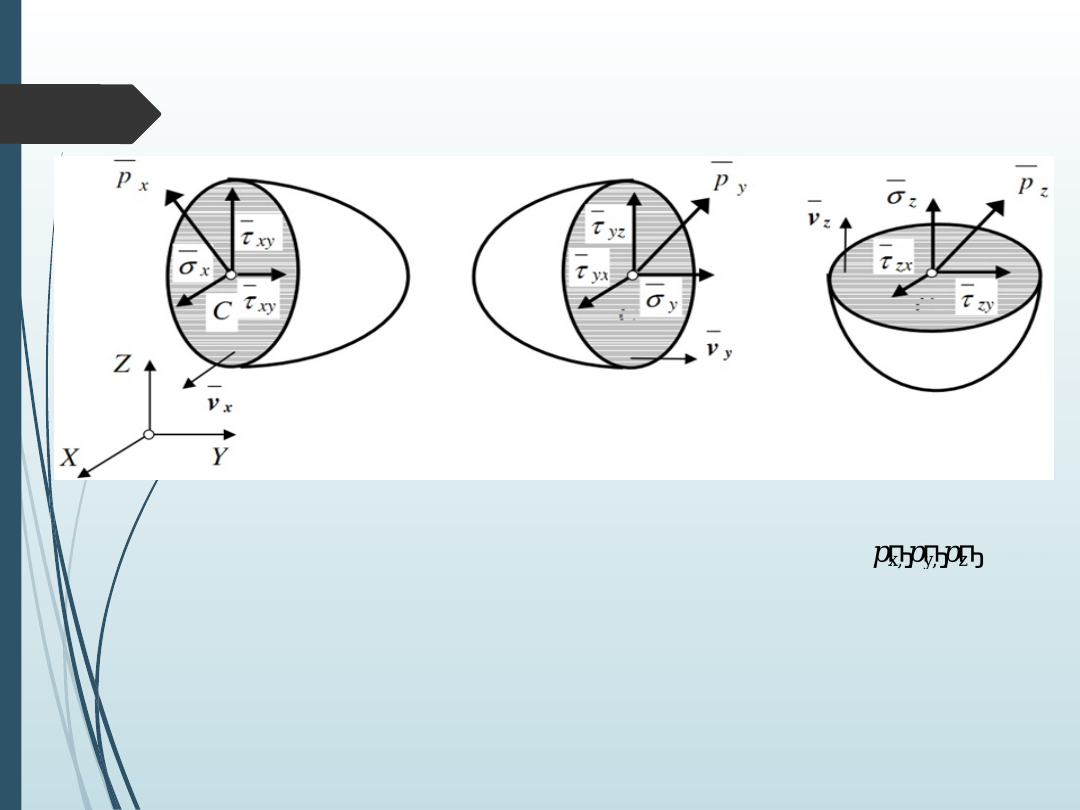
Macierz naprężeń

Dokonajmy przekroju rozważanej bryły w dowolnie wybranym punkcie C
trzema płaszczyznami prostopadłymi do osi układu (X, Y, Z). Wektory
naprężeń przyporządkowane

tym

płaszczyznom

cięcia oznaczymy,

odpowiednio

Każdy z tych wektorów naprężeń można rozłożyć na trzy
składowe równoległe do osi układu. Jedna z tych składowych
będzie normalna do płaszczyzny przecięcia a dwie pozostałe
będą do niej styczne.

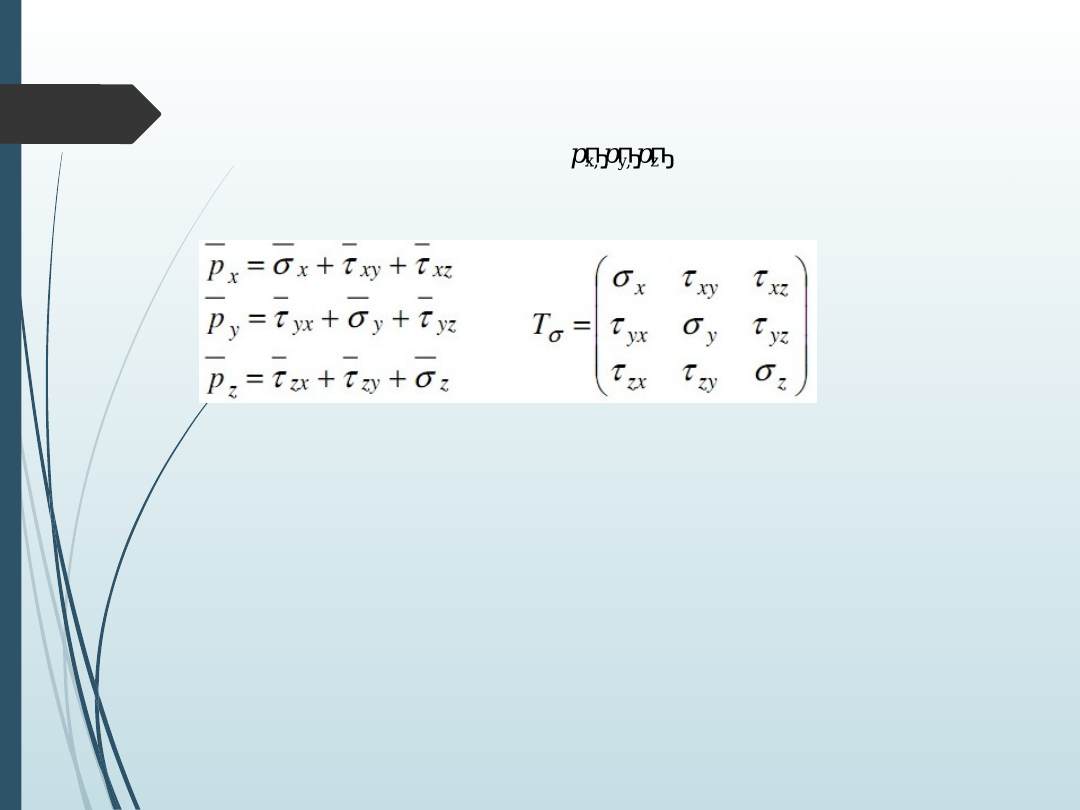
Współrzędne wektorów naprężeń oznacza się podobnie jak

ich składowe i zapisuje się je w formie macierzy naprężeń T

σ

Macierz naprężeń w punkcie to uporządkowany zbiór

współrzędnych trzech wektorów naprężeń na płaszczyznach

prostopadłych do osi układu współrzędnych.



Wiersze przedstawiają kolejne współrzędne, kolejnych wektorów

naprężeń;



Na przekątnej macierzy znajdują się naprężenia normalne ;



Poza przekątną znajdują się naprężenia styczne;

Macierz naprężeń

Za dodatnie, w macierzy naprężeń, uważamy

współrzędne takich składowych, które mają:



zwrot zgodny ze zwrotem osi do której są równoległe i zwrot
normalnej zewnętrznej płaszczyzny na której one występują także
zgodny ze zwrotem osi układu do której ta normalna jest
równoległa



zarówno składową jak i normalną o zwrotach przeciwnych do
odpowiednich osi, do których są równoległe

W każdym innym przypadku współrzędna jest ujemna.

Zgodnie z przyjętą umową naprężenie jest dodatnie jeśli

jest rozciąganie,

a ujemne jeśli jest ściskające.

Reguła podwójnej zgodności

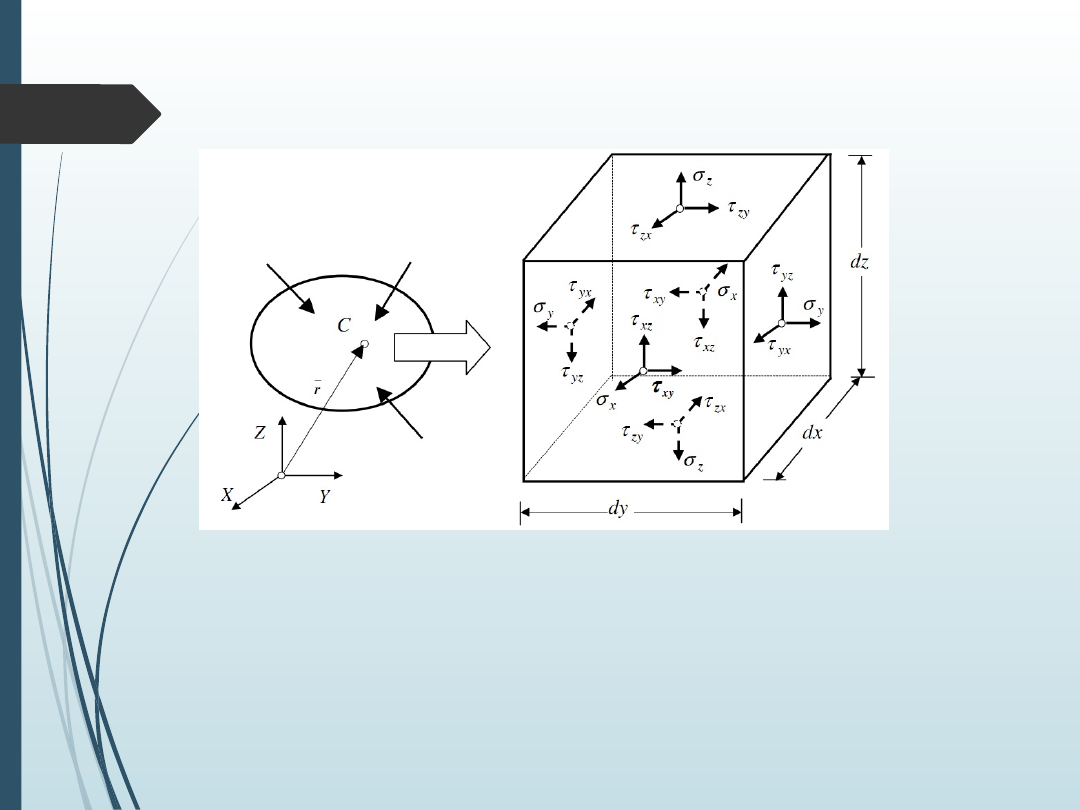
Graficzna postać macierzy
naprężeń

Punkt C jest dowolnym punktem ciała obciążonego
układem sił
i pozostającego w równowadze.

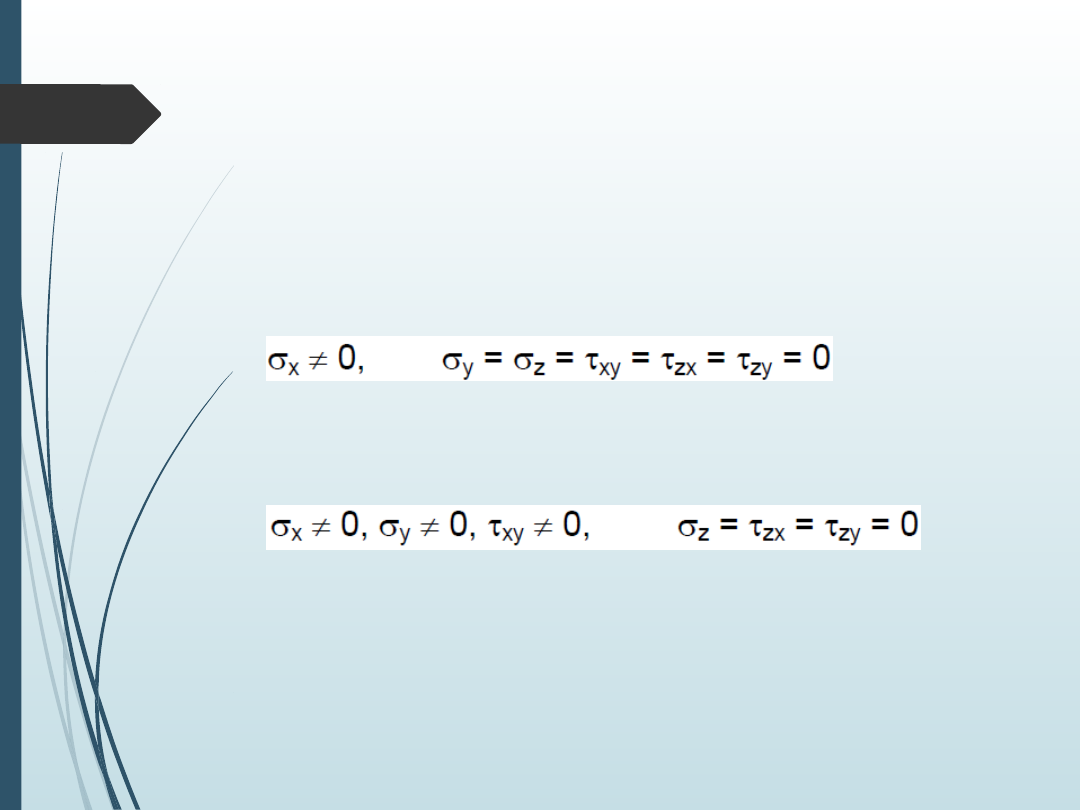
Stan naprężenia w punkcie

Wyróżniamy trzy możliwe stany naprężenia:



Jednoosiowy

–

występuje gdy wektory naprężeń przyporządkowane

dowolnym płaszczyznom cięcia bryły w danym punkcie mają ten sam kierunek



Płaski

– występuje gdy wektory naprężeń przyporządkowane dowolnym

płaszczyznom cięcia bryły w danym punkcie leżą w jednej płaszczyźnie



Przestrzenny

– występuje gdy wektory naprężeń przyporządkowane

dowolnym płaszczyznom cięcia bryły w danym punkcie są w ogólności różne

(mają różne długości, kierunki i zwroty)

.

Rozpisując warunki równowagi sił otrzymamy:

Równania różniczkowe noszą
nazwę równań równowagi
wewnętrznej lub równań
Naviera.

Równowaga sił

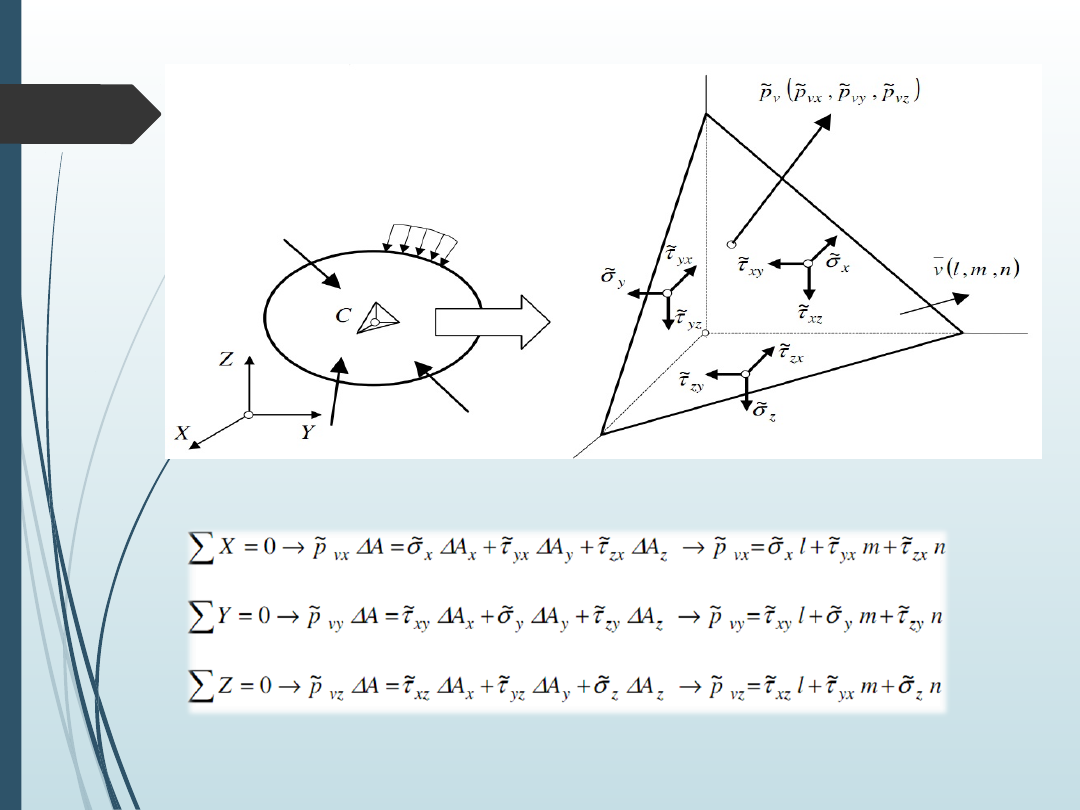
Współrzędne wektora naprężeń. Tensor naprężeń

Warunki równowagi sił działających na wycięty czworościan dają równania:

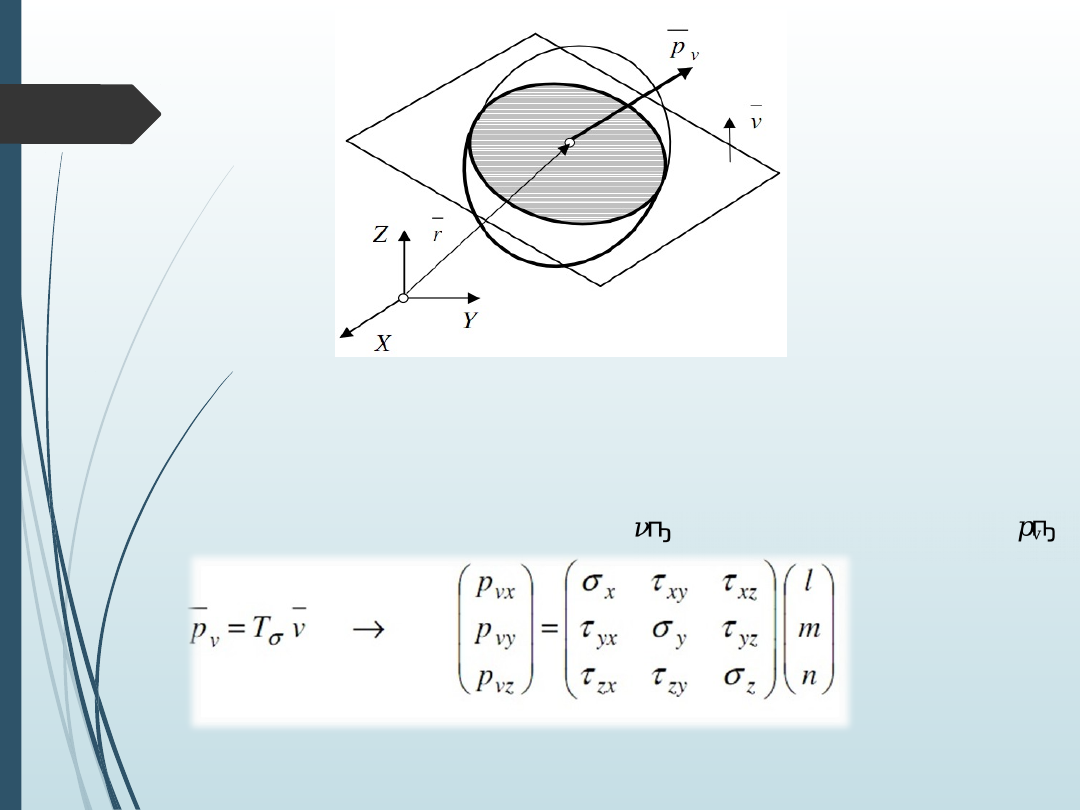
Równania dowodzą że macierz naprężeń w danym punkcie

określa w nim stan naprężenia gdyż znajomość jej elementów

pozwala na wyznaczenie

współrzędnych wektora

naprężenia na dowolnej płaszczyźnie przechodzącej przez

ten punkt.

W wyniku mnożenia naprężeń T

σ

przez wektor otrzymujemy

wektor naprężenia

Macierz naprężeń w punkcie jest wielkością, która dowolnemu

kierunkowi - normalna do płaszczyzny przecięcia bryły w tym punkcie,

przyporządkowuje wektor - wektor naprężenia na tej płaszczyźnie.

Stanowi to dowód na to, że macierz naprężeń jest tensorem drugiego

rzędu co oznacza, że jej elementy transformują się przy zmianie układu

odniesienia w pewien ściśle określony sposób zwany prawem

transformacji tensora.

Prawo transformacji tensora

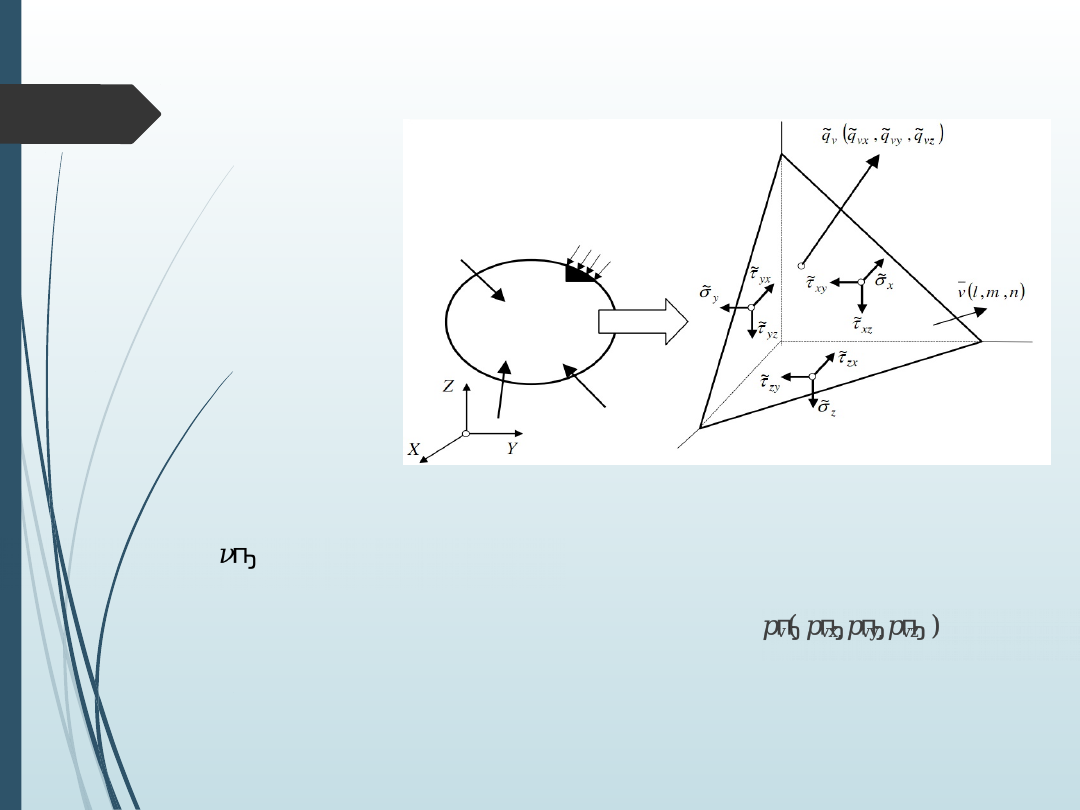
Statyczne warunki brzegowe

Z rozważanej bryły w
równowadze
wycinamy

myślowo

przy

brzegu

czworościan którego
trzy

ściany

będą

równoległe

do

płaszczyzny

układu

odniesienia, a czwarta
będzie

zawierała

element powierzchni
zewnętrznej

ΔS

o

wersorze normalnym
zewnętrznym (l, m,
n)

Analizując warunki równowagi tak wyciętego
czworościanu otrzymujemy zależności wiążące
współrzędne obciążenia bryły
w rozważanym punkcie brzegowym ze
współrzędnymi macierzy naprężeń w tym
punkcie

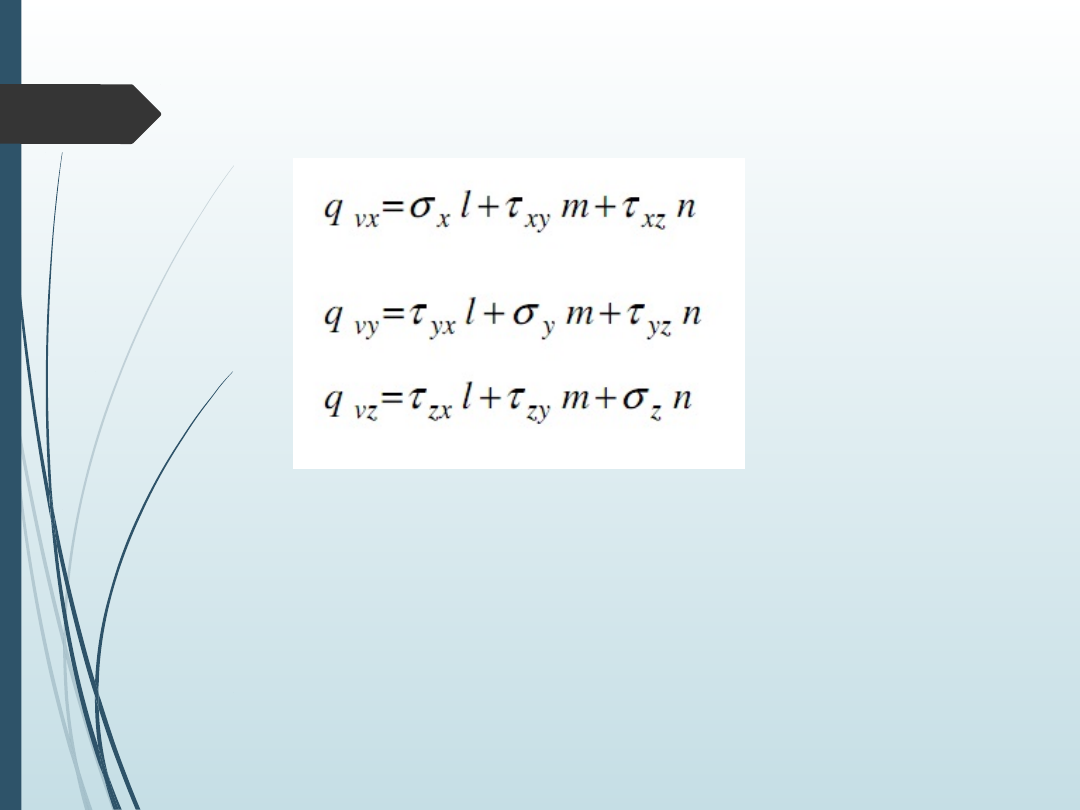
Równania te noszą nazwę statycznych

warunków brzegowych i są niezbędne przy

rozwiązywaniu równań różniczkowych

Naviera.

.

Statyczne warunki brzegowe

Teoria stanu odkształcenia

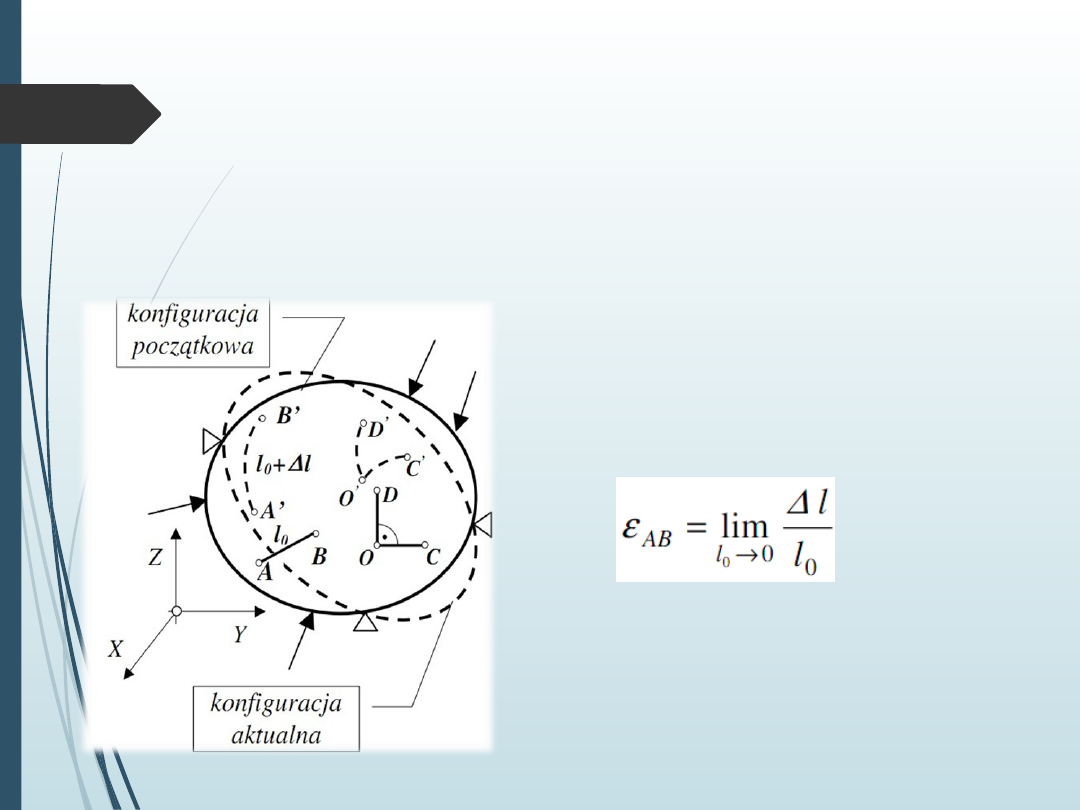
Stan odkształcenia w punkcie to nieskończony zbiór odkształceń

liniowych i kątowych wszystkich włókien przechodzących przez

ten punkt.

Odkształceniem liniowym w
punkcie A w kierunku punktu
B definiujemy jako:

Stan odkształcenia

Odkształcenie liniowe
nazywamy odkształceniem
objętościowym.

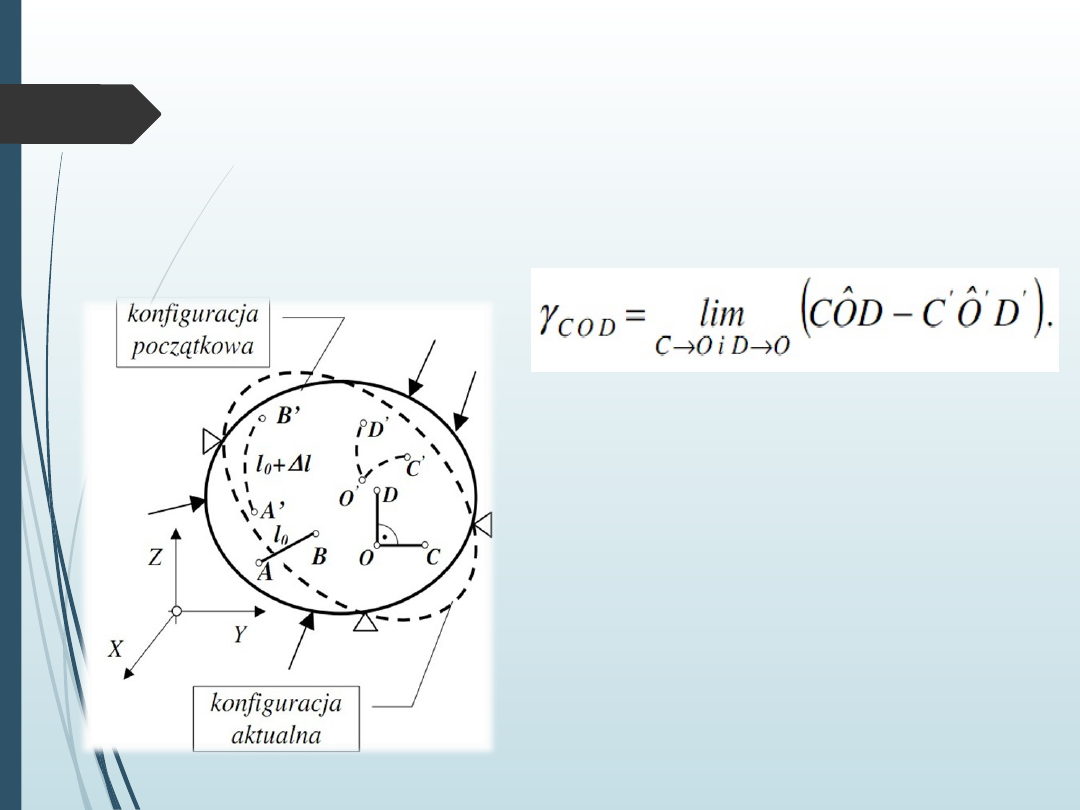
Jeżeli rozważymy dwa prostopadłe włókna przechodzące przez

wspólny punkt O w konfiguracji początkowej to ich

odkształcenie kątowe definiuje się jako:

Stan odkształcenia

Odkształcenie kątowe któremu
odpowiada zmniejszenie się kąta
prostego uważa się za dodatnie.

Odkształcenie kątowe nazywamy
odkształceniem postaciowym.

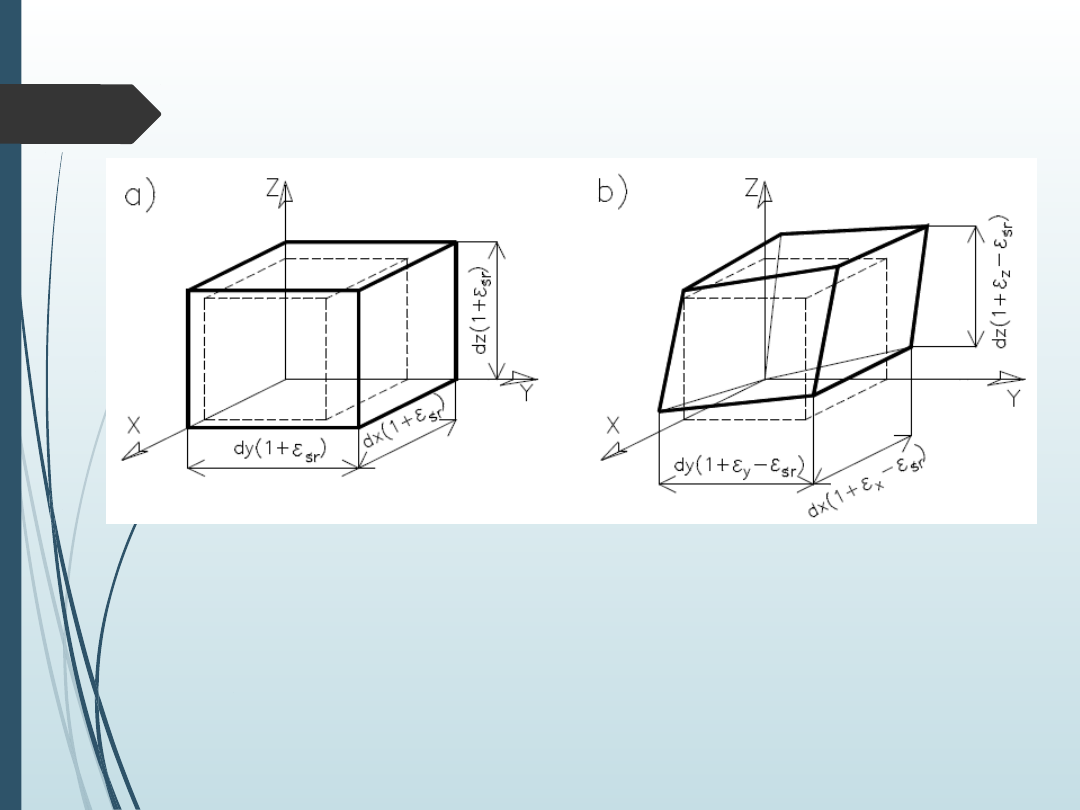
Stan odkształcenia

a) Odkształcenie czysto objętościowe

b) Odkształcenie

czysto postaciowe

Stan odkształcenia określany jest przez sześć składowych:



Wydłużenia liniowe:



Kąty odkształcenia postaciowego:

Stan odkształcenia

Macierz odkształceń

Macierz odkształceń w punkcie to uporządkowany

zbiór odkształceń liniowych i kątowych trzech

włókien przechodzących przez ten punkt i

równoległych do osi układu odniesienia.

Macierz uporządkowana jest w ten

sposób, że na przekątnej

występują odkształcenia liniowe, a

poza przekątną połówki

odkształceń kątowych.

Z definicji elementów macierzy odkształceń wynika jej symetria:

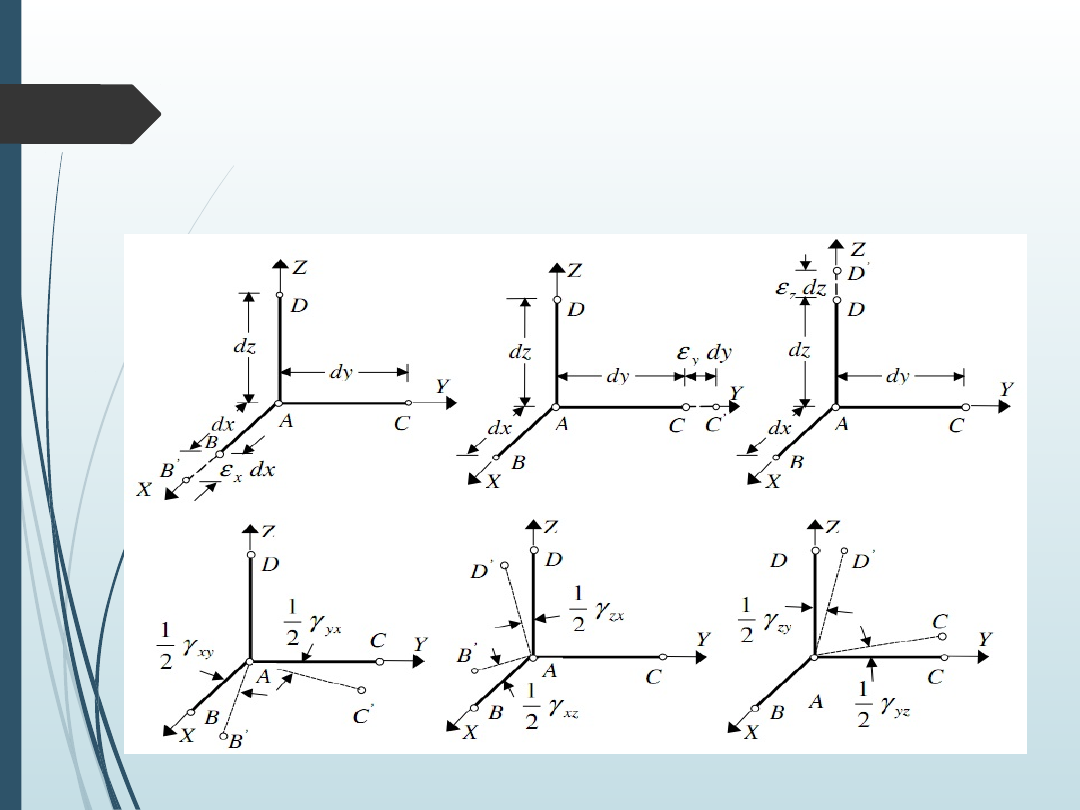
Graficzny obraz macierzy odkształceń

Aby lepiej zobrazować macierz odkształceń, można

przedstawić ją jako deformację trzech włókien,

równoległych do osi układu współrzędnych o

długościach: dx,dy,dz.

Tensor odkształceń

Macierz odkształceń jest tensorem drugiego rzędu co oznacza, że jej

elementy transformują się przy zmianie układu odniesienia w

pewien ściśle określony sposób zwany prawem transformacji

tensora, oraz, że w wyniku mnożenia jej przez jednostkowy wersor
(l, m, n) otrzymamy pewien wektor , który możemy

nazywać wektorem odkształcenia określony zależnościami

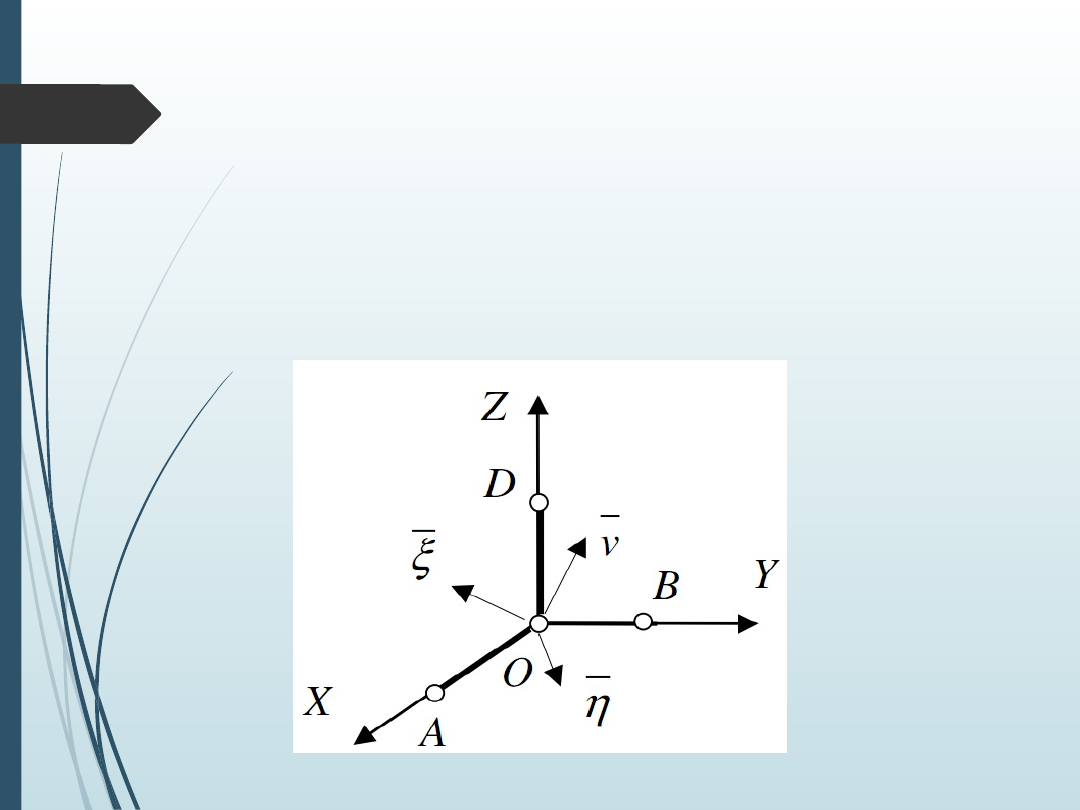
Tensor odkształceń

Znajomość macierzy odkształceń w dowolnym punkcie O

wystarcza do określenia odkształceń liniowych i

kątowych dowolnych włókien przechodzących przez ten

punkt, bo własności tensora pozwalają wyznaczyć

zależności:

Odkształcenia ekstremalne

Odkształcenia główne w danym punkcie to ekstremalne
wartości odkształceń liniowych w nim występujących. Są to
odkształcenia liniowe dwóch do siebie prostopadłych
włókien których odkształcenia kątowe są równe zero.

Wartości odkształceń głównych i ich

kierunki:

Ekstremalne odkształcenia kątowe wynoszą:

Odkształcenia ekstremalne



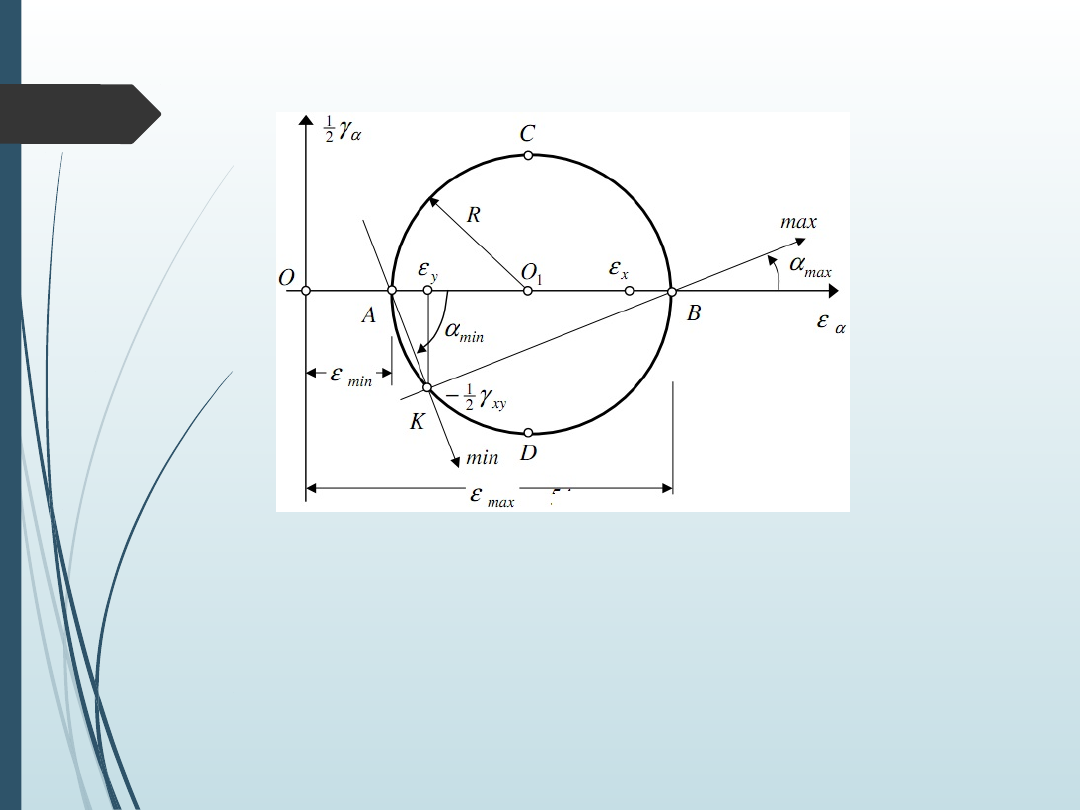
Włókna których odkształcenia kątowe są ekstremalne połowią
kąty miedzy włóknami odkształceń głównych.



Koła Mohra dla stanu odkształcenia są analogiczne jak dla stanu
naprężenia.

Koło Mohra

Prawo Hooke’a

Dla idealnie sprężystego materiału izotropowego zależności

między składowymi stanu odkształcenia i składowymi stanu

naprężenia noszą nazwę uogólnionego prawa Hooke'a.

Składowe stanu odkształcenia jako funkcje składowych

stanu naprężenia wyrażone są zależnościami:

Prawo Hooke’a

Moduł Kirchhoffa [Pa]

(moduł sprężystości

poprzecznej)

Wielkości określające sprężystość materiału:

Moduł Younga [N/m

2

]

(moduł sprężystości podłużnej)

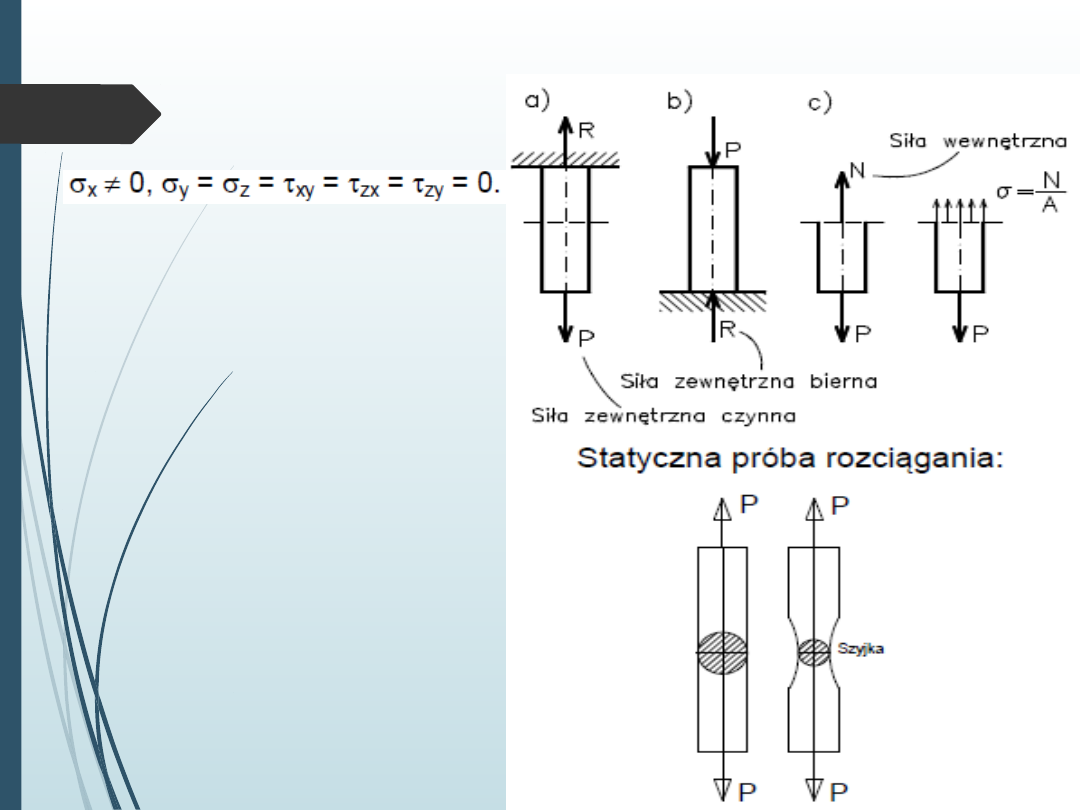
Jednoosiowe rozciąganie

Jednoosiowemu

rozciąganiu towarzyszy

trójwymiarowy stan

odkształceń – stąd

można wyjaśnić

powstawanie szyjki w

rozciąganej próbce po
przekroczeniu granicy

plastyczności

Literatura:

1. Bodnar A.: „Wytrzymałość materiałów”, Wydawnictwo

Politechniki Krakowskiej im. Tadeusza Kościuszki,
Kraków 2003

2. Piechnik S.: „Wytrzymałość materiałów”, Wydawnictwo

Politechniki Krakowskiej im. Tadeusza Kościuszki,
Kraków 2001

3. Ostwald M.: „Podstawy mechaniki” e-Skrypt Politechniki

Poznańskiej, Poznań 2013