4. ELEMENTY PŁASKIEGO STANU NAPRĘŻEŃ I ODKSZTAŁCEŃ

1

4.



4. ELEMENTY PŁASKIEGO STANU NAPRĘŻEŃ I ODKSZTAŁCEŃ

4.1. Elementy trójkątne

Do opisywania dwuwymiarowego kontinuum jako jeden z pierwszych elementów zastosowano

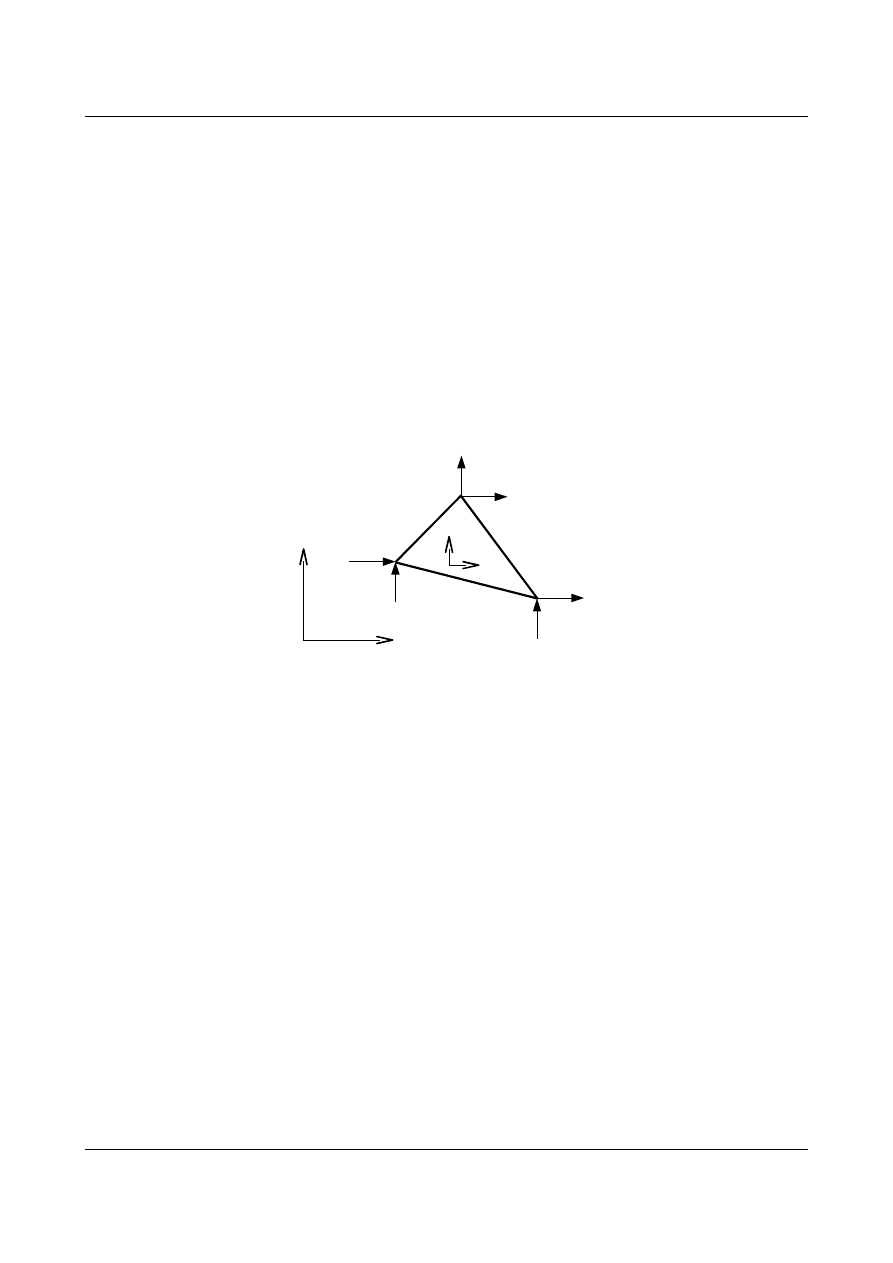
element trójkątny nazywany skrótem CST (Constant Strain Triangle). W elemencie tym wyróżnić możemy
trzy węzły (zobrazowane poprzez wierzchołki trójkąta), które mają po dwa translacyjne stopnie swobody.
Tak więc przemieszczenie dowolnego punktu elementu opisywać będziemy w układzie x0y za pomocą
dwóch składowych, które oznaczymy u i v. Kolejne przemieszczenia węzłowe oznaczymy przez d

1

do d

6

.

Odpowiadają one stopniom swobody oznaczonym na rysunku poniżej

Rys. 4.1. Element trójwęzłowy

Wektor przemieszczeń d, który opisuje deformację elementu, składa się z następujących składowych

d

=[d

1

, d

2

, d

3

, d

4

, d

5

, d

6

,

]

T

=[u

1

, v

2

, u

3

, v

4

, u

5

, v

6

,

]

T

(4.1)

Możemy przyjąć funkcje, które będą opisywać wielkości przemieszczeń u i v w postaci liniowo

zależnej od x i y:

u

=c

1

c

2

x

c

3

y

v

=c

4

c

5

x

c

6

y

(4.2)

W postaci macierzowej założoną aproksymację zmian wektora przemieszczeń

u

=[u , v]

T

możemy

zapisać

u

=gc

(4.3)

gdzie c jest wektorem stałych c

i

(na razie nieznanych), natomiast macierz geometryczna g ma postać

g

=

[

1 x y 0 0 0
0 0 0 1 x y

]

(4.4)

J.Gieczewski, M.Kończal, A.Krzysztoń, D.Mejbaum, N.Roszak, M.Wojciechowski, J.Wojtkowiak

AlmaMater

i

k

i

j

x

y

v

jk

v

ij

v

ik

u

v

d

1

d

2

d

3

d

4

d

5

d

6

4. ELEMENTY PŁASKIEGO STANU NAPRĘŻEŃ I ODKSZTAŁCEŃ

2

Jeśli podstawimy warunki brzegowe, to znaczy porównamy przemieszczenia u i v odpowiednio do

przemieszczeń węzłów w punktach i, j, k otrzymamy macierz h postaci:

h

=

[

g

i

g

j

g

k

]

=

[

1 x

i

y

i

0 0 0

0 0 0 1 x

i

y

i

1 x

j

y

j

0 0 0

0 0 0 1 x

j

y

j

1 x

k

y

k

0 0 0

0 0 0 1 x

k

y

k

]

(4.5)

która spełnia poniższe równanie macierzowe:

d

=hc

(4.6)

Z równania tego wyznaczamy wartości stałych c

i

przez znalezienie macierzy odwrotnej

h

−1

:

h

−1

=

1

2 A

ijk

[

x

j

y

k

−x

k

y

j

0

x

k

y

i

−x

i

y

k

0

x

i

y

j

−x

j

y

i

0

−y

jk

0

−y

kj

0

−y

ij

0

x

jk

0

x

kj

0

x

ij

0

0

x

j

y

k

−x

k

y

j

0

x

k

y

i

−x

i

y

k

0

x

i

y

j

−x

j

y

i

0

−y

jk

0

−y

ki

0

−y

ij

0

x

jk

0

x

ki

0

x

ij

]

(4.7)

Wpływ jednostkowego przemieszczenia w węzłach na przemieszczenia wszystkich punktów na

obszarze elementu

x

ij

=x

j

−x

i

y

ki

= y

i

− y

k

(4.8)

Funkcja kształtu jest funkcją liniową.

2 A

ijk

=∣podwójne pole powierzchni trójkąta∣=det

[

1 x

i

y

i

1 x

j

y

j

1 x

k

y

k

]

=x

ij

y

ik

−x

ik

y

ij

(4.9)

Macierz funkcji kształtu ma więc postać:

N

=gh

−1

=

[

N

1

0

N

2

0

N

3

0

0

N

1

0

N

2

0

N

3

]

(4.10)

J.Gieczewski, M.Kończal, A.Krzysztoń, D.Mejbaum, N.Roszak, M.Wojciechowski, J.Wojtkowiak

AlmaMater

4. ELEMENTY PŁASKIEGO STANU NAPRĘŻEŃ I ODKSZTAŁCEŃ

3

gdzie odpowiednie funkcje wyrażają się następującymi wzorami

N

1

=

1

2 A

ijk



x

j

y

k

−x

k

y

j

− y

jk

x

x

jk

y



(4.11)

N

2

=

1

2 A

ijk



x

k

y

i

−x

i

y

k

− y

ki

x

x

ki

y



(4.12)

N

3

=

1

2 A

ijk



x

i

y

j

−x

j

y

i

− y

ij

x

x

ij

y



(4.13)

Zależność pomiędzy przemieszczeniami węzłów d a odkształceniami elementu otrzymamy wykonując

działanie pokazane poniżej

B

=L N =

[

∂

∂ x

0

0

∂

∂ y

∂

∂ y

∂

∂ x

]

N

=

1

2 A

ijk

[

−y

jk

0

−y

ki

0

−y

ij

0

0

x

jk

0

x

ki

0

x

ij

x

jk

−y

jk

x

ki

−y

ki

x

ij

−y

ij

]

(4.14)

=Bd

(4.15)

Jeśli założymy, że mamy do czynienia z materiałem izotropowym możemy macierz konstytutywną

zapisać

D

=

E

1e

2

[

e

1

 0

 e

1

0

0

0 e

3

]

(4.16)

Gdzie przyjęte stałe

e

i

są równe:

➔

dla płaskiego stanu naprężenia

e

1

=1

e

2

=1−

e

3

=

e

2

2

(4.17)

➔

dla płaskiego stanu odkształcenia

J.Gieczewski, M.Kończal, A.Krzysztoń, D.Mejbaum, N.Roszak, M.Wojciechowski, J.Wojtkowiak

AlmaMater

4. ELEMENTY PŁASKIEGO STANU NAPRĘŻEŃ I ODKSZTAŁCEŃ

4

e

1

=1−

e

2

=1−2

e

3

=

e

2

2

(4.18)

Macierz sztywności elementu CST

K

=

∫

V

B

T

DB dV

=B

T

DBA

ijk

t

=K

1

K

2

(4.19)

gdzie przez t oznaczono grubość elementu, zaś macierze K

1

i K

2

zawierają wyrazy wywodzące się

odpowiednio tylko z odkształceń normalnych i ścinających:

K

1

=e

4

[

e

1

y

jk

2











− x

jk

y

jk

e

1

x

jk

2









e

1

y

ki

y

jk

− x

jk

y

ki

e

1

y

ki

2







− x

ki

y

jk

e

1

x

ki

x

jk

− x

ki

y

ki

e

1

x

ki

2





e

1

y

ij

y

jk

− x

jk

y

ij

e

1

y

ij

y

ki

− x

ki

y

ij

e

1

y

ij

2



− x

ij

y

jk

e

1

x

ij

x

jk

− x

ij

y

ki

e

1

x

ij

x

ki

− x

ij

y

ij

e

1

x

ij

2

]

(4.20)

K

2

=e

4

[

x

jk

2











−x

jk

y

jk

y

jk

2









x

ki

x

jk

−x

ki

y

jk

x

ki

2







−x

jk

y

ki

y

ki

y

jk

−x

ki

y

ki

y

ki

2





x

ij

x

jk

−x

ij

y

jk

x

ij

x

ki

−x

ij

y

ki

x

ij

2



−x

jk

y

ij

y

ij

y

jk

−x

ki

y

ij

y

ij

y

ki

−x

ij

y

ij

y

ij

2

]

(4.21)

Powyższe macierze są macierzami symetrycznymi .

We wzorach na K

1

i K

2

wzorach przyjęto następujące oznaczenia

e

4

=

Et

4 A

ijk

1e

2

[

e

1

 0

 e

1

0

0

0 e

3

]

e

5

=e

4

=e

3

(4.22)

4.2. Element skończony trójkątny sześciowęzłowy

J.Gieczewski, M.Kończal, A.Krzysztoń, D.Mejbaum, N.Roszak, M.Wojciechowski, J.Wojtkowiak

AlmaMater

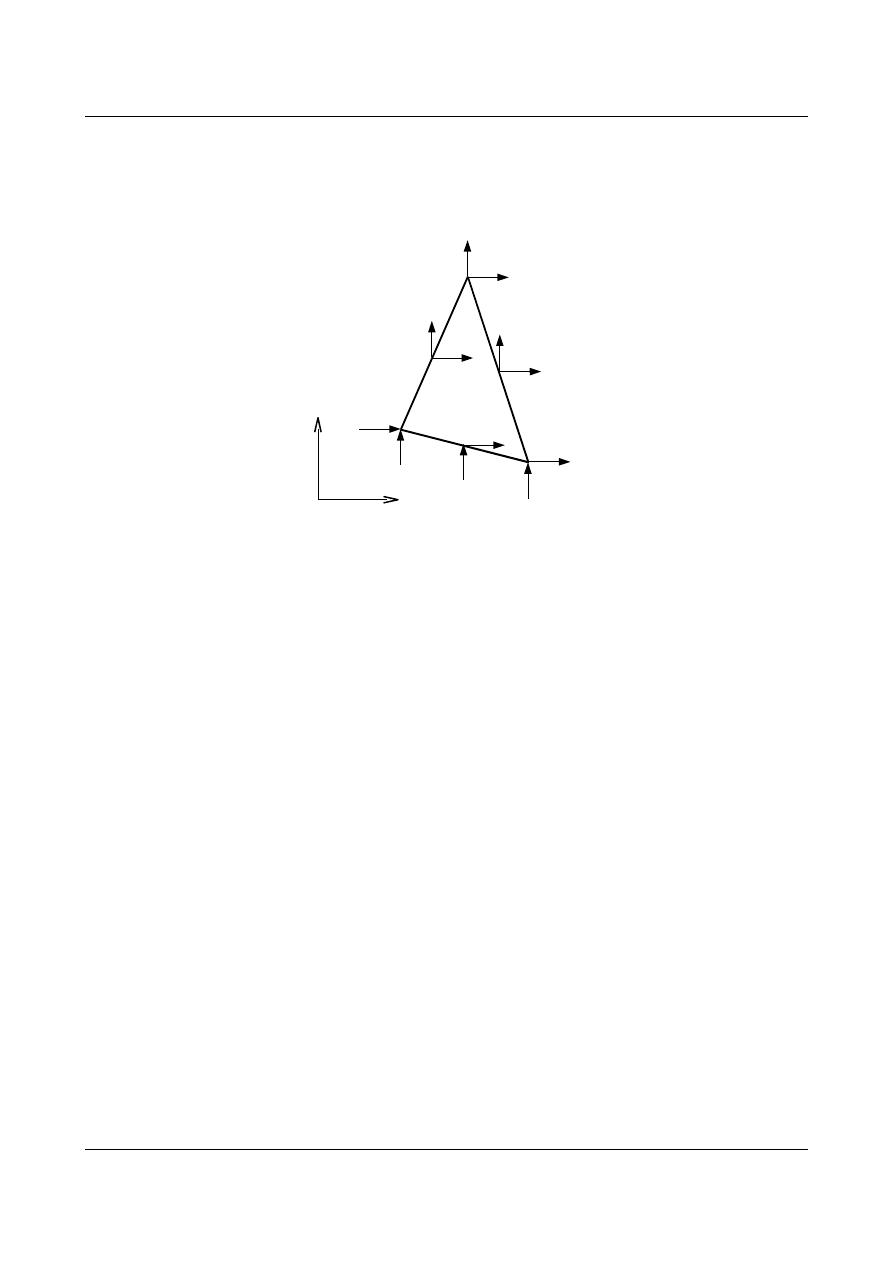
4. ELEMENTY PŁASKIEGO STANU NAPRĘŻEŃ I ODKSZTAŁCEŃ

5

Do analizy płaskich stanów naprężenia i odkształcenia możemy posłużyć się również

sześciowęzłowym elementem trójkątnym, który w literaturze jest w skrócie nazywany LST (Linear Strain
Triangle). Element ten przedstawia poniższy rysunek:

Rys. 4.2. Element sześciowęzłowy

Wektor przemieszczeń węzłowy możemy zapisać jako

d

=

[

u

1

u

2

u

3

u

4

u

5

u

6

v

1

v

2

v

3

v

4

v

5

v

6

]

T

(4.23)

Wektor przemieszczenia dowolnego punktu elementu określony jest przy pomocy dwóch składowych:

u=

[

u v

]

T

. Natomiast aproksymację każdej ze składowych przyjmuje się w postaci

u

=c

1

c

2

x

c

3

y

c

4

x

2

c

5

xy

c

6

y

2

v

=c

7

c

8

x

c

9

y

c

10

x

2

c

11

xy

c

12

y

2

(4.24)

Wektor odkształcenia możemy wyrazić jako funkcję przemieszczeń węzłów

=

[



x



y



xy

]

=

[

B

x

0

0

B

y

B

y

B

x

]

=

[

u

v

]

=Bd

(4.25)

Poszczególne wektory można zapisać następująco



x

=

[



x1



x2



x3

]



y

=

[



y1



y2



y3

]



xy

=

[



xy1



xy2



xy3

]

(4.26)

Zastosowane macierze B

i

wyrazić można jako

J.Gieczewski, M.Kończal, A.Krzysztoń, D.Mejbaum, N.Roszak, M.Wojciechowski, J.Wojtkowiak

AlmaMater

1

2

x

y

u

1

v

1

u

2

v

2

u

3

v

3

u

6

v

6

u

5

v

5

u

4

v

4

4

6

3

5

4. ELEMENTY PŁASKIEGO STANU NAPRĘŻEŃ I ODKSZTAŁCEŃ

6

B

x

=

1

2 A

[

3 y

32

−y

13

−y

21

4 y

13

0

4 y

21

−y

32

3 y

13

−y

21

4 y

32

4 y

21

0

−y

32

−y

13

3 y

21

0

4 y

13

4 y

32

]

(4.27)

B

y

=

1

2 A

[

3 x

23

−x

31

−x

12

4 x

31

0

4 x

12

−x

23

3 x

31

−x

12

4 x

23

4 x

12

0

−x

23

−x

31

3 x

12

0

4 x

31

4 x

23

]

(4.28)

4.3. Kondensacja statyczna

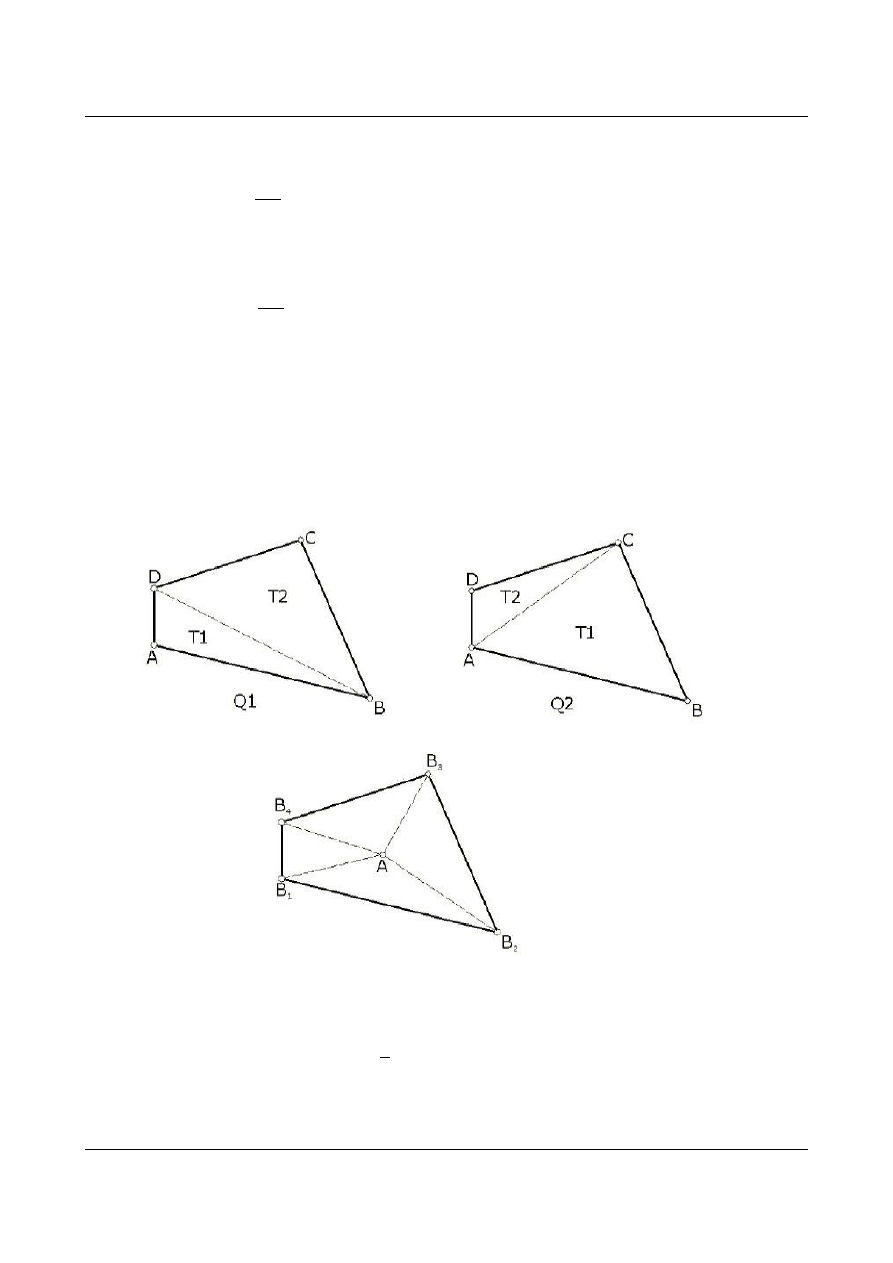
Kondensacja statyczna polega na tworzeniu elementu czterokątnego z elementów trójkątnych

(suma dwóch trójkątnych).

K

Qi

=K

T

1

K

T

2

i

=1 , 2

(4.29)

K

0

=

1
2

[ K

Q

1

K

Q

2

]

(4.30)

J.Gieczewski, M.Kończal, A.Krzysztoń, D.Mejbaum, N.Roszak, M.Wojciechowski, J.Wojtkowiak

AlmaMater

4. ELEMENTY PŁASKIEGO STANU NAPRĘŻEŃ I ODKSZTAŁCEŃ

7

[

K

AA

K

AB

K

BA

K

BB

]

⋅

[

d

A

d

B

]

=

[

p

A

p

B

]

(4.31)

K

AA

⋅d

A

K

AB

⋅d

B

= p

A

K

BA

⋅d

A

K

BB

⋅d

B

= p

B

(4.32)

Po odpowiednich przekształceniach doprowadzamy wzory do postaci

K

BA

⋅K

AA

−1

⋅ p

A

−K

AB

⋅d

B

K

BB

⋅d

B

= p

B

K

BB

−K

BA

⋅K

AA

−1

⋅K

AB

⋅d

B

= p

B

−K

BA

⋅K

AA

−1

⋅p

A

(4.33)

co skracamy do postaci

K

BB

✶

⋅d

B

= p

B

✶

(4.34)

Dokładność macierzy sztywności zależy od dyskretyzacji, otrzymujemy wynik przybliżony.

Tylko wtedy gdy obciążenia przyłożymy w węzłach, funkcja kształtu trzeciego stopnia

v

 x=a

1

a

2

x

a

3

x

2

a

4

x

3

(4.35)

Jest prawdziwą i dokładną funkcją rozwiązującą dane równanie różniczkowe. Funkcja momentów na

danym odcinku jest liniowa.

d

2

w

d x

2

=±

M

x

EI

(4.36)

Kondensacja statyczna polega na dodaniu do siebie prostych elementów po to aby tworzyć bardziej

złożone. Składanie czworokąta z trójkątów to dodanie odpowiednich sztywności.(RYSUNKI). Dochodzenie
do macierzy sztywności elementu czworokątnego może odbywać się w różny sposób. Element czworokątny
o węzłach 1,2,3,4 można złożyć z dwóch trójkątów 4,1,2 i 4,3,2 lub 1,4,3 i 1,2,3.

J.Gieczewski, M.Kończal, A.Krzysztoń, D.Mejbaum, N.Roszak, M.Wojciechowski, J.Wojtkowiak

AlmaMater