-

1

-

VII. ANALIZA STANU NAPRĘŻENIA METODĄ ELASTO-

OPTYCZNĄ

1. CELE ĆWICZENIA

1) Zapoznanie się z budową polaryskopu elastooptycznego.

2) Zapoznanie się z elastooptyczną metodą badań modelowych na przykładzie modelu płasko-

wnika poddanego rozciąganiu.

3) Określenie elastooptycznej stałej modelowej.

4) Określenie naprężeń krawędziowych w przekroju pręta osłabionego otworem.

5) Określenie współczynnika kształtu

2. WPROWADZENIE DO ĆWICZENIA

Do jednej z doświadczalnych metod analizy stanu naprężenia należy metoda elastooptyczna.

Metoda ta oparta jest na pewnych zjawiskach optycznych zachodzących w niektórych ciałach

przeźroczystych, takich jak: szkło, żywice poliestrowe, itp., które wykazują dwójłomność wy-

muszoną.

Z ciała wykazującego te własności wykonuje się model badanego elementu, poddaje obcią-

żeniu a następnie na podstawie odpowiednich praw wnioskuje się o stanie naprężenia

w rzeczywistym elemencie konstrukcji.

Prześwietlając przeźroczysty i obciążony model wiązką światła spolaryzowanego na ekranie po-

laryskopu otrzymamy obraz modelu pokryty układem jasnych i ciemnych prążków. Znajomość

rozkładu tych prążków pozwala na określenie stanu naprężenia powstałego w modelu. Przy

określaniu pola naprężeń metodami optycznymi traktujemy światło jako falę poprzeczną o okre-

ślonej długości i określonej częstotliwości.

-

2

-

3. PODSTAWY TEORETYCZNE

3.1. Zasady elastooptycznych pomiarów naprężeń

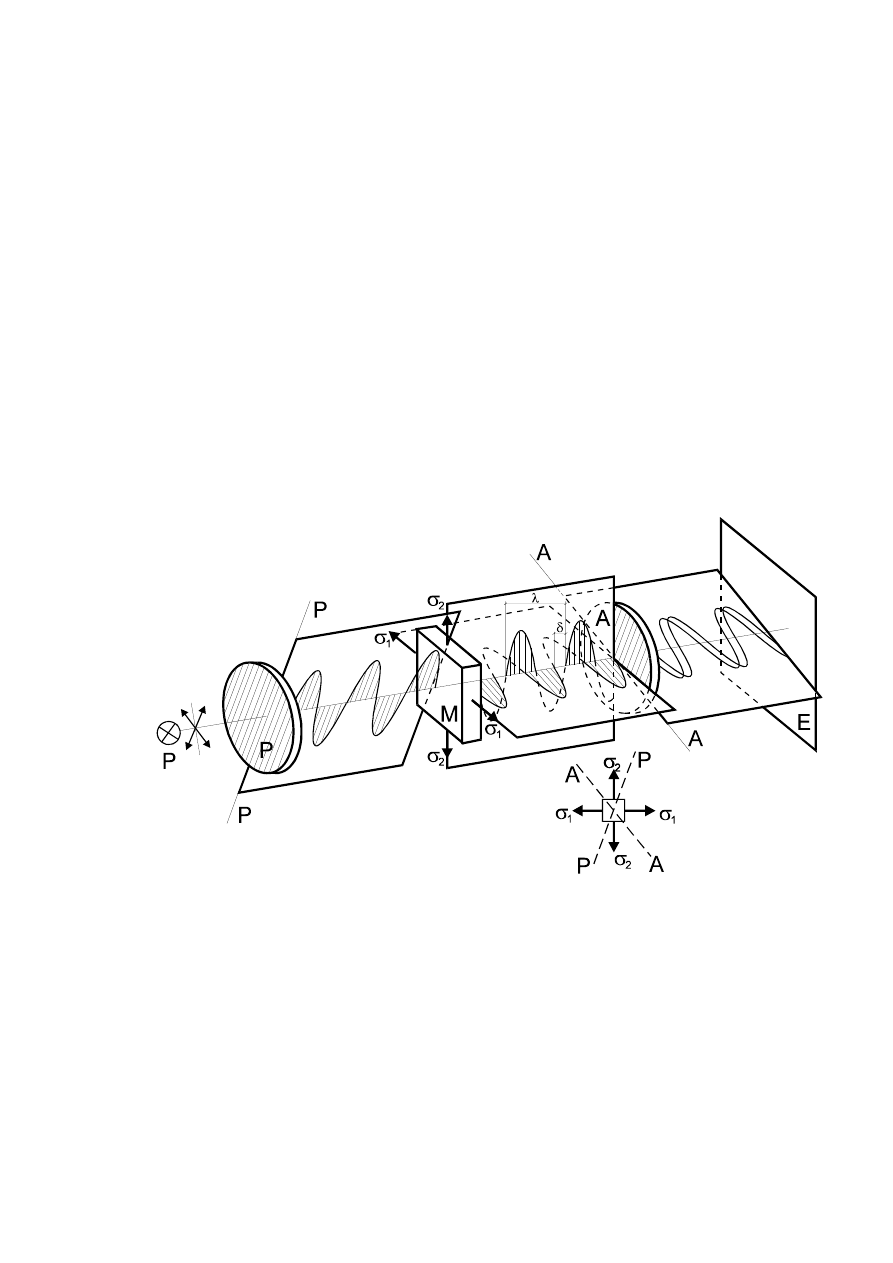
Nieuporządkowane drgania promieni świetlnych wychodzących ze źródła światła Z po

przejściu przez polaryzator zostają sprowadzone do jednej płaszczyzny tzw. płaszczyzny polary-

zacji. Spolaryzowana wiązka światła pada następnie na model M ustawiony prostopadle do kie-

runku biegu promieni i rozszczepia się w każdym punkcie modelu na dwa spolaryzowane pro-

mienie składowe.

Płaszczyzny drgań tych promieni są do siebie prostopadle i zgodne z kierunkami naprężeń

głównych s

1

i s

2

w danym punkcie modelu. Promienie składowe przebiegają przez model

z różnymi prędkościami V

1

i V

2

, co w wyniku daje ich przesunięcie liniowe d, które zachowują

po opuszczeniu płytki modelowej, biegnąc z jednakową prędkością V (rys. 3.1).

Doświadczalnie wykazano, że różnica prędkości rozszczepionych promieni spolaryzowanej

wiązki światła jest proporcjonalna do różnicy naprężeń głównych w danym punkcie modelu.

1

2

1

2

V - V = C(

-

)

σ

σ

(1)

a odpowiadające przesunięcie liniowe d wzrasta z grubością g modelu:

δ

σ

σ

= Cg(

-

)

1

2

(2)

Rys. 3.1

-

3

-

gdzie: C - stała elastooptyczna materiału modelu [cm/N]

g - grubość ścianki modelu [cm]

Przesunięcie liniowe promieni świetlnych wyraża się najczęściej wielokrotnością m długości fali

świetlnej l:

δ

λ

= m

(3)

Podstawiając związek (3) do (2) otrzymujemy podstawowe równanie elastooptyki:

m = C

g

(

-

)

1

2

λ σ

σ

(4)

lub:

1

2

g

-

= m k

σ

σ

(5)

gdzie:

kg =

gc

λ

(6)

nazywamy elastooptyczną stałą modelową (6)

m - rząd izochromy.

Jeśli teraz wychodzące z danego punktu modelu wiązki promieni świetlnych przepuścimy

przez analizator A, którego oś tworzy kąt prosty z osią polaryzatora P, to promienie składowe

zostaną sprowadzone do jednej płaszczyzny, interferując ze sobą przy zachowaniu stałego prze-

sunięcia liniowego d. Wartość tego przesunięcia nie jest jednakowa dla wszystkich punktów

modelu ze względu na różne na ogół wartości naprężeń

σ

1

i

σ

2

w różnych punktach. Ponieważ

natężenie światła opuszczającego model jest równe:

I = I

2

0

2

2

m

sin

sin

α

π

(7)

gdzie: I

0

- natężenie światła padającego na model, to na ekranie otrzymamy układ jasnych

i ciemnych prążków o jasności zależnej od przesunięcia liniowego d i kąta a nachylenia osi pola-

ryzacji do kierunku naprężenia normalnego głównego. Całkowite wygaszenie promieni (I=0) na-

stępuje wówczas, gdy jeden z kierunków naprężeń głównych pokryje się z płaszczyzną drgań

promieni spolaryzowanych, tzn., gdy α = 0, π/2, π,... lub, gdy przesunięcie liniowe d będzie
równe całkowitej wielokrotności długości fali świetlnej, czyli m = 0, 1, 2,...

Analizując obraz otrzymany na ekranie rozróżniamy dwa typowe rodzaje prążków interfe-

rencyjnych, które wyznaczają pewne wielkości charakteryzujące stan naprężenia w modelu. Je-

den rodzaj prążków określa miejsca geometryczne punktów, w których s

1

- s

2

= const. Z (7) wy-

nika, że przypadek ten zachodzi dla sin Pm = 0 czyli dla m = 0, 1, 2, .....

-

4

-

Ponieważ σ

1

- σ

2

= 2τ

max

, to prążki te są miejscami geometrycznymi punktów

o jednakowych wartościach naprężeń stycznych. Dla światła monochromatycznego prążki te

stanowią ciemne linie, natomiast w świetle białym są liniami o jednakowej barwie, stąd pocho-

dzi ich nazwa - izochromy.

Drugi rodzaj prążków interferencyjnych, zwanych izoklinami, określa miejsca geometrycz-

ne tych punktów modelu, w których kierunki naprężeń głównych pokrywają się z osiami anali-

zatora i polaryzatora. Ze wzoru (7) wynika, że przypadek ten występuje gdy sin 2

α = 0, czyli α

= n

π/2; dla n = 0, 1, 2, ...

Kąt, jaki tworzy oś optyczna polaryzatora z osią układu odniesienia nazywamy parametrem

izokliny.

Aby znaleźć kierunki naprężeń głównych w każdym punkcie modelu należy rejestrować i z o k l

i n y zmieniając każdorazowo p a r a m e t r i z o k l i n y w granicach od 0° - 90°.

Biorąc pod uwagę, że Pm nie zależy od kąta a, jednoczesny obrót polaryzatora i analizatora

nie powoduje zmiany położenia izochrom, a jedynie przemieszczenie i z o k l i n. Przy świetle

białym, na tle barwnych izochrom, izokliny są widoczne, jako ciemne linie, ponieważ wygasza-

nie promienia świetlnego zależy tylko od orientacji kierunków głównych. Znajomość izoklin

pozwala wykreślić trajektorie naprężeń głównych, czyli linie wzajemnie ortogonalne mające

tę własność, że styczne do nich w dowolnym punkcie wyznaczają kierunki naprężeń głównych.

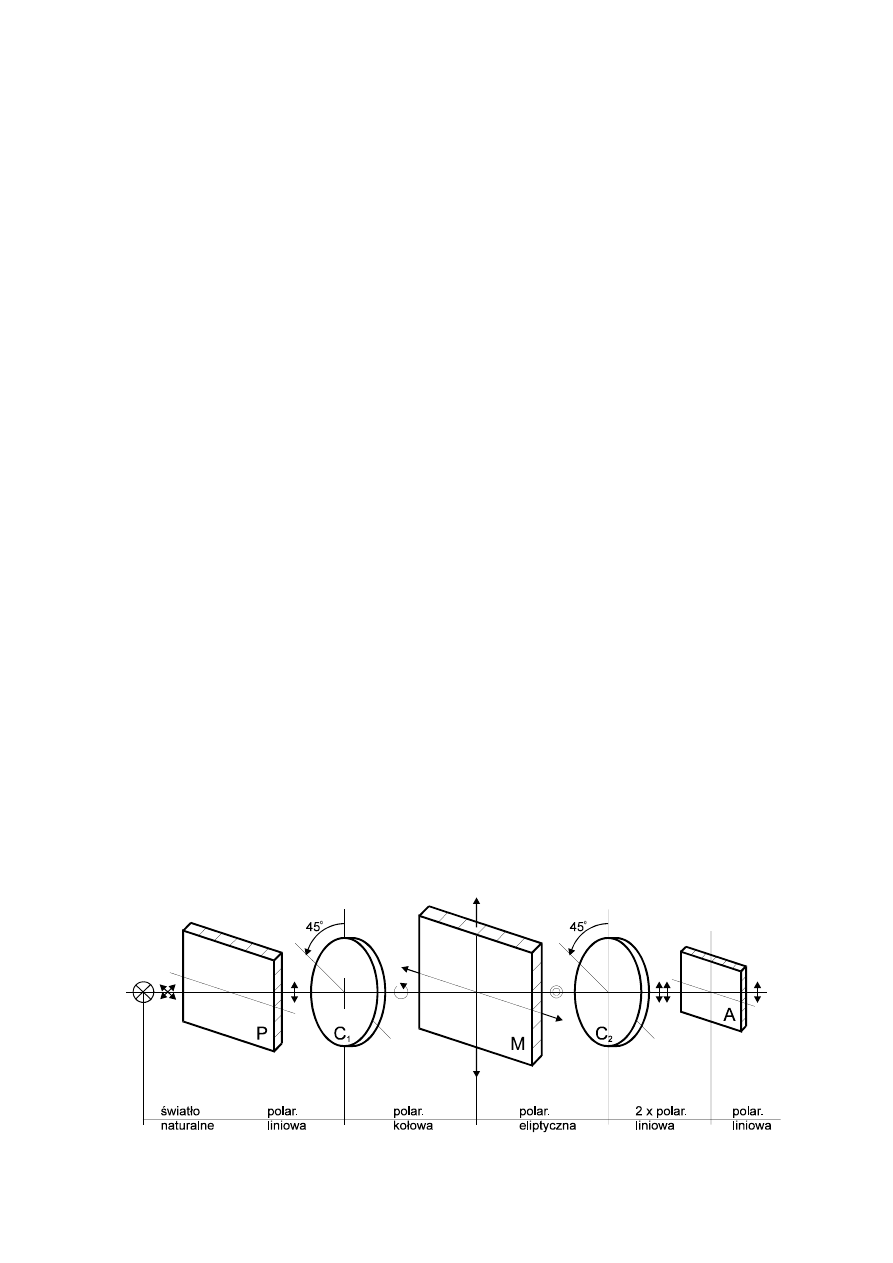
3.2. Polaryzacja kołowa

Opisana poprzednio polaryzacja świetlna, polegająca na sprowadzeniu drgań promieni

świetlnych do jednej płaszczyzny, nosi nazwę polaryzacji liniowej.

Przez wprowadzenie do układu optycznego polaryskopu ćwierćfalówek C

1

i C

2

, uzyskujemy

Rys. 3.2

-

5

-

światło spolaryzowane kołowo, nie mające uprzywilejowanego kierunku (płaszczyzny) drgań

(rys. 3.2). W przypadku polaryzacji kołowej drgania promienia świetlnego zachodzą w dwóch

wzajemnie prostopadłych płaszczyznach. Amplitudy drgań są jednakowe. Jeżeli amplitudy

drgań są różne to mamy do czynienia z polaryzacją eliptyczną.

Promień świetlny liniowo spolaryzowany po przejściu przez ćwierćfalówkę C

1

zostaje roz-

szczepiony na dwa promienie drgające w dwóch prostopadłych płaszczyznach. Po przejściu

przez model M promienie świetlne zostają spolaryzowane eliptycznie.

Ponieważ drgania eliptyczne można przedstawić w postaci sumy dwóch drgań spolaryzowa-

nych kołowo, otrzymujemy po przepuszczeniu promieni przez następną ćwierćfalówkę C

2

,

drgania spolaryzowane liniowo w dwóch prostopadłych do siebie kierunkach.

Ustawiony odpowiednio analizator A sprowadzi te drgania do jednej płaszczyzny

i w efekcie otrzymujemy polaryzację liniową. Ten rodzaj polaryzacji powoduje znikanie we

wzorze (7) czynnika sin

2

α i na ekranie widać tylko obraz izochrom.

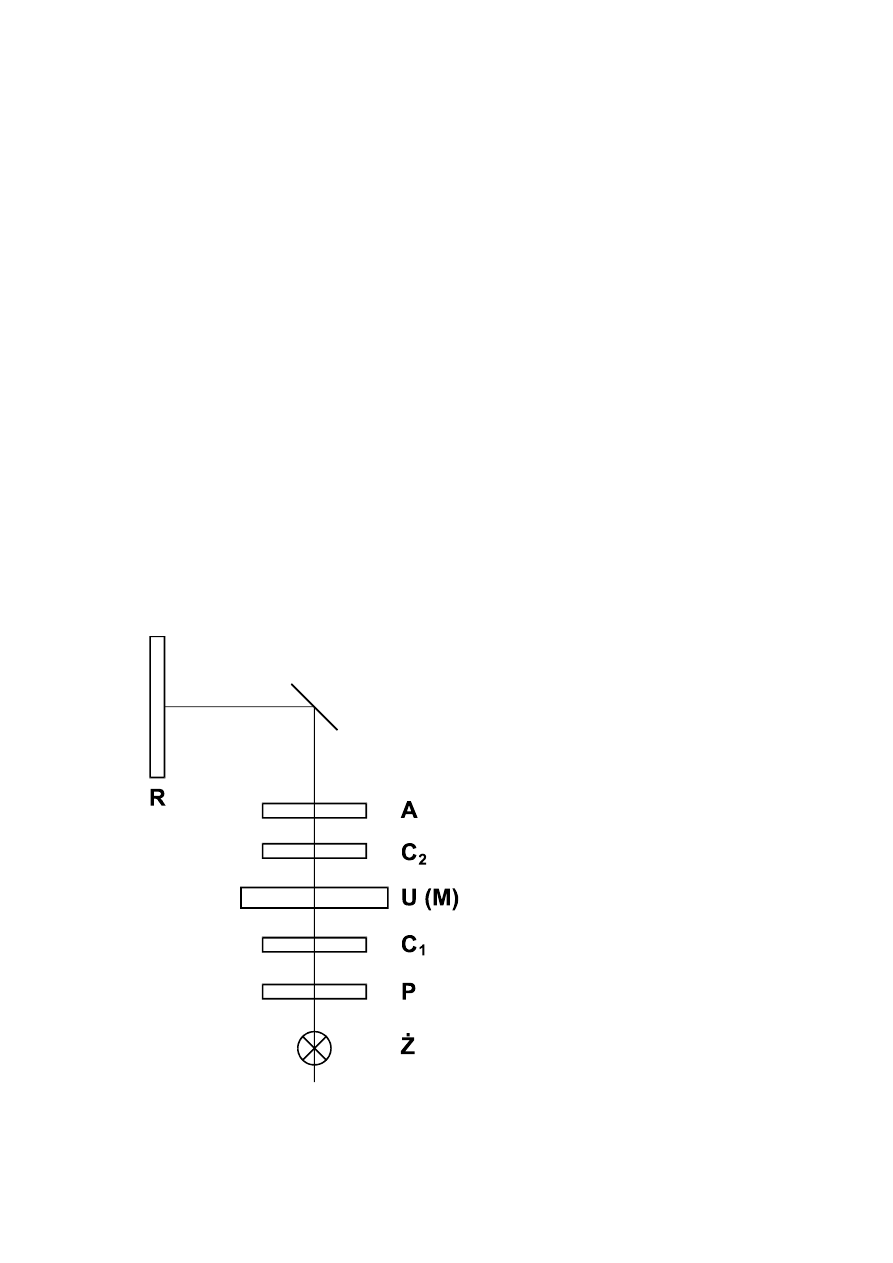
3.3. Aparatura pomiarowa

Polaryskop optyczny zastosowany w ćwi-

czeniu działa z wykorzystaniem źródła światła

zainstalowanego w rzutniku pisma. Zestaw

optyczny nakładany jest na stolik rzutnika.

Zasadniczymi częściami polaryskopu ela-

stooptycznego przedstawionego na rys. 3.3.

są:

- układ optyczny

- urządzenie obciążające

- zespół rejestrujący

W skład układu optycznego wchodzą:

- źródło światła Z

- polaryzator P

- ćwierćfalówki C

1

i C

2

- analizator A

Zespół rejestrujący R stanowi tu ekran, na

którym można obserwować izochromy

Rys. 3.3

-

6

-

i izokliny. Istnieje możliwość kreślenia tych linii przy pomocy ołówka na kalce.

Urządzenie obciążające U ma zapewnić realizację wymaganych warunków zamocowania

i obciążenia badanego modelu.

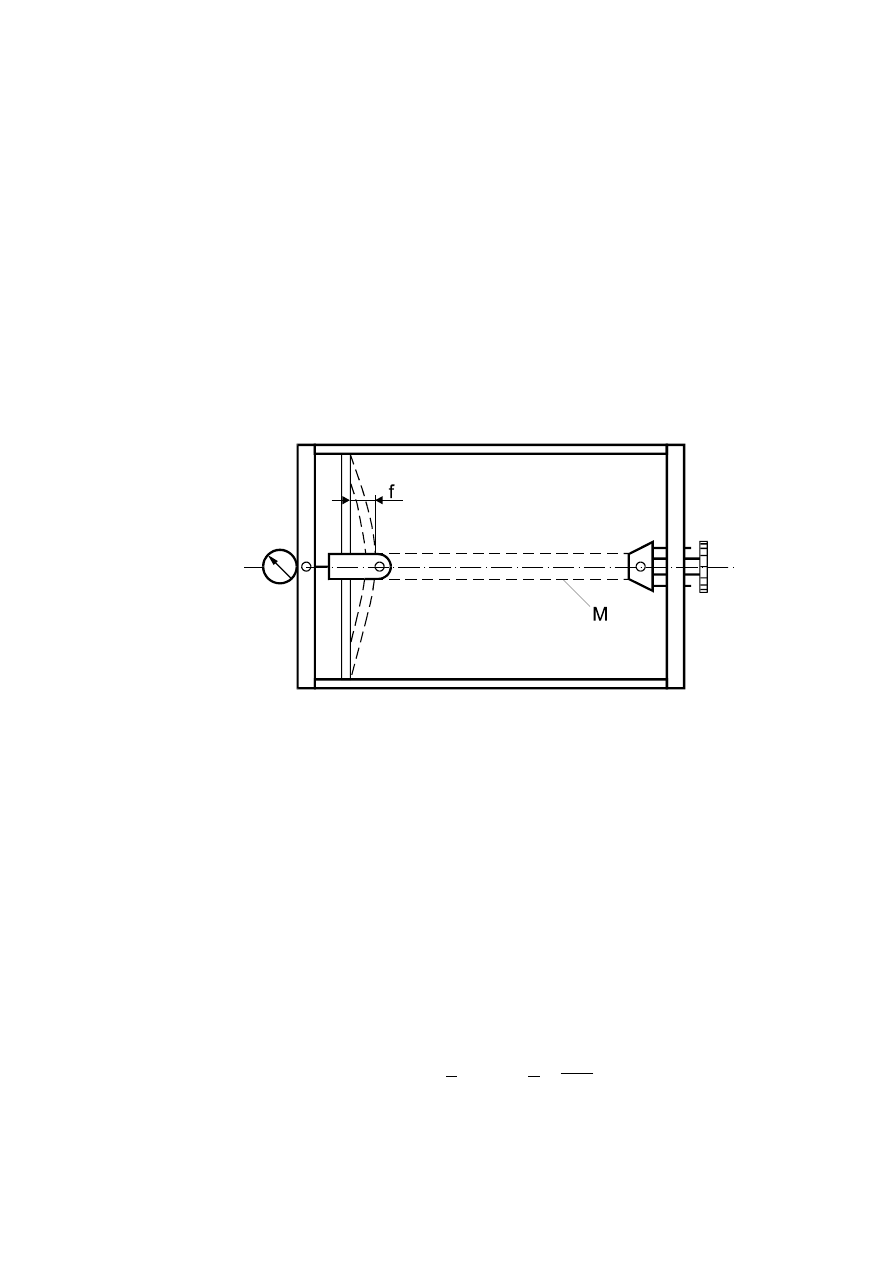
3.4. Badanie stanu naprężenia w płaskowniku poddanym rozciąganiu

Badany pręt mocowany jest dwoma końcami w uchwytach (Rys. 3.4). Jeden z nich połączo-

ny jest ze śrubą, przez pokręcenie której wywołujemy rozciąganie pręta. Drugi uchwyt połączo-

ny jest ze środkiem małej stalowej beleczki pełniącej tu rolę siłomierza. Siła rozciągająca bada-

ny pręt powoduje zginanie belki, a jej strzałkę ugięcia (f) rejestruje czujnik.

3.4.1. Wyznaczanie elastooptycznej stałej modelowej

Elastooptyczną stałą modelową wyznaczamy z podstawowego równania elastooptyki:

1

2

g

-

= m k

σ

σ

(8)

poddając rozciąganiu pręt o stałym przekroju. W pręcie tym, w każdym jego punkcie, zgodnie z

teorią pręta rozciąganego wystąpią jednakowe naprężenia σ

1

(σ

2

= 0), co da na ekranie obraz

izochrom, jako jednobarwny obszar wypełniający cały kontur pręta. Zwiększając siłę rozciągają-

cą powodować będziemy wzrost rzędu izochromy m. Kolejne jednolite barwy wystąpią przy m

= 1, 2, 3,... Dla kolejnych wartości m określamy stałą modelową k

gi

, a następnie:

g

i=1

n

gi

i=1

n

i

i

k =

1
n

k =

1
n

P

Am

Σ

Σ

(9)

Rys. 3.4

-

7

-

gdzie:

i

1i

P

A

=

σ

Wyznaczona wartość stałej modelowej jest taka sama dla wszystkich modeli pręta rozciąganego,

wykonanych z tego samego materiału i posiadających tę samą grubość. Mając elastooptyczną

stałą modelową k

g

, możemy wyznaczyć elastooptyczną stałą materiałową: k = k g

g

3.4.2. Wyznaczanie naprężeń na brzegu otworu i na krawędzi pręta

Na swobodnym brzegu otworu, jak też na zewnętrznej krawędzi pręta jedno z naprężeń

głównych jest równe zeru. Gdy przy danym obciążeniu w jednym z punktów na swobodnym

brzegu rząd izochromy wynosi m oraz σ

2

= 0, wówczas naprężenie σ

1

wyniesie:

1

p

g

= m k

σ

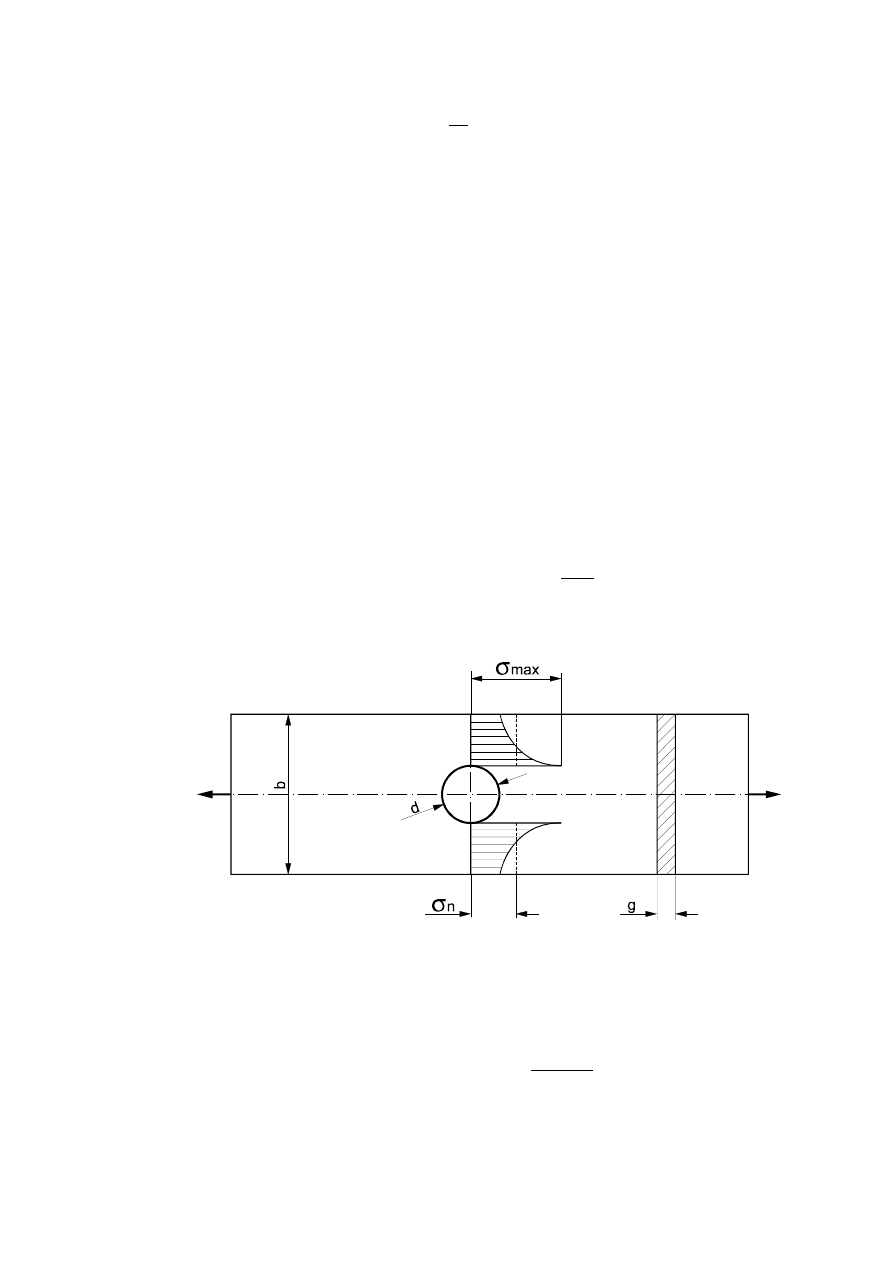
3.4.3. Wyznaczanie współczynnika kształtu dla przekroju pręta osłabionego otworem ko-

łowym

Współczynnik kształtu wyraża stosunek maksymalnych naprężeń w danym przekroju do

naprężeń

nominalnych:

k

n

=

α

σ

σ

max

Naprężenia nominalne są to naprężenia w przekroju osłabionym, określone jako iloraz siły i

pola powierzchni pozostałej części przekroju.

n

=

P

(b - d)g

σ

Naprężenia maksymalne określamy oczywiście z podstawowego równania elastooptyki.

Rys. 3.5

-

8

-

4. PRZEBIEG ĆWICZENIA

Kolejność czynności przy przeprowadzaniu ćwiczenia:

1) włączyć źródło światła,

2) ustawić plaryzator i analizator tak, aby osie ich były ze sobą skrzyżowane,

3) ustawić ćwierćfalówki - mają tworzyć z osiami polaryzatora i analizatora kąty 45

°

,

4) zamocować model w urządzeniu obciążającym,

5) stopniowo obciążać model,

6) odrysować z ekranu obraz izochrom,

7) wyłączyć prąd,

8) zmierzyć niezbędne do obliczeń wielkości.

Ćwiczenie przeprowadzić dla pełnego płaskownika (bez otworu) oraz dla płaskowników z

otworami o różnych wielkościach.

Porównać otrzymane wyniki.

5. OPRACOWANIE WYNIKÓW

5.1. Wytyczne do wykonania sprawozdania

W sprawozdaniu należy podać:

a) definicje izochromy i izokliny;

b) istotę polaryzacji liniowej i kołowej;

c) schemat układu pomiarowego do wyznaczania stałej modelowej;

d) rysunki izochrom z zaznaczonymi rzędami izochrom;

e) obliczenia stałej modelowej i elastooptycznej stałej materiałowej;

f) obliczenia naprężeń w zadanych punktach modelu;

g) obliczenia współczynnika kształtu;

h) porównanie otrzymanych wyników i wnioski.

-

9

-

6. PYTANIA KONTROLNE

1) jaki jest cel ćwiczenia?

2) co to jest elastooptyka? Jakie zjawisko optyczne wykorzystuje się w elastooptycznych ba-

daniach modelowych?

3) wyjaśnij znaczenie pojęć:

- izoklina,

-

dwójłomnść wymuszona,

-

izochroma,

- polaryzacja liniowa,

- polaryzacja kołowa.

4) co to jest rząd izokliny i rząd izochromy?

5) podać zależności pomiędzy naprężeniami a rzędem izochromy. Omówić sposób

wyprowadzania wzoru;

6) jaka jest różnica pomiędzy elastooptyczną stałą modelową a elastooptyczną stałą materia-

łową? Omówić sposób ich wyznaczania;

7) narysować i omówić schemat polaryskopu elastooptycznego z plaryzacją liniową i kołową;

8) jak wyglądają izokliny a jak izochromy w przypadku polaryzacji liniowej i kołowej dla

światła białego i monochromatycznego?

9) jak wyznaczyć naprężenia (rozkład naprężeń) w płaskim stanie naprężenia?

10) co to jest współczynnik kształtu i jak go wyznaczamy?

7. LITERATURA

1. A. Jakubowicz, C. Orłoś: "Wytrzymałość materiałów"; PWN, Warszawa 1970.

2. S. Katarzyński, S. Kocanda, M. Zakrzewski: "Badanie własności mechanicznych metali";

PWT, Warszawa 1956.

3. J. T. Pindera: "Zarys elastooptyki"; PWT, Warszawa 1953.

-

10

-

Politechnika Śląska

w Gliwicach

Wydział Mechaniczny Technologiczny

Katedra Wytrzymałości Materiałów i Metod Komputerowych

Mechaniki

Laboratorium Wytrzymałości Materiałów

Protokół z ćwiczenia Nr 7

Temat: ANALIZA STANU NAPRĘŻENIA METODĄ
ELASTOOPTYCZNĄ

Rok akademicki: . . . . . . . . . . ., Data wyk. ćwicz.: . . . . . . . . . ., Grupa: . . . . . . .

Prowadzący: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . , podpis . . . . . . . . . . . . . . . .

Studenci:

1. . . . . . . . . . . . . . . . . . . . . . . . . . ., Ocena: . . . . . . . . . . . . ,

2. . . . . . . . . . . . . . . . . . . . . . . . . . ., Ocena: . . . . . . . . . . . . ,

3. . . . . . . . . . . . . . . . . . . . . . . . . . ., Ocena: . . . . . . . . . . . . ,

4. . . . . . . . . . . . . . . . . . . . . . . . . . ., Ocena: . . . . . . . . . . . . ,

5. . . . . . . . . . . . . . . . . . . . . . . . . . ., Ocena: . . . . . . . . . . . . ,

6. . . . . . . . . . . . . . . . . . . . . . . . . . ., Ocena: . . . . . . . . . . . . ,

7. . . . . . . . . . . . . . . . . . . . . . . . . . ., Ocena: . . . . . . . . . . . . ,

8. . . . . . . . . . . . . . . . . . . . . . . . . . ., Ocena: . . . . . . . . . . . . ,

9. . . . . . . . . . . . . . . . . . . . . . . . . . ., Ocena: . . . . . . . . . . . . ,

10 . . . . . . . . . . . . . . . . . . . . . . . . . ., Ocena: . . . . . . . . . . . . ,

11. . . . . . . . . . . . . . . . . . . . . . . . . ., Ocena: . . . . . . . . . . . . ,

12. . . . . . . . . . . . . . . . . . . . . . . . . ., Ocena: . . . . . . . . . . . . ,

13 . . . . . . . . . . . . . . . . . . . . . . . . . ., Ocena: . . . . . . . . . . . . ,

14 . . . . . . . . . . . . . . . . . . . . . . . . . ., Ocena: . . . . . . . . . . . . ,

-

11

-

1. Cel ćwiczenia i opis przebiegu ćwiczenia:

. . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . .

2. Schemat układu pomiarowego

-

12

-

3. Opracowanie wyników

1)

4. Uwagi i wnioski:

. . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . .

5. Załączniki

1. Podać definicje izochromy i izokliny.

2. Podać definicję polaryzacji liniowej i kołowej.

3. Rysunki izochrom z zaznaczonymi rzędami izochrom.

4. Obliczenia stałej modelowej i elastooptycznej stałej materiałowej.

5. Obliczenia naprężeń w zadanych punktach modelu.

6. Obliczenia współczynnika kształtu.

1)

Patrz pkt. 6