A. Zaborski, Zwi zki ró niczkowe sił przekrojowych

Zwi zki ró niczkowe pomi dzy siłami przekrojowymi dla łuku

płaskiego

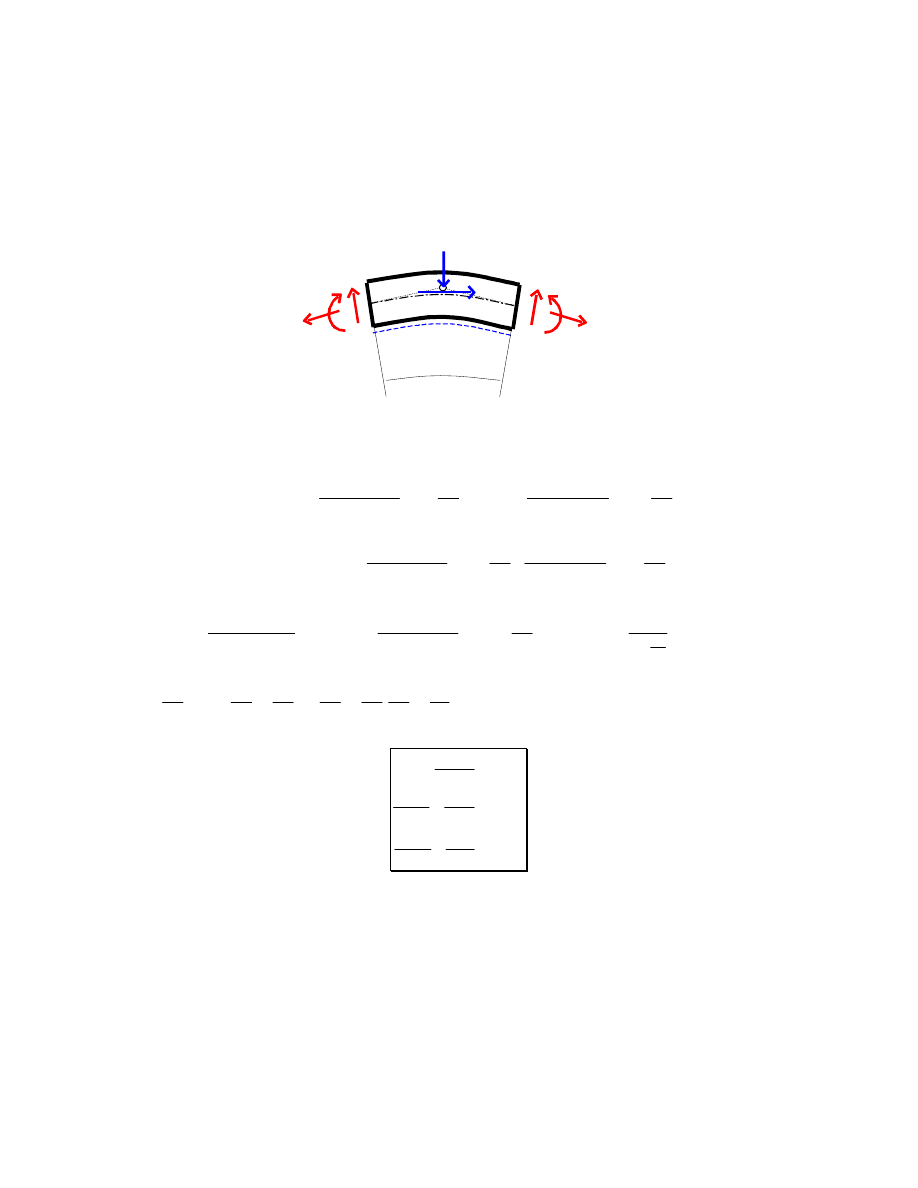
Rozpatrzmy równowag elementu o długo ci ds pr ta o osi krzywej płaskiej, obci onego

obci eniem ci głym q - normalnym do osi, oraz p - stycznym do osi. Zarówno obci enie jak

i siły przekrojowe zaznaczamy zgodnie z przyj t konwencj znakowania.

ρ

∆ϕ

A

N(s)

M(s)

Q(s)

q(s+

β∆s)∆s

p(s+

∆s)∆s

Q(s+

∆s)

M(s+

∆s)

N(s+

∆s)

Obci enia mo emy zast pi wypadkowymi, które zgodnie z tw. Lagrange’a oraz po

zaniedbaniu małych wy szego rz du przedstawia rysunek obok. Wyci ty element powinien

znajdowa si w równowadze.

Obliczaj c sum rzutów sił na pionow o symetrii, mamy:

,

0

2

sin

)

(

)

(

2

2

cos

)

(

)

(

=

∆

∆

∆

+

+

−

∆

∆

∆

+

−

∆

∆

+

−

ϕ

α

ϕ

α

β

s

ds

s

s

dN

s

N

s

ds

s

s

dQ

s

s

s

q

N

Q

dla sumy rzutów sił na o poziom :

,

0

2

cos

)

(

2

sin

)

(

)

(

2

)

(

=

∆

∆

∆

+

+

∆

∆

∆

+

+

−

∆

∆

+

ϕ

α

ϕ

α

γ

s

ds

s

s

dN

s

ds

s

s

dQ

s

Q

s

s

s

p

N

Q

a dla sumy momentów wzgl dem punktu A:

0

cos

)

(

2

tan

)

(

)

(

2

)

(

2

=

−

∆

∆

+

−

∆

∆

∆

+

+

+

∆

∆

+

−

∆

ρ

ρ

γ

ϕ

ρ

α

α

ϕ

s

s

s

p

s

ds

s

s

dQ

s

Q

s

ds

s

s

dM

Q

M

Dziel c równania przez

∆

s i uwzgl dniaj c, e dla małego k ta

∆ϕ

jest:

,

2

2

,

2

2

tan

,

2

2

sin

,

1

2

cos

ρ

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

s

∆

→

∆

∆

→

∆

∆

→

∆

→

∆

oraz e dla

∆

∆

s

f s

s

f s

→

+

→

0

(

)

( )

α

, otrzymamy ostatecznie:

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

s

p

s

Q

ds

s

dN

s

q

s

N

ds

s

dQ

s

Q

ds

s

dM

−

=

−

−

=

+

=

ρ

ρ

Pochodna momentu zginaj cego po współrz dnej łukowej jest równa sile poprzecznej (z

dokładno ci do znaku: zale nie od przyj tej konwencji znakowania). W przekroju zerowania

si siły poprzecznej moment zginaj cy osi ga warto ekstremaln .

Uwaga: Znaki w wyprowadzonych równaniach zale od przyj tej konwencji znakowania

obci e i sił przekrojowych.