Optoelektronika 

 

 

 

5 

1. Pomiar apertury numerycznej światłowodu 

1.1.  Wstęp 

W optyce geometrycznej, rozpatrując rozchodzenie się fal świetlnych przyjmuje się pew-

ne założenia upraszczające, dzięki czemu analiza wielu zjawisk jest łatwiejsza i nie wpływa 
znacząco na uzyskiwane rezultaty. 

 

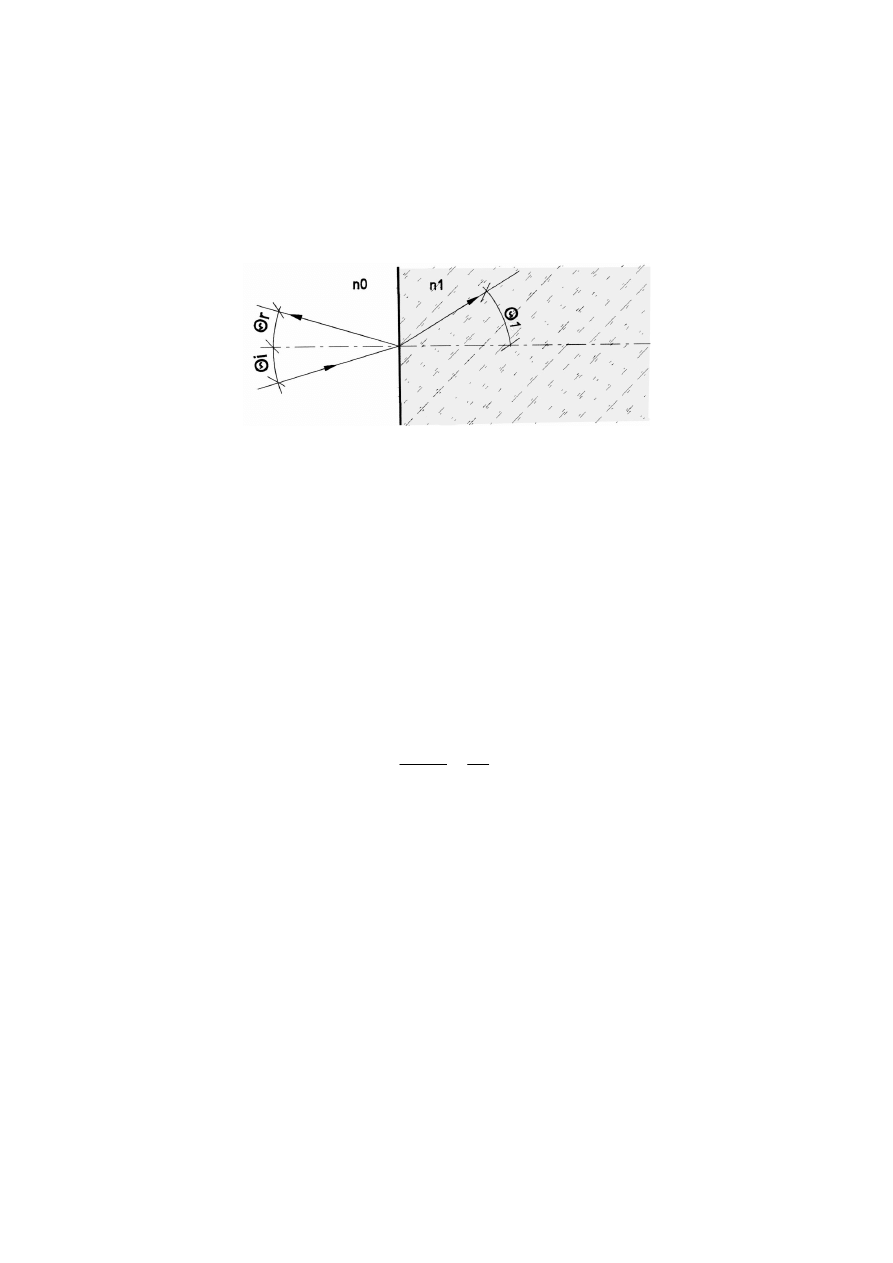
Rys. 1.1. Załamanie i odbicie promienia świetlnego na granicy dwóch ośrodków o róż-

nych współczynnikach załamania, 

1

0

n

n

<

. (

i

Θ

 - kąt padania, 

r

Θ

 - kąt odbicia, 

1

Θ

 - kąt załamania, 

1

,

0 n

n

- współczynniki załamania poszczególnych ośrodków) 

Prawa odbicia: 

2.  Promień padający, odbity i normalna do powierzchni granicznej leżą  w jednej płasz-

czyźnie. 

3.  Kąt padania jest równy kątowi odbicia. 

 

r

i

Θ

=

Θ

. 

(1.1) 

Prawa Snella dotyczą załamania promienia świetlnego: 

1.  Promień  padający,  załamany  i  normalna  do  powierzchni  granicznej  leżą  w  jednej 

płaszczyźnie. 

2.  Stosunek  sinusa  kąta  padania  do  sinusa  kąta  załamania  jest  stały  i  odpowiada  sto-

sunkowi współczynników załamania: 

 

0

1

1

sin

sin

n

n

i

=

Θ

Θ

. 

(1.2) 

Wiązka  światła  swobodnie  propagująca  się  w  ośrodku  dielektrycznym,  o  określonym 

współczynniku  załamania 

0

n

,  przechodząc  do  drugiego  ośrodka  o  innym  współczynniku 

załamania

1

n

,  zostaje  częściowo  odbita,  przy  czym  kąt  odbicia  jest  równy  kątowi  padania, 

częściowo  zaś  w  nowym  ośrodku  zostaje  załamana,  a  kąt  załamania  określa  prawo  Snella 
(1.2). Energia, jaką niosła ze sobą wiązka zostaje, więc rozdzielona pomiędzy wiązkę odbitą 
i załamaną. 

Jeśli zaczniemy obserwować wiązkę światła biegnącą w ośrodku o współczynniku zała-

mania 

1

n

 i przechodzącą do ośrodka o mniejszym współczynniku załamania 

0

n

, to zwięk-

szając kąt padania 

Θ

 na granicę ośrodków, w pewnym momencie 

gr

Θ

=

Θ3

, zauważymy, 

ż

e promień załamany ma zgodny kierunek z granicą ośrodków. Wszystkie promienie padają-

ce na granice ośrodków pod kątem większym od kąta granicznego 

gr

Θ

 (na rysunku 1.2 jest 

to promień 4) w ogóle nie przejdą do ośrodka 

0

n

, a cała energia wiązki padającej, bez żad-

nych strat zostanie w wiązce odbitej. 

Zjawisko  to  nosi  nazwę  całkowitego  wewnętrznego  odbicia  i  jest  wykorzystywane  w 

ś

wiatłowodach umożliwiając prowadzenie światła na bardzo duże odległości. 

Dla  przykładu  załóżmy,  że  ośrodkiem 

1

0

=

n

  jest  powietrze,  a  ośrodkiem 

48

,

1

0

=

n

  - 

szkło kwarcowe. Wówczas dla kąta 

(

)

1

'

3

sin

,

90

'

3

=

Θ

°

=

Θ

 ze wzoru (1.2) otrzymujemy: 

Optoelektronika 

 

 

 

6 

 

48

,

1

1

)

90

sin(

sin

=

°

Θgr

, 

°

=

Θ

5

,

42

gr

. 

 

 

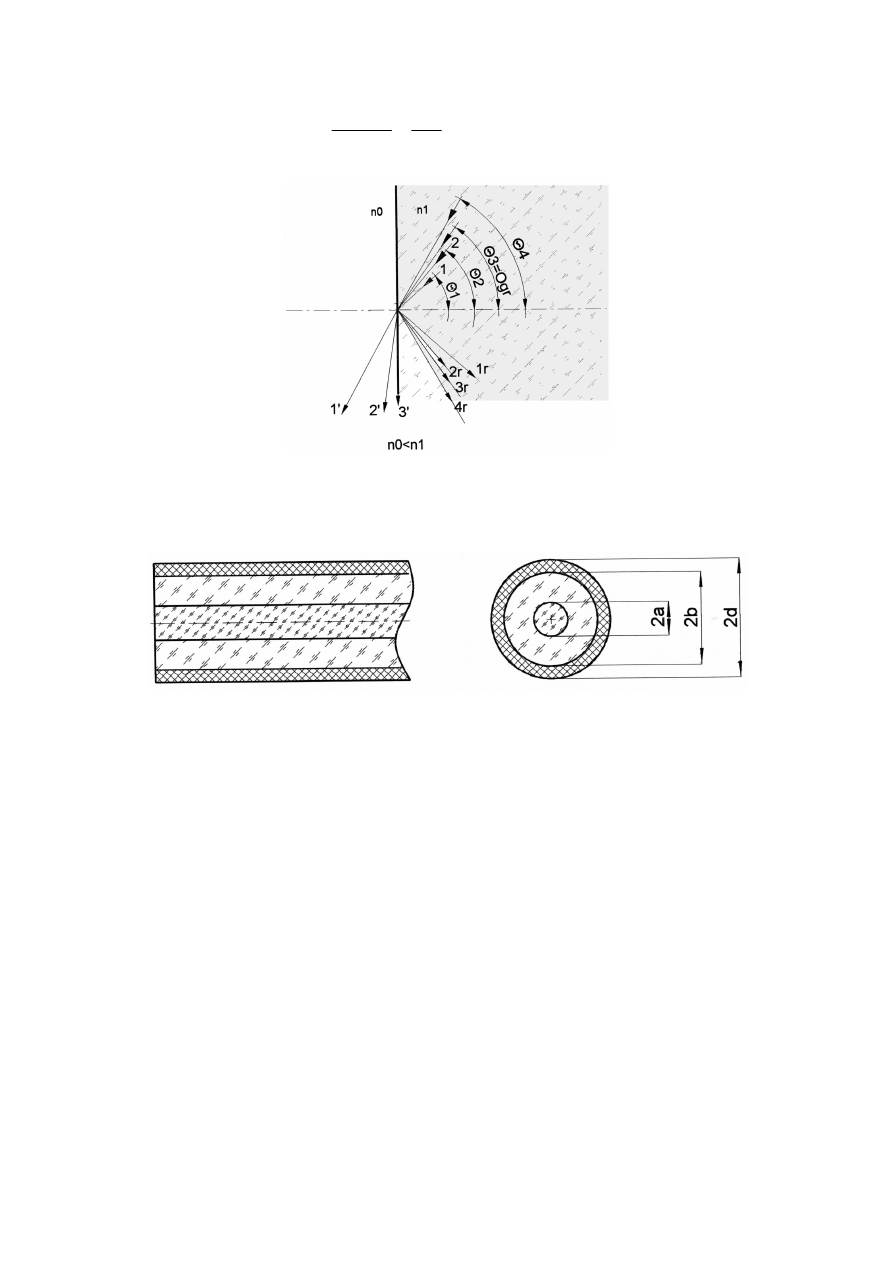
Rys. 1.2. Całkowite wewnętrzne odbicie 

Budowę  typowego  światłowodu  o  stałym  współczynniku  załamania  w  obrębie  rdzenia 

przedstawia rysunek 1.3.  

 

Rys. 1.3. Budowa światłowodu 

Podstawowe parametry takiego światłowodu to: 

- 2a - średnica rdzenia, o współczynniku załamania 

1

n

, 

- 2b - średnica płaszcza o współczynniku załamania 

1

2

n

n

<

, 

- 2d - średnica otuliny. 
 
Współczynniki  załamania  rdzenia  i  płaszcza  różnią  się  od  siebie  nieznacznie  np.: 

48

,

1

1

=

n

, 

46

,

1

2

=

n

.  Dla  takich  wartości  współczynnika  załamania  kąt  graniczny  wyniesie 

°

=

Θ

5

,

80

gr

. 

Z powyższego wynika, że aby w światłowodzie mogła propagować się fala wykorzystują-

ca  całkowite  wewnętrzne  odbicie  na  granicy  rdzeń-płaszcz,  promienie  muszą  wpadać  pod 
kątem mniejszym od kąta 

C

Θ

 w stosunku do osi światłowodu. W powyższym przykładzie kąt 

ten wynosi ok. 

°

=

Θ

13

C

 i nazywany jest kątem akceptacji światłowodu. Wartość 

C

Θ

2

 okre-

ś

la stożek akceptacji światłowodu  w obrębie, którego znajdują się promienie świetlne przyj-

mowane przez światłowód.  
Należy pamiętać, że podane wartości współczynnika załamania zależne są od długości fali, a 
więc  kąt  akceptacji  światłowodu  zależy  również  od  długości  padającej  fali.  Rysunek  1.4. 
przedstawia warunki propagacji światła w światłowodzie.  

Optoelektronika 

 

 

 

7 

 

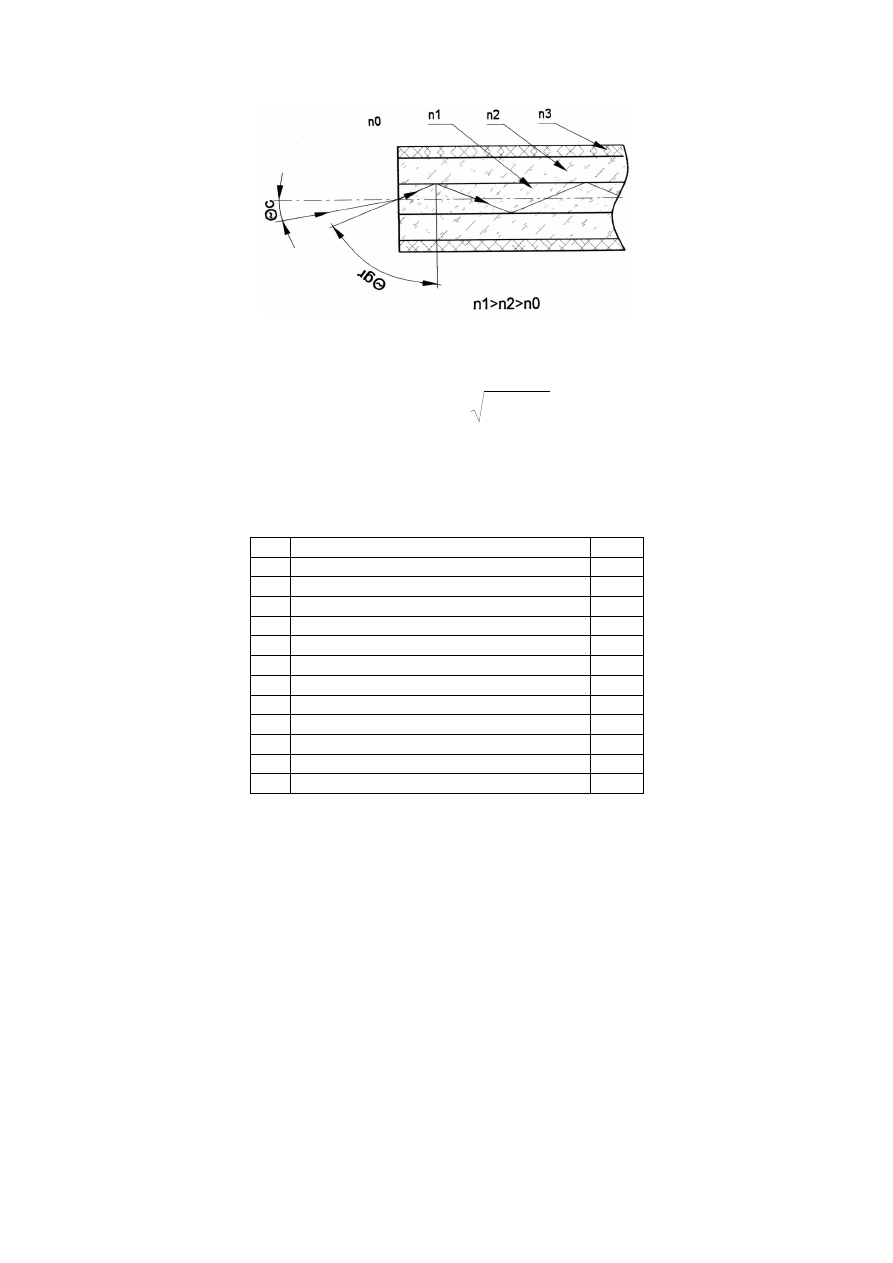
Rys. 1.4. Kąt akceptacji światłowodu 

W oparciu o kąt akceptacji definiowana jest apertura numeryczna światłowodu: 

 

2

2

2

1

sin

n

n

NA

C

−

=

Θ

=

. 

(1.3) 

1.2.  Ćwiczenie 

1.2.1. Lista potrzebnych elementów; budowa stanowiska 

L.P.  Opis 

il. szt. 

1 

Płyta podstawy 

1 

2 

Pręt mocujący 

2 

3 

Kolumna zwykła 

2 

4 

Pochylny uchwyt elementów płaskich 

2 

5 

Uchwyt małych elementów okrągłych 

2 

6 

Moduł lasera 670nm 

1 

7 

Moduł kolimatora 

1 

8 

Moduł detektora 

1 

9 

Uchwyt światłowodu 

2 

10 

Kolumna z podziałką 

1 

11 

Ś

wiatłowód wielodomowy: FT-200-EMT  1 

13 

Pozycjoner XY 

1 

1.2.2. Przebieg ćwiczenia 

 

Uwaga! Elementy regulacyjne należy zawsze dokręcać delikatnie i z wyczuciem. 
 

1.  Wstępnie  zmontuj  stanowisko  pomiarowe  zgodnie  z  planem  pokazanym  na  rys.1.5. 

Polega to na wkręceniu prętów (2) w otwory na płycie (1), a następnie zainstaluj ko-
lumny zwykłe (3) i kolumnę z podziałką (10).  

2.  Zamocuj sztywne uchwyty elementów płaskich (4), a w nich uchwyty małych elemen-

tów okrągłych (6). 

3.  Przygotuj laser: przy pomocy kolimatora (7) wyjustuj go, tak by w odległości kilku me-

trów,  obraz  plamki  był  zbliżony  gabarytowo  do  rozmiarów  plamki  obserwowanej  tuż 
za laserem. 

4.  Zainstaluj laser w uchwycie (6). 
5.  Przygotuj  trzy  odcinki  światłowodów  o  długości  ok.  1m:  wielomodowego  650nm  (w 

białej  otulinie),  wielomodowego  telekomunikacyjnego  1000nm  (w  zielonej  otulinie), 
jednodomowego telekomunikacyjnego (w brązowej otulinie).