Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

1

temów transportowychtemów transportowych

Modele sieci transportowej

Model WJN

Modele sieci transportowej

Model WJN

Modelowanie 

procesów i sys

t

Modelowanie 

procesów i sys

t

Piotr Sawicki

Piotr Sawicki

Zakład Logistyki | WMRiT 

pok. 742, tel. 665 22 49 
piotr.sawicki@put.poznan.pl |  www.put.poznan.pl/~piotr.sawicki

Zakład Logistyki | WMRiT 

pok. 742, tel. 665 22 49 
piotr.sawicki@put.poznan.pl |  www.put.poznan.pl/~piotr.sawicki

Agenda

Agenda

Æ

Wprowadzenie do przedmiotu

•

klasyfikacja modeli systemu transportowego 

(przypomnienie)

•

zakres tematyczny

•

cel zajęć

Æ

Model WJN

•

ogólne założenia

•

konstrukcja modelu

•

weryfikacja poprawności modelu

•

metoda rozwiązania 

Æ

Z t

i   d l  WJN

24

22

Piotr Sawicki /  Modelowanie procesów i systemów transportowych

Æ

Zastosowanie modelu WJN

Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

2

Wprowadzenie do przedmiotu

Klasyfikacja

Wprowadzenie do przedmiotu

Klasyfikacja

Æ

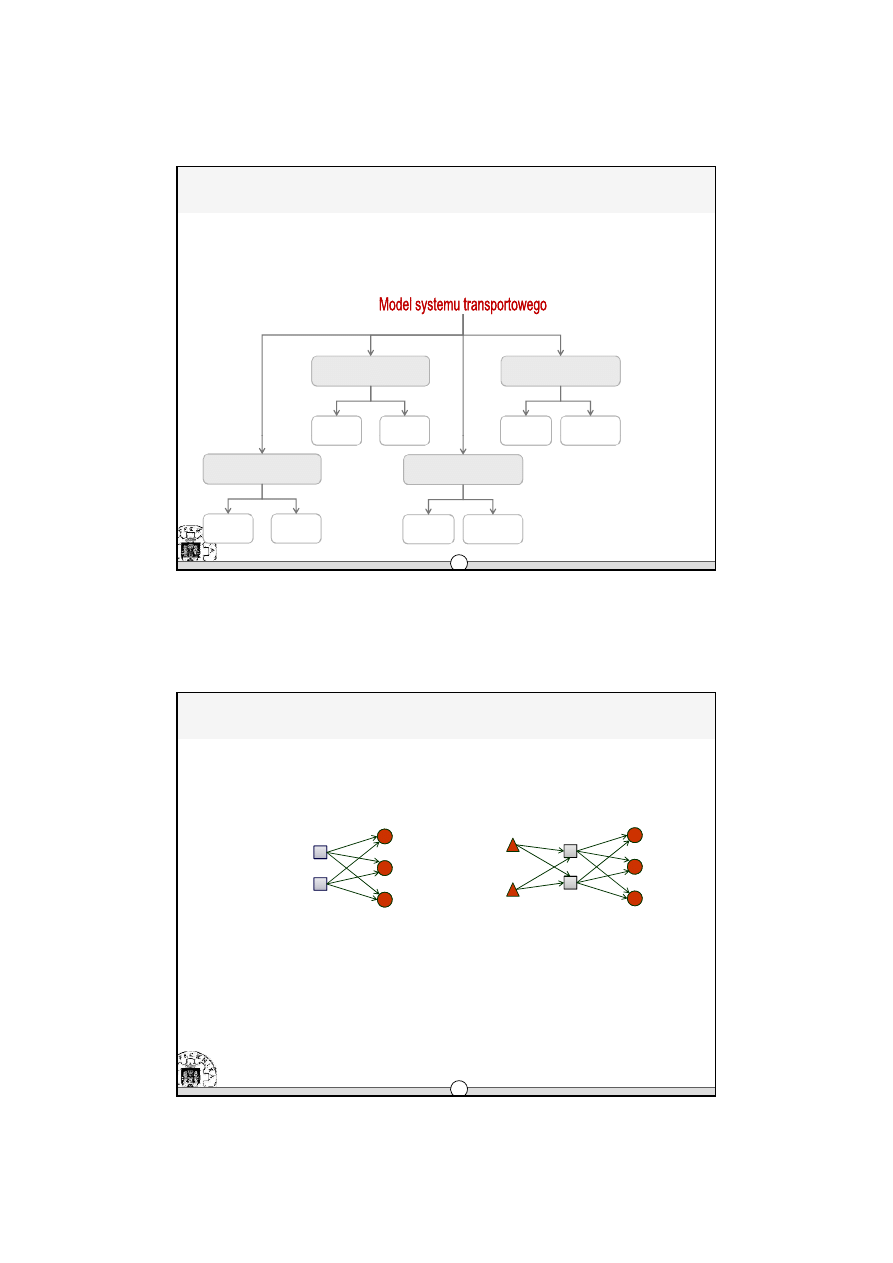
Klasyfikacja modeli systemów transportowych

Z uwagi na 

liczbę poziomów

Jedno-

poziomowy

Wielo-

poziomowy

Z uwagi na 

liczbę produktów

Jeden

produkt

Wiele

produktów

24

33

Piotr Sawicki /  Modelowanie procesów i systemów transportowych

Z uwagi na 

wielkość obiektów mag.

poziomowy

poziomowy

Ograniczona 

wielkość

Nieograniczona

wielkość

produkt

produktów

Z uwagi na 

postać zmiennej decyzyjnej

Liniowy

Nieliniowy

Wprowadzenie do przedmiotu

Klasyfikacja

Wprowadzenie do przedmiotu

Klasyfikacja

Æ

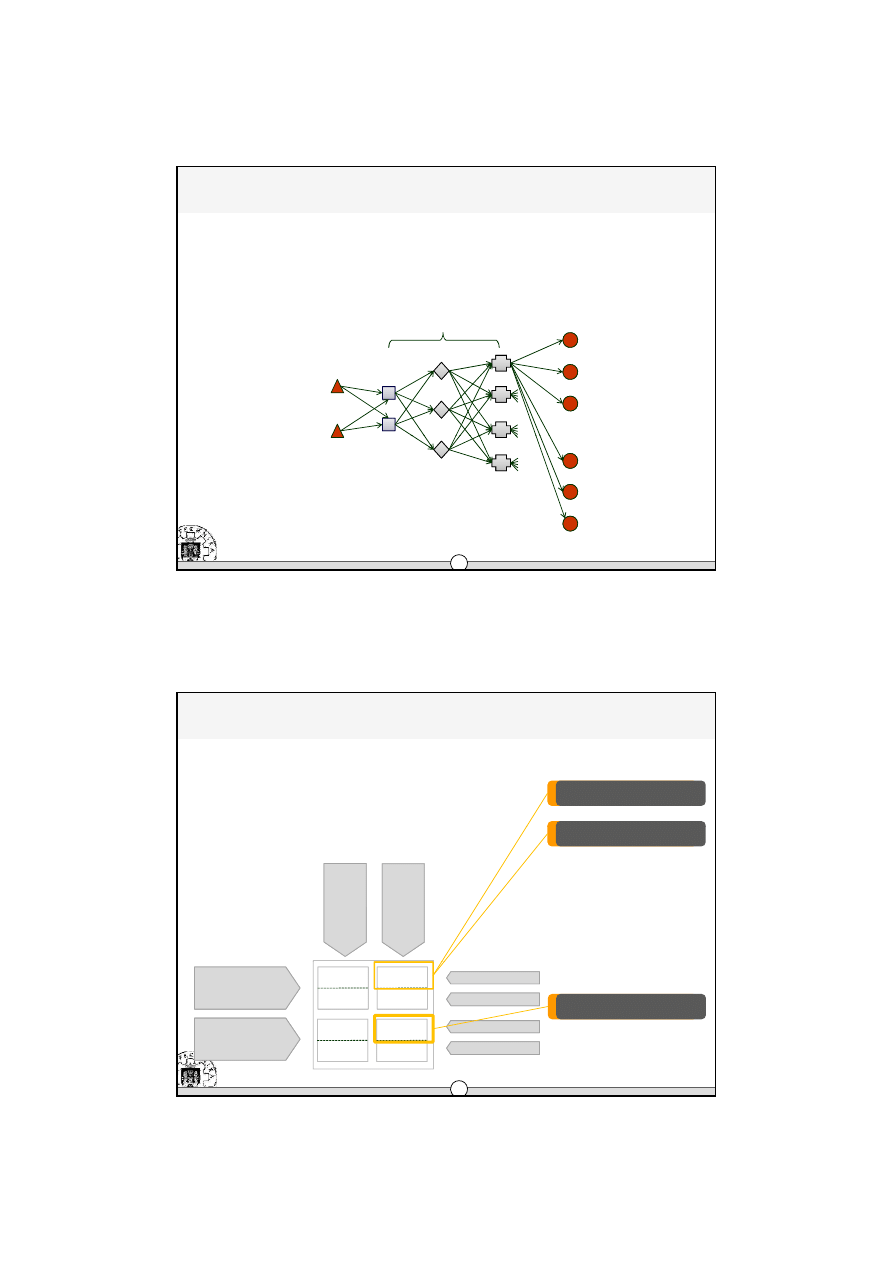
Klasyfikacja modeli systemów transportowych

•

Modele jedno-poziomowe

Obiekty

Klienci / odbiorcy

Obiekty

Klienci / odbiorcy

Dostawcy

Model  jedno-etapowy

Model  dwu-etapowy

24

44

Piotr Sawicki /  Modelowanie procesów i systemów transportowych

Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

3

Wprowadzenie do przedmiotu

Klasyfikacja

Wprowadzenie do przedmiotu

Klasyfikacja

Æ

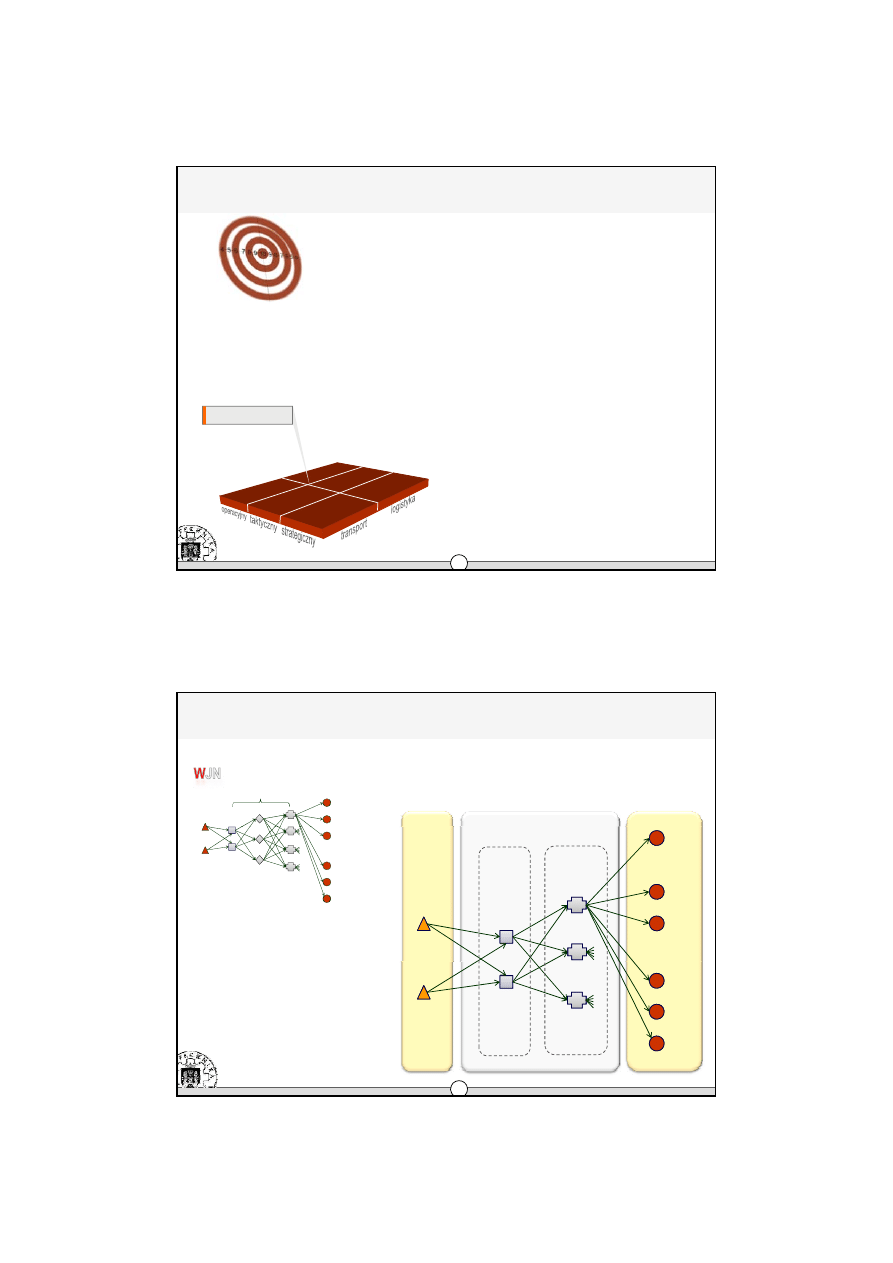
Klasyfikacja modeli systemów transportowych

•

Modele wielo-poziomowe

Obiekty

Klienci / odbiorcy

Dostawcy

(…)

24

55

Piotr Sawicki /  Modelowanie procesów i systemów transportowych

(…)

Wprowadzenie do przedmiotu

Klasyfikacja

Wprowadzenie do przedmiotu

Klasyfikacja

Æ

Klasyfikacja modeli systemów transportowych 
Æ

Gdzie jesteśmy?

Model analityczny

środek ciężkości

Model liniowy

O

graniczona 

wielko

ść

 obiekt

u (O

)

Nieograniczona 

wielko

ść

 obiekt

u (N)

Model liniowy

problem transportowo-magazynowy

24

66

Piotr Sawicki /  Modelowanie procesów i systemów transportowych

Model

jedno-poziomowy (J)

Model

wielo-poziomowy (W)

J 

J 

O

J 

W 

O

J 

J

N

J 

W 

N

W 

J 

O

W 

W

O

W 

J 

N

W 

W 

N

p

( )

Jeden produkt (J)

Wiele produktów (W)

( )

Jeden produkt (J)

Wiele produktów (W)

Model mieszany 

problem  transportowo-magazynowo-prod.

Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

4

Wprowadzenie do przedmiotu

Cel zajęć

Wprowadzenie do przedmiotu

Cel zajęć

Æ

Zasadniczy cel zajęć

•

poznanie głównych technik modelowania systemów i 
procesów transportowych

–

istota modelowanego zjawiska

–

definiowanie modelu

–

określenie ograniczeń

•

poznanie modelu typu WJN

•

weryfikacja modelu z wykorzystaniem dostępnych technik 
obliczeniowych

•

praktyczne wykorzystanie wiedzy (laboratoria)

–

analiza rzeczywistych przypadków

Zakres modelowania

24

77

Piotr Sawicki /  Modelowanie procesów i systemów transportowych

–

kształtowanie umiejętności samodzielnego modelowania

–

możliwość zweryfikowania zbudowanego modelu

Model WJN

Istota problemu 

Model WJN

Istota problemu 

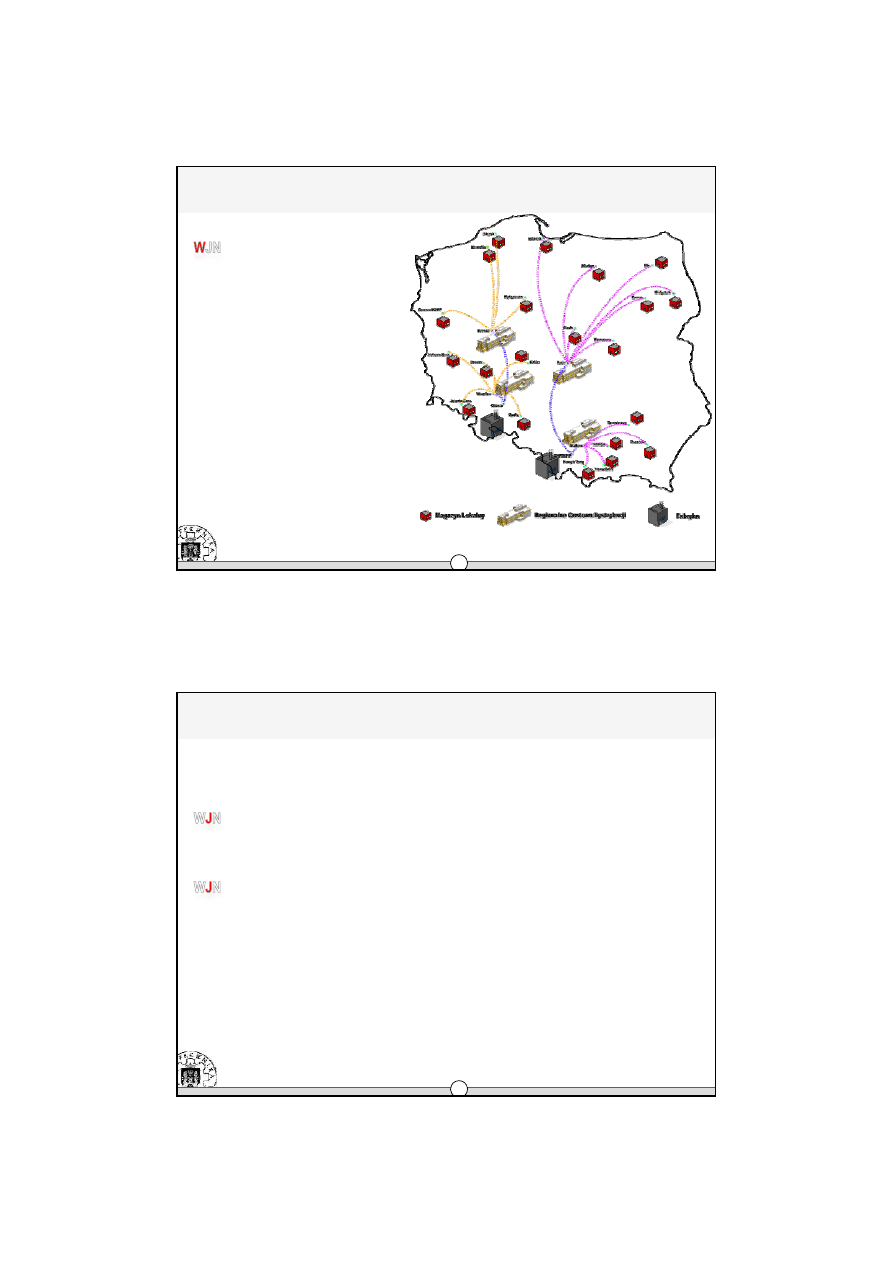
Obiekty

Klienci /odbiorcy

Dostawcy

F b ki

M

 

Obiekty

Klienci / odbiorcy

Dostawcy

(…)

Fabryki

Magazyny reg.

(…)

24

88

Piotr Sawicki /  Modelowanie procesów i systemów transportowych

Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

5

Model WJN

Istota problemu 

Model WJN

Istota problemu 

Æ

Struktura systemu (sieci)

•

wielo-poziomowa 

–

dostawca (-cy)

–

fabryka (-ki)

–

pośrednik (-cy) - RCD

pośrednik ( cy)  RCD

–

odbiorca (-y)

Æ

Kluczowe pytania

•

które fabryki i w jakim stopniu 
powinny obsługiwać 
poszczególnych odbiorców (ML)?

–

lista potencjalnych lokalizacji  
fabryk jest znana

•

przez które magazyny (RCD) 

24

99

przez które magazyny (RCD) 
powinna być realizowana 
sprzedaż do poszczególnych 
odbiorców (ML)?

–

lista lokalizacji magazynów 
(RCD) jest znana

Piotr Sawicki /  Modelowanie procesów i systemów transportowych

Model WJN

Podstawowe  założenia

Model WJN

Podstawowe  założenia

Æ

Podstawowe założenia

•

po stronie popytu (klientów)

–

znana 

{

wielkość popytu każdego z odbiorców – d

j

{

rodzaj przewożonego towaru – jednorodny produkt

•

po stronie podaży (punktów nadania)

–

nieznane

{

pojemność magazynów – pojemność nieograniczona 

–

znane

{

potencjalne lokalizacje magazynów i fabryk

{

jednostkowe koszty transportu z k-tej fabryki, przez i-ty magazyn do j-tego klienta – c

ijk

{

stały koszt funkcjonowania magazynu w i-tej lokalizacji – f

i

24

10

10

{

stały koszt przypisany do k-tej fabryki -

g

k

•

zmienne decyzyjne

–

udział zapotrzebowania j-tego klienta zaopatrywanego z k-tej fabryki przez i-ty magazyn - x

ijk

–

występowanie/brak magazynu w i-tej lokalizacji - y

i

–

występowanie/brak fabryki w k-tej lokalizacji - z

k

Piotr Sawicki /  Modelowanie procesów i systemów transportowych

Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

6

Model WJN

Modelowanie …

Model WJN

Modelowanie …

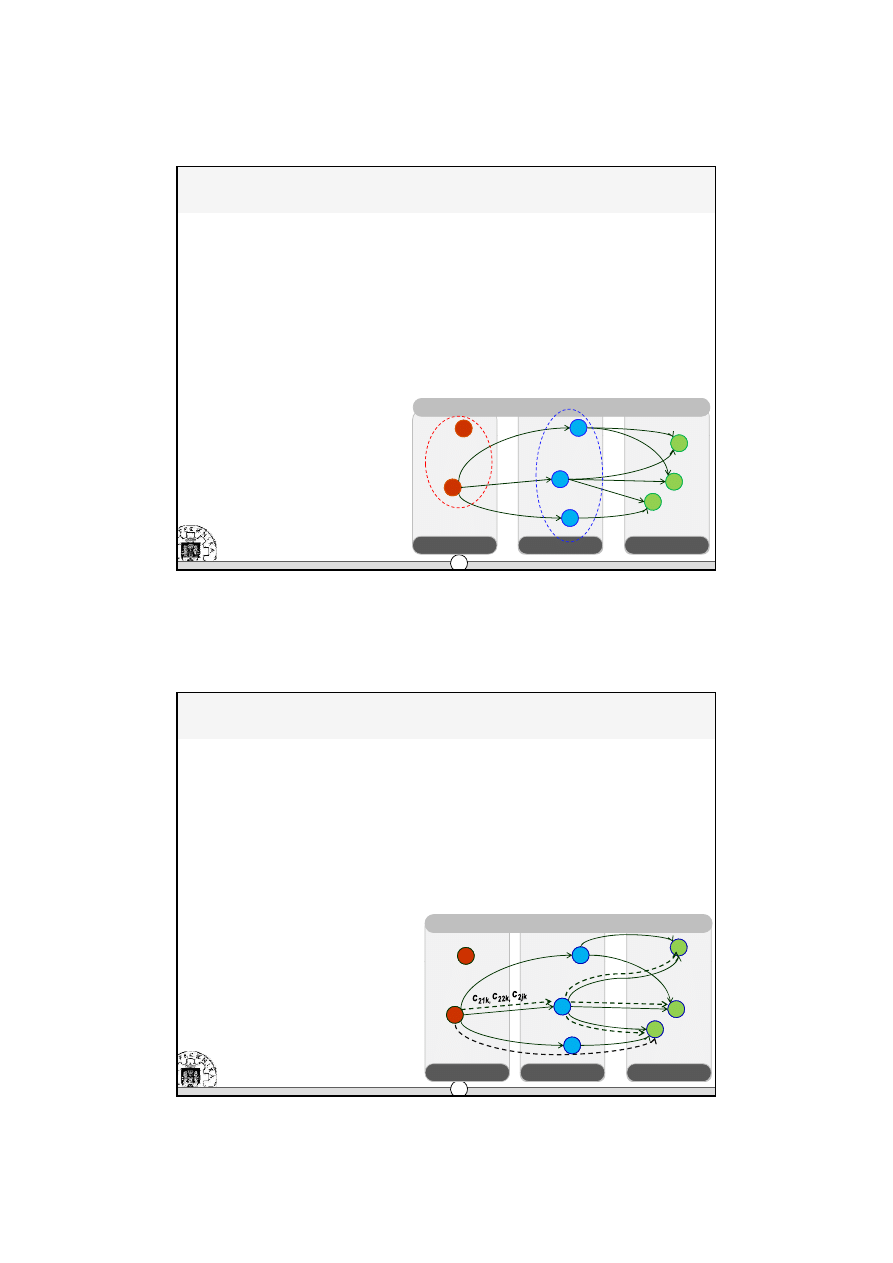
Æ

Model matematyczny

•

funkcja celu

min

KC

→

+

+

=

KP

KM

KT

gdzie:
KT – koszt transportu
KM – koszt magazynowania (RCD)
KP – koszt produkcji

1

1

Model

d

1

24

11

11

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

k

2

i

FABRYKI

RCD

KT

KLIENCI

j

2

1

d

j

d

2

KM

KP

Model WJN

Modelowanie …

Model WJN

Modelowanie …

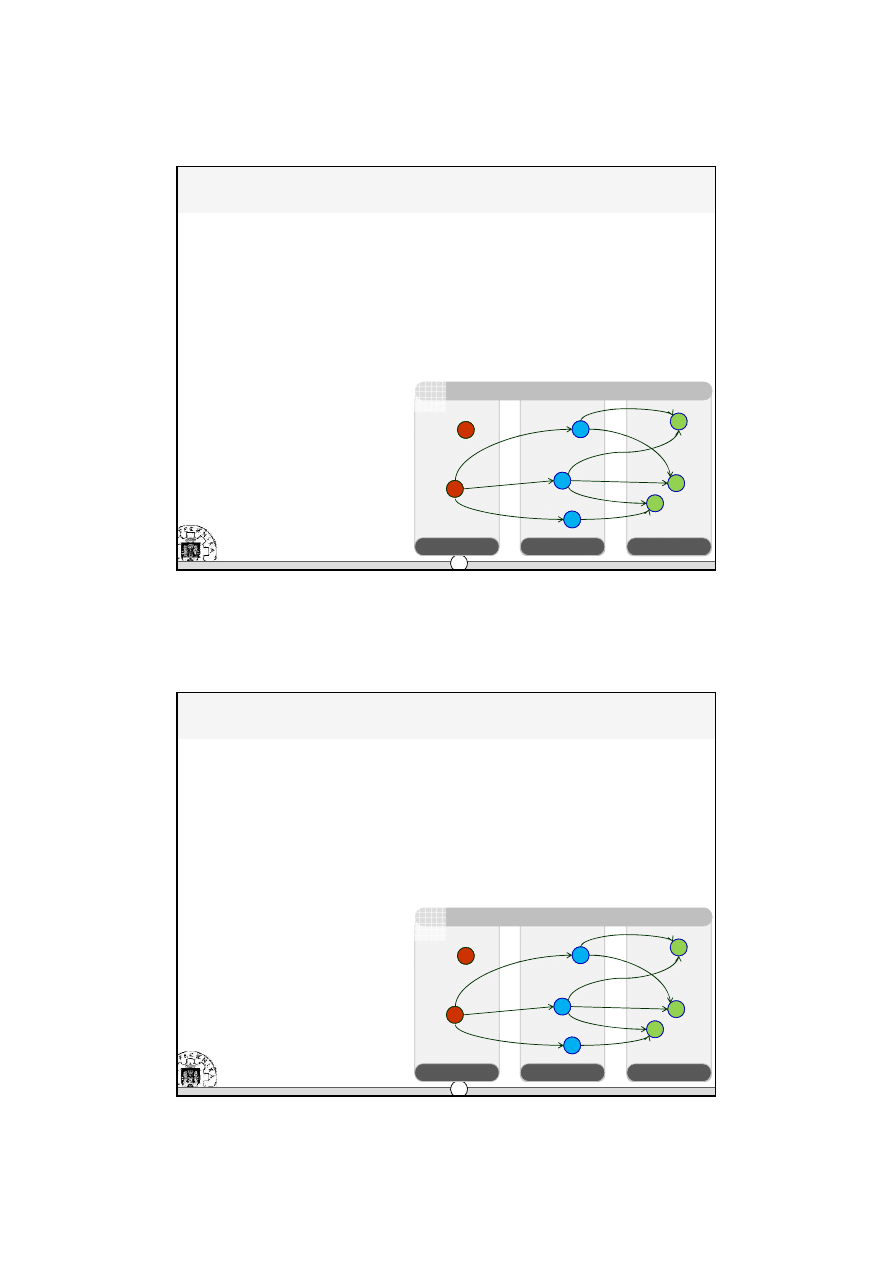
Æ

Model matematyczny

•

komponenty funkcji celu – KT (koszt transportu)

∑∑∑

=

m

i

n

j

j

ijk

ijk

p

k

d

x

c

1

1

1

KT

gdzie:
c

ijk

- jednostkowy koszt transportu z fabryki k przez magazyn i do klienta j

x

ijk

- część (udział procentowy) zapotrzebowania klienta j zaopatrywanego z fabryki k

przez magazyn i

d

j   

- zapotrzebowanie klienta j

=

=

=

i

j

k

1

1

1

1

1

Model

1

d

1

24

12

12

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

k

2

i

FABRYKI

RCD

c

ijk

ODBIORCY

j

x

ijk

2

d

j

d

2

c

2jk

c

22k

c

21k

Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

7

Model WJN

Modelowanie …

Model WJN

Modelowanie …

Æ

Model matematyczny

•

komponenty funkcji celu – KM (koszt magazynowania)

∑

=

=

m

i

i

i

y

f

1

KM

gdzie:
f

i 

- stały koszt przypisany do magazynu i

y

i  

- zmienna binarna określająca występowanie magazynu w i-tej lokalizacji

1

1

Model

1

f

1

, y

1

=

i

1

⎩

⎨

⎧

=

0

1

i

y

jeżeli jest i-ty magazyn
w przeciwnym przypadku

24

13

13

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

k

2

i

FABRYKI

RCD

ODBIORCY

j

2

f

1

, y

2

f

1

, y

i

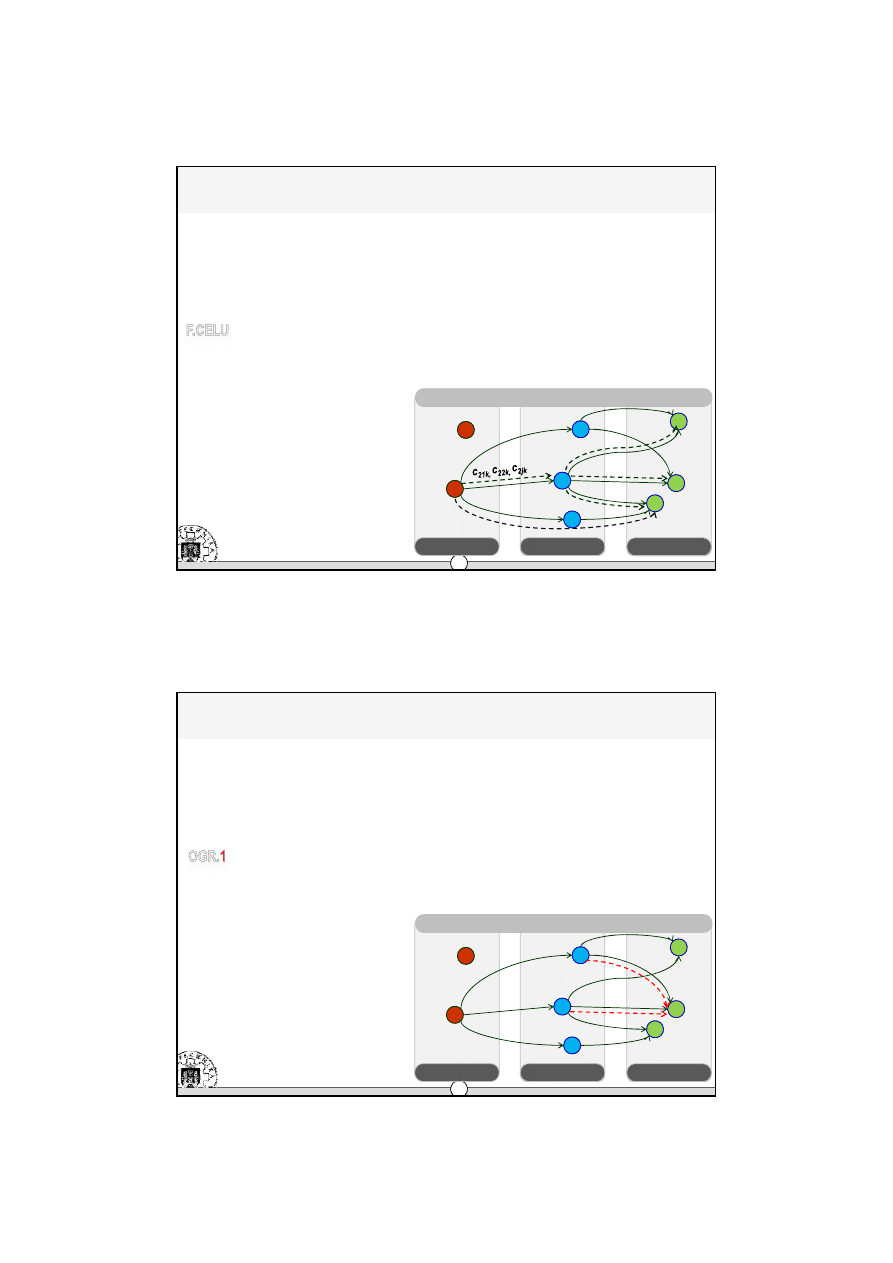
Æ

Model matematyczny

•

komponenty funkcji celu – KP (koszt produkcji)

Model WJN

Modelowanie …

Model WJN

Modelowanie …

∑

=

p

k

k

k

z

g

1

KP

gdzie:
g

k 

- stały koszt przypisany do fabryki k

z

k

- zmienna binarna określająca występowanie fabryki w k-tej lokalizacji

1

1

Model

1

=

k

1

⎩

⎨

⎧

=

0

1

k

z

jeżeli jest k-ta fabryka
w przeciwnym przypadku

g

1

, z

1

24

14

14

k

2

i

FABRYKI

RCD

ODBIORCY

j

2

g

k

, z

k

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

8

Æ

Model matematyczny

•

komponenty funkcja celu – KM (koszt magazynowania)

Model WJN

Modelowanie 

Model WJN

Modelowanie 

min

KC

→

+

+

=

KP

KM

KT

min

KC

→

+

+

=

∑

∑

∑∑∑

=

=

=

=

=

p

k

k

k

m

i

i

i

m

i

n

j

j

ijk

ijk

p

k

z

g

y

f

d

x

c

1

1

1

1

1

1

1

Model

1

d

1

X

ij1, 

g

1

, z

1

f

1

, y

1

24

15

15

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

k

2

i

FABRYKI

RCD

c

ijk

ODBIORCY

j

X

ijk, 

g

k

, z

k

2

d

j

d

2

c

2jk

c

22k

c

21k

f

1

, y

2

f

1

, y

i

Æ

Model matematyczny - ograniczenia

•

ograniczenie 1
sumaryczna wielkość dostaw z i-tego magazynu do j-tego odbiorcy (klienta) równa jest 
rzeczywistemu zapotrzebowaniu tego odbiorcy

Model WJN

Modelowanie …

Model WJN

Modelowanie …

przykład: x

1

2

+ x

2

2

= d

2

1

1

Model

1

d

1

∑

=

=

n

i

j

ij

d

x

1

24

16

16

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

k

2

i

FABRYKI

RCD

ODBIORCY

j

2

d

j

d

2

x

22

x

12

Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

9

Æ

Model matematyczny - ograniczenia

•

ograniczenie 2
zmienna decyzyjna określająca czy magazyn ma być zlokalizowany w i-tym punkcie jest 
zmienną binarną

Model WJN

Modelowanie …

Model WJN

Modelowanie …

•

ograniczenie 3
zmienna decyzyjna określająca czy fabryka ma być zlokalizowana w k-tym punkcie jest 
zmienną binarną

0

1

∪

=

i

y

1

1

Model

1

y

1

0

1

∪

=

k

z

z

1

24

17

17

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

k

2

i

FABRYKI

RCD

ODBIORCY

j

2

y

2

y

i

z

k

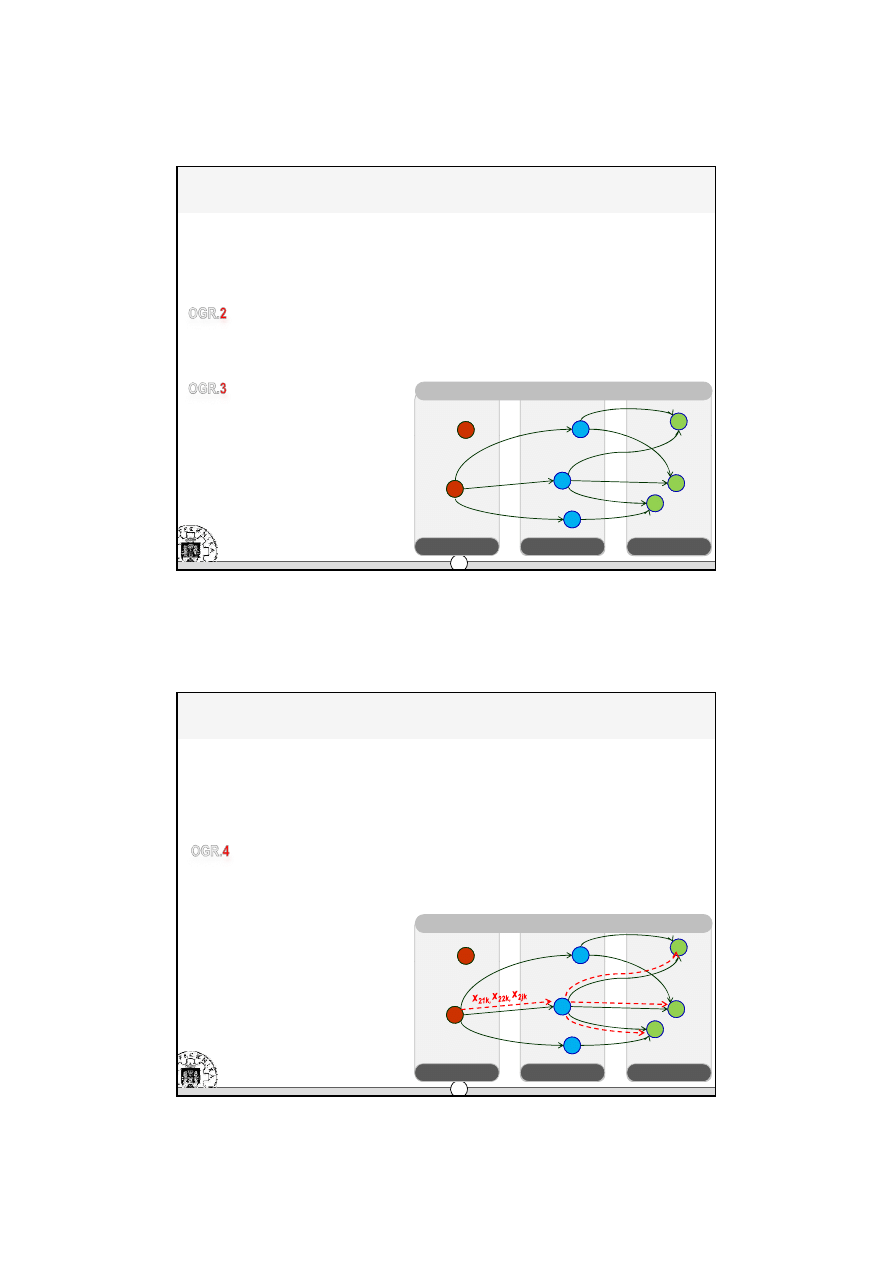
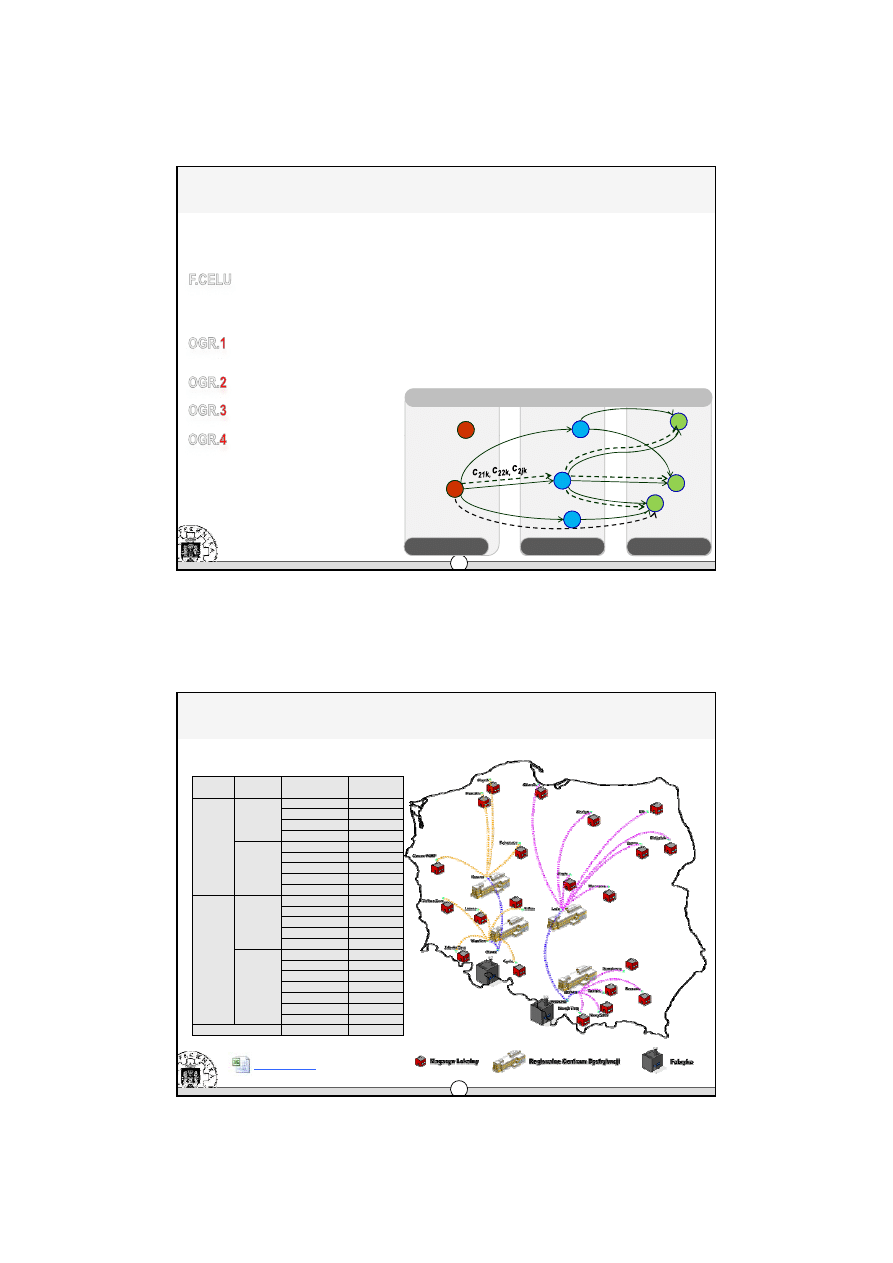
Æ

Model matematyczny - ograniczenia

•

ograniczenie 4
magazyn (RCD) powinien istnieć tylko wtedy (y

i

= 1), jeżeli uzasadniony jest przepływ 

towaru z k-tej fabryki przez i-ty magazyn do j-tego klienta 

Model WJN

Modelowanie …

Model WJN

Modelowanie …

w praktyce:

–

jeżeli dowolna ze zmiennych 
x

2

1k, 

x

2

2k, 

x

2

jk 

przyjmie 

wartość większą od 0, 
wówczas y

2

=1

i

ijk

y

x

≤

1

1

Model

1

dla k = 1, …, p  

y

1

24

18

18

–

jeżeli wszystkie ze zmiennych 
x

2

1k, 

x

2

2k, 

x

2

jk 

przyjmą 

wartość równą 0, 
wówczas y

2

=0

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

k

2

i

FABRYKI

RCD

ODBIORCY

j

2

x

2jk

x

22k

x

21k

y

2

y

i

Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

10

Æ

Model matematyczny

•

funkcja celu

Model WJN

Modelowanie …

Model WJN

Modelowanie …

min

KC

→

+

+

=

∑

∑

∑∑∑

=

=

=

=

=

p

k

k

k

m

i

i

i

m

i

n

j

j

ijk

ijk

p

k

z

g

y

f

d

x

c

1

1

1

1

1

•

ograniczenia

=

=

=

=

=

k

i

i

j

k

1

1

1

1

1

∑

=

=

n

i

j

ij

d

x

1

0

1

∪

=

i

y

0

1

∪

=

k

z

y

x

≤

1

1

Model

1

d

1

X

ij1, 

g

1

, z

1

f

1

, y

1

24

19

19

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

i

ijk

y

x

≤

k

2

i

FABRYKI

RCD

c

ijk

ODBIORCY

j

X

ijk, 

g

k

, z

k

2

d

j

d

2

c

2jk

c

22k

c

21k

f

1

, y

2

f

1

, y

i

Model WJN

Weryfikacja modelu

Model WJN

Weryfikacja modelu

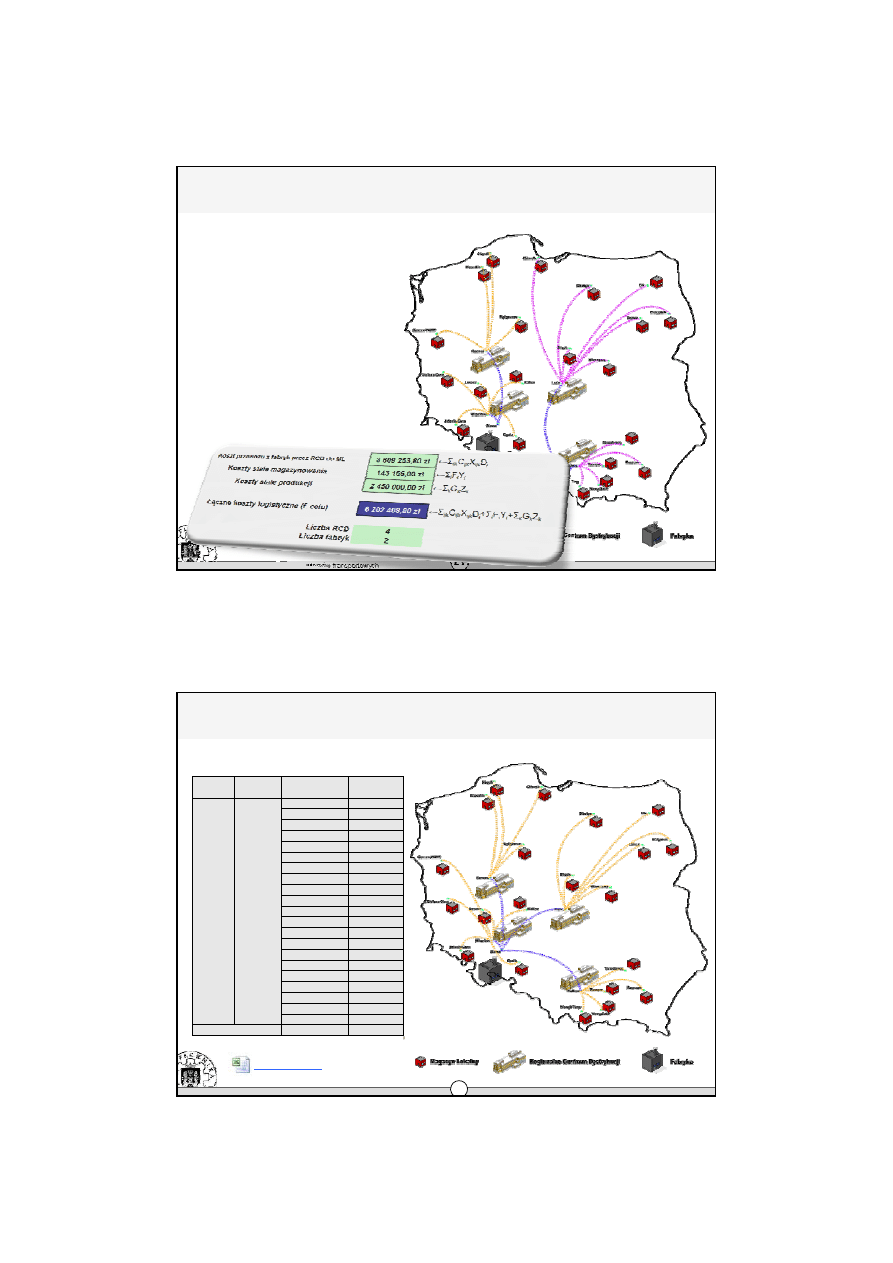
Æ

Stan aktualny

Fabryka

RCD

Odbiorca (ML)

Popyt 
[EUR]

Poznań

Słupsk

3670

Koszalin

3230

Bydgoszcz

6600

Oława

Bydgoszcz

6600

Gorzów Wlkp.

4540

Wrocław

Zielona Góra

4780

Leszno

4310

Kalisz

4240

Jelenia Góra

5590

Opole

5300

Skawina

Kraków

Tarnobrzeg

4550

Rzeszów

6430

Tarnów

4980

Nowy Sącz

5000

Nowy Targ

5900

Gdańsk

5650

24

20

20

Piotr Sawicki /  Modelowanie procesów i systemów transportowych

Skawina

Łódź

Olsztyn

4700

Ełk

5000

Łomża

4200

Białystok

4421

Płock

4765

Warszawa

6600

Suma

104456

Model stanu obecnego

Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

11

Model WJN

Weryfikacja modelu

Model WJN

Weryfikacja modelu

Æ

Stan aktualny

24

21

21

Piotr Sawicki /  Modelowanie procesów i systemów transportowych

Model WJN

Weryfikacja modelu

Model WJN

Weryfikacja modelu

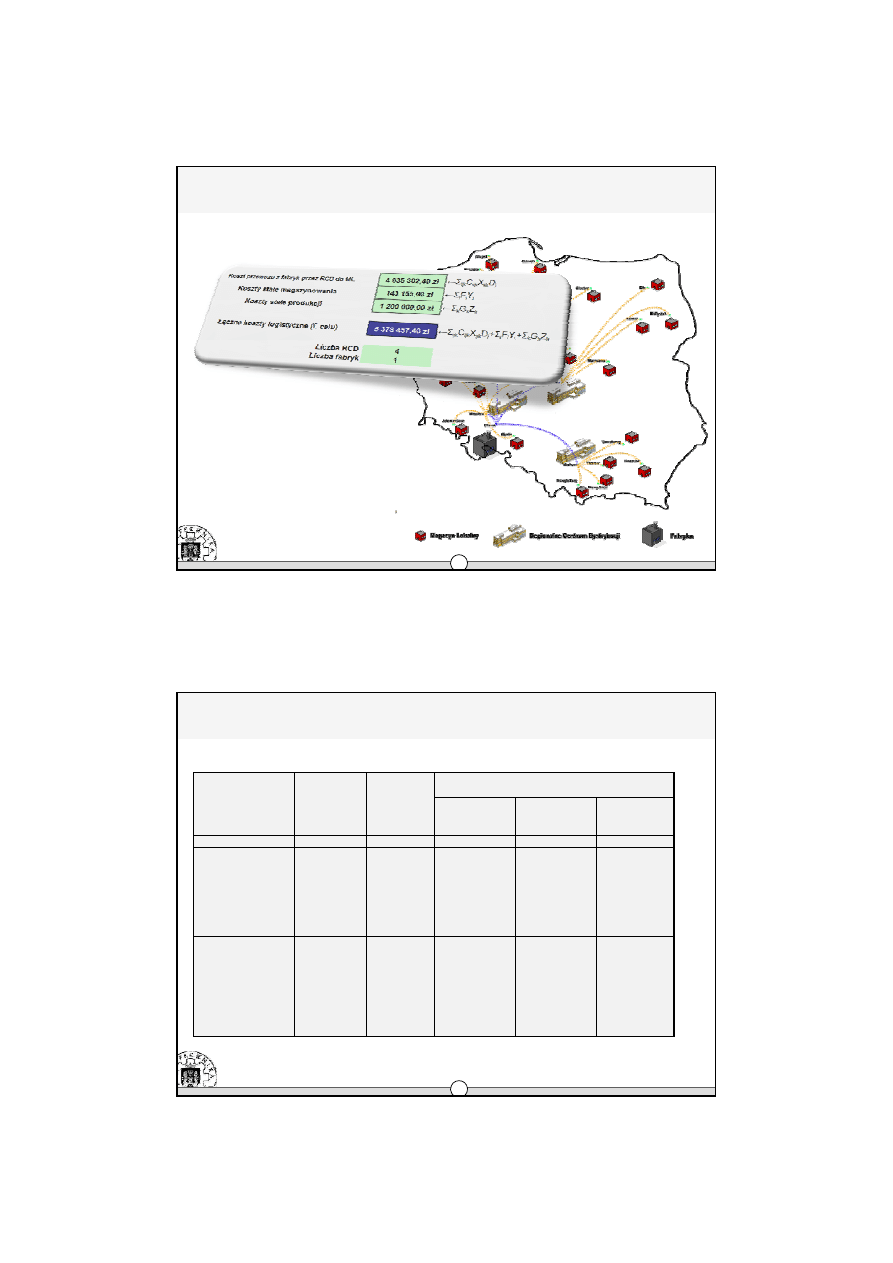
Æ

Optymalizacja – stan docelowy

Fabryka

RCD

Odbiorca (ML)

Popyt 
[EUR]

Słupsk

3670

Koszalin

3230

Bydgoszcz

6600

Oława,

Skawina

Poznań,

Wrocław,

Kraków,

Łódź

Bydgoszcz

6600

Gorzów Wlkp.

4540

Zielona Góra

4780

Leszno

4310

Kalisz

4240

Jelenia Góra

5590

Opole

5300

Tarnobrzeg

4550

Rzeszów

6430

Tarnów

4980

Nowy Sącz

5000

Nowy Targ

5900

Gdańsk

5650

24

22

22

Piotr Sawicki /  Modelowanie procesów i systemów transportowych

Olsztyn

4700

Ełk

5000

Łomża

4200

Białystok

4421

Płock

4765

Warszawa

6600

Suma

104456

Model stanu docelowego

Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

12

Model WJN

Weryfikacja modelu

Model WJN

Weryfikacja modelu

Æ

Optymalizacja – stan docelowy

24

23

23

Piotr Sawicki /  Modelowanie procesów i systemów transportowych

Podsumowanie

Porównanie wyników

Podsumowanie

Porównanie wyników

Wariant

Koszty 

logistyczne

[zł] 

Różnica w 

stosunku 

do stanu 

aktualnego 

[%]

Udział poszczególnych kosztów w kosztach 

całkowitych [%]

Transport

Magazynow.

(koszty stałe)

Produkcja

(koszty stałe)

[%]

(

y

)

(

y

)

Stan aktualny 

6 202 408,80

-

58,2

2,3

39,5

Stan aktualny 

(wariant z dwoma 

fabrykami) − 

rozwiązanie 

uzyskane w wyniku 

zastosowania 

modelu 

6 049 652,88

2,5

57

2,6

40,4

Stan aktualny 

(wariant bez 

24

24

24

Piotr Sawicki /  Modelowanie procesów i systemów transportowych

wymuszonych 

jednostek) − 

rozwiązanie 

uzyskane  w wyniku 

zastosowania 

modelu 

5 378 457,40

13,5

75

2,7

22,3

Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

13

Literatura

Literatura

Æ

Nijak D. Projekt lokalizacji sieci logistycznej z wykorzystaniem modelu 
MESUFL, Politechnika Poznańska, Poznań 2007 (praca przejściowa)

24

25

25

Piotr Sawicki /  Modelowanie procesów i systemów transportowych

temów transportowychtemów transportowych

Modele sieci transportowej

Model WJN

Modele sieci transportowej

Model WJN

Modelowanie 

procesów i sys

t

Modelowanie 

procesów i sys

t

Piotr Sawicki

Piotr Sawicki

Zakład Logistyki | WMRiT 

pok. 742, tel. 665 22 49 
piotr.sawicki@put.poznan.pl |  www.put.poznan.pl/~piotr.sawicki

Zakład Logistyki | WMRiT 

pok. 742, tel. 665 22 49 
piotr.sawicki@put.poznan.pl |  www.put.poznan.pl/~piotr.sawicki