Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

1

temów transportowychtemów transportowych

Modele sieci transportowej

Model JWN

Modele sieci transportowej

Model JWN

Modelowanie 

procesów i sys

t

Modelowanie 

procesów i sys

t

Piotr Sawicki

Piotr Sawicki

Zakład Logistyki | WMRiT 

pok. 742, tel. 665 22 49 
piotr.sawicki@put.poznan.pl |  www.put.poznan.pl/~piotr.sawicki

Zakład Logistyki | WMRiT 

pok. 742, tel. 665 22 49 
piotr.sawicki@put.poznan.pl |  www.put.poznan.pl/~piotr.sawicki

Wprowadzenie

Agenda

Wprowadzenie

Agenda

Æ

Wprowadzenie

•

cel i zakres

•

klasyfikacja modeli - przypomnienie 

Æ

Model matematyczny typu JWN

Æ

Model matematyczny typu JWN

•

ogólne założenia

•

konstrukcja modelu

•

weryfikacja poprawności modelu

•

metoda rozwiązania 

Æ

Zastosowanie modelu JWN

22

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

2

Model systemu transportowego

Klasyfikacja modeli

Model systemu transportowego

Klasyfikacja modeli

Æ

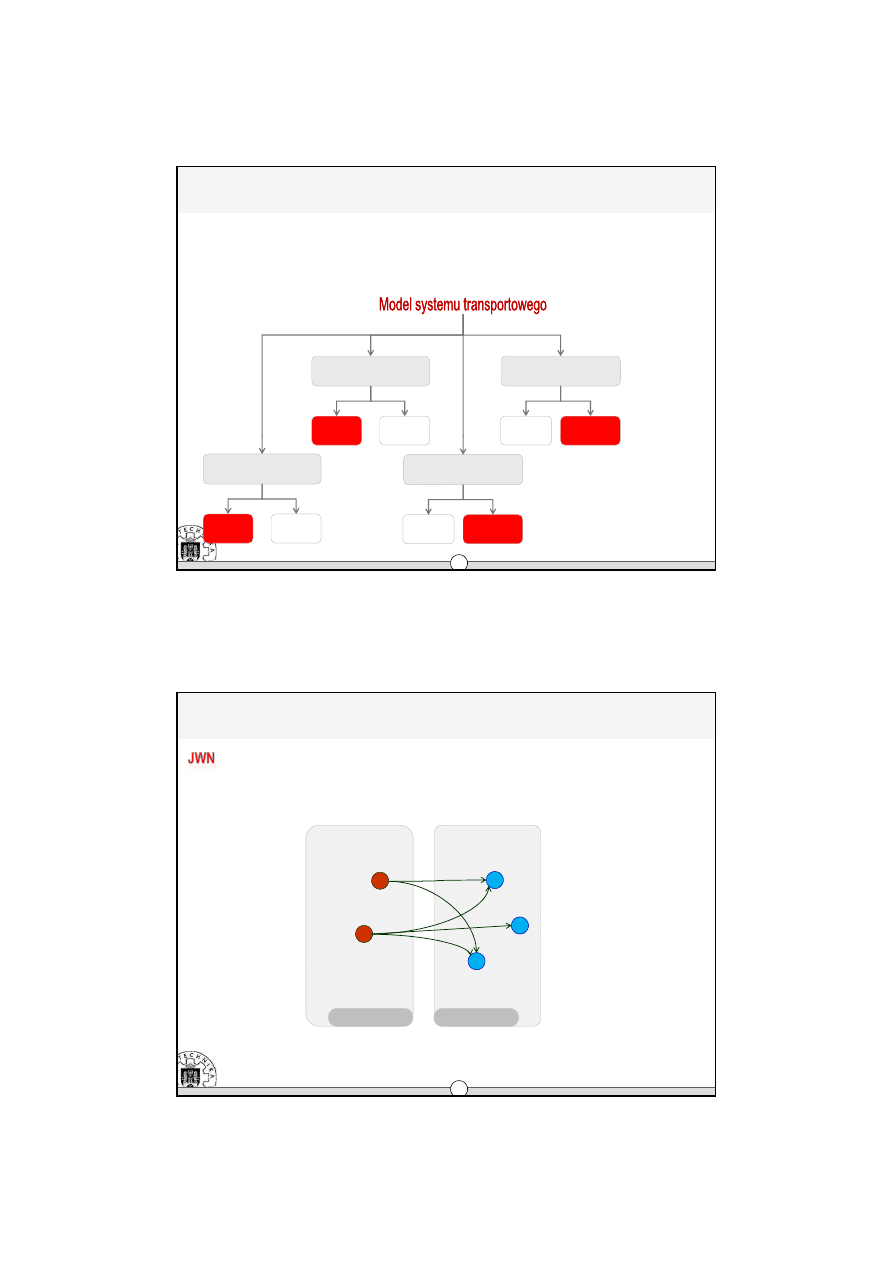
Klasyfikacja modeli systemów transportowych
- lokalizacja modelu JWN

Z uwagi na 

liczbę poziomów

Jedno-

poziomowy

Wielo-

poziomowy

Z uwagi na 

liczbę produktów

Jeden

produkt

Wiele

produktów

33

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

Z uwagi na 

wielkość obiektów mag.

poziomowy

poziomowy

Ograniczona 

wielkość

Nieograniczona

wielkość

produkt

produktów

Z uwagi na 

postać zmiennej decyzyjnej

Liniowy

Nieliniowy

Æ

Jedno-poziomowy (J), 
wielo-produktowy (W) model systemu transportowego
z nieograniczną (N) pojemnością magazynów

Model systemu transportowego

Klasyfikacja modeli

Model systemu transportowego

Klasyfikacja modeli

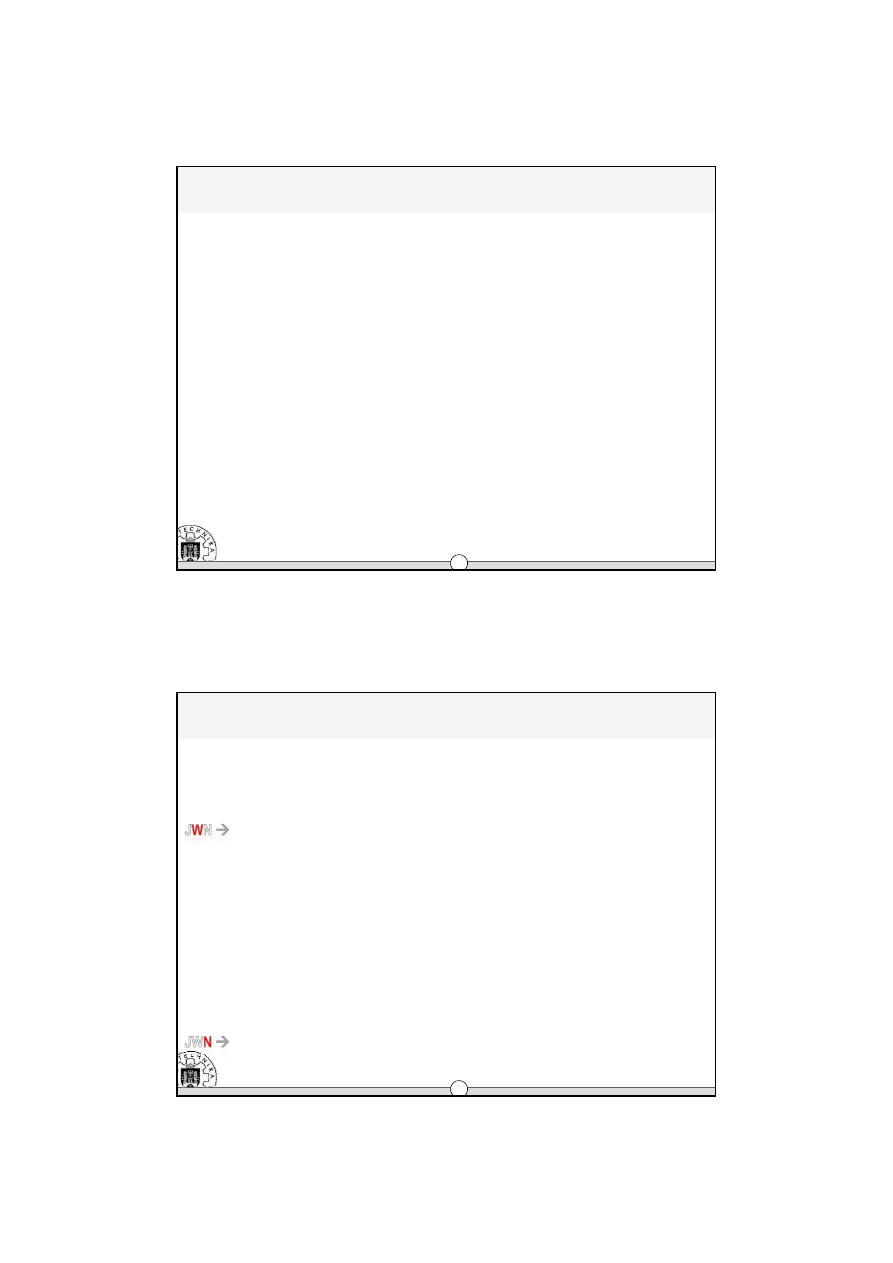
i

1

2

j

1

p=1,2,…,P

p=1,2,…,P

p=1,2,…,P

p=1,2,…,P

44

NADAWCY

ODBIORCY

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

j

p=1,2,…,P

Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

3

Model JWN

Założenia do modelowania

Model JWN

Założenia do modelowania

Æ

Podstawowe założenia

•

stosowane oznaczenia
i – indeks nadawcy (dostawcy); 

i = 1,2, …, I

j – indeks odbiorcy; 

j = 1,2, …, J

p – indeks produktu (wyrobu); 

p = 1,2, …, P

C

i

- pojemność magazynu i-tego nadawcy

D

j

- pojemność magazynu j-tego odbiorcy

55

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

D

j

pojemność magazynu j tego odbiorcy

T

jp

- zapotrzebowanie (popyt) j-tego odbiorcy na p-ty produkt

Z

ip

- potencjał (podaż) i-tego nadawcy związany z p-tym produktem

Model JWN

Założenia do modelowania

Model JWN

Założenia do modelowania

Æ

Podstawowe założenia

•

po stronie odbiorców (klientów) - j

–

znane (parametry)

{

skończona liczba odbiorców – j

{

skończona liczba produktów (wyrobów) – p; 

p ≥ 2

{

zapotrzebowanie j-tego odbiorcy na p-ty produkt -

T

jp

{

pojemność magazynu j-tego odbiorcy – D

j

•

po stronie nadawców

–

znane (parametry)

{

skończona liczba nadawców – i

{

jednostkowy koszty transportu p-tego produktu (wyrobu) z i-tego magazynu nadawcy do j-tego
magazynu odbiorcy – c

ijp

j d

k

  k

 

i  

d k   (

b )   i

  i  

d

 

66

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

{

jednostkowy koszty magazynowania p-tego produktu (wyrobu) w i-tym magazynie nadawcy –
h

ip

–

nieznane

{

ilość p-tego towaru (wyrobu) przetransportowana z i-tego magazynu nadania do j-tego
magazynu odbioru - x

ijp

(ZMIENNA DECYZYJNA)

{

pojemność magazynu (

nieograniczona

) i-tego nadawcy 

– C

i  

{

potencjał (podaż) i-tego nadawcy związany z p-tym produktem –

Z

ip

Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

4

Æ

Model matematyczny

•

funkcja celu

Model JWN

Modelowanie systemu

Model JWN

Modelowanie systemu

(

)

(

)

min

KM

KT

JWN

→

+

=

+

∑∑∑

=

=

=

I

i

J

j

P

p

ijp

ip

ijp

x

h

c

1

1

1

Minimalizacja kosztu transportowo-magazynowego funkcjonowania systemu 
logistycznego

=

=

=

i

j

p

1

1

1

1

1

c

21p

Parametry

x

21p

Zmienna decyzyjna

p=1,2,…,P

p=1,2,…,P

h

1p

1

1

77

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

2

2

j

NADAWCY

ODBIORCY

c

2jp

c

22p

2

NADAWCY

ODBIORCY

x

2jp

x

22p

p=1,2,…,P

i

p=1,2,…,P

p=1,2,…,P

p=1,2,…,P

h

2p

h

ip

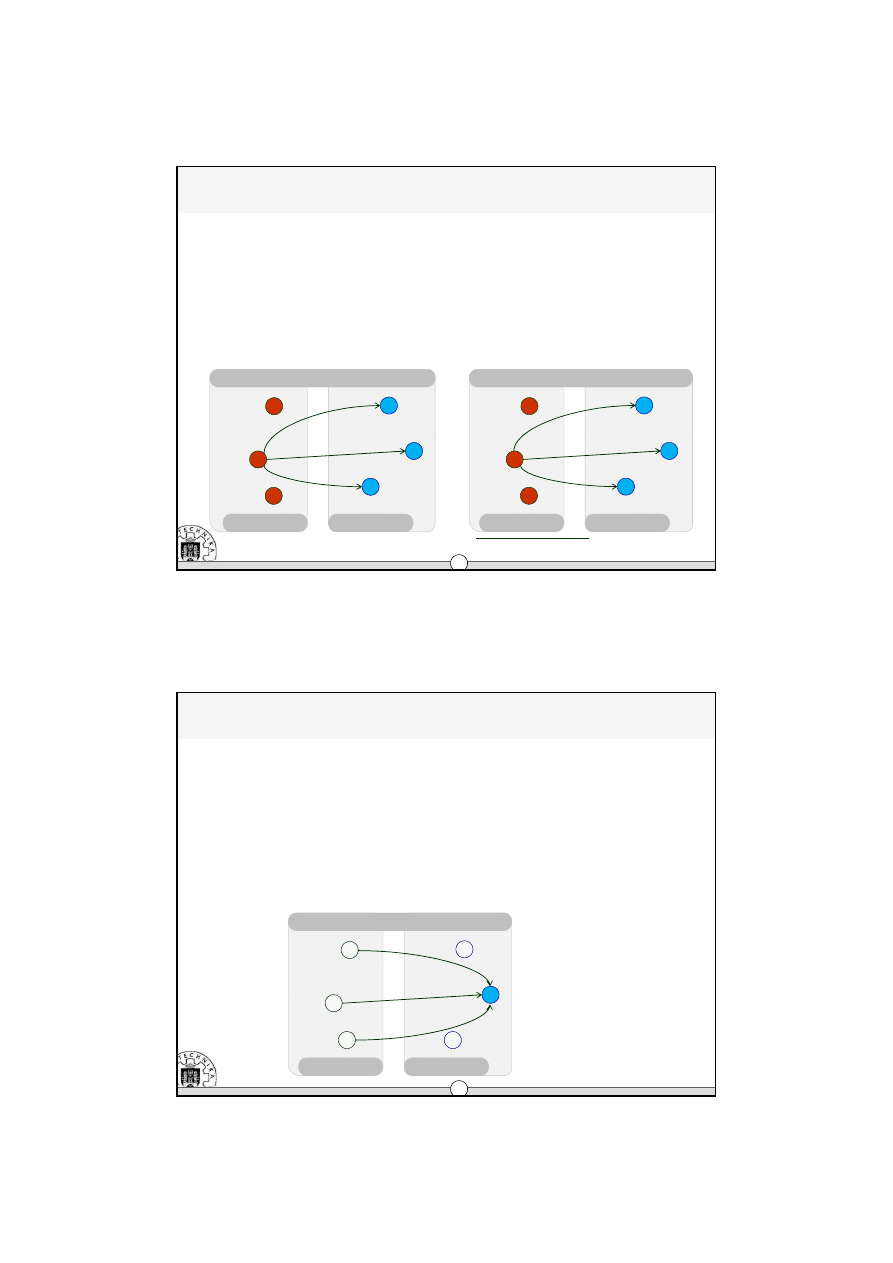
Uwaga,
Na wszystkich rysunkach zaznaczono tylko przykładowe relacje transportowe

2

j

i

Model JWN

Modelowanie systemu

Model JWN

Modelowanie systemu

Æ

Model matematyczny

•

ograniczenia po stronie odbiorców

–

popyt j-tego odbiorcy (klienta) na p-te produkty (wyroby) musi zostać w pełni zaspokojony przy 
uwzględnieniu dostaw ze wszystkich i-tych punktów nadania

I

P

np. dla p=2, i=3, j=1

x

121 

+ x

221 

+ x

321  

= T

21

oraz

P

p

J

j

T

x

jp

I

i

P

p

ijp

,...,

1,2

 ;

1,2,...,

 

  

;

=

=

∀

=

∑ ∑

=

=

1

1

1:

1:

1

1

x

12p

O

GRANICZENIE

1

p=1,2,…,P

88

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

x

122 

+ x

222 

+ x

323  

= T

22

2

2

j

NADAWCY

ODBIORCY

x

i2p

x

22p

i

p=1,2,…,P

p=1,2,…,P

p=1,2,…,P

Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

5

Model JWN

Modelowanie systemu

Model JWN

Modelowanie systemu

Æ

Model matematyczny

•

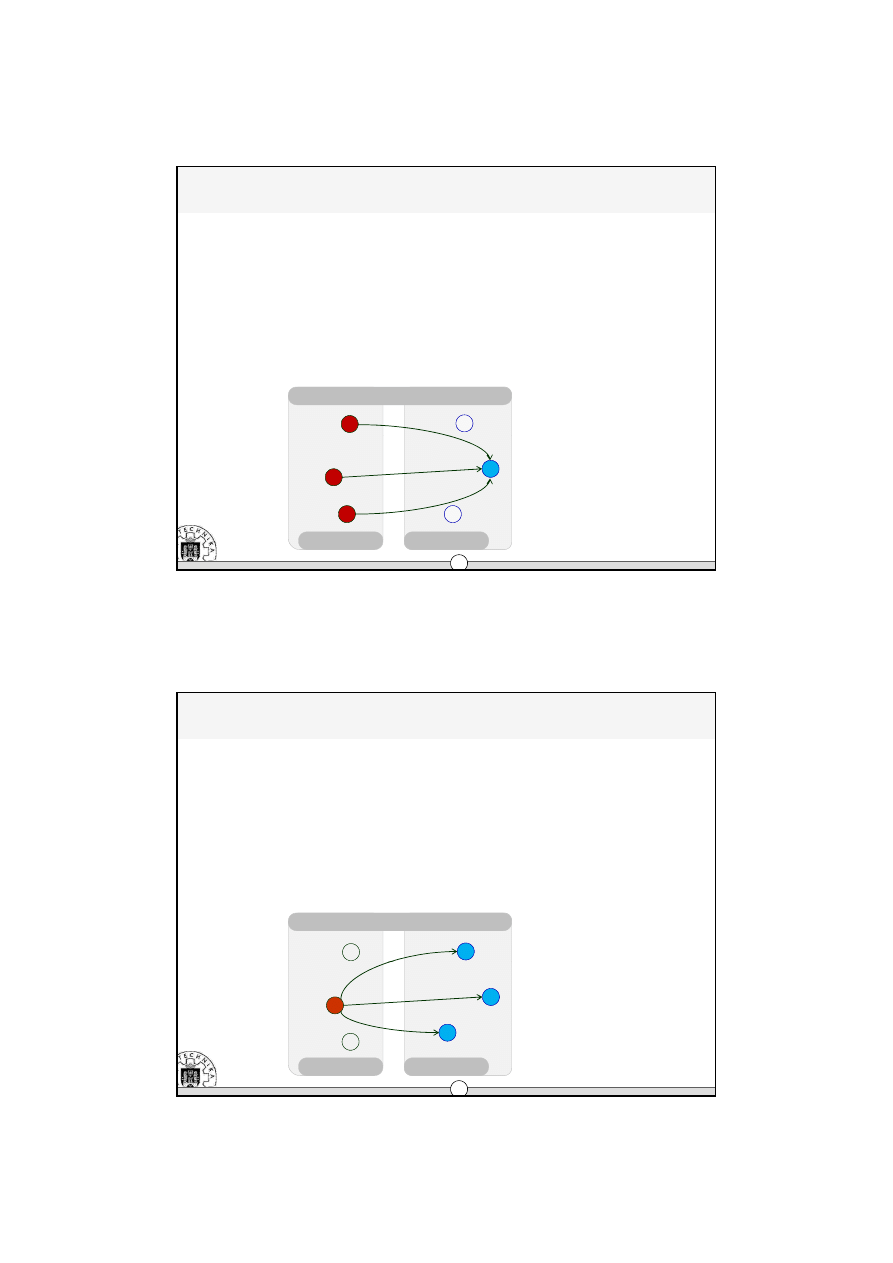
ograniczenia po stronie odbiorców

–

pojemność magazynu j-tego odbiorcy wynika z ilości zgromadzonych p-tych produktów 
(wyrobów) i jest znana

P

np. dla p=2, j=1
T

21 

+ T

21

= D

2

J

j

D

T

j

P

p

jp

1,2,...,

 

  

;

=

∀

=

∑

=1

2:

2:

1

1

x

121

O

GRANICZENIE

2

p=1

99

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

2

2

j

NADAWCY

ODBIORCY

x

i22

x

221;

x

222

i

p

p=1,2

p=2

p=1,2

Model JWN

Modelowanie systemu

Model JWN

Modelowanie systemu

Æ

Model matematyczny

•

ograniczenia po stronie nadawców

–

dostępność produktów w i-tym magazynie nadawcy wynika z zapotrzebowania obsługiwanych 
odbiorców (i jest nieznana)

J

np. dla p=2, i=1, j=3
T

12 

+ T

22 

+ T

32  

= Z

22

P

p

I

i

Z

T

ip

J

j

jp

,...,

1,2

 ;

1,2,...,

 

  

;

=

=

∀

=

∑

=1

3:

3:

O

GRANICZENIE

3

1

1

T

1p

10

10

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

NADAWCY

ODBIORCY

2

2

j

p=1,2,…,P

i

T

2p

T

jp

Z

2p

p=1,2,…,P

p=1,2,…,P

p=1,2,…,P

Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

6

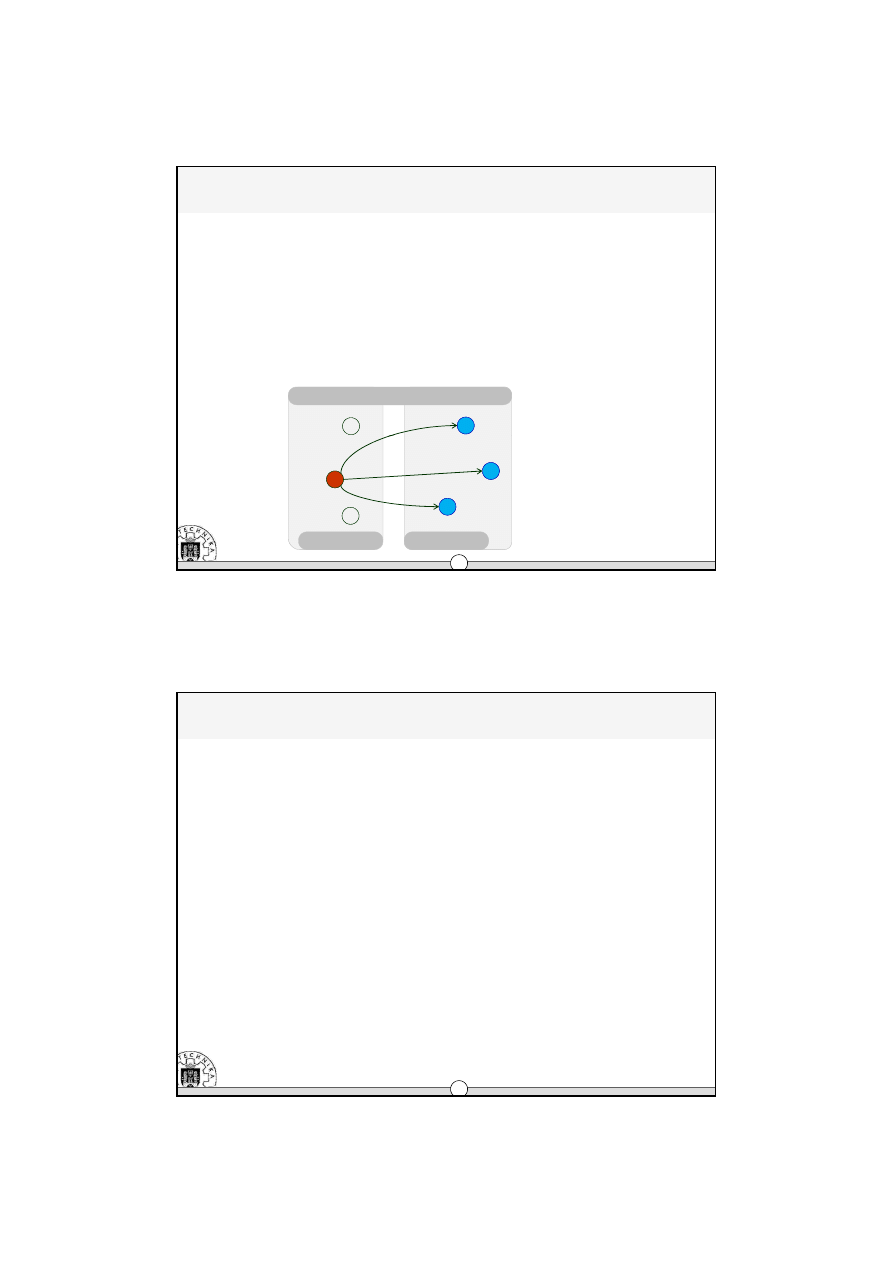
Model JWN

Modelowanie systemu

Model JWN

Modelowanie systemu

Æ

Model matematyczny

•

ograniczenia po stronie nadawców

–

pojemność i-tego magazynu nadawcy wynika z potoków towarowych  p-tych produktów 
dostarczanych do j-tych odbiorców

J

P

np. dla p=2, i=1, j=3
C

2 

= x

211 

+ x

221  

+ x

231

I

i

x

C

J

j

P

p

ijp

i

1,2,...,

 

  

;

=

∀

=

∑ ∑

=

=

1

1

4:

4:

O

GRANICZENIE

4

1

1

x

21p

p=1 2

P

11

11

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

2 

211 

221  

231

+ x

212 

+ x

222  

+ x

232

NADAWCY

ODBIORCY

2

2

j

p=1,2,…,P

i

C

i

x

2jp

x

22p

p=1,2,…,P

p=1,2,…,P

p=1,2,…,P

Model JWN

Modelowanie systemu

Model JWN

Modelowanie systemu

Æ

Model matematyczny

•

funkcja celu

(

)

(

)

min

KM

KT

JWN

→

+

=

+

∑∑∑

I

i

J

j

P

p

ijp

ip

ijp

x

h

c

1

1

1

•

ograniczenia

=

=

=

i

j

p

1

1

1

P

p

J

j

T

x

jp

I

i

P

p

ijp

,...,

1,2

 ;

1,2,...,

 

  

;

=

=

∀

=

∑∑

=

=

1

1

1:

1:

J

j

D

T

j

P

p

jp

1,2,...,

 

  

;

=

∀

=

∑

=1

2:

2:

J

12

12

P

p

I

i

Z

T

ip

J

j

jp

,...,

1,2

 ;

1,2,...,

 

  

;

=

=

∀

=

∑

=1

3:

3:

I

i

x

C

J

j

P

p

ijp

i

1,2,...,

 

  

;

=

∀

=

∑∑

=

=

1

1

4:

4:

Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

7

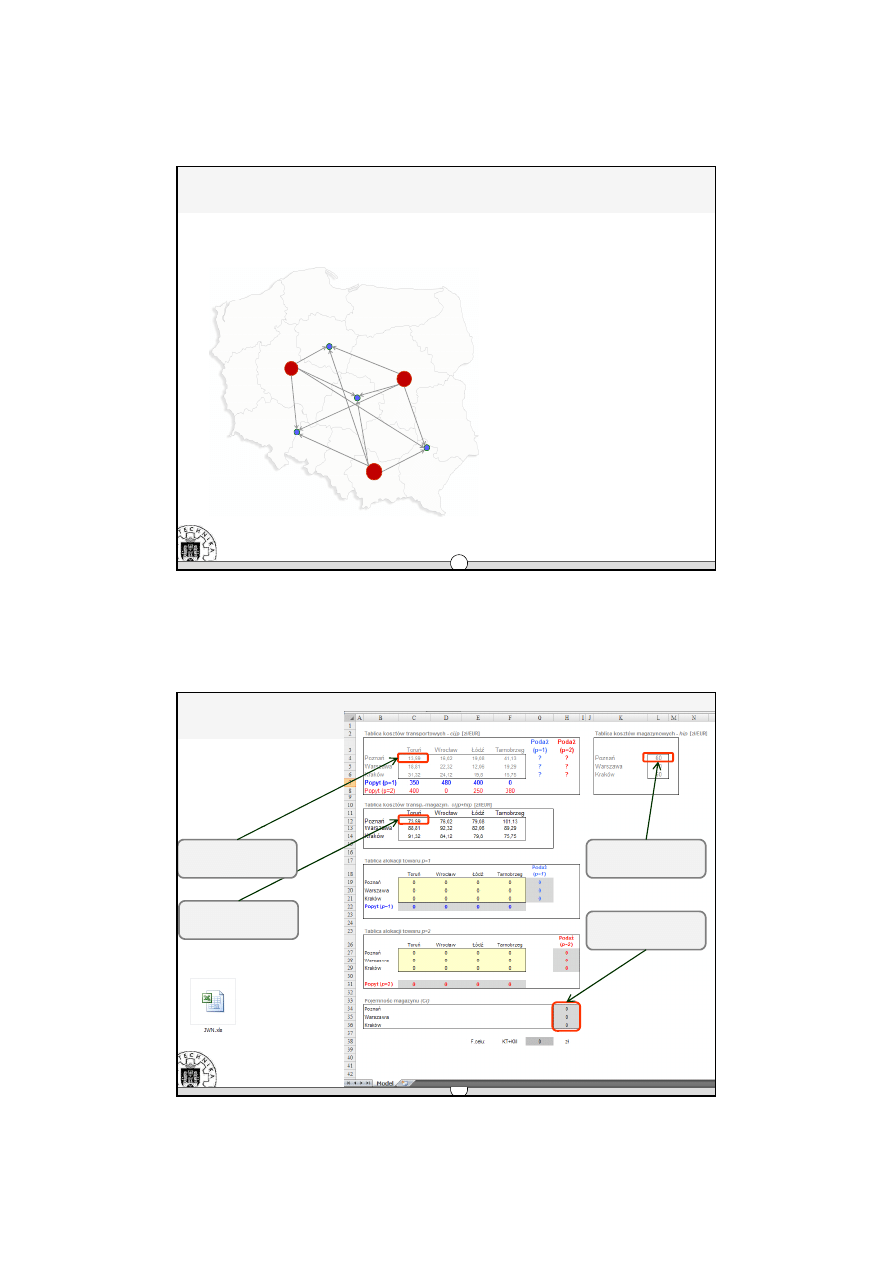
Model JWN

Zastosowanie modelu

Model JWN

Zastosowanie modelu

Æ

Analizowany problem

•

i = 3, j = 4, p=3

1

2

1

4

2

(?)

(? )

13

13

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

3

4

3

(?)

Model JWN

Zastosowanie modelu

Model JWN

Zastosowanie modelu

Koszt transportu 

i magazynowania 1 EUR

nieznana (poszukiwana) 

pojemność magazynów

Koszt transportu 

1 EUR

Koszt magazynowania 

1 EUR

14

14

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

8

Model JWN

Zastosowanie modelu

Model JWN

Zastosowanie modelu

15

15

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

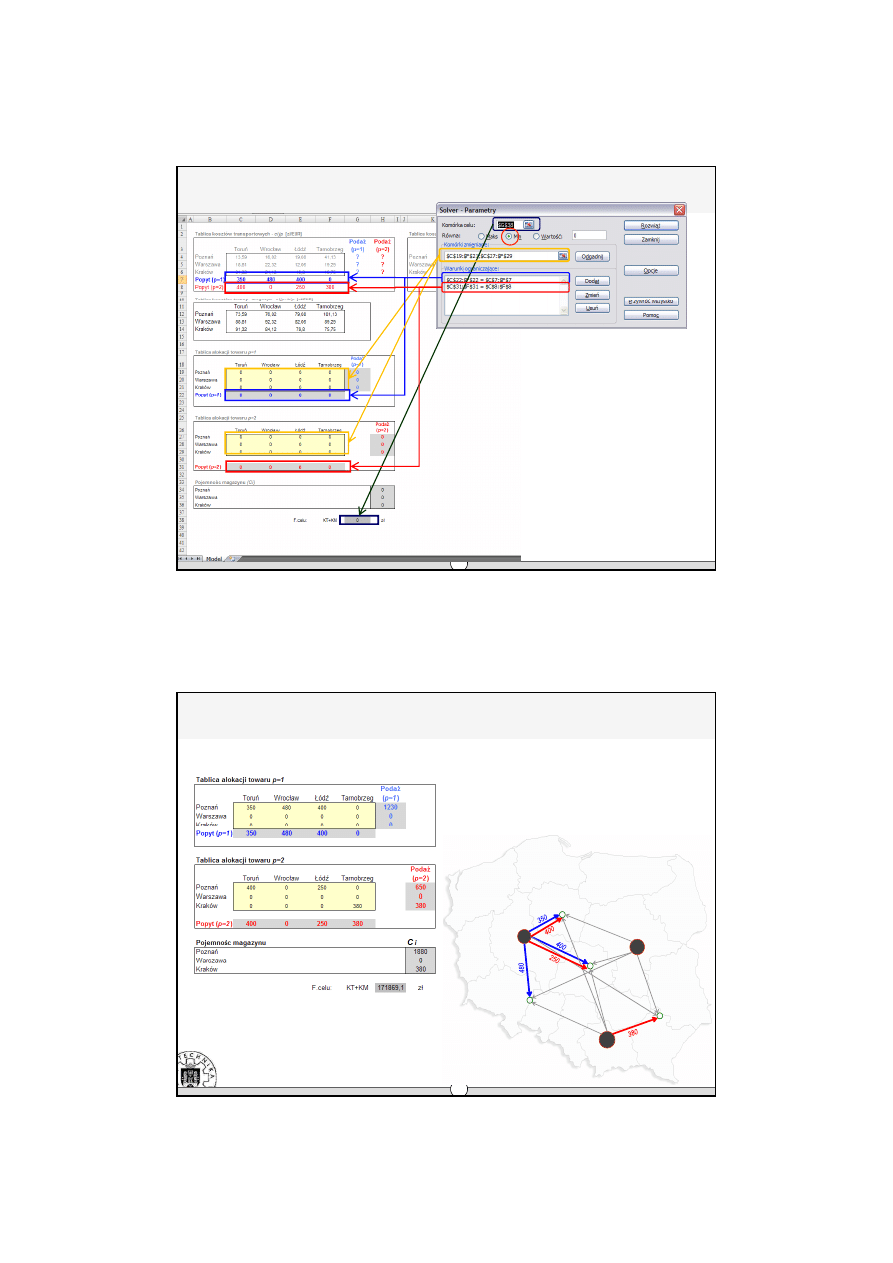
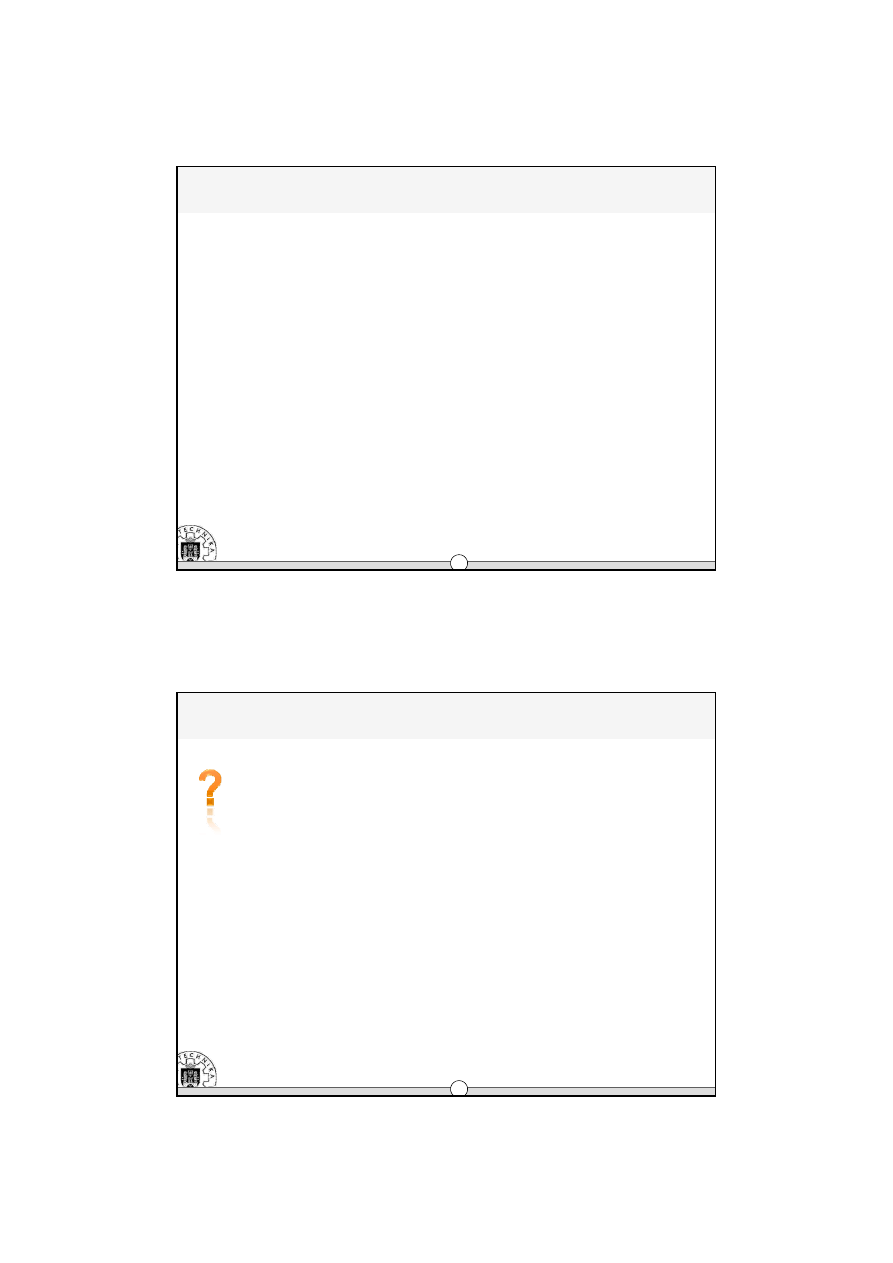
Model JWN

Zastosowanie modelu | Rozwiązanie

Model JWN

Zastosowanie modelu | Rozwiązanie

Æ

Rozwiązanie

1

2

1

2

(1880)

(0 )

(

1230 + 

650

)

16

16

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

3

4

3

(380)

(

380

)

Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

9

Podsumowanie

Podsumowanie

Æ

Zakres zastosowania modelu JWN

•

pozwala określić

–

liczbę i lokalizację magazynów w sieci

{

ile ich jest i gdzie są zlokalizowane?

d i ł  kli tó   ( dbi ó )  d  

ó   (d t

ó ) 

–

przydział klientów (odbiorców) do magazynów (dostawców) 

{

kto kogo obsługuje?

–

plan przewozowy w sieci transportowo-magazynowej (logistycznej) osobno dla każdego z 
produktów (wyrobów)

{

skąd dokąd wożony jest towar konkretnego typu?

•

zakres stosowania modelu 

–

krótkie kanały dystrybucji (dostawca - odbiorca)

–

systemy wielo-produktowe (realne przypadki biznesowe – sieci handlowe)

17

17

•

mankamenty modelu

–

nie uwzględnia stałych kosztów posiadania magazynów

–

nie pozwala dokonywać przerzutów międzymagazynowych

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

Podsumowanie

Podsumowanie

Æ

Zadanie do realizacji z zakresu modelu klasy JWN

•

zbudować model JWN uwzględniający stałe koszty 
posiadania magazynów wysyłkowych (nadawców)

•

zweryfikować jego poprawność (w opraciu o Solver)

•

porównać wyniki uzyskane dla modelu JWN bez stałych 
kosztów magazynowania

18

18

Piotr Sawicki |  Modelowanie procesów i systemów transportowych

Modelowanie procesów i systemów 
transportowych

dr inż. Piotr Sawicki

10

temów transportowychtemów transportowych

Modele sieci transportowej

Model JWN

Modele sieci transportowej

Model JWN

Modelowanie 

procesów i sys

t

Modelowanie 

procesów i sys

t

Piotr Sawicki

Piotr Sawicki

Zakład Logistyki | WMRiT 

pok. 742, tel. 665 22 49 
piotr.sawicki@put.poznan.pl |  www.put.poznan.pl/~piotr.sawicki

Zakład Logistyki | WMRiT 

pok. 742, tel. 665 22 49 
piotr.sawicki@put.poznan.pl |  www.put.poznan.pl/~piotr.sawicki