Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
1
1
1. SZACOWANIE MODELU LINIOWEGO Z DWIEMA
ZMIENNYMI OBJAŚNIAJĄCYMI
1.1 DANE DO ZADANIA
Oszacować KMNK parametry następującego modelu:
t
t
t
t
x
b
x
b
b
y
ε
+
+
+
=
2
2
1
1
0
gdzie:
y – podaż pieniądza M2 [mld zł],
x
1
– stopa redyskontowa banku centralnego,
x
2
– Produkt Krajowy Brutto [mld zł].
Ponadto:
1. Zinterpretuj wpływ zmiennych objaśniających na zmienną objaśnianą.
2. Oblicz miary dopasowania modelu i zinterpretuj je.
3. Oszacuj średnie błędy ocen parametrów modelu.
4. Oceń istotność zmiennych objaśniających i wykonaj estymację przedziałową parametrów
strukturalnych modelu.
5. Oceń istotność autokorelacji składnika losowego pierwszego rzędu testem DW.
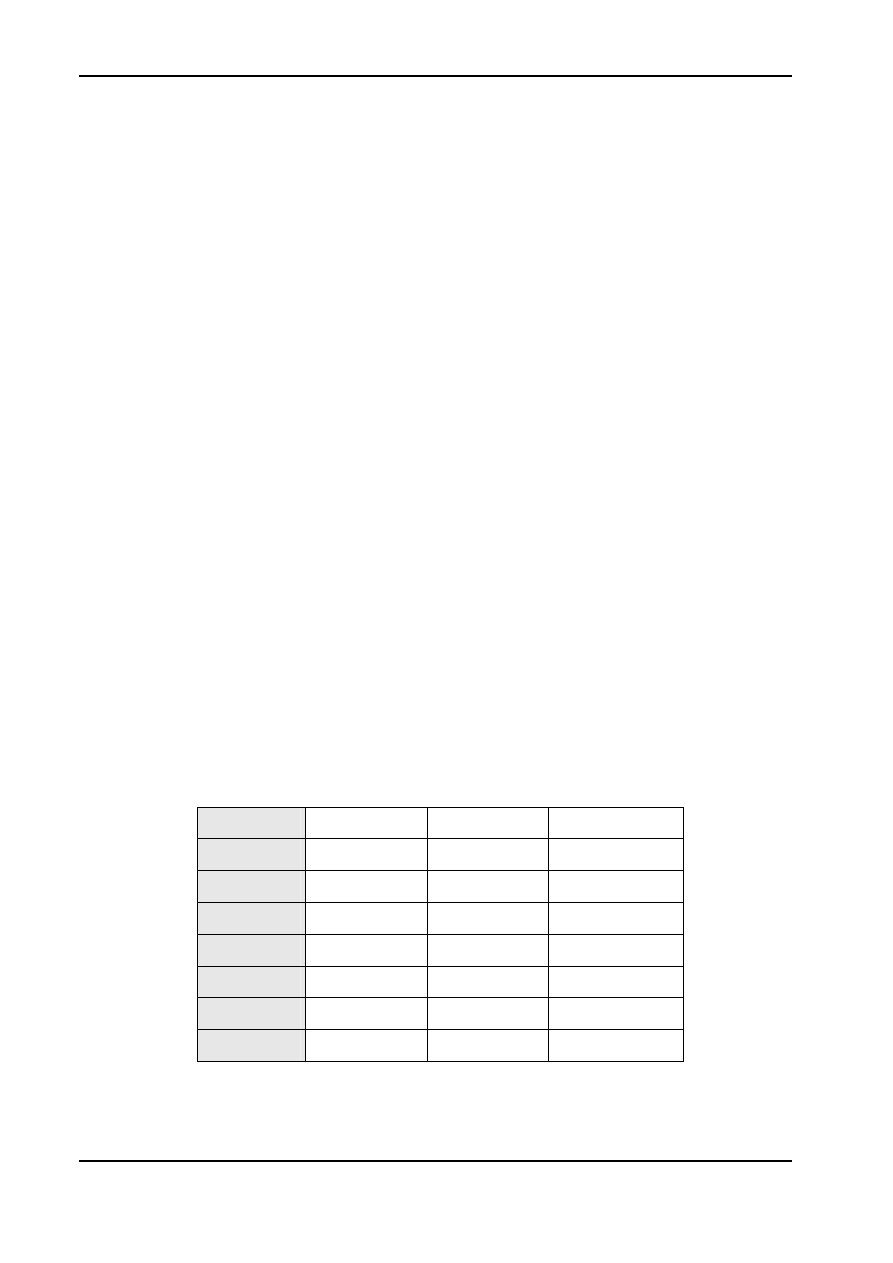
Dane do zadania przedstawia poniższa tabela.
okres y
t
x
1t
x
2t
1 23 9,5 4,5
2 25 9,25 5,1
3 27 9,25 5,7
4 28 8,75 5,8
5 32 8 6,1
6 35 7,25 7
7 40 6 8,4
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
2
2
1.2 SZACOWANIE PARAMETRÓW STRUKTURALNYCH MODELU
Estymator KMNK dla potrzeb naszego zadania zapiszemy w postaci:
(
)
y
X
X
X
b
T
T
1
ˆ
−
=
Konstruując macierz X
T
X zauważmy, że w modelu występują trzy parametry, co determinuje
wymiary tej macierzy. Posługując się schematem konstrukcyjnym tej macierzy zapiszemy, że:
( )
3
3
2
2
2
1
2
2
1
2
1
1
2
1
×
⋅
⋅
=
∑
∑
∑
∑
∑
∑
∑
∑
t
t
t
t
t
t
t
t
t
t
T
x
x
x
x
x
x
x
x
x
x
n
X
X
Natomiast macierz X
T
y przyjmie postać:
)
1
3
(
2
1
×
=
∑
∑
∑
t
t
t
t
t
T
x
y
x
y
y
y
X
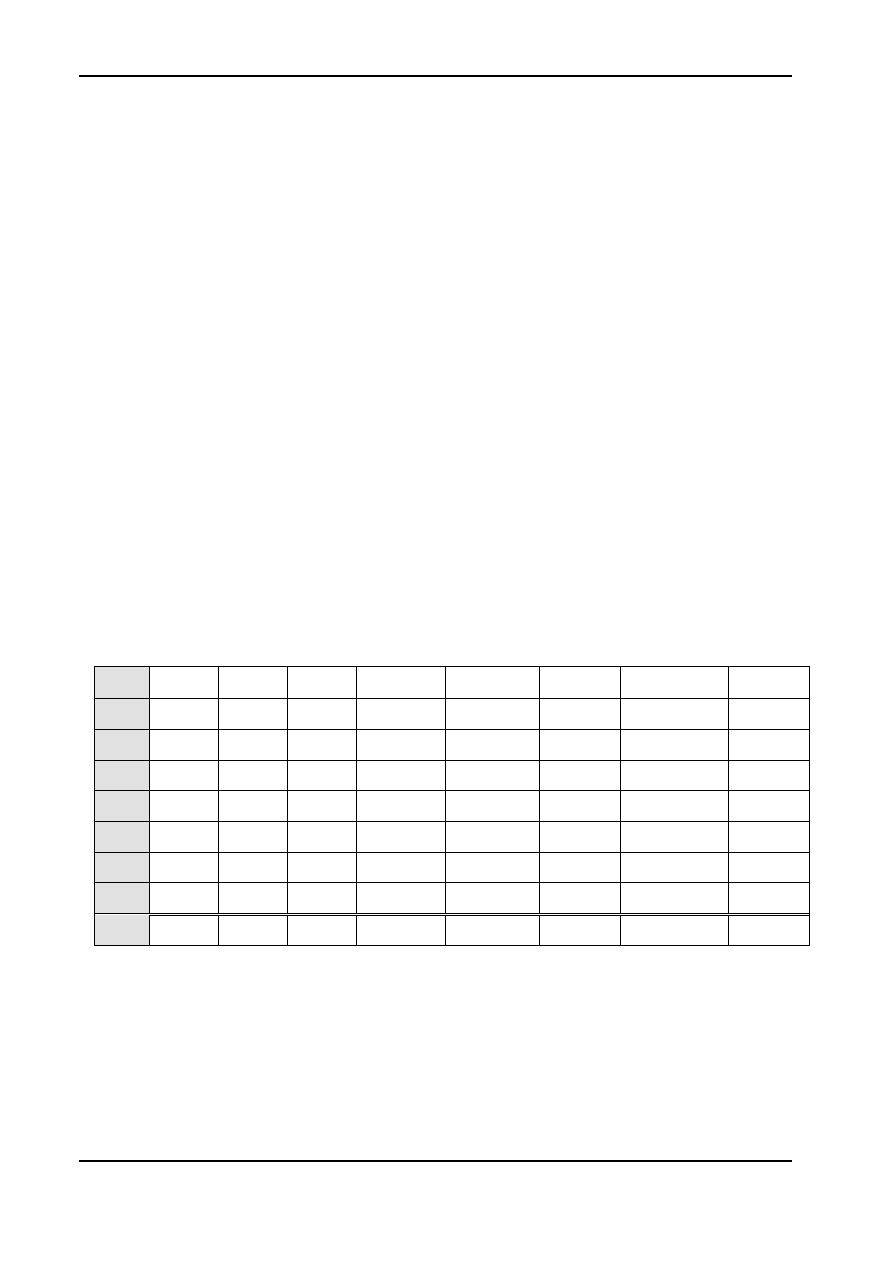
Posługując się poniższa tabelą wyznaczymy wielkości występujące w macierzach:
okres y
t
x
1t
x
2t
x
1t
x
2t
y
t
x
1t
y
t
x
2t
x
1t
2
x
2t
2
1
23 9,5 4,5 42,75 218,5 103,5 90,25 20,25
2
25 9,25 5,1 47,175 231,25 127,5 85,5625 26,01
3
27 9,25 5,7 52,725 249,75 153,9 85,5625 32,49
4
28 8,75 5,8 50,75 245 162,4 76,5625 33,64
5
32 8 6,1 48,8 256 195,2 64 37,21
6
35 7,25 7 50,75 253,75 245 52,5625 49
7
40 6 8,4 50,4 240 336 36 70,56
suma
210 58 42,6
343,35
1694,25
1323,5 490,5 269,16
Możemy zatem zapisać interesujące nas macierze następująco:
=
16
,
269
35
,
343
6
,
42
35
,
343
5
,
490
58
6
,
42
58
7
)
(
X
X
T
=
5
,
1323
25
,
1694
210
y
X
T

Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
3
3
Macierz
X
T
X należy odwrócić, zgodnie z formułą:
X
X
X
X
X
X
T
D
T
T
)
(
)
(
1
=
−
Dopełnienia algebraiczne elementów macierzy X
T
X, które wchodzą w skład macierzy (X
T
X)
D
obliczamy następująco:
C
M
ij
i j
ij
≡ −
⋅
+
(
)
1
gdzie:
|C
ij
| - dopełnienie algebraiczne elementu macierzy X
T
X dla i-tego wiersza i j-tej kolumny,
|M
ij
| - minor elementu dla i-tego wiersza i j-tej kolumny,
i
- numer wiersza,
j
- numer kolumny.
Stąd np. dla elementu 7 (wiersz 1, kolumna 1) z macierzy (X
T
X) dopełnienie jest następujące:
7575
,
14133
16
,
269
35
,
343
35
,
343
5
,
490
)
1
(
1
1
11
=
⋅
−
≡
+
C
Podobnie obliczamy dopełnienia dla pozostałych elementów i otrzymujemy macierz:
−
−
−
−
=
5
,
69
35
,
67
981
35
,
67
36
,
69
57
,
984
981
57
,
984
7575
,
14133
)
(
D
T
X
X
Następnie obliczamy wyznacznik macierzy X
T
X:
6425
,
40
=
X
X
T
Stąd ostatecznie otrzymujemy macierz odwrotną:

Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
4
4
−
−
−
−
=
−
71003
,
1
65713
,
1
13729
,
24
65713
,
1
70659
,
1
22513
,
24
13729
,
24
22513
,
24
75807
,
347
)
(
1
X
X
T
Możemy zatem obliczyć oceny parametrów strukturalnych modelu:
2
1
0
1
ˆ
ˆ
ˆ
99268
,
1
67688
,
2
05296
,
40
5
,
1323
25
,
1694
210
71003
,
1
65713
,
1
13729
,
24
65713
,
1
70659
,
1
22513
,
24
13729
,
24
22513
,
24
75807
,
347
)
(
ˆ
b
b
b
y
X
X
X
b
T
T
←
−
=
⋅
−
−
−
−
=
=
−
Mając szacunki punktowe parametrów zapiszemy model w postaci teoretycznej:
t
t
t
x
x
y
2
1
99268
,
1
67688
,
2
05296
,
40
ˆ
⋅
+
⋅
−
=
1.3 INTERPRETACJA MODELU
Na podstawie przedstawionego modelu możemy dokonać oceny wpływu zmiennych
objaśniających (stopy dyskontowej oraz PKB) na wielkość podaży pieniądza:
• wzrost stopy redyskontowej o 1 punkt procentowy powodował w badanym okresie spadek
podaży pieniądza średnio o 2,677 mld złotych (spadek stopy dyskontowej o 1 punkt
procentowy powodował w badanym okresie wzrost podaży pieniądza średnio o 2,677 mld
złotych), przy założeniu stałości zmiennej x
2
czyli PKB
• wzrost PKB o 1 mld złotych powodował w badanym okresie wzrost podaży pieniądza średnio
o 1,993 mld złotych (spadek PKB o 1 mld złotych powodował w badanym okresie spadek
podaży pieniądza średnio o 1,993 mld ), przy założeniu stałości x
1
czyli stopy redyskontowej
1.4 REPREZENTACJA GRAFICZNA UZYSKANYCH WYNIKÓW
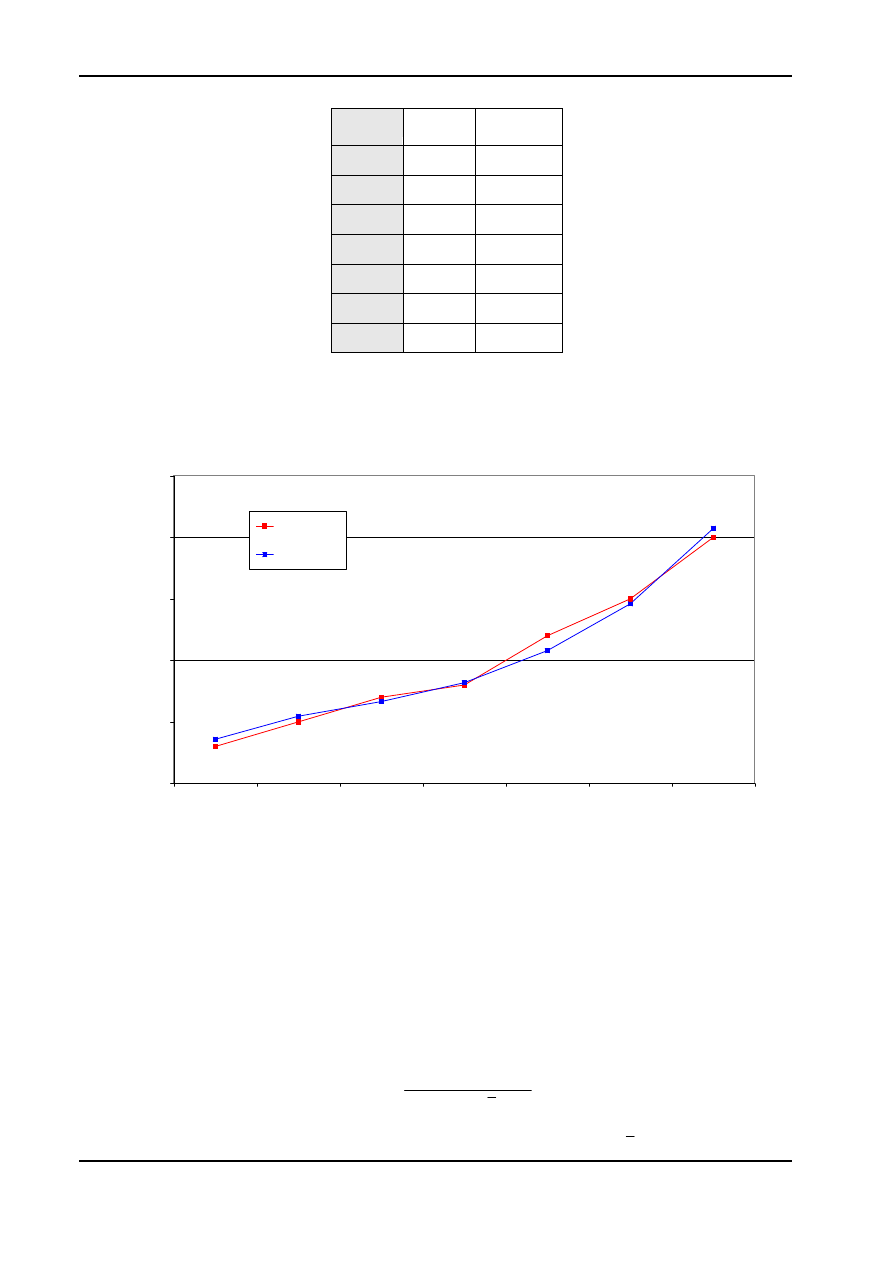
Jeżeli obliczymy na podstawie powyższego modelu teoretyczne wartości zmiennej y to
otrzymamy wartości
t
yˆ , jak przedstawiono w tabeli:
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
5
5
okres y
t
t
yˆ
1
23 23,58968
2
25 25,45451
3
27 26,65012
4
28 28,18783
5
32 30,79329
6
35 34,59436
7
40 40,73021
Na podstawie tych danych możemy wykonać wykres przedstawiający dopasowanie danych
teoretycznych zmiennej objaśnianej do danych rzeczywistych.
Jak
widać dopasowanie punktów teoretycznych do rzeczywistych jest dość dobre. Aby ocenić
dopasowanie bardziej precyzyjnie obliczamy statystyczne miary dopasowania:
1.5 MIARY DOPASOWANIA
1.
Współczynnik zbieżności
2
2
2
)
(
ˆ
)
(
∑
∑
−
−
=
y
y
b
y
X
y
t
T
T
t
ϕ
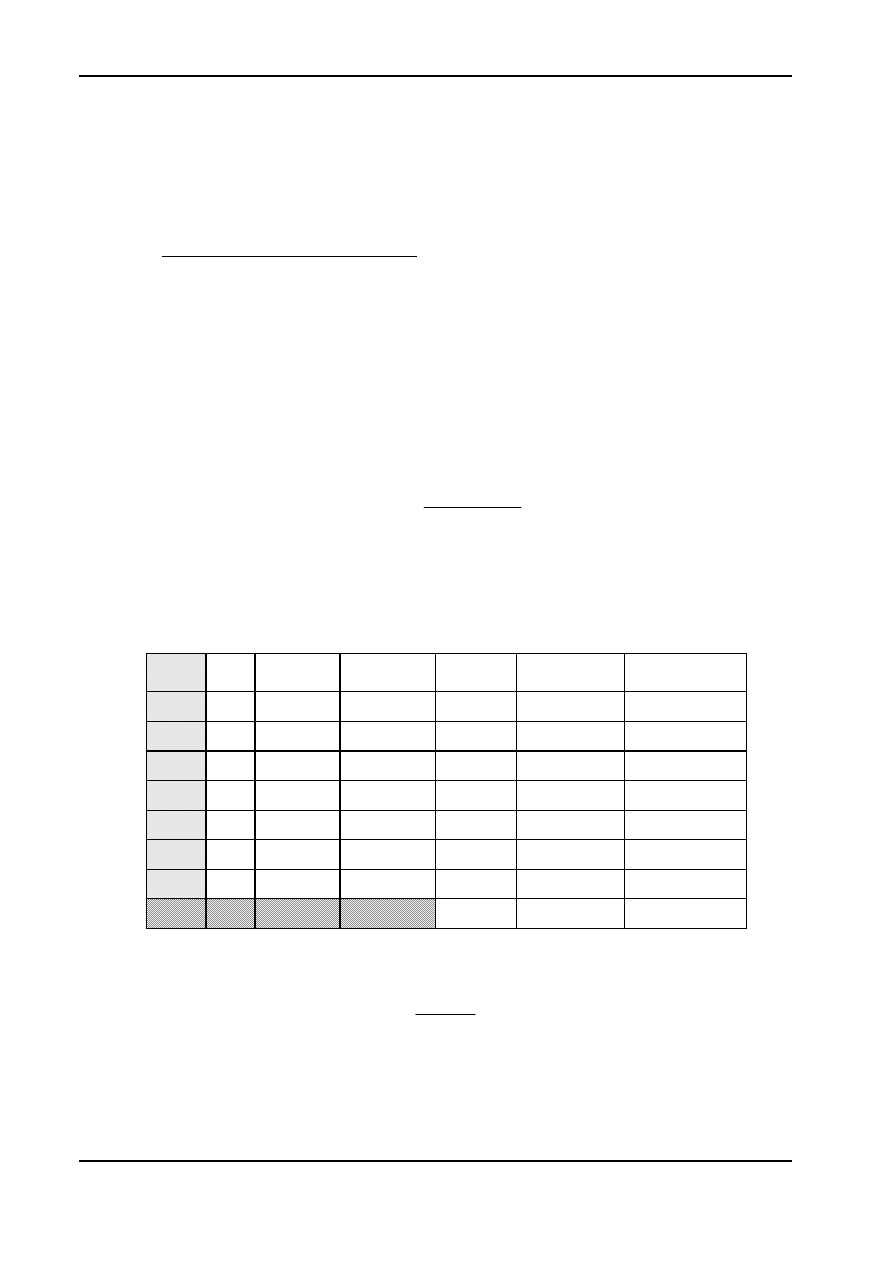
Dane do powyższej formuły obliczamy w tabeli (średnia arytmetyczna
30
=
y
):
20
25
30
35
40
45
1
2
3
4
5
6
7
y
y teoretyczne
okres
P
oda
ż pi
eni
ąd
za
[mld
z
ł]

Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
6
6
okres
2
t
y
2
)
(
y
y
t
−
1
529 49
2
625 25
3
729 9
4
784 4
5
1024 4
6
1225 25
7
1600 100
suma
6516 216
[
]
216
12964
,
6513
6516
216
99268
,
1
67688
,
2
05296
,
40
5
,
1323
25
,
1694
210
6516
2
−
=
−
⋅
−
=
ϕ
0132
,
0
2
=
ϕ
Interpretując współczynnik zbieżności powiemy, że 1,32 % całkowitej zmienności podaży
pieniądza nie zostało wyjaśnione przez model, czyli przez zmienność stopy dyskontowej x
1
oraz
zmienność PKB x
2
.
2.
Współczynnik determinacji
Współczynnik ten obliczymy korzystając ze wzoru:
9868
,
0
0132
,
0
1
1
2
2
=
−
=
−
=
ϕ
R
Powiemy, że 98,68 % całkowitej zmienności podaży pieniądza zostało wyjaśnione przez model,
czyli przez zmienność stopy dyskontowej oraz PKB.
Dodatkowo
można by obliczyć tzw. skorygowany współczynnik determinacji, który jest
dokładniejszą miarą wyjaśnionej części całkowitej wariancji zmiennej objaśnianej (oznaczamy
go
2
R ), ale pominiemy te obliczenia.

Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
7
7
3. Wariancja reszt modelu
[
]
4
12964
,
6513
6516
)
1
2
(
7
99268
,
1
67688
,
2
05296
,
40
5
,
1323
25
,
1694
210
6516
)
1
(
ˆ
)
(
ˆ
2
2
−
=
+
−
−
⋅
−
=
+
−
−
=
∑
k
n
b
y
X
y
T
T
t
ε
σ
7176
,
0
4
87036
,
2
ˆ
2
=
=
ε
σ
4. Na postawie wariancji wyznaczamy średni błąd resztowy:
8471
,
0
7176
,
0
ˆ
=
=
ε
σ
mld zł.
Wartość średniego błędu reszt wskazuje, że wartości teoretyczne
t
yˆ różnią się od wartości
empirycznych y
t
średnio o 0,8471 mld zł.
Ponieważ błąd średni regresji jest miarą bezwzględną można dodatkowo obliczyć miernik
pozwalający porównać go z wartościami zmiennej objaśnianej y. Na tej podstawie obliczamy
współczynnik zmienności losowej:
%
82
,
2
100
30
8471
,
0
100
ˆ
=
⋅
=
⋅
=
y
v
ε
σ
Powyższa wartość oznacza, że reszty modelu stanowią przeciętnie około 2,82% wartości
zmiennej objaśnianej y.
1.6 ŚREDNIE BŁĘDY OCEN PARAMETRÓW STRUKTURALNYCH MODELU
Aby
oszacować średnie błędy ocen parametrów naszego modelu należy znać szacunki wariancji
ocen parametrów. Dlatego należy wyznaczyć realizację macierzy wariancji-kowariancji ocen
parametrów.
(
)
=
−
−
−
−
⋅
=
⋅
=
−
71003
,
1
65713
,
1
13729
,
24
65713
,
1
70659
,
1
22513
,
24
13729
,
24
22513
,
24
75807
,
347
7176
,
0
ˆ
)
ˆ
(
1
2
2
X
X
b
D
T
ε
σ

Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
8
8
−
−
−
−
=
1 , 2 2 7 1 2
1 , 2 2 4 6 5
2 4 9 , 5 5 1 1 9
18916
,
1
32092
,
17
18916
,
1
38395
,
17
32092
,
17
38395
,
17
Pierwiastki
elementów
leżących na głównej przekątnej powyższej macierzy to właśnie średnie
błędy ocen parametrów, a zatem:
10775
,
1
22712
,
1
ˆ
10664
,
1
22465
,
1
ˆ
79719
,
15
55119
,
249
ˆ
2
1
0
ˆ
ˆ
ˆ
±
=
=
±
=
=
±
=
=
b
b
b
σ
σ
σ
Wobec tego możemy zapisać model w postaci uwzględniającej obliczone odchylenia
standardowe ocen parametrów:
(
)
(
)
(
)
t
t
t
x
x
y
2
10775
,
1
1
10664
,
1
79719
,
15
99268
,
1
67688
,
2
05296
,
40
ˆ
⋅
+
⋅
−
=
±
±
±
1.7 TEST ISTOTNOŚCI ZMIENNYCH OBJAŚNIAJĄCYCH
Zakładając, że składnik losowy spełnia własności normalności rozkładu, stałości wariancji oraz
braku istotnej autokorelacji możemy wykonać ocenę istotności zmiennych objaśniających modelu za
pomocą testu t-Studenta.
Dla parametru b
1
stawiamy zestaw hipotez:
H
0
: b
1
= 0, H
A
: b
1
≠ 0.
Dla parametru b
2
stawiamy zestaw hipotez:
H
0
: b
2
= 0, H
A
: b
2
≠ 0.
Obliczmy statystyki próbkowe dla parametrów b
1
i b
2
:
418
,
2
10664
,
1
67688
,
2
ˆ
ˆ
1
1
ˆ
1
ˆ
=
−
=
=
b
b
b
t
σ
799
,
1
10775
,
1
99268
,
1
ˆ
ˆ
2
2
ˆ
2
ˆ
=
=
=
b
b
b
t
σ
Przy
założeniu prawdziwości hipotez zerowych powyższe statystyki mają rozkłady t-Studenta o
n-(k+1) stopniach swobody, wobec tego, przy założonym poziomie istotności dla testu dwustronnego
(
α = 0,1), znajdujemy w tablicach statystycznych wartość krytyczną rozkładu t:

Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
9
9
132
,
2
05
,
0
2
=
= t
t
a
Porównując statystyki próbkowe z wartością krytyczną otrzymujemy:
•
2
ˆ
1
α
t
t
b
>
zatem odrzucamy hipotezę H
0
na korzyść hipotezy H
A
, czyli stwierdzamy, że
parametr b
1
istotnie różni się od 0, co oznacza, że zmienna x
1
(stopa dyskontowa banku)
istotnie wpływała w badanym okresie na podaż pieniądza,
•
2
ˆ
2
α
t
t
b
<
zatem nie ma podstaw do odrzucenia H
0
, czyli uznajemy parametr b
1
za nieistotnie
różny od 0, co oznacza, że zmienna x
2
(Produkt Krajowy Brutto) nieistotnie wpływała w
badanym okresie na podaż pieniądza.
W takim wypadku należałoby usunąć zmienną x
2
z modelu i dokonać ponownego oszacowania
modelu tylko z jednym regresorem, czyli ze zmienną objaśniającą x
1
.
1.8 PRZEDZIAŁY UFNOŚCI PARAMETRÓW STRUKTURALNYCH
Estymacja
punktowa
pozwoliła dla warunków naszego zadania znaleźć liczbowe oceny
parametrów modelu
2
1
0
ˆ
,
ˆ
,
ˆ
b
b
b
(wartości oczekiwane tych estymatorów). Ponieważ, przy spełnieniu
założeń regresji liniowej dla wielu zmiennych objaśniających, estymatory te mają rozkłady normalne
to możemy także znaleźć ich charakterystyki przedziałowe. W tym celu skonstruujemy tzw.
przedziały ufności dla parametrów analizowanego modelu, przy założonym poziomie ufności.
Załóżmy, że poziom ufności 1-
α = 0,9, a zatem konstrukcja przedziału ufności dla parametru b
i
będzie następująca:
(
)
9
,
0
ˆ
ˆ
ˆ
ˆ
ˆ
05
,
0
ˆ
05
,
0
=
⋅
+
≤
≤
⋅
−
i
i
b
i
i
b
i
t
b
b
t
b
P
σ
σ
Stąd:
(
)
(
)
(
)
9
,
0
73256
,
73
37335
,
6
79719
,
15
132
,
2
05296
,
40
79719
,
15
132
,
2
05296
,
40
ˆ
ˆ
ˆ
ˆ
0
0
ˆ
05
,
0
0
0
ˆ
05
,
0
0
0
0
=
≤
≤
=
⋅
+
≤
≤
⋅
−
=
=
⋅
+
≤
≤
⋅
−
b
P
b
P
t
b
b
t
b
P
b
b
σ
σ
Powiemy
zatem,
że oszacowany przedział jest jednym z tych przedziałów, które z
prawdopodobieństwem 0,9 pokrywają nieznany parametr b
0
.
Nie jest to (z punktu widzenia rachunku prawdopodobieństwa) ścisła interpretacja naszego
wyniku, ale dla potrzeb zadania zupełnie wystarczająca.

Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
10
10
(
)
(
)
(
)
9
,
0
31752
,
0
03624
,
5
10664
,
1
132
,
2
67688
,
2
10664
,
1
132
,
2
67688
,
2
ˆ
ˆ
ˆ
ˆ
0
0
ˆ
05
,
0
1
1
ˆ
05
,
0
1
1
1
=
−
≤
≤
−
=
⋅
+
−
≤
≤
⋅
−
−
=
=
⋅
+
≤
≤
⋅
−
b
P
b
P
t
b
b
t
b
P
b
b
σ
σ
Powiemy
zatem,
że oszacowany przedział jest jednym z tych przedziałów, które z
prawdopodobieństwem 0,9 pokrywają nieznany parametr b
1
.
(
)
(
)
(
)
9
,
0
35440
,
4
36904
,
0
10775
,
1
132
,
2
99268
,
1
10775
,
1
132
,
2
99268
,
1
ˆ
ˆ
ˆ
ˆ
0
0
ˆ
05
,
0
2
2
ˆ
05
,
0
2
2
2
=
≤
≤
−
=
⋅
+
≤
≤
⋅
−
=
=
⋅
+
≤
≤
⋅
−
b
P
b
P
t
b
b
t
b
P
b
b
σ
σ
Powiemy
zatem,
że oszacowany przedział jest jednym z tych przedziałów, które z
prawdopodobieństwem 0,9 pokrywają nieznany parametr b
2
.
1.9 TEST ŁĄCZNEJ ISTOTNOŚCI ZMIENNYCH OBJAŚNIAJĄCYCH (TEST
ISTOTNOŚCI WSPÓŁCZYNNIKA DETERMINACJI)
Posługując się uogólnionym testem Walda możemy z kolei zbadać łaczną istotność zmiennych
objaśniających (współczynnika determinacji R
2
). Hipotezy w tym teście postawimy następująco:
H
0
: parametry strukturalne b
1
i b
2
nie różnią się istotnie od 0
H
A
: przynajmniej jeden z parametrów b
1
i b
2
istotnie różni się od 0
Obliczmy
statystykę próbkową o postaci:
67
,
149
0033
,
0
4934
,
0
))
1
2
(
7
/(
0132
,
0
2
/
9868
,
0
))
1
(
/(
/
2
2
=
=
+
−
=
+
−
=
k
n
k
R
F
ϕ
Powyższa statystyka, przy założeniu prawdziwości hipotezy zerowej, ma rozkład F Fishera-
Snedecora. Dlatego wartość F należy porównać ze znalezioną w tablicach statystycznych wartością
krytyczną rozkładu F dla przyjętego poziomu istotności. Obszar krytyczny testu jest prawostronny.
Zakładając poziom istotności
α = 0,05 i mając stopnie swobody licznika k, oraz stopnie swobody
mianownika n-(k+1) odczytujemy wartość następującą:
94
,
6
)
4
,
2
(
))
1
(
,
(
05
,
0
=
=
+
−
F
k
n
k
F
α
Ponieważ zachodzi zależność
)
4
,
2
(
05
,
0
F
F
>
to odrzucamy hipotezę zerową i stwierdzamy, że
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
11
11
przynajmniej jeden z parametrów istotnie różni się od 0 (zmienne objasniające łącznie istotnie
wpływają na zmienną objaśnianą; spółczynnik determinacji R
2
jest istotny statystycznie).
1.10 TEST ISTOTNOŚCI AUTOKORELACJI SKŁADNIKA LOSOWEGO
1.10.1 TEST DURBINA-WATSONA
Aby
ocenić istotność współczynnika autokorelacji rzędu I-ego wykonamy test Durbina-Watsona.
Stawiamy następujący zestaw hipotez:
H
0
: współczynnik autokorelacji
ρ
1
nieistotnie różni się od 0,
H
A
: współczynnik autokorelacji
ρ
1
istotnie różni się od 0.
Statystyka próbkowa testu zostanie policzona na podstawie wzoru:
(
)
∑
∑
−
−
=
2
2
1
ˆ
ˆ
ˆ
t
t
t
DW
ε
ε
ε
Na podstawie oszacowanego modelu obliczamy wartości teoretyczne
t
yˆ , a następnie reszty
modelu
t
ε
ˆ .
okres
y
t
t
yˆ
t
t
t
y
y
ˆ
ˆ
−
=
ε
1
ˆ
−
t
ε
2
1
)
ˆ
ˆ
(
−
−
t
t
ε
ε
2
ˆ
t
ε
1
23 23,5897 -0,58968
-
-
0,34772
2
25 25,4545 -0,45451 -0,58968
0,01827
0,20658
3
27 26,6501 0,34988 -0,45451
0,64704
0,12242
4
28 28,1878 -0,18783 0,34988 0,28913
0,03528
5
32 30,7933 1,20671 -0,18783
1,94474
1,45614
6
35 34,5944 0,40564 1,20671 0,64171
0,16454
7
40 40,7302 -0,73021 0,40564 1,29016
0,53321
suma
4,83106 2,8659
Zatem statystyka DW wynosi:
685
,
1
8659
,
2
83106
,
4
=
=
DW
Ponieważ statystyka DW < 2 to badamy istotność autokorelacji dodatniej. Odnajdujemy w
tablicach statystycznych wartości krytyczne rozkładu DW dla ustalonego poziomu istotności (
α =

Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
12
12
0,05) oraz stopni swobody n = 7 i k = 2:
dL = 0,467; dU = 1,897.
Ponieważ zachodzi zależność: dL < DW < dU to test Durbin-Watsona nie rozstrzyga o
odrzuceniu lub nieodrzuceniu hipotezy H
0
(test jest niekonkluzywny). W takim przypadku można
posłużyć się innymi testami na istotność autokorelacji, pamiętając o ograniczeniach tych testów i
konieczności spełnienia odpowiednich założeń.
Mając obliczoną wartość DW możemy oszacować współczynnik autokorelacji I-ego rzędu
1575
,
0
2
685
,
1
1
2
1
ˆ
1
=
−
≅
−
≅
DW
ρ
Ponieważ wartość współczynnika autokorelacji dodatniej może mieścić się w przedziale
(
1
;
0
to
możemy uznać oszacowany współczynnik autokorelacji za niewielki.
1.10.2 TEST MNOZNIKA LAGRANGE’A
Ze
względu na fakt, iż test DW nie pozwolił jednoznacznie okreslic istotności autokorelacji
składnika losowego zastosujemy test mnożnika Lagrange’a (LM). Hipotezy dotyczace współczynnika
autokorelacji 1-ego rzędu są takie same, jak w teście DW. Szacujemy model pomocniczy o postaci:
t
t
t
t
t
u
x
x
u
ε
β
β
β
β
+
+
+
+
=
−1
3
2
2
1
1
0
ˆ
ˆ
Zauważmy, że w modelu pomocniczym rolę zmiennej objasnianej pełnią reszty modelu
podstawowego, zaś zmiennymi objasniającymi są wszystkie zmienne egzogeniczne modelu
podstawowego oraz reszty modelun opóźnione o jeden okres (t-1). Obliczamy współczynnik
determinacji tego modelu:
182
,
0
2
=
LM
R
Nastepnie obliczamy statystyke testową
)
1
(
2
−
⋅
=
n
R
LM
LM
o trzymujemy, że LM = 1,092.
Statystyka LM ma rozkład chi-kwadrat o 1 stopniu swobody. Zakładając poziom istotności
α = 0,05
odszukujemy w tablicach statystycznych wartość krytyczną
χ
α
2
(1) = 3,841 dla prawostronnego
obszaru krytycznego (test LM jest testem prawostronnym). Następnie porównujemy statystykę
empiryczną LM ze statystyką teoretyczną z tablicy. Reguły decyzyjne sa następujące:
LM <
χ
α
2
nie odrzucamy H
0
LM >
χ
α
2
odrzucamy H
0

Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
13
13
W
naszym
przykładzie LM <
χ
α
2
, a więc nie odrzucamy H
0
i przyjmujemy, że w modelu nie
wystepuje istotna autokorelacja 1-ego rzędu.
1.11 SZACOWANIE PARAMETRÓW MODELU PO USUNIĘCIU NIEISTOTNEJ
ZMIENNEJ
Stwierdziliśmy poprzednio, że zmienna objaśniająca x
2
nieistotnie wpływa na zmienną y. Wobec
tego usuniemy ją z modelu i oszacujemy postać zredukowaną:
t
t
t
u
x
b
b
y
+
+
=
1
1
0
Aby nie wykonywać obliczeń na piechotę posłużymy się programem komputerowym. Wyniki
szacowania przedstawiono poniżej.
Ordinary Least Squares Estimation
*******************************************************************************
Dependent variable is Y
6 observations used for estimation from 1 to 6
*******************************************************************************
Regressor Coefficient Standard Error T-Ratio[Prob]
C 71.4783 4.6259 15.4519[.000]
X1 -4.9783 .53150 -9.3665[.001]
*******************************************************************************
R-Squared .95639 R-Bar-Squared .94549
S.E. of Regression 1.0406 F-stat. F( 1, 4) 87.7307[.001]
Mean of Dependent Variable 28.3333 S.D. of Dependent Variable 4.4572
Residual Sum of Squares 4.3315 Equation Log-likelihood -7.5361
Akaike Info. Criterion -9.5361 Schwarz Bayesian Criterion -9.3279
DW-statistic 1.7078
*******************************************************************************
Na podstawie uzyskanych wyników możemy zapisać nasz model w postaci teoretycznej:
(
)
(
)
t
t
x
y
1
53150
,
0
6259
,
4
9783
,
4
4783
,
71
ˆ
⋅
−
=
±
±
Interpretując uzyskany model powiemy, że: ceteris paribus, wzrost stopy redyskontowej x
1
o
jeden punkt procentowy powodował spadek podaży pieniądza średnio o 4,9783 mld zł.
Współczynnik determinacji R
2
wynosi 0,9564, co oznacza, że 95,64 procenta całkowitej
zmienności zmiennej y zostało wyjaśnione przez model, czyli przez zmienność stopy redyskontowej
x
1
.
Na tej podstawie można obliczyć współczynnik zbieżności, który przyjmuje wartość

Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
Materiały pomocnicze do zajeć z ekonometrii SSW Chojnice 2012
Krzysztof Świetlik
14
14
0436
,
0
2
=
ϕ
. Powiemy zatem, że 4,36 procenta całkowitej wariancji zmiennej y nie zostało
wyjaśnione przez model.
Średni błąd resztowy
0406
,
1
ˆ
=
ε
σ
, a więc powiemy, że wartości teoretyczne podaży pieniądza
t
yˆ odchylają się od wartości empirycznych y
t
średnio o 1,0406 mld zł.
Aby
pokazać, czy odchylenie to jest duże, można policzyć współczynnik zmienności losowej v.
Statystyka DW
= 1,7078. Jest to wartość mniejsza od 2, zatem zestaw hipotez dla tego
przypadku postawimy następująco:
0
:
0
:
1
1
0
>
≤
ρ
ρ
A
H
H
Znajdujemy w tablicach statystycznych wartości krytyczne rozkładu DW na poziomie istotności
α = 0,05 i porównując te wartości ze statystyką DW podejmujemy decyzję dotyczącą odrzucenia lub
nieodrzucenia hipotezy zerowej H
0
.
Mając wartość DW oszacujemy współczynnik autokorelacji I-ego rzędu:
1461
,
0
2
7078
,
1
1
2
1
ˆ
1
=
−
=
−
≅
DW
ρ
Ponieważ wartość ta jest niewiele większa od 0 możemy powiedzieć, że siła autokorelacji jest w
przypadku naszego zadania znikoma.
Czytelnikowi pozostawiamy do samodzielnego zbadania istotność zmiennej objaśniającej (test t-
Studenta), istotność współczynnika determinacji (test Walda) i dokończenie testu na istotność
współczynnika autokorelacji rzędu I-ego (test Durbina-Watsona).
Wyszukiwarka
Podobne podstrony:
Model potęgowy z dwiema zmiennymi objaśniającymi
Model z jedną zmienną objaśniającą (liniowy i nieliniowy)
Model liniowy z 2 zmiennymi WZiE
MNK liniowy 2 zmienne objasniajace(1)
Model z wieloma zmiennymi objasniajacymi
Obejrzyj zależność liniową między zmiennymi
Analiza regresji między dwiema zmiennymi, Płyta farmacja Bydgoszcz, statystyka, pozostałe
W2 Dobór zmiennych objaśniających do modelu
W2 Dobór zmiennych objaśniających do modelu 2
Dobor zmiennnych objasniajacych
Analiza regresji między dwiema zmiennymi, Statystyka, statystyka(3)
Analiza regresji między dwiema zmiennymi, statystyka matematyczna(1)
Regresja liniowa dwoch zmiennych, materiały z roku 2011-2012, Semestr II, Statystyka opisowa - ćwicz
Dobor zmiennnych objasniajacych
Model liniowy holta
ekonometria wyklad model liniowy WSB 13 14
współzależność, Współczynnik korelacji liniowej oraz funkcja regresji liniowej dwóch zmiennych
MPiST 05 Model liniowy JWN
Liniowe przeksztalcenie zmienny Nieznany
więcej podobnych podstron