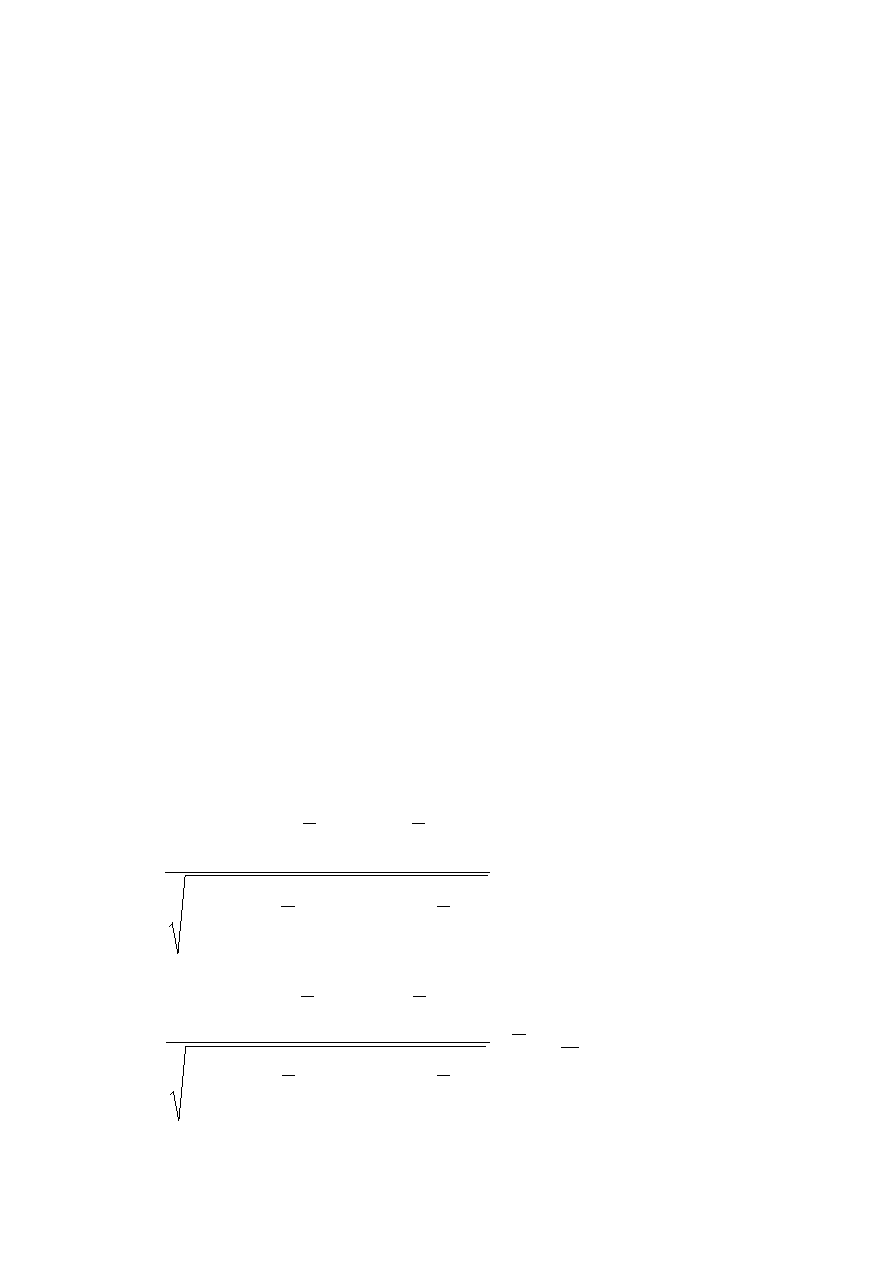
Dobór zmiennych objaśniających do modelu
ekonometrycznego
Oznaczenia:
Y
- zmienna objaśniana,
k
X
X
X
,...,
,
2
1
- potencjalne zmienne objaśniające.
Postać macierzowa:
=
n
y
y
y
Y
:
2
1
,
=
kn
n
n
k
k
x
x
x
x
x
x
x
x
x
X
..
:
:
:
:
..
..
2
1
2
22
12
1
21
11
.
Współczynniki korelacji:
=
k
r
r
r
r
R
:
3
2
1
0
,
=
1
..
:
..
:
:
:
..
1
..
1
..
1
3
2
1
3
32
31
2
23
21
1
13
12
k
k
k
k
k
k
r
r
r
r
r
r
r
r
r
r
r
r
R
,
gdzie
;
)
(
)
(
)
(
)
(
1
2
1
2
1
∑
∑
∑
=
=
=
−
⋅
−
−
⋅
−
=
n
i
m
mi
n
i
i
n
i
m
mi
i
m
x
x
y
y
x
x
y
y
r
k
m
,...,
2
,
1
=
;
)
(
)
(
)
(
)
(
1
2
1
2
1
∑
∑
∑
=
=
=
−
⋅
−
−
⋅
−
=
n
i
m
mi
n
i
l
li
n
i
m
mi
l
li
lm
x
x
x
x
x
x
x
x
r
;
1
1
∑
=
=
n
i
li
l
x
n
x
k
m
l
,...,
2
,
1
,
=
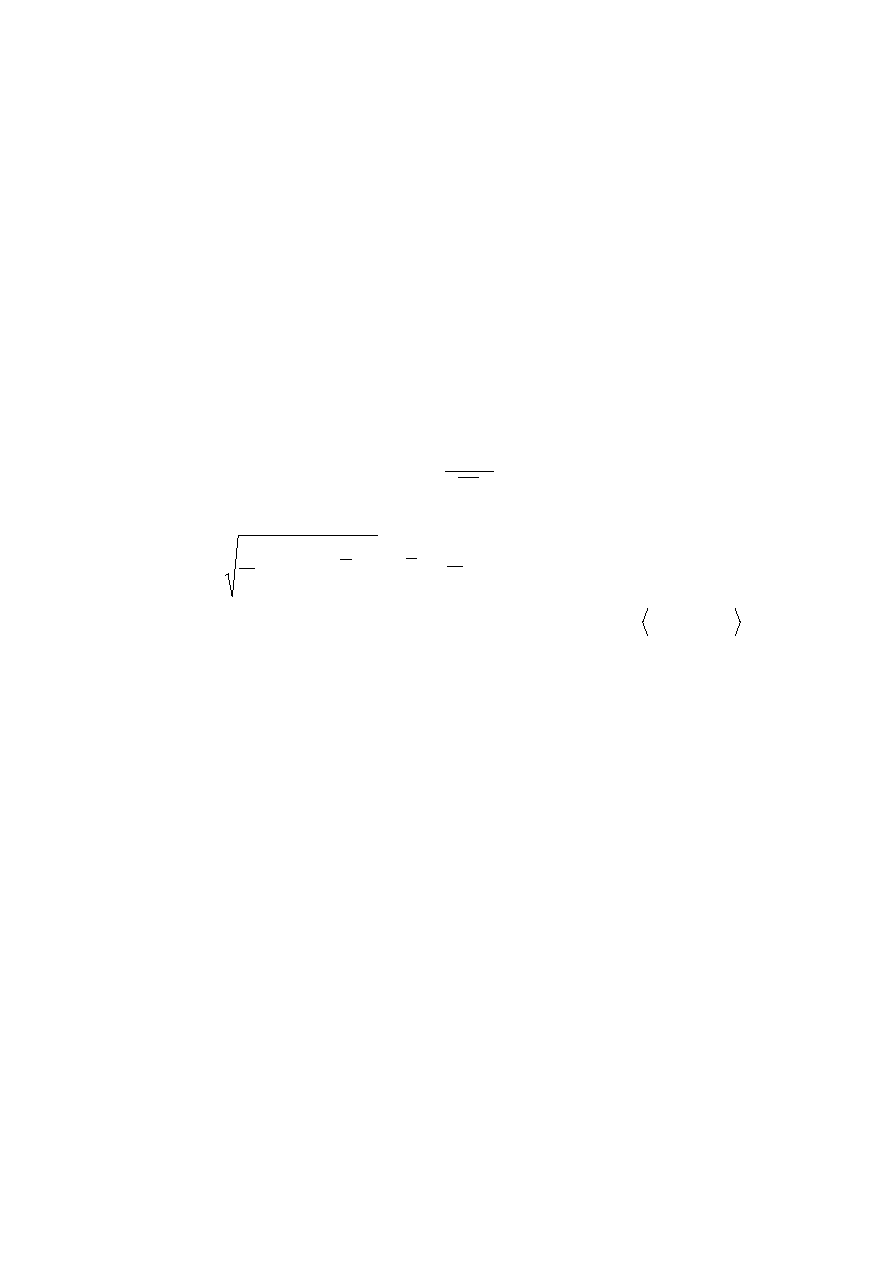
Postulaty dotyczące zmiennych objaśniających:
•
Wysoki poziom zmienności zmiennych objaśniających.
•
Zmienne
k
X
X
X
,...,
,
2
1
powinny być słabo skorelowane między sobą
a jednocześnie silnie skorelowane ze zmienną Y.
Poziom zmienności
Zmienne objaśniające
k
X
X
X
,...,
,
2
1
powinny charakteryzować się
odpowiednio wysokim poziomem zmienności mierzonym
współczynnikiem zmienności:
l
X
l
X
S
v
l
=
,
gdzie
∑
=
−
=
n
i
l
li
X
x
x
n
S
l
1
2
)
(
1
,
∑
=
=
n
i
li
l
x
n
x
1
1
dla
k
l
,...,
2
,
1
=
.
Krytyczny poziom zmienności
*
v
jest liczbą z zakresu
20
,
0
;
05
,
0
.
Ze zbioru potencjalnych zmiennych objaśniających eliminujemy te,
dla których współczynnik zmienności nie przekracza wybranej
wartości krytycznej
*
v
.
Brak współliniowości
Metody doboru zmiennych objaśniających:
•
metoda pojemności informacyjnej,
•
metoda grafowa,
•
metoda analizy współczynników korelacji.

Metoda pojemności informacyjnej.
k – liczba potencjalnych zmiennych objaśniających (pozostałych po
usunięciu zmiennych o zbyt niskim poziomie zmienności).
Zbiór potencjalnych zmiennych objaśniających
}
,...,
,
{
2
1
k
X
X
X
zawiera
1
2
−
k
niepustych podzbiorów. Każdy podzbiór z tej rodziny
numerujemy w pewnym porządku. Niech m oznacza numer
wybranego podzbioru
m
ℵ
.
Indywidualna pojemność informacyjna zmiennej
l
X będącej
elementem podzbioru
m
ℵ
:
∑
ℵ
∈
=
m
i
li
l
ml
r
r
h
|
|
2
Integralna pojemność informacyjna podzbioru
m
ℵ
:
∑
ℵ
∈
=
m
i
mi
m
h
H
Integralną pojemność informacyjną wyznacza się dla wszystkich
podzbiorów zbioru
}
,...,
,
{
2
1
k
X
X
X
. Podzbiór o największej wartości
integralnego wskaźnika pojemności informacyjnej wyznacza zmienne
objaśniające najlepsze w sensie pojemności informacyjnej.

Przykład:
W pewnej firmie przeprowadzono badania dotyczące wydajności pracy mające na celu
zbudowanie modelu ekonometrycznego opisującego wydajność pracy. W grupie
potencjalnych zmiennych objaśniających znalazły się zmienne:
1
X
- techniczne uzbrojenie pracy;
2
X
- średnie roczne płace pracowników;
3
X
- straty czasu pracy z przyczyn organizacyjno – technicznych.
Macierz i wektor korelacji:
−
−
−
−
=
1
079
,
0
181
,
0
079
,
0
1
824
,
0
181
,
0
824
,
0
1
R
−
=
210
,
0
640
,
0
520
,
0
0
R
W tym przykładzie występują 3 potencjalne zmienne objaśniające, stąd należy wyznaczyć
integralne pojemności informacyjne dla
7
1
2
3
=
−
podzbiorów potencjalnych zmiennych
objaśniających.
Lista podzbiorów:
}
{
1
1
X
=
ℵ
}
{
2
2
X
=
ℵ
}
{
3
3
X
=
ℵ
}
;
{
2
1
4
X
X
=
ℵ
}
;
{
3
1
5
X
X
=
ℵ
}
;
{
3
2
6
X
X
=
ℵ
}
;
;
{
3
2
1
7
X
X
X
=
ℵ
Podzbiór
}
{
1
1
X
=
ℵ
Indywidualny wskaźnik pojemności informacyjnej:
27
,
0
1
)
520
,
0
(
2
11
=
=
h
Integralny wskaźnik pojemności informacyjnej:
27
,
0
11
1
=
=
h
H
Podzbiór
}
{
2
2
X
=
ℵ
41
,
0
22
2
=
=
h
H
Podzbiór
}
{
3
3
X
=
ℵ
04
,
0
33
3
=
=
h
H

Podzbiór
}
;
{
2
1
4
X
X
=
ℵ
Indywidualne wskaźniki pojemności informacyjnej:
15
,
0
|
824
,
0
|
1
)
520
,
0
(
2
41
=
+
=
h
22
,
0
|
824
,
0
|
1
)
640
,
0
(
2
42
=
+
=
h
Integralny wskaźnik pojemności informacyjnej:
37
,
0
42
41
4
=
+
=
h
h
H
Podzbiór
}
;
{
3
1
5
X
X
=
ℵ
Indywidualne wskaźniki pojemności informacyjnej:
23
,
0
|
181
,
0
|
1
)
520
,
0
(
2
51
=
−
+
=
h
04
,
0
|
181
,
0
|
1
)
210
,
0
(
2
53
=
−
+
−
=
h
Integralny wskaźnik pojemności informacyjnej:
27
,
0
53
51
5
=
+
=
h
h
H
Podzbiór
}
;
{
3
2
6
X
X
=
ℵ
Indywidualne wskaźniki pojemności informacyjnej
:
48
,
0
|
079
,
0
|
1
)
640
,
0
(
2
62
=
−
+
=
h
04
,
0
|
079
,
0
|
1
)
210
,
0
(
2
63
=
−
+
−
=
h
Integralny wskaźnik pojemności informacyjnej:
52
,
0
63
62
6
=
+
=
h
h
H
Podzbiór
}
;
;
{
3
2
1
7
X
X
X
=
ℵ
Indywidualne wskaźniki pojemności informacyjnej:
13
,
0
|
181
,
0
|
|
824
,
0
|
1
)
520
,
0
(
2
71
=
−
+
+
=
h
21
,
0
|
079
,
0
|
|
824
,
0
|
1
)
640
,
0
(
2
72
=
−
+
+
=
h
03
,
0
|
181
,
0
|
|
079
,
0
|
1
)
210
,
0
(
2
73
=
−
+
−
+
−
=
h
Integralny wskaźnik pojemności informacyjnej:
37
,
0
73
72
71
7
=
+
+
=
h
h
h
H
Integralna pojemność informacyjna jest największa dla
podzbioru numer 6 co oznacza, że najlepszymi w sensie
pojemności informacyjnej zmiennymi objaśniającymi są zmienne
3
2
, X
X
.

Metoda grafowa.
1.
Wyznaczamy wartość krytyczną współczynnika korelacji
*
r
.
2.
W macierzy korelacji pomiędzy potencjalnymi zmiennymi
objaśniającymi
R
zastępujemy zerami wszystkie elementy
spełniające warunek:
*
|
|
r
r
ij
≤
tworząc macierz
'
R
.
3.
Na bazie macierzy
'
R
buduje się graf. Wierzchołkami grafu
są potencjalne zmienne objaśniające, natomiast krawędzie
odpowiadają niezerowym elementom macierzy
'
R
.
Możliwe do otrzymania grafy to:
a) jeden graf spójny, w którym każdy wierzchołek jest
połączony krawędziami z innym wierzchołkiem;
b) więcej niż jeden podgrafów spójnych, które nie
posiadają wspólnych krawędzi;
c) graf lub grafy spójne oraz graf lub grafy zerowe (bez
krawędzi);
d) grafy zerowe.
4. Do zmiennych objaśniających zalicza się:
a) zmienne, które tworzą grafy zerowe,
b) zmienne o maksymalnej liczbie krawędzi wybrane z
każdego podgrafu spójnego; jeżeli w danym podgrafie
jest więcej niż jedna zmienna o takiej samej
maksymalnej liczbie krawędzi, to wybiera się spośród
tych zmiennych najsilniej skorelowaną ze zmienną
objaśnianą.
Przykład:
Wektor i macierz korelacji:
−
−
−
−
−
−
−
−
−
−
−
−
=
1
21
,
0
1
92
,
0
11
,
0
1
07
,
0
87
,
0
28
,
0
1
18
,
0
93
,
0
03
,
0
45
,
0
1
02
,
0
21
,
0
17
,
0
21
,
0
23
,
0
1
33
,
0
12
,
0
03
,
0
52
,
0
72
,
0
13
,
0
1
R
−
−
−
=
78
,
0
01
,
0
82
,
0
73
,
0
91
,
0
54
,
0
21
,
0
0
R
Wartość krytyczna współczynnika korelacji (
05
,
0
,
25
=
=
α
n
):
39
,
0
07
,
2
2
25
07
,
2
2
2
*
=
+
−
=
r
Macierz
'
R
:
−
−
−
=
1
0
1
92
,
0
0
1
0
87
,
0
0
1
0
93
,
0
0
45
,
0
1
0
0
0
0
0
1
0
0
0
52
,
0
72
,
0
0
1
'
R
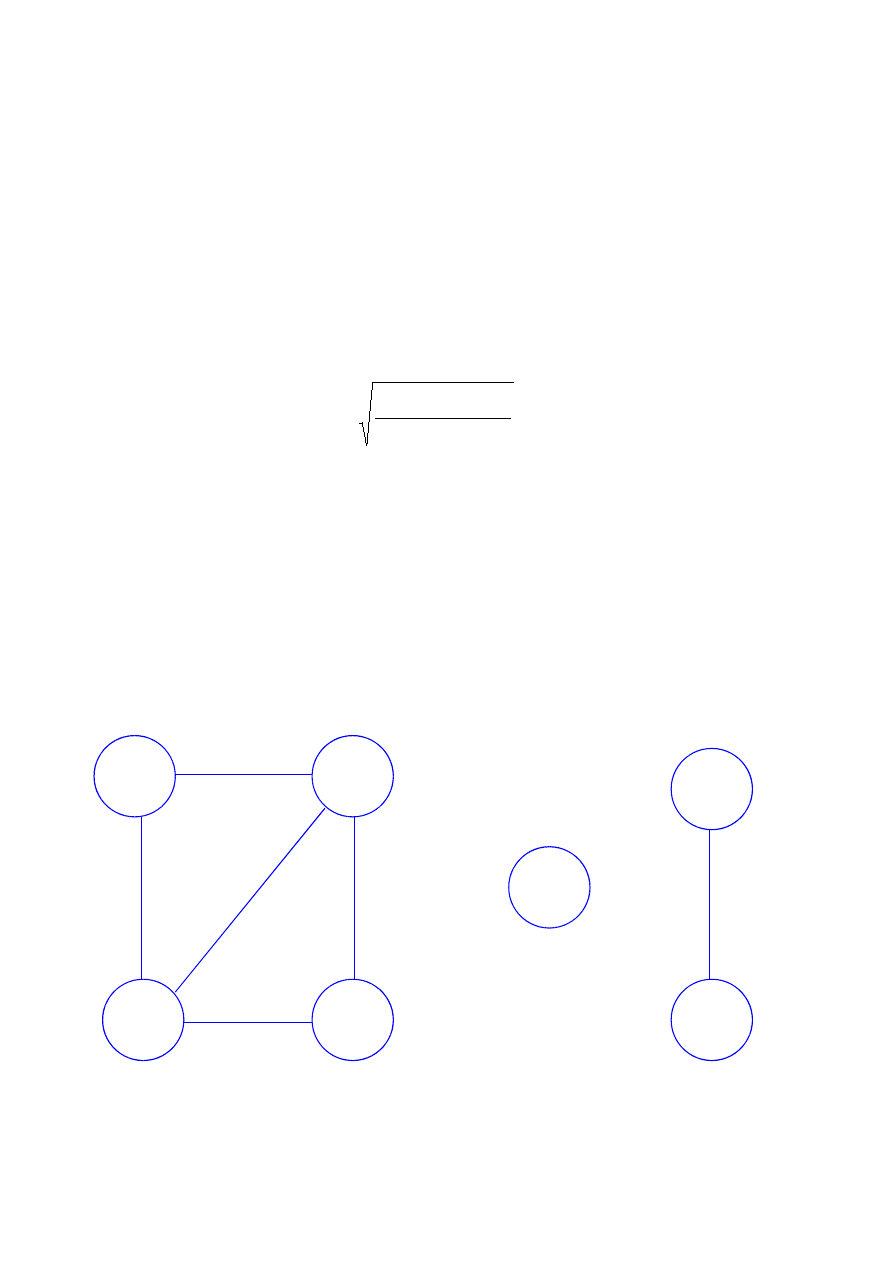
Graf:
2
3
4
5
6
7
1

Metoda analizy współczynników korelacji
Etapy prac:
1. Wyznaczenie wartości krytycznej współczynnika korelacji,
2. Wybór z grupy potencjalnych zmiennych objaśniających
zmiennej najsilniej skorelowanej ze zmienną objaśnianą,
3. Eliminacja ze zbioru potencjalnych zmiennych objaśniających
wszystkich zmiennych skorelowanych ze zmienną wybraną w
punkcie 2,
4.
Powtarzanie kroków 2, 3 do wyczerpania zbioru potencjalnych
zmiennych objaśniających.
Przykład (macierz korelacji i wektor korelacja – metoda grafowa):
1.
Wybieramy zmienną X
3
,
2.
Eliminujemy zmienne: X
1
, X
4
, X
6
,
3.
Z pozostałych zmiennych (X
2
, X
5
, X
7
) wybieramy najsilniej
skorelowaną ze zmienną objaśnianą (R
0
) czyli zmienną X
5
,
4.
Eliminujemy zmienną X
7
, ponieważ jest skorelowana z X
5
(współczynnik korelacji z macierzy R wynosi –0,92),
5.
Pozostała tylko zmienna X
2
i ją jako najsilniej skorelowaną
wybieramy do grupy zmiennych objaśniających,
6. Zbiór potencjalnych zmiennych objaśniających został
wyczerpany – koniec metody.
7.
Rezultat: zmienne objaśniające wybrane metodą analizy
współczynników korelacji to zmienne: X
3
, X
5
, X
2
Wyszukiwarka
Podobne podstrony:
W2 Dobór zmiennych objaśniających do modelu
W2 Dobór zmiennych objaśniających do modelu 2
Dobor zmiennnych objasniajacych
3 dobór zmiennych do liniowego modelu ekonometrycznego
dobór zmiennych rozw ćwiczenia2
dobór zmiennych rozw ćwiczenia2
Wyklad 5b Dobor zmiennych
MNK liniowy 2 zmienne objasniajace(1)
Wykład5, Dobór zmiennych do modelu - Hellwig, Dobór zmiennych do modelu
Model z wieloma zmiennymi objasniajacymi
W6 dobor zmiennych, Ekonometria
Model z jedną zmienną objaśniającą (liniowy i nieliniowy)
Model liniowy z dwiema zmiennymi objaśniającymi
dobor zmiennych gorski m
dobór zmiennych rozw ćwiczenia2
dobór zmiennych rozwiazania01
dobór zmiennych
więcej podobnych podstron