Metody doboru zmiennych i postaci modelu

Przy doborze zmiennych objaśniających należy kierować się na wstępie:

• zdrowym rozsądkiem i teorią dotyczącą badanego zagadnienia.

Dobór zmiennych zależy również od jakości oszacowania modelu przy danych zmiennych (wykazany brak spełnienia założeń użytej metody estymacji, takie jak dla KMNK heteroskedastyczność, autoregresyjność czy brak rozkładu normalnego reszt, wskazuje na konieczność użycia innego zestawu zmiennych objaśniających). W ten sposób budowa finalnego modelu ma charakter iteracyjny.

Przydatne w modelu są także następujące własności zmiennych objaśniających:

• silna korelacja ze zmienną objaśnianą,

• słaba (brak) korelacja między sobą (z innymi zm. objaśniającymi),

• duża zmienność,

• nielosowość.

W praktyce wykorzystuje się niekiedy techniczne metody doboru zmiennych do modelu, np.

• Metoda optymalnego wyboru predyktand (Metoda Hellwiga)

• Metoda analizy grafów (metoda Bartosiewicz)

Metoda optymalnego wyboru predyktand

Metoda optymalnego wyboru predyktand (także: metoda Hellwiga) - jedna z najczęściej stosowanych metod doboru zmiennych objaśniających do modelu ekonometrycznego; opracowana w 1969 roku przez polskiego ekonometryka prof. Zdzisława Hellwiga.

Polega na wyborze takiej kombinacji zmiennych objaśniających ze zbioru zmiennych potencjalnych, których współczynnik korelacji liniowej ze zmienną endogeniczną jest jak największy, natomiast współczynnik korelacji liniowej między zmiennymi objaśniającymi występującymi w danej kombinacji jest jak najmniejszy.

Liczba wszystkich możliwych kombinacji zmiennych objaśniających jest równa:

gdzie:

• p - liczebność zbioru zmiennych potencjalnych

Nośnikiem informacji o zmiennej endogenicznej jest potencjalna zmienna objaśniająca. Pojemność indywidualna (cząstkowa) nośnika jest dana wzorem:

gdzie:

• l = (1,2,...,L)

• j = (1,2,...,p)

• r_0j - współczynnik korelacji liniowej między zmienną endogeniczną a j-tą zmienną objaśniającą.

• r_ij - współczynnik korelacji liniowej między i-tą i j-tą zmienną objaśniającą występującą w danej kombinacji zmiennych.

Integralna pojemność informacyjna danej kombinacji potencjalnych zmiennych objaśniających jest równa sumie pojemności indywidualnych nośników wchodzących w skład danej kombinacji i jest dana wzorem:

Tak dana pojemność integralna stanowi kryterium wyboru optymalnej kombinacji zmiennych objaśniających. H_l przyjmuje wartości z przedziału < 0,1 > i jest tym większa im zmienne objaśniające są silniej skorelowane ze zmienną endogeniczną oraz im słabiej są skorelowane między sobą.

Kombinacją opytmalą jest więc ta kombinacja, której pojemność integralna jest największa.

Przykład

Dane są:

• zmienna endogeniczna Y

• zbiór potencjalnych zmiennych objaśniających
  

• wektor współczynników korelacji liniowej między zmiennymi egzogenicznymi i zmnienną endogeniczną
  

• macierz współczynników korelacji między potencjalnymi zmiennymi objaśniającymi
  

Liczba możliwych kombinacji zmiennych endogenicznych wynosi

• Kombinacje jednoelementowe:

,

,

• Kombinacje dwuelementowe:

,

,

• Kombinacje trójelementowe:

Metoda analizy grafów (metoda Bartosiewicz)

W prezentowanej metodzie zmierza się do tego, by spośród wszystkich zmiennych objaśniających wyodrębnić grupy zmiennych skorelowanych między sobą oraz znaleźć zmienne, z których żadna nie jest skorelowana z pozostałymi zmiennymi objaśniającymi. Następnie spośród tych grup zmiennych wybiera się zmienne mocniej skorelowane ze zmienną objaśnianą i wprowadza się je do relacji modelu. Do modelu wchodzą również wszystkie zmienne nieskorelowane między sobą, ale skorelowane ze zmienną objaśnianą.

Procedurę wyboru zmiennych objaśniających przedstawioną metodą realizuje się następującymi etapami:

1) Na podstawie obserwacji o zmiennych oblicza się współczynniki korelacji liniowej między zmienną objaśnianą a zmiennymi objaśniającymi oraz współczynniki korelacji między wszystkimi zmiennymi objaśniającymi. Następnie buduje się symetryczną macierz wszystkich współczynników korelacji o wymiarach (m + 1) x (m + 1).

Buduje się nową macierz R o wymiarach m x m przez wyłączenie
z macierzy W pierwszego wiersza i pierwszej kolumny:

2) Formułuje się hipotezy zerowe dotyczące współczynników korelacji w populacji generalnej H0: ρi j = 0 wobec hipotez alternatywnych H1: ρi j ≠ 0.
Oblicza się wartość krytyczną r, posługując się wzorem o postaci: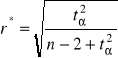
, gdzie wartość t odczytuje się dla n-2 stopni swobody.

3) Zmienne skorelowane zbyt słabo ze zmienną objaśnianą, tzn. o współczynnikach korelacji r_0j<r^* usuwa się ze zbioru danych i z macierzy korelacji R,

4) W macierzy R pozostawia się tylko współczynniki korelacji spełniające warunek r_ij>=r^*, pozostałe współczynniki przyjmuje się równe 0,

5) Na podstawie macierzy R buduje się grafy powiązań między zmiennymi objaśniającymi, tworząc w ten sposób k grafów - grup zmiennych, odpowiadających przyszłym k zmiennym objaśniającym modelu.

6) Do zmiennych objaśniających zalicza się:
a) zmienne, które w odwzorowaniu tworzą grafy zerowe (izolowane),
b) zmienne o maksymalnej liczbie łuków wybrane z każdego grafu spójnego, jeżeli w każdym grafie spójnym jest więcej niż jedna zmienna o takiej samej maksymalnej liczbie łuków, to wybiera się spośród tych zmiennych tę, która jest najbardziej skorelowana ze zmienną objaśnianą.

Źródła

• Barczak, A. S., Biolik, J.: Podstawy Ekonometrii, Wydawnictwo Akademii Ekonomicznej w Katowicach, Katowice 1999

• Goryl A. i inni: „Wprowadzenie do ekonometrii w przykładach i zadaniach”

• Witkowska D: „Podstawy ekonometrii i teorii prognozowania”

• http://pl.wikipedia.org

• www.ekonometryk.fc.pl/twww_24/ Projekt%20z%20ekonometrii.pps

---