Odwzorowania liniowe w przestrzeni wektorowej
Definicja 1. (odwzorowania liniowego)
1
2
,
1
2
1
( , , , ), ( , , , )
:
1
: (
)
( )
(
2
:
: (
)
( )
x x
X
K
x X
X K
Y K
f X
Y
f x
x
f x
f x
f
x
f x
α
α
α
∈
∈
∈
+ ⋅
+ ⋅
→
∀
+
=
+
∀
∀
= ⋅
- przestrzenie wektorowe
:
⇔
jest odwzorowaniem liniowym
2
)
WNIOSEK
:
Jeżeli f: jest liniowe to:
X
Y
→
1
0
2
( )
( )
( )
0
x
y
f
f
x
f
=
−
= −
x
Twierdzenie 1.
1
2
,
,
1
2
1
, , , ),( , , , )
:
:
: (
)
( )
(
x x
X
K
X K
Y K
f X
Y
f
x
x
f x
f x
α β
α
β
α
β
∈
∈
+ ⋅
+ ⋅
→
∀
∀
+
=
+
⇔
- przestrzenie wektorowe
jest liniowe
(
Z:
T:
2
)
Twierdzenie 2.
(
f X
∀
∀
f
1
2,
1
2
,
...,
, ,...,
1 1
2 2
1
1
2
2
, , , ), ( , , , )
:
:
:
(
...
)
( )
( ) ...
(
n
n
K
x x
x
X
n n
n
n
X K
Y K
Y
x
x
x
f x
f x
f x
α α
α
α
α
α
α
α
α
∈
∈
+ ⋅
+ ⋅
→
+
+ +
=
+
+ +
⇔
- przestrzenie wektorowe
f jest liniowe
)
Przykład 1.
(
)
(
)
(
)
(
)
(
)
(
)
( )
( )
3
1
2
3
1
2
3
, , ,
, ,
(
2 ,
,3
3
3 )
, ,
, ,
,
f
x y z
x y
z x y z x
y
z
u
x x x
v
y y y
f
u
v
f u
f v
α β
α
β
α
β
+ ⋅
=
− +
+ +
+
+
=
=
∈
+
=
+
R
3
2
→
Niech Sprawdźmy, czy jest to odwzorowanie
liniowe
?
Czy
- przestrzeń wektorowa
, że:
taka
Wykład dr Magdaleny Sękowskiej
strona 1 z 5
Część 5 –Odwzorowania liniowe
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
) (
)
(
(
) (
)
(
)
)
(
)
(
(
)
1
2
3
1
2
3
1
1
2
2
3
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
, ,
, ,
,
,
2
2
,
,
3
3
3
3
3
3
2 ,
,3
3
3
2 ,
,3
3
3
, ,
f
u
v
f
x x x
y y y
f
x
y
x
y
x
y
x
x
x
y
y
y
x
x
x
y
y
y
x
x
x
y
y
y
x
x
x x
x
x
x
x
x
y
y
y y
y
y
y
y
y
f x x x
α
β
α
β
α
β α
β
α
β
α
β
α
β
α
β
α
β
α
+
=
+
=
=
+
+
+
=
=
− +
+
−
+
+
+
+
+
+
+
+
+
+
+
+
=
=
− +
+
+
+
+
+
−
+
+
+
+
+
+
(
)
( )
( )
1
2
3
, ,
f y y y
f u
f v
β
α
β
=
+
)
=
Odwzorowanie f jest liniowe
Definicja 2.
(
)
f X
(
, , , ,
, , ,
:
X K
Y K
Y
+ ⋅
+ ⋅
→
jest liniowe
)
- przestrzenie wektorowe
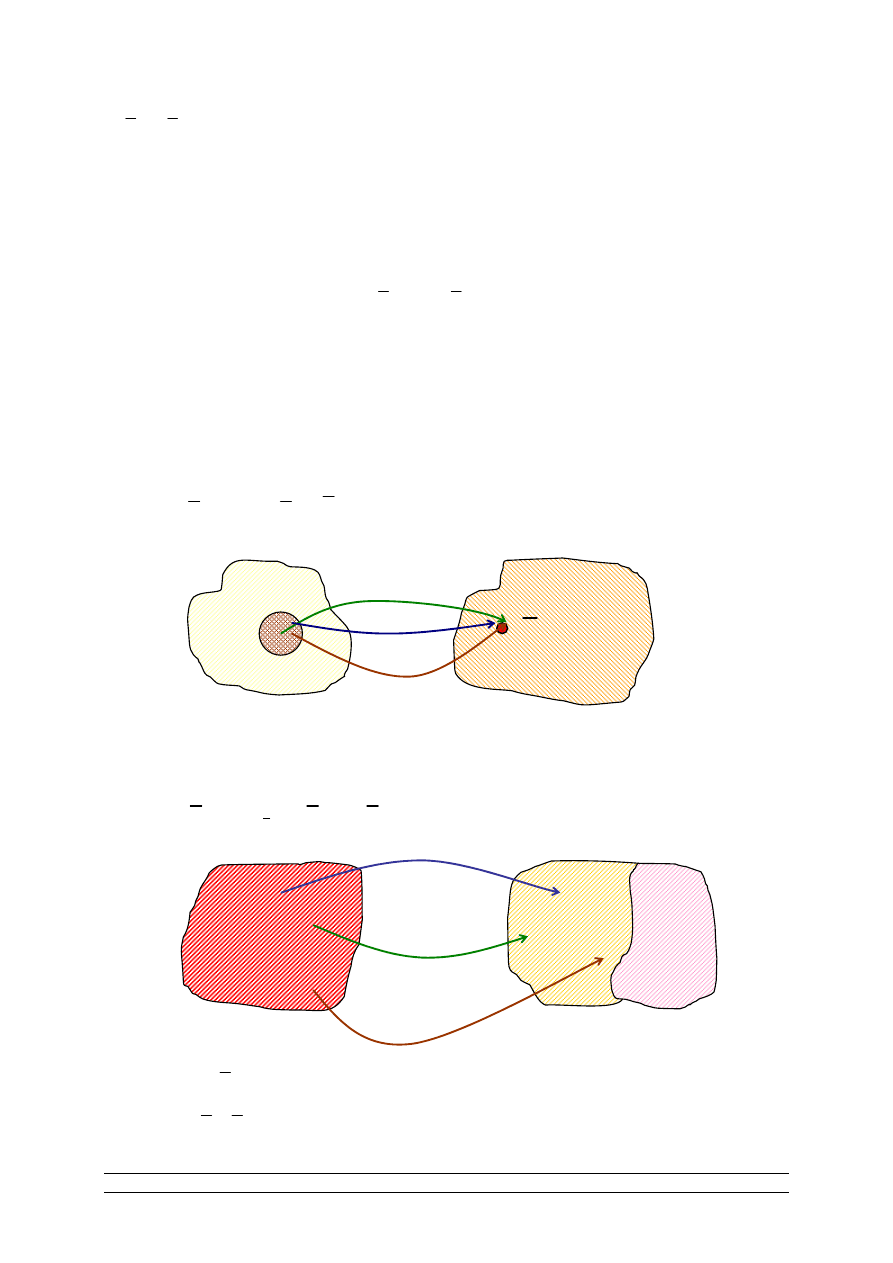
Jądrem
odwzorowania liniowego nazywamy ogół takich wektorów z
przestrzeni X, których wartość jest wektorem zerowym przestrzeni Y
Ke
( )
{
}
r :
:
0
y
f
x
X f x
=
∈
=
0
y
Y
Ker f
X
Obrazem
odwzorowania f (przeciwdziedziną, zbiorem wartości)
nazywamy zbiór
{
}
:
:
:
( )
x X
f
y Y
y
f x
∈
=
∈
∃
=
Im
WNIOSEK
:
Im f
Y
X
Ker
{ }
{
}
1
0
( ) :
f
f
f
f x x
X
−
=
=
∈
Im
Wykład dr Magdaleny Sękowskiej
strona 2 z 5
Część 5 –Odwzorowania liniowe
Twierdzenie 3.
- przestrzenie wektorowe
(
T
f
T
f
) (
)
(
)
(
)
1
2
, , , ,
, , ,
:
: Ker , , ,
: Im , , ,
X K
Y K
f X
Y
K
K
+ ⋅
+ ⋅
→
+ ⋅
+ ⋅
podprzestrzeń przestrzeni Y
podprzestrzeń przestrzeni X
i f liniowe
Twierdzenie 4.
Z:
(
X K
T:
) (
)
, , , ,
, , ,
:
dim
dim Ker
dim Im
Y K
f X
Y
X
f
+ ⋅
+ ⋅
→
=
+
jest liniowe
- przestrzenie wektorowe
f
Definicja 3.
(
) (
)
, , , ,
, , , , :
X K
Y K
f X
Y
+ ⋅
+ ⋅
→
f – liniowe
Wymiar obrazu nazywamy rzędem odwzorowania liniowego
dim Im
r
f
f
=
Definicja 4.
(
• Odwzorowanie nazywamy
monomorfizmem
, jeżeli jest liniowe i
injektywne (różnowartościowe)
) (
)
, , , ,
, , ,
:
X K
Y K
f X
Y
+ ⋅
+ ⋅
→
- przestrzenie wektorowe
• Odwzorowanie nazywamy
epimorfizmem
, jeżeli jest linowe i
surrjektywne (Im f=Y)
• Odwzorowanie nazywamy
izomorfizmem
, jeżeli jest liniowe i bijektywne
Twierdzenie 5.
Z:
(
) (
)
, , , ,
, , ,
:
X K
Y K
f X
Y
+ ⋅
+ ⋅
→
- przestrzenie wektorowe
f - liniowe
{ }
Ker
0
f
⇔
=
T:
f jest injektywne
Twierdzenie 6.
Z
X
f
dim
T
f
(
) (
)
:
, , , ,
, , ,
:
,
: dim Im
K
Y K
X
Y f
monomorfizm
X
n
n
+ ⋅
+ ⋅
→
−
=
=
- przestrzenie wektorowe
Wykład dr Magdaleny Sękowskiej
strona 3 z 5
Część 5 –Odwzorowania liniowe
Definicja 5.
(
)
X
(
, , , ,
, , ,
:
:
X K
Y K
Y
f X
+ ⋅
+ ⋅
⇔ ∃
→
∼
Mówimy, że X i Y są przestrzeniami izomorficznymi
Y
i f - izomorfizm
)
- przestrzenie wektorowe
WNIOSEK:
X
Twierdzenie 7.
Z
X
T X
dim
dim
Y
X
⇒
=
∼
Y
)
im
(
) (
:
, , , ,
, , ,
:
dim
d
K
Y K
Y
X
Y
+ ⋅
+ ⋅
⇔
=
∼
- przestrzenie wektorowe
Definicja 6.
(
)
L
(
)
(
) {
, , , ,
, , ,
,
:
: :
X K
Y K
X Y
f f X
Y
+ ⋅
+ ⋅
=
→
- przestrzenie wektorowe
}
∧
f - liniowe
Twierdzenie 7.
Z
X
T
X
Gdzie - dodawanie odwzorowań
⊕
(
) (
(
)
(
:
, , , ,
, , ,
:
,
, , ,
K
Y K
Y K
+ ⋅
+ ⋅
⊕
L
)
)
- przestrzenie wektorowe
Jest przestrzenią wektorową
- mnożenie odwzorowań przez skalary z ciała K
Definicja 7.
(
f
)
, , ,
:
X K
X
X
+ ⋅
→
∧
f - liniowe
Odwzorowanie liniowe przestrzeni w samą siebie nazywamy
endomorfizmem
UWAGA
Z
X
T g
(
) (
) (
(
)
(
)
(
)
:
, , , ,
, , , ,
, , ,
,
,
:
,
K
U K
Y K
f
X U
g
U Y
f
X Y
+ ⋅
+ ⋅
+ ⋅
∈
∧ ∈
∈
L
L
L
)
- przestrzenie wektorowe
Wykład dr Magdaleny Sękowskiej
strona 4 z 5
Część 5 –Odwzorowania liniowe
Definicja 8.
(
Wykład dr Magdaleny Sękowskiej
strona 5 z 5
Część 5 –Odwzorowania liniowe
(
)
, , ,
, , ,
X K
K K
+ ⋅
+ ⋅
)
Każde ciało może być traktowane jako
przestrzeń wektorowa nad samym sobą
Odwzorowanie liniowe f: X -> K nazywamy formą liniową
WNIOSEK
(
(
)
)
,
, , ,
X U K
+ ⋅
L
Zbiór form liniowych z dodawaniem i mnożeniem
odwzorowań przez skalar z ciała K jest
przestrzenią wektorową
Definicja 9.
(
(
(
)
)
)
,
, , ,
', , ,
X U K
X
X K
+ ⋅ =
+ ⋅
L
- przestrzeń
dualna
do przestrzeni X (przestrzeń form
liniowych określonych nad przestrzenią X)
'