6.04.21
Odwzorowanie
podstawowych obiektów
rysunkowych
Zapis konstrukcji

6.04.21
Odwzorowanie podstawowych obiektów rysunkowych
2
Podstawowe obiekty rysunkowe
Punkt
Odcinek
Prosta
Płaszczyzna

6.04.21
Odwzorowanie podstawowych obiektów rysunkowych
3
Punkt
• Rzut punktu na jedną rzutnię
• Rzut punktu na dwie rzutnie
• Rzut punktu na trzy rzutnie
• Konstrukcja trzeciego rzutu
6.04.21
Odwzorowanie prostych obiektów rysunkowych - punkt
4
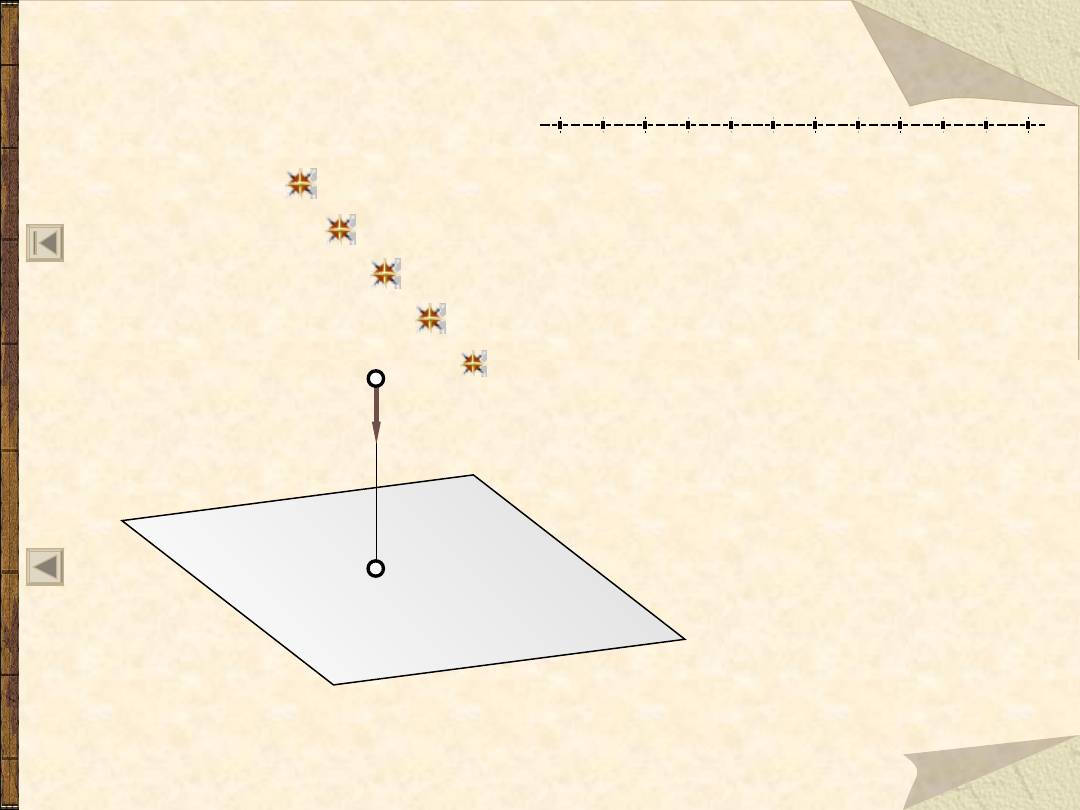
Rzut punktu na jedną rzutnię
A
A’
A - punkt w przestrzeni
A’ – rzut punktu na płaszczyznę
a
– prosta rzutująca
K
a
K - kierunek rzutowania
– płaszczyzna rzutowania
6.04.21
Odwzorowanie prostych obiektów rysunkowych - punkt
5
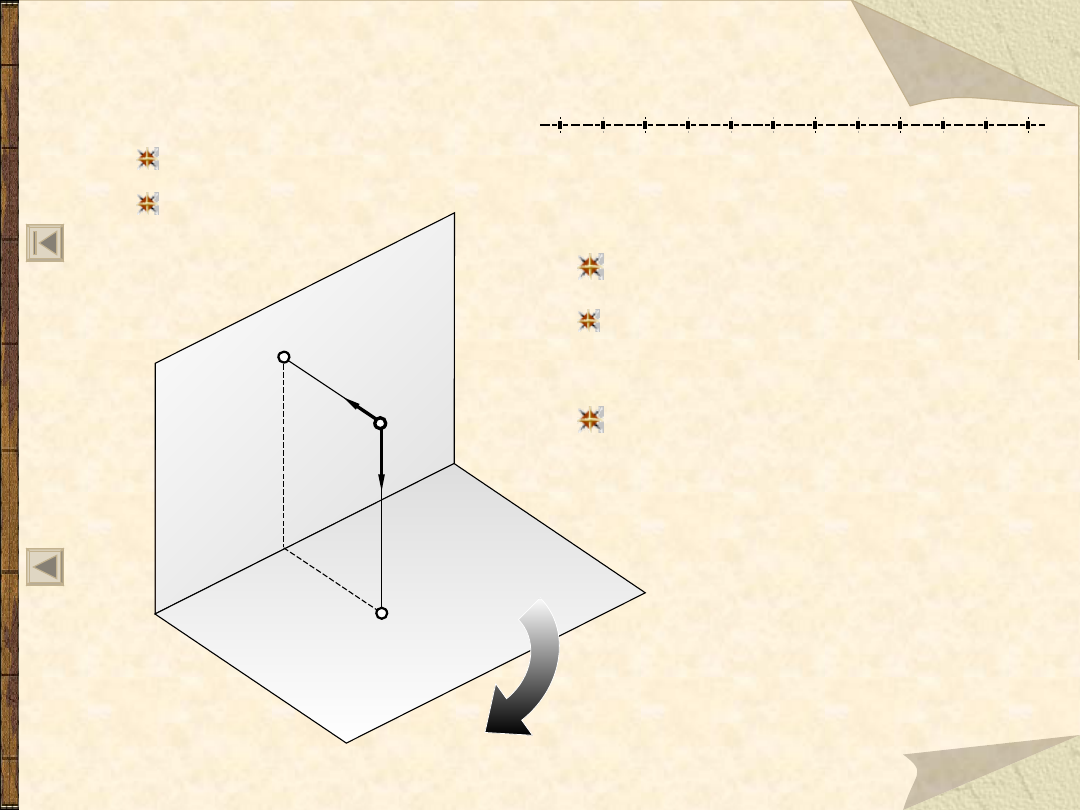
Rzut punktu na dwie rzutnie
A", B", C" ... - rzuty
punktów A, B, C ... na
płaszczyznę II
x – oś rzutni
A’
A
”
A
x
I – pionowa płaszczyzna rzutów (rzutnia pionowa)
A’, B’, C’ ... rzut punktów
A, B, C ... na płaszczyznę I
II – pozioma płaszczyzna rzutów (rzutnia pozioma)
6.04.21
Odwzorowanie prostych obiektów rysunkowych - punkt
6
x
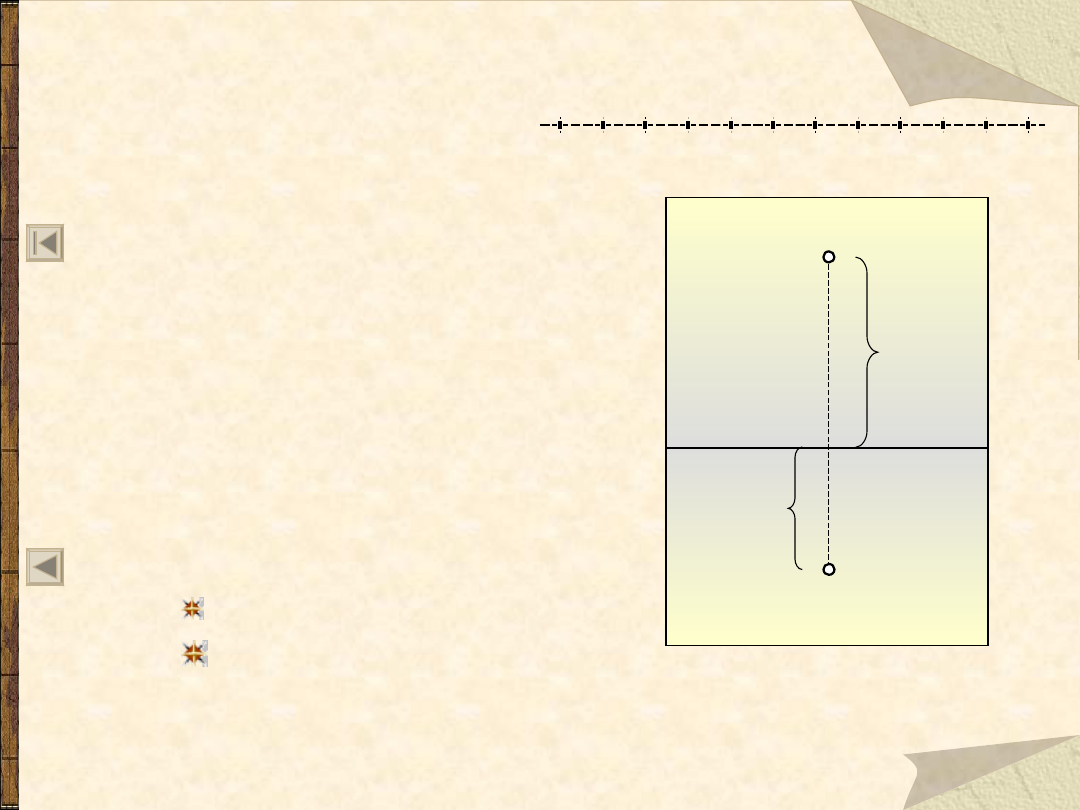
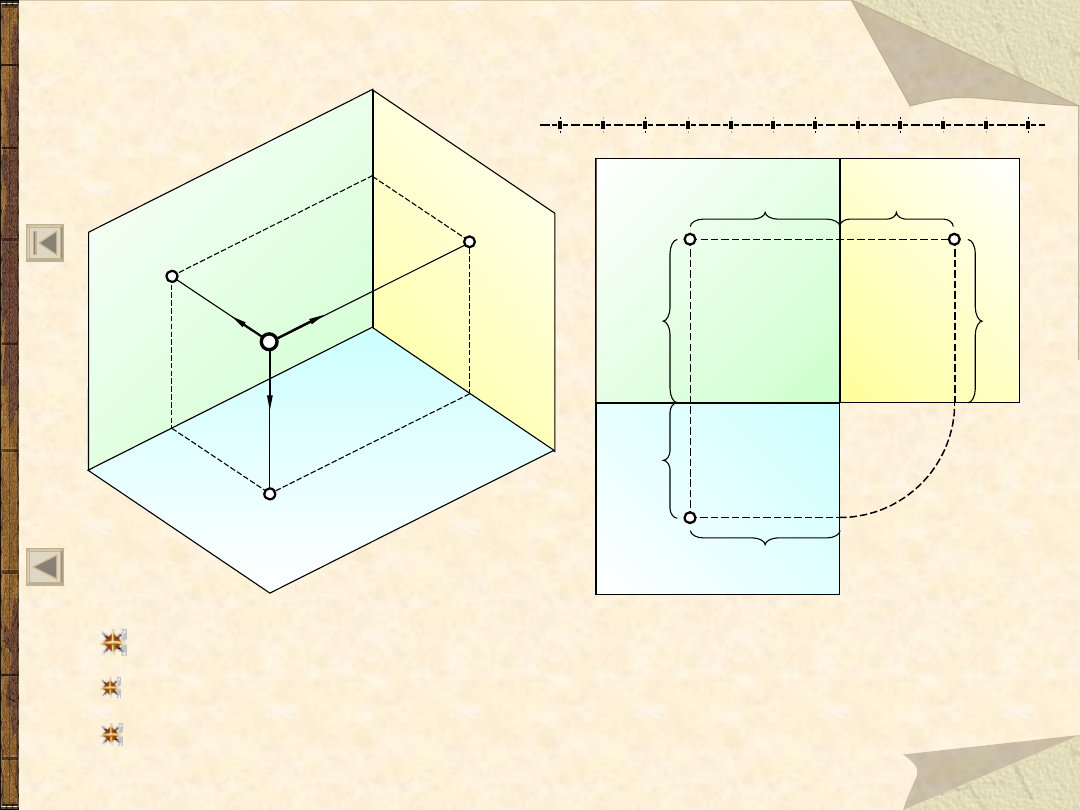
Rzut punktu na dwie rzutnie
w płaszczyźnie rysunku
Sprowadzamy obie rzutnie do
jednej płaszczyzny rysunku.
g – głębokość punktu
h
g
A
”
A’
h – wysokość punktu
Rzut pionowy A’ i poziomy
A” dowolnego punktu A w
przestrzeni, znajdują się
zawsze na jednej prostej
odnoszącej, prostopadłej
do osi x.
6.04.21
Odwzorowanie prostych obiektów rysunkowych - punkt
7
y
y
z
0
x
y
z
0
x
Rzut punktu na trzy rzutnie
III – płaszczyzna boczna rzutowania (rzutnia boczna)
A
A’
A
”
A”’
A’
h
g
s
s
g
h
s
– szerokość punktu
A’", B’", C’" ... - rzut punktów A, B, C ... na płaszczyznę III
A
”
A”
’

6.04.21
Odwzorowanie prostych obiektów rysunkowych - punkt
8
Rzut pionowy A’ i boczny A”’ dowolnego punktu A
znajdującego się w przestrzeni, leżą na jednej prostej
odnoszącej, prostopadłej do osi z.
Rzut poziomy A” i boczny A”’ dowolnego punktu A
znajdującego się w przestrzeni, leżą na jednej prostej
odnoszącej, prostopadłej do osi y.
Aby jednoznacznie określić położenie punktu w
układzie trzech rzutni, musimy mieć trzy
współrzędne określające jego odległość od tych
płaszczyzn: szerokość (x), głębokość (y) i
wysokość (z).
W układzie trzech rzutni możliwych jest osiem położeń
punktu.
6.04.21
Odwzorowanie prostych obiektów rysunkowych - punkt
9
x
y
y
z
0
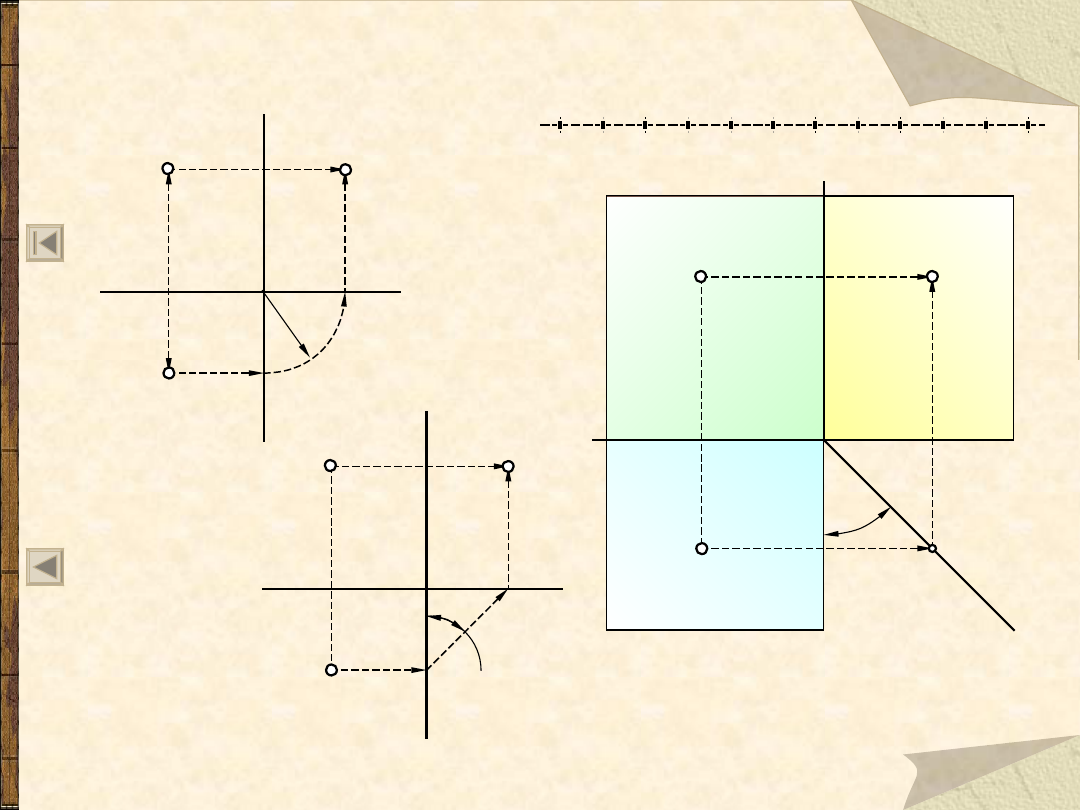
Konstrukcja trzeciego rzutu
A
”
A”
’
A’
x
y
y
z
0
A”
’
A
”
A’
45
0
x
y
y
z
0
A”
’
A’
45
0
r
A
”

6.04.21
Odwzorowanie podstawowych obiektów rysunkowych
10
Odcinek
Rzut odcinka na jedną rzutnię
Rzut odcinka na dwie rzutnie
- położenie dowolne
Rzut odcinka na dwie rzutnie
- przypadki szczególne
Rzut odcinka na trzy rzutnie
6.04.21
Odwzorowanie prostych obiektów rysunkowych - odcinek
11
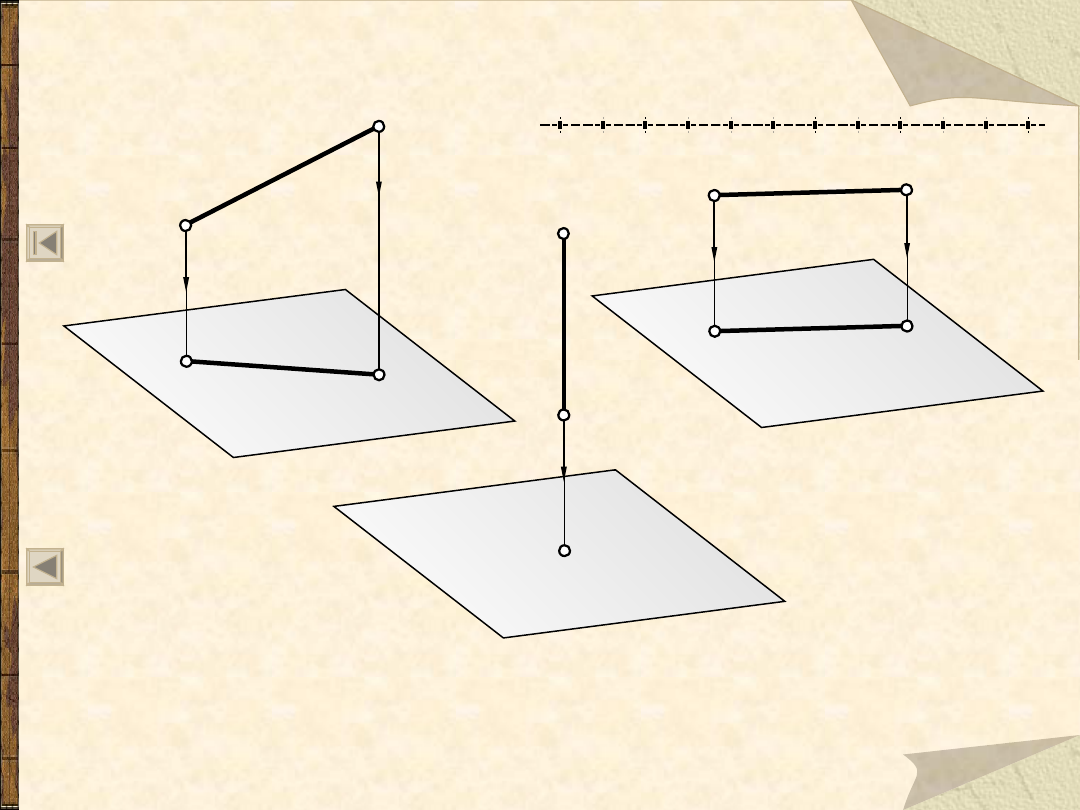
Rzut odcinka na jedną rzutnię
Jeżeli odcinek
jest prostopadły do rzutni,
to jego rzutem jest punkt.
Jeżeli odcinek jest równo-
legły do rzutni, to rzut
tego odcinka jest równy
danemu odcinkowi
A’B’ = AB
A
A’
B
B
’
A
A’=B
’
B
A
A’
B
B
’
6.04.21
Odwzorowanie prostych obiektów rysunkowych - odcinek
12
x
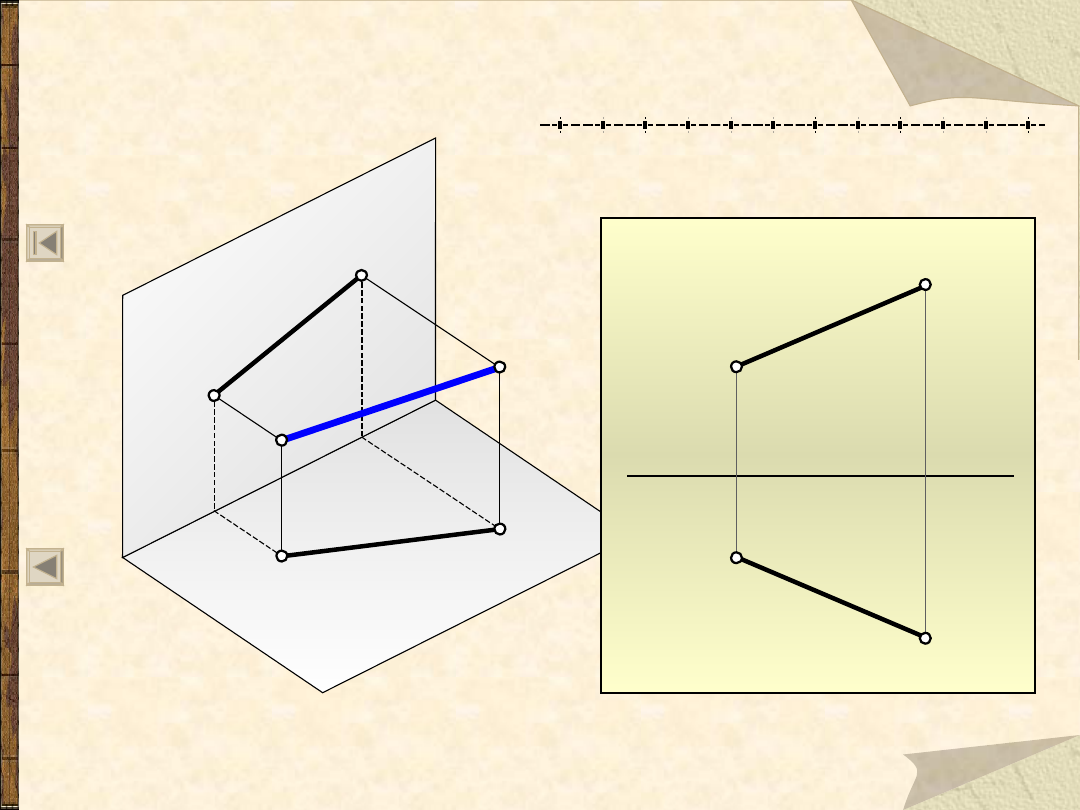
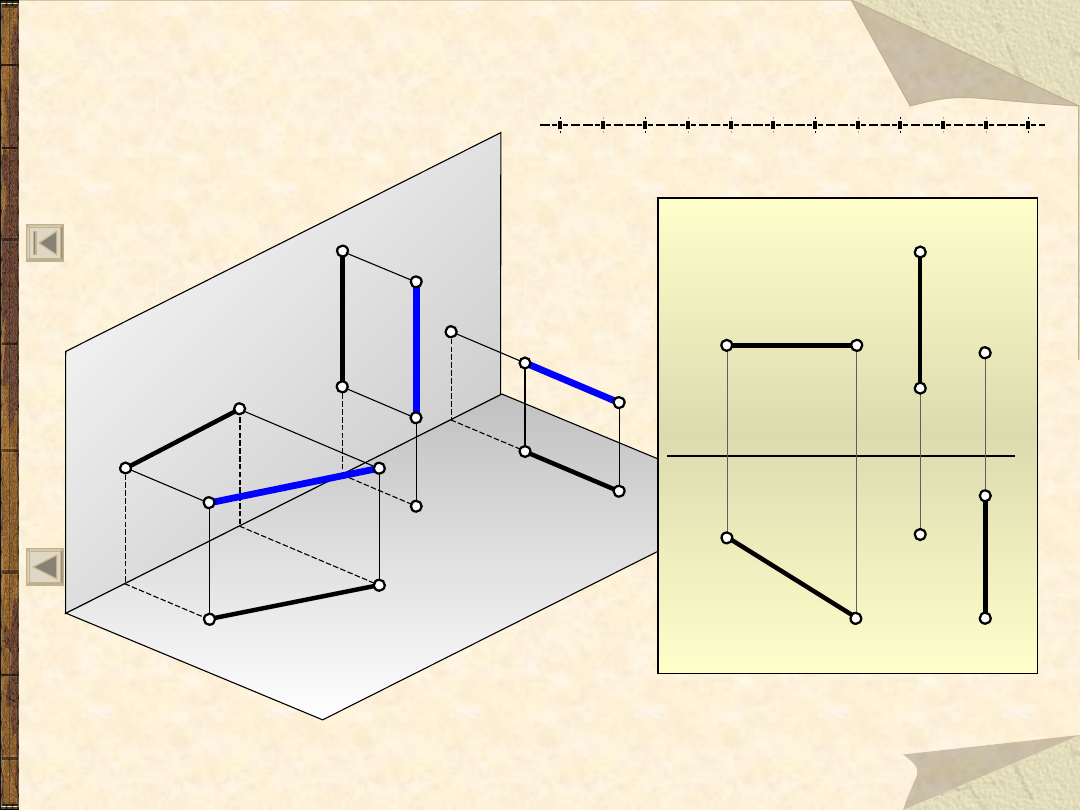
Rzut odcinka na dwie rzutnie
- położenie dowolne
A
”
B
”
A’
B’
A
B
x
A
”
B
”
A’
B’
6.04.21
Odwzorowanie prostych obiektów rysunkowych
13
x
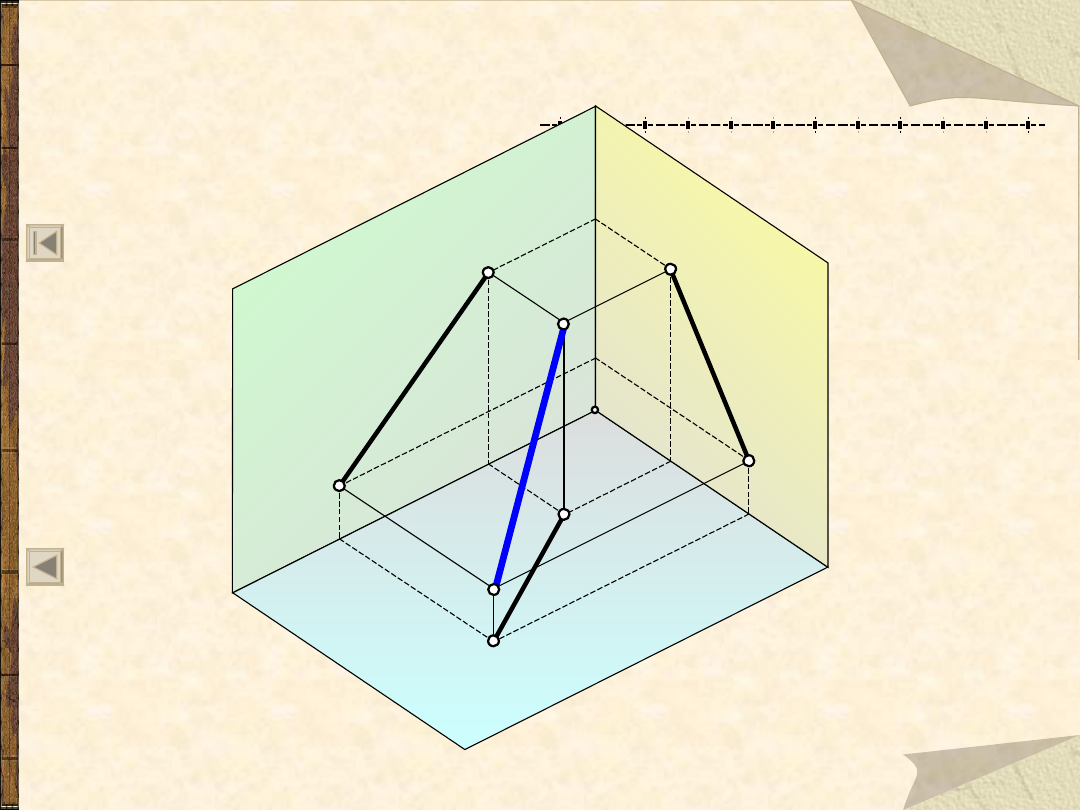
Rzut odcinka na dwie rzutnie
- przypadki szczególne
A
”
B
”
A’
B’
A
B
D
C
C’
D’
C”=D
”
F
”
E
”
E”=F
”
x
A
”
B
”
A’
B’
E’=F
’
C”=D
”
E
”
F
”
C’
D’
E
F
6.04.21
Odwzorowanie prostych obiektów rysunkowych
14
x
y
z
0
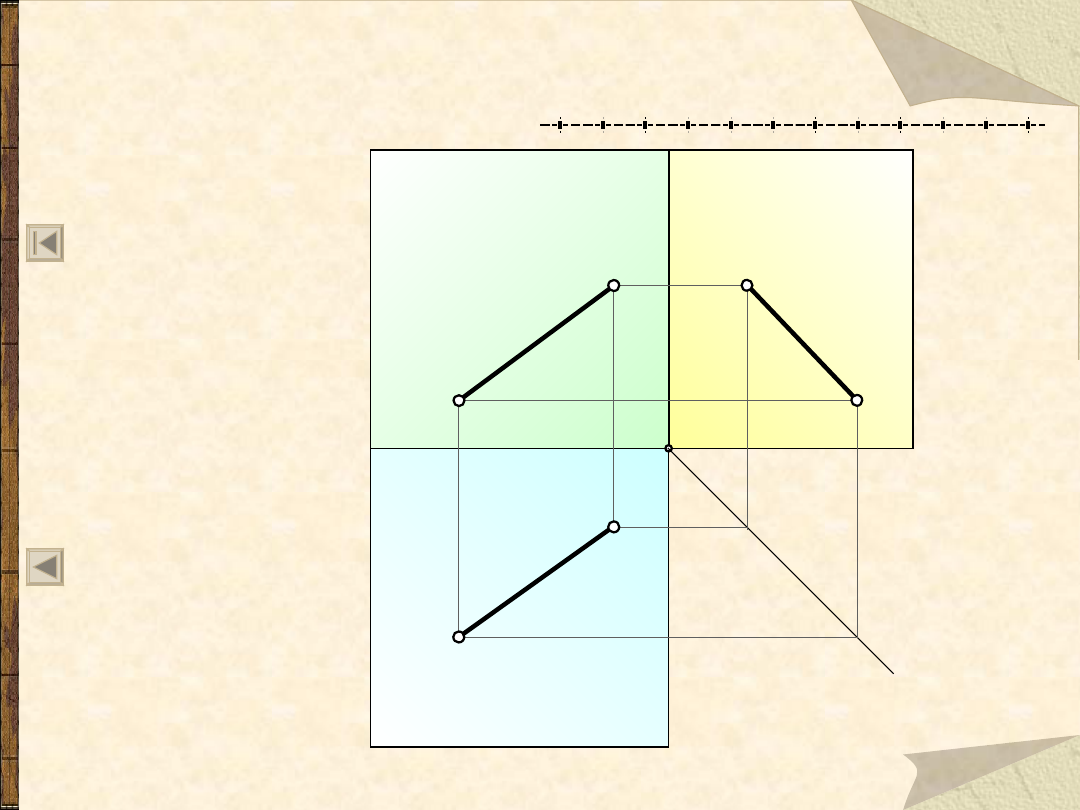
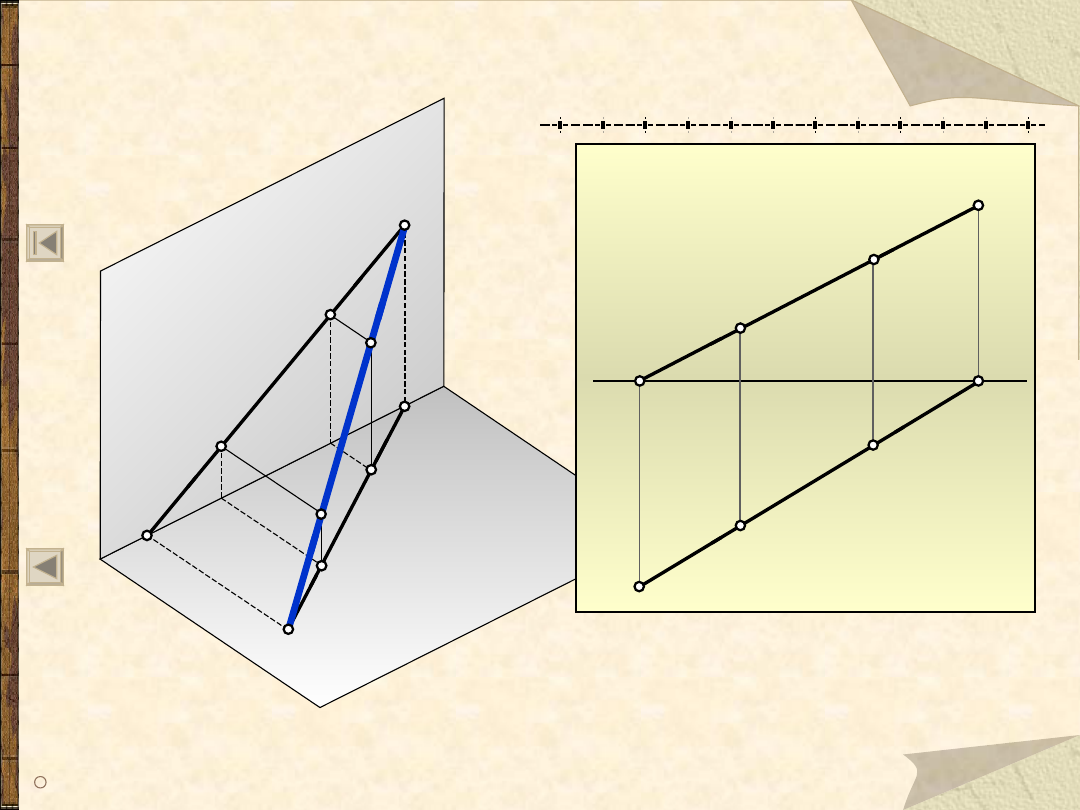
Rzut odcinka na trzy rzutnie
- położenie dowolne
A
B
A”’
B’
”
A’
B’
A
”
B
”
6.04.21
Odwzorowanie prostych obiektów rysunkowych
15
x
y
y
z
0
A’
B’
A
”
B
”
A”
’
B”
’

6.04.21
Odwzorowanie podstawowych obiektów rysunkowych
16
Prosta
Prosta i jej ślady
Wzajemne położenie dwu prostych
• równoległe
• przecinające się
• prostopadłe
• wichrowate
Prosta na płaszczyźnie
(1)
• Prosta dowolna
(2)
• Prosta pozioma
• Prosta czołowa
Punkt na płaszczyźnie
• Punkt na płaszczyźnie szczególnej
6.04.21
Odwzorowanie prostych obiektów rysunkowych
17
x
Prosta i jej ślady
H
k
- ślad poziomy prostej k
x
V
k
– ślad pionowy prostej k
k
”
k’
k
H
k
’
B
’
A
’
A
”
B
”
A
B
V
k
”
V
k
=V
k
’
V
k
”
H
k
’
H
k
= H
k
”
k
”
k’
B
’
A
’
A
”
B
”
V
k
=V
k
’
H
k
= H
k
”
6.04.21
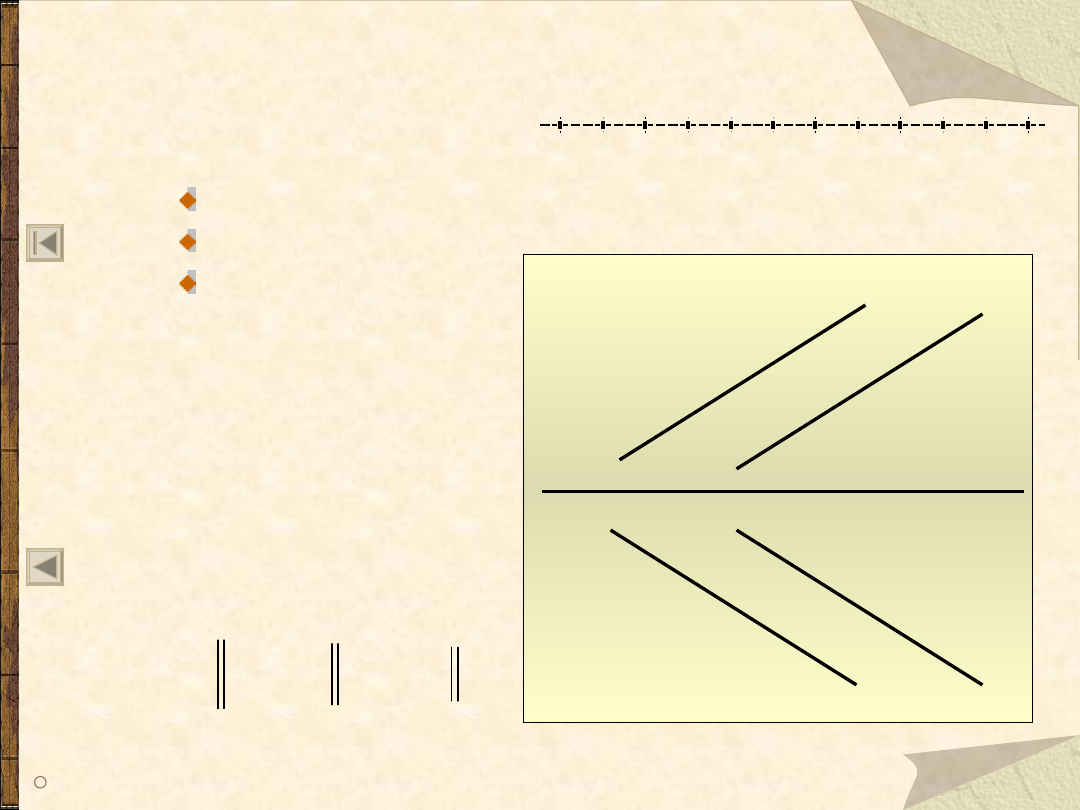
Wzajemne położenia dwu prostych
18
Proste równoległe
Dwie proste w przestrzeni mogą być:
wzajemnie do siebie równoległe
przecinające się
wichrowate
b
a
b
a
b
a
"
"
'
'
x
b
”
a’
b
’
a
”
6.04.21
Wzajemne położenia dwu prostych
19
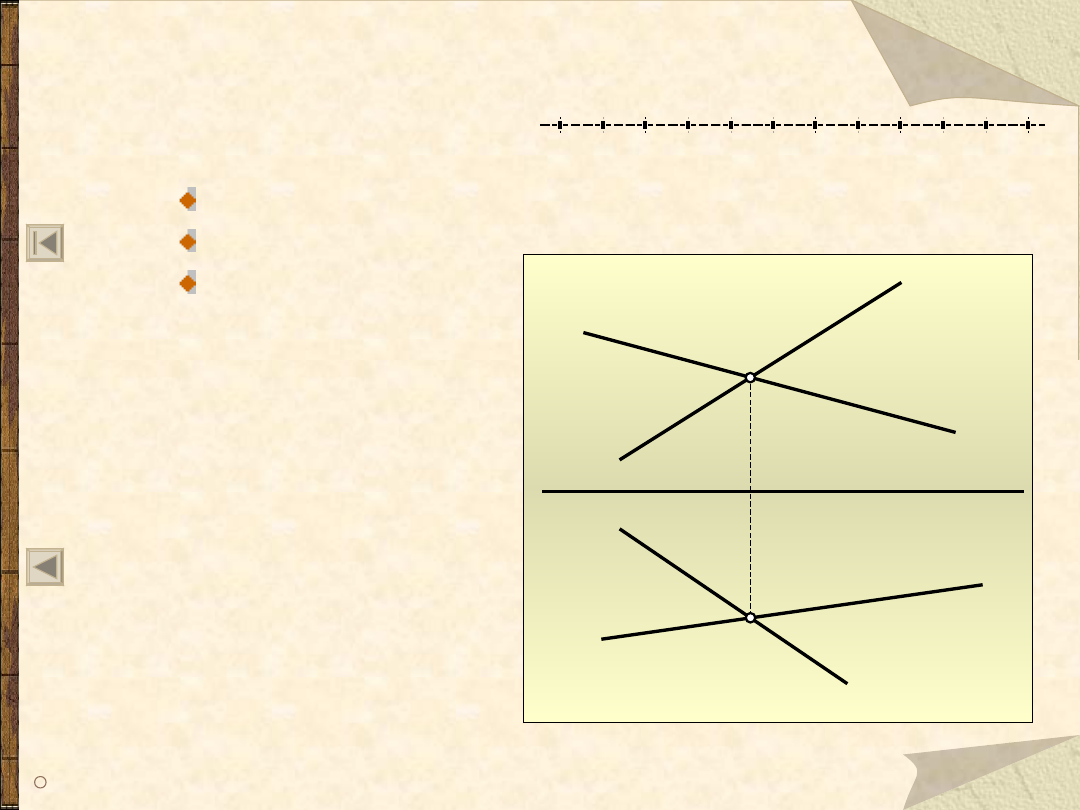
Proste przecinające się
Dwie proste w przestrzeni mogą być:
wzajemnie do siebie równoległe
przecinające się
wichrowate
x
a’
b
”
b
’
a
”
A
”
A’
'
'
'
'
b
A
a
A
"
"
"
"
b
A
a
A
b
A
a
A
6.04.21
Wzajemne położenia dwu prostych
20
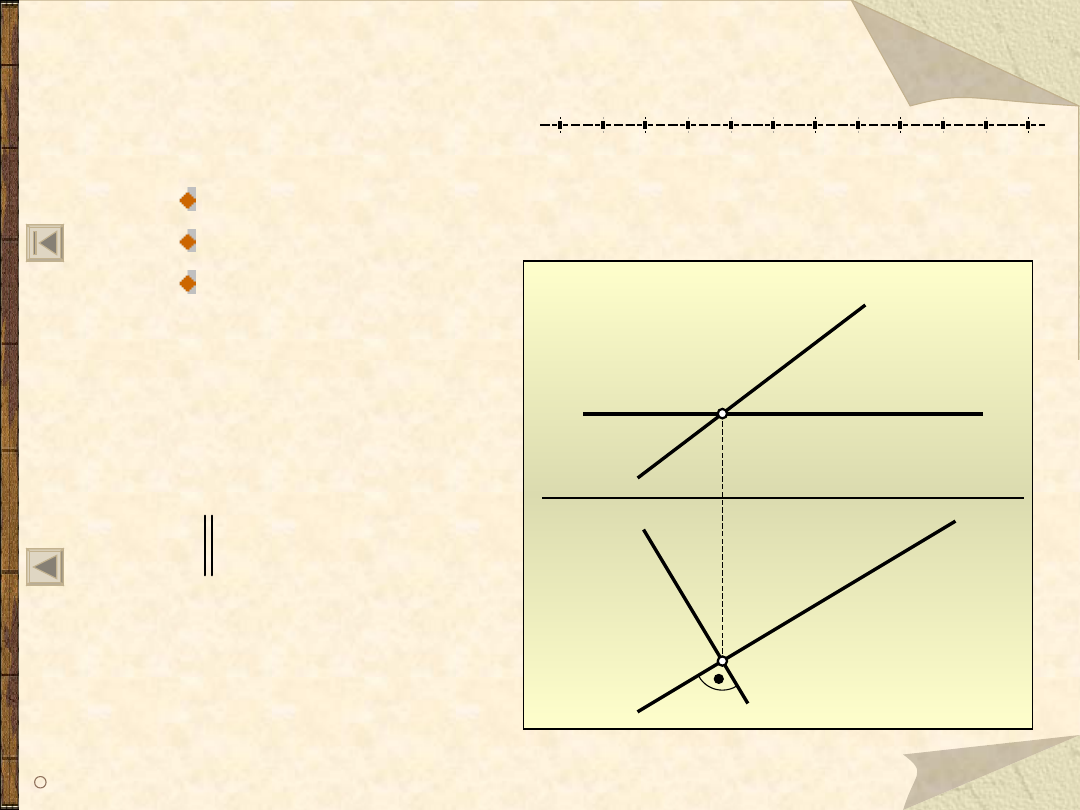
Proste prostopadłe
Dwie proste w przestrzeni mogą być:
wzajemnie do siebie równoległe
przecinające się – wzajemnie prostopadłe
wichrowate
x
a’
b
”
b
’
a
”
A’
A
”
"
"
'
b
a
x
b
b
a
b
A
a
A
6.04.21
Wzajemne położenia dwu prostych
21
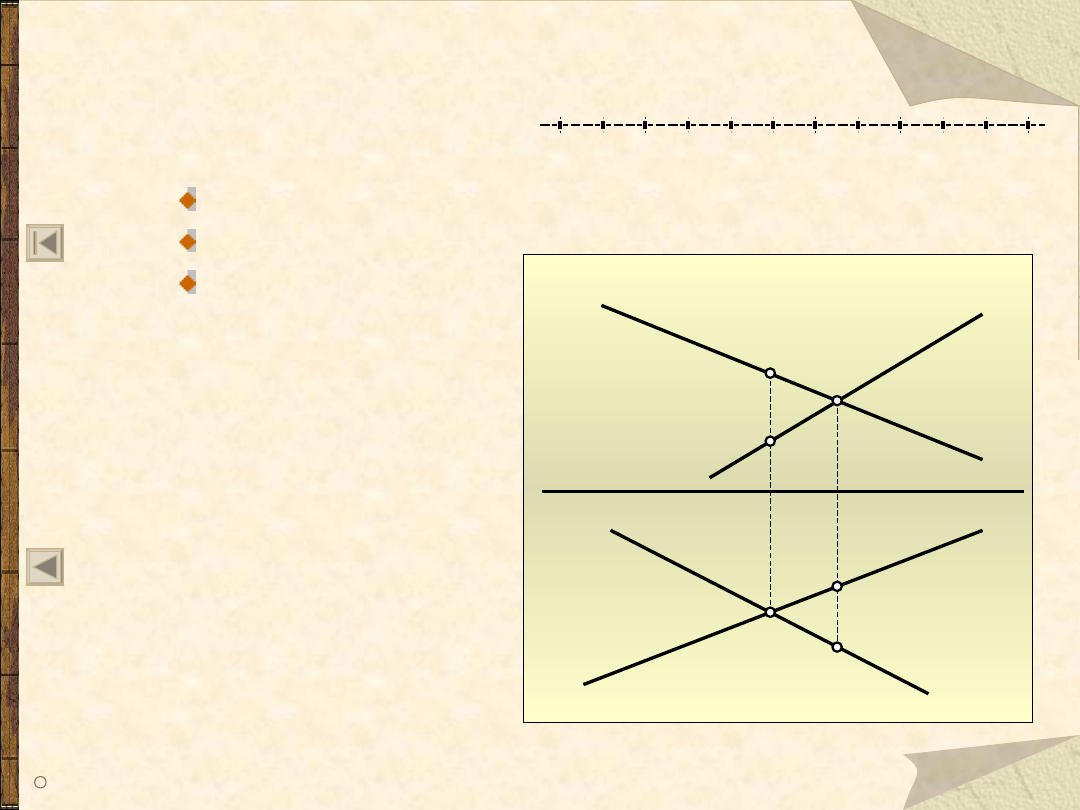
Proste wichrowate
Dwie proste w przestrzeni mogą być:
wzajemnie do siebie równoległe
przecinające się
wichrowate
x
a’
b
”
b
’
a
”
C’
A’
D
”
B
”
B’=D
’
A”=C
”
a
B
A
b
D
C
"
"
'
'
C
A
D
B
b
a
6.04.21
Przynależność elementów w rzucie równoległym
22
b”
b’
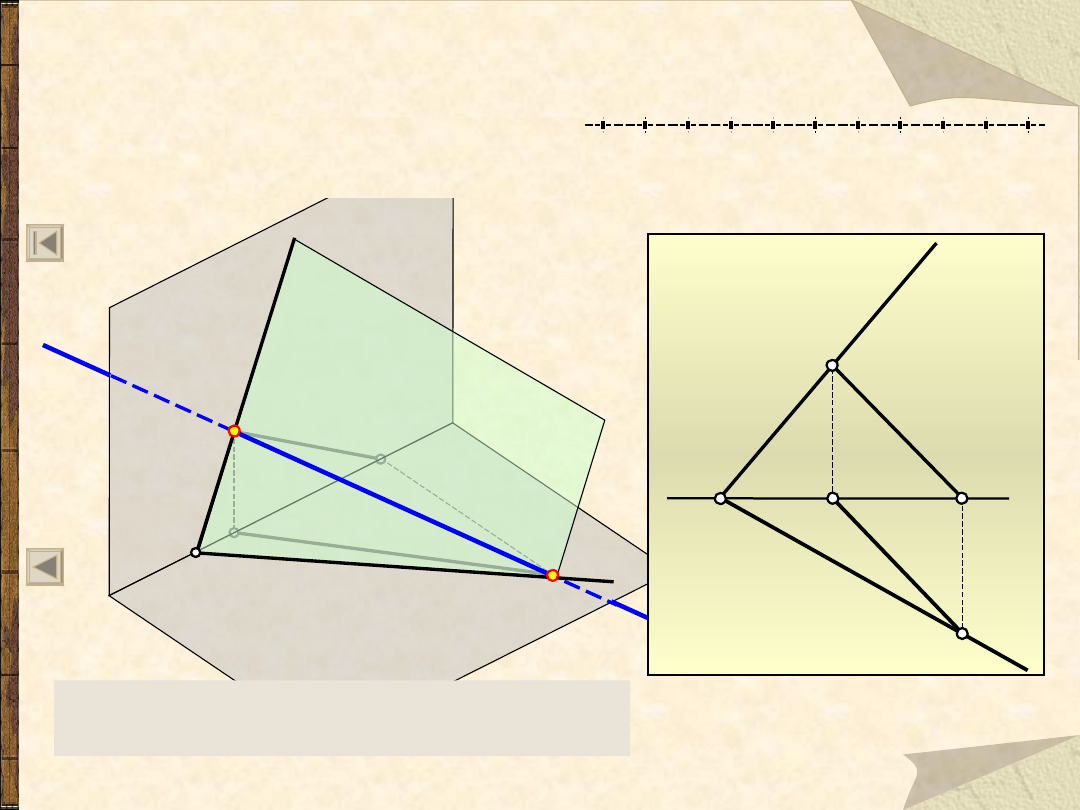
Prosta na płaszczyźnie
(1)
x
V
b
b
v
h
H
b
Prosta b leży na płaszczyźnie,
jeżeli jej ślady
V
b
i H
b
leżą na odpowiednich śladach
v
i
h
płaszczyzny
.
b
h
H
v
V
b
b
... jeżeli ma z nią, co najmniej,
dwa punkty wspólne.
x
h
v
b
”
b’
V
b
H
b
6.04.21
Przynależność elementów w rzucie równoległym
23
x
b’
b”
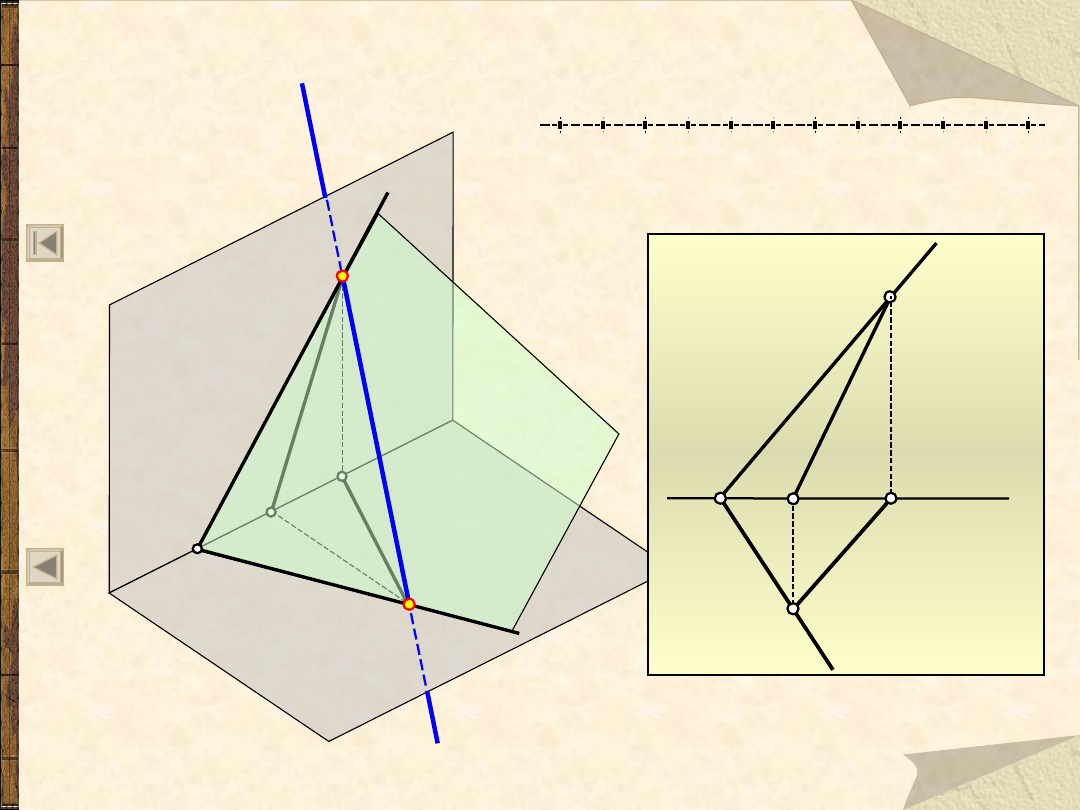
Prosta na płaszczyźnie
(2)
v
h
x
b’
b
h
v
b
”
V
b
H
b
H
b
V
b
6.04.21
Przynależność elementów w rzucie równoległym
24
Z wielu prostych leżących na płaszczyźnie najbardziej interesują
nas proste w położeniu szczególnym:
prosta równoległa do rzutni poziomej, tzw. prosta
pozioma
prosta równoległa do rzutni pionowej, tzw. prosta czołowa
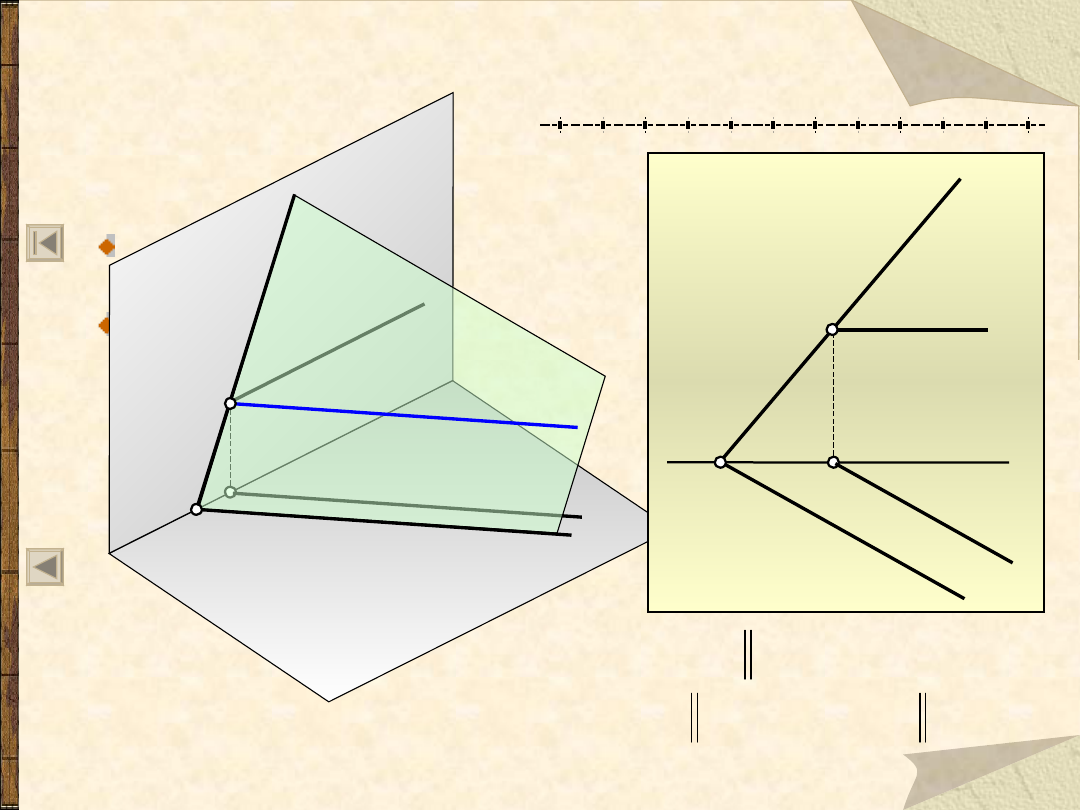
Prosta pozioma na płaszczyźnie
x
x
b”
b’
h
v
b
”
b’
V
b
h
v
b
V
b
Jeżeli:
II
b
b
to:
v
V
x
b
b
'
h
b"
6.04.21
Przynależność elementów w rzucie równoległym
25
Z wielu prostych leżących na płaszczyźnie najbardziej interesują
nas proste w położeniu szczególnym:
prosta równoległa do rzutni poziomej, tzw. prosta pozioma
prosta równoległa do rzutni pionowej
, tzw. prosta
czołowa
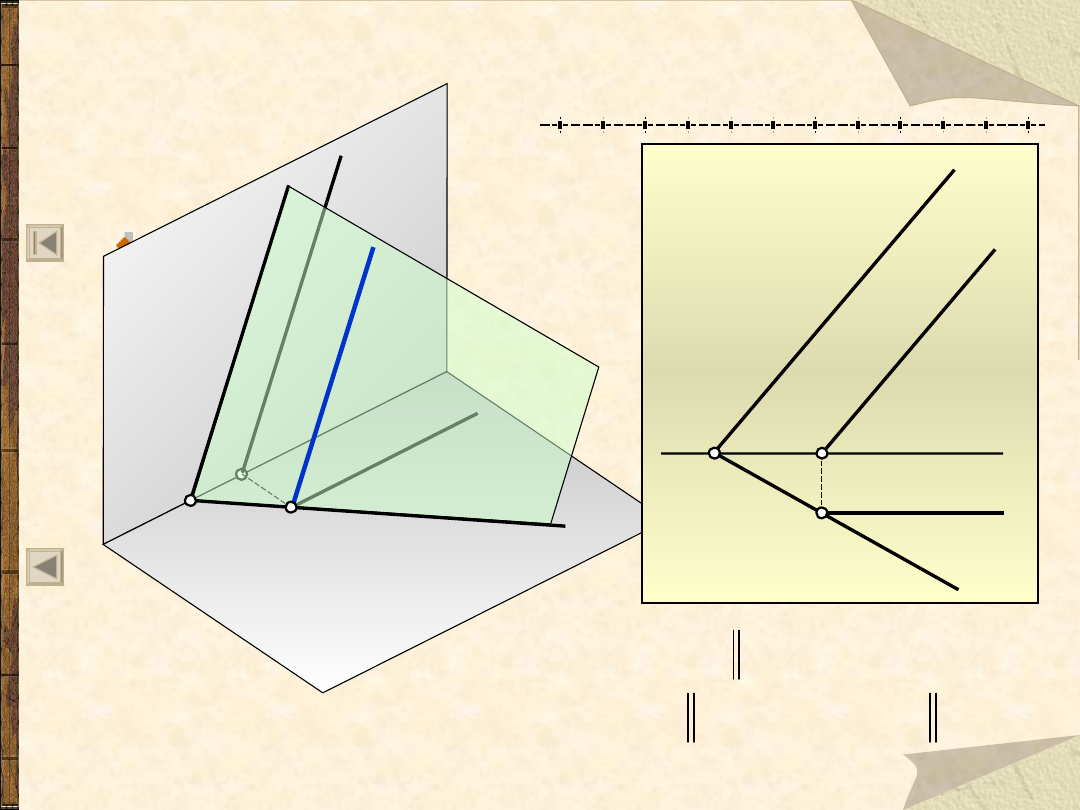
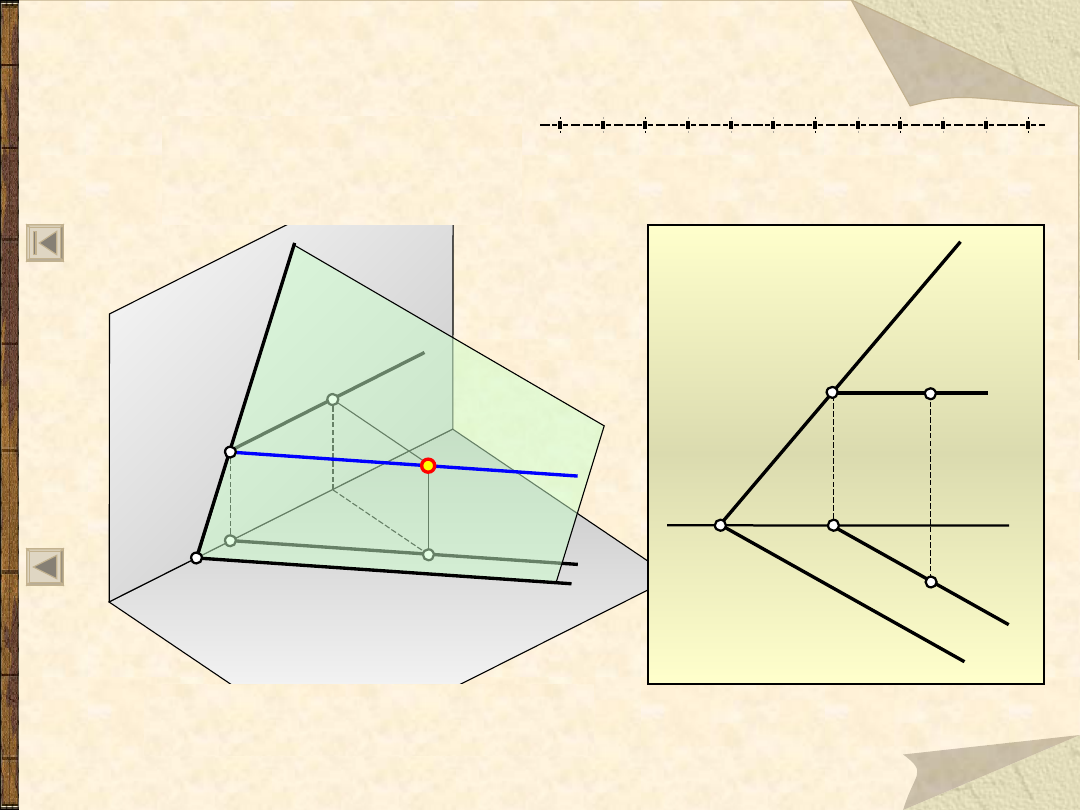
Prosta czołowa na płaszczyźnie
x
x
b”
h
v
b
”
b’
b’
H
b
b
h
v
H
b
Jeżeli:
I
b
b
to:
h
H
x
b
b
"
v
b'
6.04.21
Przynależność elementów w rzucie równoległym
26
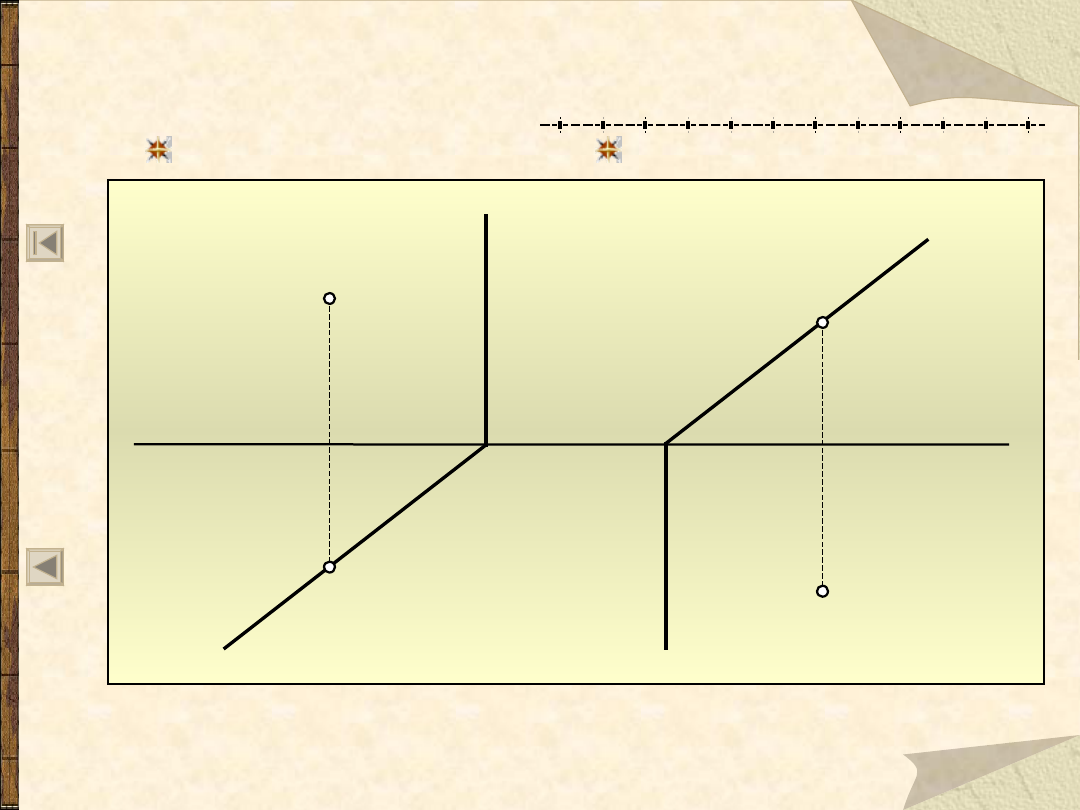
Punkt na płaszczyźnie
x
x
Punkt P leży na płaszczyźnie
, jeżeli jego rzuty leżą na
odpowiednich rzutach prostej należącej do tej płaszczyzny.
b”
b’
P”
P’
h
v
b
”
b’
V
b
P’
P”
h
v
b
P
P
jeżeli
"
"
'
'
b
P
b
P
b
V
b
6.04.21
Przynależność elementów w rzucie równoległym
27
Punkt na płaszczyźnie szczególnej
poziomo rzutującej
pionowo rzutującej
x
h
v
v
h
A”
B’
B”
A’
h
A
A
"...)
(
,...)
(
v
B
B
'...)
(
,...)
(
6.04.21
Odwzorowanie podstawowych obiektów rysunkowych
28
Płaszczyzna
Odwzorowanie płaszczyzn
Odwzorowanie płaszczyzn
Płaszczyzna w układzie dwóch rzutni
Płaszczyzna w układzie dwóch rzutni
Szczególne położenia płaszczyzn
Szczególne położenia płaszczyzn
• Płaszczyzna pionowo rzutująca
• Płaszczyzna poziomo rzutująca
• Płaszczyzna bocznie rzutująca
• Płaszczyzny równoległe do rzutni
Wzajemne położenia dwu płaszczyzn
Wzajemne położenia dwu płaszczyzn
• Płaszczyzny równoległe
• Płaszczyzny dowolne przecinające się
• Płaszczyzna pozioma i dowolna
• Płaszczyzna dowolna i czołowa
• Płaszczyzny prostopadłe
Wzajemne położenia prostej i płaszczyzny
Wzajemne położenia prostej i płaszczyzny
• Prosta równoległa
• Prosta przebijająca
• Prosta prostopadła

6.04.21
Odwzorowanie prostych obiektów rysunkowych
29
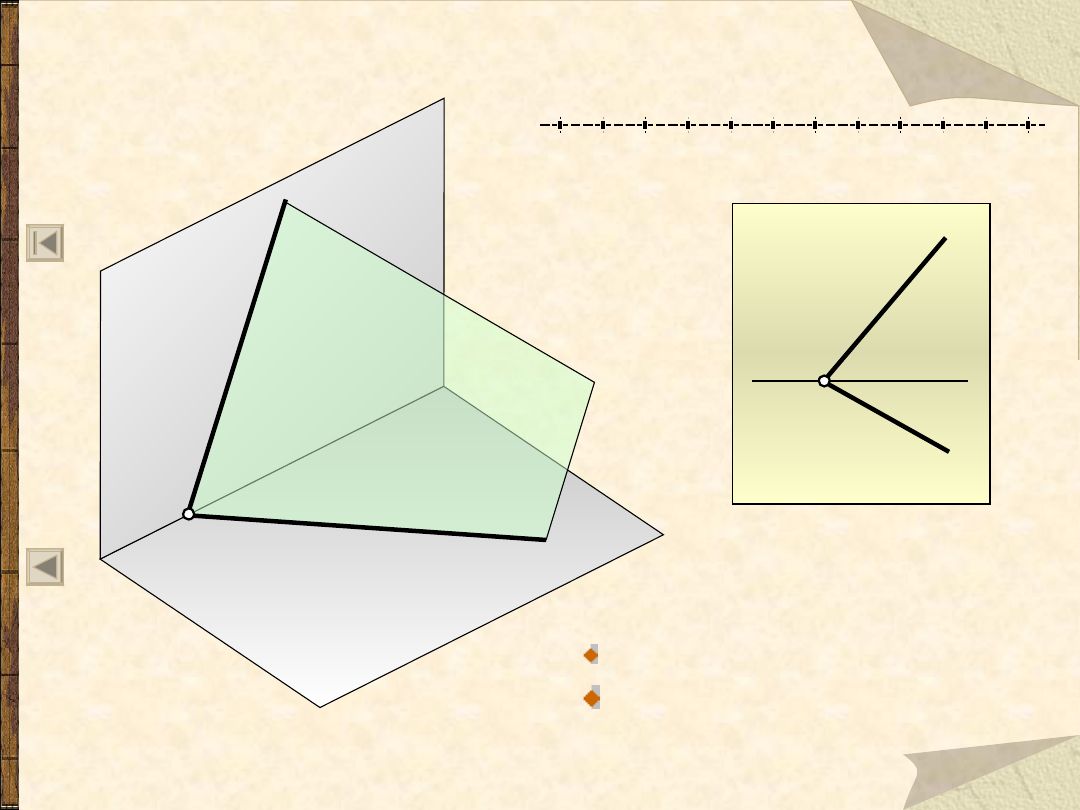
Odwzorowanie płaszczyzn
Położenie płaszczyzny w przestrzeni może być
wyznaczone przez:
trzy punkty nie leżące na jednej prostej;
prostą i punkt nie leżący na niej;
dwie przecinające się proste;
dwie proste równoległe.
Możliwe położenia płaszczyzn względem rzutni:
położenie dowolne;
prostopadłość tylko do jednej rzutni (płaszczyzna
rzutująca);
prostopadłość do dwu rzutni (równoległość do
trzeciej).
6.04.21
Odwzorowanie prostych obiektów rysunkowych
30
x
Płaszczyzna w układzie dwóch rzutni
h
- ślad poziomy płaszczyzny
X
h
v
x
h
v
X
v
– ślad pionowy płaszczyzny
h
v
x
X
6.04.21
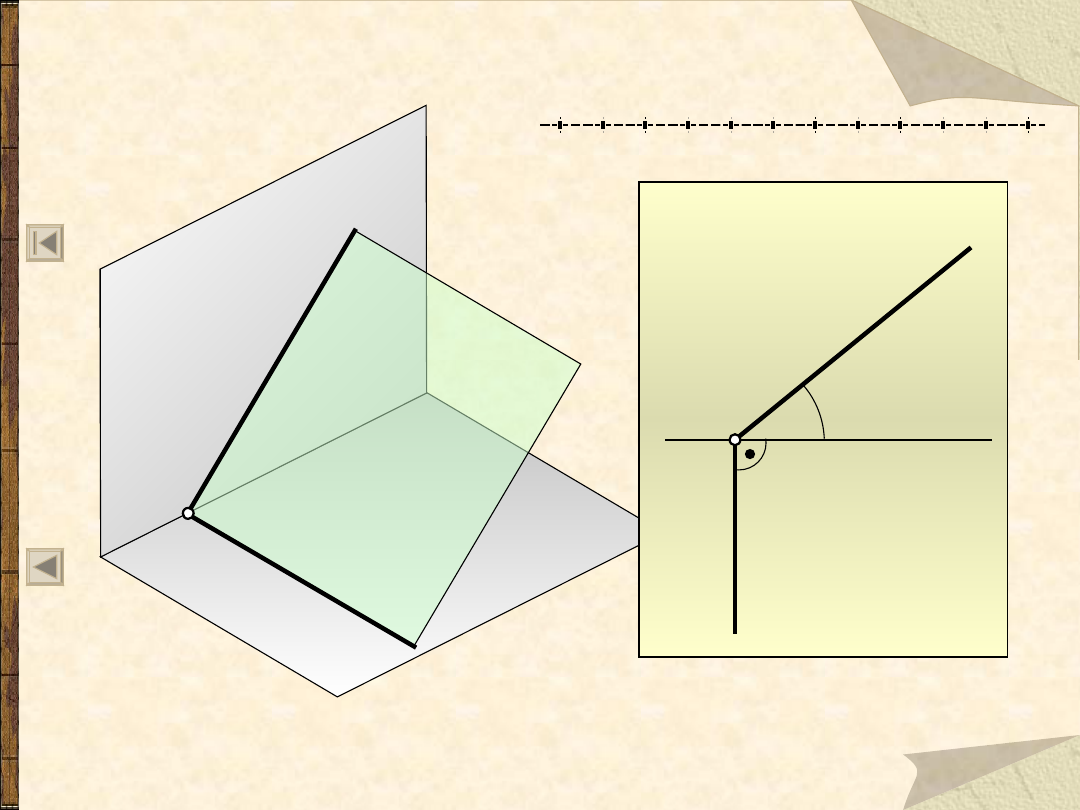
Szczególne położenia płaszczyzn
31
x
Płaszczyzna pionowo rzutująca
h
v
x
h
v
X
X
6.04.21
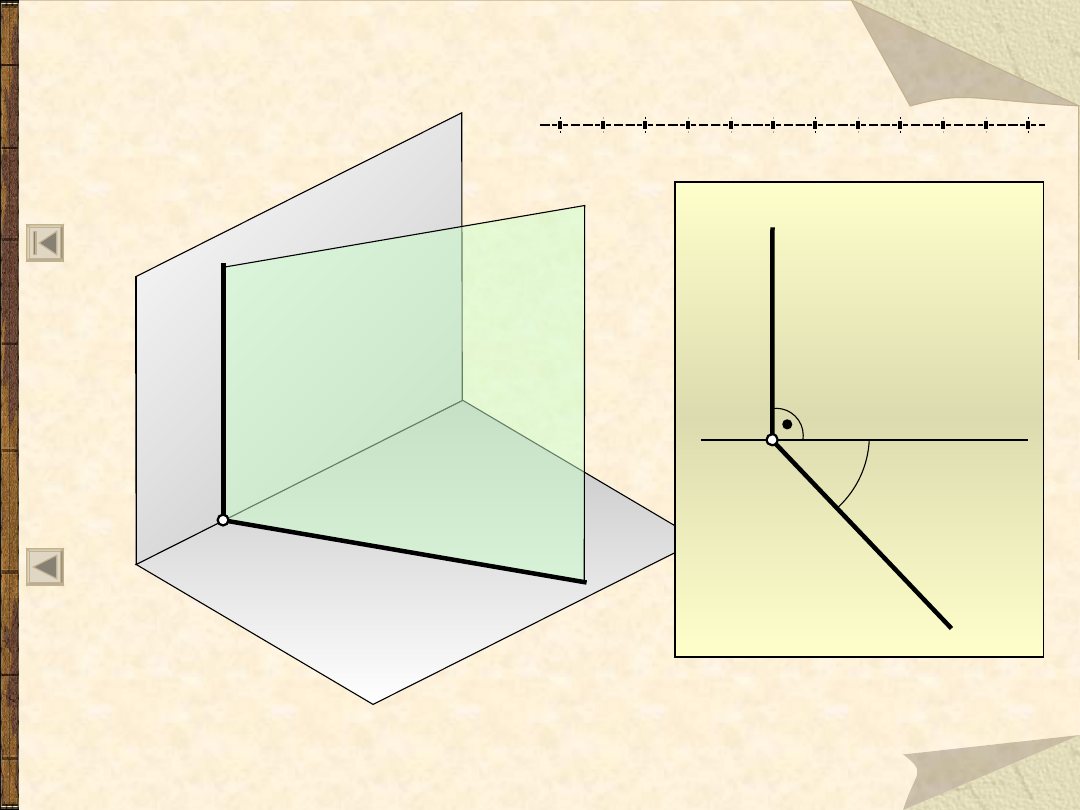
Szczególne położenia płaszczyzn
32
x
Płaszczyzna poziomo rzutująca
h
v
x
h
v
X
X
6.04.21
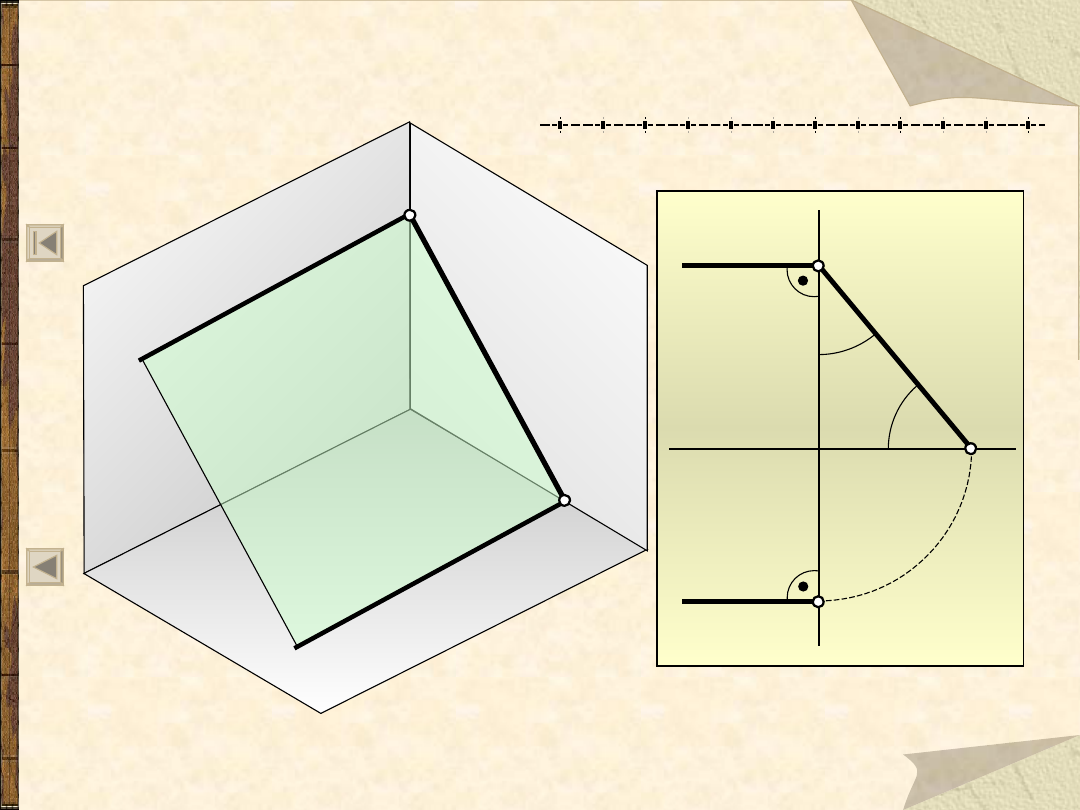
Szczególne położenia płaszczyzn
33
x
0
y
z
Płaszczyzna bocznie rzutująca
h
v
k
x
h
v
y
z
y
k
0
Z
Y
Z
Y
6.04.21
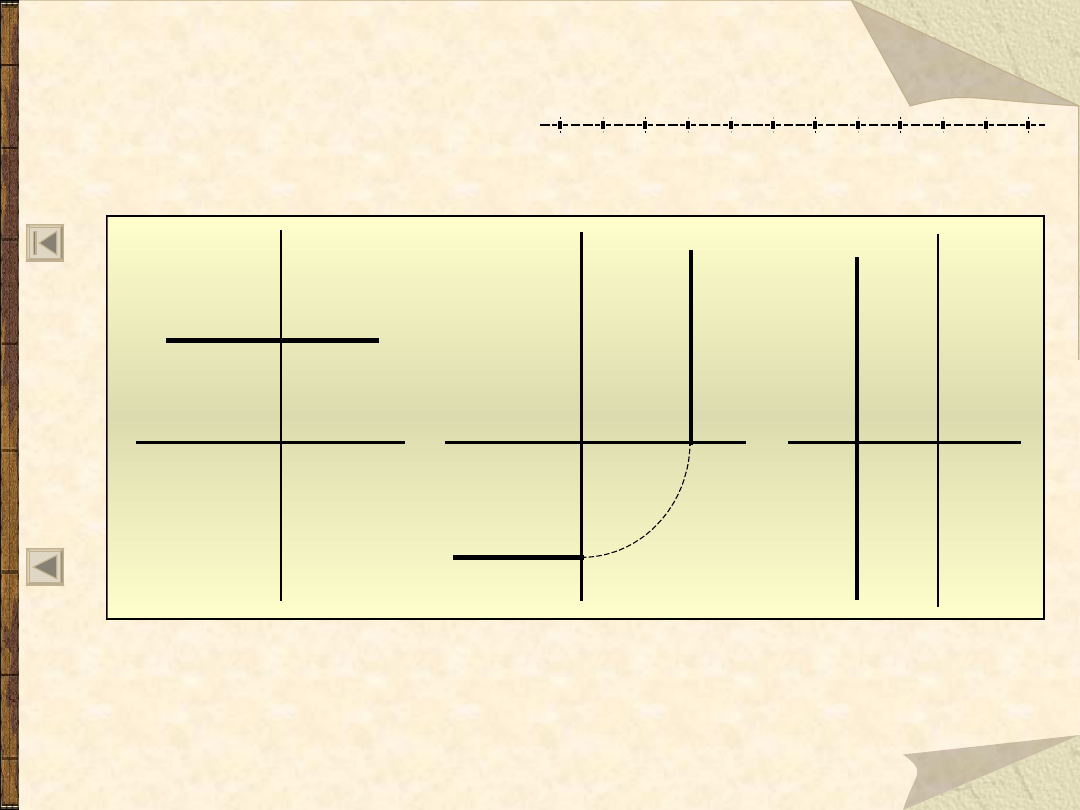
Szczególne położenia płaszczyzn
34
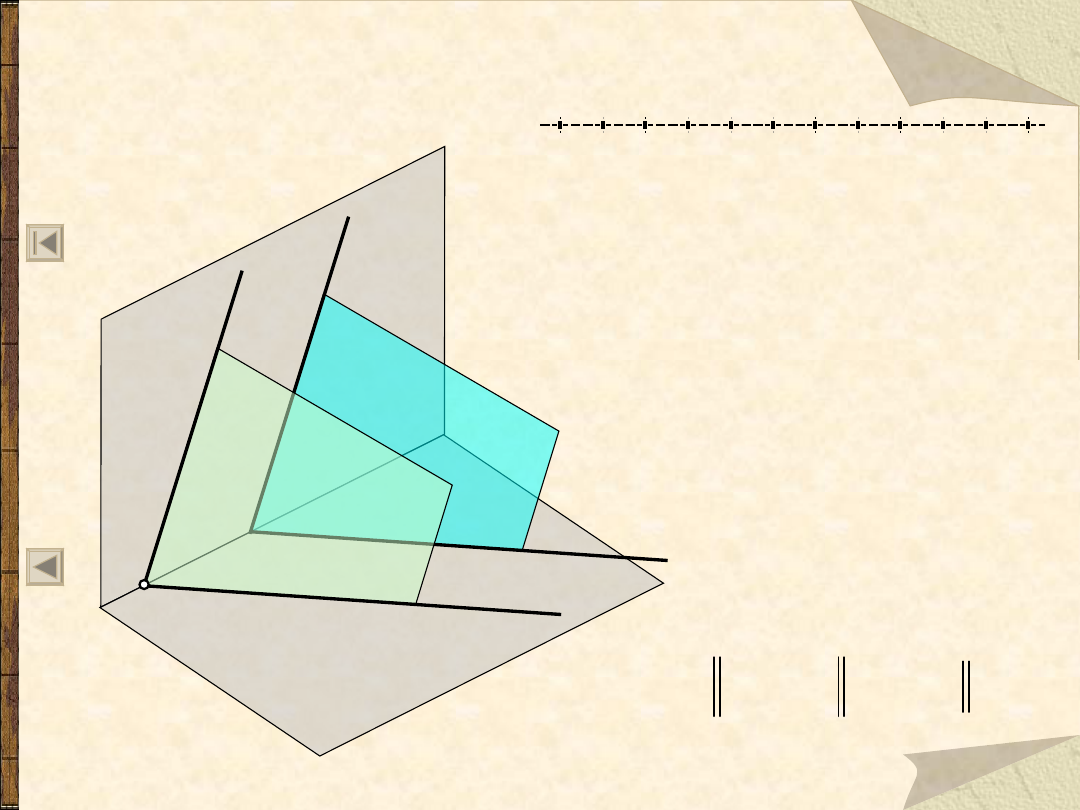
Płaszczyzny równoległe do rzutni
h
x
y
z
y
0
k
x
y
z
y
0
v
k
x
y
z
y
0
h
v
6.04.21
Wzajemne położenia dwu płaszczyzn
35
x
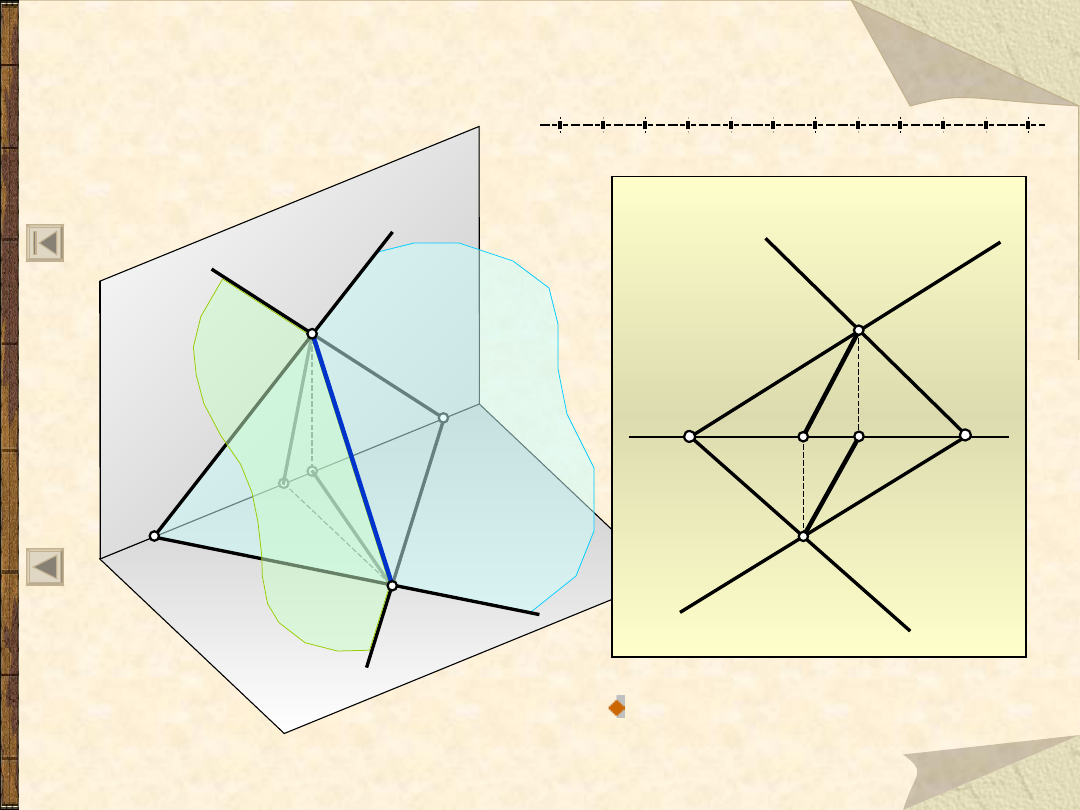
Płaszczyzny równoległe
Płaszczyzna
jest równoległa
do
, jeżeli dwie proste
przecinające się jednej
płaszczyzny są odpowiednio
równoległe do co najmniej
dwu prostych przecinających
się drugiej płaszczyzny.
Dwie płaszczyzny
i
są równoległe,
jeżeli jednoimienne
ich ślady są do
siebie równoległe.
h
h
v
v
v
h
v
h
6.04.21
Wzajemne położenia dwu płaszczyzn
36
x
v
h
X
k’
k”
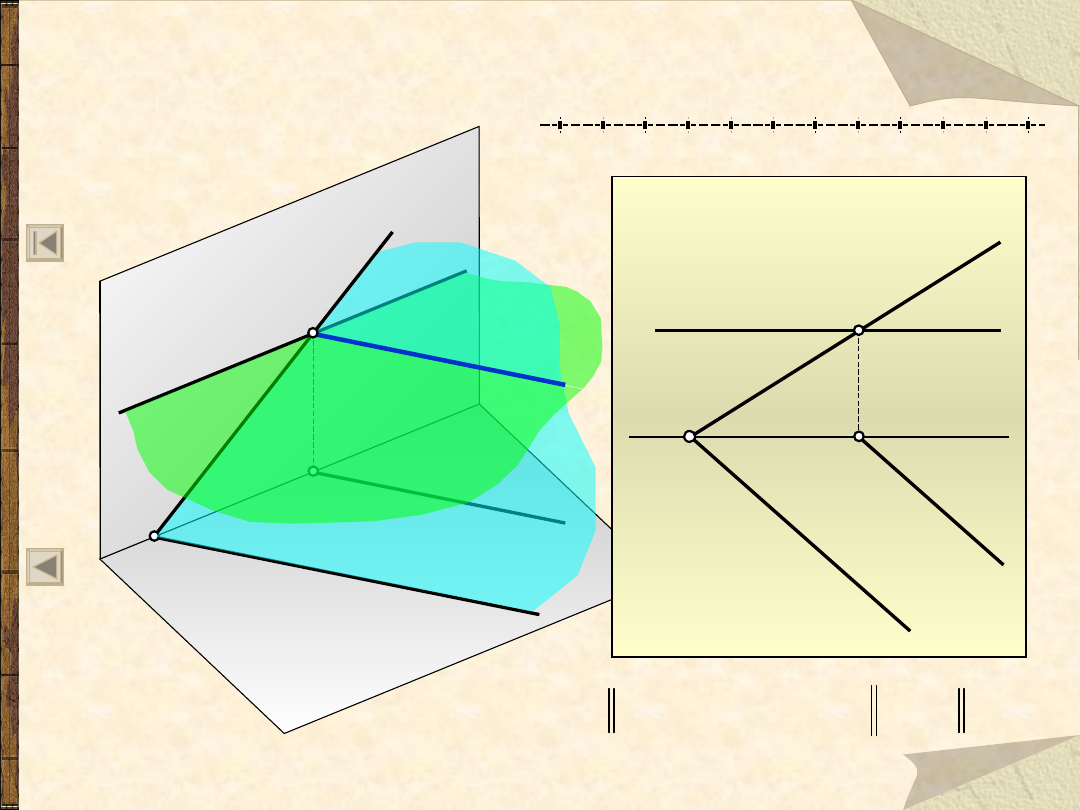
Płaszczyzny dowolne przecinające się
k - krawędź płaszczyzn
x
h
v
X
v
h
X
k’
k
”
v
h
H
k
V
k
X
k
H
k
V
k
6.04.21
Wzajemne położenia dwu płaszczyzn
37
x
v
k
”
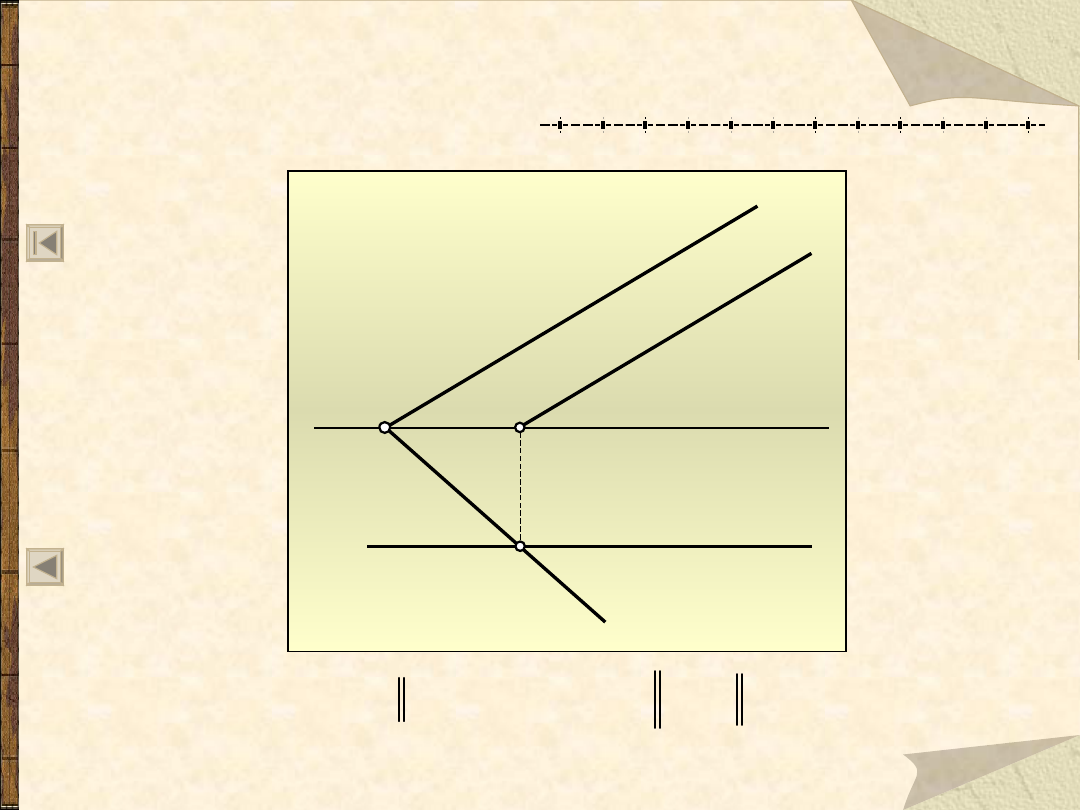
Przecinające się płaszczyzny:
pozioma i dowolna
x
h
v
X
v
h
X
k’
k’
k
v
k
”
V
k
V
k
h
k
x
k
k
II
"
'
6.04.21
Wzajemne położenia dwu płaszczyzn
38
Przecinające się płaszczyzny: czołowa
i dowolna
x
h
v
X
k’
h
k
”
H
k
h
k
x
k
k
I
'
"
I
I
I
H’
k
6.04.21
Wzajemne położenia dwu płaszczyzn
39
h
v
b’
x
b”
b
v
Prostopadłość płaszczyzn
b
h
b
v
b
"
'
b
v
b'
Płaszczyzna
jest prostopadła
do płaszczyzny
, jeżeli
zawiera co najmniej jedną
prostą prostopadłą
do płaszczyzny
.
6.04.21
Wzajemne połozenia prostej i płaszczyzny
40
Równoległość prostej i płaszczyzny
Prosta m jest równoległa
do płaszczyzny
gdy
jest równoległa do
prostej n należącej do
tej płaszczyzny.
x
h
v
n
”
m’
n’
m”
H
n
V
n
m
n
m
n
m
n
"
"
'
'
6.04.21
Wzajemne połozenia prostej i płaszczyzny
41
Prosta i płaszczyzna
w położeniu ogólnym
x
h
v
k’
m’
m”
H
k
P’
P”
k”
X
h
v
V
k
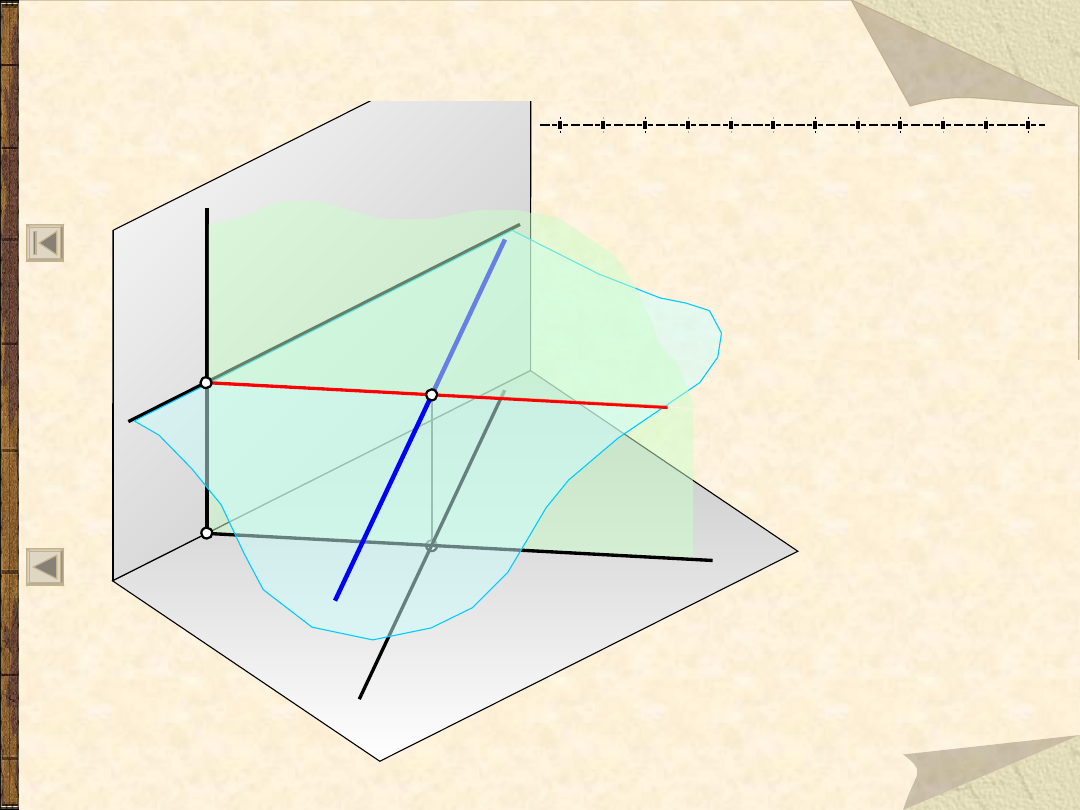
6.04.21
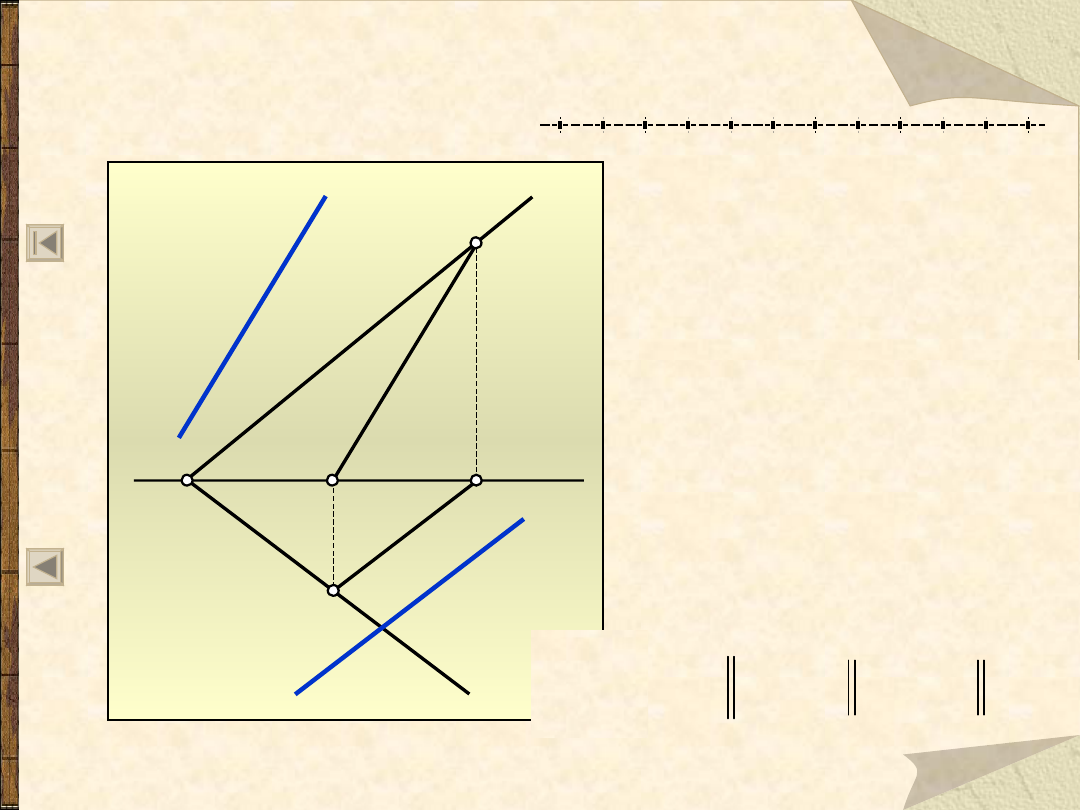
Wzajemne połozenia prostej i płaszczyzny
42
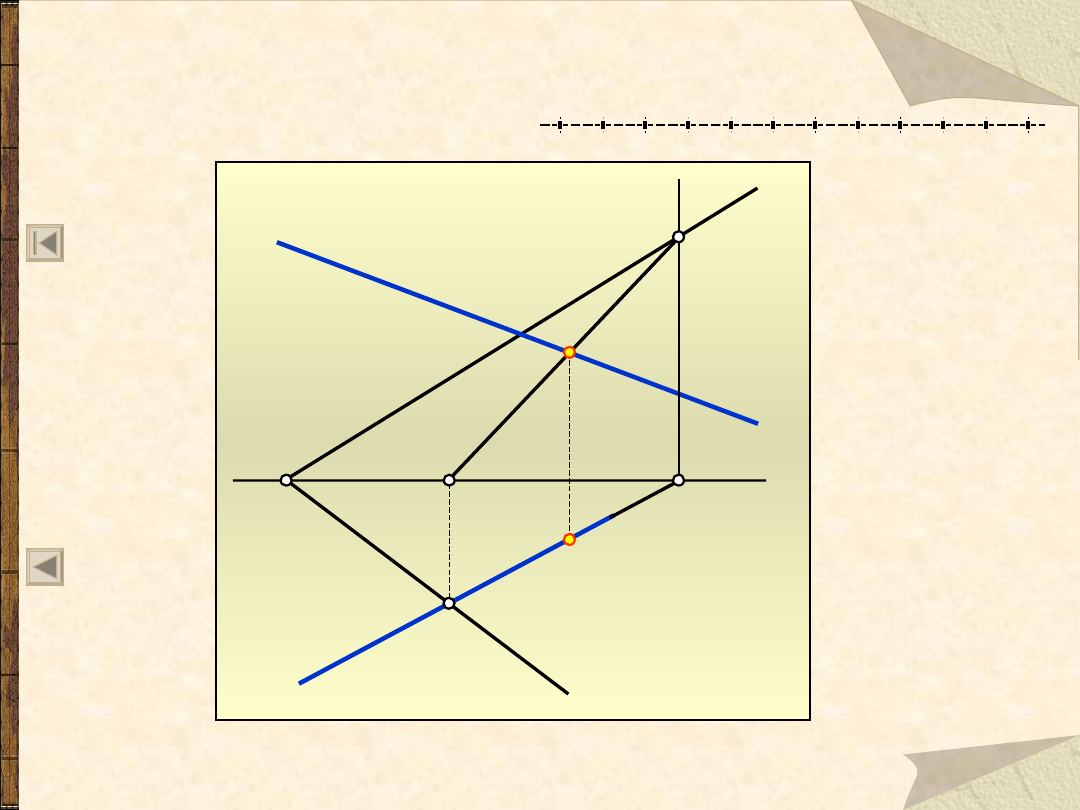
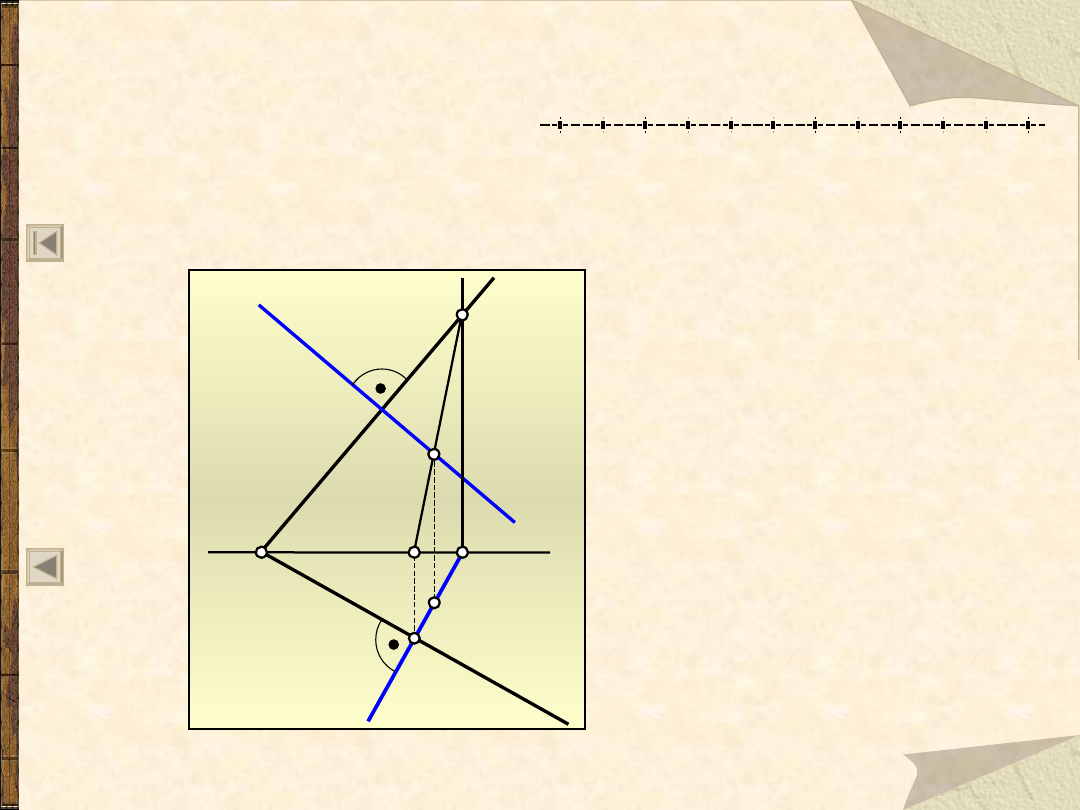
Prostopadłość prostej i płaszczyzny
Prosta jest prostopadła do płaszczyzny gdy jest
prostopadła do co najmniej dwóch prostych
przecinających się, należących do tej płaszczyzny.
Prosta przebija płaszczy-
znę pod kątem prostym,
jeżeli jej rzuty są prosto-
padłe do odpowiednich
śladów płaszczyzny.
Warunek konieczny
i wystarczający.
b
h
b
v
b
"
'
x
h
v
b
”
b’
h
v
k’
k”
P’
P
”
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
Wyszukiwarka
Podobne podstrony:
05 Odwzorowywanie obiektow na plas (2)
05 Wykonywanie podstawowych operacji ślusarskich
05 Sporządzanie podstawowego asortymentu potraw z owoców
05 Wykonywanie podstawowych robót malarskich
wykład-V-05.11.2012 BEZ-RYSUNKÓW, Praca Socjalna UŚ, zarządzanie i organizacja w pomocy społecznej
Odwzorowanie modelu obiektowego na DDL-1, Informatyka, SEMESTR IV, Projektowanie
05 odwzorowania linioweid 5542 Nieznany (2)
STUDIUM PRZYPADKU na podstawie analizy rysunku rodziny, analiza rysunku dziecka
ASEUT 2015 2016 MGR S1 PODSTAWOWE OBIEKTY REGULACJI W INSTALACJACH HYDRAULICZNYCH UCZ W1
Ćw 02 Rysowanie podstawowych obiektów graficznych – funkcje paska „Rysuj”
2 1 PODSTAWOWE ZASADY RYSUNKU TECHNICZNEGO
Pedagogika kompleks, Pedagogika specjalna - dział pedagogiki którego podstawowym obiektem zaintereso
odwzorowania, podstawy geodezji z geomatyką
05 Wykonywanie podstawowych operacji
Charakterystyka rodzajowa podstawowych obiektow hotelarskich, Hotelarstwo
więcej podobnych podstron