1

PRACA I ENERGIA

Praca
- wykonana przez stala sile.

- wykonana przez sile zmienna

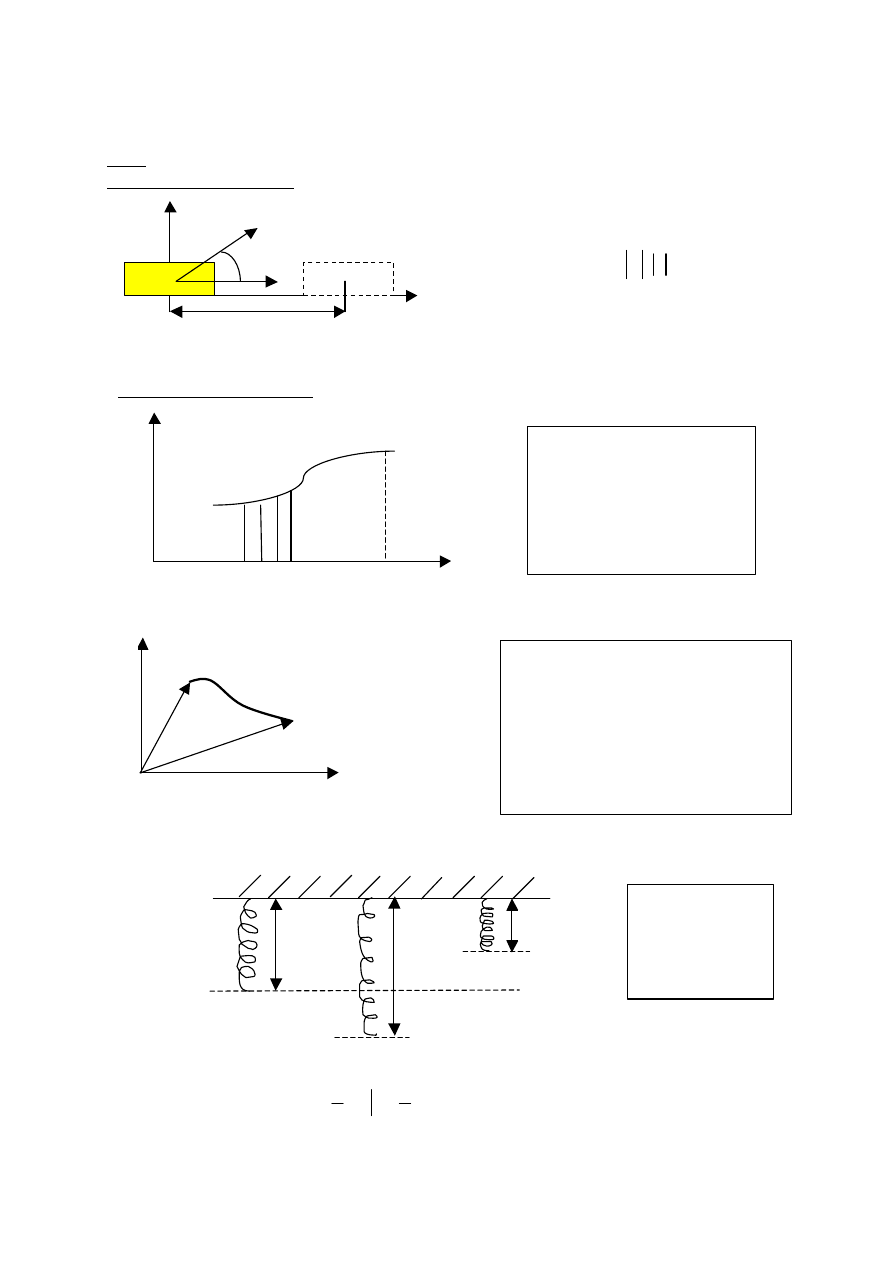
Ogólnie – prace sily na pewnym odcinku drogi definiujemy

W szczególnym przypadku
W = F · r

F = const, r - droga – linia prosta majaca kierunek sily

Przyklad - sprezyna przymocowana do sciany.

F’(x) – sila przeciwnie skierowana do sily sprezystosci F(x) dla x

1

= 0 i x

2

= x,

W

12

=½kx

2

r

2

r

1

F

x

y

x

0

x

x

a Fcosa

d

F

x

2

F(x)

? x

x

1

x

∆

W = F

∆

x

∑

∆

=

2

1

12

x

x

x

F

W

r

r

∫

∑

=

∆

=

→

∆

2

1

2

1

0

12

lim

x

x

x

x

x

Fdx

x

F

W

∫

⋅

=

2

1

r

r

r

d

F

W

r

r

r

1

– wektor wodzacy w

poczatkowym punkcie drogi
r

2

– wektor wodzacy w koncowym

punkcie drogi, po której porusza sie
punkt.

F = -k(x-x

0

)

Prawo
Hooke’a,
F = -kx

α

α

cos

cos

Fs

W

s

F

s

F

W

=

⋅

⋅

=

•

=

r

r

v

r

W = F·s dla F

||

s;

α = 0

0

W = F·s = 0 dla F

⊥

s;

α = 90

0

∫

∫

=

=

=

=

x

x

x

kx

kx

kxdx

dx

x

F

W

0

0

2

0

2

2

1

2

1

)

(

'

2

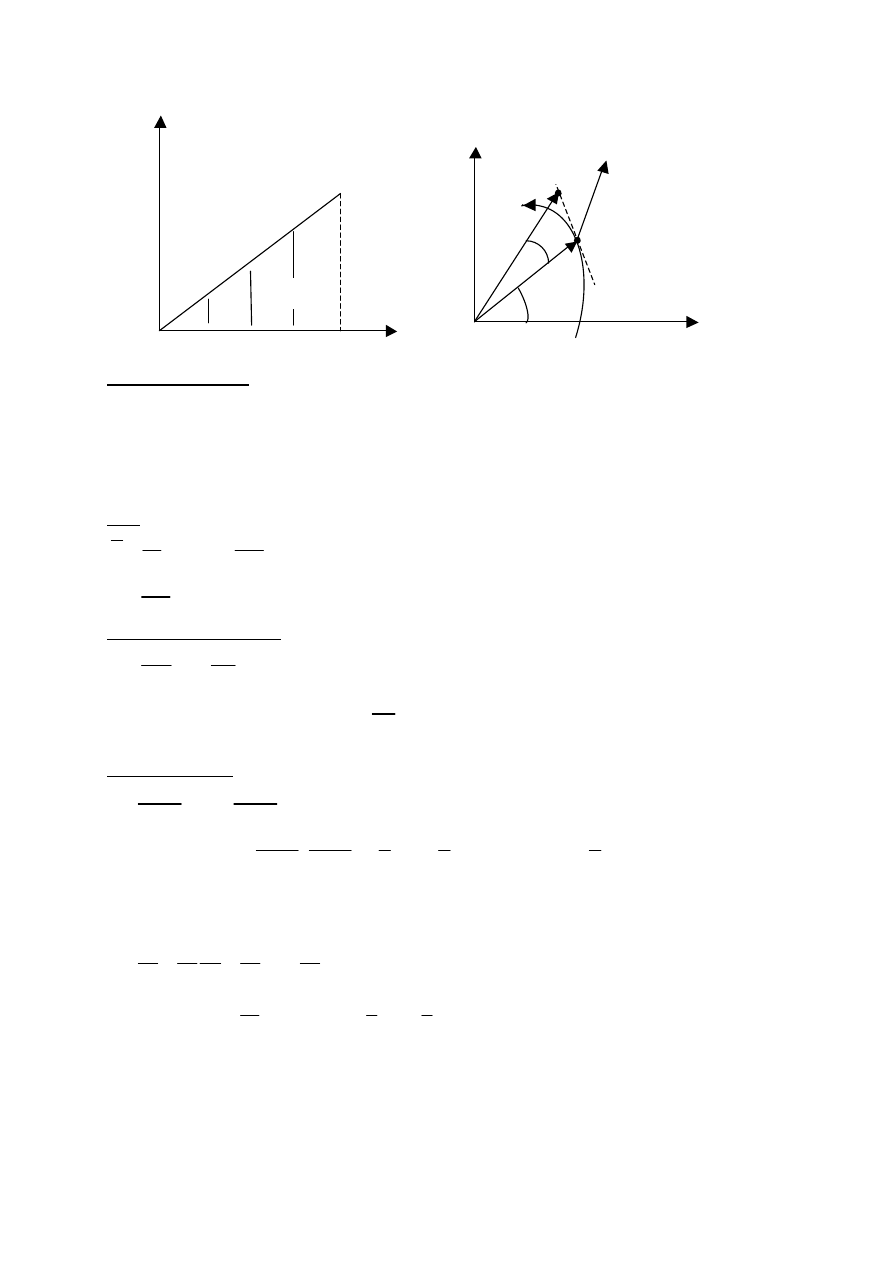
W ruchu obrotowym
ds = rd

θ

, Fcos

ϕ

– skladowa sily F w kierunku ds

ϕ

θ

θ

ϕ

ϕ

cos

cos

cos

Fr

M

bo

d

M

dW

d

Fr

ds

F

s

d

F

dW

=

=

=

=

=

r

r

M – wartosc chwilowego momentu sily dzialajacego na cialo sztywne wzgledem osi 0.

Moc

t

W

P

=

dt

dW

P

=

jednostka [J/s] = [W]

dt

dW

P

=

jesli W ~ t

wtedy P =W/t

Moc w ruchu obrotowym

dt

d

a

Md

dW

bo

M

P

M

dt

d

M

dt

dW

P

θ

ω

θ

ω

ω

θ

=

=

=

=

=

=

,

Energia kinetyczna

t

v

v

x

t

v

v

a

2

,

0

0

+

=

−

=

2

0

2

0

0

2

1

2

1

2

max

mv

mv

t

v

v

t

v

v

m

x

F

W

−

=

+

⋅

−

=

=

=

i

2

2

1

mv

E

k

=

dx

dv

v

v

dx

dv

dt

dx

dx

dv

dt

dv

a

=

=

=

=

k

k

k

E

E

E

W

∆

=

−

=

0

Twierdzenie o pracy i energii

0

,

=

∆

=

=

k

E

W

const

v

v, v

0

– predkosc punktu materialnego na koncu i poczatku drogi

F

x

kx

F’= kx

½ kx

2

x

f

d?

r(t+dt)

?

P

F

ds

P(t+dt)

r(t)

O

y

x

v

0

– predkosc czastki w chwili t=0

v – predkosc w chwili t

∫

∫

=

=

x

x

Fdx

s

d

F

W

0

r

r

2

0

2

2

1

2

1

0

0

0

mv

mv

dv

mv

dx

dx

dv

mv

Fdx

W

v

v

x

x

x

x

−

=

=

=

=

∫

∫

∫

3

W ruchu obrotowym
E

k

= ½I

ω

2

gdy M – moment sily = const,

ϕ

- obrót o pewinien kat

W = M

ϕ = ∆E

k

= Fs

E

k

= ½mv

2

+ ½I

ω

2

ωα

ω

ω

ω

ω

I

dt

d

I

dt

d

I

I

dt

d

dt

dW

=

=

=

=

2

2

2

1

)

2

1

(

α

ωα

ω

I

M

I

M

=

=

II zasada dynamiki dla ruchu obrotowego ciala sztywnego

Energia potencjalna

k

x
x

E

mv

mv

Fdx

W

∆

=

−

=

=

∫

2

0

2

2

1

2

1

0

∆

E

k

= -

∆

E

p

dx

x

F

x

E

x

E

zatem

dx

x

F

E

czyli

Fdx

E

x
x

p

p

x
x

p

x
x

k

)

(

)

(

)

(

)

(

0

0

0

0

∫

∫

∫

=

−

−

=

∆

=

∆

const

mv

x

E

mv

x

E

E

mv

mv

Fdx

x

E

x

E

p

p

k

x
x

p

p

=

+

=

+

∆

−

=

−

=

=

−

∫

2

0

0

2

2

2

0

0

2

1

)

(

2

1

)

(

lub

2

1

2

1

)

(

)

(

0

Prawo zachowania energii kinetycznej i potencjalnej.

2

2

1

)

(

mv

x

E

E

E

E

p

k

p

+

=

+

=

∫

∆

=

−

−

=

p

p

E

dx

x

f

bo

x

E

dx

d

x

F

)

(

)

(

)

(

Zasada zachowania energii mechanicznej

const

mv

mgh

=

+

2

2

1

h – wysokosc punktu materialnego od powierzchni Ziemi

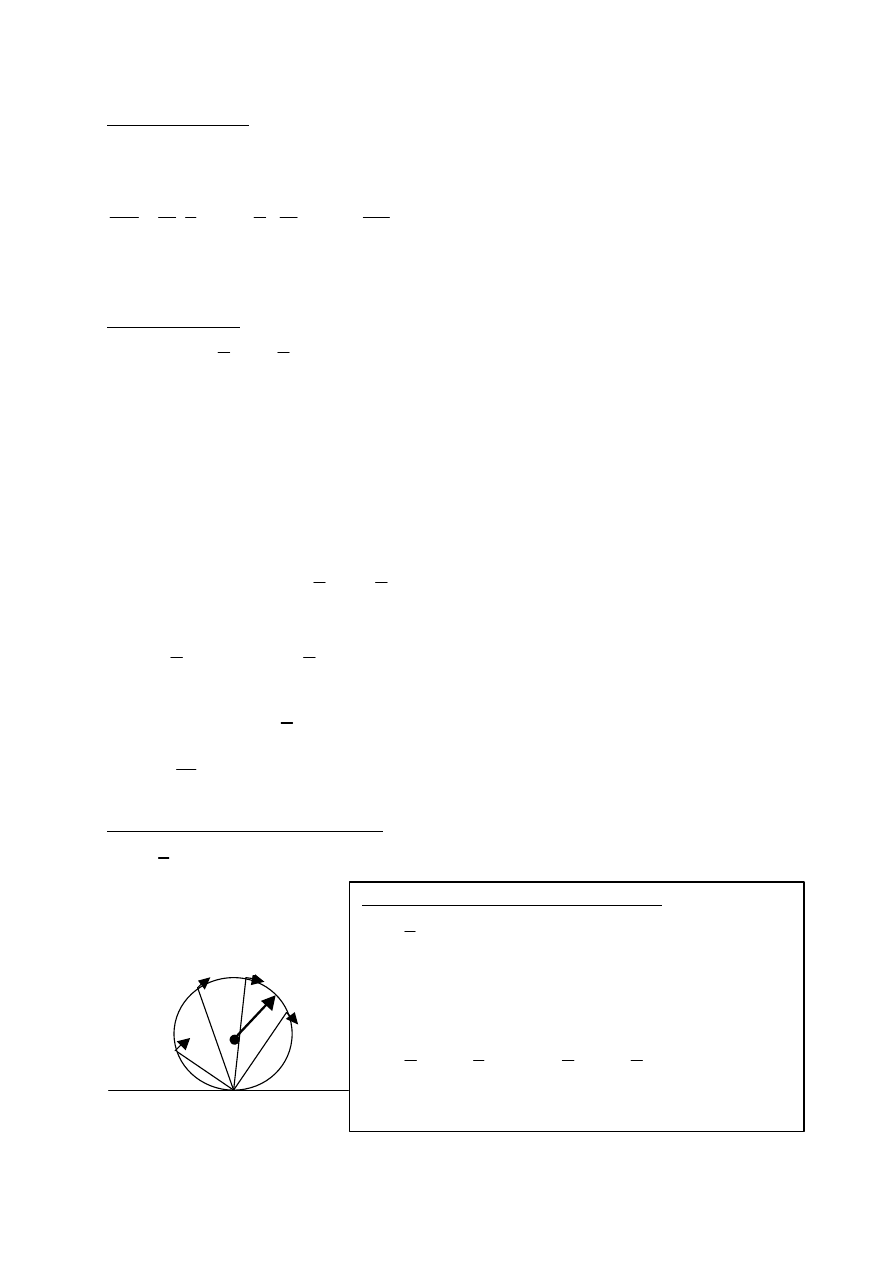
P

R

v

0

Ruch postepowo-obrotowy ciala sztywnego

2

2

1

ω

p

k

I

E

=

i

I

p

= I

0

+ MR

2

I

p

– moment bezwladnosci wzgl. osi przechodzacej przez

pkt. P,
I

0

– moment bezwladnosci wzgl. osi równoleglej do osi

przechodzacej przez srodek ciezkosci, czyli

0

2

0

2

0

2

2

2

0

,

2

1

2

1

2

1

2

1

v

R

bo

Mv

I

MR

I

E

k

=

+

=

+

=

ω

ω

ω

ω

v

0

= R? – jest predkoscia liniowa srodka masy cylindra

wzgledem nieruchomego pkt. P