
Laboratorium Cyfrowego Przetwarzania Sygnałów
Ćwiczenie 2 – Dyskretne sygnały stochastyczne - analiza widmowa i korelacyjna
- 1 -
Wydział Elektryczny
Zakład Automatyki
LABORATORIUM CYFROWEGO PRZETWARZANIA SYGNAŁÓW
Ćwiczenie 2
Dyskretne sygnały stochastyczne - analiza widmowa i korelacyjna
1. Cel ćwiczenia
• Opanowanie podstawowych pojęć: funkcji korelacji i widma mocy stacjonarnego procesu
stochastycznego.
• Przećwiczenie sposobów estymacji charakterystyk sygnałów stochastycznych i interpretacji
wyników obliczeń komputerowych.
• Zapoznanie się z metodami analizy liniowych układów dyskretnych przetwarzających sygnały
stochastyczne.
2. Podstawy teoretyczne
2.1. Pojęcia podstawowe
Pod pojęciem dyskretnego procesu (sygnału) stochastycznego x(n) będziemy rozumieć zbiór
funkcji x
1
(n), x
2
(n), ... będących realizacjami tego procesu (Rys. 1). Dla ustalonej chwili czasu
(indeksu) n
1
wielkość x(n
1
) jest zmienną losową (wartością procesu losowego w chwili n
1
), którą
charakteryzuje funkcja gęstości prawdopodobieństwa p
x
(x
1
, n
1
) (PDF – probability density function).
Obserwacjom podlegają jedynie realizacje zmiennych losowych, ale dalej nie będziemy stosować dla
nich odrębnych oznaczeń i przez x(n
k
) będziemy rozumieć - w zależności od kontekstu - zmienną
losową lub wartość jej realizacji.
Do pełnego opisu procesu losowego potrzebna jest znajomość wszystkich k-wymiarowych PDF
zmiennych losowych x(n
1
), x(n
2
),..., x(n
k
) w dowolnie wybranych chwilach czasowych {n
1
, n
2
,..., n
k
}.
W wielu zagadnieniach praktycznych wystarczy wiedzieć, w jaki sposób właściwości procesu
losowego x(n) w punkcie n=n
1
zależą od jego właściwości w punkcie n=n
2
. Do określenia tej
zależności wystarcza znajomość dwuwymiarowej PDF
1
2
( , )
xx
p n n
zmiennych losowych x(n
1
) i x(n
2
)
w chwilach n
1
i n
2
. Można wtedy wyznaczyć podstawowe wielkości, tzw. statystyki, opisujące sygnał
stochastyczny.
Najważniejsze wielkości charakteryzujące dyskretny proces losowy o wartościach rzeczywistych
są następujące (wzory są podane dla procesów o wartościach ciągłych x oraz dyskretnych
(skwantowanych) xi, i=1,2,…,M; px(x,n) – gęstość prawdopodobieństwa w chwili n)
Wartość średnia (oczekiwana) procesu x(n):
∫
∞
∞
−
=
=
dx
n
x
xp
n
x
E
n
m
x
x
)
,
(
)]
(
[
)
(
albo
( )
[ ( )]
( , )
x
i
x
i
i
m n
E x n
x p x n
=
=
∑
(2.1)
Średnia kwadratowa (moc średnia) sygnału (gwiazdka oznacza wielkość sprzężoną):
2
2
( )
[ ( )]
( , )
x
x
P n
E x n
x p x n dx
∞
−∞
=
=
∫
albo
2
2
( )
[ ( )]
( , )
x
i
x
i
i
P n
E x n
x p x n
=
=
∑
(2.2)
Laboratorium Cyfrowego Przetwarzania Sygnałów
Ćwiczenie 2 – Dyskretne sygnały stochastyczne - analiza widmowa i korelacyjna
- 2 -
x
1
(n)
x
2
(n)
x(n
1
)
x(n
2
)
n
x
3
(n)
Realizacje procesu X(n)
Realizacje zmiennych losowych
Rys. 1. Ilustracja pojęcia: dyskretny proces stochastyczny
Wariancja (moc składowej zmiennej):
2
2
2
2
( ) var[ ( )]
{[ ( )
( )] }
[ ( )]
( )
x
x
x
n
x n
E x n
m n
E x n
m n
σ
=
=
−
=
−
(2.3)
Funkcja autokorelacji zmiennych losowych x(n
1
) i x(n
2
) sygnału:
1
2
1
2
1
2
1
2
1
2
( , )
[ ( ) ( )]
( ) ( )
( , , ) ( ) ( )
xx
xx
R n n
E x n x n
x n x n p x n n dx n dx n
∞ ∞
−∞ −∞
=
=
∫ ∫
albo
1
2
1
2
1
2
( , )
[ ( ) ( )]
[ ( ), ( )]
xx
i
j
xx
i
j
i
j
R n n
E x n x n
x x p x n x n
=
=
∑∑
(2.4)
(jest to prawdopodobieństwo łączne: Prob[x(n
1
)=x
i
∧ x(n
2
)=x
j
].
Funkcja autokowariancji zmiennych losowych x(n
1
) i x(n
2
) sygnału:
1
2
1
1
2
2
( , )
{[ ( )
( )][ ( )
( )]}
xx
x
x
C n n
E x n
m n
x n
m n
=
−
−
(2.5)
(dla sygnałów o zerowych wartościach średnich korelacja i kowariancja są sobie równe; w
szczególności kowariancja
2
( , )
xx
x
C n n
= σ
).
W analogiczny sposób definiuje się funkcje korelacji i kowariancji wzajemnej dwóch sygnałów
losowych x(n) i y(n), np. kowariancja wzajemna:
1
2
1
1
2
2
( , )
{[ ( )
( )][ ( )
( )]}
xy
x
y
C n n
E x n
m n
y n
m n
=
−
−
(2.6)
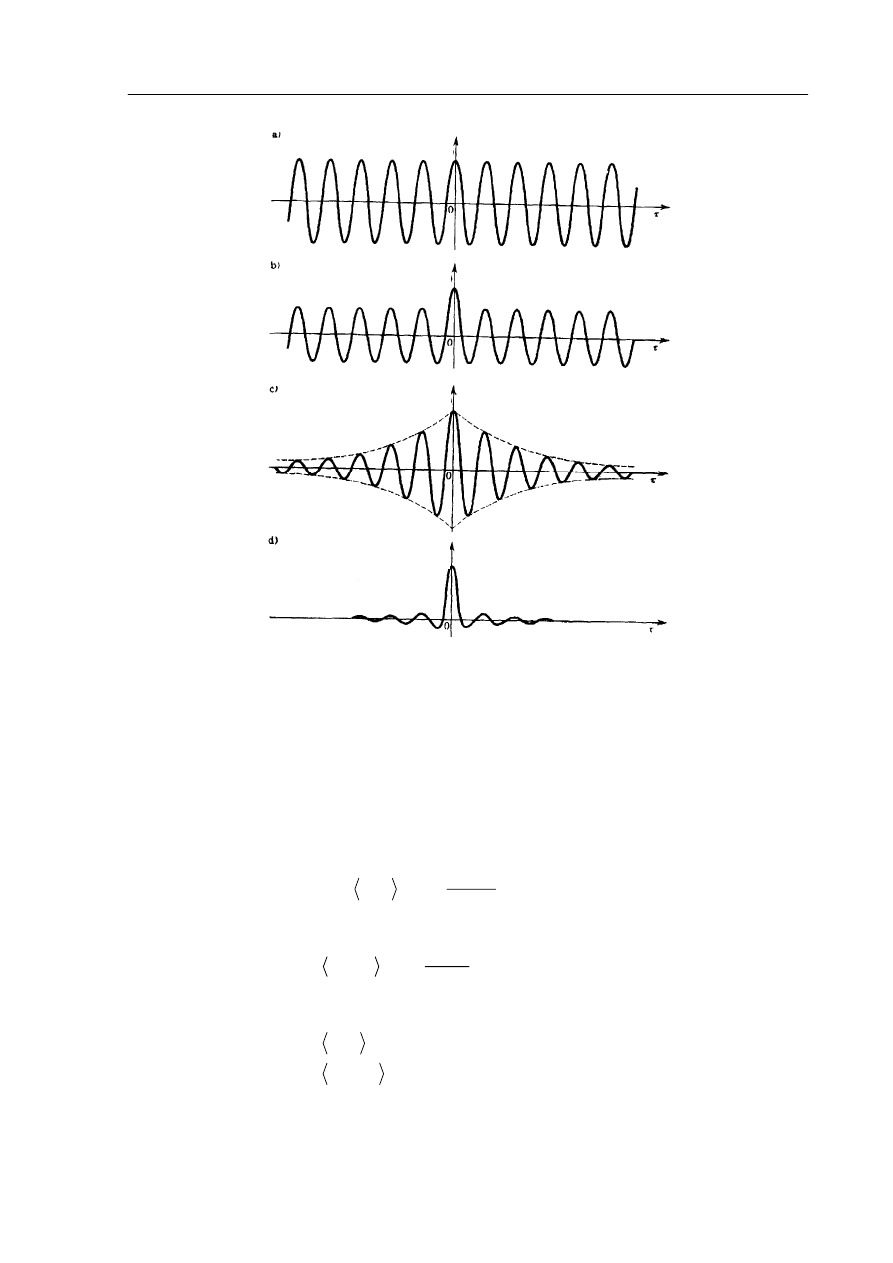
Autokorelacja jest funkcją deterministyczną i najważniejszą wielkością charakteryzującą
sygnał stochastyczny w dziedzinie czasu. Na Rys. 2 pokazane są przykładowe wykresy autokorelacji
sygnałów różnego typu.
2.2. Sygnały stacjonarne i ergodyczne
Jeżeli statystyki procesu losowego nie zmieniają się w czasie, tzn. p
x
(x, n
1
)=p
x
(x, n
2
), to nazywamy
ten proces stacjonarnym. Ograniczymy się dalej do analizy procesów stacjonarnych w szerszym
sensie, których rozkłady prawdopodobieństwa mogą się zmieniać w czasie, ale spełnione są
następujące warunki:
średnia
x
x
m
n
m
=
)
(
oraz wariancja
2
2
)
(
x
x
n
σ
=
σ
są stałe,
autokorelacja
)
(
)
(
)
,
(
1
2
2
1
m
R
n
n
R
n
n
R
xx
xx
xx
=
−
=
nie zależy od wyboru chwil n
1
i n
2
, a tylko
od odległości m= n
2
-n
1
między zmiennymi losowymi x(n
1
) i x(n
2
), których wzajemne zależności
(korelacje) są analizowane.
Laboratorium Cyfrowego Przetwarzania Sygnałów
Ćwiczenie 2 – Dyskretne sygnały stochastyczne - analiza widmowa i korelacyjna
- 3 -
Rys. 2 Przebiegi funkcji autokorelacji sygnałów: a) sinusoidalnego, b) sinusoidalnego z szumem
losowym, c) szumu wąskopasmowego, d) szumu szerokopasmowego
Wyznaczanie tzw. zespołowych statystyk (2.1)-(2.5) wymaga uśredniania po realizacjach procesu.
Często jednak nie dysponujemy zbiorem realizacji procesu {x
k
(n)}, k=1,2,..., ale pojedynczą realizacją
(dla jednej wartości wskaźnika k), na podstawie której mamy wnioskować o właściwościach całego
procesu x(n). Zamiast uśredniania po realizacjach trzeba wtedy stosować uśrednianie po czasie dla
obserwowanej realizacji x(n) sygnału. Wymaga to skorzystania z tzw. hipotezy ergodycznej, czyli
przyjęcia założenia, że dla badanego procesu średnie po realizacjach są równe średnim czasowym.
Zdefiniujemy średnie czasowe
〈⋅〉 stacjonarnego sygnału losowego x(n).
wartość średnia:
∑
−
=
∞
→
+
=
N
N
n
N
n
x
N
n
x
)
(
1
2
1
lim
)
(
(2.7)
czasowa funkcja autokorelacji:
1
( )
lim
( ) (
)
2
1
N
xx
N
n
N
R m
x n x n m
N
→∞
=−
=
+
+
∑
(2.8)
Sygnał X(n) nazywamy ergodycznym, jeżeli średnie czasowe są równe odpowiednim średnim
statystycznym, tzn.:
1
2
),
(
)
(
const
)
(
n
n
m
m
R
m
R
m
n
x
xx
xx
x
−
=
=
=
=
(2.9)
W przeprowadzanych eksperymentach numerycznych będziemy operować na realizacjach
sygnałów losowych i obliczać średnie czasowe skończonych ciągów próbek jako estymaty
zespołowych statystyk sygnału.
R
xx
(
τ)
R
xx
(
τ)
R
xx
(
τ)
R
xx
(
τ)

Laboratorium Cyfrowego Przetwarzania Sygnałów
Ćwiczenie 2 – Dyskretne sygnały stochastyczne - analiza widmowa i korelacyjna
- 4 -
2.3. Widmo mocy sygnału losowego
Jeżeli odległe w czasie zmienne losowe stacjonarnego sygnału dyskretnego x(n) stają się od siebie
niezależne, to zanika kowariancja sygnału:
0
)
(
lim
=
∞
→
m
C
xx
m
i można wyznaczyć jej transformatę Z.
Obszar zbieżności transformaty zawiera okrąg jednostkowy |z|=1, a zatem istnieje odpowiednia
transformata Fouriera dla z=e
j
Ω
. Widmowa gęstość mocy (widmo mocy) P
xx
(
Ω) jest transformatą
Fouriera kowariancji sygnału x(n):
∑
∞
−∞
=
Ω
−
=
Ω
m
jm
xx
xx
e
m
C
P
)
(
)
(
(2.10)
gdzie
Ω=ω/f
s
jest pulsacją kątową unormowaną względem częstotliwości próbkowania f
s
=1/T
s
.
Widmo mocy jest najważniejszą wielkością opisującą właściwości sygnału losowego w dziedzinie
częstotliwości
. W przypadku sygnałów o zerowej wartości średniej (m
x
=0) autokowariancję w (2.10)
można zastąpić równoważną autokorelacją R
xx
(m). Funkcja P
xx
(
Ω) określa wtedy moc sygnału
przypadającą na jednostkę unormowanej pulsacji
Ω.
Właściwości widma mocy:
• P
xx
(
Ω) jest funkcją okresową o okresie 2π,
• jeżeli x(n) jest sygnałem o wartościach rzeczywistych, to jego widmo mocy jest funkcją
nieujemną i parzystą, tzn. P
xx
(
Ω)=P
xx
(-
Ω),
• całka oznaczona widma mocy sygnału o zerowej średniej (m
x
=0)
∫
Ω
Ω
Ω
Ω
2
1
)
(
d
P
xx
określa moc średnią moc sygnału w zakresie pulsacji
2
1
Ω
≤
Ω
≤
Ω
. Całka obliczona w całym
zakresie częstotliwości określa całkowitą moc (energię) sygnału.
Znając widmo mocy można określić wartości autokowariancji jako współczynniki rozwinięcia
widma w szereg Fouriera:
∫
π
π
−
Ω
Ω
Ω
π
=
d
e
P
m
C
jm
xx
xx
)
(
2
1
)
(
(2.11)
W szczególności dla m=0 zależność (2.11) określa wariancję sygnału
)
0
(
2
xx
x
C
=
σ
.
W analogiczny sposób definiuje się widmo mocy wzajemnej dwóch sygnałów:
∑
∞
−∞
=
Ω
−
=
Ω
m
jm
xy
xy
e
m
C
P
)
(
)
(
(2.12)
2.4. Klasyczne metody estymacji autokowariancji i widma mocy
W wielu zastosowaniach praktycznych właściwości procesu losowego X(n) trzeba oceniać na
podstawie znajomości tylko jednej jego realizacji x(n) obserwowanej w skończonym przedziale czasu.
Powstaje więc problem estymacji (oszacowania) wartości średniej, wariancji, funkcji kowariancji
(korelacji) i widma mocy na podstawie skończonego ciągu N próbek x
0
(n), n=0,1,...,N-1. Zakłada się
przy tym, że analizowany sygnał jest stacjonarny (w szerszym sensie) i ergodyczny.
Najczęściej stosowane estymatory (oznaczane symbolami z daszkiem) z próbek są określone w
sposób następujący:
estymator wartości średniej (największej wiarygodności):
1
0
1
ˆ
( )
N
x
n
m
x n
N
−
=
=
∑
(2.13)
estymator (największej wiarygodności) wariancji sygnału o nieznanej wartości średniej:
1
2
2
0
1
ˆ
ˆ
[var( )]
[ ( )
]
N
x
x
n
E
x
x n
m
N
−
=
σ =
=
−
∑
(2.14)

Laboratorium Cyfrowego Przetwarzania Sygnałów
Ćwiczenie 2 – Dyskretne sygnały stochastyczne - analiza widmowa i korelacyjna
- 5 -
estymator funkcji autokorelacji (również autokowariancji w przypadku sygnału o zerowej wartoś-
ci średniej, m
x
=0):
| | 1
0
1
ˆ ( )
( ) (
),
(
1)
1
N m
xx
n
R m
x n x n m
N
m N
N
− −
=
=
⋅
+
−
− ≤ ≤ −
∑
(2.15)
estymator widma mocy PSD (wyliczany na podstawie estymatora korelacji w przypadku m
x
=0):
∑
−
−
−
=
Ω
−
=
Ω
1
)
1
(
)
(
ˆ
1
)
(
ˆ
N
N
m
jm
xx
xx
e
m
R
N
P
(2.16)
Zauważmy, że dla różnych realizacji procesu losowego (różnych pomiarów) otrzymamy różne
wartości lub przebiegi funkcji estymatorów, ponieważ one same są zmiennymi losowymi (
2
ˆ
i
ˆ
x
x
m
σ
)
lub procesami losowymi (
)
(
ˆ
i
)
(
ˆ
Ω
Ω
xx
xx
P
R
).
2.5. Jakość estymacji
Przypuśćmy, że pewien (nieznany) parametr
α procesu stochastycznego oceniamy wyznaczając
jego estymator
αˆ
. Jakość estymatora ocenia się na podstawie oszacowania jego dwóch parametrów:
obciążenia estymatora (ang. bias):
ˆ
ˆ
( )
[ ]
B
E
α = α − α
(2.17)
wariancji estymatora:
2
2
ˆ
ˆ
ˆ
ˆ
var
[(
[ ]) ]
E
E
α
α =
α − α
= σ
(2.18)
Obciążenie jest odchyleniem wartości oczekiwanej estymatora od rzeczywistej wartości parametru, a
wariancja - miarą skupienia wartości estymatora wokół przeciętnej
]
ˆ
[
α
E
. Dobry estymator powinien
mieć jak najmniejsze obciążenie i wariancję (najlepiej równe zero). Często estymator o małym
obciążeniu ma dużą wariancję lub na odwrót. Z tego powodu jakość estymatora ocenia się podając
błąd średniokwadratowy
2
2
2
ˆ
ˆ
[(
) ]
E
B
α
α − α
=
+ σ
(2.19)
uwzględniający oba wymienione wskaźniki jakości. Wymaga się, aby estymator był zgodny, tzn.
zbieżny do wartości rzeczywistej estymowanego parametru przy liczbie próbek
∞
→
N
(obciążenie i
wariancja dążące do 0):
1
)
ˆ
(
lim
=
α
=
α
∞
→
N
N
Prob
(2.20)
Zastosujemy opisane wskaźniki jakości estymacji do oceny estymatorów z próbek przedstawionych
w pkt.2.4 dla stacjonarnego gaussowskiego procesu stochastycznego:
estymator wartości średniej (2.13) jest nieobciążony, a jego wariancja
N
m
x
x
/
]
ˆ
var[
2
σ
=
(gdzie
2
x
σ
jest rzeczywistą wariancją procesu), a więc estymator jest zgodny,
estymator wariancji (2.14) jest obciążony:
2
2
ˆ
[ ] (
1)
/
x
x
B
N
N
σ =
− σ
, a jego wariancja
]
ˆ
var[
2
x
σ
jest
proporcjonalna do 1/N, jest to zatem estymator zgodny,
estymator (2.15) funkcji autokorelacji jest obciążony:
)
(
|
|
)]
(
ˆ
[
m
R
N
m
m
R
B
xx
xx
=
(2.21)
(widać, że błąd estymacji jest duży na krańcach rekordu danych, tzn. dla |m|
→N), a jego
wariancja
)]
(
ˆ
var[
m
R
xx
jest proporcjonalna do
N
m
R
xx
/
)
(
2
. W związku z tym niekiedy stosuje się
nieobciążony estymator autokorelacji (kompensujący błędy na krańcach rekordu danych)
| | 1
'
0
1
ˆ ( )
( ) (
),
| |
N m
xx
n
R m
x n x n m
N
m
− −
=
=
⋅
+
−
∑
(2.22)
ale błąd średniokwadratowy takiego estymatora jest większy niż dla estymatora (2.15).
estymator widma mocy (2.16) nie jest estymatorem zgodnym, jest obciążony, a jego wariancja
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
Ω
Ω
+
Ω
=
Ω
sin
sin
1
)
(
)]
(
ˆ
var[
2
N
N
P
P
xx
xx
(2.23)
Laboratorium Cyfrowego Przetwarzania Sygnałów
Ćwiczenie 2 – Dyskretne sygnały stochastyczne - analiza widmowa i korelacyjna
- 6 -
jest proporcjonalna do kwadratu estymowanego widma. Właściwości te sprawiają, że fluktuacje
wokół prawdziwych wartości widma mocy są duże i nie maleją w miarę zwiększania liczby
próbek N. Są to wady, które dyskwalifikują estymator (2.16) jako użyteczne narzędzie
obliczeniowe.
2.6. Periodogram jako estymata widma mocy
Ponieważ, jak widzieliśmy, transformata Fouriera (2.16) zgodnej estymaty kowariancji nie jest
zgodnym estymatorem PSD (tzn. nie dąży do wartości prawdziwych przy wzroście liczby próbek N),
w praktyce stosuje się metody, które pomijają etap estymacji funkcji
)
(
ˆ
m
R
xx
i umożliwiają estymację
widma bezpośrednio z ciągu próbek x(n) poddawanych dyskretnemu przekształceniu Fouriera DFT.
Obliczanym w ten sposób estymatorem widma mocy jest periodogram zdefiniowany jako:
2
)
(
1
)
(
ˆ
)
(
m
j
m
xx
m
N
e
X
N
P
I
Ω
=
Ω
=
Ω
(2.24)
gdzie
)]
(
[
)
(
n
x
DFT
e
X
m
j
=
Ω
. Estymacja widma mocy metodami cyfrowymi sprowadza się więc do
wyznaczenia (najczęściej za pomocą algorytmu FFT) periodogramu ciągu próbek x(n), n=0,1,...,N-1,
dla skończonego zbioru pulsacji
1
,...,
1
,
0
,
2
−
=
π
=
Ω
N
m
N
m
m
. Stosując przekształcenie odwrotne
)]
(
[
m
N
I
IDFT
Ω
można wyznaczyć estymatę funkcji autokorelacji
)
(
ˆ
m
R
xx
.
Periodogram jest estymatorem PSD niezgodnym i o dużej wariancji:
)
(
)]
(
var[
2
Ω
≅
Ω
xx
N
P
I
, co
daje „poszarpane” obrazy widma mocy niezależnie od liczby próbek.
2.7. Uśrednianie periodogramów – estymacja z wygładzaniem widma
W celu uzyskania zgodnego estymatora PSD, czyli zmniejszenia wariancji estymacji przy wzroście
liczby próbek N, stosuje się uśrednianie pewnej liczby niezależnych periodogramów (metoda
Bartletta).
Procedura obliczeniowa jest następująca:
1) Ciąg danych {x(n): n=0,1,...,N-1} dzieli się na K segmentów
)
(
)
(
n
x
i
, i=1,2,..,K o długości M
każdy (N=KM).
2) Oblicza się K krótszych periodogramów
2
)
(
)
(
|
)]
(
[
|
1
)
(
n
x
DFT
M
I
i
m
i
M
=
Ω
.
3) Wyznacza się estymatę Bartletta PSD w postaci:
∑
=
Ω
=
Ω
K
i
m
i
M
m
B
xx
I
K
P
1
)
(
)
(
1
)
(
ˆ
(2.25)
W przypadku, kiedy periodogramy są od siebie niezależne, wariancja estymaty Bartletta
)
(
1
)]
(
var[
1
)]
(
ˆ
var[
2
Ω
≈
Ω
=
Ω
xx
M
B
xx
P
K
I
K
P
(2.26)
a obciążenie jest większe niż dla pojedynczego dłuższego periodogramu. Estymata (2.25) jest więc
zgodna, co oznacza wygładzenie widma przy wzroście N, ale ze względu na krótsze segmenty danych
pogarsza się rozdzielczość częstotliwościowa estymaty.
Ulepszoną metodą uśredniania zmodyfikowanych periodogramów jest metoda Welcha.
Modyfikacja polega na nałożeniu na segmenty danych przed obliczaniem periodogramów okna
czasowego różnego od prostokątnego. Zmodyfikowane periodogramy mają postać:
2
)
(
)
(
|
)]
(
)
(
[
|
1
)
(
n
w
n
x
DFT
MF
I
i
m
W
i
M
⋅
=
Ω
(2.27)
gdzie w(n) jest funkcją okna czasowego, a F jest czynnikiem normującym energię (jest to energia
sygnału okna)

Laboratorium Cyfrowego Przetwarzania Sygnałów
Ćwiczenie 2 – Dyskretne sygnały stochastyczne - analiza widmowa i korelacyjna
- 7 -
∑
−
=
=
1
0
2
)
(
1
M
k
k
w
M
F
(2.28)
niezbędnym do zapewnienia asymptotycznej nieobciążoności (przy
∞
→
K
).
W celu zwiększenia liczby segmentów K (zmniejszenia wariancji estymatora) bez zmniejszania
ich długości M (tzn. rozdzielczości widmowej) stosuje się podział na segmenty nakładające się na
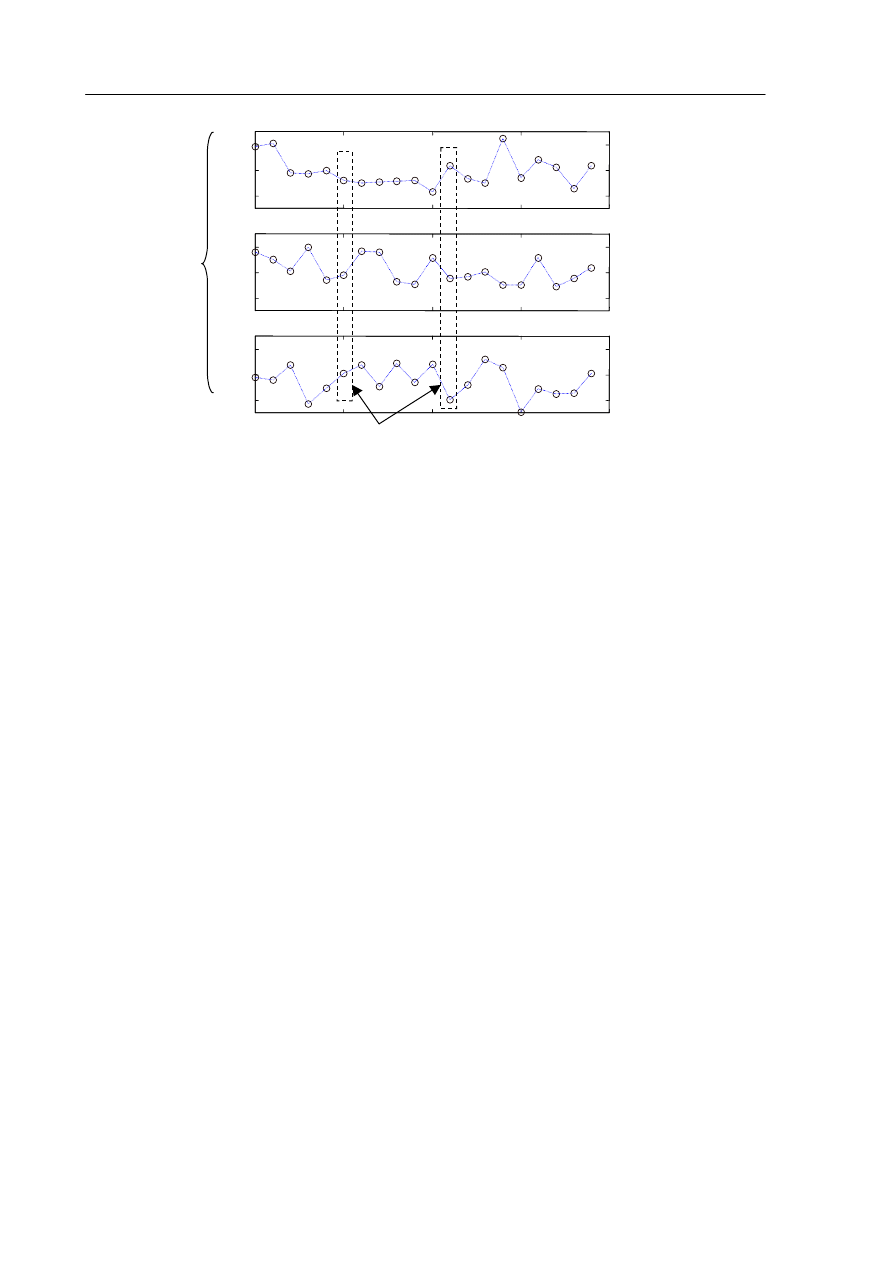
siebie (overlapping, Rys. 3). Periodogramy stają się wtedy jednak zależne od siebie, co zwiększa
wariancję. Zależność periodogramów segmentów zachodzących na siebie jest mniejsza po nałożeniu
na segmenty (przed obliczeniem periodogramów) okien dążących do zera na krańcach (np. okna
Hanninga). Powoduje to, że metoda Welcha z nakładaniem się segmentów zapewnia estymację o
mniejszej wariancji w porównaniu z metodą Bartletta.
Rys. 3. Podział ciągu danych na segmenty do wyznaczania krótszych periodogramów:
a) segmenty nie nakładające się, b) segmenty nakładające się
2.8. Przetwarzanie sygnałów stochastycznych przez liniowy układ dyskretny
Dyskretny układ (filtr) liniowy z wejściem x(n) i wyjściem y(n) może być w pełni
scharakteryzowany przez podanie jego transmitancji dyskretnej:
N
N
N
N
z
a
z
a
z
b
z
b
b
z
X
z
Y
z
H
−
−
−
−
+
+
+
+
+
+
=
=
…
…
1
1
1
1
0
1
)
(
)
(
)
(
(2.29)
przy zerowych warunkach początkowych. Transmitancja filtra stanowi transformatę Z jego
charakterystyki impulsowej h(n) (odpowiedzi na sygnał x(n)=1 dla n=0 i x(n)=0 dla n
≠0):
)]
(
[
Z
)
(
n
h
z
H
=
(2.30)
Sygnał na wyjściu układu jest splotem sygnału na jego wejściu i charakterystyki impulsowej:
∑
∞
−∞
=
−
=
∗
=
k
k
n
x
k
h
n
x
n
h
n
y
)
(
)
(
)
(
)
(
)
(
(2.31)
Charakterystyka widmowa
)
(
Ω
j
e
H
filtra jest transmitancją H(z) obliczaną dla
Ω
=
j
e
z
(na okręgu
jednostkowym). Charakterystyka amplitudowa filtra stanowi moduł A(
Ω)=|
)
(
Ω
j
e
H
|, a
charakterystyka fazowa argument
ϕ
(
Ω)=arg[
)
(
Ω
j
e
H
] charakterystyki widmowej.
Jeżeli sygnał wejściowy x(n) jest sygnałem stochastycznym o znanej średniej, wariancji i funkcji
autokorelacji, to (w stanie ustalonym po odpowiednio długim czasie od pojawienia się wymuszenia)
sygnał wyjściowy y(n) jest również sygnałem stochastycznym o parametrach zależnych od
parametrów sygnału wejściowego i od charakterystyki widmowej (lub impulsowej) filtra.
Laboratorium Cyfrowego Przetwarzania Sygnałów
Ćwiczenie 2 – Dyskretne sygnały stochastyczne - analiza widmowa i korelacyjna
- 8 -
Pomiędzy statystykami sygnału wejściowego i wyjściowego zachodzą w stanie ustalonym
następujące zależności:
• wartość średnia sygnału losowego na wyjściu:
x
j
y
m
e
H
m
)
(
0
=
(2.32)
• funkcja autokorelacji procesu wyjściowego:
)
(
)
(
)
(
m
v
m
R
m
R
xx
yy
∗
=
,
gdzie
)
(
)
(
)
(
)
(
)
(
m
h
m
h
k
n
h
k
h
m
v
k
−
∗
=
+
=
∑
∞
−∞
=
(2.33)
• jeżeli sygnał wejściowy ma zerową wartość średnią (m
x
=0), a transformatę Z funkcji autokorelacji
dowolnego sygnału y(n) oznaczymy jako S
yy
(z)=Z[R
yy
(m)], to:
)
(
)
/
1
(
)
(
)
(
z
S
z
H
z
H
z
S
xx
yy
⋅
⋅
=
,
(2.34)
a widmo mocy
Ω
=
=
Ω
j
e
z
yy
yy
z
S
P
|
)
(
)
(
sygnału wyjściowego:
)
(
)
(
)
(
2
Ω
=
Ω
Ω
xx
j
yy
P
e
H
P
(2.35)
• funkcja korelacji wzajemnej sygnałów wejściowego i wyjściowego:
)
(
)
(
)
(
m
R
m
h
m
R
xx
xy
∗
=
(2.36)
skąd wynika, że funkcja widma mocy wzajemnej (w ogólności funkcja zespolona)
)
(
)
(
)
(
Ω
=
Ω
Ω
xx
j
xy
P
e
H
P
(2.37)
Szczególną rolę jako sygnał pobudzający wejście filtra odgrywa tzw. szum biały, wyidealizowany
sygnał losowy, który ma tę właściwość, że kolejne próbki nie są ze sobą skorelowane, tzn.
⎩
⎨
⎧
≠
=
σ
=
0
dla
0
0
dla
)
(
2
m
m
m
R
x
xx
(2.38)
Widmo mocy szumu białego ma w całym zakresie częstotliwości wartość stałą:
π
≤
Ω
≤
π
−
σ
=
Ω
dla
)
(
2
x
xx
P
(2.39)
W analizie procesów losowych szum biały jest w pewnym sensie odpowiednikiem
deterministycznego sygnału impulsowego (impulsu jednostkowego w przypadku sygnałów
dyskretnych w czasie).
Zależność (2.35) stanowi podstawę do modelowania sygnałów losowych o określonym widmie
mocy („kolorowych”) za pomocą szumu białego przepuszczanego przez stabilny układ liniowy o
odpowiedniej transmitancji (Rys. 4).
Na podstawie (2.37) można wyznaczyć zależność pozwalającą na identyfikację charakterystyki
widmowej nieznanego układu dyskretnego na podstawie obserwacji realizacji sygnałów losowych
na wejściu i wyjściu (teoretycznie najlepszym sygnałem wejściowym jest szum biały, ponieważ
obejmuje całe pasmo częstotliwości i pobudza wszystkie składowe dynamiki układu):
.
)
(
)
(
)
(
Ω
Ω
=
Ω
xx
xy
j
P
P
e
H
(2.40)
Przykład: Na wejście filtra o transmitancji H(z)=0.5[1+z
-1
] podawany jest szum biały. Równanie
różnicowe wiążące wyjście z wejściem filtra ma postać: y(n)=0.5[x(n)+x(n-1)]. Próbki y(n) i y(n+1)
sygnału losowego na wyjściu zależą więc od tej samej próbki x(n) sygnału wejściowego, a zatem są ze
sobą skorelowane, co oznacza, że R
yy
(1)
≠0. Wartości funkcji autokorelacji R
yy
(m)=0 dla m>1.
Laboratorium Cyfrowego Przetwarzania Sygnałów
Ćwiczenie 2 – Dyskretne sygnały stochastyczne - analiza widmowa i korelacyjna
- 9 -
0
0 . 1
0 . 2
0 . 3
0 . 4
0 . 5
0
2
4
6
8
1 0
Rys. 4 Widmo mocy szumu na wyjściu filtra środkowoprzepustowego o transmitancji H(z)
pobudzanego szumem białym o wariancji
1
2
=
σ
x
2.9. Detekcja sygnału w szumie - filtr dopasowany do sygnału
Filtry dopasowane są filtrami optymalnymi z punktu widzenia zdolności do wykrywania impulsu
sygnału użytecznego s(n) w silnym szumie. Stanowią one m.in. jeden z podstawowych elementów
układów radarowych.
Charakterystykę impulsową filtra dopasowanego do sygnału deterministycznego s(n) o
skończonym czasie trwania równym N+1 określa się jako sprzężenie sygnału odwrócone w czasie (w
przypadku zespolonych sygnałów modulowanych należy wziąć zespolone sprzężenie s
*
(-n) ):
( )
(
),
0,1,...,
h n
s n
n
N
= −
=
(2.41)
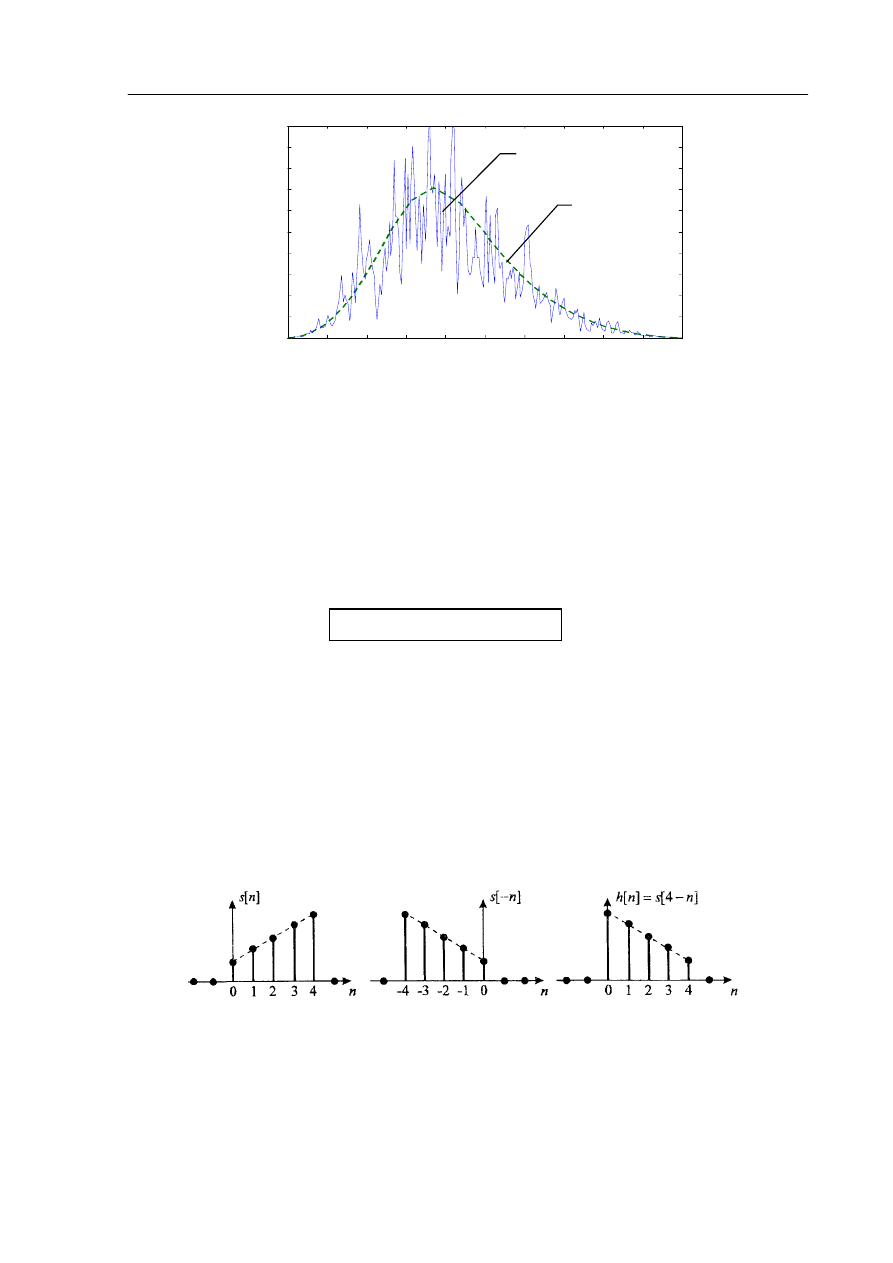
Aby otrzymać filtr przyczynowy charakterystykę tę należy przesunąć o N względem sygnału (Rys. 5):
h(n) = s(N-n).
(2.42)
Sygnał na wyjściu filtra pobudzanego sygnałe, do którego filtr jest dopasowany, jest (zgodnie z (2.31)
równe:
0
0
( )
( ) (
)
(
) (
)
n
n
k
k
y n
h k s n k
s N k s n k
=
=
=
−
=
−
−
∑
∑
(2.43)
Dla n=N otrzymujemy na wyjściu wartość maksymalną równę energii impulsu s(n):
2
0
0
( )
(
) (
)
| ( ) |
N
N
k
m
y N
s N k s N k
s m
=
=
=
−
−
=
∑
∑
(2.44)
Rys. 5 Sygnał s(n) o skończonej długości (N=4) i odpowiedź impulsowa h(n)=s(N-n)
przyczynowego filtra FIR dopasowanego do sygnału s(n)
A zatem w określonej chwili (n=N) czasu próbka sygnału wyjściowego określa energię sygnału
użytecznego (maksymalną wartość funkcji korelacji sygnału dopasowanego i wejściowego) i wtedy
odpowiedź filtra osiąga maksimum. W układach radarowych wysyłane impulsy stanowią sygnał s(n),
widmo mocy P
yy
(
Ω)
|H(e
j
Ω
)|
2
Ω/2π
P
yy
|H|
2

Laboratorium Cyfrowego Przetwarzania Sygnałów
Ćwiczenie 2 – Dyskretne sygnały stochastyczne - analiza widmowa i korelacyjna
- 10 -
który wraca do anteny w formie opóźnionej s(n-n
0
)+szum. Wyjście filtra dopasowanego osiąga wtedy
maksimum dla n=N+n
0
.
Największą efektywność detekcji uzyskuje się dla impulsów s(n), których autokorelacja bardzo
szybko zanika do zera. Filtr dopasowany reaguje wtedy bardzo skupionym impulsem wyjściowym.
Właściwość taką ma stosowana w układach radarowych funkcja „chirp” (sinusoida z liniowo
modulowaną częstotliwością), której ciągła wersja ma postać:
2
1 dla
( )
( )
,
( )
0 dla pozostaych
W
j
t
T
T t T
s t
p t e
p t
t
π
− ≤ ≤
⎧
=
= ⎨
⎩
(2.45)
gdzie 2T jest czasem trwania impulsu, a W – szerokością przemiatanego zakresu częstotliwości.
Literatura
1. Oppenheim A.V., Schafer R.W.: „Cyfrowe przetwarzanie sygnałów”, WKiŁ, 1979.
2. Praca zbiorowa pod red. A. Dąbrowskiego: „Przetwarzanie sygnałów przy użyciu procesorów sygnałowych”,
Wyd. Politechniki Poznańskiej, 1998.
3. Szbatin J.: „Podstawy teorii sygnałów”, WKiŁ, 1982.
4. Praca zbiorowa pod red. A. Wojtkiewicza: „Cyfrowe przetwarzanie sygnałów”, preskrypt lab., Oficyna Wyd.
Politechniki Warszawskiej, 1997.
5. Brandt S.: „Analiza danych”, PWN, 1998.
Opracował: Dr inż. Janusz Baran
Częstochowa, 1999

Laboratorium Cyfrowego Przetwarzania Sygnałów
Ćwiczenie 2 – Dyskretne sygnały stochastyczne - analiza widmowa i korelacyjna
- 11 -
3. Obliczenia komputerowe - zadania do wykonania
3.1. Klasyczne metody estymacji widma mocy i autokorelacji
Eksperymenty będą przeprowadzane na przykładzie sygnału losowego będącego gaussowskim
szumem białym. Ciąg próbek (wektor wierszowy ) o długości N stanowiący realizację takiego sygnału
(o średniej m
x
=0 i wariancji
σ
x
2
=1) można w Matlabie wygenerować za pomocą polecenia:
>> x=randn(1,N);
które wykorzystuje generator liczb pseudolosowych. Ze względu na losowe generowanie realizacji
sygnałów uzyskiwane w ćwiczeniu wyniki nie są w dokładnie powtarzalne.
Estymatę funkcji autokorelacji R
xx
(m) realizacji sygnału oblicza funkcja
>> Rxx=xcorr(x);
(help xcorr daje opis ewentualnych dodatkowych parametrów).
Do wygenerowania macierzy R realizacji procesu losowego o długości N każda służy procedura
>> X=c2_noise(R,N);
gdzie poszczególne realizacje są wierszami macierzy X.
A.
Wygenerować R=20 realizacji białego szumu gaussowskiego o długości N=128 każda:
>> X=c2_noise(20,128);
Na wykresach w oknie 1 porównać (nie rejestrować wykresów w tym punkcie) zakres zmienności
przykładowej realizacji oraz realizacji uśrednionej (uśrednianie następuje po kolumnach macierzy X,
czyli dla realizacji zmiennych losowych x(n) dla ustalonego indeksu n), a w oknie komend Matlaba
porównać obliczone dla nich liczbowe wartości wariancji. Na wykresie w oknie 2 zaobserwować
estymatę autokorelacji R
xx
(m) sygnału uśrednionego (unormowaną tak, aby R
xx
(0)=1).
B.
Wyznaczyć periodogramy wygenerowanych sygnałów losowych korzystając z funkcji
>> PER=c2_per(X,L);
i przyjmując L=256 (L jest liczbą punktów transformaty DFT użytej do obliczania periodogramów).
Peridogramy poszczególnych realizacji mieszczą się w wierszach macierzy wynikowej PER.
Porównać wariancje przykładowego periodogramu jednej z realizacji oraz periodogramu
stanowiącego ich średnią (wartości liczbowe są podane w oknie komend Matlaba).
C.
Zaobserwować i zarejestrować charakter zmian (w rozdzielczości i stopniu "poszarpania"
periodogramów ) wynikających ze zmiany
• długości N generowanych realizacji procesu:
>>
X=c2_noise(10,1024);
>>PER=c2_per(X,1024);
• liczby realizacji R (uśrednianie po większej liczbie realizacji powoduje zmniejszenie wariancji):
>>
X=c2_noise(200,128);
>>PER=c2_per(X,256);
Do praktycznego wyznaczania estymaty widma mocy P
xx
(
ω) stosuje się metody (Bartletta i
Welcha) podziału ciągu próbek na segmenty (które mogą na siebie zachodzić) i uśredniania
obliczonych dla nich krótszych periodogramów. Realizuje je funkcja PSD (power spectrum density):
>> [Pxx, f]=psd(x, ndft, fs, win, ovlap);
Znaczenie parametrów wejściowych jest następujące:
x
- wektor realizacji sygnału,
ndft
- liczba punktów DFT,
fs
-
częstotliwość próbkowania (do skalowania wektora wynikowego f częstotliwości, w
przypadku skali unormowanej należy zadawać fs=1),
win
- typ i długość M okna (segmentu danych); w metodzie Bartletta stosuje się okno
prostokątne boxcar(M), w metodzie Welcha okno Hanninga: hanning(M),
ovlap
- szerokość obszaru nakładania się segmentów.
D.
Wydrukować i przeanalizować (opcja File | Open M-file) zawartość pliku skryptowego
c2_bart.m
, który oblicza periodogram zwykły oraz periodogramy uśredniane metodą Bartletta.
>> c2_bart(M,ovlap,A)

Laboratorium Cyfrowego Przetwarzania Sygnałów
Ćwiczenie 2 – Dyskretne sygnały stochastyczne - analiza widmowa i korelacyjna
- 12 -
gdzie: M – długość segmentu (długość całego rekordu N=512),
ovlap
– długość nakładających się odcinków segmentów (ovlap<M),
A
– amplituda składowej harmonicznej dodawanej do szumu (domyślnie A=0.5).
Przeprowadzić obliczenia i porównać wyniki dla przypadków, kiedy sygnał zawiera jedynie szum:
c2_bart(128,64,0)
(amplituda A=0) oraz szum i składową harmoniczną (A=0.5). Dla
przypadku ze składową harmoniczną porównać wyniki dla (M=128,ovlap=0) oraz (M=128,
ovlap=64)
.
• Porównać wariancję priodogramu i estymaty Bartletta (z nakładaniem się segmentów i bez)
oraz rozdzielczość widma (szerokość prążków). Jaka jest liczba segmentów (przy tej samej
długości M) w przypadku z nakładaniem i bez? Zwrócić uwagę na wygładzenie widma
uzyskanego metodą Bartletta w porównaniu z periodogramem i poszerzenie jego prążków.
• Dlaczego na wykresie w skali logarytmicznej (dB) występuje przeliczene 10⋅log
10
(P
xx
)?
E.
Wydrukować i przeanalizować skrypt c2_welch.m, który oblicza estymaty widma mocy
metodą Bartletta (okno prostokątne) oraz metodą Welcha z oknem Hanninga (w obu przypadkach
z nakładaniem segmentów). Uruchomić skrypt
>> c2_welch
i zarejestrować otrzymane wyniki (domyślna wartość amplitudy składowej sinusoidalnej sygnału
A=0.5
). Zbadać szanse na wykrycie w PSD składowej harmonicznej o mniejszej amplitudzie
A=0.25
dla kilku realizacji sygnału x(n) uruchamiając kilkakrotnie funkcję z parametrami
>> c2_welch(0.25,128,64)
F.
Weryfikacja właściwości estymat funkcji autokorelacji opisanych we wprowadzeniu
teoretycznym. Należy wydrukować i przeanalizować zawartość pliku skryptowego
>> c2_akor(signal)
Estymaty mogą być obliczane dla jednego z trzech różnych sygnałów o skończonej długości:
detrministycznego sygnału sinusoidalnego (x=sin(2*pi*0.2*[0:N-1]);), signal=1,
szumu białego (x=randn(1,N);), signal=2,
sinusoidy z szumem (suma dwóch powyższych), signal=3.
Funkcja oblicza 3 estymaty autokorelacji:
estymatę obciążoną (z dzieleniem sumy przez N – liczbę próbek),
estymatę nieobciążoną (z dzieleniem sumy przez N-|m|, gdzie m oznacza przesunięcie
sygnałów)
jako odwrotną transformatę Fouriera IDFT periodogramu sygnału.
Sygnał deterministyczny służy jako sygnał testowy właściwości estymat, ponieważ jego
autokorelację można wyliczyć analitycznie (do wykonania w sprawozdaniu).
Uruchomić procedurę i przeanalizować wyniki dla poszczególnych sygnałów. Która estymata
jest lepsza dla sygnału deterministycznego, a która dla losowego i dlaczego (zakładając, że
rzeczywiste sygnały są nieograniczonych w czasie)?
Wyjaśnić, skąd biorą się wartości zerowe na krańcach przedziału estymaty obciążonej i
dlaczego estymata nieobciążona autokorelacji szumu białego ma dużą (fałszywą) wariancję na
krańcach przedziału?
3.2. Przetwarzanie sygnału losowego przez układ liniowy
W tym punkcie badane będą odpowiedzi liniowego układu dyskretnego o transmitancji H(z)
postaci (2.29) na pobudzenie sygnałem losowym (szumem białym). Transmitancja H(z)= B(z)/A(z)
opisuje filtr o nieskończonej odpowiedzi impulsowej (IIR). Jeśli wielomian w mianowniku A(z)=1, to
mamy do czynienia z filtrem o skończonej odpowiedzi impulsowej (FIR), którego wszystkie bieguny
są równe zero.
A.
W pierwszym punkcie badany będzie filtr II rzędu. Do badania jego odpowiedzi służy funkcja
c2_ford2(B,A)
, wewnątrz której automatycznie generowany jest szum pobudzający filtr.
Należy zadać parametry (jest to filtr dolnoprzepustowy) i wywołać funkcję:
>> B=[0,0,0.25]; A=[1,-1,0.25];
(B=[b
0
, b
1
, b
2
], A=[a
0
, a
1
, a
2
])
>> y=c2_ford2(B,A);

Laboratorium Cyfrowego Przetwarzania Sygnałów
Ćwiczenie 2 – Dyskretne sygnały stochastyczne - analiza widmowa i korelacyjna
- 13 -
a następnie obejrzeć obciążoną estymatę autokorelacji (unormowaną do R
xx
(0)=1) i widmo mocy P
yy
sygnału wyjściowego filtra przy pomocy funkcji (lewostronne argumenty wyjściowe można
pomijać, ale wyniki będę wtedy tracone po zakończeniu funkcji
):
>> [R,m,P,f]=c2_rxpx(y);
(Znaczenie wyników: R
yy
(m) i P
yy
(f))
Zarejestrować otrzymane wyniki. Powtórzyć obliczenia dla filtra pasmowoprzepustowego:
>> B=[1,0,-1]; A=[1,-cos(pi/3),0.25];
>> y=c2_ford2(B,A);
>> c2_rxpx(y);
Sprawdzić zgodność „obwiedni” widma sygnału wyjściowego filtra z kształtem charakterystyki
amplitudowej (jaka jest zależność analityczna?).
Powtórzyć obliczenia autokorelacji i widma mocy i zaobserwować ewentualne zmiany po
wyeliminowaniu z odpowiedzi filtra początkowych próbek (np. 128) stanowiących stan
nieustalony:
>> c2_rxpx(y(129:512));
Wyniki w skali logarytmicznej daje analogiczna funkcja c2_rxpxd(), którą można w razie
potrzeby wykorzystać. Najbardziej interesujący zakres funkcji autokorelacji w pobliżu zera można
powiększyć przez przeskalowanie osi górnego wykresu:
>> subplot(211), axis([-30,30,-1,1])
Zaobserwować, ile próbek autokorelacji (w otoczeniu zera) ma wartość znacząco różną od zera (jak
się to ma do rzędu filtra?). Co dzieje się z szumem nieskorelowanym x po przejściu przez filtr?
Uzasadnić stwierdzenie, że filtr „koloryzuje” szum biały.
B.
Badanie koloryzowania szumu białego przez filtr N-tego rzędu (filtr dolno- lub górnoprzepustowy
Butterwortha 8 rzędu). Wydrukować i przeanalizować zawartość pliku skryptowego
c2_fordn.m
. Parametry wejściowe tej funkcji to:
x – wektor pobudzenia (opcjonalny),
option – wybór filtra dolnoprzepustowego (option=1 – domyślnie) lub
górnoprzepustowego (option=2)
Funkcja wywołana bez parametrów sama generuje gaussowski szum biały.
Wywołać funkcję z option=1 i 2 i przeprowadzić analizę jak w poprzednim punkcie:
>> y=c2_fordn([],1);
>> c2_rxpxd(y);
3.3. Identyfikacja nieznanego układu liniowego
Zadanie polega na wyznaczeniu estymaty charakterystyki częstotliwościowej nieznanego filtra na
podstawie pomiaru sygnałów: wejściowego i wyjściowego filtra. Jest to tzw. identyfikacja
nieparametryczna. Do jej przeprowadzenia służy procedura
>>c2_ident(filtr, signal);
która wykreśla charakterystyki amplitudowe.
A.
Wydrukować i przeanalizować zawartość pliku skryptowego c2_ident.m. W procedurze
istnieje możliwość wybrania do identyfikacji danych generowanych przez:
filtr dolnoprzepustowy Butterwortha 4. rzędu o nieskończonej odpowiedzi impulsowej IIR
(parametr filtr=1):
[B,A]=butter(4,0.4)
filtr dolnoprzepustowy o skończonej odpowiedzi impulsowej (FIR) 14. rzędu (filtr=2):
B=fir1(14,0.2,boxcar(15)); A=1;
oraz jednego z dwóch sygnałów wejściowych:
szumu białego (parametr signal=1)
lub sygnału sinusoidalnego o częstotliwości unormowanej f
n
=0.02 (signal=2):
Zauważyć, że w danych do funkcji estymacji tfe pomija się no początkowych próbek symulacji
filtra (w jakim celu?).
B.
Przeprowadzić eksperymenty dla obu filtrów z pobudzeniem szumem białym lub sygnałem
harmonicznym o stałej częstotliwości (4 przypadki).
Ocenić i wyjaśnić możliwość identyfikacji przy pobudzeniu harmonicznym.

Laboratorium Cyfrowego Przetwarzania Sygnałów
Ćwiczenie 2 – Dyskretne sygnały stochastyczne - analiza widmowa i korelacyjna
- 14 -
Zaobserwować i wyjaśnić różnice dokładności identyfikacji charakterystyki amplitudowej w
zależności od tego, czy odpowiedź impulsowa układu jest skończona (filtr FIR) czy nie (filtr
Butterwortha).
3.4. Badanie korelacji wzajemnej sygnałów
Eksperyment jest ilustracją analizy korelacyjnej dwóch sygnałów x(n) i y(n), gdzie drugi jest
przesuniętą w czasie i zakłóconą wersją pierwszego. Obliczenia realizuje funkcja:
>> c2_korxy(signal,sig2,no)
gdzie: signal – rodzaj sygnału użytecznego: odcinek sinusoidy (signal=1) lub sygnał losowy
(model np. sygnału mowy, signal=2),
sig2
– wariancja szumu zakłócającego (domyślnie 0.01),
no
≥0 – przesunięcie sygnałów w czasie (domyślnie 100).
A.
Wydrukować i przeanalizować zawartość pliku c2_korxy.m. Przeprowadzić obliczenia dla obu
typów sygnałów z zakłóceniem i bez (4 przypadki), np.
>> c2_korxy(1,0)
oznacza, że x(n) zawiera odcinek sinusoidy, a y(n) nie jest zakłócony szumem. Zmienić
przesunięcie no i zaobserwować związaną z tym zmianę położenia maksimum korelacji R
xy
(m).
B.
(*) Powtórzyć obliczenia zwiększając sig2 (do ok.1) w celu sprawdzenia, do jakiego stosunku
sygnału do zakłócenia (SNR – signal-to-noise ratio) widać jeszcze maksimum korelacji.
3.5. Detekcja sygnału w szumie – filtr dopasowany
Problem polega na wykrywaniu znanego sygnału (skończonego impulsu s(n)) w obecności szumu
przy pomocy filtra dopasowanego do sygnału. Charakterystyka impulsowa filtra dopasowanego
h(n)=s
*
(-n) (sprzężenie i odwrócenie w czasie, charakterystyka ta określa jednocześnie współczynniki
transmitancji filtra FIR). Obliczenia przeprowadza funkcja
>>c2_fdop(signal,A)
;
A.
Wydrukować i przeanalizować zawartość pliku skryptowego c2_fdop.m. Procedura umożliwia
wybranie jednego z trzech sygnałów s(n), do którego dopasowany będzie filtr:
impuls prostokątny o amplitudzie A (signal=1):
s=A*ones(1,M);
impuls z sygnałem harmonicznym o stałej częstotliwości f0 (signal=2):
f0=0.05; s=A*exp(j*2*pi*f0*(1:M));
impuls o liniowo modulowanej częstotliwości (tzw. LFM chirp) (signal=3):
p=2; s=A*dchirp(M,p);
Syntezę filtra dopasowanego do sygnału s realizuje w programie instrukcja:
h=conj(s(M:-1:1));
Przebieg sygnału LFM chirp można obejrzeć za pomocą polecenia (parametry przykładowe)
>> dchirp(300,3);
Sygnałem zakłócającym jest gaussowski szum biały o jednostkowej wariancji. Domyślna wartość
wartość A=0.5 amplitudy impulsu użytecznego jest na tyle mała, że jest on niewidoczny w szumie.
B.
Przeprowadzić symulacje dla każdego z wymienionych sygnałów i porównać skuteczność detekcji
odbitego impulsu (amplitudę i rozmycie odpowiedzi filtra dopasowanego oraz czas
odpowiadający jej maksimum; w oknie komend Matlaba podawane są współrzędne maksimum
odpowiedzi filtra).
C.
(*) Sprawdzić – odpowiednio modyfikując procedurę - czy korzystając z filtra dopasowanego do
impulsu prostokątnego można wykryć impuls LFM i wyjaśnić wynik testu.
4. Opracowanie sprawozdania
W sprawozdaniu należy zawrzeć zarejestrowane wyniki eksperymentów numerycznych z
odpowiednimi opisami oraz wyjaśnieniami problemów wskazanych w pkt. 3 dokonanymi na
podstawie informacji teoretycznych z pkt.2.
Wyszukiwarka
Podobne podstrony:
dsp lab1 id 144058 Nieznany
lab2 7 id 259265 Nieznany
dsp lab7 id 144062 Nieznany
bd lab2 id 81995 Nieznany (2)
JPPO Lab2 id 228821 Nieznany
AKiSO lab2 id 53766 Nieznany
lab2 9 id 259271 Nieznany
bsi lab2 id 93526 Nieznany
PAiRAII Instr 2007 lab2 id 3455 Nieznany
Protokol Siko Lab2 id 402771 Nieznany
lab2(1) 4 id 259343 Nieznany
lab2 8 id 259268 Nieznany
Instrukcja Lab2 id 216873 Nieznany
BHP i lab2 id 84433 Nieznany (2)
kap lab2 id 231164 Nieznany
lab2 1 id 259287 Nieznany
lab2 5 id 259259 Nieznany
dsp lab5 id 144060 Nieznany
więcej podobnych podstron